II. THEORETICAL ANALYSIS

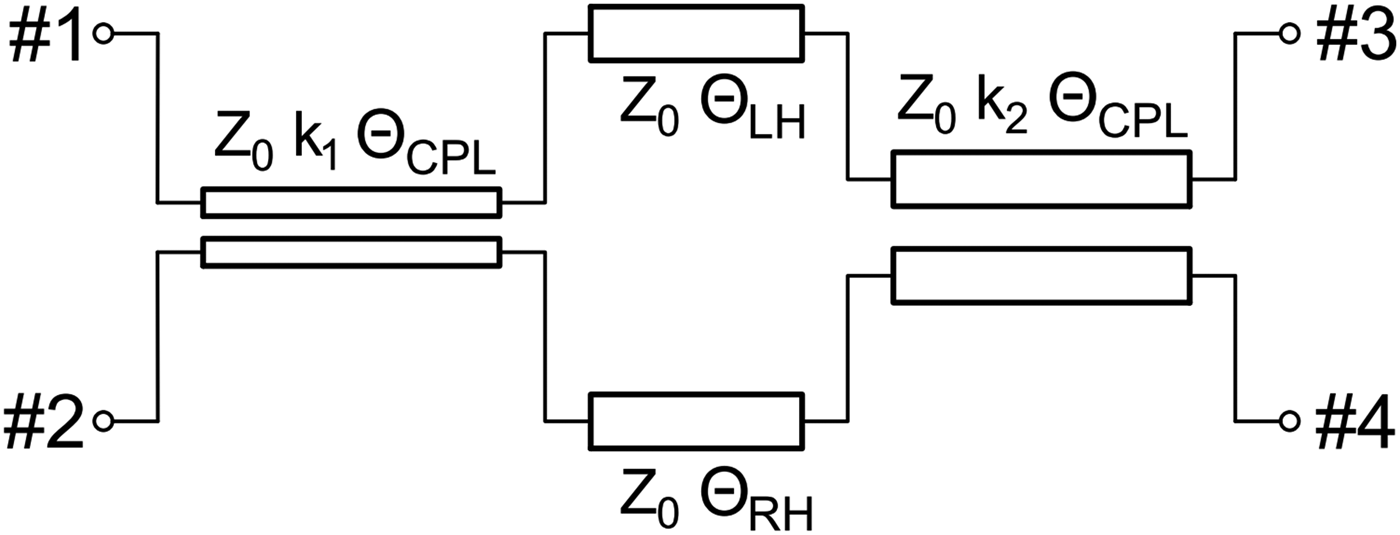
A generic schematic of the proposed directional coupler consisting of two coupled-line sections having equal electrical length connected with the use of LH and RH uncoupled transmission lines is presented in Fig. 1. Such a coupler's structure can provide broadband equal-ripple frequency characteristics being similar to the frequency characteristics of the classic two-section coupled-line directional couplers. Simultaneously, the presented network allows for significant reduction of the required coupling coefficients. The proposed structure is described by: Z ₀ – characteristic impedance, k ₁, k ₂ – the coupling coefficients of the coupled-line sections and Θ_LH, Θ_RH, Θ_CPL – the electrical lengths of LH, RH uncoupled transmission lines and coupled-line sections, respectively. The coupling characteristic of the presented directional coupler can be expressed as follows [Reference Park and Lee17]:

Fig. 1. A generic schematic of the proposed directional coupler consisting of tightly and loosely coupled-line sections connected by LH and RH uncoupled transmission lines.

(1)$$S_{21}=\displaystyle{{C_1+\lpar {T_1^2 - C_1^2 } \rpar C_2 E_{LH} E_{RH} } \over {1 - C_1 C_2 E_{LH} E_{RH} }}.$$

The coefficients C _i, T _i (i = 1, 2) are the coupling and transmission coefficients, respectively, of particular coupled-line sections, given by the well-known formulas [Reference Mongia, Bahl and Bhartia18]:

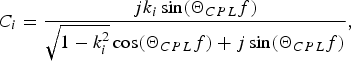(2)$$C_i=\displaystyle{{jk_i \sin \lpar {\Theta_{CPL} f} \rpar } \over {\sqrt {1 - k_i ^2 } \cos \lpar {\Theta_{CPL} f} \rpar +j\sin \lpar {\Theta_{CPL} f} \rpar }}\comma \; $$

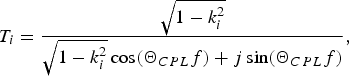(3)$$T_i=\displaystyle{{\sqrt {1 - k_i ^2 } } \over {\sqrt {1 - k_i ^2 } \cos \lpar {\Theta_{CPL} f} \rpar +j\sin \lpar {\Theta_{CPL} f} \rpar }}\comma \; $$

where Θ_CPL is the electrical length of the coupled-line sections and f is the normalized frequency. The remaining factors E _LH and E _RH are the transmission coefficients of the ideal LH and RH uncoupled transmission lines, respectively:

(4)$$E_{LH}=\cos \left({\displaystyle{{\vert {\Theta_{LH} } \vert } \over f}} \right)+j\sin \left({\displaystyle{{\vert {\Theta_{LH} } \vert } \over f}} \right)\comma \; $$

(5)$$E_{RH}=\cos \lpar {\Theta_{RH} f} \rpar - j\sin \lpar {\Theta_{RH} f} \rpar .$$

The derivation of the 3 dB coupler's parameters ensuring an equal-ripple frequency response leads to the equations that cannot be solved analytically; therefore, a numerical procedure has been utilized. It is based on the minimization of the following expression:

(6)$$D=\max \lcub X \rcub - \min \lcub X \rcub \comma \; $$

where X indicate a three-element vector having the form:

(7)$$X=\lcub {\vert {S_{21} \lpar {f_1 } \rpar } \vert \comma \; \vert {S_{31} \lpar {f_2 } \rpar } \vert \comma \; \vert {S_{21} \lpar {f_3 } \rpar } \vert } \rcub $$

in which f ₁ and f ₃ are the frequencies, at which the coupling characteristic S ₂₁ has its local maxima and f ₂ is the frequency, at which the coupling characteristic has its local minimum. The exemplary frequency response obtained for initial values of coupler's parameters is illustrated in Fig. 2. It can be observed that D = 0 can be obtained only for equal-ripple frequency characteristics. Assuming that the investigated coupler is lossless, i.e.:

(8)$$\vert {S_{31} \lpar f\rpar } \vert =\sqrt {1 - \vert {S_{21} \lpar f\rpar } \vert ^2 } .$$

Fig. 2. Graphical explanation of the factor D utilized in the numerical procedure for calculating the coupler's parameters. The minimized value of D corresponds to an equal-ripple frequency response.

Equation (7) can be expressed using only coupling characteristic S ₂₁:

(9)$$X=\left\{{\vert {S_{21} \lpar f_1 \rpar } \vert \comma \; \sqrt {1 - \vert {S_{21} \lpar f_2 \rpar } \vert^2 }\comma \; \vert {S_{21} \lpar f_3 \rpar } \vert } \right\}\comma \; $$

which constitutes the final form utilized in the numerical procedure.

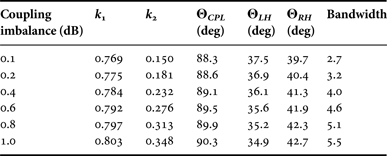
The obtained results are presented in Fig. 3, where the values of bandwidth BW (defined as a ratio of maximum and minimum frequencies, at which coupling characteristic satisfies the assumed coupling imbalance), coupling imbalance δ _C and electrical lengths Θ_LH, Θ_RH, and Θ_CPL have been plotted versus the coupling coefficients k ₁ and k ₂. The plotted shapes include all possible solutions for which an equal-ripple response is obtained. As it is seen, the proposed network features high flexibility in a choice of the coupler's parameters. It can be observed, that the proposed approach allows for the design of a 3 dB coupler with the assumed bandwidth with the use of different coupling coefficients k ₁ and k ₂. On the other hand, having fixed the maximum available coupling coefficient k ₁ = k _max, one can realize 3 dB couplers with different bandwidths. Such a feature, not obtainable in case of the classic coupled-line directional couplers, significantly increases the flexibility of couplers' practical realization. By analyzing Figs 3(d) and 3(e), one can see that in general the reduction of tight coupling coefficient k ₁ requires the extension of the LH and RH uncoupled transmission-line sections. Simultaneously, by the slight increase of the weaker coupling coefficient k ₂, the initially assumed bandwidth can be preserved in contrary to the classic coupled-line couplers, in which the reduction of tight coupling coefficient results implicitly in the bandwidth reduction (Table 1).

Fig. 3. Parameters of the proposed 3 dB coupler ensuring equal-ripple frequency characteristics vs. coupling coefficients k ₁ and k ₂: bandwidth (a), coupling imbalance (b) the electrical length of the coupled-line sections (c), the electrical lengths of RH and LH uncoupled transmission lines (d) and (e), respectively. The white area represents the set of coupling coefficients, using which the equal-ripple frequency response with the coupling imbalance δ _C≤1 dB cannot be obtained. Assumed resolution of coupling coefficients Δ_k = 0.001.

Table 1. Parameters of the proposed 3 dB directional coupler ensuring equal-ripple frequency characteristics for different coupling imbalance

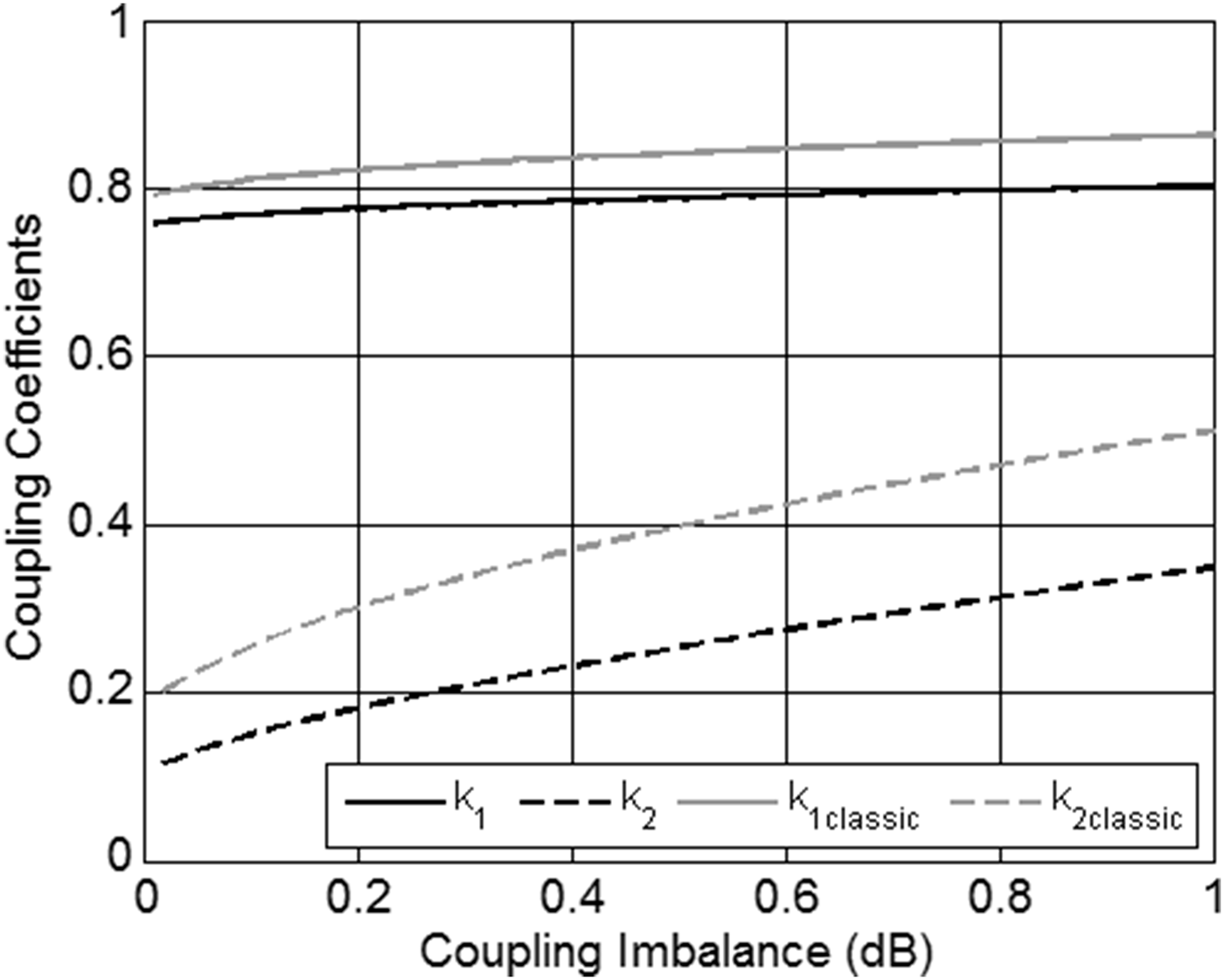
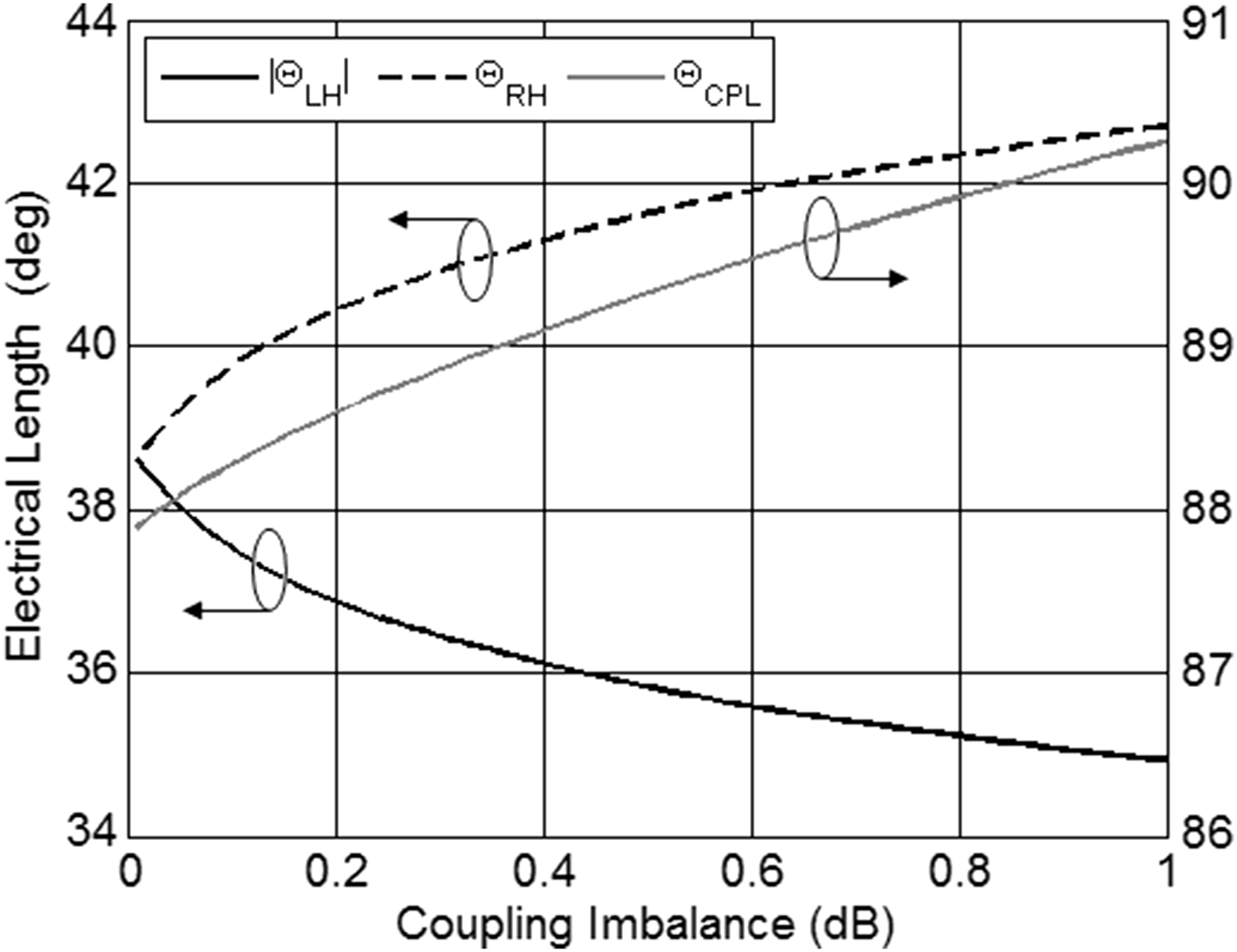
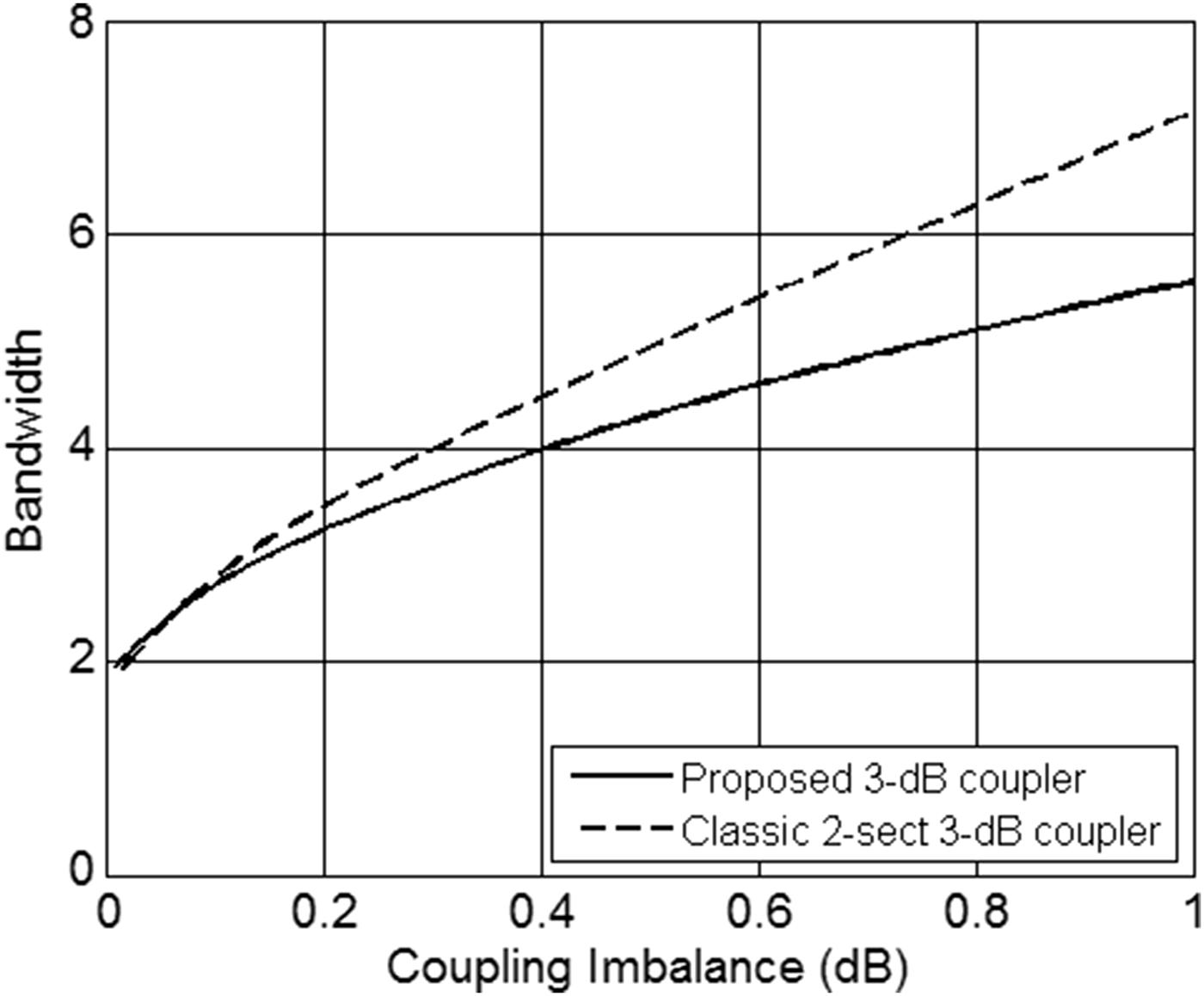
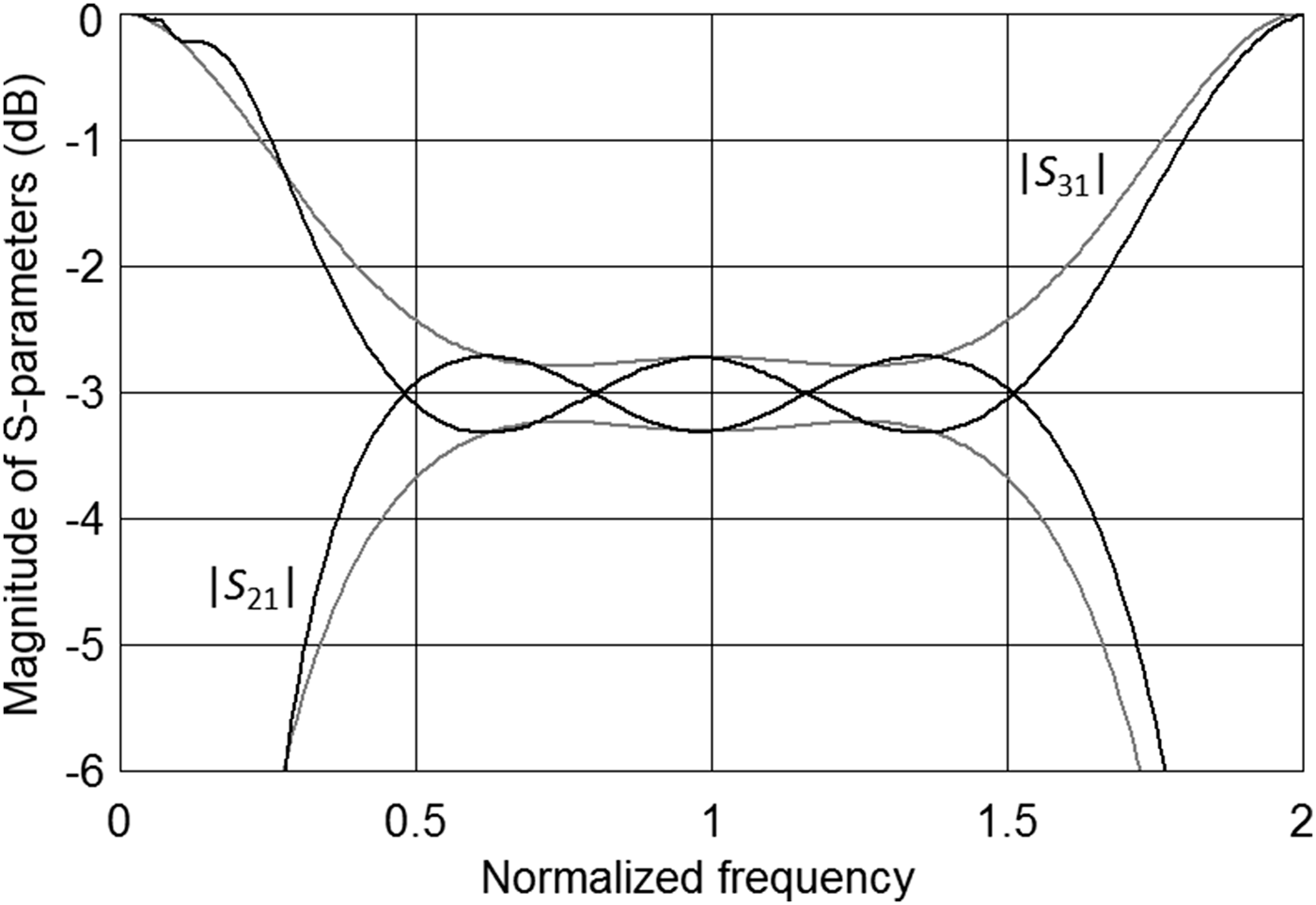
To compare the presented approach to the classic two-section coupled-line directional coupler, for each value of the coupling imbalance δ _C ≤ ±1.0 dB the set of coupler's parameters, ensuring the widest obtainable bandwidth has been chosen. Such a condition results in the choice of the maximum coupling coefficient k ₁ and the minimum electrical lengths of the LH and RH transmission lines, which corresponds to the upper edge of the shapes presented in Fig. 3 (the corresponding data is listed in Table 1). The comparison is shown in Figs. 4–6. As seen, despite of the chosen maximum coupling coefficient, it is still significantly lower than the one related to the classic two-section coupled-line coupler. The difference k _classic – k _1max varies from 0.035 (0.38 dB) to 0.061 (0.63 dB) depending on the coupling imbalance. Figure 7 presents the exemplary ideal frequency response with the coupling imbalance δ _C = ±0.3 dB compared to the classic directional coupler consisting of two quarter-wave-long coupled-line sections having the same coupling coefficients as in case of the proposed 3 dB directional coupler. As seen, the proposed approach allows for the design of a 3 dB coupler featuring equal-ripple frequency characteristics utilizing significantly reduced coupling coefficient, what cannot be achieved with the use of the classic two-section coupled-line directional coupler. Nevertheless, as a trade-off, the proposed structure results in slight decrease of the operational bandwidth in comparison with the classic solution.

Fig. 4. The coupling coefficients ensuring equal-ripple frequency characteristics and the maximum bandwidth of the proposed 3 dB directional coupler versus its coupling imbalance compared to the coupling coefficients of the classic two-section directional coupler.

Fig. 5. Electrical lengths of particular components ensuring equal-ripple frequency characteristics and the maximum bandwidth of the proposed 3 dB directional coupler versus its coupling imbalance.

Fig. 6. The maximum bandwidth of the proposed 3 dB directional coupler versus its coupling imbalance compared with the bandwidth of the classic two-section directional coupler having the corresponding coupling imbalance.

Fig. 7. The exemplary ideal frequency response of the proposed 3 dB directional coupler with the coupling imbalance δ _C = ±0.3 dB (black lines) compared with the classic directional coupler consisting of two coupled-line sections having the electrical length equal to 90° and the same coupling coefficients (gray lines).

III. EXPERIMENTAL RESULTS

The proposed method has been experimentally verified by the design and measurements of an exemplary two-section 3 dB asymmetric directional coupler operating at the center frequency of 1.5 GHz. The chosen dielectric structure is presented in Fig. 8(a), in which the conditions for ideal coupled-line section realization are not met, i.e. the capacitive and inductive coupling coefficients are not equal. To equalize the coupling coefficients, and therefore, to improve directivity and impedance match of the resulting coupled-line sections, a method proposed in [Reference Gruszczynski and Wincza19] has been used. In the chosen dielectric structure the maximum coupling level equals k _max = 0.75 (C = 2.5 dB). In order to realize a two-section asymmetric coupler having the nominal coupling C = 3 dB with coupling imbalance δ _C = ±0.25 dB, based on the analysis presented in Section II, coupled-line sections having electrical lengths Θ_CPL = 89.6° and coupling coefficients k ₁ = k _max = 0.75 and k ₂ = 0.129 need to be connected using LH and RH transmission lines having electrical lengths Θ_LH = 80.8° and Θ_RH = 88.8°, respectively. The resulting bandwidth equals BW = 2.9. On the other hand, to obtain the same nominal coupling and imbalance in a classic configuration [Reference Levy16], the following coupling coefficients are required k _1classic = 0.824 and k _2classic = 0.315, whereas the resulting bandwidth equals BW _classic = 3.7. By comparing coupling coefficients of tightly coupled sections of both couplers, it is seen that the required coupling coefficient is reduced in the proposed solution by the factor of k ₁/k _1classic = 0.91 at the expense of bandwidth reduction of BW/BW _classic = 0.78.

Fig. 8. Cross-sectional view of dielectric structure (a) and pictures of the manufactured 3 dB two-section asymmetric directional coupler where tightly and loosely coupled sections are connected using RH and LH transmission line sections: top side view of assembled coupler (b), view of the top metallization layer (c) and view of the bottom metallization layer (d).

The LH section has been physically realized with the use of a two-section T-type LC equivalent circuit. The elements' values have been calculated according to [Reference Sorocki, Piekarz, Wincza and Gruszczynski20] and are equal L _LH = 7.52 nH and C _LH = 3.01 pF. The required inductors have been realized using high-impedance transmission-line sections, whereas capacitors have been realized using 2.7 pF SMD 0402 chip capacitors, what enforced a slight circuit tuning. Parasitic reactances introduced by the transition regions between physically realized coupled and uncoupled lines, have been compensated using lumped capacitances [Reference Gruszczynski, Wincza and Sachse21].

The designed circuit has been electromagnetically calculated using AWR Microwave Office software, manufactured and measured. Photographs of the circuit are presented in Figs 8(b)–8(d), whereas the simulation and measurement results are shown in Fig. 9. As it is seen, the developed coupler features equal power split with imbalance δ _C = ±0.4 dB. The isolation is better than 18 dB and return losses are better than 15 dB over the entire operational bandwidth being equal to BW = 3.

Fig. 9. Calculated (dotted lines) and measured (solid lines) amplitude characteristics of the designed 3 dB two-section asymmetric directional coupler.

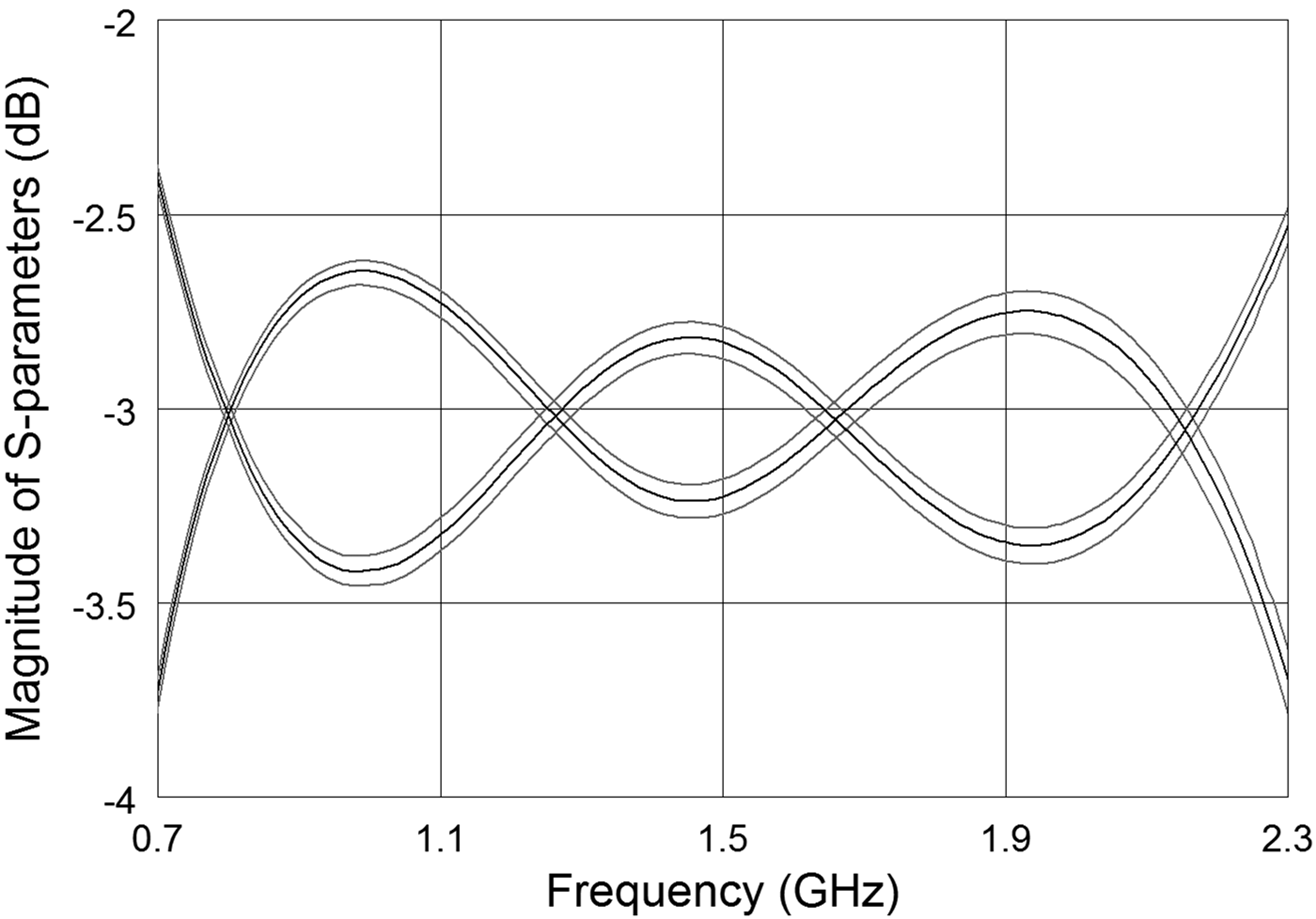
Furthermore, the tolerance of physical dimensions on the frequency response has been verified. The entire coupler's structure has been electromagnetically analyzed for the widths of coupled lines being deteriorated by ±20 µm (typical tolerance values for PCB manufacturing processes). The calculated coupling and transmission coefficients are given in Fig. 10. As it is seen the deterioration of frequency response resulting from the manufacturing tolerance is insignificant.

Fig. 10. Deterioration of the frequency response for the designed 3 dB directional coupler resulting from ±20 µm tolerance of the coupled line width. Results of electromagnetic calculations.