I. INTRODUCTION
Synthetic aperture radar (SAR) [Reference Cumming and Wong1] is a powerful remote-sensing technique that enables surveying at any time and under any weather conditions. The ability of SAR to process complex information leads to good resolution images. Due to these features, SAR finds extensive applications not only in the military but also in civil domain. In the military, it finds use in battleground surveillance, attack management, battle damage assessment, etc. [Reference Goj2–Reference Bezvesilniy, Gorovyi and Vavriv4].
As SAR is now used by every country for its security and surveillance purpose, it is also important for any country to hide its important military targets from enemy SAR. Therefore, it becomes important to do the jamming of SAR of enemy. Jamming of SAR is more difficult than jamming of radar because SAR possess high processing gain. Therefore, research on jamming and anti-jamming of SAR has gained a lot of attention both from academician and researchers [Reference Cumming and Wong1, Reference Goj2].
Two types of SAR jamming methods are available in the literature. One is active jamming and other is passive jamming [Reference Nan and Changwen5]. In active jamming, the electromagnetic signal is transmitted to corrupt the jamming signal, whereas in passive jamming, a jamming signal is generated from electromagnetic scattering of strong-reflecting objects. Passive-jamming methods generally make use of large quantities of reflectors, such as chaff, to protect a certain area from being observed by SAR.
Active jamming comprises barrage and deceptive jamming. Barrage jamming involves adding a noise signal to the original echo so as to cover the objects of interest [Reference Garmatyuk and Narayanan6, Reference Garmatyuk and Narayanan7]. This type of jamming is produced easily, but requires the high power of jammer; so, it is not preferred practically. A better alternative is to use deceptive jamming. Deceptive jamming involves generating a signal that resembles the original echo signal, so that false targets are generated in the SAR image [Reference Yan, Guoqing and Yu8–Reference Zhou, Zhao, Tao, Bai, Chen and Sun10].
This paper includes conventional Range Doppler Algorithm (RDA), which is based on fast Fourier transform (FFT) and RDA using fractional Fourier transform (RDA–FRFT) to generate SAR images [Reference Akliouat, Smara and Bouchemakh11–Reference El-Mashed, Zahran, Dessouky, El-Kordy and Abd El-Samie13].
Different models for jamming SAR are available. Zhou et al. [Reference Zhou, Zhao, Tao, Bai, Chen and Sun10] proposed an efficient algorithm for large scene deceptive jamming against the SAR. It involved breaking the jamming scene template into sub-templates performing the desired operations and then incorporating all the sub-templates together.
To efficiently implement passive jamming, Xu et al. [Reference Xu, Feng and Wang14] introduced a micro-Doppler method to create virtual objects, as jamming strips, on the SAR image. This jamming method utilized a spinning reflector in order to cover some regions, which actually increase the jamming area. Many more jamming models have been proposed over the years [Reference Zhao, Zhou, Tao, Zhang and Bao15–Reference Huang and Zhou21].
II JAMMING MODEL
The main function of the jammer is to generate a jamming signal for the deception template and mix it with the backscattered radiations of the actual area [Reference Liu, Wang, Pan, Dai and Feng16]. The term deception template stands for deceptive electromagnetic signatures that may consist of a virtual scene or many virtual objects that are to be created by the jammer. The working of jammer may be briefed as [Reference Liu, Wang, Pan, Dai and Feng16]:
• Detection and interception of the signal emitted by SAR.
• Modulating the intercepted signal in accordance with the deception template.
• At last, the above-generated signal is transmitted back to radar and is mixed with the backscattered radiations of the actual area.
The SAR platform trajectory coincides with the azimuth axis. In the deception template for depicting the backscattering coefficients of the artificial scatterers, a coordinate system (U, V) has been launched with (x j, y j) are the coordinates of jammer and (x d, y d) are the coordinates of a deception template center. In the deception template, point P 0 represents an artificial point scatterer. The coordinates of P 0 in the system (U, V) are (u, v); σ (U, V) is its backscattering coefficient; 
$\emptyset (x)$ is the immediate squint angle of P 0; D J (x) is the immediate distance from the jammer to SAR antenna and D(x, u, v) is the immediate distance from P 0 to SAR antenna (Fig. 1).
Fig. 1. Geometry for jamming and imaging in the slant plane.
The defocusing of fake or virtual scatterers is the main problem that any jamming technique needs to tackle. The algorithm proposed by Liu et al. [Reference Liu, Wang, Pan, Dai and Feng16] was able to get rid of this problem to a huge extent; but if we replace FFT by FRFT, we achieve even better-focused scatterers.
FFT can be defined as the generalized form of Fourier transform. A supplementary degree of freedom (order of the transform), which gives significant gains is enabled using FRFT. The FRFT of a signal x(t) is given as [Reference Capus and Brown22, Reference Capus, Rzhanov and Linnett23]:
$$X_P \left( {t,u} \right) = F^P \left[ {x\left( t \right)} \right] = \mathop \int \nolimits_{ - \infty} ^\infty x(t)K_\alpha (t,u)dt,$$where F P[.] = FRFT operator
$K_\alpha \left( {t,u} \right)$ the kernel of FRFT
$$\eqalign{& K_\alpha \left( {t,u} \right) \cr & = \left\{ {\matrix{{\sqrt {\displaystyle{{1 - jcot\left( \alpha \right)} \over {2\pi}}} \exp \left( {j\displaystyle{{t^2 + u^2} \over 2}\cot \left( \alpha \right)\!-\!tu\csc \left( \alpha \right)} \right),\alpha \ne n\pi} \hfill \cr {\delta \left( {t - u} \right),\; \; \; \alpha = 2n\pi} \hfill \cr {\delta \left( {t + u} \right),\; \; \; \alpha = (2n + 1)\pi,}\hfill\cr}} \right.}$$where α = P(π/2), P ∈ R.
III. JAMMING SIGNAL GENERATION
Inspired by a frequency-domain three-stage algorithm proposed by Liu et al. [Reference Liu, Wang, Pan, Dai and Feng16], we propose an algorithm for generating a jamming signal that makes use of FFT for processing the signals. The flow chart of the proposed algorithm is given in Fig. 2.
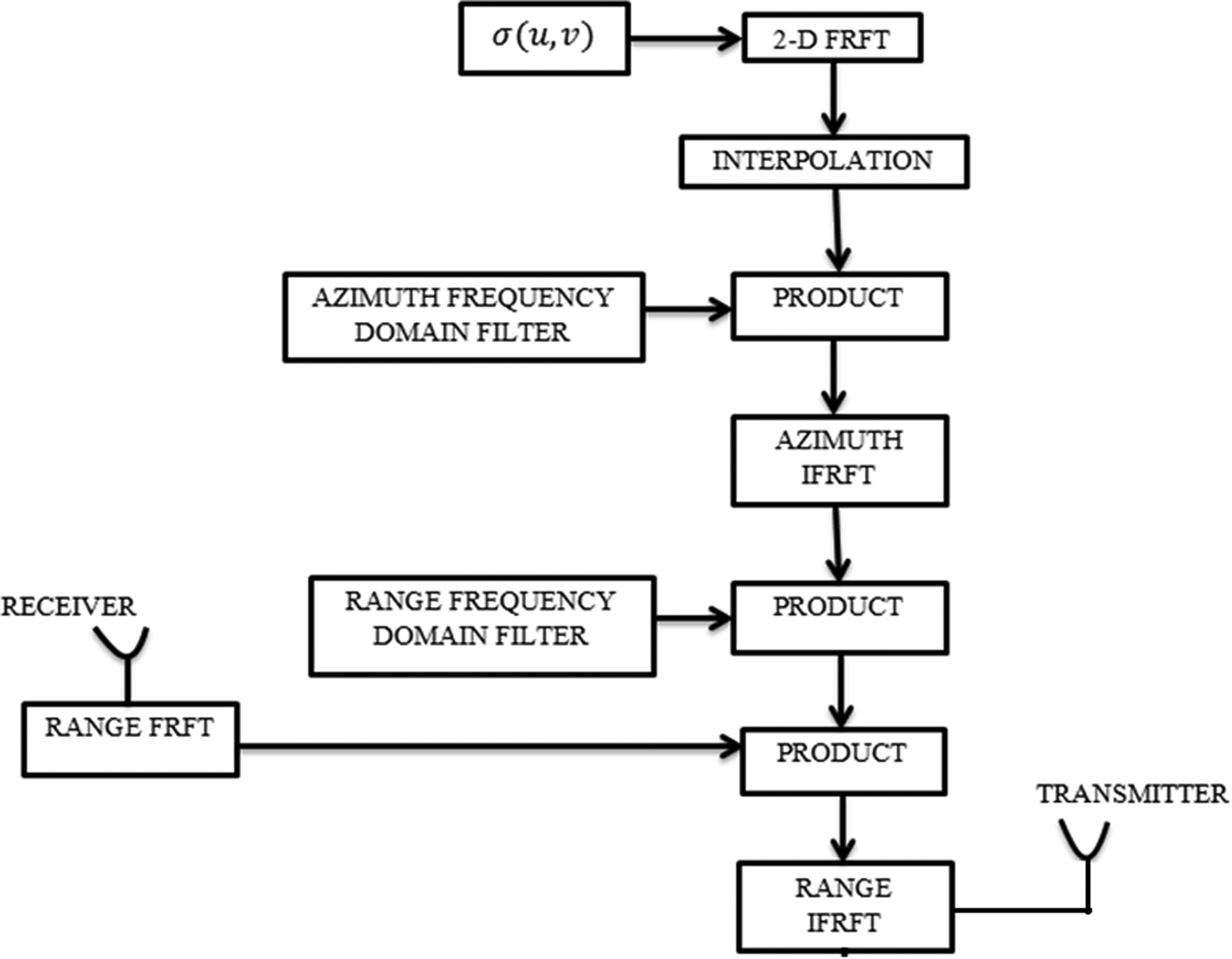
Fig. 2. Flowchart for jamming signal generation.
Let m tx represent the transmitted SAR signal. If the carrier frequency is represented by f c; chirp pulse duration,Tp r; range chirp, K rg; then the transmitted signal can be represented as
$$m_{tx} = W(t)\cos \left( {2\pi f_c + \pi K_{rg} t^2} \right),$$where W represents the pulse envelope. The jammer intercepts and receives the signal transmitted by SAR. Let m int (t, n) represent the intercepted signal; where t represents the time in range direction, and n is the time in the azimuth direction. The various sub-blocks of jamming signal generation are presented below:
(A) RANGE FRFT: Taking FRFT of the intercepted signal along the range direction, such that
(4)
$$S_1 (u_t, n) = \int m_{int} \left( {t,n} \right).K_\alpha (t,u_t )dt.$$(B) Next step is to take two-dimensional (2D) FRFT of σ(u, v)d let the value be represented by S (u t, u n). After this step, a 2D interpolation is performed so as to remove any non-uniformity in the samples.
(C) AZIMUTH FILTERING: Next step is to perform matched filtering along the azimuth direction. For this we take FRFT of the reference signal along the azimuth direction. The reference signal for azimuth frequency domain filter is:
(5)where K az azimuth chirp rate. Taking FRFT of the signal given in equation (5), we get$$S_a = e^{j\pi K_{az} n}, $$(6)$$S_a (u_n ) = \int S_{a\,} (n).K_\alpha (u_n, n)dn.$$
After multiplying S(u t, u n) and S a (u n) we get
$$M_1 (u_t, u_n ) = S(u_t, u_n ).\; S_a (u_n ).$$(D) AZIMUTH INVERSE FRFT: Taking inverse FRFT (IFRFT) of equation (7) along the azimuth direction, we get
(8)$$M_2 (u_t, n) = \int M_1 (u_t, u_n ).K_{ - \alpha} (u_n, n)du_n $$(E) RANGE FILTERING: Next step is to perform matched filtering along the range direction. For this, we take FRFT of the reference signal along the range direction. The reference signal for range frequency domain filter is:
(9)where K rg is the range chirp rate; and t d is the delay time. Taking FRFT of the signal given in equation (9), we get$$S_r = e^{j\pi K_{rg} (t - t_d )^2}, $$(10)$$S_r (u_t ) = \int S_r (n).K_\alpha (t,u_t )dt.$$
By multiplying equations (8) and (10), we get
$$M_3 (u_t, n) = M_2 (u_t, n).S_r (u_t ). $$Thereafter, multiplying equations (4) and (11), we get
$$M_4 (u_t, n) = M_3 (u_t, n).S_1 (u_t, n). $$(F) RANGE IFRFT: Taking IFRFT of signal obtained in equation (12) along the range direction, we get
(13)where M 5 (t, n) is the jamming signal generated, which is transmitted toward the radar, where it gets mixed with the original echo signal of the actual scene. Thus, the jammed signal is generated at SAR.$$M_5 (t,n) = \int M_4 (u_t, n).K_{ - \alpha} (t,u_t )du_t, $$
IV. RESULTS
In this section, the performance of proposed algorithm is given and compared with the method given by Liu et al. [Reference Liu, Wang, Pan, Dai and Feng16]. For the performance comparison, two different scenarios have been considered in this paper. In the first scenario, a template with two airplanes has been considered and results are shown in Fig. 3. For the second scenario, a template with some random object has been taken and the results are shown in Fig. 6.
Fig. 3. Images obtained using proposed and the method given in [Reference Liu, Wang, Pan, Dai and Feng16] for the first scenario. (a) Original scene template. (b) Deception template. (c) Actual SAR image of an original scene using RDA–FRFT. (d) Actual SAR image of an original scene using RDA [Reference Liu, Wang, Pan, Dai and Feng16]. (e) Actual SAR image of deceptive template using RDA–FRFT. (f) Actual SAR image of deceptive template using RDA [Reference Liu, Wang, Pan, Dai and Feng16]. (g) Jammed image obtained using RDA–FRFT. (h) Jammed image obtained using RDA [Reference Liu, Wang, Pan, Dai and Feng16].
For the first scenario, the images obtained using proposed and available algorithms [Reference Liu, Wang, Pan, Dai and Feng16] are given in Fig. 3. Fig. 3(a) is the template of original scene (two airplanes) that is required to be protected by jamming. Fig. 3(b) is the template of illusion scene (deception template). Figures 3(c), 3(e), and 3(g) are generated using RDA-FRFT, whereas Figs 3(d), 3(f), and 3(h) are generated using RDA algorithm as given by Liu, et al. in [Reference Liu, Wang, Pan, Dai and Feng16]. Figures 3(c) and 3(d) represent the SAR image of the original scene that we want to protect. Figures 3(e) and 3(f) represent the SAR image of illusion scene that the jammer has created to confuse it with the actual scene. Due to this reason, the deception template is considered as a mirrored version of the original scene. Figures 3(g) and 3(h) represent the jammed image, which the SAR will form under the effect of jamming. From the jammed image, we can say that it becomes difficult to differentiate between the actual and the false airplanes (Table 1).
Table 1. SAR simulation parameters.
Although, the same original scene template has been considered for generating SAR image, but there is a difference in the size of the image generated by RDA and RDA–FRFT. The presence of chirp function in the transmitted signal is the main reason behind this. It is an established fact that FRFT localizes chirp function better than Fourier transforms [Reference Ozaktas, Zalevsky and Kutay24]. Due to this characteristic of FRFT, the image generated by RDA–FRFT seems to be clearer.
Figures 4 and 5 represent the jamming signal of the illusion scene created above using the method presented by Liu et al. [Reference Liu, Wang, Pan, Dai and Feng16] and the proposed method respectively. From Figs 4 and 5, it can be said that a more focused jamming signal is obtained using the proposed method since it clearly describes the location of the two false airplanes. So, we obtain well-focused false scatterers.
Fig. 4. Jamming signal generated using the method given in [Reference Liu, Wang, Pan, Dai and Feng16].
Fig. 5. Jamming signal generated using the proposed algorithm.
For the second scenario of random objects, the images obtained using proposed and the methods given in [Reference Liu, Wang, Pan, Dai and Feng16] are given in Fig. 6. Figure 6(a) is the template of original scene (random objects) that is required to be protected by jamming. Fig. 6(b) is the template of illusion scene (deception template). Figures 6(c), 6(e), and 6(g) are generated using RDA–FRFT, whereas Figs 6(d), 6(f) and 6(h) are generated using the RDA algorithm as given by Liu et al. in [Reference Liu, Wang, Pan, Dai and Feng16]. Figures 6(c) and 6(d) represent the SAR image of the original scene that we want to protect. Figures 6(e) and 6(f) represent the SAR image of illusion scene that the jammer has created to confuse it with the actual scene. To hide the information of original scene from the SAR, deception template is generated from the basic shape of the original target. Figures 6(g) and 6(h) represent the jammed image, which the SAR will form under the effect of jamming. It is clearly visible from Figs 6(g) and 6(h) that the actual and false scene is merged in one SAR image and hence it becomes difficult to differentiate between the actual and the false objects. Also, the images obtained using RDA–FRFT is clearer than RDA [Reference Liu, Wang, Pan, Dai and Feng16].
Fig. 6. Images obtained using proposed and the method given in [Reference Liu, Wang, Pan, Dai and Feng16] for the second scenario. (a) Original scene template. (b) Deception Template. (c) Actual SAR image of an original scene using RDA–FRFT. d) Actual SAR image of an original scene using RDA [Reference Liu, Wang, Pan, Dai and Feng16]. (e) Actual SAR image of deceptive template using RDA–FRFT. (f) Actual SAR image of deceptive template using RDA [Reference Liu, Wang, Pan, Dai and Feng16]. (g) Jammed image obtained using RDA–FRFT. (h) Jammed image obtained using RDA [Reference Liu, Wang, Pan, Dai and Feng16].
Figures 7 and 8 represent the jamming signal of the illusion scene created above using the method presented by Liu et al. [Reference Liu, Wang, Pan, Dai and Feng16] and the proposed method for processing the signals, respectively.
Fig. 7. Jamming signal generated using the method given in [Reference Liu, Wang, Pan, Dai and Feng16].
Fig. 8. Jamming signal generated using the proposed algorithm.
From Figs 7 and 8, it can be said that a more focused jamming signal is obtained using the proposed algorithm. So, we obtain well-focused false scatterers. We observe some side lobes because uncorrelated noise is present at all times and frequencies, so for such a noise no linear relationship exists between time and frequency. This implies that the noise will spread over the entire domain.
V. CONCLUSION
In this paper, a new algorithm is proposed for deceptive jamming of SAR. The proposed algorithm is based on the use of FRFT. A supplementary degree of freedom (order of the transform), which gives significant gains is enabled using FRFT. Jamming of SAR using FRFT can help get rid of defocusing of the virtual scatterers and maintain a reasonable computational load. As shown in Figs 4, 5, 7 and 8, it can be concluded that Jamming signal generated using the proposed algorithm is more focused as compared with the one obtained using FFT.
Hem Dutt Joshi has completed his B.Tech. in ECE in the year July 1999 from Barkatullah University, Bhopal. He did his M.E. in Communication Control and Networking (CCN) from M.I.T.S., Gwalior in the year 2004. He worked as Assistant Professor in JUET, Guna from 2006 to 2013. Currently, he is working as Assistant Professor in Thapar University, Patiala. His research include wireless communication systems, OFDM, MIMO-OFDM, Antenna designing. He is a life member of the Institution of Electronics and Telecommunications Engineers (IETE), India.
Ms. Ravneet Kaur received a Bachelor in technology degree in ECE from Punjab technical university, Jalandhar (BBSBEC, Fatehgarh Sahib) in 2014 and completed Masters of Engineering from Thapar University, Patiala in the field of Electronics and Communication. Her main research interests are signal processing, image processing, and wireless communication.
Dr. Ashutosh Kumar Singh has completed his B.Tech in I&E Engineering in year 2001 from M.I.E.T., Meerut. He joined M.I.T.S., Gwalior as M. Tech student in Microwave Engineering in year 2003. After completing his M. Tech. in 2005 he has joined JIET, Guna as Lecturer. Later on, he has awarded Ph.D. degree in the year 2011 from JUET Guna. Later on, in the year 2015 he has shifted to TU, Patiala, where he is currently working as Assistant Professor.
Amit Mishra received the B.E. degree in electronics engineering from Marathwada University, Aurangabad, India in 1992 and the M.Tech. degree in the engineering systems and Ph.D. degree in soft computing systems from the Dayalbagh Educational Institute (DEI), Agra, and Jamia Millia Islamia (Central University), Delhi, India in 2002 and 2010 respectively. Currently, he is working as assistant professor in the department of electronics and communication engineering, Thapar University, Patiala, Punjab, India. His current interests include design of neural network architecture, OFDM wireless communication systems, nonlinear signal processing and optimization.
