Introduction
The search for low-mass extrasolar planets is very important in developing an answer to the question ‘Are we alone in the universe?’. Studies in this context have defined a zone for human life called the habitable zone (HZ), which reaches from 0.93 AU to 1.37 AU in our Solar System (according to the work by Kasting et al. (Reference Kasting, Whitmire and Reynolds1993)). For defining the boundaries, Kasting et al. (Reference Kasting, Whitmire and Reynolds1993) based their work on a planet with a terrestrial ocean of superficial water, the carbonate–silicate cycle (which controls the CO2 level in the atmosphere) and a surface temperature that is above freezing in the HZ. In the outer region (for semi-major axes a>1.37 AU) CO2 condenses in the atmosphere producing, CO2 clouds that can affect the temperature–CO2 coupling significantly.
For the inner region (a<0.93 AU) H2O becomes a major atmospheric compound and is rapidly lost to space after ultraviolet (UV) photolysis. More recent studies find a potentially larger HZ for a Sun-like star – see e.g. Forget & Pierrehumbert (Reference Forget and Pierrehumbert1997) or Mischna et al. (Reference Mischna, Kasting, Pavlov and Freedman2000); both studies included CO2 cloud effects.
From the given border of the Sun's HZ one can see that the size of the HZ is limited to a small region, depending on the spectral type and the age of the host star. Therefore the planet's eccentricity has to be sufficiently small if we require that the planet's orbit is completely within the HZ. In dynamical studies we distinguish different types of HZ, depending on the position of the giant planet in the system (see Fig. 1).
(1) The outer HZ (OHZ), where the HZ is outside the giant planet's orbit, as for systems hosting a hot Jupiter.
(2) The inner HZ (IHZ), where the HZ is between the host star and the detected giant planet, as in the Solar System.
(3) The giant planet HZ (GP-HZ) where the detected giant planet moves in the HZ. In this case we can only expect so-called habitable moons (see Fig. 1, (3a)) or habitable Trojan planets (Fig. 1, (3b)) (see Laughlin & Chambers (Reference Laughlin and Chambers2002), Dvorak et al. (Reference Dvorak, Pilat-Lohinger, Schwarz and Freistetter2004) and Érdi & Sándor (Reference Érdi and Sándor2005) ).

Fig. 1. Different types of habitable zone – a classification from the dynamical point of view depending on the position of the giant planet's orbit.
The study of habitability is certainly an interdisciplinary venture including astrophysical, biological, geophysical and chemical studies. It is well known that the evolution of a biosphere is a process that occurs over a long time; therefore, it is obvious that long-term orbital stability in the HZ is one of the basic requirements. This emphasizes the importance of such numerical investigations for known and future extrasolar planetary systems (EPS). Two approaches are used:
(i) to study certain detected extrasolar planetary systems concerning stability or planetary formation, or
(ii) to perform general numerical studies that can be applied to many of the discovered system.
If we classify three types of planetary systems as follows then results of general stability studies are available for systems in groups (1) and (3):
(1) single-star single-planet systems;
(2) single-star multi-planet systems;
(3) planets in double-star systems.
From observations we know that most EPS are part of class (1), for which we can apply the general studies of Sándor et al. (Reference Sándor, Süli., Érdi, Pilat-Lohinger and Dvorak2007) and Schwarz et al. (Reference Schwarz, Dvorak, Süli and Érdi2007). Systems of class (2) are more complicated from the dynamical point of view. Stable planetary motion is restricted to certain regions of the phase space of a system due to the gravitational interactions between the celestial bodies. Due to the diversity of these systems there are no global stability studies available. To date we have knowledge of more than 30 multi-planet systems. The necessity of verifying the dynamical stability of such systems was demonstrated by Ferraz-Mello (2005a), who showed in a numerical simulation that the two planets of HD82943 might end in a catastrophe after about 50 000 years when using the orbital parameters given by the observations. Stability studies for planets of class (3) are also very important due to the perturbations of the second star and the fact that more than 60% of the stars in the Solar neighbourhood build double or multiple star systems (see Duquennoy & Mayor Reference Duquennoy and Mayor1991). For the future we expect an increasing number of planets to be found in binary systems.
In this paper a brief overview of the motion of terrestrial planets is given for the three classes of planetary systems, and some general stability studies as well as applications to real EPS will be shown. First, a description of the dynamical model and the numerical methods will be given.
Dynamical models and computations
For general stability studies it is necessary to use the appropriate dynamical model. If one has to study a large set of orbital parameters the computations will be very time-consuming, therefore it is advisable to choose a model that enables efficient computation time. In dynamical astronomy it is common to use the so-called elliptic restricted three body problem (ERTBP), which describes the motion of a small body (of negligible mass) in the gravitational field of two primary bodies (that are either a star and a giant planet or two stars). This massless body has no influence on the motion of the two massive bodies, so that they move on Keplerian orbits around their centre of mass.
Numerous test computations have shown that this model provides good results for a system where the mass of one body is small compared with those of the other two. For larger masses of the third body the results of the ERTBP can be considered as a first approximation but should be examined additionally using e.g. the three body problem.
To determine whether a planet might be considered as ‘habitable planet’ from the dynamical point of view, it is useful to calculate the maximum eccentricity (max-e) of its orbit over the whole integration time. The max-e stability maps of the HZ indicate clearly the stable regions in a system. This method has been successfully applied to studies of extrasolar planetary systems (e.g. Dvorak et al. Reference Dvorak, Pilat-Lohinger, Funk and Freistetter2003a; Funk et al. Reference Funk, Pilat-Lohinger, Dvorak, Freistetter and Érdi2004, Reference Funk, Schwarz, Pilat-Lohinger, Süli and Dvorak2009; Dvorak et al. Reference Dvorak, Pilat-Lohinger, Schwarz and Freistetter2004; Érdi et al. Reference Érdi, Dvorak, Sándor and Pilat-Lohinger2004; Pilat-Lohinger & Funk Reference Pilat-Lohinger and Funk2006).
Besides the use of simple model it is also useful to apply methods that allow shorter computational runs, where the dynamical state of motion is determined via a so-called chaos indicator that indicates fairly quickly whether the motion is stable or chaotic. ‘Stable’ means that trajectories are located in an ordered region of the phase space, while ‘chaotic’ regions are characterized by instabilities due to chaotic diffusion of the trajectories. Most chaos indicators are based on the Lyapunov characteristic exponent. In this paper only the two methods that have been used for different numerical studies presented in the following sections will be described, in brief.
The fast Lyapunov indicator (see Froeschlé et al. Reference Froeschlé, Lega and Gonczi1997) is a numerical tool to distinguish quickly between regular and chaotic motion, since orbits in a chaotic region show an exponential growth of the largest tangent vector (for details see Froeschlé et al. (Reference Froeschlé, Lega and Gonczi1997) ). For most chaotic orbits only a small number of primary revolutions are needed to determine the orbital behaviour. This method has often been applied to studies of extrasolar planetary systems (e.g. Pilat-Lohinger & Dvorak Reference Pilat-Lohinger and Dvorak2002; Dvorak et al. Reference Dvorak, Pilat-Lohinger, Funk and Freistetter2003a, Reference Dvorak, Pilat-Lohinger, Funk and Freistetterb; Pilat-Lohinger et al. Reference Pilat-Lohinger, Funk and Dvorak2003; Bois et al. Reference Bois, Kiseleva-Eggleton, Rambaux and Pilat-Lohinger2003; Érdi et al. Reference Érdi, Dvorak, Sándor and Pilat-Lohinger2004; Pilat-Lohinger Reference Pilat-Lohinger, Knezevic and Milani2005; Sándor et al. Reference Sándor, Süli., Érdi, Pilat-Lohinger and Dvorak2007).
Another fast method is the relative Lyapunov indicator (Sándor et al. 2000, Reference Sándor, Érdi, Széll and Funk2004) which measures the convergence of the finite time Lyapunov indicators to the maximum Lyapunov characteristic exponent of two very close orbits. This method is extremely fast in determining the dynamical behaviour of individual orbits (e.g. sticky orbits, Sándor et al. (Reference Sándor, Érdi, Széll and Funk2004) ). Whenever both methods have been applied to a particular system, the results were found to be in good agreement.
Single-star single-planet systems
It is well known that most of the EPS build simple two-body systems, which are certainly stable. However, we cannot exclude that all these systems host no other planets – maybe there are small terrestrial planets hidden. It is interesting therefore to study the orbital motion of additional low-massive planets in these systems. Since they are very numerous, it is advisable to use results of general stability studies.
The so-called ‘Exocatalogue’ (see Sándor et al. Reference Sándor, Süli., Érdi, Pilat-Lohinger and Dvorak2007) is an example for such a general study. It provides 92 stability maps covering 23 mass ratios (MR=m 2/(m 1+m 2)) of a star and a giant planet (ranging from 0.0001 to 0.05). In this numerical study the semi-major axis of the giant planet (a gp) was set to unity and its eccentricity (e gp) was varied from 0 to 0.5. For the giant planet two starting positions were used – where the mean anomaly (M gp) is either 0 or 180 degrees. Using the ERTBP as dynamical model, Sándor et al. (Reference Sándor, Süli., Érdi, Pilat-Lohinger and Dvorak2007) studied (i) the region between the host star and the giant planet (inner region), where the test planets have starting positions between 0.1 and 0.9; and (ii) the region outside the giant planet (outer region) from 1.1 to 4. To use the results of the Exocatalogue one has to calculate the MR, to find the appropriate stability map. Then the dimensionless units have to be converted to the systems' units. For a more convenient application we installed the online tool ‘ExoStab’ (available at http://univie.ac.at/adg/exostab).
When using ExoStab one is asked to enter some basic parameters of a planetary system, such as the masses of the host star and the known giant planet, the distance between these two bodies, the eccentricity of the giant planet and its uncertainty. Further input depends on the option chosen by the user:
(i) stability of an additional planet;
(ii) stability of the HZ;
(iii) stability of an additional planet with respect to the HZ.
A detailed description of ExoStab is published by Pilat-Lohinger et al. (Reference Pilat-Lohinger, Eggl and Winkler2009). According to the input, ExoStab searches the corresponding result of the Exocatalogue and generates a stability map using colour codes, where blue defines the zone of stable motion and green to red indicates chaotic behaviour (while in the Exocatalogue stable regions are yellow or orange, and dark orange to black mark chaotic motion).
As an example, ExoStab has been applied to the ESP HD143361. The resulting stability map is given in Fig. 2. and shows a linear decrease of the stable region (blue area) when increasing the eccentricity of the giant planet. Additionally, one can recognize vertical green lines that indicate perturbations within the stable region due to mean motion resonances (MMRs) with respect to the giant planet. The rectangle marks the HZ (depending on the selection made by the user the rectangle could also mark the region where a newly discovered planet is expected, and whether this region corresponds to the HZ). Its position and size is given in x-direction by the defined borders of the HZ and in y-direction by the error of the giant planet's eccentricity. A magnification of the area within the rectangle (see Fig. 3) is also provided when using ExoStab, which displays more details of this region.

Fig. 2. Stability map for fictitious small planets in the extrasolar planetary system HD143361 created by ExoStab. Blue area labels the stable motion; green to red indicates chaotic motion. Vertical green lines mark the locations of mean motion resonances.

Fig. 3. Magnification of the region within the rectangle of Fig. 2, which corresponds to the habitable zone.
Limitations of the application of ExoStab are due to the chosen dynamical model and initial configuration. The stability maps are mostly valid for small planets (e.g. terrestrial planets) and low-eccentric motion (e<0.2) since the computations were performed in the ERTBP. Moreover, currently only the results of nearly circular motion of the low-mass planets are available. A mutual inclination of the planet to the plane of the giant planet is also not yet included.
Multi-planetary systems
For such systems it is difficult to perform general stability studies, since the number of orbital parameters that has to be varied is large. From the more than 30 multi-planet systems that have been discovered up to May 2009 we know that most systems have only two planets; there are eight systems hosting three planets, two systems with four and one system has five planets.
From the dynamical point of view, we distinguish four classes of multi-planet systems (according to Ferraz-Mello et al. (2005b)), which are based on the mutual distance between the planets and the orbital eccentricities, described below.
Class 1 – planets in mean-motion resonance (MMR)
Planets of this class move in eccentric orbits that are relatively close to each other, so that strong gravitational interactions have to be expected. Such systems remain stable, if the two planets are in MMR, i.e. if the ratio of the orbital periods of two planets is close to a ratio of two integers. An MMR can be written as (p+q)/q, where p and q are integers and the latter represents the order of the resonance. Whether a system is in resonance or not can be verified by the behaviour of the critical angles of a MMR, which are defined as:
where λi, i=1, 2, are the mean longitudes of the planets and ![]() i, i=1, 2, are the longitudes of perihelion. If one of these angles oscillates then the system is inside a resonance. There are many examples of planet pairs in MMRs, e.g. GJ 876, 55 Cnc, HD829422, HD202206, HD160691, Ups And.
i, i=1, 2, are the longitudes of perihelion. If one of these angles oscillates then the system is inside a resonance. There are many examples of planet pairs in MMRs, e.g. GJ 876, 55 Cnc, HD829422, HD202206, HD160691, Ups And.
Class 2 – low-eccentricity near-resonant planet pairs
Planets of this class have low-eccentric orbits, therefore it is not necessary that they are in MMR in order to exclude close encounters. Our Solar System belongs to this group as does the recently discovered OGLE-06-109L system (Gaudi et al. Reference Gaudi2008), which shows similar characteristics to the Solar System. For Jupiter–Saturn analogues, a comprehensive stability study has been carried out by Pilat-Lohinger et al. (Reference Pilat-Lohinger, Süli, Robutel and Freistetter2008a), where the mass of Saturn was increased by factors of 2–40 and its initial semi-major axis was varied from 8 to 11 AU.
When studying the perturbations of different Jupiter–Saturn configurations on the motion in the HZ, we observe a curved band of higher eccentricity (see Fig. 4) corresponding to a secular frequency with respect to the peri-astron of Jupiter (known as g5 frequency in the Solar System).

Fig. 4. Maximum eccentricity map for Earth-like planets influences by Jupiter and Saturn. The x-axis shows the different initial semi-major axis of the massless Earth-like planets and the y-axis shows the different semi-major axis of Saturn. The grid size in x is 0.02 AU and in y 0.1 AU. The vertical black solid lines indicate the positions of Venus (V), Earth (E) and Mars (M) and the horizontal solid line shows the semi-major axis of Saturn (Sat) in the Solar System. The horizontal dashed lines label the positions of different mean motion resonances of Saturn and Jupiter. Different grey shadings belong to different maximum eccentricities (see the scaling). The arched band of higher eccentricity belongs to the secular frequency g5.
For the Solar System masses of Jupiter and Saturn one can see that the orbital region of Venus is influenced by the g5 frequency which increases the eccentricity (>0.2) in this area. In Pilat-Lohinger et al. (Reference Pilat-Lohinger, Robutel, Süli and Freistetter2008b) it is shown that the only way to decease the eccentricity at Venus position is to add the Earth to the dynamical system.
Results of systems with larger Saturn mass show that this secular perturbation is shifted towards the outer region of the HZ. Venus is then found in the low-eccentric region. However, the Earth is now influenced by this secular perturbation and eccentricities of 0.27 were observed.
Adding a third giant planet to the systems, the results of the Jupiter–Saturn system and the Jupiter–Saturn–Uranus system were similar when using the masses of the Solar System.
An increase of Saturn's mass indicated an influence of the third giant planet (for details see Pilat-Lohinger et al. Reference Pilat-Lohinger, Robutel, Süli and Freistetter2008b).
Class 3 – non-resonant planets with significant secular dynamics
Such planet pairs can have strong gravitational interactions, where long-term variations are ascribed to secular perturbations, large variations of the eccentricities and dynamical effects such as the alignment and anti-alignment for the apsidal lines (see Michtchenko & Malhotra Reference Michtchenko and Malhotra2004). For the long-term stability of such a system, it is not necessary that the planets are in MMR. Examples are 55 Cnc (e and b), HD169830, HD37124.
Class 4 – hierarchical planet pairs
This is a class of planet pairs with a large ratio of their orbital periods: P1/P2>10. In this case, the gravitational interactions are not so strong as in class 3, and the probability of a capture in a MMR is negligible. The weaker interactions lead to stable motion in the numerical simulations, even if the orbits of the planets are not as well determined. Examples are HD168443, HD74156, HD38529.
For a detailed description of the interesting topic about dynamics of multi-planetary systems, see Ferraz-Mello et al. (2005b) or Michtchenko et al. (Reference Michtchenko, Ferraz-Mello, Beaugé and Dvorak2007).
Planets in binary systems
Studies of planetary motion in binary systems are very important due to the fact that more than 60% of the stars in the Solar neighbourhood build double or multiple star systems (see Duquennoy & Mayor Reference Duquennoy and Mayor1991). It is obvious that in such systems the stable planetary motion is restricted to certain regions of the phase space due to the gravitational perturbations of the second star.
From the dynamical point of view, we distinguish three types of motion in double star systems (according to Dvorak Reference Dvorak1984):
(i) the satellite-type (or S-type) motion, where the planet orbits one stellar component;
(ii) the planet-type (or P-type) motion, where the planet surrounds both stars in a very distant orbit; and
(iii) the libration-type (or L-type) motion, where the planet moves in the same orbit as the secondary but 60° ahead or behind; furthermore, they are locked in 1:1 MMR.
To date (May, 2009) 43 double and multiple star systems (37 binaries and six triples) are known that harbour at least one planet (Mugrauer & Neuhäuser Reference Mugrauer and Neuhäuser2009). From the observations, one can see that the S-type motion is the most interesting one, since all detected extrasolar planets in binary systems orbit one of the stars.
The P-type motion will become interesting when planets are discovered in very close binaries. In principal we know that planetary motion around both stars is only stable for distances (from the mass-centre) larger than twice the distance of the two stars. In the case of high eccentric motion of the binary (around 0.7) the planet's distance has to be more than four times that of the two stars to be stable. For details see e.g. Dvorak (Reference Dvorak1984, Reference Dvorak1986), Rabl & Dvorak (Reference Rabl and Dvorak1988), Dvorak et al. (Reference Dvorak, Froeschlé and Froeschlé1989), Holman & Wiegert (Reference Holman and Wiegert1999), Pilat-Lohinger et al. (Reference Pilat-Lohinger, Funk and Dvorak2003), Pilat-Lohinger & Dvorak (Reference Pilat-Lohinger, Dvorak and Dvorak2007).
The third type of motion (L-type motion), where the planet librates around one of the two Lagrangian triangular points of one of the stars, is not so interesting for planetary motion in double stars due to a limitation in the MR of the two stars:
This motion is more interesting for single-star, giant planet systems, where the limit of the MR is easily fulfilled.
Due to these facts details will only be given for S-type motion, which is currently the type of most interest. From the binaries hosting one or more planets, only four can be considered as close double stars, where the separation of the two stars is around 20 AU. If only one planet is detected in such a system, it is possible to verify the stability of the planetary motion via general stability studies like the ones by Rabl & Dvorak (Reference Rabl and Dvorak1988), Holman & Wiegert (Reference Holman and Wiegert1999), or Pilat-Lohinger & Dvorak (Reference Pilat-Lohinger and Dvorak2002). All these studies used the ERTBP and determined the stable region as a function of the binary's MR and its eccentricity. An eccentricity of the planetary motion was only considered in the paper by Pilat-Lohinger & Dvorak (Reference Pilat-Lohinger and Dvorak2002). The general conditions for these studies are the following:
(i) m 1 is the host star about which the planet moves;
(ii) the second star m 2 is at 1 AU and starts either from the pericentre or from the apocentre;
(iii) the eccentricity of the binaries is increased from 0 to 0.8 in steps of 0.1;
(iv) the semi-major axis of the test planets (TPs) is between 0.1 and 0.9 AU;
(v) the TPs were placed at four different starting positions (mean anomaly=0°, 90°, 180° or 270°);
(vi) the planet's eccentricity was varied between 0 and 0.5 (only in Pilat-Lohinger & Dvorak Reference Pilat-Lohinger and Dvorak2002).
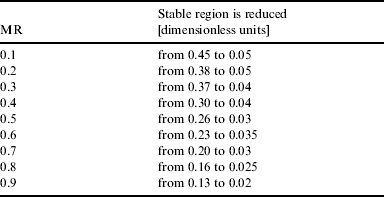
The result for circular planetary motion is summarized in Fig. 5 and Table 1, which show a shrinking stable region (z-axis) for the different MRs when the eccentricity of the binary (x-axis) is increased from 0 to 0.8.

Fig. 5. Border of stable motion for S-type orbits in binary systems for different mass ratios (y-axis) and different eccentricities of the binary (x-axis). The z-axis shows the maximum distance from the host-star for which stable motion was found independent on the starting position.
Table 1. Borders of stable motion for different mass-ratios (MR) – from circular motion to high eccentric motion (e=0.8) of the binary
In the study by Pilat-Lohinger & Dvorak (Reference Pilat-Lohinger and Dvorak2002) it was shown that the influence of the planet's eccentricity is not so strong. However, even if the size of the stable region does not indicate a strong dependence on the planet's eccentricity, it is not negligible.
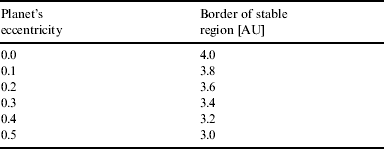
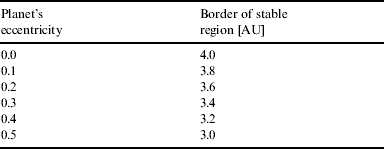
This will be demonstrated using the real binary system Gamma Cephei, which hosts a giant planet of about 1.6 Jupiter-masses). The MR of the binary is 0.2 and the binary's eccentricity is about 0.4. Even if the observed eccentricity of Cep b is only 0.11 we show the reduction of the stable zone for eccentricities up to 0.5. Using 20 AU as separation for the two stars the results shown in Table 2 were found.
Table 2. Border of the stable motion of gamma Cep A for different eccentricities of the detected giant planet
It is clearly seen that for a planet close to the border of the stable region it is also necessary to take into account its eccentricity, otherwise a planet which is thought to move in the stable area (when using the results of circular planetary motion) is already in the chaotic zone due to its eccentricity. In this case it would be necessary to improve the orbital fit from which the orbital parameters have been determined.
Planets in the habitable zone of double star systems
The dynamical behaviour of planets in the HZ of a binary star will be discussed for three real systems (Gliese 86, HD41004 AB and Gamma Cephei), which are examples of the different HZs shown in Fig. 1.
Habitable zone of Gliese 86
The binary Gliese 86 consists of a K1 main sequence star of 0.7 Solar masses and a white dwarf with a minimum mass of 0.55 Solar masses at a distance of about 21 AU (Mugrauer & Neuhäuser Reference Mugrauer and Neuhäuser2005). Queloz et al. (Reference Queloz, Mayor, Weber, Blicha, Burnet, Confino, Naef, Pepe, Santos and Udry2000) have found a close-in planet at 0.11 AU to K1 V star with an orbital period of less than 16 days. Due to the CORALIE measurements a minimum mass of four Jupiter masses was determined.
The HZ of a K1 V star is approximately between 0.4 and 0.9 AU, that is, outside the orbit of the detected giant planet. Therefore, this system is an example of the first type of HZ (i.e. OHZ).
Since the gas giant moves at 0.11 AU on a nearly circular orbit, its gravitational influence on the HZ is not significant. A detailed study examining the influence of a massive close-in planet on the HZ of Gliese 86 is in progress.
For such systems it is certainly more important to have knowledge regarding region in which the giant planet has been formed and if the migration of the gas giant through the HZ allows the existence of terrestrial planets in this region. A first study which examines this problem has been published by Raymond et al. (Reference Raymond, Mandell and Sigurdsson2006).
Habitable zone of HD41004A
HD41004 AB can be divided into two subsystems, with a projected distance of the two stellar components between 20 and 23 AU according to different observations. Both stars have a sub-stellar companion: (i) a planet of 2.3 Jupiter masses orbits HD41004A (a K1 V star) at a distance between 1.31 and 1.7 AU in a quite high eccentric motion (between 0.39 and 0.74) – see Zucker et al. (Reference Zucker, Mazeh, Santos, Udry and Mayor2004) ; and (ii) a brown dwarf of more than 18 Jupiter-masses moves around HD41004B (a M2 V star) in about 1.328 days.
The HZ of HD41004A is located between the star and the orbit of the giant planet and is therefore a second-type HZ (i.e. IHZ; as in the Solar System). Stability studies of terrestrial planets in this system have shown that the first orbital parameter set would allow long-term stable motion in the HZ, which is limited to the inner region of the HZ (up to 0.7 AU), but only if the eccentricities of the binary and of the planet are not too high (<0.3). The stable region is fragmented into several stable strips due to MMRs with the detected giant planet: the 4:1 MMR is near 0.52 AU, the 7:2 MMR is near 0.57 AU, the 3:1 MMR is near 0.63 AU and the 8:3 MMR is near 0.68 AU (for details see Pilat-Lohinger & Funk Reference Pilat-Lohinger, Eggl and Winkler2009).
Habitable zone of Gamma Cephei
This binary consists of a K1 IV star (of 1.6 Solar masses) and a M4 V star (of 0.4 Solar masses). Cochran et al. (Reference Cochran, Hatzes, Endl, Paulson, Walker, Campbell and Yang2002) discovered a planet of about 1.7 Jupiter masses moving at about 2 AU in a low eccentric orbit around the K1 star. In the previous section it was shown that the long-term stability of this planet was confirmed by general stability studies.
The HZ of a 1.6 Solar mass star extends approximately from 1.6 to 3.2 AU. Since the giant planet moves in the HZ, this system is an example for the third type HZ (i.e. GP-HZ), so that habitable Trojan-type planets or habitable moons could be possible in this planetary system. The stability of these motions has still to be studied.
Conclusions
In this paper the dynamical evolution of planets in different planetary systems was discussed. Following a classification into (1) single-star single-planet systems, (2) single-star multi-planet systems and (3) planets in double stars, a short overview discussing stability of planetary motion in the different systems has been given.
In case of single-star single-planet systems, which build stable two-body systems, the general stability study of Sándor et al. (Reference Sándor, Süli., Érdi, Pilat-Lohinger and Dvorak2007) – the so-called Exocatalogue – and the online tool ExoStab (Pilat-Lohinger et al. Reference Pilat-Lohinger, Eggl and Winkler2009) were discussed. From these studies one gets information about the stability of an additional small planet moving inside or outside the giant planet's orbit, which is certainly interesting for the detection of Earth-like planets in such systems.
For multi-planetary systems it is too difficult to perform general stability studies, since too many orbital parameters have to be varied. From the dynamical point of view, different groups of multi-planetary systems can be distinguished, but in principal the different EPS have to be studied separately.
The stability of planetary motion in binary systems can be determined via general stability studies – using the ones by Dvorak (Reference Dvorak1984, Reference Dvorak1986), Rabl & Dvorak (Reference Rabl and Dvorak1988), Dvorak et al. Reference Dvorak, Froeschlé and Froeschlé1989, Holman & Wiegert Reference Holman and Wiegert1999, Pilat-Lohinger & Dvorak Reference Pilat-Lohinger and Dvorak2002, Pilat-Lohinger et al. Reference Pilat-Lohinger, Funk and Dvorak2003 – if only one giant planet has been discovered. It was shown that the size of the stable region depends mainly on the MR of the binary and its eccentricity. However, the planet's eccentricity should not be ignored, especially if the planet was found close to the border of stable motion.
In case of a multi-planetary system in a close binary, the stability of the whole system has to be examined, since no general studies are available. It is well known that such investigations are very important, since more than 60% of the stars in the Solar neighbourhood build double or multiple star systems. Therefore, we expect an increasing number of planets to be discovered in binary systems in the future.
Summarizing the different studies, one can see that only for simple systems, such as a star accompanied by a giant planet or by a second star, general stability studies to verify the dynamical behaviour of a third small celestial body are possible. In these systems the dynamics depend mainly on the masses and the eccentricity of the two massive bodies, and perturbations within the stable region result from MMRs. In the case of multi-planetary systems, additional secular resonances and three-body resonances occur that certainly yields a more complicated dynamical structure of the phase space.
Acknowledgment
EP-L wishes to acknowledge the support by the Austrian FWF (project P19569-N16).