Introduction
Nucleic acids and proteins currently form the basis for the informational content in living organisms. The formation of these macromolecules is highly regulated today, and the question of how the molecules themselves and the complex mechanism of regulation could have originated from the much simpler inorganic and organic compounds present in the early solar system is still open (Bada Reference Bada2004). A lot of effort has been expended on the spontaneous formation of the precursors of informational molecules (nucleotides and amino acids) from the compounds present in the early atmosphere (Rode Reference Rode1999), meteorites and comets (Muñoz Caro et al. Reference Muñoz Caro, Meierhenrich, Schutte, Barbier, Arcones Segovia, Rosenbauer, Thiemann, Brack and Greenberg2002), but very little is known about the processes at the base of the formation of functional macromolecules like proteins from their monomeric constituents. The primitive conditions on Earth and the various routes for the formation of amino acids and peptides were reviewed by Rode (Reference Rode1999), who also provided a rationale for favouring polypeptides over RNA as the first replicating species, based on their higher chemical stability. Another open question concerning RNA and proteins is the origin of their informational content. Nucleic acids contain the information necessary to build proteins, and in turn proteins derive their structural or catalytic properties from their amino acid sequence and structure, so it has to be determined how the correct sequences and structures developed in primitive polypeptides, which could not have formed by decoding any information in pre-existing nucleic acids. The accepted paradigm is by way of selection from a large number of random combinations of primary structures governed by chance. However, there are unresolved questions regarding the practical realization of this process. First, it has to be determined how the overall number of possible polypeptides and the number of actually catalytically active polypeptides compare and how both of these numbers relate to the mean time of the reactivity for peptide bond formation and the available time (~0.5 Gyr) between the cooling of the Earth's crust and the first fossilized unicellular organisms (Rode Reference Rode1999). Second, given the spontaneous formation of catalytic polypeptides, we need to know whether their concentrations were sufficient to actually act on various substrates and form species which would not otherwise form spontaneously in the prebiotic environment. It is logically necessary that the species generated by the catalytic process would themselves act as new substrates, thus enhancing the chemical diversity of the early Earth with the other constituents of living organisms, like lipids and sugars. In order to be able to answer some of these questions quantitatively, it is necessary to build a model of the process of polymerization under reasonable assumptions regarding the physicochemical conditions of the prebiotic environment, being aware that too many assumptions would oversimplify the problem making the ensuing answers unrealistic, while, on the other hand, taking into consideration too many factors would quickly make the model mathematically and computationally intractable.
After the previous quantitative analysis (Canepa Reference Canepa2013) of the catalytic requirement of the (isothermal) prebiotic aqueous environment that would allow the formation of polypeptides with the minimum length required to exhibit catalytic properties, this work examines the consequences of the spontaneous formation of a mixture of polypeptides of various lengths on the diversity of the prebiotic oceanic chemistry on the early Earth. Following the formation of proto-enzymes in the presence of chemical species acting as substrates, we may envision the development of a more complex chemistry until a kinetic cycle of reactions involving self-replicating species was reached. We assume the presence of a continuous source of amino acids that would keep the monomer concentration constant. It is an established fact that micrometeorites, interplanetary dust particles (IDP), and carbonaceous chondrites presently deliver amino acids to the Earth (Anders Reference Anders1989), and many experiments have shown that amino acids could have formed in the early atmosphere subjected to various energy sources. The model developed in this work assumes the presence of an ideal amino acid source; it is immaterial if the source is endogenous or external to the planet Earth.
Model and simulation
We briefly summarize in this section the key results of a previous investigation (Canepa Reference Canepa2013) that are needed before we may proceed to analyse the concentration of the chemical species formed by the catalytic activity of the polypeptides. These results will be used in the next section, and we refer the reader to Canepa (Reference Canepa2013) for further details. An active enzyme with n amino acid residues could have formed spontaneously from its monomeric components in a catalytic environment given an appropriate source of amino acids. The fraction α of constrained amino acid (De Ley Reference De Ley1968), the set p of available amino acids, the oceanic volume V, and the probability p− αn that a particular polypeptide of length n and concentration x n would exhibit catalytic properties are related by
$$f = x_n VN_A p^{ - {\rm \alpha} n}, $$
where N A is the Avogadro number, and f can be thought of as the number of molecules of catalytic polypeptides in the whole volume or the ratio between the total number of molecules of length n and the number of possible primary structures. Setting f ≅ 1, we determined the minimal requirements of the catalytic environment and the amino acid source that allowed the formation of a catalytic polypeptide, regardless of its concentration.
In the presence of an amino acid source with the ability to keep the concentration of monomers x 1 constant, the formation of the peptide with n residues is governed by the equation
$$\dot x_n = {\rm \eta} x_1 x_{n - 1} - {\rm \omega} x_n, $$
with solution
$$x_n = {\rm \zeta} ^{n - 1} x_1 [1 - Q{\rm (}n - 1,\,{\rm \omega} t{\rm )}],$$
where Q(n−1, ωt) is the ratio between the incomplete and complete gamma function of Euler
$$Q{\rm (}n - 1,\,{\rm \omega} t{\rm )} = \displaystyle{{{\rm \Gamma (}n - 1,\,{\rm \omega} t{\rm )}} \over {{\rm \Gamma (}n - 1{\rm )}}}.$$
We define ζ = (ω−ω h )/ω as the ratio between the rate of peptide formation over the overall reaction rate (peptide formation plus hydrolysis). The interval of variation of the parameter ζ describes the various effects that the environment might have had on the rate of formation of the peptide bond in polypeptides. The value ζ = 1/2 implies equal rates for the formation of the peptide bond and its hydrolysis. On the other hand, values of ζ near unity describe very effective catalysis by either chemical species in solution or mineral surfaces. The proper frequency of the reactive system ω = ηx 1 + η h xw is given in terms of the bimolecular rate coefficient for peptide bond formation (η) and the rate coefficient for hydrolysis (η h ). The key parameter ζ expresses the catalytic efficiency of the polymerization and it will represent the independent variable in the following discussion. In this context, both the frequency for hydrolysis ω h = η h xw and the frequency for spontaneous amino acid polymerization ω determine the time scale of the problem. Both depend on the reaction rate coefficients, which in turn are functions of temperature. The experimental value for the hydrolysis of glycyl-glycine (6.3 × 10 − 11 s−1) (Radzicka & Wolfenden Reference Radzicka and Wolfenden1996) will be used in all the calculations, thus neglecting the contributions of the temperature gradient of the ocean, the lowered pH of the surface waters, and the degradative effect of radiolysis and photolysis on the polypeptides. Since we consider the rate coefficients for amino acid hydrolysis to be constant, we will obtain upper bounds to the final concentrations of polypeptides and products of catalysis.
It was shown that the inflection point of Q at ωt = n−2 is reached in a time span lower than ≈ 105 yr, so that it may be safely assumed that, for periods of time of the order of 1 Gyr, the dynamics of the possible formation of polypeptides of length n in the presence of catalysis affords a geometric progression with the terms
$$x_n = {\rm \zeta} ^{n - 1} x_1, $$
for the stationary concentration x n of polypeptides.
This work concerns the necessary conditions allowing the formation of significant amounts of products of the chemical transformations of pre-existing substrates promoted by the polypeptides through their own catalytic properties. Consequently, we must determine the required concentration of the polypeptides affording f ≫ 1.
Equation (5) was linked to the relation between the source s of monomeric amino acids and their concentration at steady state by the relation
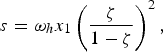$$s = {\rm \omega} _h x_1 \left( {\displaystyle{{\rm \zeta}\over {1 - {\rm \zeta}}}}\right)^2 , $$
having defined the source s = 4πR 2φ/(VN A ) in terms of the incoming flux φ of amino acids. We note that a smaller volume of the sea with respect to the present-day value would have increased the value of the source. For the purpose of calculation (all calculations were performed with the program Scilab: Scilab Enterprises (2012). Scilab: Free and Open Source software for numerical computation (OS, Version 5.XX) [Software]. Available from: http://www.scilab.org), in this work we use s = 2.83 × 10− 20 M s−1, the mean value of Chyba et al. (Reference Chyba, Thomas, Brookshaw and Sagan1990) estimate, and s/ω h = 4.49 × 10 − 10 M for glycyl-glycine. At steady state we obtained, for the concentration of polypeptides of length n,
$$x_n = \displaystyle{s \over {{\rm \omega} _h}} (1 - {\rm \zeta} )^2 {\rm \zeta} ^{n - 3}. $$
The efficiency of a catalyst promoting the condensation of the amino acids is also given by the ratio of the rate coefficient for catalysed formation of the polypeptide to the corresponding rate coefficient for hydrolysis
$$\displaystyle{{\rm \eta}\over {{\rm \eta} _h}}= \displaystyle{{x_w {\rm \omega} _h}\over s}\left( {\displaystyle{{\rm \zeta}\over {1 - {\rm \zeta}}}}\right)^3. $$
In particular, we note that the concentration of polypeptides has a maximum for the value of the catalytic efficiency ζ m = (n − 3)/(n − 1), corresponding to η/η h = (x w ω h /8s)(n−3)3 = 1.41 × 1016 for n = 100, a value attained by the most efficient of the present-day enzymes (Fig. 1). The catalytic efficiency ζ m maximizing x n , the frequency ω expressing the reactivity of the polypeptides towards their formation or hydrolysis, and the ratio η/η h are given in Table 1 for different values of n. The effect of catalysis on the dynamics of the concentrations of all the polymers of different lengths was found to be essential. This investigation begins by determining the concentration of catalytic polypeptides of given lengths in steady-state conditions. The choice of the minimum value of n that allows for catalytic features is somehow speculative. Short polypeptides, even dipeptides, have been shown to possess the ability to promote at pH = 10 the formation of the peptide bond between model systems such as ethyl- or thioesters of amino acids and amino acid derivatives such as the amide of leucine (Lee et al. Reference Lee, Granja, Martinez, Severin and Ghadiri1996; Gorlero et al. Reference Gorlero, Wieczorek, Adamala, Giorgi, Schininà, Stano and Luisi2009). However, free amino acids do not react in the same conditions, probably because the high values of pH generating the nucleophile NH2 from NH3 + at the same time deprotonates the carboxylic group to COO−, thus impairing the reactivity of the electrophile.
Fig. 1. Plot of the logarithm of the ratio η/η h (equation 8) versus the catalytic efficiency ζ and the amino acid source s for p = 10 and α = 0.10.
Table 1. Frequency ω of reactivity of the polypeptides and the required ratio η/ηh between the polymerization rate coefficient to the hydrolysis rate coefficient for the values of the catalytic efficiency ζm maximizing the concentration of active polypeptides at various values of n, p = 10, and α = 0.10
Results
We first observe that not every combination of amino acids in a given sequence corresponds to a catalytic polypeptide. In order to be an effective catalyst, a polypeptide must have specific structural properties resulting in its ability to bind a substrate and to promote its chemical transformation. This ability is summarized by the value of the ratio k 2/k M in the Michaelis–Menten mechanism of enzyme catalysis. The concentration of catalytically active polypeptides is (x n ) cat = x n p− αn , where the fraction α of constrained amino acid residues in specific positions in the chain implies catalytic activity. Plots of (x n ) cat are shown in Fig. 2 for p = 10, α = 0.10 and n = 60, 80, 100, ostensibly showing the dramatic effect of the values of these parameters on the concentration of a polypeptide of given length.
Fig. 2. Logarithm of the molar concentration of the species x n (blue) and of the catalytic polypeptides x n p− αn (red) given by equation (7) for p = 10 and α = 0.10. Solid lines are for n = 20, dashed lines for n = 60, and dash-dot lines for n = 100.
We now turn our attention to the formation of possible reaction products catalysed by the polypeptides by considering as active catalysts all polypeptides with αn amino acid residues constrained. The Michaelis–Menten reaction rate for the transformation of a generic substrate z is proportional to the product of the concentration of the catalyst (x n ) cat , and z. The rate coefficient λ for the process can be deduced considering that, in the primordial oceanic conditions, the concentration of any substrate was small compared to typical values of the Michaelis constant k M . The ratio k 2/k M is an indication of the catalytic ability of a polypeptide in promoting a chemical reaction on a substrate (z→u), and it must not be confused with the parameter ζ, relating to the catalytic process forming the polypeptides. We also safely assume that the concentration z of a substrate was larger than the typical steady-state concentration of the catalyst (x n ) cat , and, for the sake of simplicity, assume the source of z to be of the same intensity as the source of amino acids. If the condition (x n ) cat ≪ z ≪ k M is satisfied, the dynamics of the substrate follows the equation
$$\dot z = s - {\rm \lambda} z,\quad {\rm \lambda}= \displaystyle{{k_2}\over {k_M}} x_n^0 p^{ - {\rm \alpha} n} , $$
with solution
$$\displaystyle{z \over {z_0}}= {\rm e}^{ - {\rm \lambda} t} + \displaystyle{s \over {z_0 {\rm \lambda}}} (1 - {\rm e}^{ - {\rm \lambda} t} ).$$
In this context
$x_n^0 $
in the expression for λ is the stationary concentration (equation (7)) of polypeptide of length n when it reaches catalytic capability. For the purpose of calculation, we attribute to z
0 (the concentration of the substrate before the onset of catalysis) the value estimated by Pierazzo and Chyba (Thomas et al. Reference Thomas, Hicks, Chyba and McKay2006) for the oceanic glycine concentration from electrical discharge and cometary input 4.0 Gyr ago (2.4 × 10
−
9 M). Using this estimate, we obtain s/z
0 = 1.18 × 10
−
11 s−1, a value close to ω
h
. The frequencies s/z
0, λ, and ω are plotted in Fig. 3 for k
2/k
M
= 1.0 × 103 M−1 s−1, p = 10, α = 0.10, and three different values of n. The frequency ω of polymerization is of the order 10
−
2 yr−1 for most values of ζ, except around ζ ≈ 1. The corresponding frequency λ for the reactivity of the substrates is many orders of magnitude lower. Without catalysis (λ = 0), z would follow the law
$$\displaystyle{z \over {z_0}}= 1 + \displaystyle{{st} \over {z_0}}, $$
and the concentration of the reaction product u is thus given by the difference between equations (11) and (10)
$$\displaystyle{u \over {z_0}}= (1 - {\rm e}^{ - {\rm \lambda} t} )\left( {1 - \displaystyle{s \over {z_0 {\rm \lambda}}}} \right) + \displaystyle{{st} \over {z_0}}. $$
Fig. 3. Logarithm of the frequencies (in yr−1) s/z 0 (dashed lines), λ (solid lines), and ω (dash-dot line) versus the catalytic efficiency ζ for k 2/k M = 1.0 × 103 M−1 s−1, p = 10, and α = 0.10. The effect of different values of n is also shown: n = 20 (green), n = 60 (blue), and n = 100 (red).
In all the cases where λt is small (n > 60), the concentration of the product may be approximated as u/z 0 ≅ λt(1 − λt/2 + st/2z 0). With the selected source and t = 0.5 Gyr we have u/z 0 ≈ 10 − 6−105 for the above-mentioned value of z 0, even with the low values of the product-forming frequency (λ ≈ 10 − 20 − 10 − 9 yr−1). The effect of n on these values is dramatic. Only polypeptides with a relatively low value of n may form a non-negligible concentration of product, and it should be determined if such a low value of n is compatible with the assumed catalytic efficiency k 2/k M ≈ 103 M−1 s−1. A surface plot of equation (12) versus ζ and the wide range of s estimated by taking into account the lunar cratering record (Hartmann et al. Reference Hartmann, Ryder, Dones and Grinspoon2000) is shown in Fig. 4. The surface plot shows the effect of values of the amino acid source significantly in excess of the estimated contribution from micrometeorites. In fact, the source is related to the flux φ of the amino acids and the depth of the water h through the equation s = φ/h. It can thus be conceived that regions of shallow waters may have actually caused a locally increased value of s with a corresponding linear increase in λ. It is also possible that the production of more complex amino acid species from amino acids of simple structure would have increased over time the value of p. In this case, equation (9) would involve a nonlinear function p(u). However, we know that p would not increase by more than a factor of two, decreasing the value of λ by a factor of 2−αn . To clarify the effect of an increasing p, we compute the state variables with the values p = 10 (Table 2), and p = 20 (Table 3). The catalytic efficiency is set to the value maximizing equation (7), i.e. ζ m = (n − 3)/(n − 1). Comparing the data in Tables 2 and 3, we see that the increase of p does not change the concentration of products obtained through catalytic polypeptides of low length. At higher values of n, however, the increase of p makes significant concentrations of the products u even more unattainable in the time frame t = 0.5 Gyr.
Fig. 4. Plots of the ratio u(t)/z 0 at t = 0.5 Gyr versus the catalytic efficiency ζ and the amino acid source s for n = 60, k 2/k M = 1.0 × 103 M−1 s−1, p = 10, α = 0.10, and z 0 = 2.4 × 10 − 9 M given by equation (12).
Table 2. For various values of n, p = 10, α = 0.10, k2/kM = 1.0 × 103 M−1 s−1, ζ = ζm, and z0 = 2.4 × 10 − 9 M are given: the probability p−αn, the molar concentration of catalytic polypeptides (xn)cat, the frequency λ of the catalysed reactions, the value λt, and the concentration of products u(t)/z0 at t = 0.5 Gyr given by equation (12)
Table 3. For various values of n, p = 20, α = 0.10, k2/kM = 1.0 × 103 M−1 s−1, ζ = ζm, and z0 = 2.4 × 10− 9 M are given: the probability p−αn, the molar concentration of catalytic polypeptides (xn)cat, the frequency λ of the catalysed reactions, the value λt, and the concentration of products u(t)/z0 at t = 0.5 Gyr given by equation (12)
For most values of n, the proper time for reaction (λ−1) greatly exceeds the age of the universe (τ u ), indicating that the catalysed process would be much slower than the available time for chemical evolution. Imposing the constraint λ−1 = τ u would imply in all cases values of k 2/k M in excess of the limit 1010 M−1 s−1 for diffusion-controlled reactions. The data in Table 2 also show that the value of f (the number of molecules of catalytic polypeptides of a given length) sharply decreases with growing n, but the limit value f = 1 is never reached. The number of catalytic polypeptides is quite large, of the order p αn , making the number of chemical species likely limited by the number of substrates with initial concentration z 0.
For the sake of completeness, we also consider the case of a discontinued source of amino acids. In this case, an effective polypeptide from the point of view of its catalytic properties could not be re-formed in the next generation of polypeptides, its mean life being only ω−1 = (1−ζ)/ω h ≈ 10 yr. This also limits the number of catalytic processes per unit time to fω. Consequently, the concentration of the catalytic species would follow the equation
$$(\dot x_n )_{{\rm cat}} = - {\rm \omega (}x_n {\rm )}_{{\rm cat}} , $$
and the dynamics of the substrate the equation
$$\dot z = s - {\rm \lambda} \,{\rm e}^{ - {\rm \omega} t} z,$$
with solution
$$\displaystyle{z \over {z_0}} = {\rm e}^{ - ({\rm \lambda} /{\rm \omega )(}1 - {\rm e}^{ - {\rm \omega} t} {\rm )}} - \displaystyle{s \over {z_0 {\rm \omega}}} {\rm e}^{({\rm \lambda} /{\rm \omega )(e}^{ - {\rm \omega} t} {\rm )}} \int_{a_1} ^{a_2} {\displaystyle{{{\rm d\xi}} \over {{\rm ln\xi}}}},$$
where a
1 = e−λ/ω and
$a_2 = {\rm e}^{ - ({\rm \lambda} /{\rm \omega )(e}^{ - {\rm \omega} t} {\rm )}} $
. The difference between equations (11) and (15) gives the concentration of the reaction product u
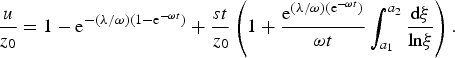$$\displaystyle{u \over {z_0}} = 1 - {\rm e}^{ - ({\rm \lambda} /{\rm \omega )(}1 - {\rm e}^{ - {\rm \omega} t} {\rm )}} + \displaystyle{{st} \over {z_0}} \left( {1 + \displaystyle{{{\rm e}^{({\rm \lambda} /{\rm \omega )(e}^{ - {\rm \omega} t} {\rm )}}} \over {{\rm \omega} t}}\int_{a_1} ^{a_2} {\displaystyle{{{\rm d\xi}} \over {{\rm ln\xi}}}}} \right).$$
Its asymptotic behaviour for ωt ≫ 1 is u ∞ /z 0 = 1 − e− λ/ω. An approximate expression for equation (16) in terms of elementary functions may be obtained for λ/ω ≪ 1. In this case ξ ≈ 1 and the logarithmic integral in equation (16) may be written as
$$\int_{a_1} ^{a_2} {\displaystyle{{{\rm d\xi}} \over {{\rm ln\xi}}}} \cong \int_{a_1} ^{a_2} {\displaystyle{{{\rm d\xi}} \over {{\rm \xi} - 1}} = {\rm ln}\displaystyle{{a_2 - 1} \over {a_1 - 1}} \cong - {\rm \omega} t}, $$
obtaining
$$\displaystyle{u \over {z_0}} = 1 - {\rm e}^{ - ({\rm \lambda} /{\rm \omega )(}1 - {\rm e}^{ - {\rm \omega} t} {\rm )}} + \displaystyle{{st} \over {z_0}} (1 - {\rm e}^{({\rm \lambda} /{\rm \omega )(e}^{ - {\rm \omega} t} {\rm )}} ).$$
In all cases under investigation λ/ω ≪ 1, and equation (18) may be approximated with the expression
$$\displaystyle{u \over {z_0}} \cong \displaystyle{{\rm \lambda} \over {\rm \omega}} \left[ {1 - \left( {1 + \displaystyle{{st} \over {z_0}}} \right){\rm e}^{ - {\rm \omega} t}} \right],$$
with the asymptotic limit u ∞ /z 0 = λ/ω. Since we have now excluded the survival of a catalytic species for more than one generation of polypeptides, if we want to attain catalysis and a significant build-up of u, we must equate the mean life for the transformation of a substrate (λ−1) to the mean life of the catalytic species (ω−1), obtaining
$$(1 - {\rm \zeta} )^3 {\rm \zeta} ^{n - 3} = \displaystyle{{{\rm \omega} _h^2 p^{{\rm \alpha} n}} \over {sk_2 /k_M}}. $$
Equation (20) does not have solutions for the values of the parameters used up to this point, and we can find solutions only by considerably raising the value of either the amino acid source or the rate coefficient k
2/k
M
(or both) by a combined factor of 9 × 105. A plot of equation (20) and its solution
$\bar \zeta $
, obtained with the unrealistic value s = 2.55 × 10
−
14 M s−1, is shown in Fig. 5. Higher values of n, p, α or lower values of s do not afford solutions to equation (20), that is, the half-life of transformation of a substrate would be longer than the mean life of the catalytic species (x
n
)
cat
, lowering the efficiency of the production of new chemical species. With λ = ω, a
1 = e
−1, a
2 = e−e−ωt
, and the asymptotic condition ωt ≫ 1, the concentration of the product is u
∞
/z
0 = 1−e−
1 ≅ 0.63.
Fig. 5. Plot of equation (20), the expression for optimal condition (λ = ω) for the formation of products after turning off the amino acid source, versus the catalytic efficiency ζ for n = 60, p = 10, α = 0.1, z
0 = 2.4 × 10
−
9 M, and k
2/k
M
= 1.0 × 103 M−1 s−1. The solution is
$\bar \zeta = 0.9717$
, the initial source s = 2.55 × 10
−
14 M s−1, the molar concentration of catalytic polypeptides (x
n
)
cat
= 6.30 × 10
−
14 M, the frequency of formation of the polypeptides (which equals the frequency λ of the catalysed reactions) ω = 0.0704 yr−1, and the required ratio between the polymerization rate coefficient to the hydrolysis rate coefficient η/η
h
= 5.59 × 109.
Discussion
The present-day amino acid flux on Earth was estimated to be around 3.0 × 107 kg yr−1 (Matrajt et al. Reference Matrajt, Pizzarello, Taylor and Brownlee2004) with an amino acid content of 869 nmol g−1. These figures translate into an amino acid source s of 5.90 × 10 − 25 M s−1 for the present mass of the ocean (1.4 × 1021 kg). To account for the increased bombardment rate based on the lunar cratering record of 3.8 to 4.5 Gyr ago (Hartmann et al. Reference Hartmann, Ryder, Dones and Grinspoon2000), we multiply by a factor of 102 to 107 to obtain 5.90 × 10 − 23<s<5.90 × 10 − 18 M s−1. A somewhat narrower interval for s is given by the estimate of Chyba et al. (Reference Chyba, Thomas, Brookshaw and Sagan1990) of 108 − 1010 kg yr−1 of organic carbon with a 3% content of amino acids, that translates into a source of 2.83 × 10 − 21<s< 2.83 × 10 − 19 M s−1 of glycine. We may also mention the flux of organic carbon in IDPs of 3.6 × 1010 kg yr−1 that survived re-entry on the early Earth proposed by Wilson (Reference Wilson2009). Assuming again a 3% content of amino acids, we obtain for glycine s = 1.02 × 10 − 18 M s−1. It was shown (Canepa Reference Canepa2013) that, besides the intensity of the source, the length of the spontaneously formed polypeptides depends on how many types of monomeric units are involved in the formation of the chain, the fraction α of constrained amino acids, the intensity of the source s, and the catalytic efficiency for their formation ζ. Brack (Reference Brack1993) reviewed the chemical species with the ability to promote the condensation of amino acid monomers (i.e. increase ζ) and discussed the conformational and chemical properties of the resulting polypeptides according to both the nature of the side chain in the constituent amino acids and their chirality. Among the condensing agents are carbodiimides, clays, surfactant aggregates, polyphosphates, and N-carboxyanhydrides.
In conclusion, significant amounts of products might have been synthesized in a prebiotic environment containing spontaneously formed polypeptides with catalytic properties only in the assumption that the ratio between the rate coefficients for the formation of the peptide bond and its hydrolysis exceeds ~1015, and the fraction of conserved amino acid residues in the catalyst does not exceed 0.1. In this case, if the catalytic properties emerge for n ≈ 60, the concentration of products exceeds z 0 for k 2/k M = 1.0 × 103 M−1 s−1 and n ≤ 100. A final consideration is due with regard to the parameter k 2/k M , which in present day enzymes assumes a wide range of values. We have no means to guess how prebiotic polypeptides would position within that range, and we selected a value for the purpose of calculations that would be considered rather low for the evolved enzymes. However, if the prebiotic species would exhibit a value of k 2/k M significantly different from 1.0 × 103 M−1 s−1, λ would be correspondingly altered, with consequent dramatic changes in the concentrations u of the products of catalysis given in Table 2. These are the products of transformation of a generic substrate z by a catalytic polypeptide which was spontaneously formed from its constituent amino acids in an aqueous environment, itself endowed with the catalytic ability to promote the formation of the peptide bond summarized by the parameter ζ. One should bear in mind that, while the dependence of λ from k 2/k M is linear, the dependence from ζ is not, according to equation (7). The formation of products of catalysis with concentrations at least of the same order as the starting substrates seems thus to be unlikely under the conditions assumed in this work. A high ability of the aqueous environment to form polypeptides (ζ) and a substantial catalytic power of polypeptides with limited length (k 2/k M ) are both necessary to afford significant amounts of products. The change to this picture caused by the presence of autocatalytic species, i.e. polypeptides catalysing the formation of the peptide bond could be the subject of forthcoming investigations.
Conclusions
-
1. The steady-state concentration of polypeptides of length n, formed in the primordial ocean upon an incoming flux of monomeric amino acids in the presence of catalysis with efficiency ζ is x n = (s/ω h )(1 − ζ)2ζ n− 3.
-
2. Using about one half of the present-day values for the average length n of the catalytic polypeptides, the size of the amino acid set p, the fraction α of constrained amino acid residues within a polypeptide, the value of the catalytic efficiency ζ m maximizing the spontaneous synthesis of the polypeptides, and the value k 2/k M = 1.0 × 103 M−1 s−1 for the catalytic ability to promote chemical transformations, we obtain ω−1 ≈10 yr and λ−1 ≈109 − 1020 yr for the polypeptide mean life and the substrate mean life, respectively. The ratio of the rate coefficient for the catalysed formation of the polypeptides to the corresponding rate coefficient for its hydrolysis exhibits the typical values of evolved enzymes.
-
3. For polypeptides with αn constrained amino acids in specific locations along the chain, the catalysed formation of products u enriching the chemical diversity of the prebiotic ocean gives concentrations of the order u(t)/z 0 ≅ 10 − 6−105 after 0.5 Gyr.
-
4. The value of the amino acid source s found by imposing the condition λ = ω would be questionably high. Within this constraint, both the catalytic species and its substrates exhibit an average life ≈102 yr, with the asymptotic concentration of the products being u ∞ /z 0 = 0.63.
