Introduction
Since the discovery of the first exoplanets (Latham et al. Reference Latham, Stefanik, Mazeh, Mayor and Burki1989, Wolszczan & Frail Reference Wolszczan and Frail1992, Mayor & Queloz Reference Mayor and Queloz1995), this field has experienced a series of major steps: discovery of the first transiting planets, spectroscopic investigation of their atmosphere, discovery of circumbinary planets, planets detected by direct imaging, etc. Here we anticipate a new step, the probable future discovery of exo-moons and their investigation. Since there are many moons in the Solar System, and six large moons (The Moon, Io, Europa, Ganymede, Callisto and Titan), it would be surprising that some of the more than 1800 exoplanets discovered todayFootnote 1 do not have companions. After the first paper on the detection of exo-moons (Sartoretti & Schneider Reference Sartoretti and Schneider1999), specific searches dedicated to these objects have recently started (Kipping et al. Reference Kipping, Bakos, Buchhave, Nesvorny and Schmitt2012). In this paper, we investigate new detection approaches and some applications to the characterization of planetary systems. We first review the a priori constraints in the framework of formation models. Of course these a priori constraints will have to be tested by future observations. We then review present and future possible methods for the detection and characterization of exo-moons.
This paper is programmatic in the sense that some aspects of exo-moons will not be observable before some time. But, after all, the detection of molecules by transits was also considered as futuristic when it was proposed (Schneider Reference Schneider, Tran Thanh Van, Tran Thanh Van, Mounoulou, Schneider and McKay1991).
Why exo-moons
By ‘exo-moon’ we define an object of size larger than few kilometres (not to be mistaken with ring particles) in the orbit around an exoplanet. Without surprise the investigation of exo-moons is interesting from two perspectives. First, it is a test of theories of formation of planetary systems. It is also well known since the paper by Williams et al. (Reference Williams, Kasting and Wade1997) that they offer, in addition to telluric exoplanets in the habitable zone (HZ) of their parent star, other types of abodes for life. Habitable exo-moons are the moons in orbit around planets lying in the circumstellar HZ. Note nevertheless that the habitability of an exo-moon of a large mass planet in the HZ may depend on its history (Heller & Barnes Reference Heller and Barnes2014; Reynolds et al. Reference Reynolds, McKay and Kasting1987). But there is an additional type of potentially habitable exo-moons: moons around cold giant planets, heated by the tidal effects of their primary (Scharf Reference Scharf2006). To be habitable an exo-moon has to retain its atmosphere and therefore to have a size of at least 1000 km (unless life appears in a subsurface ocean) (Huang Reference Huang1960). In addition to these two interests for exo-moons, there are two others. If a planet has a large companion, the latter has an impact on its effective characteristics, namely its mass (inferred from radial velocity or astrometric measurements) and its spectrum. If one mistakes a planet–moon system with a single planet, the planet mass is overestimated and the atmospheric composition (and temperature in the near-infrared) is incorrect (see also Williams & Knacke Reference Williams and Knacke2004). This aspect has an important consequence for future searches for biosignatures. Indeed, it is often claimed that the simultaneous detection of water (H2O), oxygen (O2)/ozone, methane (CH4) and carbon dioxide on an exoplanet would constitute a serious hint for a biological activity on the planet. But if in reality what is observed is a moon–planet system with some gases on one component of the system and the others on the other component, the simultaneity argument disappears. The possibility of this configuration is strengthened by the possibility of abiotic oxygen-dominated atmospheres on terrestrial HZ planets (Wordsworth & Pierrehumbert Reference Wordsworth and Pierrehumbert2014). If such a planet or moon lies in a moon–planet system with water and/or methane in the other component, the biological interpretation of the simultaneous presence of O2, H2O and CH4 could be misleading. One can also make use of exo-moons for the measurement of the some planet characteristics, as will be shown in the section ‘Application of the detection of exo-moons to planet characteristics’.
Another argument for the importance of a moon for planet habitability has been put forward by Laskar et al. (Reference Laskar, Joutel and Robutel1993). The presence of a (sufficiently close and/or massive) moon stabilizes the planet axis in a multiplanet system (see also Sasaki & Barnes Reference Sasaki and Barnes2014). This is interesting from a geophysical point of view and we investigate in the section ‘Application of the detection of exo-moons to planet characteristics’ how to use the moon to determine the planet axis. Nevertheless, if a chaotic planet axis may indeed affect in some way the planet habitability, we do not know to what extent. If a change in the planet axis modifies the habitable regions of the planet in 1 Myr, life may have time to migrate to adapt itself to the planet axis reversal (see also the discussion by Li & Batygin Reference Li and Batygin2014). It will be interesting, in some decades when the appropriate space missions will be launched, to see if the presence of biosignatures on planets are correlated with the presence of a moon.
Finally, as pointed out by Ward & Brownlee (Reference Ward and Brownlee2000), the presence of a large moon is likely to affect other planet characteristics, such as ocean mixing, plate tectonics and tides.
Theories of exo-moon formation, a priori characteristics and some questions
While the main purpose of the present paper is the benefits and detectability of exo-moon properties, we briefly discuss the a priori constraints on exo-moon parameters. These a priori constraints should be kept in mind, although they should not constrain searches for exo-moons since the experience of the past 20 years in exoplanetary science shows that a priori theoretical prejudices (such as the planetary orbit size and eccentricity) can be contradicted by observations.
In the absence of already detected exo-moons, our Solar System is the only source of data for satellite formation and orbital evolution (Rosenblatt & Charnoz Reference Rosenblatt and Charnoz2012; Sasaki et al. Reference Sasaki, Stewart and Ida2010). It is common to distinguish between the so-called regular and irregular satellites. The former class characterizes moons that are prograde and evolve close to their primary (typically few to few tens of their planet's radius) with small inclination and eccentricity. On the contrary, the irregular satellites evolved very far from their primary, prograde or retrograde, with any eccentricity and inclination (see Fig. 1). The clear distinction between such two classes is not a mere coincidence, but most probably the result of a different formation environment. While regular moons are thought to be formed by accretion in a circumplanetary disc (Canup & Ward Reference Canup and Ward2002, Reference Canup and Ward2006), irregular satellites must have been captured objects or possibly formed by moon–moon scattering (Perets & Payne Reference Perets and Payne2014). Three different mechanisms have been invoked for captures (see Jewitt & Haghighipour Reference Jewitt and Haghighipour2007 and references therein). Two of them (pull-down capture and gas-drag capture) are taking place during the formation of the planet at the early stage of the Solar System. On the other hand, a third mechanism suggests that captures could occurred during the Late Heavy Bombardment about 500–800 Myr after the formation of our Solar System (Gomes et al. Reference Gomes, Levison, Tsiganis and Morbidelli2005; Morbidelli et al. Reference Morbidelli, Levison, Tsiganis and Gomes2005; Tsiganis et al. Reference Tsiganis, Gomes, Morbidelli and Levison2005).
Fig. 1. The different families of satellites of Jupiter (Copyright IMCCE – Paris Observatory).
Even though most irregular satellites have a typical size of few to several tens of kilometres, capture of large moons are not excluded with a crucial example in Neptune's satellite Triton (Agnor & Hamilton Reference Agnor and Hamilton2006). As a consequence, capture mechanisms may offer large exo-moons with any inclination with respect to the primary's equator. On the other hand, and despite capture process, significant eccentricity for large moons may be prevented due to tidal dissipation within the satellites. Indeed, the tidal torque acting on a large satellite will tend the rotation of the moon to be eventually synchronous to its mean motion (a state called 1 : 1 spin–orbit resonance). Once such state is reached (which is the case of all large moons in our Solar System including Triton), orbital energy will go on decreasing because of tidal dissipation, but this time with negligible exchange of angular momentum. As a consequence, eccentricity will also decrease, unless orbital resonances with another moon exists to counteract eccentricity damping (like the pair Enceladus and Dione in the Saturn System, or the Galilean satellites Io, Europa and Ganymede involved in the so-called Laplace resonance). Hence, it is not surprising that Triton's eccentricity is today almost zero. In fact, detecting a single exo-moon of large size close to a planet with high eccentricity sounds rather unlikely, a priori.
Regular moons are believed to be formed in the vicinity of their primary during its accretion process in the planet's subnebulae (Canup & Ward Reference Canup and Ward2002). A typical system is the four large Galilean moons. For long it has been believed that the main moons of Saturn formed similarly 4.5 Gyr ago. However, recent models suggest that at least some of the mid-sized moons (with typical radius of few to several hundreds of kilometres) could have formed much later in the history of our Solar System (Charnoz et al. Reference Charnoz, Crida, Castillo-Rogez, Lainey, Dones, Karatekin, Tobie, Mathis, Le Poncin-Lafitte and Salmon2011), possibly after disruption of a large moon (Canup Reference Canup2010). Such process could also apply to some of the main Uranian moons (Crida & Charnoz Reference Crida and Charnoz2012), but not for the Galilean System. All in all, moons lying not far to the equatorial plane of their primary are expected in this case. Multiplicity of moons allow for possible significant eccentricities thanks to orbital resonances and possible inclinations of few degrees.
A population of small moons evolving close to their primary can be seen on the four giant planets of our Solar System. While the Neptunian moon Proteus can reach a mean radius of about 210 km, most of the inner moons of these four planets are small with radii typically of few tens of kilometres. Their small size made them sensitive to destructive impacts. In particular, computation of their lifetime suggests few hundreds of millions of years for some of the Uranian and Neptunian moons only (Colwell et al. Reference Colwell, Esposito and Bundy2000). As a consequence these bodies are believed to be remnants of more massive moons, first shattered into rings and then re-accreted from rings evolving beyond the Roche limit. A complete cycle between ring and moon formation is likely to be at process in these systems. In the case of Saturn, inner moon formation at the outer edge of the rings may even well be sustained up to now (Charnoz et al. Reference Charnoz, Salomon and Crida2010).
While the formation process for regular moons suggests small inclinations, planets may suffer strong obliquity variations due to torque exerted from other planets and their parent star. In the Solar System, Mars has been found to suffer strong chaotic behaviour with variation of obliquity up to 60° (Laskar et al. Reference Laskar, Joutel and Robutel1993; Touma & Wisdom Reference Touma and Wisdom1993). Nevertheless, when the moons are not too far (i.e. when they are more sensitive to the oblateness of their primary J 2 than the star gravitational pull) a locking mechanism first studied for low inclinations by (Goldreich Reference Goldreich1965) and more recently for large inclinations by Gurfil et al. (Reference Gurfil, Lainey and Efroimsky2007) forces the moons to stay close to the equatorial plane of their primary even under large variations of the primary's obliquity. As a consequence, exo-moons with large inclinations will remain a clue for past orbital evolution and formation.
With these a priori considerations in mind, one may ask if different configurations may not be present in other planetary systems: Canup (Reference Canup2010) suggests that the mass ratio between the circumplanetary material and the planet itself is universally around a few 10−4. Could it result in a single exo-moon of about four times the Ganymede mass? If it holds for a 20 Jupiter mass exoplanet, could it lead to a 20 Ganymede mass exo-moon?
It is an empirical fact that many astronomical objects can be binary: binary galaxies, stars, brown dwarfs, asteroids and other small objects. Why not ‘binary planets’? They have first been suggested by Cabrera & Schneider (Reference Cabrera and Schneider2007) and investigated with quantitative simulations first by Podsiadlowski et al. (Reference Podsiadlowski, Rappaport, Fregeau and Mardling2010) and later on by Ochiai et al. (Reference Ochiai, Nagasawa and Ida2014). The latter authors claim that around 15% of migrated planets in the 1–10 AU range should be binary. Given that they are easily detectable by transit and microlensing, this fraction should be soon compared with observations. They would be identical with planet–moon systems, where the moon size and mass have the same order of magnitude than for those of the parent planet. Such a configuration exists for the Pluto–Charon system and, given the diversity and surprises experienced up to now in exoplanetology, we suggest that such binarity could exist for giant planets (i.e. for instance binary Jupiters).
The investigation of exo-moons may also help to clarify circumplanetary dust suggested to result from the collision of exo-moon swarms (Kennedy & Wyatt Reference Kennedy and Wyatt2011; Wyatt et al. Reference Wyatt, Booth, Payne and Churcher2010).
Detection methods of exo-moons
Before we develop new methods to characterize exo-moons, for completeness we briefly outline some of their methods of detection and present findings.
Transits
Planet transit time variation (TTV)
The exo-moon is indirectly detected, and its mass and circumplanetary orbit constrained, by the wobble of the parent planet around the moon–planet barycenter (TTV Sartoretti & Schneider (Reference Sartoretti and Schneider1999) and transit duration variation (TDV Kipping Reference Kipping2011)). This approach requires several to many transits. Indeed, it makes use of the relation between deviation TTV of individual transit at a time t (relative to an arbitrary origin) and the moon mass M moon and circumplanetary semi-major axis a moon according to the formula (assuming circular planetary and exo-lunar orbits):
$${\rm TTV}(t) = (a_{{\rm moon}} {\rm /}V_{{\rm pl}} {\rm )cos(2\pi} t{\rm /}P_{{\rm moon}} {\rm )(}M_{{\rm moon}} {\rm /}M_{{\rm pl}} {\rm ),}$$where V pl is the planet velocity and P moon the moon circumplanetary orbital period. The exo-lunar parameters can only be extracted from a ‘TTV curve’ with at least a few data points. See Kipping (Reference Kipping2011) Forgan & Kipping (Reference Kipping2011) for a detailed discussion.
Moon transit
The moon can be detected, its radius measured and its orbit constrained by the detection of the moon transit itself (Sartoretti & Schneider Reference Sartoretti and Schneider1999). This approach requires only one or few transits, depending on the signal to noise ratio. Indeed, if the moon itself is transiting it adds the stellar flux drop due to the planet its own transit, with a different depth (ΔF/F)moon for a stellar flux F, duration D moon and time of transit T moon.
The depth ΔF moon, gives the moon size, D moon gives the inclination of the moon orbit, with an impact parameter b, and T moon gives the sky projection of the moon–planet separation at the time of transit according to the formulae
$$({\rm \Delta} F{\rm /}F)_{{\rm moon}} {\rm = (}R_{{\rm moon}} {\rm /}R_{{\rm st}} {\rm )}^2, $$
$$D_{{\rm moon}} {\rm = (}P_{{\rm pl}} {\rm /\pi )}\sqrt {R_{{\rm st}}^2 - b_{{\rm moon}}^2 {\rm /}a_{{\rm pl}}}. $$To detect individual exo-lunar transits at a five level, the signal to noise ratio for the stellar photometry must be better than (1/5)(ΔF/F)moon during one transit.
Moon transit spectroscopy
When the moon transit is detectable with a sufficient signal-to-noise ratio, they can be used to detect the moon atmosphere by spectroscopic observations of the transit and constrain its properties (Kipping et al. Reference Kipping, Fossey, Campanella, Schneider, Tinetti, Vincent Coudé du, Gelino and Ribas2010).
Moon-induced Rossiter effect
Suppose a transiting planet orbiting a star clock-wise compared to the stellar rotation, in the stellar equatorial plane. During the first half of the transit the planet hides parts of the stellar surface going towards the observer and therefore blue-shifted. There is thus a lack of stellar flux in the blue wings of the stellar spectral line. It results a net apparent redshift of the star. Similarly in the second half of the transit there is an apparent blueshift of the star. The global spectral shift variation is symmetric in time. This phenomenon is known as the Rossiter–McLaughlin effect. If the planet orbit is not in the star equatorial plane the spectral shift curve is not symmetric in time and the asymmetry is related to the planet orbit inclination relative to the stellar rotation. This non inclination has been observed for several transiting hot Jupiters (Triaud et al. Reference Triaud, Queloz and Bouchy2009). Similarly the exo-moon can induce an effective apparent radial velocity variation of the parent star during the transit (Simon et al. Reference Simon, Szabo, SzatMary and Kiss2010) and constrain the exo-lunar orbital plane.
Transits: present findings
Up to now (March 2014) no exo-moon has been detected. Space facilities have frequently been used to rule out the presence of moons around extrasolar planets (Brown et al. Reference Brown, Charbonneau, Gilliland, Noyes and Burrows2001; Pont et al. Reference Pont, Gilliland, Moutou, Charbonneau, Bouchy, Brown, Mayor, Queloz, Santos and Udry2007; Deeg et al. Reference Deeg., Moutou, Erikson, Csizmadia, Tingley, Barge, Bruntt, Havel, Aigrain and Almenara2010; Szabo et al. Reference Simon, Szabo, SzatMary and Kiss2012). Kipping et al. (Reference Kipping, Bakos, Buchhave, Nesvorny and Schmitt2012, Reference Kipping, Forgan, Hartman, Nesvorny, Bakos, Schmitt and Buchhave2013b) have started a systematic search for moons around extrasolar planets taking the advantage of the simultaneous change in several quantities including the transit timing and transit duration (TD) changes produced by the presence of satellites (Kipping Reference Kipping2009a, Reference Kippingb). However, until now only negative results have been reported. In a first systematic search, Kipping et al. (Reference Kipping, Nesvorny, Buchhave, Hartman, Bakos and Schmitt2014) have studied eight planetary candidates from the Kepler mission (Batalha et al. Reference Batalha, Rowe, Bryson, Barclay, Burke, Caldwell, Christiansen, Mullaly, Thompson and Brown2013) with an automatic algorithm that identifies viable satellite hosts. They have set an upper limit of 4% to the mass ratio between the planet and any possible satellite for several super-Earth candidates (as a reference, the mass-ratio of the Earth–moon system 1%). In a second paper, Kipping et al. (Reference Kipping, Forgan, Hartman, Nesvorny, Bakos, Schmitt and Buchhave2013a) studied the case of Kepler-22b (Borucki et al. Reference Borucki, Koch, Batalha, Bryson, Rowe, Fressin, Torres, Caldwell, Christensen-Dalsgaard and Cochran2012), a 2.4 Earth-radius planet, excluding the existence of moons with masses larger than half the mass of the Earth, although the photometric analysis of the light curve would have allowed the detection of satellites with the size of the Earth's Moon.
It results that no binary giant planet (like putative binary Jupiters) has been discovered by transit today. This negative result may be explained by the difficulty to form binary planets by capture during migration (Gong et al. Reference Gong, Zhou, Xie and Wu2013; Williams Reference Williams2013). It nevertheless leaves open the possibility to have binary telluric planets.
Microlensing
The detection of exo-moons by gravitational amplification of a passing background star is similar to the detection of exoplanets by the same method (Han & Han Reference Han and Han2002). When the image of a distant background star passes close to a planetary companion of a star, the star–planet system makes a temporary amplification of the background star flux. The same approach can be used to detect exo-moons. The amplification factor and its duration provide (poor) constrains on the exo-moon mass and on the moon–planet separation projected onto the sky plane at the time of amplification. An exo-moon candidate may have been detected by microlensing in the event MOA-2011-BLG-262 (Skowron et al. Reference Skowron, Udalski, Szymanski, Kubiak, Pietrzynski, Soszynski, Poleski, Ulacsyk, Pietrukowicz and Kozlowski2013).
Direct imaging
Of course the most obvious way to detect exo-moons by direct imaging would be to separate them from their parent planet in a high angular resolution image. But it requires large interferometers with baselines of at least 400 m combined with a high contrast device Schneider et al. (Reference Schneider, Léger and Fridlund2010).
A more indirect method, feasible with future ground-based 30 m-class or space-based 3 m-class telescopes, is to make use of moon–planet ‘phenomena’ (Fig. 1). The phenomena are the mutual influence of the planet and the moon on their photometric properties. They are of four types:
a. the shadow of the moon projected on the illuminated region of the planet makes, during its passage, a temporary flux drop of the planet brightness;
b. the moon transiting the illuminated part of the planet makes similarly a flux drop of the planet;
c. the disappearance of the moon in the planet umbra suppresses completely its contribution to the planet+moon brightness; and
d. the disappearance of the moon behind the planet also suppresses its contribution to the planet+moon brightness.
To these four phenomena already described in Cabrera & Schneider (Reference Cabrera and Schneider2007) we add a fifth phenomenon: the moon shadow on the planet can also take place during the moon transit (Phase 2 in Fig. 1). The geometric probability p=R pl/a moon of these phenomena is not negligible. For our Jupiter and Saturn it is typically 10% and up to 17% for Io.
Moons can also be detected by their own thermal emission when they are tidally heated by their parent planet (Peters & Turner Reference Peters and Turner2013).
Planet velocimetry and astrometry
A moon induces a wobble on the parent planet it is orbiting. This wobble can be detected by radial velocity variations (Snellen et al. Reference Snellen, de Kok, de Mooij and Albrecht2010) or astrometric measurements of the planet. With a 100 m extremely large telescope (ELT) an Earth-mass moon on a Io-type orbit around a 1 Jupiter mass planet could be detected in a 600 h campaign with a R=10 000 spectrograph (Ardeberg Reference Ardeberg and Hook2005a). Unfortunately the European ELT has been downsized from 100 to 40 m, leaving presently to no hope for this measurement. An Earth-mass moon lying on a Callisto-like orbit around a 1 Jupiter-mass orbit at 10 pc would induce a wobble of the planet of 0.7 milli-arcsec (Ardeberg Reference Ardeberg and Hook2005b). This value is to be compared with the accuracy 
$(1/\sqrt N )({\rm \lambda} /D)$ of the measured planet position with N photons at a wavelength λ with a telescope of diameter D. This accuracy 0.2 milli-arcsec is for a planet detected with 1000 photons at a wavelength 1 μm with a 40 m telescope (we leave aside problems of thermal and mechanical stability of the focal plane).
Applications to the characterization of exo-moons
Let us develop the principles of methods to apply these detection approaches to the determination of some parameters of exo-moons.
Moon–star transits
Here we assume that the moon transit is directly seen in the light curve (note that it is possible that the moon is transiting and the planet not). When a moon transiting the parent star has the same impact parameter (relative to the star centre) than its parent planet, the moon and planet TD are the same. But generally, the planet and moon impact parameters are different, due to the planet or moon orbital inclinations, or both. It therefore leads to different TD for the moon and the planet, giving a measurement of the relative moon–planet inclination, if the phase of the moon on its orbit is known (see the discussion of the ‘TDV–TIP effect’ in Kipping Reference Kipping2011).
When transiting exoplanets disappear behind their parent star, they can make a detectable secondary transit if they are sufficiently close to their parent star to have a significant reflected or thermal flux. It is not clear if such close-in planet can have exo-moons. In principle, the orbital stability criterion a moon<0.3a planet(M planet/3M star)1/3 can be fulfilled down to a planet=0.05 AU for a 1 M Jup mass planet. In that case, similarly to exoplanets, when the exo-moon passes behind the parent star the depth of this secondary transit in the infrared constrains its thermal emission, if the moon size is determined from primary transits in visible light. The timing of this secondary transit, compared with the timing of the parent star secondary transit, also constrains the eccentricity of the moon orbit around its parent planet, in the same way that the timing of the planet secondary transit constrains (where e and ω are the orbit eccentricity and periapsis argument).
Moon orbital elements from moon–planet transits in direct imaging
The comparison between (optical) reflected light and (infrared) thermal emission of moon–planet phenomena in direct imaging provides constrains on the exo-lunar and planetary thermal properties. When disappearing in the planet umbra, the exo-moon cools down and its infrared thermal radiation drops down to some extent. The speed and amount of thermal radiation loss provide information on the exo-moon thermal inertia and thus on the composition of its surface. The same argument holds for the exo-moon shadow on the planet which provides constrains on the planet surface thermal inertia (if the signal to noise ratio is sufficient). The mutual phenomena (planet–moon transits and shadows) can be used for some characterization of the moon orbit around the planet.
Moon orbit inclination
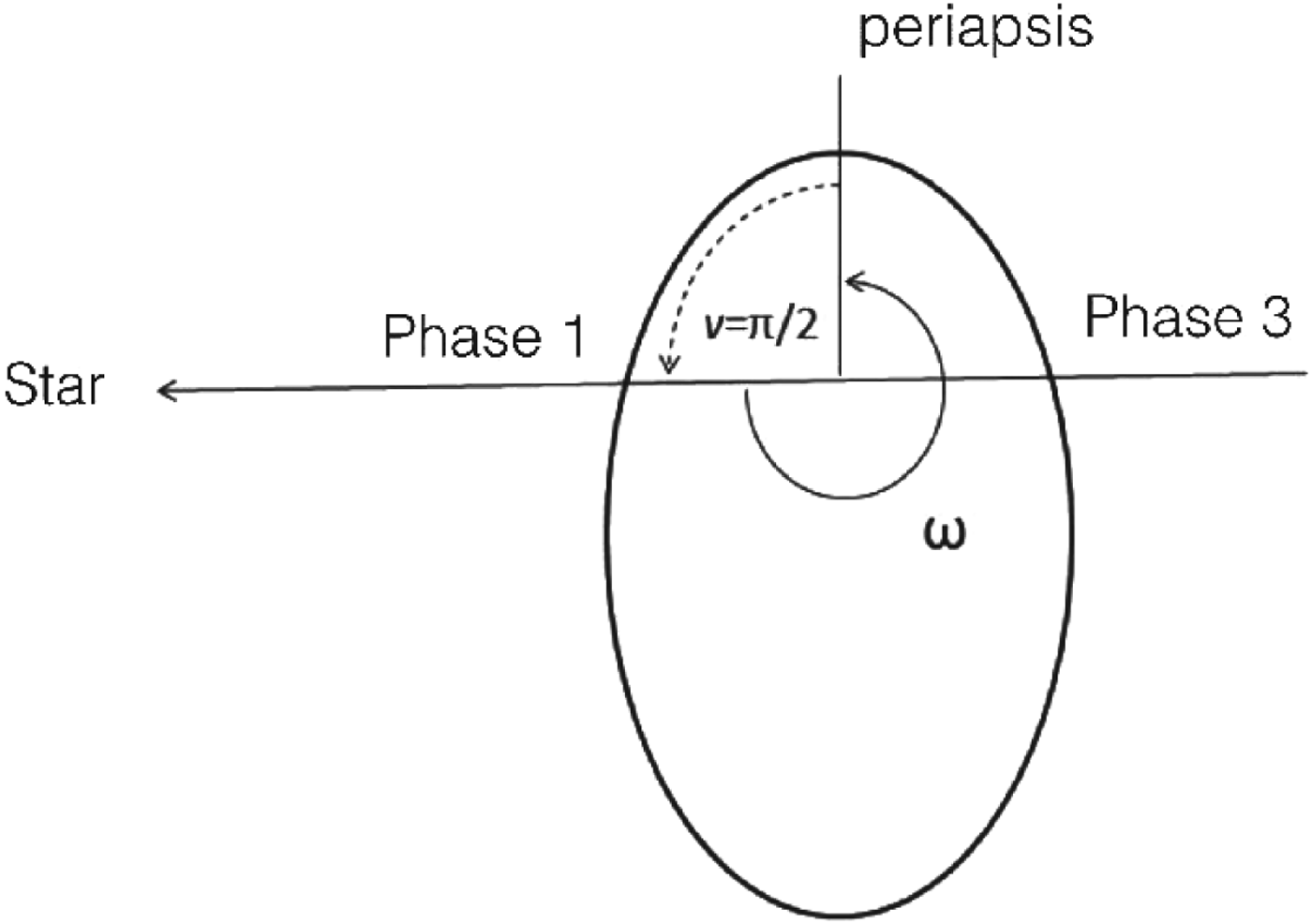
As shown in Figures 4 to 7 Cabrera and Schneider (Reference Cabrera and Schneider2007), the inclination of the moon orbit in the sky plane can be derived from the relative durations of Phases 1–5 of the moon–planet phenomena (see fig 2).
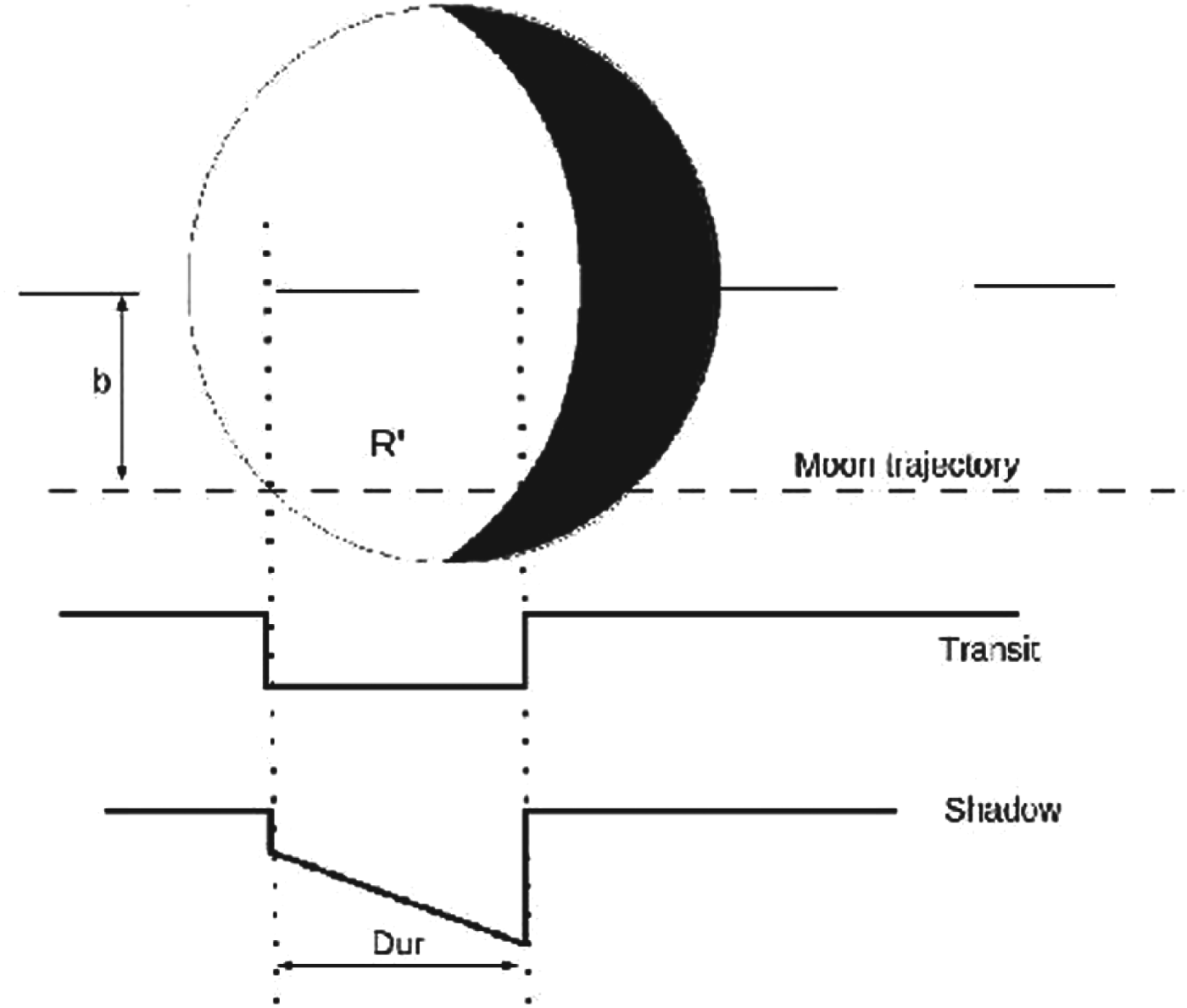
Fig. 2. The duration Dur for moon transits and the shadow of the moon on the planet in direct imaging. The duration depends on two parameters: the moon or shadow impact parameter b and the phase of the parent star planet on its trajectory around the parent star. The latter determines the fraction of the planet illuminated by the parent star.
Semi-major axis a moon
For moons transiting their parent planets, the semi-major axis a moon can be inferred from the TD Durmoon by the relation (assuming a non-eccentric orbits)
$$a_{{\rm moon}} = \displaystyle{{R_{{\rm pl}}^{\rm \prime}} \over {\rm \pi}} \displaystyle{{P_{{\rm moon}}} \over {{\rm Dur}_{{\rm moon}}}} $$For eccentric orbits see our Appendix 1 and Kipping et al. (Reference Kipping, Bakos, Buchhave, Nesvorny and Schmitt2012).
In this relation, 
${R}_{{\rm pl}}^{\rm \prime} $ designates the length of the transit segment of the illuminated part of the planet (Fig. 3). It is inferred from the planet radius and the moon orbital inclination around the planet. The latter can be deduced from the ratio of the moon–planet phenomenon to the moon orbital period (Cabrera & Schneider Reference Cabrera and Schneider2007).
Fig. 3. Top: The five phases of the moon–planet phenomena. Bottom: Their impact on the light curve of the global moon+planet flux in direct imaging.
Even if the moon is not transiting its planet it generally projects a shadow on the illuminated part of the planet, provided the moon orbital plane around the planet is close to the planet orbital plane around the star, regardless the inclination of the latter orbit. Then the same argument applies when the TD is replaced by the shadow phenomenon duration.
Eccentricity and longitude of periapsis
For circular orbits the times of the events 3, 4 and 5 (Fig. 1) are given by P moon/4, P moon/2 and 3P moon/4. When the orbit is eccentric, there is a difference with respect to these values. The eccentricity and the longitude of periapsis can then be obtained by fitting these differences with the Keplerian motion of the moon. We give in Appendix 1 the equations relating these differences to the eccentricity e.
Application of the detection of exo-moons to planet characteristics
Let us finally give the principles of the application of the detection approaches to the characterization of the parent planet.
Planet mass
The planet mass determination has been investigated in Kipping et al. (Reference Kipping, Fossey, Campanella, Schneider, Tinetti, Vincent Coudé du, Gelino and Ribas2010) from the planet star transits. Here we discuss the case of non-transiting planets. One of the embarrassing weaknesses of planet detection by direct imaging is that for many cases the planet mass cannot be derived from radial velocity or astrometric measurements of the parent star. It can often only be roughly estimated from its spectrum and planet atmospheric models. This happens when the stellar characteristics are not appropriate for high precision radial velocity of astrometric measurements, or when the planet orbit is too wide.
If the moon is transiting its parent planet with a period P moon, we have seen in subsection ‘Semi-major axis a moon’ how to determine the moon semi-major axis a moon. The planet mass M pl is then directly derived from the orbit period P moon of the moon around its planet by
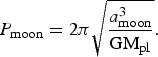$$P_{{\rm moon}} = {\rm 2\pi} \sqrt {\displaystyle{{a_{{\rm moon}}^3} \over {{\rm GM}_{{\rm pl}}}}}. $$Planet oblateness and spin axis
Barnes & Fortney (Reference Barnes and Fortney2003) have proposed to infer the transiting planet oblateness from the shape of the transit light curve. It would require extremely precise photometry. Another approach, applicable also to non-transiting planets, is to make use of the timing of moon–planet events in direct imaging. If the planet has an oblateness (characterized at first order by the parameter J 2) it can be inferred from the precession of the node and/or periapsis of lunar inclined and/or eccentric orbits. See Appendix 2 for details.
Planet rotation axis
As we have seen in the section ‘Detection methods of exo-moons’, it is likely that large moons evolving close to their primary, lie in the planet equatorial plane. Such assumption may even be taken for granted if more than one moon is seen evolving on the same plane in the system. Therefore measuring the inclination of the moon orbit, as described in subsection ‘Moon orbit inclination’, provides a way to determine the planet rotation axis. Indeed, for moons making their own detectable transit in addition to the planet transit, in addition to the moon orbit inclination (relative to the sky plane), the time difference between the planet and moon transits gives an additional parameter convertible in a second angle fully characterizing the moon orbital plane. That axis may be compared with the planet orbit plane and thus gives insight on the dynamics of the planetary system.
Conclusion
The transit of parent stars by the moon is today and in the near future the easiest way to detect moons. But moon–planet phenomena are more suited for the characterization of these moons and their use for the parent planet characterization. These phenomena are also more frequent than transits of the parent star. Indeed, it is likely that moons exist only at planet semi-major axis larger than say 0.5 AU, giving a transit probability of 1%, while planet/moon event have a typical probability of 10%. And for the astrometry and velocimetry of the parent planet, it can even be performed in every case.
The required instrumentation does not exist today but future projects for the 2030 decade (Quirrenbach et al. Reference Quirrenbach2013) may provide instruments to implement the detection and investigation methods described here.
Acknowledgements
We thank the two referees for their detailed and useful comments.
Appendix 1
In this appendix, we first investigate the variation of phenomenon duration as a function of eccentricity of the orbit. Then, we consider time spent between different phases.
Phenomenon duration
Phenomena durations for the circular case are given in (Cabrera & Schneider Reference Cabrera and Schneider2007). In the following, we are using the same notations.
As already shown in (Cabrera & Schneider Reference Cabrera and Schneider2007), we have for Phase 4 in the circular case
$${\rm \Delta} T_4 = \displaystyle{{{\rm 2}R_{{\rm pl}}} \over {na_c}} = \displaystyle{{P_c R_{{\rm pl}}} \over {{\rm \pi} a_c}}. $$In the eccentric case, we no longer have dv/dt=n, where v denotes the true anomaly of the moon (see Fig. 1). Moreover, a c should now be replaced by the changing radial distance r. In particular, we have:
$$\displaystyle{{{\rm d}v} \over {{\rm d}t}} = \displaystyle{{n(1{\rm +} e\,{\rm cos}\,v)^2} \over {(1 - e^2 )^{3/2}}} \quad {\rm and}\quad r{\rm =} \displaystyle{{a_c (1 - e^2 )} \over {1 + e\,{\rm cos}\,v}}.$$Using these expressions, we now have
$${\rm \Delta} T_4 = \displaystyle{{{\rm 2}R_{{\rm pl}}} \over {na_c}} \times \displaystyle{{\sqrt {1 - e^2}} \over {\left( {1{\rm +} e\,{\rm cos}\,v} \right)}}.$$
Maximum and minimum duration will occur for respectively ω=π and ω=0. As a consequence, we have 
$\displaystyle{{{\rm \Delta} T_{4_{\rm Max}} - {\rm \Delta} T_{4_{\rm Min}}} \over {{\rm \Delta} T_{4_\circ}}} = \displaystyle{{2e} \over {\sqrt {1 - e^2}}},$ where Δ
${{\rm \Delta} T_{4_\circ }}$ refers to the circular case.
For a Titan/Saturn-like configuration (e=0.03), the difference is 12%; leading to a deviation from a circular orbit of ±15 min (1 h peak to peak).
Time spend between phases
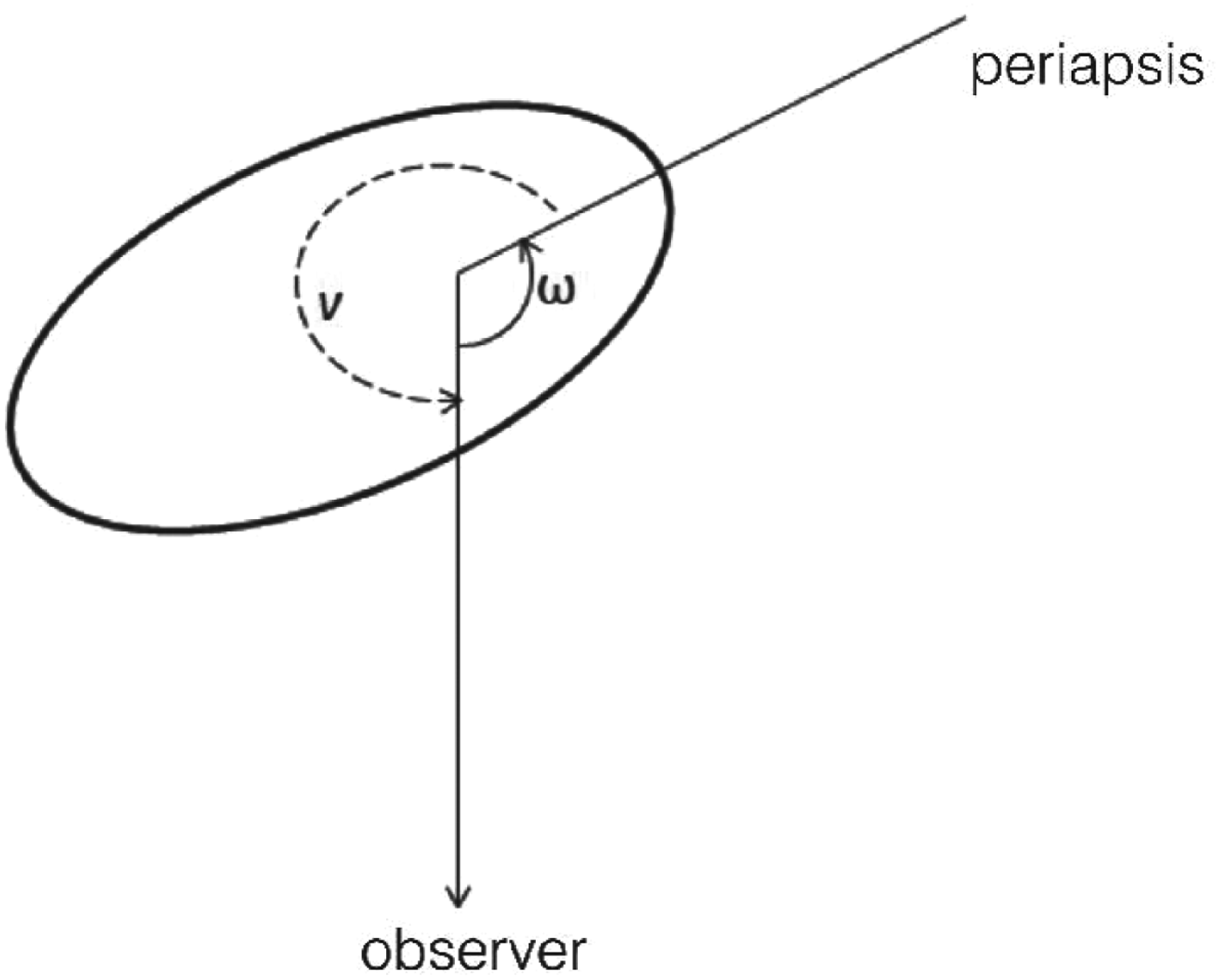
Let us now consider the time spent between Phases 3 and 1 (see Fig. 4). It is twice the time taken by the moon to go from its periapsis to the point where v=π/2. Introducing the eccentric anomaly E (Duriez Reference Duriez2002), we have
Fig. 4. Geometry of the true anomaly of the moon.
At v=π/2,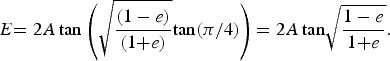 
$E{\rm = 2}A\,{\rm tan}\left( {\sqrt {\displaystyle{{(1 - e)} \over {(1{\rm +} e)}}} {\rm tan(\pi /}4{\rm )}} \right){\rm = 2}A\,{\rm tan}\sqrt {\displaystyle{{1 - e} \over {1{\rm +} e}}}. $ Introducing Kepler's equation, we have for this time interval
$${\rm \Delta} T_{v{\rm = 0,\pi} /2} = \displaystyle{M \over n} = \displaystyle{{E - e\,\sin E} \over n}.$$The time interval between Phases 1 and 3 thus is
$${\rm \Delta} T_{{\rm 13}} = \displaystyle{{{\rm 2}M} \over n} = \displaystyle{{4A\,{\rm tan}\sqrt {\displaystyle{{1 - e} \over {1{\rm +} e}}} - {\rm 2}e\,{\rm sin}\left( {{\rm 2}A\,{\rm tan}\sqrt {\displaystyle{{1 - e} \over {1{\rm +} e}}}} \right)} \over n}.$$For a Titan/Saturn-like configuration, the deviation with respect to e=0 would be 7.5 h, and so 15 h differences between Phases 1–3 and Phases 3–1.
The time spent between Phases 2–4 and Phases 4–2 is exactly similar (Fig. 5).
Fig. 5. Geometry of maximum time differences between Phases 1 and 3 events for an eccentric orbit. Similar time differences will arise when the moon enters Phase 3 with a true anomaly equal to π/2.
Appendix 2
The precession of the orbit of an exo-moon induced by the J 2 coefficient of its primary can be assessed analytically. Expanding the disturbing function in Keplerian elements and after averaging, the secular variation to first order of angular Keplerian elements can be obtained. While a full derivation is given in Duriez (Reference Duriez2002), here we simply recall the expressions
$$n_M {\rm =} n_o {\rm +} \displaystyle{3 \over 4}n_o J_2 \displaystyle{{a_e^2} \over {a_o^2}} \displaystyle{{(2 - {\rm 3sin}^2 i_o )} \over {\left( {1 - e_o^2} \right)^{3/2}}}, $$
$$n_{\rm \omega} = \displaystyle{3 \over 4}n_o J_2 \displaystyle{{a_e^2} \over {a_o^2}} \displaystyle{{(4 - {\rm 5sin}^2 i_o )} \over {\left( {1 - e_o^2} \right)^2}}, $$
$$n_\Omega = - \displaystyle{3 \over 2}n_o J_2 \displaystyle{{a_e^2} \over {a_o^2}} \displaystyle{{{\rm cos}i_o} \over {\left( {1 - e_o^2} \right)^2}}, $$and
$$M{\rm =} M_o {\rm +} n_M t,$$
$${\rm \omega = \omega} _o {\rm +} n_{\rm \omega} t,$$
$$\Omega = \Omega _o {\rm + n}_\Omega t,$$where M is the mean anomaly, ω and Ω are the argument of the periapsis and of the node. Ωo and Ωo are their respective value at the initial epoch t=0.
a o, eo, no and i o are the semi-major axis, eccentricity, mean motion and inclination in absence of the perturbation associated to J 2. a e is the equatorial radius of the planet.
