Introduction
As a result of the noteworthy success of the Alvarez hypothesis (Alvarez et al., Reference Alvarez, Alvarez, Asaro and Michel1980; Alvarez, Reference Alvarez1997) ascribing the mass extinction of dinosaurs and many other species at the end of the Cretaceous period to a cometary impact and the apparent recurrence of other mass extinctions on timescales between 20 and 40 million years, many investigators have sought for a periodic astrophysical phenomenon that might provide a root cause for such events. These explanations have included a hypothesis advanced by Raup and Sepkowski in the 1980s (Raup and Sepkowski, Reference Raup and Sepkowski1984; Muller, Reference Muller1988; Raup Reference Raup1999) that the sun might have a dim stellar companion, dubbed ‘Nemesis’, in a highly elliptical orbit taking it from deep interstellar space into the Oort cloud every 26 million years. At perihelion it would then destabilize many Oort cloud objects from their orbits, causing them to fall into the inner solar system, with the resulting cometary bombardment causing mass extinctions. This explanation has been falsified by the failure of extensive searches to find such a Nemesis star. More recently, Randall (Randall and Reece, Reference Randall and Reece2014; Randall, Reference Randall2015) has proposed that periodic Oort Cloud destabilization could be caused by the gravitational influence of a disk of dark matter orbiting the galaxy, which interacts with our Solar System during its periodic passage through said disk. This hypothesis has yet to be falsified. However, the existence of such a disk has yet to be found and moreover, it has yet to be convincingly shown that the recurrence of mass extinctions on Earth is truly periodic. On the contrary, those advocating periodicity have proposed a large variety of periods typically ranging between 25 and 38 million years. It is apparent that by superimposing such varying periods virtually any impact event could be included. Therefore the evidence at hand seems to better support the hypothesis that major impacts are random events that occur with a probabilistic frequency on the order of 30 million years, rather than the result of a periodic causal phenomenon.
In this paper, I will examine an alternative hypothesis ascribing intermittent increases in the rate of cometary bombardments to the destabilization of Oort Cloud objects by random encounters of the solar system with passing stars. Such a hypothesis was proposed and examined by Heisler et al. (Reference Heisler, Tremaine and Alcock1987), who came to the conclusion that such a mechanism would only result in bombardments with characteristic frequencies on the order of once every 100 million years, which is insufficient to explain the data. However, those investigators used a computer model, making their analysis impossible to review and moreover, employed assumptions, notably that destabilization events require encounters with stars of solar mass, that are untrue and which result in an unjustified reduction in the estimate of the collision frequency. Since that time, however, further consideration has been given to this hypothesis by a number of authors, with varying conclusions (Stern, Reference Stern1987; Weissman Reference Weisman1997; Fouchard et al., Reference Fouchard, Froeschle, Rickman, Valsecchi, Benest, Froelich and Lega2008a, Reference Fouchard, Frieschle, Breiter, Ratajczak, Valsecchi, Rickman, Benest, Froelich and Lega2008b, Reference Fouchard, Froeschle, Rickman and Valsecchi2011; Feng and Bailer-Jones, Reference Feng and Bailer-Jones2014, Reference Feng and Bailer-Jones2015 and Mamajek et al., Reference Mamajek, Barenfeld, Ivanov and Kniazev2015).
In the following sections, I will set forth an analytic model for calculating the frequency of interstellar encounters. It will be seen that the rates calculated are entirely consistent with the observed characteristic frequency of cometary events.
An analytic model for interstellar encounters
We begin by considering our region of the galaxy as a gas, with stars as particles with a characteristic density. For our Sun's galactic neighboūrhood, extending outward for thousands of light years, this density, D, is approximately 0.003 stars per cubic light year. These stars, however, are not static or moving together in complete synchrony, but rather have random velocities with respect to each other on the order of ten km/s. For the purpose of analysis, we will, therefore, take the Sun's random velocity with respect to this star field to be 10 km s−1, or 2 AU year−1. Then, depending upon what we consider to be the effective encounter distance, R, there will be a mean free path between encounters, L, given by:
In Fig. 1 below, we show the results of equation 1, with D = 0.003 stars per cubic light year, L given in light years and R given in AU.
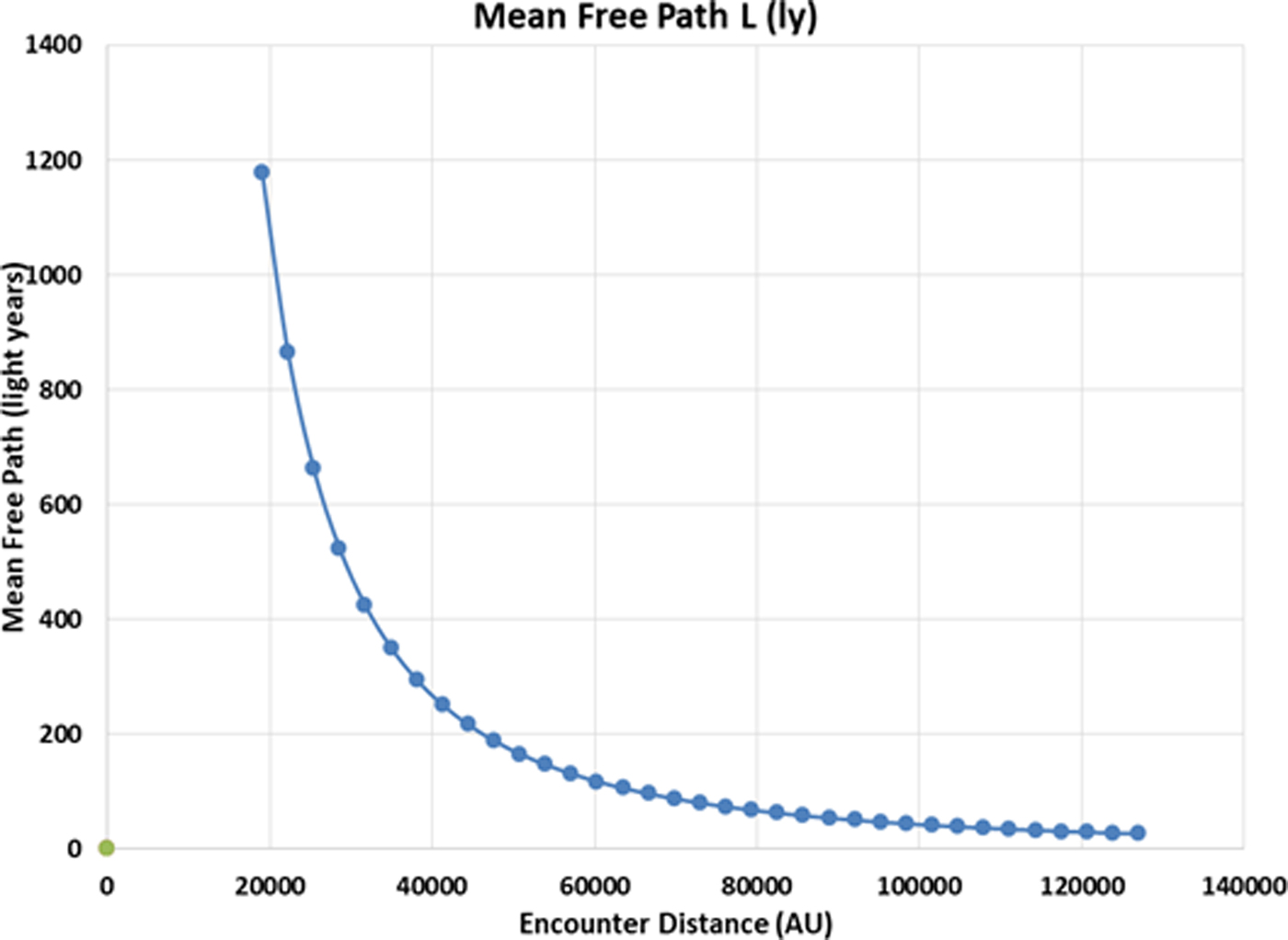
Fig. 1. Mean free path in light years between stellar encounters as a function of encounter distance (horizontal axis) given in AU.
The characteristic time between encounters, τ, is then given by the mean free path, L, divided by the sun's velocity, V, with respect to the star field.
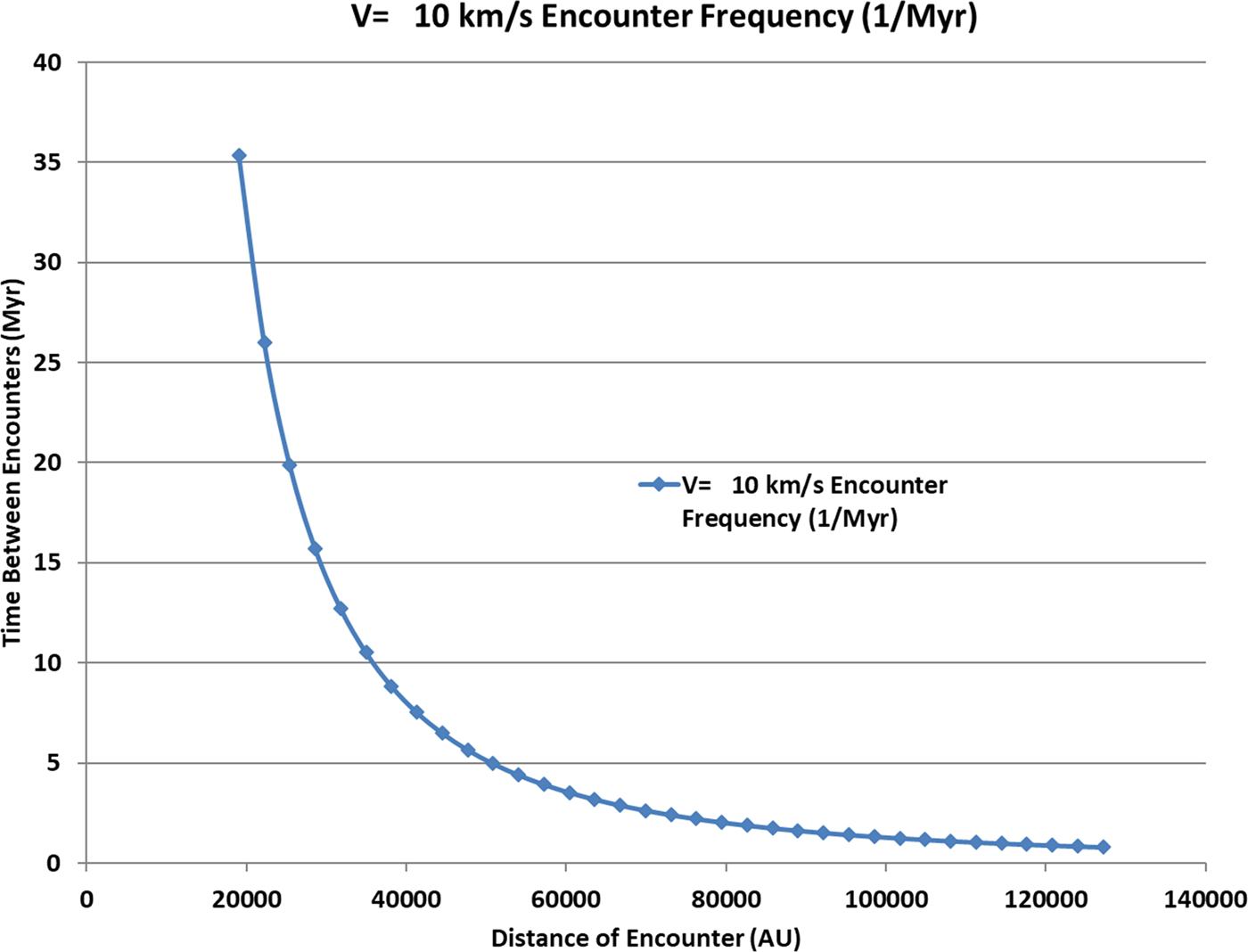
The results of equation (2) are presented in Fig. 2.
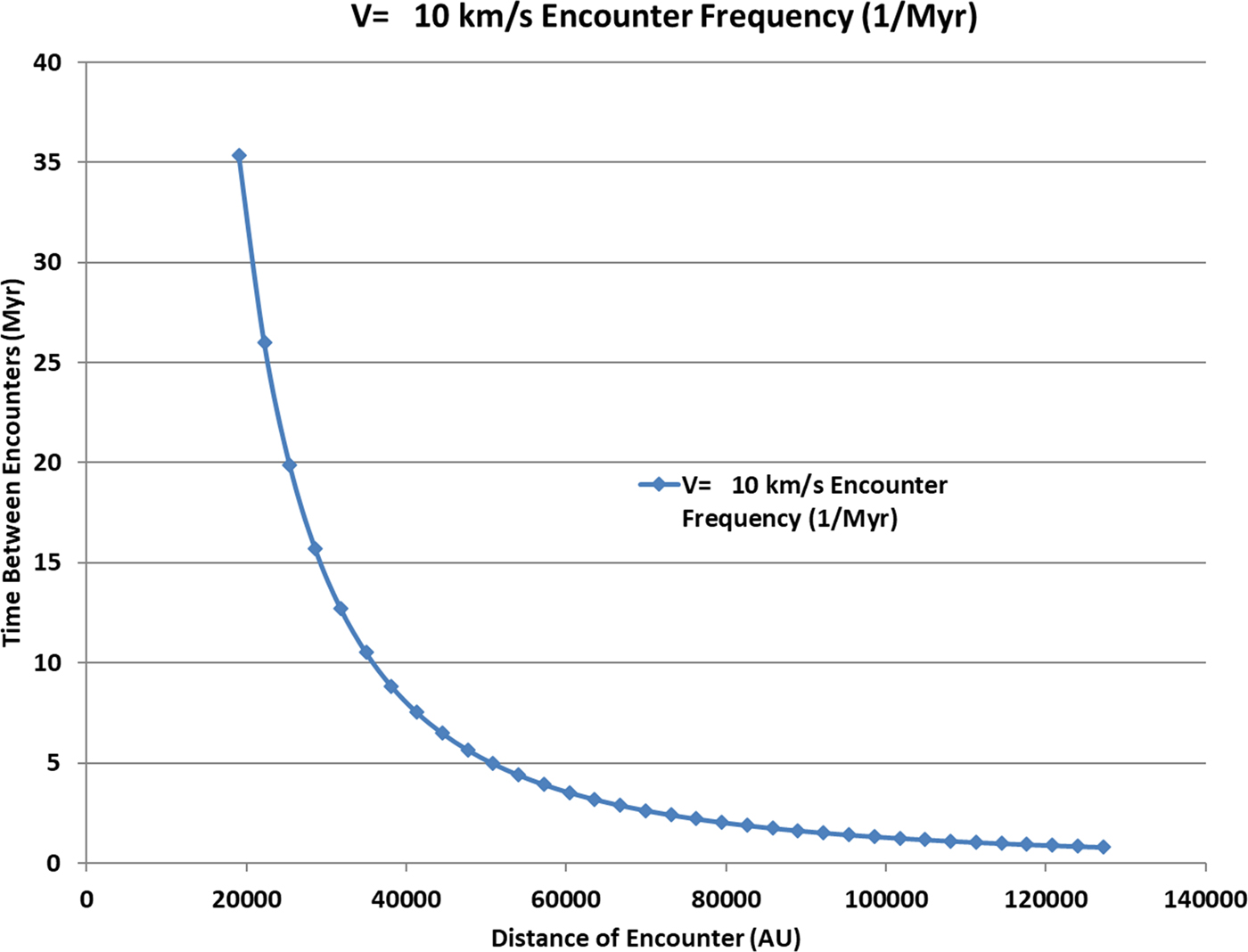
Fig. 2. Characteristic encounter frequency between sun and neighbouring stars as a function of encounter distance (AU).
Examining Fig. 2, we see that the characteristic frequency of 1 encounter every 26 million years occurs if the distance of effective encounter is taken as 22 000 AU. This is a remarkable result because an encounter at 22 000 AU would send the alien star right through the heart of the sun's Oort cloud, while the sun would be travelling through the outer regions of the Oort Cloud of a common M dwarf.
Now the sun's Oort cloud extends to at least 30 000 AU, with some estimates taking it to 100 000 AU. It is also believed to contain something on the order of trillion objects of cometary size. If we take the effective radius of the sun's Oort Cloud to be 40 000 AU and the number of objects to be a trillion, then the average density of objects within the Oort Cloud would be on the order of 4 per 1000 cubic AU, or a spacing of four objects per cube 10 AU on a side. We note also that the sun is among the larger stars, with smaller stars outnumbering those of solar size or larger by about 10:1. In fact, the most common stars are type M dwarfs, which might typically have masses around a quarter of our Sun. It is unclear whether such low-mass stars have Oort clouds, but there is a strong theoretical basis to believe that they do. (Brasser et al., Reference Brasser, Duncan and Levison2008; Levison et al., Reference Levison, Duncan, Brasser and Kaufmann2010, Hughes et al., Reference Hughes, Duchêne and Matthews2018). I make that assumption accordingly. However, because gravitational attraction is linear with mass but inversely proportional to the square of the distance, such objects would exert gravitational acceleration equal to that of our Sun at half the distance. Therefore, if the sun can retain Oort Cloud objects at the distance of 40 000 AU, such an M dwarf would be expected to be equally able to retain an Oort Cloud of its own out to a radius of 20 000 AU.
So it should be understood that two Oort Clouds are involved in the encounter, that of our Sun and that of the visiting dwarf. In a typical encounter, the dwarf will penetrate deeper into the sun's Oort Cloud than the sun penetrates the dwarf's, but both will come much closer to Oort Cloud objects of the other than either are to their own Oort cloud.
Furthermore, the destabilization of the sun's own Oort Cloud objects to produce bombardment of the home solar system cannot be the mechanism responsible for periodic or characteristic frequency mass extinctions. This is so because an Oort Cloud object at 20 000 AU destabilized to fly into the inner solar system would have a period of 1 million years. Over the past 400 years of telescopic astronomy by competent scientists, we have observed thousands of cometary visits to the inner solar system, without one striking the Earth. This proves that any given comet is likely to visit the inner solar system many times before it strikes a planet. But if the attrition rate was <1 impact per hundred visits, which it demonstrably is, then the number of million-year period comets precipitated by a stellar encounter falling into the inner solar system would be nearly as great 13 million years after the encounter (i.e. at the presumed periodic minimum) as 1 million years after. In other words, even if hordes of such long-period comets were dispatched with true 26 million year periodicity, they would still arrive nearly constantly, creating no appreciable signal to noise in the impact record.
So while self-bombardment of the solar system by its own Oort Cloud objects is certainly possible, it cannot explain any periodicity or characteristic frequency of extinction events. In contrast, if the sun were to destabilize the Oort Cloud visiting star by passing right through it, impacts could occur quite quickly. Let us examine this possibility.
How close does a visiting star need to come to the Oort Cloud object of another to turn it into a comet? A good approximate criterion for this might be a distance such that the net change in velocity Δv imposed by the visiting star on the Oort Cloud object is greater than the encounter velocity, V, between the two solar systems. That is disruption occurs if:
The acceleration, A, exerted by a star decreases as m/r2, where r is the range between the star and the Oort cloud object and m is the mass of the star traveling through the cloud in suns and r is the distance in AU and time is given in years.
The Δv is then given approximately by A times the time of encounter between the star and the Oort Cloud object. This is given approximately by r/V, where V, as before, is the velocity of the star with respect to the other solar system (10 km s−1 = 2 AU yr−1). So, for disruption to occur we have:
Or, if m = 1 and V = 2:
In which case we find that r < 10 AU.
So the sun can capture visiting star Oort Cloud objects if it passes within 10 AU of them. If the visiting star is a K dwarf with a mass of 0.6 Suns, it would have to come with 6 AU of one of our Oort cloud objects to have chance to capture it; if it were an M dwarf with 0.3 solar masses it would have to come within 3 AU.
Of course, any given visiting star Oort cloud object disrupted by our Sun would only have a small probability of striking the Earth. How many shots would the alien star get?
If the sun were to travel through the alien star's Oort Cloud at a range of 20 000 AU, it would probably be in the cloud for about that distance. Assuming a disruption range of 10 AU, it would sweep out a path with a volume of π(102) 20 000 = 6.3 million cubic AU. Assuming 4 Oort cloud objects per 1000 cubic AU, this implies that approximately 25 000 alien cloud objects could potentially be captured per pass, providing a significant chance of impact events to follow.
The great majority of impacts caused by disrupted objects would no doubt be delivered to gas-giants type planets. However, with such a large number of objects released per pass, Earth-sized worlds would likely be impacted as well. The most impacts on minor planets could be expected to occur shortly after the encounter before the larger planets had time to sweep up the debris. Thus the number and size of the major planets in a solar system would be a significant factor in determining the sharpness of the impact-rate peak.
Smaller stars, having shorter disruption ranges, would experience less impacts per event, with the number going as the square of the star's mass. Still, even small M stars would be able to capture several thousand per encounter.
Once their orbits are disrupted, the destabilized Oort cloud objects can fall into their target solar systems very swiftly. For example, a dwarf star Oort cloud object destabilized into a cometary orbit by our Sun at a typical range of 10 AU would have a semi-major axis of about 6 AU with a period of 15 years, allowing it to reach perihelion the first time in as little as 7.5 years. A solar Oort cloud object destabilized by the M dwarf at a range from it of 3 AU would have a period of as little as 3 years. If the encounter range between the two stars is 20 000 AU and their relative motion is 2 AU yr−1 (10 km s−1) the duration of the encounter will be around 10 000 years. Therefore, given the short periods of the comets created by the encounter, it is highly probable that planets in each of the two solar systems involved will be impacted while the other star is still in the neighbourhood.
Since the radius of the Oort Cloud of a star scales as the square root of the mass of the star, a dwarf star could pass through the sun's Oort cloud while the sun remains outside of the Oort Cloud of the dwarf. In such an encounter, the dwarf's solar system would be bombarded by objects from the sun's Oort Cloud while the sun's solar system would remain unaffected. Thus while our Solar System might be experiencing bombardments every 30 million years from a star field with a typical stellar mass of 0.25 Suns and Oort field radii of 30 000 AU, its own Oort Cloud, with a radius of 60 000 AU, would simultaneously be delivering bombardments to one of the surrounding dwarfs every 7.5 million years.
It may be noted that these timescales and rates are very approximate order of magnitude estimates. However, while purportedly more precise estimates could be made by integrating over distribution functions, the input data for such calculations are uncertain by much larger factors than the uncertainty caused by the approximations used. By making use of the simpler model presented here, calculations may more readily be checked or reexamined using alternative assumptions.
It is also useful to examine which type of stars deliver the most bombardments to our own Solar System. Larger stars have bigger Oort Clouds but are fewer in number. A weighted average of each type is therefore necessary. The results of such an analysis are presented in Table 1.
Table 1. Comparative responsibility of star types for cometary bombardment of our Solar System

In Table 1, ‘Base F’ is the frequency of encounters per Gyr with such stars assuming that they were present with an average density of 0.003 per cubic light year (i.e. that all stars were of their type.) This base frequency is then multiplied by the stellar fraction to calculate the weighted average of the number of encounters per Gyr resulting from that star type presented in the final column.
It can be seen that while large (G and F) stars could be responsible for as many as ~14 cometary bombardments of our Solar System every billion years (i.e. an average of 1 every 70 Myr, in fair agreement with the earlier analysis of Heisler et al. (Reference Heisler, Tremaine and Alcock1987)), four times as many bombardments are likely to be launched by smaller, but more common, K and M stars.
The calculated total encounter frequency of 47.2 Gyr−1 (1 per 21 Myr) is a bit high. This suggests that the assumption that the sun's effective Oort Cloud radius of 40 000 AU may be slightly excessive. If an effective radius of 36 000 AU for a star of 1 solar mass is assumed, then a frequency of 37.2 encounters per Gyr (1 per 27 million years) results, in good agreement with available data.
Consequences for evolution
The above analysis has significant potential consequences for astrobiology. If we estimate that each Oort Cloud object disrupted has an average mass of 1 billion tons, then an encounter at 20 000 AU would appear to have the potential to import about 25 trillion tons of mass from another solar system into our own. Of course, only a tiny fraction of it would hit the Earth. But even so, the potential to transfer biological material is evident.
This is so because impacts can cause the material to be ejected from a solar system at velocities on the order of 20 km s−1, which is considerably faster than the 10 km s−1 relative velocity of the two stars. Indeed, dust thrown up from the Earth by an impact event could be driven outward by the pressure of sunlight at speeds on the order of 30 km s−1 (Zubrin, Reference Zubrin2017). Therefore, since impacts are likely to occur while the other star is still close by, it is possible that impacts can cause the material to be ejected from each of the two solar systems that will subsequently hit the other. Furthermore, even if ejected material fails to hit the passing solar system, it could become captured in the home solar system's Oort Cloud. Such material, as well as dust particles containing microbes previously driven outward by the pressure of sunlight, could be stored for long periods in Oort Cloud objects in deep freeze under effective ice shielding until a subsequent encounter with a different passing stellar system causes it to be released and transferred at that time.
In either case, microbes in the transferred material would only have to survive a transfer of ~ 20 000 AU or about 0.3 light years, a factor of 20 or more, less than the ~5–10 light years that would be typically required to travel from one solar system to another. This would sharply increase their probability of surviving the trip. In consequence, the mechanism proposed significantly strengthens the case for lithopanspermia. (Melosh, Reference Melosh1988; Zubrin, Reference Zubrin2001, Hornek et al., Reference Hornek, Klaus and Mancinelli2010). Thus, like warships in the age of fighting sail, which had global reach but limited artillery range, solar systems greatly improve their chances of scoring hits by discharging their biological broadsides only when their counterparts are passing close by.
It may also be noted that with a typical time between incoming encounters of 25 million years, it is probable that our Solar System has had about 140 incoming-delivery encounters with other stars since life first appeared on Earth some 3.6 billion years ago (Drake, Reference Drake2017). If each encounter with a dwarf star typically releases 1000 solar system Oort cloud objects, then our Solar System has been responsible for releasing some 140 000 objects into others over this period. But, as a large G star, the sun probably delivered at least three times as many bombardments on other stellar systems as it received. Thus, while we have only travelled through the Oort clouds of other, mostly dwarf, stars 140 times, dwarf stars have probably travelled through our own Oort Cloud about 420 times. If only 10% of encounters actually result in the transfer of microbial life from the Earth to another solar system, then we have been responsible for seeding 42 other solar systems with life. If each of these were then to act as a similar microbial transmitter, the result would be billions of inhabited worlds seeded by the Earth.
We also note that the encounter frequency experienced by any particular star resulting from the mechanism described in this paper increases linearly in proportion to the local stellar number density, while the volumetric encounter rate (the number of encounters occurring in any region of space per unit time) increases as the square of the number density. This has interesting implications because a case can be made that the rate of mass extinctions of Earthy is slower than optimal for the evolution of advanced life. For example, it would appear that terrestrial life would be further advanced today if the K-T event had occurred sooner. The biosphere more than recovered from that event within 5 million years, sporting a very promising array of mammals and birds to replace the dinosaurs. So perhaps a typical impact rate of 15 million years might encourage more rapid progress. On the other hand, if impacts were too frequent, there could be insufficient recovery and redevelopment time for new types of creatures to explore and develop their full evolutionary potential before the next event. This suggests that regions of the galaxy somewhat further towards its center with perhaps double our local stellar population density might be the home of the most advanced species and civilizations, while those with much higher high or lower local stellar densities might be comparatively primitive.
So while we may not live in the best of all possible worlds, at least we live in one of the better ones.
Conclusions
We conclude that the observed characteristic frequency of cometary impacts on Earth of ~1 per 25 Myr is not caused by a periodic astrophysical phenomenon, but is a simple consequence of the random motion of the sun with respect to the surrounding star field. We further conclude that stars of every type contribute to this bombard, but that the predominant role is played by common dwarf stars, not by rare large ones as previously assumed. We further find that the large majority of Oort cloud objects destabilized from their orbits to become comets entering a solar system do not originate that solar system, but from that of the other star engaged in the encounter. Since these immigrant objects are destabilized from their orbits at distances on the order of 2–20 AU, they can enter their new home solar systems on timescales of years or decades following the encounter, not the millions of years that might be required of Oort Cloud objects originating in the home system some 20 000 AU from the home star. Therefore impact events resulting from the interstellar encounters can occur while the two stars are still near each other. As a result, dust or other debris thrown up by such impacts on each solar system could reach the other. Alternatively, such dust of debris could reach the home system's Oort Cloud and be stored there for long periods until it is delivered riding its comet into another solar system during a subsequent encounter event. In either case, interstellar travel by microbes contained within such dust or debris would only require transits of ~0.3 light years, greatly increasing the odds of survival compared to transits of 5–10 light years that might be required under non-encounter conditions. We also observe that solar systems with large stars, like our Sun, because they have more extensive Oort Clouds than most stars, deliver more cometary bombardments on other solar system than they themselves receive. Thus, because it is about 3 times as massive as the average star, our Sun has probably delivered bombardments to other solar systems with three times the frequency that our own Solar System has received, firing off over 400 such bombardments in the time since life is known to have appeared on Earth. Consequently, if microbes can survive transits on the order of 20 000 AU, our Solar System may have been responsible for spreading the seeds of life to many others.