Introduction
The study of the thermochemical behaviour of micrometeoroids (MMs) entering Earth's atmosphere is of crucial interest for planetary and astrobiological science, since these objects represent a large fraction of the total annual input of extraterrestrial matter into the biosphere (Jenniskens et al. Reference Jenniskens, Wilson, Packan, Laux, Krüger, Boyd, Popova and Fonda1998). Actually, many works in the past (Anders Reference Anders1989; Maurette et al. Reference Maurette, Beccard, Bonny, Brack, Christophe, Veyssiere and Battrick1990, Reference Maurette, Brack, Kurat, Perreau and Engrand1995; Jenniskens et al. Reference Jenniskens, Wilson, Packan, Laux, Krüger, Boyd, Popova and Fonda1998; Maurette Reference Maurette2006) suggested that micrometeorites might be the major carrier of extraterrestrial C-rich compounds reaching Earth's surface. Recent studies actually focus on the possible survival of amino acids (Glavin and Bada Reference Glavin and Bada2001) and organic compounds during the atmospheric entry of interplanetary dust particles and MMs (Matrajt et al. Reference Matrajt, Brownlee, Sadilek and Kruse2006). In particular, in Matrajt et al. (Reference Matrajt, Brownlee, Sadilek and Kruse2006), experimental pulse-heating analyses on three different organic substances have been performed, and the authors conclude that these molecules are able to survive the atmospheric entry heating, thanks to a combination of a microporous structure of the grain and the presence of sublimation processes.
In this context, the analysis of a peculiar class of materials, that we may call ‘white soft minerals’ (WSM) including calcite, magnesite, gypsum, talc, might represent a key point in panspermia theory, as these materials are often associated with the presence of organic matter (Gooding et al. Reference Gooding, Wentworth and Zolensky1988; Pizzarello et al. Reference Pizzarello, Cooper and Flynn2006; Orofino et al. Reference Orofino, Blanco, D'Elia, Fonti and Licchelli2009; Yabuta et al. Reference Yabuta, Uesugi, Naraoka, Ito, Kilcoyne, Sandford, Kitajima, Mita, Takano, Yada, Karouji, Ishibashi, Okada and Abe2014; D'Elia et al. Reference D'Elia, Blanco, Galiano, Orofino, Fonti, Mancarella, Guido, Russo and Mastandrea2017).
In the present work, we investigate the thermochemistry of the atmospheric entry of pure anhydrous CaSO4 MMs. The attention to this composition is justified by several findings. Calcium sulphate grains (possibly, gypsum) have been identified in SNC (shergottites, nakhlites and chassignites) martian meteorites Nakhla, EETA 7901 and Chassigny (Gooding et al. Reference Gooding, Wentworth and Zolensky1988; Wentworth and Gooding Reference Wentworth and Gooding1988; Gooding Reference Gooding1992; Wentworth and Gooding Reference Wentworth and Gooding1994), supporting the idea that these sulphates might be of extraterrestrial origin. Actually, calcium sulphate has been identified on Mars surface (Gendrin et al. Reference Gendrin, Mangold, Bibring, Langevin, Gondet, Poulet, Bonello, Quantin, Mustard, Arvidson and Le Mouélic2005; Langevin et al. Reference Langevin, Poulet, Bibring and Gondet2005) by OMEGA/Mars Express, in association with the martian past aqueous activity. Opportunity rover found probable calcium sulphate veins at martian Endeavour Crater (Squyres et al. Reference Squyres, Arvidson, Bell, Calef, Clark, Cohen, Crumpler, de Souza, Farrand, Gellert, Grant, Herkenhoff, Hurowitz, Johnson, Jolliff, Knoll, Li, McLennan, Ming, Mittlefehldt, Parker, Paulsen, Rice, Ruff, Schröder, Yen and Zacny2012); calcium sulphate veins, most of them hydrated and some anhydrous, have been analyzed by ChemChem/Curiosity at martian Gale Crater (McLennan et al. Reference McLennan, Anderson, Bell, Bridges, Calef, Campbell, Clark, Clegg, Conrad, Cousin, Des Marais, Dromart, Dyar, Edgar, Ehlmann, Fabre, Forni, Gasnault, Gellert, Gordon, Grant, Grotzinger, Gupta, Herkenhoff, Hurowitz, King, Le Mouélic, Leshin, Léveillé, Lewis, Mangold, Maurice, Ming, Morris, Nachon, Newsom, Ollila, Perrett, Rice, Schmidt, Schwenzer, Stack, Stolper, Sumner, Treiman, VanBommel, Vaniman, Vasavada, Wiens and Yingst2014; Nachon et al. Reference Nachon, Clegg, Mangold, Schröder, Kah, Dromart, Ollila, Johnson, Oehler and Bridges2014). These discoveries might help the understanding of past aqueous processes on Mars and, consequently, the presence of ancient environment able to support life forms.
Although organic molecules are often associated with evaporitic materials, only recently a paleontological interest in detecting organic compounds in sulphate minerals has arisen. Several terrestrial gypsum deposits have been analysed, in close connection with gypsum discovery on Mars and with their remarkable similarity with Earth sediments, and diverse microfossil organisms have been detected in many of these ancient deposits (Australia, Chile, Italy, Jordan, Mexico, Perú, USA) (Aubrey et al. Reference Aubrey, Cleaves, Chalmers, Skelley, Mathies, Grunthaner, Ehrenfreund and Bada2006; Dong et al. Reference Dong, Rech, Jiang, Sun and Buck2007; López-Lozano et al. Reference López-Lozano, Eguiarte, Bonilla-Rosso, García-Oliva, Martínez-Piedragil, Rooks and Souza2012; Schopf et al. Reference Schopf, Farmer, Foster, Kudryavtsev, Gallardo and Espinoza2012; Benison and Karmanocky Reference Benison and Karmanocky2014). Moreover, impact craters are of great interest for life evidence: in particular, Haugton impact crater (Canada) presents hydrothermal gypsum deposits, which are a favourable habitat for microbial colonies (Parnell et al. Reference Parnell, Lee, Cockell and Osinski2004). These discoveries demonstrate that organic compounds are well preserved in terrestrial sulphate minerals and strongly suggest that these materials should represent the main goal in the search for organic compounds and evidence of past life on Mars.
In view of the importance of calcium sulphate in its association with organic matter, the study of the atmospheric entry of CaSO4 MMs might represent a fundamental issue in the astrobiological context.
On entering Earth's atmosphere, MMs experience several physical and chemical modifications (Genge et al. Reference Genge, Grady and Hutchison1997): collisions with atmospheric atoms, deceleration, evaporation, ablation, heating, decomposition. Thermal effects experienced by MMs entering Earth's atmosphere have been extensively studied, from a theoretical (Love and Brownlee Reference Love and Brownlee1991; Toppani et al. Reference Toppani, Libourel, Engrand and Maurette2001; Opik Reference Opik2004; Micca Longo and Longo Reference Micca Longo and Longo2017a,Reference Micca Longo and Longob) and an experimental (Füri et al. Reference Füri, Aléon-Toppani, Marty, Libourel and Zimmermann2013; Suttle et al. Reference Suttle, Genge, Folco and Russell2017) point of view. Various numerical models have been developed (Flynn Reference Flynn1989; Love and Brownlee Reference Love and Brownlee1991; Briani et al. Reference Briani, Pace, Shore, Pupillo, Passaro and Aiello2013; Bisceglia et al. Reference Bisceglia, Micca Longo and Longo2017; Micca Longo and Longo Reference Micca Longo and Longo2017a,Reference Micca Longo and Longob) in order to simulate the various interactions between the MMs and Earth's atmosphere. These previous works focus on more common micrometeorites materials, i.e. silicates, and introduce the study of carbonates, which are very promising in the context of astrobiology. In particular, very recent studies (Micca Longo and Longo Reference Micca Longo and Longo2017a,Reference Micca Longo and Longob) focus on the atmospheric entry of pure magnesite MMs and of MMs with a mixed composition of calcite and magnesite, respectively. The entry model has been developed in relation with the idea that carbonates might act as cooling materials, in the context of astrobiology and of the delivery of organic matter from Space to the Earth (Bisceglia et al. Reference Bisceglia, Micca Longo and Longo2017).
In this work, our entry model (Micca Longo and Longo Reference Micca Longo and Longo2017a,Reference Micca Longo and Longob) has been modified in order to undertake the thermochemical analysis of anhydrous calcium sulphate MMs. The aim of the present study is to understand whether CaSO4 might provide a sort of thermal protection to organic matter, in view of its possible delivery from Space to Earth. Such grains are envisaged to be a result of an impact ejection on planetary surfaces with water present (at the time of the impact or in the past). In an organic delivery scenario, they may enter the atmosphere as such, or be produced by the fragmentation of a fragile larger body at high altitudes. In order to reduce the number of parameters involved, in this work, we will consider a scenario of pristine chemically pure grains entering the atmosphere as such. For this purpose, thermochemical properties of this specific test mineral need to be known, in order to include them during the entry scenarios.
Thermochemistry of the entry model
The atmospheric entry model has been already described in previous papers (Micca Longo and Longo Reference Micca Longo and Longo2017a,Reference Micca Longo and Longob). Accordingly, we provide here a characterization of specific features for anhydrous CaSO4, while shortly reviewing the algorithm.
MMs are treated as a homogeneous and isothermal sphere, with a constant density of 3 gr cm−3 and a pure CaSO4 composition. The isothermal hypothesis is supported by Biot number analysis: considering temperatures and grain radii involved in our case study, the Biot number is much smaller than one (~ 10−4) so that the body temperature can be considered uniform. This hypothesis is thoroughly discussed in the next sections. We assume that the material is porous enough to allow the SO3 diffusion and the chemical mixing.
The model includes two equations for two cartesian components of velocity in the vertical entry plane xy, the effect of gravity, drag forces, Earth's curvature and the current atmospheric density profile (Rees Reference Rees1989).
The micrometer size of grains allows us to exclude fluid dynamics: the mean free path of air molecules at the considered altitudes is larger than the MM dimension. Therefore, the interaction between the MMs and the air molecules is always direct.
Concerning the thermochemistry of the entry process, the input power given by air molecules to the MM is:
$$P_{\rm in}={\kappa' \over 2}\rho_{\rm atm}{\pi}r^2v^3 $$r is the grain radius, v is the entry speed and κ′ is the heat transfer coefficient in a collision between two free atoms (Opik Reference Opik2004):
$$\kappa'={2\tilde m \over (1+\tilde m)^2} $$where 
$\tilde m = 14.5/A_{\rm t}$ and A t is the atomic weight. Considering the atomic weights of the species involved in calcium sulphate, in this work, we assume κ′ = 0.4.
The input power is balanced by radiative and evaporative energy losses:
$$P_{\rm out}=4{\pi}r^2({\epsilon}{\sigma}T^4 + H_{\rm v} Cp_{\rm v}\sqrt{m_{\rm mol}/T}) $$where ε is the body's emissivity (here we assume ε = 1), σ is the Stefan–Boltzmann constant, T is the temperature, H v is the latent heat of vaporization, C is 4.377 × 10−5 (cgs units), p v is the vapour pressure, m mol is the molecular weight. All evaporation is assumed to take place in a vacuum.
Since evaporation affects both particle's temperature and mass, it is possible to evaluate the mass loss rate:
$$\dot{m}=4{\pi}r^2 Cp_{\rm v} \sqrt{m_{\rm mol}/T}$$At sufficiently high temperatures, anhydrous calcium sulphate decomposes to calcium oxide and sulphur trioxide: CaSO4 → CaO + SO3. In this respect, a model based on a well-mixed and ideal solid mixture has been developed, in order to evaluate the grain behaviour during its passage through Earth's atmosphere. The Langmuir law allows us to calculate the evaporation rate, per unit time and area, as stated in Bisceglia et al. (Reference Bisceglia, Micca Longo and Longo2017), in terms of the vapour pressure for the solid mixture CaSO4/CaO that may be estimated using Raoult’s law:
$$p_{{\rm SO}_3} = {\rm e}^{-{\Delta G_0(T) \over RT}}\chi_{{\rm CaSO}_4} $$where 
$\chi _{{\rm CaSO}_4}$ is the mole fraction of CaSO4 in the grain and ΔG 0(T) is calculated using specific thermodynamic data of ΔH f and ΔS 0 for the chemical species involved (CaSO4, CaO and SO3).
$\chi _{{\rm CaSO}_4}$ is calculated using stoichiometry:
$$\chi_{{\rm CaSO}_4}= {m-m_{\rm min} \over m_0-m_{\rm min}} $$m 0 represent the mass of the object when it is composed by pure sulphate and m min is the minimum mass in which all sulphate is turned into CaO:
$$m_{\rm min}={M_{\rm CaO} \over M_{{\rm CaSO}_4}}m_0 $$where M CaO and 
$M_{{\rm CaSO}_4}$ are the molecular weights of the pure oxide and of the anhydrite, respectively.
In these calculations, as already stated, we have assumed that the body temperature is uniform and this hypothesis is confirmed by an estimate of the Biot number, assuming radiative cooling. Several works in the past have modelled the internal temperature profile of MMs (Szydlik and Flynn Reference Szydlik and Flynn1992, Reference Szydlik and Flynn1997), leading to a relevant temperature gradient during the heating pulse. Since an estimate, based only on the Biot number, cannot account for evaporation cooling, we have built up a simple two concentric zone model, which is presented in the appendix. Results show that the temperature differences between these two zones are irrelevant, so for micro-sized grains, the thermal gradient is negligible (as resulting from the Biot number analysis). A plot showing very small temperature differences between the inner (T 1) and the outer zone (T 2) is displayed in figure 1.
Fig. 1. Temperature differences between the inner and the outer zone in the MM concentric model.
Comparison with the methodology of the aforementioned works shows that the authors (Szydlik and Flynn Reference Szydlik and Flynn1992, Reference Szydlik and Flynn1997) assumed a very low diffusivity (~ 1 × 10−10 m2 s−1), more than three order of magnitudes lower than that suitable for CaSO4 (~ 7 × 10−7 m2 s−1, in our model).
Results and discussion
The model has been implemented as a Fortran code; all simulations begin at 190 km altitude, and the Leapfrog method has been used with a time step of 1 ms. 0° indicates vertical downward fall.
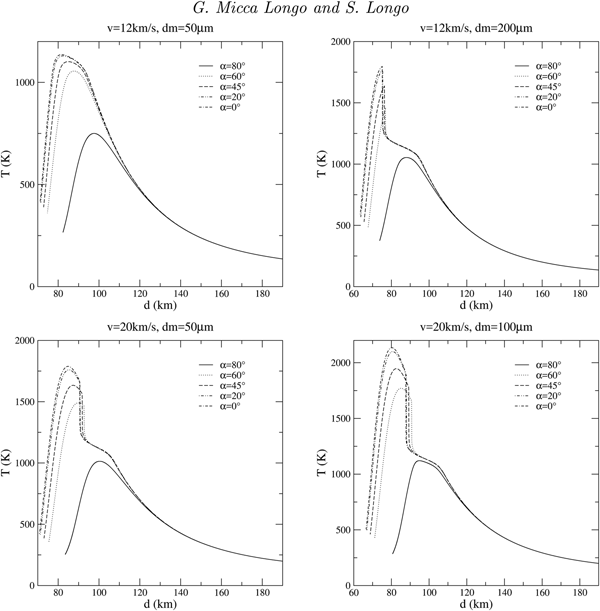
Several entry scenarios, showing the thermal history of the grain during its passage through the atmosphere, are plotted in figure 2 as a function of the quota d.
Fig. 2. Thermal curves for different entry scenarios (α is the entry angle, v is the entry velocity and dm is the meteoroid diameter) of an anhydrous calcium sulphate MM.
For the corresponding entry scenarios, it is possible to plot the sulphate fraction χ as a function of the quota d (figure 3).
Fig. 3. Mole fraction of sulphate 
$\chi _{{\rm CaSO}_4}$ in the grain, during entry scenarios.
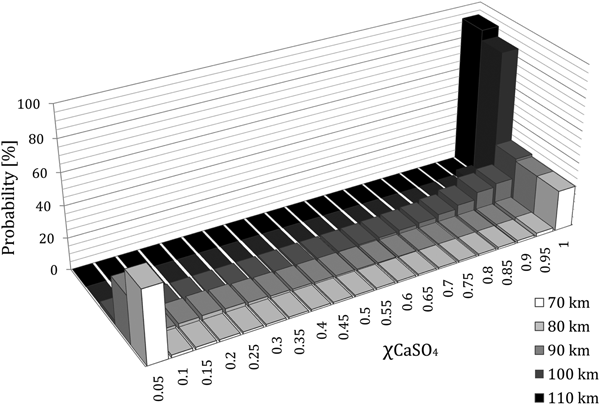
Histograms showing sulphate occurrences at different altitudes (figure 4) and at the ground (figure 5) are reported. A Monte Carlo calculation has been performed, using speed, angle and grain mass distributions from Love and Brownlee (Reference Love and Brownlee1991). As mentioned in a recent paper (Micca Longo and Longo Reference Micca Longo and Longo2017a), the use of such distributions, established for the asteroidal matter, is kind of arbitrary in the case of non-silicate grains; nevertheless, this choice allows us to perform a first statistical evaluation based on well-known literature data. Of the considered 105 entry events, 7.8% lead to the MMs escape from the atmosphere. This estimate and, in general, the evaluation of grazing entries, that will be shown later, are possible only using a 2D model and accounting for Earth's curvature. It must be noted that in the model, since the equations used do not apply to subsonic flight, any trajectory is interrupted when the motion is no more supersonic. Therefore, assuming that decelerated particles keep falling at their terminal speed, their composition is included in the statistics at all quotas below that of formal termination.
Fig. 4. Calcium sulphate fraction occurrences at different altitudes.
Fig. 5. Calcium sulphate fraction occurrences on ground.
Our study shows that, for most trajectories, anhydrite MMs are actually able to survive the atmospheric entry with a partial decomposition; after deceleration, these grains are able to reach Earth's surface substantially unaltered. In this perspective, anhydrous CaSO4 MMs offer an encouraging scenario for the delivery of organic matter from Space to Earth, in view of the aforementioned association between sulphate minerals and organic matter.
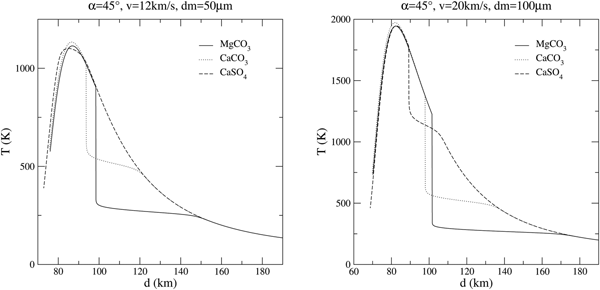
Even compared with calcium and magnesium carbonates, anhydrous calcium sulphate is a much promising material from an astrobiological point of view. Comparisons among the thermal history during the atmospheric entry of these three minerals (MgCO3, CaCO3 and CaSO4) are plotted in figure 6.
Fig. 6. Comparison among MgCO3, CaCO3 and CaSO4 MM in two typical entry scenarios.
The difference in these thermal trends is due to the different standard formation enthalpies of the materials considered (
$\Delta H_{{\rm MgCO}_3} = -1095.797\,{\rm kJ}\,{\rm mol^{-1}}$, 
$\Delta H_{{\rm CaCO}_3} = -1206.9\,{\rm kJ}\,{\rm mol^{-1}}$, 
$\Delta H_{{\rm CaSO}_4} = -1434.52\,{\rm kJ} \,{\rm mol^{-1}}$). It is evident that a larger enthalpy leads to higher temperatures, consequently to a lower volatility and a greater dissipation; indeed, shifting from magnesite to calcite and anhydrite, the grain offers a better thermal protection. Figure 6 also shows that CaSO4, in view of its interesting intermediate volatility between carbonates and silicates, may actually reduce the duration of the heat peak in a substantial way. More volatile materials are able to keep a very low equilibration temperature but the chemical reservoir of carbonates is soon exhausted. This happens, for the most probable entry conditions, at high altitudes (~ 100 km) for CaCO3. A grain of CaSO4 is able to keep strong chemical cooling until about 80 km altitude.
On the other hand, a greater standard formation enthalpy for silicates leads to such a low volatility that temperatures are substantially controlled by radiation.
In this respect, plots showing the radiative and evaporative energy losses contributions are shown in figure 7 for few anhydrite MM entry scenarios.
Fig. 7. Radiative and evaporative energy losses during CaSO4 MM atmospheric entry.
Figure 7 shows that substantial evaporative cooling is offered by a CaSO4 grain at altitudes between 90 km and 80 km.
From about 80 km downwards, further heating mechanisms, that are not considered in this paper, may provide the additional thermal mitigation, which might be able to produce a scenario of ‘cold’ organic matter delivery. For example, the mean free path of air molecules decreases rapidly with altitude and becomes comparable with micrograin dimensions at about 70 km downwards: this produce conditions for thermal dissipation far from the grain, in the air shock wave and in the ‘evaporation cap’ hit by air molecules. Further studies should, therefore, consider this issue for the case of CaSO4 or other materials of comparable volatility.
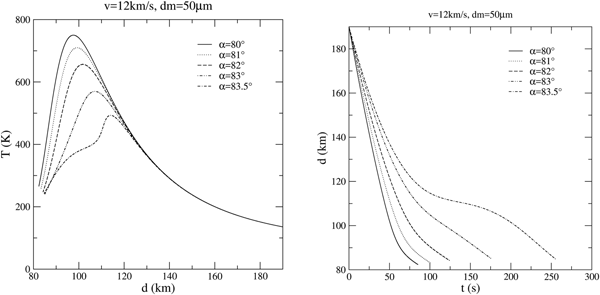
Grazing trajectories provide quite an interesting behaviour, since it is the main scenario in which larger grains are able to survive the atmospheric entry without melting (Love and Brownlee Reference Love and Brownlee1991; Hunten Reference Hunten1997). In figure 8, few thermal histories (temperature versus quota) and actual trajectories (quota versus time) are plotted for these grazing angles.
Fig. 8. Grazing entry scenarios.
As can be seen, the smooth deceleration experienced in these cases leads to longer entry times and modest heating.
Additional thermal protection may be produced by water in the mineral grain. Indeed, anhydrite has a strong affinity for water and forms more complex compositions, such as bassanite CaSO4 · 0.5(H2O) and gypsum CaSO4 · 2H2O; therefore, they might be even more promising materials. A scenario implying these phases could not be studied with the present model because it requires simultaneous equilibria and a description of the interaction of the H2O and SO3 species inside grain pores.
Conclusions
The conclusions of this paper can be grouped into two kinds of considerations. First of all, our calculations demonstrate that CaSO4 is a remarkable material for the organic matter survival in Space and its dissemination scenario, remarkably never considered in this light in past literature. Present calculations actually show that anhydrous calcium sulphate can survive the atmospheric entry substantially unaltered or only partially decomposed, reaching Earth's surface and that its chemical decomposition may actually mitigate the thermally induced damage of embedded organic matter.
On the other hand, this and our previous studies raise a case for what we called here ‘white soft minerals’, that should be intended as a wide class of mineral phases which share low hardness, lack of colour when pure, non-negligible and sometimes high capability to incorporate water, frequent association with life environments on Earth and finally a significant capacity of heat dissipation via chemical decomposition and/or dehydration of their solid solution with water. Although sparing previous works have considered water bearing silicates and much recently carbonates, these mineral phases have never been considered in the past as a unity in the context of astrobiology. This paper adds CaSO4 as a remarkable candidate material and formulates a strong suggestion that such minerals may become the subject for future studies in planetology and astrobiology.
Acknowledgments
The present research is part of the activities of the PON Apulia Space, which is acknowledged for partial financial support.
Appendix
A first estimate of the thermal gradient inside a CaSO4 MM during its atmospheric entry is presented here.
The MM (which is considered spherical, as stated in section ‘Thermochemistry of the entry model’) is divided into two concentric zones, an internal (index 1) and an external one (index 2); its density is constant (3 g cm−3). What we want to simulate is the heat transfer between these two shells, in order to evaluate the temperature difference (if there is any) between the inner and the outer zone of the grain during the atmospheric entry.
At the beginning, when the MM is about to enter the atmosphere, the temperature is uniform and in equilibrium with the solar radiation. In order to have a first evaluation of the initial temperature of the grain, a balance between the radiation losses and the solar radiation gain is assumed.
$$S \sigma T^4={\Phi S \over 4} $$where S in the grain surface, T its temperature, σ is the Stefan-Boltzmann constant and Φ is the solar constant (1367 Wm−2).
During the descent through the atmosphere, a heat flux arises between the two concentric shells (thermal conduction); in general, the Fourier law is assumed to be valid:
$${{\rm d}Q \over {\rm d}t}=-kS \nabla T $$where Q is the heat exchanged between the two zones and k is the thermal conductivity of the anhydrite grain (~ 2 WmK−1).
In order to write the temperature equations, we have to consider the inner and the outer zone separately. For the inner zone, only thermal conduction needs to be accounted:
$${{\rm d}T_1 \over {\rm d}t}= - {kS_1 \nabla T \over \rho V_1 c_{\rm v}} $$where S 1 is the internal surface and V 1 its volume, ρ is its density and c v is the specific heat.
For the outer zone, radiative and evaporative losses must be taken into account:
$${{\rm d}T_2 \over {\rm d}t}={kS_1 \nabla T \over \rho V_2 c_{\rm v}} - {S_2 \sigma T_2^4 \over \rho V_2 c_{\rm v}}-{S_2H(T) \over \rho V_2 c_{\rm v}}+{S_2 P_{\rm in} \over \rho V_2 c_{\rm v}} $$In equation A.4, the first term is the Fourier law for the outer zone in balance with the inner one. The second term represents the radiation heat losses (ε = 1). The third term describes the evaporation heat losses, that derives from the decomposition of CaSO4 to calcium oxide and sulphur trioxide. H(T) represents the energy loss per unit time and unit surface:
$$PH(T)={\Delta H^f J(T) \over N_{\rm A}} $$where N A os the Avogadro number. J(T) is the number of evaporating molecules per unit time and surface:
$$J(T)={\,p(T) \over 4Tk_B}\sqrt{{8k_BT \over \pi m_{{\rm SO}_3}}} $$p(T) is the vapour pressure, calculated as in equation 5, k B is the Boltzmann constant and 
$m_{{\rm SO}_3}$ is the mass of the gaseous component SO3.
The last term of equation A.4 is an estimate of the absorbed thermal power per surface unit. During the atmospheric entry, the energy input P in must be considered. We included a Gaussian fit of the P in resulting from the complete atmospheric entry model, valid for conditions of entry speed v entry = 12 km s−1, entry angle α entry = 45° and MM diameter dm = 100 μm.
The results, collected for a grain of 100 μm diameter, show that the difference between T 1 and T 2 is very small (figure 1).
Therefore, the assumption of isothermal grains for MMs is acceptable for the conditions of the present study.
