Futility of Linnaean Classification

Species cannot form clear-cut categories if we admit evolution which imposes mutability. Of course, this pre-supposes Darwinian rather than Lamarckian evolution. Similarly, there may be no clear demarcation between non-life and life if the latter evolves from the former. For instance, Strecker synthesis of amino acids is a chemical process while the reverse Krebs cycle is a biological process. There must be intermediate processes which allow the evolution of the biological from the inorganic (Szostak. Reference Szostak2012). One possibility in this specific case might be through the hydrolysis of thioesters CH₃–CO–SCH₃ formed from CO and CH₂SH catalysed by FeS minerals (Wachtershauser Reference Wachtershauser1992). Similarly, self-organization through far-from-equilibrium thermodynamics exhibits increasing degrees of complexity from physical to biological manifestations – Benard cells in convecting fluids at Rayleigh number beyond 1760 are a physical phenomenon; the Belousov–Zhabotinski reaction is a chemical phenomenon of greater complexity; and the Kauffman NK model of autocatalysis is a pre-biological phenomenon of still greater complexity. Such self-organization involves local interactions between components resulting in emergent global properties without any central control or supervision. Self-organization is a commonly exploited property of biological systems. For example, self-organization of the global cytoskeletal architecture of eukaryotic cells is emergent from the reaction–diffusion effects of individual cytoskeletal filaments.

Furthermore, lack of categorizability was manifest in early biological evolution. It is believed that the last universal common ancestor (LUCA) that eventually diverged into the three main domains of Archaea, Bacteria and Eukarya was constituted from a community of cellular organisms that were engaged in lateral gene transfer with elevated mutation rates rather than vertical gene inheritance (Woese Reference Woese1998). RNA-based genetic translation was simple, acting on multiple and redundant short genetic segments, and was error-prone, limiting protein sizes. Different progenitors possessed different metabolic capabilities which would be shared through lateral gene transfer. This is compatible with the curious incidence of genes shared by archaea and bacteria simultaneously with the genetic replication mechanism shared by archaea and eukarya, yet there appear to be strong similarities in DNA polymerases across all three domains. There was thus no single evolutionary cell line prior to the divergence of the great domains whence individual evolutionary cell lines were established. If so, the early origins of life are shrouded - no wonder that we seek to gain insights a la Richard Feynman (‘what I cannot create, I do not understand’).

The demarcation of life/non-life illustrates the limitations of logic classification – such limitations in logic have been well known in artificial intelligence because logic admits no contradiction (x and not-x cannot both be true), no change over time (x is true or false at all times), and no exclusion (x is either true or false). This was the reason for the introduction of degrees of truth through a veritable host of shades of grey – Bayesian, Dempster–Shaferian, non-monotonic, circumscriptive, modal, temporal and fuzzy logics – into artificial intelligence. The most extreme variation of this is non-well-founded (NWF) set theory which eschews logic almost entirely (Stepney Reference Stepney2012). Bruylants et al. (Reference Bruylants, Bartik and Reisse2010) favoured a fuzzy definition of life though, if pressed, my preference would be for a Bayesian approach for its greater rigour and versatility. As an example of greyness, there is debate over the nature of viruses which are commonly classified as non-life. However, viruses may be controversially characterized as alive in the sense that they are complex evolving organisms integrated into their host's molecular machinery for their own replication – in this phase of the viral lifecycle, the infected host cell is a viral cell (Forterre Reference Forterre2010). Viruses are highly efficient replicators because their host provides the replicating machinery that is hijacked by the virus. Viruses are an example of the difficulty in differentiating between life/non-life and the degrees of uncertainty involved. Indeed, from the folk perspective with which we opened our discussion, they are very much alive because they are ‘germs’ (though the pre-scientific miasma folk theory would not have viewed viral infections as being transmitted through living organisms).

Metabolism

All physicochemical reactions tend towards the lowest Gibbs free energy state according to the second law of thermodynamics. Living systems maintain themselves in a far-from-equilibrium state through the consumption of external energy. Metabolism is a network of chemical reactions and implies that the provision and consumption of energy are necessary to maintain and grow itself. Due to the second law of thermodynamics, this energy must be supplied from the environment. Such thermodynamically open systems form dissipative structures characterized by energy dissipation through dynamically stable structures under far-from-equilibrium conditions. It has been suggested that life creates more entropy in the universe through dissipative processes over ecological timescales than non-life, essentially driven by their efficient consumption of energy (Ulanowicz & Hannon Reference Ulanowicz and Hannon1987). A high-energy gradient in the environment is limited in its dissipative capability, creating local, highly ordered complex structures (life) far from thermal equilibrium to increase energy dissipation (Schneider & Kay Reference Schneider and Kay1994). Biological processes exploit captured energy to move far away from thermodynamic equilibrium to a state of low entropy with respect to the environment by storing the maximum exergy available (the maximum exergy principle) (Jorgensen & Fath Reference Jorgensen and Fath2004). Exergy is defined as the energy available for useful work. The maximum exergy principle is a version of Le Chatelier's principle that energy inputs shift equilibrium compositions of reaction systems. From this, metabolism may be defined as a system of self-maintenance that controls energy flows through the system (Moreno Bergareche & Ruiz-Mirazo Reference Moreno Bergareche and Ruiz-Mirazo1999). This management of energy with precise control of energy flows is essential to organize the material construction of metabolic substrates. We may regard metabolism powered by energy sources as a fundamental ingredient of life. The most basic form of metabolism for the generation of energy is the physicochemical redox couple involving electron donors and electron acceptors, such as anoxygenic photosynthesis by green and purple sulphur bacteria. They reduce sulphate as the electron acceptor (oxidant) to release H₂S as an electron donor for the reduction of CO₂.

Physical metabolism involving both material and energy processes is a necessary component of life (Boden Reference Boden2003). This disavows artificial life which considers only informational and evolutionary aspects of life without consideration of physicality. If the autopoietic aspect of self-production is an essential component of life, then evolutionary robots are excluded because while their evolved behaviours are informational, their bodies are artificially pre-constructed without metabolic exchange with the environment. Furthermore, evolutionary algorithms are driven by user-defined fitness functions rather than the open-ended evolution of biology. Contrarily, a self-replicating machine is fundamentally self-created from its physical environment where self-replication is an extension of self-repair which itself is a form of self-maintenance. Its capability to create physical copies of itself from the environment is a form of self-production so this would admit self-replicating machines to the ranks of life.

Encapsulation

The autopoietic definition of life proposes that life is a cellular system capable of self-production and self-maintenance through a network of processes within a self-made boundary that adapts to its environment (Bich & Damiano Reference Bich and Damiano2007; Damiano & Luigi Luisi Reference Damiano and Luigi Luisi2010). Self-production implies that genetic information is available while self-maintenance necessitates that there are metabolic processes. Autopoiesis emphasizes identity (referred to as autonomy) as a continuous and dynamic self-regeneration – a process of autopoietic self-organization (Maturana Reference Maturana1975). Structural identity and physical integrity of the lifeform – the cell – is derivative from the processes it encapsulates from its environment, i.e. metabolism. It is this metabolic activity that allows the entity to adapt to its environment through a continuous cycling of anabolic and catabolic processes, i.e. self-production and self-maintenance are the result of the same underlying process. An autopoietic system involves homeostatic processes that are autocatalytic as a whole by continually producing and recycling its components. An illustrative minimal autopoietic model is based on a two-dimensional (2D) cellular array which may be occupied by one of three types of particles: S (substrate), K (catalyst) and L (link) subject to three chemical reactions (Varela et al. Reference Varela, Maturana and Uribe1974):

$${\rm Production}\!:{\rm S} + {\rm S} + {\rm K} \to {\rm L} + {\rm K}$$

$${\rm Bonding}\!:\,{\rm L} + {\rm L} \to - {\rm L} = {\rm L} - $$

$${\rm Disintegration}\!:\,{\rm L} \to {\rm S} + {\rm S}\, {\rm (spontaneous)}$$

Chains of L particles can form a closed membrane that is permeable to S particles but impermeable to K and L particles, i.e. cell membrane structures. Initially, at least one K particle is enclosed within an L-membrane through which S particles permeate. These S particles are catalysed by K within the membrane to increase the concentration of L particles which cannot escape. As internal stresses build, the membrane ruptures due to disintegration. However, the high concentration of L ensures that they will seal the L-chain membrane. This models a continual cycle of anabolism and catabolism of the L-membrane. This cycle generates a steady state of the form:

$${\textstyle{{{\rm d}x} \over {{\rm d}t}}} = kx - gx$$

where k is growth rate and g is decay rate. Dynamic equilibrium occurs when k = g such that dx/dt = 0. The inhibition of bonding of L particles near chains of L particles is an essential feature in autopoietic modelling to prevent premature L-chain formation (McMullin & Varela Reference McMullin and Varela1997). This computational model and others (Schwegler & Tarumi Reference Schwegler and Tarumi1986; Cui & Friedman Reference Cui and Friedman1999) prove the computability of autopoiesis (McMullin Reference McMullin2004), refuting postulations that autopoiesis is non-computable.

Membrane-enclosed vesicles that separate self from non-self are an important property of life (Weber Reference Weber2010). The importance of a cell membrane to separate an internally controlled environment from the external environment has long been recognized, but both the coacervate and proteinoid concepts were implausible in lacking continuity with biological membranes. Intriguingly, lipid-like amphiphilic compounds such as PAHs, pyrene and fluoranthene have been extracted from the Murchison meteorite (Deamer & Pashley Reference Deamer and Pashley1989). Amphiphilic molecules comprise a polar hydrophilic tail and hydrophobic head which induces them to spontaneously self-assemble into vesicles as proto-cells (Deamer et al. Reference Deamer, Dworkin, Sandford, Bernstein and Allamandola2002). Self-assembly is spontaneous with amphiphilic molecules – they form a single-layer surface membrane on water with hydrophobic heads oriented above the surface and hydrophilic tails in the water. High concentrations of phospholipids form a double layer which encloses vesicles formed by high surface tension. Amphiphilic molecules may form via Fischer–Tropsch reactions catalysed on mineral surfaces. The membrane must be semipermeable to allow the flow of selective materials and energy. Self-assembling lipid membranes are an obvious candidate for early biological membranes. Reverse micelles may represent a minimal autopoietic system (Luigi Luisi & Varela Reference Luigi Luisi and Varela1989). They spontaneously self-organize into cells within which host aqueous chemical reactions produce its boundary surfactants (comprising a polar head and aliphatic tail). Alternatively, proto-membranes may have been iron/sulphur-based, formed near hydrothermal vents (Martin & Russell Reference Martin and Russell2003). The vesicles enclose polymers which may be formed in a number of plausible ways. Simple precursors to organic molecules that underlie biology can be synthesized into polymers in Miller–Urey-type reactions catalysed by clays under reducing conditions (such as CH₄ + NH₃ + H₂ or CO₂ + H₂ + N₂ or CH₄ + H₂O + N₂ atmospheres) with an energy source by Strecker condensation. Formaldehyde can be synthesized by photochemical reactions in Earth's primitive atmosphere as the primary step towards biochemical materials (Pinto et al. Reference Pinto, Gladstone and Yung1980):

$${\rm C}{\rm O}_{\rm 2} + {\rm 2}{\rm H}_{\rm 2} \to {\rm H}_{\rm 2}{\rm CO} + {\rm H}_{\rm 2}{\rm O}$$

From formaldehyde, many biological molecules may be synthesized:

1. (a) Production of the pentose sugar ribose:

   $${\rm 5}{\rm H}_{\rm 2}{\rm CO} \to {\rm C}_{\rm 5}{\rm H}_{{\rm 1}0}{\rm O}_{\rm 5}$$

2. (b) HCN may be synthesized under primitive Earth conditions (Oro et al. Reference Oro, Kimball, Fritz and Master1959):

   $${\rm H}_{\rm 2}{\rm CO} + {\rm N}{\rm H}_{\rm 2}{\rm OH} \to {\rm HCN} + {\rm 2}{\rm H}_{\rm 2}{\rm O}$$

3. (c) Amino acid glycine may be produced from HCN:

   $${\rm 3HCN} + {\rm 2}{\rm H}_{\rm 2}{\rm O} \to {\rm C}_{\rm 2}{\rm H}_{\rm 5}{\rm O}_{\rm 2}{\rm N} + {\rm C}{\rm N}_{\rm 2}{\rm H}_{\rm 2}$$

4. (d) The purine base adenine may be produced from HCN:

   $${\rm 5HCN} \to {\rm C}_{\rm 5}{\rm H}_{\rm 5}{\rm N}_{\rm 5}$$

Although Miller–Urey-type reactions have been questioned as pre-biotic processes on early Earth, similarly synthesized biochemical products may be concentrated into protocells by semi-permeable membranes that form spontaneously from phospholipids in water. More complex, multi-compartment lipid vesicles represent models of artificial cells in which multi-step biochemical reactions can be implemented (Elani et al. Reference Elani, Law and Ces2014). There have even been suggestions that a minimum of two membranes can implement computing functions (Paun, 2000). Liposomes are engineered vesicles for delivering drugs to the human body formed from the hydrophobic/hydrophilic properties of amphiphilic lipids in water (Mozafari Reference Mozafari2005). Self-assembled membrane bilayer vesicles formed by self-assembly of lipids constitute a minimal protocell – embedded primitive pigments such as porphyrins can convert photonic energy into electrochemical proton gradients for phosphorylation (Morowitz et al. Reference Morowitz, Heinz and Deamer1988). The cytoskeleton network of actin, microtubules and intermediate filaments in biological cells are fundamental in providing the basis for cell shape, compartmentation and intracellular traffic. The incorporation of hydrogel fibrillary networks self-assembled by hydrophobic interactions and hydrogen bonds in liposomes presents a simplified artificial analogue of a biological cell with an internal cytoskeleton (Brizard & van Esch Reference Brizard and van Esch2009). Artificial cells must include information-laden replicating molecules, polymerases to catalyse replicating molecules, and a translation system to convert genetic information into protein synthesis instructions (Pohorille & Deamer Reference Pohorille and Deamer2002). The protocell of the RNA world is premised on two RNA replicating molecules – one as a genomic template and the other as a ribozyme that catalyses the synthesis of amphiphilic lipids for the membrane (Szostak et al. Reference Szostak, Bartel and Luigi Luisi2001). Vesicles can then reproduce through amphiphilic growth until the lipid capsule becomes unstable and fissions into two vesicles. These arguments suggest that encapsulation from the environment is an essential feature of life.

Self-replication

The autopoietic view of life does not consider self-replication specifically, so autopoiesis may be regarded as a necessary but not sufficient condition for life (Luigi Luisi Reference Luigi Luisi2003; Froese & Stewart Reference Froese and Stewart2010). Indeed, according to autopoietic theory, reproduction is not a necessary property of living systems, but is merely a derivative property enabled by the unity of the living system for that unity to be multiplied (Varela et al. Reference Varela, Maturana and Uribe1974). It is conceivable that a living organism could exist that was incapable of self-replication – such an organism would have to emerge without any evolutionary heritage through pure self-organization. It has been suggested that a spontaneously emerging self-replicator on Earth would not have possessed an overall complexity exceeding 100–200 bits over the background environment (Jacobson Reference Jacobson1959). A necessary adjunct to autopoiesis is autogenesis which emphasizes the emergence of self-replication (Csanyi & Kampus Reference Csanyi and Kampus1985). Autopoiesis has been proposed to be part of a larger concept of (M, R) systems where M, metabolic activity and R, repair activity collectively imply that self-repairing metabolism is capable of replication (Letelier et al. Reference Letelier, Marin and Mpoodoziz2003). This implies that not all replicating systems are autopoietic. Autopoietic systems are further characterized by operational closure where metabolic processes feed into each other in a circular causal network. Autopoiesis must be supplemented with an open-ended evolution property (Ruiz-Mirazo et al. Reference Ruiz-Mirazo, Pereto and Moreno2004), for it is the evolutionary process that yields increased organismic complexity over time (Saunders & Ho, Reference Saunders and Ho1976).

Evolution is a learning process whereby information is extracted from the environment and incorporated into the lifeform. Darwinian evolution is a universal phenomenon premised on the notion of stored (genetic) information for which three properties occur: (i) variation (errors) due to random genetic mutation, (ii) selection favouring fitter individuals to a specific environment and (iii) inheritance whereby fitter individuals copy their characteristics onto the next generation through their offspring. The last implies the ability to generate copies, i.e. self-replication. Evolutionary capacity thus implies a self-reproductive capacity for mutation to operate during the copying process. Using λ-calculus, it has been demonstrated that self-replication logically precedes self-maintenance (Fontana & Buss Reference Fontana and Buss1994). By definition, autopoietic systems are to be differentiated from allopoietic systems. The latter converts raw material into a product (comprising an organized conjunction of those materials) other than itself, an example being a factory. Clearly, by definition, a self-replicating entity is not an allopoietic system because it yields products of itself. ‘The living is a factory that makes itself from within’ (Luigi Luisi Reference Luigi Luisi2003). Self-replication may thus be viewed as an essential ingredient of life. The so-called mule problem is readily dismissed in that reproductive capacity is potential rather than actual. Furthermore, evolutionary capacity is a property of populations rather than individuals – mules are part of an evolving gene pool of a population (Chodasewicz Reference Chodasewicz2014).

The earliest form of replication may have been uncoded and implemented through autocatalytic sets of organic polymers with Lamarckian inheritance (Gabora Reference Gabora2006). Regardless of the nature of early self-replication, life may have emerged when a non-metabolic replicator acquired metabolism to exploit external energy sources. It thus acquired purposefulness (Pross Reference Pross2008). Purposefulness as a characteristic of life has its roots in physicochemical reactions of metabolism during replication. Purposefulness arises through dynamic kinetic stability maintained by a persistent metabolism as distinct from thermodynamic stability representing a state of maximum decay. Kinetic stability is a unique property of persistent replicating systems and is dependent on the environment (Pross Reference Pross2005a). The competition for finite resources imposes a trend towards increasing kinetic stability –survival of the most stable. Complex replicators are kinetically more stable than simple replicators, hence driving evolution towards greater complexity (Pross Reference Pross2005b). These arguments suggest that self-replication is indeed, an essential property of life.

The definition of life is implicit in the origin of life question of whether metabolism or self-replication was the first property of life to emerge. In terrestrial life, folded molecular chains effectively implement computational processes as program strings, while molecular encoding in genes acts as a blueprint for the construction of these molecular chains, and through templating, the molecular codes implement their self-reproduction (Laing Reference Laing1975). The two aspects of life – genotype and phenotype – appear inextricable.

The RNA world attempts to circumvent the chicken-and-the-egg problem of metabolism versus genetic replication (Lazcano Reference Lazcano2010). RNA comprises a phosphate–ribose–phosphate backbone with nucleotide links forming a chain polymer. Within the RNA world, RNA acts as both a store of genetic information and as an organic catalyst for metabolic activity. This RNA world was enabled by its possession of both genotype (as RNA bases) and phenotype (as ribozymes). Information is held in the nucleotide base sequence while its folding pattern forms the catalytic structure. It suggests that RNA polymers (ribozymes) could catalyse their own synthesis and self-replicate, thereby establishing both metabolism and self-replication, perhaps encapsulated within a vesicle. The rRNA of the ribosome is a type of ribozyme. RNA replicase is an RNA molecule that is a template for genetic information and acts as an RNA polymerase to replicate itself. A simple protocell would comprise RNA replicase within a vesicle using nucleoside triphosphate (NTP) for energy (Szostak et al. Reference Szostak, Bartel and Luigi Luisi2001). As a single RNA molecule cannot simultaneously act as template and polymerase, two RNA molecules are required. Hence, molecular networks of RNA are required to sustain cooperative cycles of production (Pross & Pascal Reference Pross and Pascal2013). RNA replication requires the RNA replicase protein which begs the need for a supporting metabolism, i.e. an interconnected gene–metabolism–encapsulation triumvirate network (Rasmussen et al. Reference Rasmussen, Chen, Nilsson and Abe2003). Autocatalysis involves the presence of a product catalysing the original reagents – thus RNA acts as a template for assembling further RNA molecules. The emergence of genetic encoding of metabolic and lipid reaction rates is believed to involve some kind of autocatalytic feedback mechanism (Hordijk Reference Hordijk2013). Alternatively, peptide nucleic acid (PNA) has a hydrophobic polypeptide rather than phosphate–sugar backbone but with the same base pairing as DNA or RNA. PNA can act as an electron relay system with modifications. PNA replicates through ligation rather than the ribozymes that act as their own replicase required of RNA replication. The insertion of non-organic material into a proto-organism emphasizing a building blocks approach offers one possible transition between non-living and living matter (Rasmussen et al. Reference Rasmussen, Chen, Nilsson and Abe2003). However, the existence of RNA rather than PNA in today's terrestrial biology as a mediator between DNA and proteins favours the RNA world. RNA performs multiple functions – mRNA constitutes transportation mechanisms, tRNA constitutes jigs and rRNA constitutes the planner and controller for the ribosomes. However, RNA replication is more prone to error than DNA replication, and so subject to strong evolutionary processes. The DNA–protein world may have emerged from the RNA world through retroviral-like mechanisms. A protocell containing a self-replicating catalytic DNA may have represented the first living organism. Although specific to life on earth, the RNA world incorporated metabolism, self-replication and encapsulation. Life then is a collective set of properties.

Control systems

Cybernetic systems are another necessary and complementary component of living systems involving specific sensory inputs triggering specific actions, i.e. its internal processes are adapted to its environment (Bourgine & Stewart Reference Bourgine and Stewart2004). This implies that control mechanisms are an essential feature of life.

It may be instructive to examine synthetic biology in the Feynman tradition that creating yields understanding. To create artificial cells, simple biological cells may be simplified further (top-down) or assembled de novo from scratch from biological and non-biological materials (bottom-up) (Rasmussen et al. Reference Rasmussen, Chen, Deamer, Krakauer, Packard, Stadler and Bedau2004). In bottom-up synthesis, lipid vesicles may be self-assembled by amphiphilic aggregation encapsulating self-replicating RNA or the simpler PNA. Synthetic biology is also a bottom-up process that blurs the distinction between naturally evolved living organisms whose only goal is survival and human-designed and manufactured machines of inorganic material that serve human-dictated purposes (the latter being the subject-matter of this paper). In synthetic biology, new functionality to biological cells (acting as a chassis) can be introduced to complement natural biological nucleic acid/protein biochemistry (Benner & Sismour Reference Benner and Sismour2005). Self-replication in biology occurs through molecular template copying of genetic information which encodes physical properties of the lifeform. This requires molecular pattern recognition of which Watson–Crick pairing of large purines with small pyramidines (A–T and G–C) through hydrogen bonds is an example. An indispensable part of this recognition process is the phosphate–ribose backbone with its repeating charge. Shuffling hydrogen bond links permits the addition of four further base pairs forming a synthetic genetic alphabet (Sismour & Benner Reference Sismour and Benner2005). Similarly in proteins, different amino acids from the standard 20 can be introduced. Amino acids in polypeptide chains interact with each other due to their folding. Artificial polypeptides can be constructed from amphiphilic side chains of amino acids that replicate specific protein folding (Deming Reference Deming1997). This complements pre-existing biology within the constraints of biochemistry. Synthetic biology is exploring the limits of life further by attempting to re-design the biological realm to construct genetically engineered machines (Gibbs Reference Gibbs2004). There are three main thrusts: (i) synthesis of a minimal protocell; (ii) synthesis of minimal genomes; (iii) genetically engineered machines. Synthetic biology applies an engineering philosophy to biological components to build engineering functions from those biological components. It is the complement to the self-replicating machine concept explored later which uses engineered components to build a (biological) self-replication function. The major thrust of synthetic biology is the manufacture of a library or toolbox of logical functions from standardized biological genes that can yield biological components assembled to implement a specific device (McDaniel & Weiss Reference McDaniel and Weiss2005). These genetic segments of DNA – BioBricks – encode for biological components that implement known characteristics such as logic gates, sensors, actuators, etc that can be assembled like molecular Lego into cellular circuits such as logical implication and even more complex logics such as filters and feedback loops (Endy Reference Endy2005). Bistable switches have been developed which can act as memory elements which are heritable from one generation to the next. Similarly, the inverter BioBrick implements a NOT function which, with the AND BioBrick, provides logical universality through the composite NAND operator. These would be expressed within synthetic cells acting as chassis organisms. Nevertheless, they would retain their autopoietic character including self-production and self-reproduction and so be subject to evolutionary pressures. Hence, it would be human-designed in origin but will exist as a biological organism (Deplazes & Huppenbauer Reference Deplazes and Huppenbauer2009). This follows a similar logic to the self-replicating machine. However, in the Registry of Standard Biological Parts, many of the synthetic biology parts were of poor quality and did not function reliably, did not work when combined into circuits, were too complex to use, induced complex undesired reactions in the host cell, and desired functions often operated periodically rather continuously (Kwok Reference Kwok2010). These difficulties will not plague the engineered self-replicating machine presented later. There are more severe limits to synthetic biology (Zakeri & Carr Reference Zakeri and Carr2015). The chief problem in creating biological circuits is their long operation times compared with electronic circuits. Furthermore, as designed genetic circuits become larger and more complex, there is an increasing probability of mutation or genetic rearrangement. As manufactured functionality does not improve the fitness of the chassis organisms, there will be selection pressure to evolve out that functionality over time. Indeed, this occurs very rapidly, suggesting that fears of synthetic organisms escaping and engaging in damaging interactions with the outside environment are unfounded (Tucker & Zilinskas Reference Tucker and Zilinskas2006). Building in redundancy may improve the robustness and stability of the synthetic function but it will not suppress evolutionary processes. If a mechanism is found to suppress evolution, then these synthetic organisms would no longer be alive (Schark Reference Schark2012). Autopoiesis would be compromised because continuous self-regeneration would no longer operate. The organism would have a complex organization but no longer any self-organization capacity. However, it has been asserted that self-organization with complex global phenomena emerging from simple local microscopic phenomena is, in fact, a functional property of life (Bedau Reference Bedau, Varela and Bourgine1992).

Movement in some form is implicit in biological systems in order to acquire and transport nutrients (see the Appendix on molecular motors). All molecular motors convert chemical energy into mechanical work. Switching between biological conformations which is fundamental to biological molecules may be regarded as a form of self-assembly which can be described formally as graph grammars (Klavins Reference Klavins2004). Molecular motors evolved from such molecular switches – kinesin, myosin and G proteins appear to have evolved from an ancestral nucleotide-binding protein while F₁-ATP synthase seems to have evolved from a different nucleotide-binding protein (Vale Reference Vale1999). Kinesins comprise a superfamily that has evolved a diverse set of functions through gene duplication while dynein molecular motors appear to have been conserved (Goldstein Reference Goldstein2001). All however evolved in early eukaryotes in a wide variety of cargo-handling types, sometimes with different motors recruited for similar functions – actin is used for membrane transport in plant cells while microtubules are used for the same in animal cells (Vale Reference Vale2003). While certain motors may be dominant in different species, mitotic kinesins are common to all eukaryotes. Porters – such as kinesin – that walk along microtubules have high duty ratio while rowers – such as myosin – that operate in teams have low duty ratio. Kinesin is the most abundant motor in most eukaryotic cells and is similar to myosin insofar as they both comprise two heavy chains and two light chains. The heavy chains fold into the two globular heads each containing the ATPase sites. Kinesin is the smallest motor protein of ~340 amino acids compared with ~850 amino acids of myosin and ~1000 amino acids of dynein. Kinesin and myosin motors respectively share a common core structure and function by ATP-powered conformation changes (Kull et al. Reference Kull, Sablin, Lau, Fletterick and Vale1996; Vale & Milligan Reference Vale and Milligan2000). One common feature in both motors is the almost identical γ-phosphate sensor to detect presence or absence of a single phosphate (ADP/ATP) – it comprises two loops that form hydrogen bonds with the γ phosphate. The relay loop moves like a piston with an upstroke on phosphate binding and downstroke on phosphate release. Kinesin and myosin appear to have evolved from a common ancestor with G proteins. Myosin V is a special myosin which transports organelles along actin filaments; kinesins have evolved similar mechanisms for multi-step motion. Motors also operate in prokaryotes. Plasmid and chromosome segregation in mitosing prokaryotic cells is undertaken by homologues of actin filaments acting as cables (Gerdes et al. Reference Gerdes, Meller-Jensen, Ebersbach, Kruse and Nordstrom2004). Furthermore, these and other actin-like proteins such as MreB and ParM act like centromeres for plasmid segregation during mitosis (Egelman Reference Egelman2003). MreB cell shape proteins form large spirals in rod-shaped bacterial cells acting as a precursor cytoskeleton – MreB proteins are absent in spherical bacteria, however. MreB proteins have a similar structure to filamentous actin in eukaryotes and indicate that the eukaryotic cytoskeleton originated in the prokaryotic domain (van den Ent et al. Reference van den Ent, Amos and Lowe2001a).

Bacterial FtsZ (filamentous temperature-sensitive) protein involved in bacterial mitosis is similar to eukaryotic tubulin that is the basis of its cytoskeleton (van den Ent et al. Reference van den Ent, Amos and Lowe2001b). FtsZ is a ubiquitous and highly conserved GTPase in most eubacteria including chloroplasts and mitochondria and is common in archaea. Although there is limited amino acid homology (10–18%) between FtsZ and α- and β-tubulins of eukaryotes, they are similar in structure with common folds suggesting a common evolutionary origin. In eukaryotic cells, however, chromosome segregation during mitosis is undertaken by microtubule fibres fixed to the centromere which pull the chromosomes apart (Taylor Reference Taylor2001). Eukaryotic cells can form extended mitochondrial filaments forming cable networks connected by intermitochondrial junctions for the transmission of energy through the cell (Skulachev Reference Skulachev2001). It has been suggested that fibres are a ubiquitous feature of biological material – they form the cytoskeleton as the basis for cytoplasmic streaming, cilia and flagella movement, chromosome migration, cytokinesis and muscle contraction (Frixione Reference Frixione2000). The cyclic reaction of a motor protein with a cytoskeletal fibre is a common architecture – the myosin motor on actin filaments and the dynein and kinesin motors on microtubule filaments. On binding with the filament, the motor protein in each case undergoes a conformation change (power stroke) to generate a movement step. The motor then releases the filament before rejoining further up the filament for a repeated step.

Bacterial flagella are powered by motors that can rotate in either direction (Blair Reference Blair1995). When the bacterial motor turns counter-clockwise, the filaments of the flagellum form a bundle that propels the cell along a smooth trajectory. If a motor reverses direction clockwise, the bundle unfolds into an array of individual uncoordinated movements generating tumbling. Typical motion is essentially alternation between runs and tumbles, i.e. a random walk. Directionality involves controlling the frequency of reversals in response to sensory detection of stimulants. The detection of attractor stimulants such as glucose suppresses the clockwise tumbling. Conversely, clockwise runs in unfavourable directions are suppressed by repellants. When bound to a repellant, Tar protein receptors in the cell membrane stimulate autophosphorylation of CheA which transfers its phosphate group to CheY. Phosphated CheY then interacts with the flagellar motor to increase the probability of tumbling by clockwise rotation of its flagellar motor. When bound to an attractor, CheY remains unphosphorylated and increases the probability of straight swimming by anticlockwise rotation of the flagellar motor. In fact, it is the change in concentration over time that is measured, requiring a short-term memory capability implemented by methylation of the chemoreceptors. Hence, the bacterium propels itself in the direction of higher concentrations of nutrients. Bacteria can also form highly complex colonies with the emergent functional and cognitive properties of a multicellular super-organism. These bacterial communities exhibit a number of modes of inter-cell biochemical signalling such as quorum sensing and chemotactic sensing (Ben-Jacobs Reference Ben-Jacobs2009).

In prokaryotes, most movement is passive though it is essential as a life function nonetheless. In terrestrial water-laden environments, nutrients flow passively so that static organisms can intercept them. Once acquired, these nutrients are ingested by bacteria and migrate within the bacterial cell by passive diffusive processes. Some bacteria have invented rotary motors to drive flagella to move in search of nutrients more efficiently. Furthermore, in some bacteria, the rudiments of internal transport tracks have evolved. In eukaryotes, such tracks are adopted for internal movement of cargo within the cell. They are also spanned by linear ‘legged’ motors which tend to be large in comparison with rotary motors. Is it not conceivable for some postulated exo-bacteria to have evolved proto-tracks spanned by bacterial rotary motors similar to a rack-and-pinion gear in, perhaps, a more hostile environment? My contention is that movement to acquire and transport nutrients is a necessary condition for life, a consideration not usually appreciated given that Earth's environment often provides this facility for free at the scale of bacteria. Furthermore, internal/external is defined relative to an enclosing membrane – movement internally and externally achieves the same goal of accessing resources for consumption. We contend that movement implies a cybernetic control system as a necessary condition of life.

Life as a list of properties

Hence, we are back to a list of properties of life embedded in an environment from which it must consume resources. The properties of life may be ascertained from the bacterial genome and its coding – a typical bacterial genome comprises 30% non-protein coding genes, 10% for energy metabolism, 17% for genetic transcription and translation, 12% for cell transport and 8% to cell envelope proteins such as adhesins (Bloom Reference Bloom1995). Our generalized list of properties is thus:

1. (i) Self-maintenance and growth through metabolic processes through the ingestion of matter and energy and the excretion of waste;

2. (ii) Self-boundary through cellular encapsulation from the environment by constructive metabolism;

3. (iii) Self-reproduction capability and therefore capacity to evolve in response to environmental pressures;

4. (iv) Cybernetic facility through adaptive control system mechanisms to adapt to the environment.

The unofficial NASA definition of life attributed to Gerald Joyce is: ‘Life is a self-sustained chemical system capable of undergoing Darwinian evolution’. Although there are dissenters to this definition (Luisi Reference Luisi1998), it is succinct and there are a number of characteristics implicit in this definition. Chemical system implies metabolic biochemistry and Darwinian evolution requires self-reproduction. As a chemical system, it excludes artificial life but does not exclude engineered life. Capacity for Darwinian evolution does not require life to have an evolutionary history, only an evolutionary future, though an evolutionary past may be inferred in natural systems. All life on the Earth is carbon-based involving water as the fundamental biochemical solvent and most astrobiology work is premised on this. The lack of detection of organic material on Mars by Viking's gas chromatograph mass spectrometer (though this result has since been contested) trumped the detection of labelled CO₂ from its labelled release experiment on that basis (the overall conclusion has not changed even in the light of contested measurements). Hypothetical silicon-based life or liquid ammonia as a biochemical solvent has not been entertained seriously. For instance, Si does not form double sp or triple sp² bonds but its d orbitals do permit the formation of dπ–pπ bonds. Nevertheless, there have been attempts to consider life from a broader perspective (Schulze-Makuch & Irwin Reference Schulze-Makuch and Irwin2008). The work presented here is part of an ongoing research programme that will explore several key open issues in engineered life including ‘How does life arise from the nonliving?’ (Bedau et al. Reference Bedau, McCaskill, Packard, Rasmussen, Adami, Green, Ikegami, Kaneko and Ray2000). In doing so, we retain the control system property of life. As pointed out in (Brack & Trouble Reference Brack and Trouble2010), robotics has been emulating many of the characteristics of life including replicating and evolving behavioural properties through genetic algorithms (Eiben Reference Eiben2014). Evolutionary robotics involves using genetic algorithms to evolve neural networks to implement specific behaviours on physical robots. Of great interest is coevolution of both behaviour and bodily morphology. Robotics to date, however, has not yet demonstrated self-replication of bodily form. This is what we explore here.

Self-replicating automata

Looking to artificial life as an exploration of non-terrestrial life, the key motivation is to broaden from life-as-we-know-it to life-as-it-could-be (Umerez Reference Umerez2010). There are three approaches: (a) soft artificial life involving software simulations; (b) hard artificial life involving hardware implementations; (c) wet artificial life involving chemical implementations (Bedau Reference Bedau2003). Our approach is a combination of all three to form a fourth approach: (d) engineered life involving manufacturing physical resources.

Cellular automata (CA) constitute the main modelling environment for artificial life. Indeed, there are many examples of CA models of different biological phenomena including developmental biology (Ermentrout & Edelatein-Keshet Reference Ermentrout and Edelatein-Keshet1993; Calabretta Reference Calabretta, Bandini, Serra and Suggi Liverani1998). CA are highly abstract but serve to illustrate the logic of life divorced from the physicality of life. CA comprise a chain (1D) or lattice (2D) of cells, each of which can be in one of a finite number k of possible states. They are updated every discrete timestep with a well-defined transition rule that depends on the state of its R neighbours. The simplest CA is a 1D string of cells, the states (with two states 0 and 1) of which are dependent on the flanking neighbours. For 2D arrays, there are two commonly adopted neighbourhoods: the von Neumann neighbourhood consists of the R = 4 neighbouring cells to the north, south, east and west; the Moore neighbourhood consists of the R = 8 neighbouring cells to the north, south, east, west, north-east, south-east, north-west and south-west. Hence, each cell is a finite state machine with transition rules applied only locally based on the local neighbouring states. The CA can simulate different Wolfram universes of logic (Wolfram Reference Wolfram2002): in class 1, initial configurations evolve to a fixed configuration; in class 2, initial configurations evolve to a periodic cycle of configurations; in class 3, initial configurations evolve into chaotic behaviour; in class 4, initial configurations evolve complex localized structures with global behaviours. Class 1 and 2 CAs exhibit only localized information transmission (λ = 0); in class 3 and 4 CAs, information transfer is however global (λ > 0). The dynamic Langton λ factor which varies from 0 to (1–1/k) – defined as the fraction of active output states in the rule table – attempts to quantify these classes and defines a critical value λ_c that corresponds to class 4 at the ‘edge of chaos’. It has been suggested that this class possesses the capacity for universal computation but it has been questioned whether CAs can be quantified in this fashion. Nevertheless, the notion of computability in CAs is an important property which defines the capacity of the specific CA (Mitchell Reference Mitchell, Gramss, Bornholdt, Gross and Mitchell1998). Central to computability is the Turing machine and the limit imposed by the Turing halting problem that there exists no general algorithm that can predict whether an algorithm halts, i.e. halting is undecidable (Turing Reference Turing1937). However, halting is decidable in a two-state CA with a von Neumann neighbourhood. The simplest CAs that support universal computation have k = 18 and R = 3 in 1D and k = 3 and R = 3 in 2D (Wolfram Reference Wolfram1985). A 1D CA with (m + n + 2) states can simulate a Turing machine with n states and m alphabetic letters.

Conway's Game of ‘Life’ is a CA system of 2D cells that illustrates the phenomenon of emergence. Each cell has two (binary) states – it is either alive (1) or dead (0). The next state is determined by the state of its eight neighbours (Moore neighbourhood) according to specific local rules. If there are three living neighbours, its state is alive; if there are two or less or four or more living neighbours, the cell dies of loneliness or overcrowding respectively. From the interaction of such simple cells, highly ordered complex structures can emerge (Crutchfield Reference Crutchfield1994) – the glider is a local pattern that moves through the CA array diagonally as an integrated unit. The glider gun configuration emits regularly spaced gliders every 30 time steps. If a glider encounters a square block of four cells, they collide and mutually disintegrate – a law of physics that is not specified in the CA rule set. Hence, complex structures can emerge from very simple cell rules. Although the rules are local, they can yield globally emergent phenomena such as universal computation. ‘Life’ is capable of universal computation by exploiting glider guns and gliders. Logic functions are constructed by interacting streams of gliders. For example, a NOT gate is implemented by two perpendicular gliders colliding and annihilating each other. AND/OR gates can be implemented similarly while memory is implemented through circulating gliders. Of course, such implementations of universal computation are cumbersome and impractical. Artificial chemistry (AC) such as Squirm3 has successfully modelled the emergence of self-replicating molecules (Hutton Reference Hutton2002). AC is a form of CA that defines a triple (S,R,A) where S = set of all possible molecules, R = set of collision rules and A = algorithm defining physical rules. Unlike CAs, artificial chemistries do not constrain the movement of molecules to a regular grid. Bonds are formed between atoms on collision but bonds can be broken by reactions. A set of eight reactions defining how two different atoms combine to form molecules are sufficient to permit the spontaneous emergence of self-replicators from a primordial soup of atoms.

The first systematic consideration of self-replicating machines was that of John von Neumann (von Neumann & Burks Reference von Neumann and Burks1966). His 2D CA-based self-replicating machine required each cell to have 29 states including an inactive state. The CA model comprised five major subsystems: (i) a program of instructions; (ii) a sequencer; (iii) a controller; (iv) a constructor arm; and (v) a workspace environment. A more physically realistic kinematic model of the von Neumann self-replicator comprised eight different components in two major systems – four logic components for control signals and four mechanical elements for structure and mobility. The two major subsystems were: (i) a tape unit, itself comprising a linear memory tape and a tape control unit, i.e. a universal Turing machine (computer); (ii) a constructing unit comprises a robot arm and an arm control unit, i.e. a universal constructor. The control program is stored on the memory tape that instructs the robotic arm to select, acquire and assemble components from a sea of pre-fabricated constituent parts in the working environment – in effect, it was a self-assembling machine. The construction unit signals the tape unit and reads the instructions as a set of (x ₀, y ₀) start coordinates and (Δx, Δy) movements for the robot arm. Thus, the universal Turing machine and the universal constructor send sequences of signals to each other to control the construction of the machine according to the program blueprint. The robotic arm picks up a part from the environment and inspects it to compare it with the program's specifications. If correct, it joins this new part with the ongoing assembly. The robotic arm model of the universal constructor is essentially a pick-and-place assembly manipulator. If the tape constitutes a description of itself, the constructor arm builds a copy of itself. It then copies its program and inserts it into the new machine. The machine (analogous to proteins) that is constructed is determined by the construction program stored on the memory tape (analogous to DNA) – it is a universal constructor comprising a universal Turing machine to store and interpret information on the program tape and a robotic arm to act on those instructions to build the phenotypic expression of those genetic instructions. The universal constructor can construct any machine specified on its tape given the required raw materials, energy and information. One such program is a self-specification to construct a copy of itself – a self-replicating machine (Freitas & Merkle Reference Freitas and Merkle2004). To pass on this self-replication capability, the tape must be copied into the offspring. Thus, the instructions on the tape are used in two ways – first, it is read and interpreted (and so executed) during construction (analogous to biological translation) then it is read passively (uninterpreted) during copying (analogous to biological transcription). A computer model of the von Neumann self-replicator has been simulated (Pesavento Reference Pesavento1995). In biology, the process is more complex. During transcription, the nucleotide base sequence of a strand of DNA is transcribed onto messenger mRNA with the complementary sequence. During translation, mRNA is associated with a ribosome (constructed from one large 50s and one small 30s ribosomal rRNA and proteins) to map to the equivalent amino acid sequences. The mRNA sequence is encoded into triplets, usually beginning AUG and ending with stop codons UAG, UAA or UGA. The mapping process is realized through tRNA and aminoacyl-synthetases with tRNA acting as an adapter molecule between mRNA and an amino acid. There are at least 64 different types of tRNA and specific types of aminoacyl-synthetase. mRNA is aligned with the ribosome to ensure that the ribosome reads the mRNA codons.

Simplifications to von Neumann's formulation exploit sheathed loops where the instruction sequence structure is surrounded by a sheath to provide a path for signal propagation. The sheathed loop was a modified Codd periodic emitter loop which implemented a time-delay/memory function which formed the basis of Codd's 8-state self-replicator (Hutton Reference Hutton2009). Data sequences circulating around the instruction loop would intercept the origin of the constructing arm causing a copy to propagate along the arm and causing it to extend or bend. If the data sequence is a replication code, then the sheathed loop becomes self-replicating with the arm printing a second loop that detaches and replicates ad infinitum (Langton Reference Langton1984). The Langton replicating sheathed loop of 86 active eight-state cells with 219 transition rules allowed abandonment of universal construction. The Langton loop is a pure self-replicator in which a closed loop transmits signals to perform the dual function of both interpreted and uninterpreted instructions. Replacing the sheath around the instruction loop with a growth cap at the tip of the constructing arm retains simple self-reproducing structures of 32 active eight-state cells with 177 transition rules (Reggia et al. Reference Reggia, Armentrout, Chou and Peg1993). In fact, even smaller self-replicating entities are permissible such as six active eight-state cells with 91 transition rules and 12 active six-state cells with 46 transition rules. Hence, universal construction is sufficient but not necessary for self-replication. Such pure self-replicators are not universal constructors and are highly simplified (analogous to prions) but cannot be considered models of life. We submit that universal construction is a universal feature of life.

The self-replicating machine concept – which reads its self-description – can be logically extended to a machine that can self-replicate by self-inspection, i.e. examine itself to infer a complete structural description of itself (Laing Reference Laing1979). The key capability is an active cellular string in sliding contact with another passive cellular string that accesses the passive string data. Hence, a universal constructor can, by self-inspection, can construct a copy of itself. This is biologically implausible as it represents a Lamarckian evolutionary process. However, the ability to self-inspect provides a mechanism for self-repair with reference to pre-existing instructions. The Godel machine is a further extension which is a universal computing machine that can rewrite itself if a proof search embedded in the initial algorithm can prove that the rewrite yields rewards to a utility function, i.e. it is a learning algorithm that interacts with its environment (Schmidhuber Reference Schmidhuber, Goertzel and Pennachin2007). Learning algorithms are premised on the notion that the future is a reflection of the past (as is evolution). In this way, such self-changes through self-introspection (in essence, self-consciousness) allow the system to step outside of itself thereby circumventing the limits of a closed arithmetic system. Self-reproduction by self-inspection rather than a stored program of instructions has been demonstrated in the form of analogue control circuitry (Suthakorn & Chirikjian Reference Suthakorn, Chirikjian, Ang and Khatib2006). Such circuitry is 2D in nature so does not possess volume, thereby ensuring that the system is completely observable. The system observed the configuration of colour-coded electronic components serially using a phototransistor sensor mounted on a Cartesian gantry system. It selected a copy of the currently observed component from a feeder. By serially observing the circuit components, component copies were assembled in sequence until the entire circuit was replicated. Of course, self-replication by self-inspection requires complete self-observability, a condition that in general will not be valid. Self-inspection illustrates that the logic of self-replication opens up possibilities that go far beyond the strictures of life on Earth and may be of interest to the astrobiological community.

Notwithstanding all this, von Neumann's self-replicator is more a self-assembling system rather than a self-replicating system as it involves assembling a series of parts or components to construct a complete configuration. A recent example of such a self-assembling system employed a set of cubes, each of which was divided into two halves that could rotate relative to each other in a diagonal plane (Zykov et al. Reference Zykov, Mytilinaios, Adams and Lipson2005). Each face of the cube was equipped with an electromagnet permitting cubes to attach to each other. A tower of such cubes can pick up other cubes in its environment to construct a copy of the tower, i.e. self-replicate after a fashion. Self-assembling structures are widespread in both chemistry and biology. Although molecular self-assembly is ubiquitous in the biological world, we shall not consider it further here. The environment in reality constitutes a soil of raw material rather than a sea of ready-made components. Practical self-replication involves extracting and processing materials into complete parts or components. An early example of this concept for the terrestrial environment was the artificial living plant concept which was to absorb air, water and soil as raw materials using solar energy to construct copies of itself (Moore Reference Moore1956).

For our self-replicating machine, we are attempting to demonstrate 3D printing of electric motors (the basis of the constructing arm) and electronic circuitry based on vacuum tubes (the basis of the computer) as the fundamental components of a self-replicating machine. These critical components will provide an existence proof that a 3D printer-based self-replicating machine can be constructed. We approach our self-replicating machine through four major biological principles.

Biological Principle 1: materials closure

The first issue to consider is the materials and component inventory required to construct our self-replicating machine. Materials (food) must be acquired from the environment – for an autotroph, this is inorganic material for both engineered and biological organisms. In the case of the Moon, the lunar regolith must be transformed into elementary parts to be assembled into the final product – this is in-situ resource utilization (ISRU). Self-replicating machines on the Moon were proposed in an early study (Freitas & Gilbreath Reference Freitas and Gilbreath1980) and subsequently developed further but the latter were self-assembling concepts based on Lego bricks (Chirikjian et al. Reference Chirikjian, Zhou and Suthakorn2002; Ellery Reference Ellery2016a,Reference Elleryb,Reference Elleryc). We begin with a raw materials list for our self-replicating machine. The materials ingested by the self-replicator are also the first radical departure from the materials adopted in synthetic biology. Engineering metals have high strength and stiffness (robust) – commonly metals – while biological materials have low strength and stiffness but high toughness and elasticity (adaptable) – commonly non-metallic elastomers – which is particularly useful for mechanical energy storage (Ellery et al. Reference Ellery2004). Biological materials are synthesized at moderate temperatures through the use of catalysts while engineering materials are manufactured at high temperature. An interesting question that emerges is ‘is life restricted to low-temperature regimes?’ Enzymes are biological catalysts that serve to increase the rate of biochemical reactions. If organic material is the elan of life, then life will be restricted to moderate temperature regimes. However, it is the chemical reaction that constitutes metabolic function, the enzyme merely facilitating it. If the logic of life is independent of its material substrate, then there is no reason why engineering materials cannot provide the basis for life. There are some precedents for such a notion.

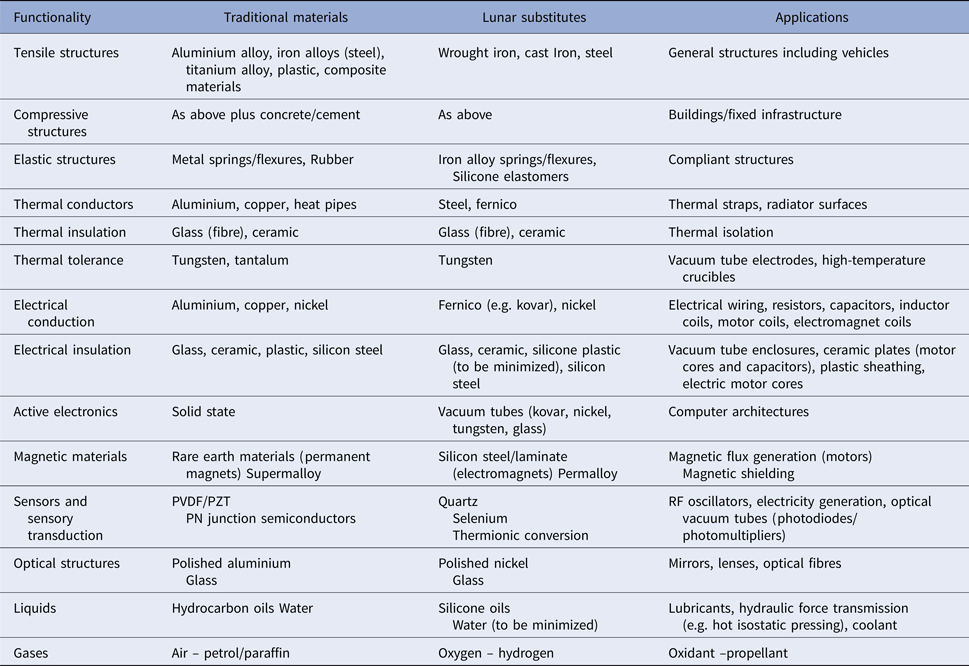
Clays are non-organic minerals that provide surfaces and cavities that constrain the formation of 3D conformation structures from simple precursors such as HCN, HCHO, etc. It has been postulated that biological catalysts evolved from inorganic catalysts such as mineral surfaces (Cairns-Smith Reference Cairns-Smith1990). Montmorillonite (Al₄(Si₄O₁₀)₂(OH)₄.xH₂O) clay may have acted as one of the first organic catalysts in the origin of life through the RNA world (Ferris Reference Ferris2005) and perhaps even prior to the RNA world as the first medium of genetic information storage (Cairns-Smith Reference Cairns-Smith1987). The clays montmorillonite and illite provide catalytic mineral surfaces for the polymerization of 20–50 monomer-long oligomers of nucleotides and amino acids, respectively (Ferris et al. Reference Ferris, Hill, Liu and Orgel1996). Montmorillonite, in particular, can catalyse the polymerization of oligopeptides and oligonucleotides (Schwartz Reference Schwartz1996). Montmorillonite may have catalysed the synthesis of RNA polymers of length greater than 40 bases in length as required to act as both template and catalyst (Ferris et al. Reference Ferris, Joshi, Wang, Miyakawa and Huang2004). Specific catalysts for polymerization and replication could be implemented using clays within a protocell. The postulated RNA world was probably preceded by inorganic replicators such as crystal defects in clays, and mineral surfaces may have provided key metabolic processes in a protocell (Wachtershauser Reference Wachtershauser1990). Inorganic metabolism such as the iron–sulphur world is consistent with hydrothermal vents with such proto-metabolism, possibly enhanced with hypercyclic feedback systems (Szostak et al. Reference Szostak, Wasik and Blazewicz2016). If a catalyst (inorganic or organic) is replaced or supplemented by higher thermal energy, the chemical reaction is still hastened. Does this absolve it of its biological character? We suggest not. Rather than CHONPS, we are adopting a minimal suite of engineering materials that can implement all the functions required of a self-replicator in its environment – we focus on the Moon for a number of reasons not relevant to this argument (Ellery Reference Ellery2016a,Reference Elleryb,Reference Elleryc). This approach brings to mind the emphasis placed on physicochemical processes on the nature of life (Schultze-Makuch & Irwin Reference Schultze-Makuch and Irwin2004). Our self-replicator must extract its restricted set of feedstock materials – iron, silicon, nickel, cobalt, tungsten, selenium, silica-based glass, silicone plastic (siloxanes) and water – from raw materials (mineral ores). The restricted range of required materials must be able to implement all the material functions required – compressive/tensile structures (bones/tendon), thermal insulation and conduction (fat/bloodstream), electrical conduction and insulation (axons/myelin), switching logic (neurons), etc. – whilst minimizing the infrastructure required to extract it (Table 1).

Table 1. Materials inventory required for a lunar photolithoautroph

This materials inventory can be readily extracted from surface lunar minerals and near-surface NiFe asteroid material on the Moon. Over the aeons, solar wind has deposited volatiles at an average rate of 3 × 10⁸ particles cm⁻² s⁻¹ into the top few mm of soil. However, impact gardening has impregnated this material to a depth of a few metres. Solar wind comprises 96% H₂ which has accumulated into a regolith concentration of 20–200 ppm (average ~120 ppm) plus almost 4% He³ (with a He³/He⁴ ratio of 3 × 10⁻⁴ by mass) plus many minor constituents including carbon compounds. The common lunar mineral ilmenite (FeTiO₃) in the 35–55 µm grain size range also preferentially adsorbs these volatiles compared with other minerals with the degree of volatile-enrichment increasing at finer grain sizes ~10 µm. Loosely bound volatiles may be thermally evolved from surface regolith at temperatures of 600°C to release 75% of the volatile inventory (this increases to 86% at 700°C, 95% at 800°C and 100% close to 1000°C). Although dominated by H₂, additional volatiles – SO₂, CO/CO₂/CH₄, N₂, F₂, Cl₂, etc. will be released. Carbon in the form of CO, CO₂ and CH₄ volatiles is relatively scarce compared with mineral resources with an average abundance of 120 ppm (Fegley & Swindle Reference Fegley, Swindle, Lewis, Matthews and Gurrieri1993). Fractional distillation may be employed to separate the gas fractions due to their well-separated condensation temperatures – He (4.2 K), H₂ (20 K), N₂ (77 K), CO (81 K), CH₄ (109 K), CO₂ (194 K) and H₂O (373 K). The synthesis of silicone oils and silicone plastics from syngas-derived from lunar volatiles is outlined in (Ellery Reference Ellery2016a,Reference Elleryb,Reference Elleryc). Silicones are chosen over hydrocarbons for their radiation hardness, high-temperature tolerance, functional properties and economic consumption of carbon.

Heating the mineral ilmenite to ~1000°C in the presence of H₂ reduces it to pure Fe, TiO₂ and H₂O: FeTiO₃ + H₂ → Fe + TiO₂ + H₂O. The water may be electrolysed to recycle the H₂ and store O₂: 2H₂O → 2H₂ + O₂. Iron forms the basis of our self-replicator's tissue but it requires the addition of further elements to provide a range of alloys for different functions – Ni, Co, Si, W and Se. In lunar regolith, Fe, Ni and Co particles are associated together as 5–60 µm inclusions in troilite of meteoritic origin (Wittmann & Korotev Reference Wittmann and Korotev2013). However, it would be desirable to gain access to these materials in more concentrated form. The cobalt content of lunar and terrestrial mantles is similar. The Ni/Co ratio of the Moon's mantle and the Earth's mantle are similar to that of chondrites (Ringwood & Seifert Reference Ringwood and Seifert1986) (Table 2). This suggests that the Moon's abundance of Ni should be similar to that of Earth's mantle. However, Ni is depleted in the lunar mantle by a factor of 3 suggesting a Ni-rich metal lunar core. This constitutes evidence that the Moon was derived from the Earth's mantle after the Earth's core had formed. Nevertheless, lunar igneous rock often contains high Ni (up to 56%) and Co (up to 9%) content in FeNi metal inclusions, especially olivines but sometimes also in plagioclase. Lunar mantle olivine ((Mg,Fe)₂SiO₄) offers the highest source of associated Ni and Co favouring the lunar south pole Aitken basin where lunar mantle material may have been excavated – however, the crater shallowness suggests that no mantle material was in fact excavated (Wieczorek & Phillips Reference Wieczorek and Phillips1999). The two chief question marks concern the availability of tungsten which is a critical material for thermionic processes and selenium for its photosensitive response. On the Earth, tungsten has an average concentration of 1–2 mg kg⁻¹ and is typically found as wolframite ((Fe,Mn)WO₄) and scheelite (CaWO₄). It is enriched in several rock-forming minerals including igneous Fe–Ti oxide minerals which can contain up to 10 mg kg⁻¹ W. Its availability on the Moon is limited.

Table 2. Ni and Co abundances in the lunar source material (ppm) [adapted from Ringwood A & Seifert S (1986)]

Meteoritic material is the most likely material to contain high concentrations of iron, nickel, cobalt and tungsten (Ellery Reference Ellery2016a,Reference Elleryb,Reference Elleryc). A NASA proposal to capture a small ~1 m diameter asteroid and re-direct it into lunar orbit offers a potential solution. If a NiFe asteroid were to be selected, a ready source of Ni, Co, W and Se would be available although it would require orbital access. However, asteroidal material is available on the Moon itself. The three largest terrestrial impact craters on Earth are the 250–300 km diameter Vredefort cater in South Africa (2.02 Gy old), the 200 km diameter Sudbury crater in Canada (1.85 Gy old), and the 170 km diameter Chicxulub crater in the Mexico Yucatan (65 My old). Large terrestrial impact craters such as the Vredefort South Africa and Sudbury Canada craters are sources of gold–uranium and nickel–cobalt–platinum, respectively (Reimold et al. Reference Reimold, Koeberl, Gibson, Dressler, Koebert and Henkel2005). The Vredefort deposits were formed from pre-existing archaean deposits prior to impact while the Sudbury Ni–Cu sulphide deposits were formed by the impactor itself. Most Sudbury ores are associated with a sublayer at the base of a 2.5 km thick elliptical igneous lens 27 × 60 km² in extent with surrounding dikes. Large extraterrestrial impact craters might be expected to yield similar metallic sources. Mascons are high gravitational anomalies on the Moon which are believed to be formed by impact excavation (Melosh et al. Reference Melosh, Freed, Johnson, Blair, Andrews-Hanna, Neumann, Phillips, Smith, Solomon, Wieczorek and Zuber2013; Montesi Reference Montesi2013). Mantle material slowly flowed into the basin causing uplift of the basin as it cooled and contracted, increasing its density. Hence, it is generally concluded that asteroid material of the impactor was vaporized and either escaped into space or was diffused over the lunar surface to form the 1–2% of the meteoritic material in the lunar regolith. However, it is possible that there may be asteroidal ores located within 500 m of the lunar surface if some of the asteroid material survived impact. Low-velocity impacts of small meteorites up to 3 km s⁻¹ permits partial survival of the impactor which will have accumulated over the aeons (Bland et al. Reference Bland, Cintala, Horz and Cressey2001). At high-impact angles, higher impact velocities of 7 km s⁻¹ permit the survival of impactor material which remains localized at the centre of the resulting crater (Bland et al. Reference Bland, Artemieva, Collins, Bottke, Bussey and Joy2008). The fraction of surviving material is directly related to the impact angle, however. Around 2.6% of lunar craters will retain more than 50% of the impacting material – this correlates with at least 600 craters exceeding 10 km in diameter in the highlands and 70 craters of similar dimensions in the mare regions. Such craters may be identified by thin breccia lens thicknesses. These offer potential sources of asteroidal material on the Moon. Strong magnetic anomalies in the northern rim of the South Pole Aitken basin on the lunar farside indicate that they originate from magnetic iron minerals of the impactor (Wieczorek et al. Reference Wieczorek, Weiss and Steart2012; Collins Reference Collins2012). Most of the metallic core of the 200 km diameter asteroid impactor which struck from south to north at 15 km s⁻¹ at a 45° angle was retained in downrange ejecta. In general, most projectile material from near vertical impact velocities below 12 km s⁻¹ appears to fragment but they survive and concentrate into the central peak of the craters created (Yue et al. Reference Yue, Johnson, Monton, Melosh, Di, Hu and Liu2013). The rest of the impactor material is dispersed in ejecta blanket, the crater floor and rim. The olivine in many lunar crater peaks is of asteroidal rather than lunar mantle origin. Beyond 14 km s⁻¹ impact speeds, however, vaporization of the projectile material occurs. Metals appear to have the high survivability to hypervelocity impacts suggesting their incidence in crater floors, walls and ejecta blankets as metal particle fragments (McDermott et al. Reference McDermott, Price, Cole and Burchell2016). This suggests that there will be significant near-surface regions of the Moon which will host high concentrations of NiFe material and its associated Co, W and Se resources (Table 3).

Table 3. Essential iron alloys

Both iron and nickel are plentiful in NiFe meteoritic sources. Cobalt is commonly found in association with Ni. If both are in sulphide form with troilite, they can be reduced with hydrogen by smelting at high temperature and pressure. Tungsten inclusions in NiFe meteoritic material represent one of the most accessible sources of tungsten. Forging by hammer, press, rolling or die is essential for tungsten. Tungsten has the highest melting point of all metals at 3422°C. As a structural material, it may be used for rocket engine linings but it is an essential ingredient in vacuum tube cathodes. It is processed in the non-molten state through powder metallurgy. Selenium is also a required resource for its photosensitive character necessary in light sensors and arrays of our engineered lifeform. Se/Te weight ratio of ~20 is approximately constant in stony meteorites while the Se abundance averages ~25 ppm Si in both stony and carbonaceous meteorites (Akafa Reference Akafa1966; Schuindewolf Reference Schuindewolf1980). Meteoritic sources are thus favoured for both elements W and Se.

There are material commonalities to our engineered creature and biological organisms. Important elements for the LUCA organism may have been Fe, Ni, Co and W metals (amongst others such as Mn, Mo, Cu, Zn and V) at temperatures ~100°C under high pressure maintained by hydrothermal flow reactors (Wachtershausen Reference Wachtershausen2006). These materials bear many similarities to our self-replicating machine's materials, though the biological temperature regimes are much more modest. Pioneer ligands included S and S₂ (sulphides) and others such as SH, H₂O, OH, CO and CN, many of which are available as volatiles in the lunar regolith. Metal sulphides such as troilite/pyrite are common in nickel-iron meteorite material. Iron has an important role in ancient biochemical systems prior to oxygenation of the Earth's atmosphere. Early ecosystems on Earth were driven by the anaerobic cycling of H₂ and Fe²⁺ by phototrophs (Canfield et al. Reference Canfield, Rosing and Bjerrum2006). Banded iron formations from 3.8 By ago indicate Fe²⁺ was dissolved in ocean waters. Iron cycling occurred between Fe₃O₄ and Fe²⁺ in solution in a Fe²⁺/Fe³⁺ redox couple (Weber et al. Reference Weber, Achenbach and Coates2006). Insoluble Fe₃O₄ is the electron acceptor that is produced through anoxygenic photosynthesis with ferrous Fe²⁺ in solution as the electron donor (Bird et al. Reference Bird, Bonnefoy and Newman2011):

$${\rm 4F}{\rm e}^{{\rm 2} +} + {\rm C}{\rm O}_{\rm 2} + {\rm 11}{\rm H}_{\rm 2}{\rm O} \to {\rm C}{\rm H}_{\rm 2}{\rm O} + {\rm 4Fe(OH}{\rm )}_{\rm 3} + {\rm 8}{\rm H}^ + $$

Fe²⁺ is then recycled by iron-reducing bacteria. Mars has large deposits of iron oxide for which the Tinto River Basin with its iron-based geomicrobiology is an analogue (Amils et al. Reference Amils, Fernandez-Remolar, Gomez, Aguilera, Gonzalez-Toril and Rodriguez2003). Its acidic waters are enriched in ferric iron and sulphates supporting iron oxidizers and iron reducers. Pyrite FeS₂ is common under anaerobic conditions such as hydrothermal vents where it is a constituent of chimneys. It is formed from hydrothermal H₂S and Fe²⁺ in solution: FeS + H₂S → FeS₂ + 2H⁺ + 2e⁻. Pyrite offers a powerful chemoautotrophic energy source through the oxidative formation of pyrite from troilite and hydrogen sulphide (Wachtershauser Reference Wachtershauser1990). Pyrite may also act as a reduction source for catalysing the formation of iron–sulphur enzymes NAD(P)H and FADH₂ (Wachtershauser Reference Wachtershauser1992). Anaerobic oxidation of ferrous (FeII) to ferric (FeIII) iron by purple non-sulphur bacteria may have preceded oxygenic photosynthesis during the Archaean (Widdel et al. Reference Widdel, Schnell, Easing, Ehrenreich, Assmus and Schink1983). Pyrite minerals are commonly contaminated by FeS, CoS₂ and NiS₂ and have a typical Se content of 0.05% but may be enriched up to 0.9%. Finally, today, magnetotactic bacteria synthesize magnetite crystals inside magnetosomes (Rawlings et al. Reference Rawlings, Bramble and Staniland2012). Hence, iron has an important role to play in biology. Likewise, it has a central role in the metabolism and tissue of our engineered creature.

The natural lunar glass is ubiquitous on the Moon – typically 20–25% of lunar regolith – caused by impact heating followed by rapid quenching but it is not suitable for optical applications. Fused quartz/silica is the best option though it is produced by melting and shaping high-purity silica at 2000°C (compared with ~1000°C for soda lime glass). It has superior optical and thermal properties compared with most other types of glass and has a low thermal expansion coefficient (~5.5 × 10⁻⁷/°C). This makes fused silica suitable for lenses, polished mirrors, vacuum tubes, glassware and other transparent optical components across the IR–ultraviolet (UV) range. As well as glass, quartz is a piezoelectric material that may be deployed for displacement sensing and derivative measurements (Kolesar & Dyson Reference Kolesar and Dyson1995). Silica and its variant quartz are rare on the Moon due to the low water content of the Moon. It can be manufactured by deposition from silicates with the action of strong acids similar to natural weathering. For example, acid leaching by hot hydrochloric acid is a viable approach to reducing anorthite while avoiding high temperatures:

$${\rm CaA}{\rm l}_{\rm 2}{\rm S}{\rm i}_{\rm 2}{\rm O}_{\rm 8} + {\rm 8HCl} + {\rm 2}{\rm H}_{\rm 2}{\rm O} \to {\rm CaC}{\rm l}_{\rm 2} + {\rm 2AlC}{\rm l}_{\rm 3}.{\rm 6}{\rm H}_{\rm 2}{\rm O} + {\rm 2Si}{\rm O}_{\rm 2}$$

There are plastic pre-ceramic resins that can be 3D printed as a plastic gel into structures which are then fired into a high-temperature ceramic releasing much of its organic component (Wogan Reference Wogan2016). These pre-ceramic polymers are composed of mixtures of siloxanes and silazanes which are extruded. When pyrolized in the presence of UV light, the two polymers cross-link and form silicon oxycarbide ceramic structures. A simpler approach is to employ silicone plastics as precursors to ceramics without the need for silazanes (Narisawa Reference Narisawa2010). There are two options: silicone may be oxidized into silica or reduced to silicon carbide. In all cases, it requires a post-processing thermal step following 3D printing. Silicon carbide may be created by heating silica and carbon at 2400°C for an extended period – this far in excess of the temperatures required for metal extraction from minerals. However, pyrolysis of silicone at 1100°C yields SiO_xC_y which may be converted to silicon carbide by carbothermic reduction with excess C at 1800°C:

$${\rm Si}{\rm O}_x{\rm C}_y \to {\rm SiC} + x{\rm CO} + (y - x - {\rm 1}){\rm C}$$

This imposes slightly more modest temperatures though the rarity of carbon sources suggests SiC should be reserved for specialized roles such as ball milling. Alternatively, silicone may be converted to silica by flame combustion in oxygen:

$${\rm Si}{\rm O}_x{\rm C}_y + \left( {{\rm 1} - x + {\rm 2}y} \right){\rm O}_{\rm 2} \to {\rm Si}{\rm O}_{\rm 2} + y{\rm C}{\rm O}_{\rm 2}$$

This would not have the hardiness of SiC but provides a mechanism for 3D printing ceramics without extreme temperatures. Silica is commonly used in biological systems –diatom shells, phytoliths in grasses, and spicules of sponges. Silicon has also been suggested as a replacement for carbon through its redox reactions between silica solid and silane (SiH₄) gas. Such a silicon-based metabolism would require quite extreme conditions and the solidity of silica does present certain difficulties for its excretion.

Biomining is simpler and less energy-intensive than pyrometallurgy, offering a biological component to engineered self-replication. Of particular relevance is the biooxidation of sulphide deposits such as iron pyrite by Thiobacillus ferrooxidans in a cultured medium with ferrous iron as the energy source (Acevedo Reference Acevedo2000; Cockell Reference Cockell2011). Synthetic biology may introduce additional extraterrestrial applications such as enhanced biomining and biocement production, biological control systems (Menezes et al. Reference Menezes, Montague, Cumbers, Hogan and Arkin2015) and photosynthetic bacteria for capturing solar energy as a biofuel (Way et al. Reference Way, Silver and Howard2011). However, biomining using microorganisms as catalysts are unlikely to be feasible for extraterrestrial processing in the near term, especially on the Moon.

Biological Principle 2: solar energy for metabolism

Energy is essential for living entities to maintain their metabolic activity and growth. Whereas photosynthesis in chloroplasts is driven by pigment molecules which operate at moderate temperatures, the self-replicating machine autotroph uses thermal energy. Thermosynthesis has been suggested as a plausible energy source for extraterrestrial biota, though it was envisaged to apply to low-temperature gradients within ices (Muller Reference Muller2003). Such thermosynthesis would offer very low-quality energy but it is plausible that much higher temperature gradients might occur at hydrothermal vents with temperatures of 400 + °C under high pressure. Industrial temperatures offer even higher energy sources clearly beyond the capacity for carbon-based biology.

To extract our feedstock for the 3D printers, an intense source of thermal energy is required. Our self-replicator uses hearth-based chemistry to extract its restricted set of feedstocks materials. The primary energy source is solar energy which is captured and concentrated using solar concentrators – parabolic mirrors or Fresnel lenses. Solar furnaces using Fresnel lenses can provide the required temperatures for thermochemical extraction from minerals. Fresnel lenses concentrate sunlight onto a single focus – they are flat with a sculpted contour to reduce weight. They have not been discovered by biological evolution almost certainly because the advantage of Fresnel lenses over biconics is only apparent for much larger geometries than biological eyes. The temperature regimes our creature requires for its metabolism far exceed that of even Pyrolobus fumarii which like all terrestrial organisms is restricted by the limits of carbon-based organics. A silicon-based lifeform may not be so limited in temperature tolerance. The Fresnel lens-based thermal source allows us to create a local controlled environment for the self-replication process to be undertaken in a structured encapsulated environment to minimize variability in metabolic processes. This locally controlled environment begins with using Fresnel lenses to thermally fuse local lunar regolith at 1200–1500°C, thereby paving it into the glass to control the incidence of dust. This is the first step towards encapsulation.

Thermal energy can be converted into electrical energy through thermionic emission (implemented in vacuum tubes) (Ellery Reference Ellery2016a,Reference Elleryb,Reference Elleryc). This focusses light energy onto a small volume as heat onto the cathode of a vacuum tube. The cathode emits electric current through thermionic emission with an efficiency of around 5–20%. This may be enhanced significantly through PETE (photon-enhancement of thermionic emission) using photosensitive coatings (such as Se) (Schwede et al. Reference Schwede, Bargstin, Riley, Hardin, Rosenthal, Sun, Schmitt, Pianetta, Howe, Shen and Melosh2010). Thus, electric power is generated to enable the growth of the self-replicating machine. Both forms of energy – thermal and electrical – are required for our artificial creature's metabolism. Energy may be stored mechanically in motorized flywheels. According to Boden (Reference Boden2003), the first fundamental law of bioenergetics requires that a living organism must convert environmental energy into smaller energy currency units that can be tapped incrementally to power metabolic activity. In biological systems, it is ATP that provides this currency in discrete packages. In our self-replicating machine, flywheel energy storage provides a continuously tappable energy mechanism. It is not inconceivable that the bacterial flagellar motor could have evolved and been co-opted into a nanoscale-flywheel-type of organelle for storing biological energy (without the flagellum itself). Multiple flywheels in random orientations within the cell would sum to zero total angular momentum. Furthermore, as conceived in spacecraft (Varatharajoo Reference Varatharajoo2004), flywheels could provide combined energy storage and angular momentum control of cellular tumbling. The same two components discussed later for actuation and information processing – motors and vacuum tubes respectively – provide the basis for energy generation and storage respectively for our self-replicator. This multifunctional aspect of component use is common in biology where a component evolved for one task (such as feathers for thermal insulation) is co-opted for another task (control surfaces for bird flight). Motors are the central component in flywheels (electromechanical batteries) which offer high-energy densities. They provide the basis for all motive machines including 3D printers, other manufacturing processes and for energy storage (as flywheels); vacuum tubes provide the basis for all active electronics and energy generation (through thermionic conversion) (Ellery Reference Ellery2016d).

Biological Principle 3: manipulation of the environment

The feedstock to which our creature has access is fed to our ribosome which comprises a set of 3D printers for different material types. In biological 3D protein construction, 1D polypeptide strings are constructed from amino acid modules in a ribosomal assembly line using tRNA coding keys. The origin of tRNA–amino acid encoding is unknown, whether it is an arbitrary frozen accident or due to a specific physicochemical interaction (Edwards Reference Edwards1998). Coevolution theory suggests that the coding scheme evolved from relative positioning of precursor amino acids and tRNA on pyrite mineral surfaces. Polypeptide strings automatically configure themselves into their appropriate 3D shape. In our artificial creature, the construction process is not an assembly line, rather a suite of 3D printers. The artificial 3D structure is constructed from a series of modular 2D layers that are built into their appropriate 3D shape layer-by-layer. Furthermore, this 3D printed structure is employed in its entire volume rather than localized to active regions of the surface of a biological protein – this, of course, is a result of the difference of scale between the macroscopic engineered structure and the molecular biological structure. Our self-replicating machine is based on a 3D printing concept inspired by the RepRap 3D printer (Jones et al. Reference Jones, Haufe, Sells, Iravani, Olliver, Palmer and Bowyer2011). RepRap is a partially self-replicating 3D printer that can print its own plastic parts (Fig. 1). It cannot, however, replicate: (i) its steel bars; (ii) its connecting metal nuts and bolts; (iii) its glass work platform; (iv) its electric motors; (v) its electronics boards; (vi) nor can it self-assemble. Such additive manufacturing is well established for constructing structures of different materials such as plastics (fused deposition modelling), metals (electron beam freeform fabrication) and ceramics (selective laser sintering). All 3D printing involves relative motion between a printing head (xy-direction) and a work platform (z-direction). They are in effect Cartesian robots – all robots from rovers to drills to manipulators are kinematic configurations of electric motors. Hence, electric motors are central to our self-replicating machine.

Fig. 1. Assembled RepRap 3D printer.

The key components of the self-replicating machine are electric motors and electronics which can both be constructed from the available material set we considered earlier. These components are the fundamental components of any kinematic machine – 3D printers, manipulators, roving vehicles, drilling/milling machines, lathes, etc. The core of any robot is its actuators, sensors and controllers. Actuation involves manipulating the local environment – an essential pre-requisite of life. Our own experiments using shape memory alloys as artificial muscles driving a rotary shaft using cams illustrated the concept of an artificial linear bio-inspired motor but it was inferior in performance to the electromagnetic motor (Ellery Reference Ellery2015). We have been applying 3D printing methods to the construction of DC electric motors of different types. Although we have yet to 3D print an entire electric motor, we have 3D printed motor cores and are working in printing coils and electromagnets to complete the assembly (Fig. 2). In our self-replicating machine, the nature of the self/non-self-boundary is more fluid than in biological systems – its internal space is defined by its internal thermochemical processing, 3D printing, etc. Its external space is less clear as it must forage to acquire its nutrients for which it deploys rovers to perform extractive processes – they effectively extend ‘pseudopodia’ into the environment. The goal is to demonstrate 3D printing of electric motors and electronic control systems as the basic components of any kinematic machine. We thus next consider information-processing control systems.

Fig. 2. Polylactic acid (PLA)-based 3D printed motor core with 45% iron powder loading.

Biological Principle 4: information processing

It has been proposed that the Turing machine does not constitute a general model of computing (Goldin & Wegner Reference Goldin, Wegner, Cooper, Lowe and Torenvliet2005). Natural computation is a physical process that cannot be fully described by a Turing machine (MacLennan Reference MacLennan2004). Hence, there are physical machines that cannot be simulated by any Turing machine. The Turing machine model cannot account for interactivity with the environment of the real world because it is abstract rather than physical. Interacting computational units have emergent properties that are not algorithmic. A special Turing machine concept relevant to biological information processing is the interactive Turing machine. Biological organisms interact with their environment allowing for perpetual learning and so possess super-Turing capabilities (Wierdermann & van Leeuwen Reference Wierdermann and van Leeuwen2002). This concept may be abstracted as the interactive Turing machine with advice. Interactive Turing machines have perpetual exchange of information with their environment – essentially infinite computations. This models any cognitive system equipped with sensors to acquire information from the environment and effectors with which to modify that environment. This process is ongoing and continuous. This capacity by itself however, lies within the power of the universal Turing machine through its input/output tapes. The key to introducing super-Turing capabilities lies with the admission of unpredictability to its computations. This is introduced to the Turing machine as advice to implement non-computable external information. The advice takes the form of a separate advice tape that computes the advice value on its tape in a single step. The Turing machine with advice models computability with interaction with the external environment. The advice tape models inputs from a social community of interactive Turing machines – the advice is non-computable within the Turing machine itself. Hence, the interactive Turing machine with advice constitutes a super-Turing machine. A corollary of this suggests that the physical version of the Church-Turing thesis (every finite physical process subject to physical laws can be simulated by a universal Turing machine operating a finite program) (Deutsch Reference Deutsch1985) is incorrect and that biological neural function cannot be implemented by a universal Turing machine.

Our interest in feedback control systems is reminiscent of a cybernetic definition of life emphasizing multiple feedback control systems as a major characteristic (Korzeniewski Reference Korzeniewski2001). We need to 3D print computational control systems for those motors, i.e. electronics. The vacuum tube – constructed from our restricted suite of materials in a relatively simple geometric configuration – should lend itself to 3D printing (TBD). A typical triode has a simple construction comprising a heated tungsten cathode surrounded by a nickel control grid and a nickel anode enclosed in a glass tube. The control grid voltage controls the current between the cathode and anode. It provides the basis for electronic amplification and switching (Han & Meyyappan Reference Han and Meyyappan2014). Solid state electronics requires too many specialized reagents and conditions to be incorporated into a practical self-replication scheme. The vacuum tube may potentially supersede solid-state transistors for unconventional applications as they have a high tolerance to temperature and radiation (Teuscher Reference Teuscher2014). Self-replication technology is one such unconventional application. In fact, vacuum channel transistors are under development in which a thin layer of SiO₂ insulates a gate electrode from the upper source and drain electrodes (Han & Meyyappan (Reference Han and Meyyappan2014)). The cathode and anode are sharpened into points to intensify the electric field at the tips emitted via field emission. The distance between the cathode and anode is less than the electron mean free path (200 nm in the air or 1 µm in He) – in a vacuum, this is not a constraint. However, the bulky nature of traditional vacuum tubes does not lend itself to traditional general purpose computational architectures.

Digital computations require many more devices than analogue circuits for the same function – the addition of two numbers requires hundreds of transistors. It requires Boolean circuits of size O(n ^1+e) to compute multiplications with an error e > 0. For this reason, we adopt neural network architectures over traditional computer architectures to compensate for the larger size of vacuum tubes over solid-state transistors. The complexity of a neural network increases only as the logarithm of the task complexity unlike the exponential increase in circuit complexity of digital architectures. Similarly, to train a neural network of N nodes and W weights, m random training samples are required such that $m \ge O\left( {{\textstyle{W \over e}}\log {\textstyle{N \over e}}} \right)$ where 0 < e ≤ 1, e = acceptable error fraction (Baum & Haussler Reference Baum and Haussler1989). Neural net circuits can incorporate vacuum tubes rather than difficult-to-manufacture solid state circuitry but without the scaling problem of digital circuitry. To that end, we have adopted a simple analogue neuron circuit as our computing element modified from the Yamashita–Nakaruma neuron (Yamashita &Nakamura Reference Yamashita and Nakamura2007; Larson & Ellery Reference Larson and Ellery2015) (Fig. 3).

Fig. 3. Analogue neuron circuit – part of a two-neuron circuit for rover obstacle avoidance behaviour.

The electronic neuron models the nonlinear input–output relation where the output is given by:

$$y_i = f\left( {\sum\limits_{\,j = 0}^n {w_{ij}} x_i} \right)$$

where x _i = input, w _ij = weighting factor, f(.) = non-linear squashing function. The weight matrix of the network of neurons determines the functionality of the network. Simple reactive behaviours have been implemented readily using these analogue neurons. Braitenburg vehicles comprise two sensors, left and right, and two motors to drive their respective wheels, left and right. The connections between the sensors and the motors determine the vehicle's behaviour. We have demonstrated a two-neuron circuit implementing a Braitenburg control architecture of BV2/BV3 class (Braitenburg Reference Braitenburg1984) performing automatic obstacle avoidance on a simple desktop mobile robot.

Artificial neural networks can implement any nonlinear mapping function and are Turing-complete (Siegelmann & Sontag Reference Siegelmann and Sontag1995) perhaps even offering super-Turing capabilities (Siegelmann Reference Siegelmann1995). Neural nets are efficient as universal Turing machines. Recurrent neural nets with feedback are more powerful than standard feedforward neural nets (Goudreau et al. Reference Goudreau, Giles, Chakradhar and Chen1994). A neural network simulator with r = m + n + 2 layers of neurons and two sets of recurrent connection weights with feedback can simulate in real time a Turing machine with m-symbols and n-states (Sun et al. Reference Sun, Chen, Lee and Giles1991). The Siegelmann–Sontag universal neural network-based Turing machine comprised 886 neurons, though this has been reduced in more recent work to 96 then 25 and finally to just 9 switched affine neurons that implement Boolean functions (Siegelmann & Margenstern Reference Siegelmann and Margenstern1999). A recurrent neural network with rational weights is computationally equivalent to a Turing machine model of digital computing machines. The computational capacity of recurrent neural networks may be enhanced beyond that of the Turing machine using real-valued weights which offer the infinite precision of analogue information (Balcazar et al. Reference Balcazar, Gavalda and Siegelmann1997). This allows them to compute non-recursive functions. The recurrent neural network with real weights offers super-Turing capabilities as an interactive Turing machine with advice (Cabessa & Siegelmann Reference Cabessa and Siegelmann2012). Hence, neurons with rational weights yield Turing machine capability but neurons with real weights are more powerful than Turing machines (Margenstein Reference Margenstein2000). Analogue recurrent neural networks are equivalent to oracle Turing machines. An oracle machine is a black box augmenting a Turing machine that makes a decision in a single step even if that decision is complex. The Turing machine can copy symbols onto the oracle tape. The oracle is not a Turing machine itself. The oracle itself has its own tape and read/write head but has special states – Query and Response. When the machine reads the Query state, the read/write head subsequently moves to the next square and writes the Response (yes/no) as a solution in a single step. State Yes or No depends on whether the current string is on the oracle tape. The oracle introduces the possibility of inputting new non-deterministic or non-computable data to the machine. An example of a decision is the halting problem where the oracle determines whether the Turing machine halts given its inputs, i.e. the oracle augments the Turing machine with non-computable capabilities. As a physical adjunct circuit, the Wheatstone bridge can act as an oracle to a Turing machine extending the computational powers of such a system beyond the Church-Turing limit (Beggs et al. Reference Beggs, Costa and Tucker2010). It is the measurement of a physical process – in this case, measurement of analogue electrical resistance by the Wheatstone bridge – that extends the computational power of the abstract Turing machine. We select the analogue neural network (to which feedback connections can be added) as the computational architecture of choice yielding greater computational capabilities over traditional computational architectures. Evolving recurrent neural networks where synaptic weights change over time (i.e. learning) are equivalent to interactive Turing machines with advice, i.e. they are capable of super-Turing computations – this is the case for both rational and real weights (Cabessa Reference Cabessa, Villa, Wermter, Weber, Duch, Honkela, Koprinkova-Hristova, Magg, Palm and Villa2014). In rational-weighted recurrent neural networks, these super-Turing capabilities can only be realized if the synaptic weights evolve in a non-recursive manner – recursive learning limits such networks to Turing-computable functions. However, in real-weighted recurrent neural networks, there are no such requirements for the learning to achieve super-Turing capacities. Super-Turing machines include analogue recurrent neural networks with real-valued nonlinear squashing functions (Teuscher & Sipper Reference Teuscher and Sipper2002). Hence, our analogue neuron may offer super-Turing capabilities when in recurrent configuration. These circuits – based on vacuum tube active components – are to be 3D printed. The core of our universal Turing machine segment is a 3D printer which takes data stored in magnetic core memory (based on the same technology as motors) and prints out analogue neural net circuits that physically encapsulate programs. It is envisaged that such neural network circuits implement specific programs printed by a 3D printer (representing the read–write head of a universal Turing machine) according to information held in magnetic core memory (based on the same principles and materials as an electric motor). Embedded software interacts with its underlying hardware and is subject to temporal constraints on execution time, this constraint being undecidable for Turing machines (Lee Reference Lee2005). The analogue neural net is an extreme version of the embedded software in that the software is embedded in the connection weights without the temporal undecidability problem. Although the analogue neuron is far simpler than the biological neuron, it nevertheless implements basic functions of information processing and transmission.

Noise can be exploited to advantage – dithering is the process of imposing random mechanical vibrations onto motors to compensate for sticking behaviour. This is an example of stochastic resonance (Wiesenfeld & Moss Reference Wiesenfeld and Moss1995). Similarly, biological neurons, by virtue of their nonlinearity, can exploit stochastic resonance to enhance the detectability of small signals by amplifying the combined signal and noise to overcome the threshold for detection. The noise signal from broadband background entrains and resonates with the low signal to amplify it. Stochastic resonance requires low levels of noise otherwise excessive noise will swamp it – the signal-to-noise ratio rises with noise to an optimal value and then decreases. Analogue neurons are characterized by constant low levels of intrinsic noise but above a threshold they fire digitally, thereby amplifying a low signal. Networks of neurons provide the ability to handle signals with a range of amplitudes and noise levels. Hence, analogue neural circuits offer the prospect of exploiting stochastic resonance for enhanced signal processing.

Biological and analogue neural systems go beyond Turing machines because they are self-modifying and computationally open so cannot be captured in an algorithm. This is precisely the realm of autonomic computing which emphasizes self-configuration, self-optimization, self-repair and self-protection (Kephart & Chess Reference Kephart and Chess2003). Hence, our adoption of analogue recurrent neural networks offers similar computational capabilities as biological systems.