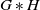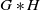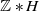1. Introduction
Weak amenability was introduced by Cowling and Haagerup [Reference Cowling and Haagerup3] as a generalisation of amenability in the context of approximation properties of operator algebras. Before receiving that name, this property was first studied by de Cannière and Haagerup [Reference de Cannière and Haagerup5] for discrete subgroups of
$\operatorname{SO}_0(n,1)$
. Although weak amenability can be defined for general locally compact groups by means of approximate identities of the Fourier algebra, in this paper we will restrict ourselves to countable discrete groups. We refer the reader to [Reference Cowling and Haagerup3] for the general definition.
Let G be a countable group. We say that G is weakly amenable if there exists a sequence of finitely supported functions
$\varphi_n\,{:}\,G\to\mathbb{C}$
converging pointwise to 1, and a constant
$C\geq 1$
such that
\begin{align*}\sup_{n\in\mathbb{N}}\|\varphi_n\|_{B_2(G)}\leq C.\end{align*}
Here
$B_2(G)$
stands for the space of Herz–Schur multipliers on G. See Section 2 for details. The Cowling–Haagerup constant
$\boldsymbol\Lambda(G)$
is the infimum of all
$C\geq 1$
such that the condition above holds. If G is not weakly amenable, we set
$\boldsymbol\Lambda(G)=\infty$
.
Recall that a group G is amenable if and only if there exists a sequence of finitely supported, positive definite functions
$\varphi_n\,{:}\,G\to\mathbb{C}$
converging pointwise to 1; see for example [Reference Brown and Ozawa2, Section 2.6]. The fact that every positive definite function
$\varphi\,{:}\,G\to\mathbb{C}$
satisfies
$\|\varphi\|_{B_2(G)}=\varphi(e)$
implies that every amenable group G is weakly amenable with
$\boldsymbol\Lambda(G)=1$
. The converse is not true since free groups satisfy
$\boldsymbol\Lambda(\mathbb{F}_n)=1$
for all
$n\geq 1$
.
Weak amenability is known to be preserved by taking direct products and subgroups; however, it is not known if it is stable under free products. For a pair of groups G, H, the free product
$G\ast H$
is the group of words in G and H, where the group operation is defined by concatenation. See for example [Reference Löh11, Section 2.3.2] for the formal definition. The question of weak amenability of free products remains open in general, but some particular cases are well understood.
Bożejko and Picardello [Reference Bożejko and Picardello1] showed that the free product of amenable groups is weakly amenable with Cowling–Haagerup constant 1. The proof of this result exploits in a very clever way the geometry of trees, and the techniques developed in that paper proved to be very fruitful in the study of weak amenability from a geometric point of view.
Generalising Bożejko and Picardello’s result, Ricard and Xu [Reference Ricard and Xu14] proved that if G and H are weakly amenable groups with
$\boldsymbol\Lambda(G)=\boldsymbol\Lambda(H)=1$
, then
$G\ast H$
is weakly amenable with
$\boldsymbol\Lambda(G\ast H)=1$
. In this case, the approach is quite different, as they prove a more general theorem for reduced free products of
$\operatorname{C}^*$
-algebras, obtaining the result for groups as a corollary.
In [Reference Guentner, Reckwerdt and Tessera7], Guentner, Reckwerdt and Tessera studied weak amenability for relatively hyperbolic groups. A particular case of their result says that, if H is hyperbolic and G has polynomial growth, then
$G\ast H$
is weakly amenable. This result builds on Ozawa’s work [Reference Ozawa13], where he shows that all hyperbolic groups are weakly amenable.
The aim of this paper is to prove the following.
Proposition 1.1 Let G be an amenable group and let H be a hyperbolic group. Then the free product
$G\ast H$
is weakly amenable.
The proof relies on the notion of orbit equivalence of group actions, which we review in Section 3.
2. Weak amenability
We will give now the precise definition of weak amenability. For this, we need to talk first about Schur multipliers. For more details, we refer the reader to [Reference Brown and Ozawa2, Appendix D].
Let X be a set and let
$\ell_2(X)$
denote the Hilbert space of complex-valued, square-summable functions on X. We denote by
$\delta_x$
(
$x\in X$
) the elements of the canonical orthonormal basis of
$\ell_2(X)$
. Let
$T\,{:}\,\ell_2(X)\to\ell_2(X)$
be a bounded linear operator. We define its matrix coefficients
$(T_{x,y})$
by
\begin{align*}T_{x,y}=\langle T\delta_y,\delta_x\rangle,\quad\forall x,y\in X.\end{align*}
Observe that an operator T is completely determined by its matrix coefficients
$(T_{x,y})_{x,y\in X}$
. We say that a function
$\psi\,{:}\,X\times X\to\mathbb{C}$
is a Schur multiplier on X if the map
\begin{align}M_\psi \,{:}\, (T_{x,y}) \mapsto (\psi(x,y)T_{x,y})\end{align}
is well defined in the algebra of bounded operators
$\mathcal{B}(\ell_2(X))$
. In this case,
$M_\psi$
is automatically continuous.
Now, let G be a countable group. We say that
$\varphi\,{:}\,G\to\mathbb{C}$
is a Herz–Schur multiplier on G if the function
$\psi\,{:}\,G\times G\to\mathbb{C}$
given by
\begin{align*}\psi(t,s)=\varphi(s^{-1}t),\quad\forall s,t\in G,\end{align*}
is a Schur multiplier on G. We denote the space of Herz–Schur multipliers by
$B_2(G),$
and we endow it with the norm
\begin{align*}\|\varphi\|_{B_2(G)}=\|M_\psi\|,\end{align*}
where
$M_\psi$
is the bounded linear map on
$\mathcal{B}(\ell_2(G))$
defined as in (2.1).
We say that G is weakly amenable if there exists a sequence of finitely supported Herz–Schur multipliers
$\varphi_n\,{:}\,G\to\mathbb{C}$
converging pointwise to 1, and a constant
$C\geq 1$
such that
\begin{align*}\sup_{n\in\mathbb{N}}\|\varphi_n\|_{B_2(G)}\leq C.\end{align*}
We define the Cowling–Haagerup constant
$\boldsymbol\Lambda(G)$
as the infimum of all
$C\geq 1$
such that the condition above holds.
Recall that a finitely generated group is hyperbolic if its Cayley graph is hyperbolic. For more details, we refer the reader to [Reference Löh11, Section 7]. The following result is essential for our purposes.
Theorem 2.1 (Ozawa) Let H be a hyperbolic group. Then H is weakly amenable.
Observe that this theorem does not provide a bound on the Cowling–Haagerup constant of H. And, in fact, there is no such bound. More precisely, it was proved in [Reference Cowling and Haagerup3] that every cocompact lattice
$\Gamma$
in
$\operatorname{Sp}(n,1)$
satisfies
\begin{align*}\boldsymbol\Lambda(\Gamma)=2n-1,\end{align*}
and such lattices are hyperbolic for all n.
Cowling and Zimmer [Reference Cowling and Zimmer4] exploited this fact in order to show that two lattices
$\Gamma<\operatorname{Sp}(n,1)$
and
$\Lambda<\operatorname{Sp}(m,1)$
cannot be orbit equivalent if
$n\neq m$
.
3. Orbit equivalence
A key concept in the study of measured group theory is the notion of orbit equivalence for group actions. We refer the reader to [Reference Furman6] for a detailed treatment of this subject. In this article, we will only focus on its connection with weak amenability, as devised by Cowling and Zimmer [Reference Cowling and Zimmer4].
Let G and H be countable groups, and let
$G\curvearrowright(X,\mu)$
,
$H\curvearrowright(Y,\nu)$
be measure preserving actions on standard non-atomic probability measure spaces. We say that these actions are orbit equivalent if there exists a measure space isomorphism
$T\,{:}\,(X,\mu)\to (Y,\nu)$
sending G-orbits onto H-orbits. We call T an orbit equivalence between
$G\curvearrowright(X,\mu)$
and
$H\curvearrowright(Y,\nu)$
. We will write
$G\sim_{OE}H$
if such actions and such an orbit equivalence exist. See [Reference Furman6, Section 2.2] for more details.
Theorem 3.1
(Cowling--Zimmer) Let G and H be countable groups such that
$G\sim_{OE}H$
. Then
$\boldsymbol\Lambda(G)=\boldsymbol\Lambda(H)$
.
Remark 3.2 This result was later extended by Jolissaint [Reference Jolissaint10] to measure equivalent groups. Recently, Ishan [Reference Ishan8] extended this even further to the context of von Neumann equivalence of groups, which was introduced in [Reference Ishan, Peterson and Ruth9].
A very important result concerning orbit equivalence of amenable groups was proved by Ornstein and Weiss [Reference Ornstein and Weiss12].
Theorem 3.3 (Ornstein--Weiss) Any two ergodic probability measure preserving actions of any two infinite countable amenable groups are orbit equivalent.
In particular, every infinite countable amenable group G satisfies
$G\sim_{OE}\mathbb{Z}$
.
Proof of Proposition 1.1. If G is finite, then
$G\ast H$
is hyperbolic, and so it is weakly amenable by Theorem 2.1. Assume now that G is infinite. Since G is amenable, by Theorem 3.3, we have
$G\sim_{OE}\mathbb{Z}$
. Since the relation
$\sim_{OE}$
is preserved by free products (see [Reference Furman6, Section 3]), this implies that
\begin{align*}G\ast H\sim_{OE}\mathbb{Z}\ast H.\end{align*}
Hence, by Theorem 3.1,
\begin{align*}\boldsymbol\Lambda(G\ast H)=\boldsymbol\Lambda(\mathbb{Z}\ast H).\end{align*}
On the other hand, since H and
$\mathbb{Z}$
are both hyperbolic, so is
$\mathbb{Z}\ast H$
. Therefore, by Theorem 2.1,
\begin{align*}\boldsymbol\Lambda(\mathbb{Z}\ast H) < \infty.\end{align*}
This shows that
\begin{align*}\boldsymbol\Lambda(G\ast H) < \infty,\end{align*}
which finishes the proof.
Acknowledgment
This work is supported by the Ministry of Science and Higher Education of the Russian Federation, agreement
$\mathcal{N}_{\underline{0}}$
075–15–2019–1619.
