Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T14:37:01.175Z Has data issue: false hasContentIssue false
  • English
  • Français

REDUCTIONS OF POINTS ON ALGEBRAIC GROUPS, II

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry Algebraic groups

Published online by Cambridge University Press:  28 July 2020

PETER BRUIN  and
ANTONELLA PERUCCA
PETER BRUIN
Affiliation:
Mathematisch Instituut, Universiteit Leiden, Postbus 9512, 2300 RA Leiden, The Netherlands, e-mail: P.J.Bruin@math.leidenuniv.nl
ANTONELLA PERUCCA
Affiliation:
Department of Mathematics, University of Luxembourg, 6, Avenue de la Fonte, 4364 Esch-sur-Alzette, Luxembourg, e-mail: antonella.perucca@uni.lu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be the product of an abelian variety and a torus over a number field K, and let 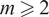$$m \ge 2$$ be a square-free integer. If 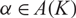$\alpha \in A(K)$ is a point of infinite order, we consider the set of primes 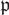$\mathfrak p$ of K such that the reduction 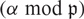$(\alpha \bmod \mathfrak p)$ is well defined and has order coprime to m. This set admits a natural density, which we are able to express as a finite sum of products of 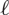$\ell$ -adic integrals, where 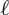$\ell$ varies in the set of prime divisors of m. We deduce that the density is a rational number, whose denominator is bounded (up to powers of m) in a very strong sense. This extends the results of the paper Reductions of points on algebraic groups by Davide Lombardo and the second author, where the case m prime is established.

MSC classification

Primary: 11F80: Galois representations
Secondary: 14L10: Group varieties 11G05: Elliptic curves over global fields 11G10: Abelian varieties of dimension $> 1$
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 2 , May 2021 , pp. 484 - 502
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

References

Jones, N., Almost all elliptic curves are Serre curves, Trans. Amer. Math. Soc. 362(3) (2010), 1547–1570.CrossRefGoogle Scholar
Jones, R. and Rouse, J., Galois theory of iterated endomorphisms, Proc. Lond. Math. Soc. (3) 100(3) (2010), 763–794. Appendix A by Jeffrey D. Achter.CrossRefGoogle Scholar
Lombardo, D. and Perucca, A., The 1-eigenspace for matrices in $\rm {GL}_2(\mathbb{Z}_\ell)$ , New York J. Math. 23 (2017), 897–925.Google Scholar
Lombardo, D. and Perucca, A., Reductions of points on algebraic groups, J. Inst. Math. Jussieu (2020), 1–33. doi: 10.1017/S1474748019000598.CrossRefGoogle Scholar
Perucca, A., Prescribing valuations of the order of a point in the reductions of abelian varieties and tori, J. Number Theory 129 (2009), 469–476.CrossRefGoogle Scholar
Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques, Invent. Math. 15(4) (1972), 259–331.CrossRefGoogle Scholar
Sutherland, A. V., Computing images of Galois representations attached to elliptic curves, Forum Math. Sigma 4(e4) (2016), 79.CrossRefGoogle Scholar
The LMFDB Collaboration, The L-functions and modular forms database (2016). http://www.lmfdb.org.Google Scholar
The Sage Developers, SageMath, the Sage Mathematics Software System (Version 7.3) (2016). http://www.sagemath.org.Google Scholar