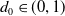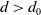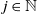1. Introduction
The study of random groups is one way to approach questions of the form “Does a typical group have property P?” To answer this question, one needs to choose a model of random groups and then calculate the probability that property P is satisfied. Generally speaking, we are interested in the asymptotic behavior of this probability as some constraint goes to infinity.
There are many models of random groups (an excellent introduction to this topic is [Reference Ollivier11]), the most studied of which is the Gromov density model, first introduced by Gromov in [Reference Gromov3]. In this model, a group presentation is chosen uniformly at random by fixing the number of generators and choosing cyclically reduced relators of a certain length. The number of relators chosen is controlled by a fixed constant called the density. One then analyzes the probability of a property being satisfied as both the length and the number of relators goes to infinity. This probability generally tends to 0 or 1, and in many important cases, there is a sharp threshold
![]() $d_0$
, so that for densities above
$d_0$
, so that for densities above
![]() $d_0$
the probability is 1, and below
$d_0$
the probability is 1, and below
![]() $d_0$
the probability is 0 (or vice versa). Some examples of this phase shift behavior include properties such as hyperbolicity [Reference Gromov3,Reference Ollivier10], small cancelation [Reference Gromov3], and satisfying Dehn’s algorithm [Reference Ollivier12].
$d_0$
the probability is 0 (or vice versa). Some examples of this phase shift behavior include properties such as hyperbolicity [Reference Gromov3,Reference Ollivier10], small cancelation [Reference Gromov3], and satisfying Dehn’s algorithm [Reference Ollivier12].
It is known that there is a sharp threshold for Kazhdan’s Property (T); however, its precise value is unknown. Property (T) was introduced by Kazhdan in [Reference Kazdan4] as a tool to study lattices in Lie groups, but turned out to be important in several areas of mathematics and computer science, especially in the study of expander graphs (for more information, see [Reference Lubotzky6]). In [Reference Żuk14], Żuk stated and sketched a proof that for
![]() $d>1/3$
, random groups in the triangular Gromov density model satisfy, with overwhelming probability, Property (T). Ollivier sketched an extension of this to the Gromov denisty model in [Reference Ollivier11], and Kotowski-Kotowski completed the proof in [Reference Kotowski and Kotowski5].
$d>1/3$
, random groups in the triangular Gromov density model satisfy, with overwhelming probability, Property (T). Ollivier sketched an extension of this to the Gromov denisty model in [Reference Ollivier11], and Kotowski-Kotowski completed the proof in [Reference Kotowski and Kotowski5].
Similarly, we do not yet know a sharp threshold for cubulation of random groups (i.e. admitting a cocompact action on a CAT(0) cube complex without a global fixed point). In [Reference Mackay and Przytycki7], Mackay-Przytycki built on the work of Ollivier-Wise [Reference Ollivier and Wise13] to show that at densities
![]() $d<5/24$
, Gromov random groups are, with probability 1, cubulated. This bound was improved to
$d<5/24$
, Gromov random groups are, with probability 1, cubulated. This bound was improved to
![]() $d<3/14$
in [Reference Montee8] using a generalization of the methods in [Reference Mackay and Przytycki7].
$d<3/14$
in [Reference Montee8] using a generalization of the methods in [Reference Mackay and Przytycki7].
For infinite hyperbolic groups, being cubulated and having Property (T) are mutually exclusive, so together these results show that the sharp threshold at which Gromov random groups fail to satisfy Property (T) must be between 1/3 and 3/14.
In order to prove his theorem, Żuk introduced a new model of random groups, called the triangular model. This was extended to the square model in [Reference Odrzygozdz9], and in [Reference Ashcroft and Roney-Dougal1], this was further generalized this to a class of models, here called the k-gonal models. Roughly speaking, as k approaches infinity the behavior of k-gonal random groups should reflect the behavior of Gromov random groups. Odrzygóźdź showed that in the 6-gonal model,
![]() $d=1/3$
is the sharp threshold at which the probability of a group satisfying Property (T) switches from 1 to 0. Figure 1 illustrates what is currently known about values of the sharp threshold for Property (T) in the k-gonal models.
$d=1/3$
is the sharp threshold at which the probability of a group satisfying Property (T) switches from 1 to 0. Figure 1 illustrates what is currently known about values of the sharp threshold for Property (T) in the k-gonal models.

Figure 1. Possible values of the sharp threshold for Property (T) in the k-gonal models. Red indicates (some of the) results from this paper.
In this paper, we show that show that any upper bound on the sharp threshold for Property (T) in the positive k-gonal model gives an upper bound in the jk-gonal model for all
![]() $j \in \mathbb{N}$
. More precisely, we prove the following theorem:
$j \in \mathbb{N}$
. More precisely, we prove the following theorem:
Theorem 1.1. Let
![]() $d_0$
be some fixed value in
$d_0$
be some fixed value in
![]() $(0, 1)$
, and suppose that with overwhelming probability a random group at density
$(0, 1)$
, and suppose that with overwhelming probability a random group at density
![]() $d>d_0$
in
$d>d_0$
in
![]() $\mathcal{M}^+_{k}(n, d)$
satisfies Property (T). Then for any
$\mathcal{M}^+_{k}(n, d)$
satisfies Property (T). Then for any
![]() $d^{\prime} \in (d_0, d)$
and for any
$d^{\prime} \in (d_0, d)$
and for any
![]() $j \in \mathbb{N}$
, with overwhelming probability a random group in
$j \in \mathbb{N}$
, with overwhelming probability a random group in
![]() $\mathcal{M}_{jk}(n, d^{\prime})$
or
$\mathcal{M}_{jk}(n, d^{\prime})$
or
![]() $\mathcal{M}^+_{jk}(n, d^{\prime})$
satisfies Property (T).
$\mathcal{M}^+_{jk}(n, d^{\prime})$
satisfies Property (T).
In particular, this improves the known upper bounds in the 3j-gonal models from
![]() $1/2$
to
$1/2$
to
![]() $1/3$
. It also shows that to find upper bounds for the sharp threshold of Property (T), it suffices to investigate the positive k-gonal models. Further, this provides evidence supporting the following conjecture:
$1/3$
. It also shows that to find upper bounds for the sharp threshold of Property (T), it suffices to investigate the positive k-gonal models. Further, this provides evidence supporting the following conjecture:
Conjecture 1.2. Let
![]() $d_{(T)}(k)$
denote the sharp threshold for Property (T) in the k-gonal model. Then
$d_{(T)}(k)$
denote the sharp threshold for Property (T) in the k-gonal model. Then
![]() $\lim_{k \to \infty} d_{(T)}(k)$
exists and is equal to the sharp threshold of the Gromov model.
$\lim_{k \to \infty} d_{(T)}(k)$
exists and is equal to the sharp threshold of the Gromov model.
2. Background
We begin by defining the k-gonal model of random groups.
Definition 2.1 ([Reference Ashcroft and Roney-Dougal1]). Fix a set S of cardinality n. The k-gonal model of random groups, denoted
![]() $\mathcal{M}_k(n, d),$
is the set of group presentations
$\mathcal{M}_k(n, d),$
is the set of group presentations
![]() $\langle S|R\rangle$
such that R is a set of
$\langle S|R\rangle$
such that R is a set of
![]() $(2n-1)^{kd}$
cyclically reduced words on
$(2n-1)^{kd}$
cyclically reduced words on
![]() $S\cup S^{-1}$
of length k, along with the uniform probability measure. We say that a k-gonal random group at density d satisfies a property P with overwhelming probability, abbreviated w.o.p, if
$S\cup S^{-1}$
of length k, along with the uniform probability measure. We say that a k-gonal random group at density d satisfies a property P with overwhelming probability, abbreviated w.o.p, if
A related family of models of random groups restricts possible relators to positive words, i.e. words on S but not on
![]() $S^{-1}$
. These are called the positive k-gonal models of random groups and are denoted
$S^{-1}$
. These are called the positive k-gonal models of random groups and are denoted
![]() $\mathcal{M}^+_k(n, d).$
We will relax the condition on the number of relators in this model and require that the number of relators be
$\mathcal{M}^+_k(n, d).$
We will relax the condition on the number of relators in this model and require that the number of relators be
![]() $ f(n) \approx (2n-1)^{kd}$
, where “
$ f(n) \approx (2n-1)^{kd}$
, where “
![]() $\approx$
” means that
$\approx$
” means that
![]() $\lim_{n\to \infty} f(n)/(2n-1)^{kd}$
is a finite constant. The definition of satisfying property P w.o.p. will not depend on this detail.
$\lim_{n\to \infty} f(n)/(2n-1)^{kd}$
is a finite constant. The definition of satisfying property P w.o.p. will not depend on this detail.
We now define (Kazhdan’s) Property (T) for discrete, finitely generated groups. The notation is suggestive—the idea of Property (T) is that the trivial representation of the group must be isolated in some metric. More formally, we can define this property via (almost) invariant vectors: Let
![]() $\Gamma$
be a finite generated group with finitely generating set S. If
$\Gamma$
be a finite generated group with finitely generating set S. If
![]() $\mathcal{H}$
is a Hilbert space and
$\mathcal{H}$
is a Hilbert space and
![]() $\pi\,:\, \Gamma \to U(\mathcal{H})$
is a unitary representation of
$\pi\,:\, \Gamma \to U(\mathcal{H})$
is a unitary representation of
![]() $\Gamma$
on
$\Gamma$
on
![]() $\mathcal{H}$
, then
$\mathcal{H}$
, then
![]() $\pi$
has almost invariant vectors if, for every
$\pi$
has almost invariant vectors if, for every
![]() $\varepsilon>0$
, there exists some
$\varepsilon>0$
, there exists some
![]() $u_\varepsilon \in \mathcal{H}$
such that for every
$u_\varepsilon \in \mathcal{H}$
such that for every
![]() $s \in S$
,
$s \in S$
,
![]() $\|\pi(s)u_\varepsilon - u_\varepsilon\| < \varepsilon\|u_\varepsilon\|.$
A vector
$\|\pi(s)u_\varepsilon - u_\varepsilon\| < \varepsilon\|u_\varepsilon\|.$
A vector
![]() $u \in \mathcal{H}$
is invariant if
$u \in \mathcal{H}$
is invariant if
![]() $\pi(g)(u) = u$
for every
$\pi(g)(u) = u$
for every
![]() $g \in \Gamma$
.
$g \in \Gamma$
.
Definition 2.2 ([Reference Kazdan4]). A finitely generated group
![]() $\Gamma$
has Property (T) if, for every
$\Gamma$
has Property (T) if, for every
![]() $\mathcal{H}$
and
$\mathcal{H}$
and
![]() $\pi$
, the following holds: if
$\pi$
, the following holds: if
![]() $\pi$
has almost invariant vectors, then
$\pi$
has almost invariant vectors, then
![]() $\pi$
has a nonzero invariant vector.
$\pi$
has a nonzero invariant vector.
The first results towards demonstrating Property (T) in random groups were first stated in [Reference Żuk14] and fully proved in [Reference Kotowski and Kotowski5]. The proof involved passing between several different models of random groups and analyzing spectral properties of random graphs.
Theorem 2.3 ([Reference Kotowski and Kotowski5] Theorem 3.14). A random group in
![]() $\mathcal{M}^+_3(n, d^{\prime})$
with density
$\mathcal{M}^+_3(n, d^{\prime})$
with density
![]() $d^{\prime}>1/3$
satisfies Property (T) with overwhelming probability.
$d^{\prime}>1/3$
satisfies Property (T) with overwhelming probability.
In fact, they also showed that this is true in
![]() $\mathcal{M}_3(n, d)$
and in the Gromov model of random groups (at the same density).
$\mathcal{M}_3(n, d)$
and in the Gromov model of random groups (at the same density).
Remark 2.4. Property (T) is preserved by surjections and finite extensions (see [Reference Kotowski and Kotowski5] Remark 2.10 and [Reference Bekka, de la Harpe and Valette2] Theorem 1.7.1). In other words, if
![]() $H$
is a group with Property (T) and
$H$
is a group with Property (T) and
![]() $H$
surjects onto
$H$
surjects onto
![]() $H'$
, then
$H'$
, then
![]() $H'$
has Property (T), and if
$H'$
has Property (T), and if
![]() $\textrm{H} \stackrel{f.i.}{\leq} \textrm{H}^{\prime\prime}$
is a subgroup of finite index, then
$\textrm{H} \stackrel{f.i.}{\leq} \textrm{H}^{\prime\prime}$
is a subgroup of finite index, then
![]() $H''$
has Property (T).
$H''$
has Property (T).
The tempting argument is to say if
![]() $G \in \mathcal{M}_{jk}(n, d)$
then
$G \in \mathcal{M}_{jk}(n, d)$
then
![]() $G = \langle S | R \rangle$
and any relator in R can be interpreted as a word of length k over the alphabet of words of length j on
$G = \langle S | R \rangle$
and any relator in R can be interpreted as a word of length k over the alphabet of words of length j on
![]() $S \cup S^{-1}$
, denoted
$S \cup S^{-1}$
, denoted
![]() $|W_j|$
. Then, G is in
$|W_j|$
. Then, G is in
![]() $\mathcal{M}_k(|W_j|, d).$
However, as is pointed out in [Reference Kotowski and Kotowski5], problems arise around the requirement that relators be reduced. In particular, a word of length kj is a word of length k in the alphabet of words of length j; however, a reduced word of length k in the alphabet of words of length j might not be reduced as a word of length jk. So we must first consider an intermediate group,
$\mathcal{M}_k(|W_j|, d).$
However, as is pointed out in [Reference Kotowski and Kotowski5], problems arise around the requirement that relators be reduced. In particular, a word of length kj is a word of length k in the alphabet of words of length j; however, a reduced word of length k in the alphabet of words of length j might not be reduced as a word of length jk. So we must first consider an intermediate group,
![]() $G^+$
, whose relators are positive words on S. This removes the reduction problem, and we can safely interpret this group as a random group in
$G^+$
, whose relators are positive words on S. This removes the reduction problem, and we can safely interpret this group as a random group in
![]() $\mathcal{M}_k^+(n, d)$
.
$\mathcal{M}_k^+(n, d)$
.
The method of proof closely follows the argument used to prove Theorem 4.3 in [Reference Odrzygozdz9], which shows that groups in the 6-gonal model w.o.p. satisfy Property (T). In particular, to prove that a random group
![]() $G \in \mathcal{M}_{jk}(n,d)$
satisfies Property (T), we construct two groups
$G \in \mathcal{M}_{jk}(n,d)$
satisfies Property (T), we construct two groups
![]() $G^+$
and
$G^+$
and
![]() $\Gamma$
so that
$\Gamma$
so that
and then show that
![]() $\Gamma$
satisfies Property (T).
$\Gamma$
satisfies Property (T).
There are two parts to this proof. The first is showing that
![]() $\phi(\Gamma)$
is finite index in
$\phi(\Gamma)$
is finite index in
![]() $G^+$
. We find a finite set of coset representatives to prove this explicitly, generalizing the method used in [Reference Odrzygozdz9]. The second is in showing that the group
$G^+$
. We find a finite set of coset representatives to prove this explicitly, generalizing the method used in [Reference Odrzygozdz9]. The second is in showing that the group
![]() $\Gamma$
can be interpreted as a typical representative of random groups in
$\Gamma$
can be interpreted as a typical representative of random groups in
![]() $\mathcal{M}^+_k(m, d^{\prime})$
for
$\mathcal{M}^+_k(m, d^{\prime})$
for
![]() $d^{\prime} >1/3.$
For this part of the argument, we mimic the method developed in the proof of Theorem A in [Reference Kotowski and Kotowski5].
$d^{\prime} >1/3.$
For this part of the argument, we mimic the method developed in the proof of Theorem A in [Reference Kotowski and Kotowski5].
3. Property (T) in jk-gonal models
Fix a generating set S of cardinality n. Let
![]() $W^+$
be the set of positive words on S and let
$W^+$
be the set of positive words on S and let
![]() $W_j$
be the words of length j on S. For any set R of words on S, let
$W_j$
be the words of length j on S. For any set R of words on S, let
![]() $R^+ = R \cap W^+$
. Then for any group
$R^+ = R \cap W^+$
. Then for any group
![]() $G = \langle S | R\rangle$
in
$G = \langle S | R\rangle$
in
![]() $\mathcal{M}_{jk}(n, d)$
, there is a group
$\mathcal{M}_{jk}(n, d)$
, there is a group
![]() $G^+ = \langle S | R^+\rangle$
that surjects onto G.
$G^+ = \langle S | R^+\rangle$
that surjects onto G.
Since G is in the jk-gonal model, every word in R and
![]() $R^+$
has length jk. There is a natural injective map
$R^+$
has length jk. There is a natural injective map
![]() $\phi: W^+_j \to F(S)$
, where F(S) denotes the free group on S, given by the labeling on each word in
$\phi: W^+_j \to F(S)$
, where F(S) denotes the free group on S, given by the labeling on each word in
![]() $W^+_j$
. Define
$W^+_j$
. Define
![]() $R^+_k = \phi^{-1}(R^+)$
and notice that every word in
$R^+_k = \phi^{-1}(R^+)$
and notice that every word in
![]() $R^+_k$
has length k over
$R^+_k$
has length k over
![]() $W_j^+$
. Let
$W_j^+$
. Let
![]() $\Gamma = \langle W_j^+ | R^+_k \rangle$
. Then,
$\Gamma = \langle W_j^+ | R^+_k \rangle$
. Then,
![]() $\phi$
induces a homomorphism, also denoted
$\phi$
induces a homomorphism, also denoted
![]() $\phi$
, mapping
$\phi$
, mapping
![]() $\Gamma \to G^+$
.
$\Gamma \to G^+$
.
Note also that
![]() $|R^+_k| = |\phi(R^+_k)| = |R^+|,$
so if
$|R^+_k| = |\phi(R^+_k)| = |R^+|,$
so if
![]() $G^+ \in \mathcal{M}^+_{jk}(n, d^{\prime}),$
then
$G^+ \in \mathcal{M}^+_{jk}(n, d^{\prime}),$
then
![]() $\Gamma \in \mathcal{M}^+_k(|W^+_j|, d^{\prime})$
. Furthermore, this map takes the uniform probability distribution on
$\Gamma \in \mathcal{M}^+_k(|W^+_j|, d^{\prime})$
. Furthermore, this map takes the uniform probability distribution on
![]() $\mathcal{M}^+_{jk}(n, d^{\prime})$
to the uniform probability distribution on
$\mathcal{M}^+_{jk}(n, d^{\prime})$
to the uniform probability distribution on
![]() $\mathcal{M}^+_k(|W^+_j|, d^{\prime})$
, because
$\mathcal{M}^+_k(|W^+_j|, d^{\prime})$
, because
![]() $\phi$
induces a 1-1 map on possible sets of relators.
$\phi$
induces a 1-1 map on possible sets of relators.
We will show that
![]() $\phi(\Gamma)$
is a finite index subgroup of
$\phi(\Gamma)$
is a finite index subgroup of
![]() $G^+$
by finding an explicit set of coset representatives of
$G^+$
by finding an explicit set of coset representatives of
![]() $\phi(\Gamma)$
in
$\phi(\Gamma)$
in
![]() $G^+$
. We note that an element of
$G^+$
. We note that an element of
![]() $G^+$
is in
$G^+$
is in
![]() $\phi(\Gamma)$
if and only if it is expressible as a string of words of length k, all of which are positive or the inverse thereof. We do this by inserting trivial words that allow us to group positive and negative letters into subwords of length j.
$\phi(\Gamma)$
if and only if it is expressible as a string of words of length k, all of which are positive or the inverse thereof. We do this by inserting trivial words that allow us to group positive and negative letters into subwords of length j.
In the following proof, for any word w,
![]() $|w|_j$
denotes the word length of w modulo j.
$|w|_j$
denotes the word length of w modulo j.
Lemma 3.1.
![]() $\phi(\Gamma)$
is a finite index subgroup of
$\phi(\Gamma)$
is a finite index subgroup of
![]() $G^+$
.
$G^+$
.
Proof. Let w be a word on
![]() $S \cup S^{-1}$
. Without loss of generality, assume that the first letter of w is in
$S \cup S^{-1}$
. Without loss of generality, assume that the first letter of w is in
![]() $S^{-1}$
. Then, w can be written as
$S^{-1}$
. Then, w can be written as
where
![]() $\{a_i\}$
are positive words on S,
$\{a_i\}$
are positive words on S,
![]() $\{A_i\}$
are negative words on S, and
$\{A_i\}$
are negative words on S, and
![]() $a_1$
might be empty.
$a_1$
might be empty.
Let x be a positive word of length
![]() $j - |a_1|_j$
and let y be a positive word of length
$j - |a_1|_j$
and let y be a positive word of length
![]() $j - |A_1x^{-1}|_j$
. Then, we have
$j - |A_1x^{-1}|_j$
. Then, we have
Note that
![]() $xa_1$
is a positive word with length divisible by j, and
$xa_1$
is a positive word with length divisible by j, and
![]() $y^{-1}A_1 x^{-1}$
is a negative word with length divisible by j. Therefore,
$y^{-1}A_1 x^{-1}$
is a negative word with length divisible by j. Therefore,
![]() $w = A_\ell a_\ell \cdots A_2 a^{\prime}_2 u,$
where
$w = A_\ell a_\ell \cdots A_2 a^{\prime}_2 u,$
where
![]() $u \in \phi(\Gamma)$
. By induction, we see that
$u \in \phi(\Gamma)$
. By induction, we see that
![]() $w \in A^{\prime}_\ell\phi(\Gamma)$
where
$w \in A^{\prime}_\ell\phi(\Gamma)$
where
![]() $A^{\prime}_\ell$
is a positive word on S. Then,
$A^{\prime}_\ell$
is a positive word on S. Then,
![]() $A^{\prime}_\ell = a z,$
where j divides
$A^{\prime}_\ell = a z,$
where j divides
![]() $|z|$
and
$|z|$
and
![]() $|a|< j$
, so
$|a|< j$
, so
![]() $z \in \phi(\Gamma)$
. Therefore,
$z \in \phi(\Gamma)$
. Therefore,
![]() $w = azv$
, where
$w = azv$
, where
![]() $zv \in \phi(\Gamma)$
and
$zv \in \phi(\Gamma)$
and
![]() $|a| < j$
.
$|a| < j$
.
Thus, the (finite) set of words of length
![]() $< j$
contains a transversal of
$< j$
contains a transversal of
![]() $\phi(\Gamma)$
in
$\phi(\Gamma)$
in
![]() $G^+$
, and
$G^+$
, and
![]() $\phi(\Gamma)$
has finite index in
$\phi(\Gamma)$
has finite index in
![]() $G^+$
.
$G^+$
.
We are now ready to prove Theorem 1.1:
Theorem 1.1. Let
![]() $d_0$
be some fixed value in
$d_0$
be some fixed value in
![]() $(0, 1)$
, and suppose that with overwhelming probability a random group at density
$(0, 1)$
, and suppose that with overwhelming probability a random group at density
![]() $d > d_0$
in
$d > d_0$
in
![]() $M_k^+(n,d)$
satisfies Property (T). Then for any
$M_k^+(n,d)$
satisfies Property (T). Then for any
![]() $d^{\prime}\in(d_0,d)$
and for any
$d^{\prime}\in(d_0,d)$
and for any
![]() $j\in\mathbb{N}$
, with overwhelming probability a random group in
$j\in\mathbb{N}$
, with overwhelming probability a random group in
![]() $\mathcal{M}_{jk}(n, d^{\prime})$
or
$\mathcal{M}_{jk}(n, d^{\prime})$
or
![]() $\mathcal{M}^+_{jk}(n, d^{\prime})$
satisfies Property (T).
$\mathcal{M}^+_{jk}(n, d^{\prime})$
satisfies Property (T).
Proof. We first show that a random group
![]() $G^+$
in
$G^+$
in
![]() $\mathcal{M}^+_{kj}(n, d)$
has Property (T). Let
$\mathcal{M}^+_{kj}(n, d)$
has Property (T). Let
![]() $m = |W^+_{j}|$
. By the construction above, given such a
$m = |W^+_{j}|$
. By the construction above, given such a
![]() $G^+$
we can find a group
$G^+$
we can find a group
![]() $\Gamma$
in
$\Gamma$
in
![]() $\mathcal{M}^+_k(m, d)$
and a map
$\mathcal{M}^+_k(m, d)$
and a map
![]() $\phi: \Gamma \to G^+$
. The distribution induced on
$\phi: \Gamma \to G^+$
. The distribution induced on
![]() $\mathcal{M}^+_k(m, d)$
in this way is uniform and by Lemma 3.1
$\mathcal{M}^+_k(m, d)$
in this way is uniform and by Lemma 3.1
![]() $\phi(\Gamma)$
is a finite index subgroup of
$\phi(\Gamma)$
is a finite index subgroup of
![]() $G^+$
. Since
$G^+$
. Since
![]() $\Gamma$
satisfies Property (T) with overwhelming probability, by Remark 2.4, so does
$\Gamma$
satisfies Property (T) with overwhelming probability, by Remark 2.4, so does
![]() $G^+$
.
$G^+$
.
Now let
![]() $G =\langle S|R\rangle$
be a group in
$G =\langle S|R\rangle$
be a group in
![]() $\mathcal{M}_{kj}(n, d).$
Note that
$\mathcal{M}_{kj}(n, d).$
Note that
![]() $|W^+_j| > \frac{1}{2^j}|W_j|.$
Therefore, the expected number of elements of
$|W^+_j| > \frac{1}{2^j}|W_j|.$
Therefore, the expected number of elements of
![]() $R^+$
is at least
$R^+$
is at least
![]() $\frac{1}{2^j}|R|> \frac{1}{2^j}|R| = \frac{1}{2^j}(2n-1)^{kjd} > 2(2n-1)^{kjd^{\prime}}$
, for any
$\frac{1}{2^j}|R|> \frac{1}{2^j}|R| = \frac{1}{2^j}(2n-1)^{kjd} > 2(2n-1)^{kjd^{\prime}}$
, for any
![]() $d^{\prime}<d$
and sufficiently large n. The Chernoff bound then implies that with overwhelming probability,
$d^{\prime}<d$
and sufficiently large n. The Chernoff bound then implies that with overwhelming probability,
![]() $|R^+| > (2n-1)^{kjd^{\prime}}.$
$|R^+| > (2n-1)^{kjd^{\prime}}.$
Fix
![]() $d^{\prime} \in (d_0, d)$
. If we enumerate the elements of
$d^{\prime} \in (d_0, d)$
. If we enumerate the elements of
![]() $W^+_j$
and take R
′ to be the set of the first
$W^+_j$
and take R
′ to be the set of the first
![]() $(2n-1)^{kjd^{\prime}}$
elements of
$(2n-1)^{kjd^{\prime}}$
elements of
![]() $W^+_j$
which are in R, we can find a group
$W^+_j$
which are in R, we can find a group
![]() $G^+ \langle S | R^{\prime}\rangle\in \mathcal{M}^+_{kj}(n, d^{\prime})$
that surjects onto G. This gives a uniform distribution on
$G^+ \langle S | R^{\prime}\rangle\in \mathcal{M}^+_{kj}(n, d^{\prime})$
that surjects onto G. This gives a uniform distribution on
![]() $\mathcal{M}^+_{kj}(n, d^{\prime})$
, so w.o.p
$\mathcal{M}^+_{kj}(n, d^{\prime})$
, so w.o.p
![]() $G^+$
satisfies Property (T), and by Remark 2.4 so does G.
$G^+$
satisfies Property (T), and by Remark 2.4 so does G.
By Theorem 3.14 in [Reference Kotowski and Kotowski5], with overwhelming probability random groups in
![]() $\mathcal{M}^+_3(n, d)$
satisfy Property (T) at density
$\mathcal{M}^+_3(n, d)$
satisfy Property (T) at density
![]() $d>1/3$
. By applying Theorem 1, we get the following result.
$d>1/3$
. By applying Theorem 1, we get the following result.
Corollary 3.2. For each
![]() $k \in \mathbb{N}$
, with overwhelming probability, a random group at density
$k \in \mathbb{N}$
, with overwhelming probability, a random group at density
![]() $d>1/3$
in
$d>1/3$
in
![]() $\mathcal{M}_{3k}(n, d)$
or
$\mathcal{M}_{3k}(n, d)$
or
![]() $\mathcal{M}^+_{3k}(n, d)$
satisfies Property (T).
$\mathcal{M}^+_{3k}(n, d)$
satisfies Property (T).
Acknowledgements
I would like to thank Danny Calegari and Tomasz Odrzygóźdź for valuable comments and feedback. This research was partially supported by a Clare Boothe Luce Professorship in Mathematics from the Henry Luce Foundation.