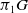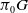1. Introduction
It is a classical fact that, for a path-connected CW-complex X and for a topological group G, the set of topological types of principal G-bundles over X is in bijection with the set [X, BG] of free homotopy classes of maps from X to the classifying space BG of G. It is, however, many times useful to have a more explicit classification of such bundles, that is, to have a more detailed description of the set [X, BG], for example, in terms of characteristic classes.
In this note, we provide such a description in a setting which is quite classical, and hence which ought to be very well known. We obtain an explicit and complete classification of G-bundles over a two-dimensional connected finite CW-complex X, for any Lie group G with
$\pi_0G$
abelianFootnote 1, in terms of cohomology classes. This includes two classical cases. Firstly, if G is connected, such bundles are classified by the cohomology group
$H^2(X,\pi_1G)$
. Secondly, there is a natural action of
$\pi_0G$
on
$\pi_1G$
, and if this action is trivial, then G-bundles over X are classified by the product
$H^1(X,\pi_0G)\times H^2(X,\pi_1G)$
. Nonetheless, such
$\pi_0G$
-action can be nontrivial and, somehow surprisingly, this case does not seem to have been explicitly treated so far. An instance where this phenomenon occurs is the case of the projective orthogonal group of even rank, which we explicitly deal with as an example.
The importance of the topological classification of principal G-bundles over any finite, two-dimensional, CW-complex by itself or by its connections with other areas of Mathematics and Physics is obvious, so the mentioned untreated case deserves to be considered. This is the purpose of this article. Just to give an example where such a topological classification plays an important role, consider the following. Suppose G is semisimple and consider the space
$\mathcal{R}(X,G)=\textrm{Hom}^{red}(\pi_1X,G)/G$
of reductive representations
$\rho:\pi_1X\to G$
modulo the G-action by conjugation. These spaces, or spaces deeply related to them, arise from several different natural points of view (Physics, Gauge Theory, Hyperbolic Geometry, etc.) and have been intensively studied in the past decades, mostly in the case X is a closed oriented surface, where deep connections arise with the theory of holomorphic vector bundles [Reference Narasimhan and Seshadri13] and also with the theory of Higgs bundles, under the so-called non-abelian Hodge correspondence (there are many references for this subject: the seminal paper is [Reference Hitchin8] and an overview and other references may be found for instance in [Reference Wentworth and Courses21]). However, the spaces
$\mathcal{R}(X,G)$
have also been studied for compact, non-orientable surfaces [Reference Baird1,Reference Baird2,9,Reference Schaffhauser17] and even for any finite two-dimensional CW-complex [Reference Daskalopoulos, Mese and Wilkin3]. Now, the topological type of G-bundles over X provides a way to distinguish certain connected components of
$\mathcal{R}(X,G)$
and to give a lower bound on the number of such components (e.g., it is known that if G is a complex Lie group and X is an orientable closed surface, such bound is exact [Reference García-Prada and Oliveira5]). Hence, the theorem of this article gives a way to achieve this for any Lie group G with
$\pi_0G$
abelian.
To give a hint on the classification theorem, note first that if a G-bundle over X is given by the homotopy class of a map
$X\to BG$
, then the homotopy class of composite
$X\to BG\to B\pi_0G$
defines a topological invariant
$\mu_1\in [X,B\pi_0G]\cong H^1(X,\pi_0G)$
of the given G-bundle, measuring the obstruction to reduce its structure group to the identity component of G. Having this, the classification result (see Theorem 2.2) states that there is a bijection between the subset of [X, BG] consisting of isomorphism classes of principal G-bundles over X with invariant
$\mu_1\in H^1(X,\pi_0G)$
and the quotient set
$H^2(X,\pi_1\mathcal{G}_{\mu_1})/\pi_0G$
. Here,
$\pi_1\mathcal{G}_{\mu_1}$
denotes the local system obtained from
$\mu_1$
and from a natural action of
$\pi_0G$
in
$\pi_1G$
and where
$\pi_0G$
acts on
$H^2(X,\pi_1\mathcal{G}_{\mu_1})$
also via the same action of
$\pi_0G$
in
$\pi_1G$
.
2. The classification and examples
2.1 A first topological invariant
Let X be a path-connected two-dimensional CW-complex. Let also G be a Lie group, with (discrete) group of connected components
$\pi_0G$
. Recall that isomorphism classes of principal G-bundles over X are topologically classified by the set [X, BG] of free homotopy classes of maps from X to the classifying space BG. There is a natural map
\begin{equation}\chi\,{:}\,[X,BG]\to[X,B\pi_0G], \ \ \ \chi([f])=[p_{0,*}\circ f],\end{equation}
where
$p_{0,*}\,{:}\,BG\to B\pi_0G$
is the map induced from the canonical projection
$p_0\,{:}\,G\to\pi_0G$
.
From here one readily defines a first topological invariant of a G-bundle E over X.
Definition 2.1. Let E be a G-bundle over X represented by a map
$f\,{:}\,X\to BG$
. Define
$$\mu_1(E)=\chi([f])\in [X,B\pi_0G].$$
Since
$B\pi_0G$
is the Eilenberg–Maclane space
$K(\pi_0G,1)$
, it follows that
$[X,B\pi_0G]\cong H^1(X,\pi_0G)$
.
$\mu_1(E)$
is obviously a topological invariant of E and it represents the isomorphism class of the
$\pi_0G$
-bundle on X obtained from E through the projection
$G\to\pi_0G$
.
From now on, we fix an element
$\mu_1\in [X,B\pi_0G]$
and our task is to classify G-bundles E on X such that
$\mu_1(E)=\mu_1$
.
2.2 The classification theorem and examples
Notice that the action:
$$\Psi\,{:}\,G\longrightarrow\operatorname{Aut}(G),$$
of G on itself by conjugation induces an action of
$\pi_0G$
on the higher homotopy groups
$\pi_iG$
(by
$\pi_iG$
we always mean homotopy groups based at the identity of G): for
$a\in G$
, consider the induced automorphism
$\Psi(a)_*\,{:}\,\pi_iG\to\pi_iG$
and, if
$b\in G$
is in the same component as a, then
$\Psi(a)$
is homotopic to
$\Psi(b)$
via a path joining a and b, hence
$\Psi(a)_*=\Psi(b)_*$
.
In particular, we are interested in the action of
$\pi_0G$
on
$\pi_1G$
, which we will denote by
\begin{equation} \Psi(-)_*\,{:}\,\pi_0G\longrightarrow\operatorname{Aut}(\pi_1G).\end{equation}
Assume now, once and for all, that the group
$\pi_0G$
is abelian and consider the homomorphism in
$\pi_1$
,
$\mu_{1*}\,{:}\,\pi_1X\to\pi_0G$
, induced from the invariant
$\mu_1\,{:}\,X\to B\pi_0G$
that we have previously fixed (recall that
$\pi_0G=\pi_1(B\pi_0G)$
). Given this, we have an induced action of
$\pi_1X$
on
$\pi_1G$
:
\begin{equation}\Psi(-)_*\circ \mu_{1*}\,{:}\,\pi_1X\longrightarrow\operatorname{Aut}(\pi_1G),\end{equation}
and so this action defines a local system
$\pi_1\mathcal{G}_{\mu_1}$
on X.
Let
$H^*(X,\pi_1\mathcal{G}_{\mu_1})$
be the cohomology of X with values in the local system
$\pi_1\mathcal{G}_{\mu_1}$
. Recall that this is the cohomology of the cochain complex
$C^*_{\mathbb{Z}[\pi_1X]}(\widetilde{X},\pi_1G)=\textrm{Hom}_{\mathbb{Z}[\pi_1X]}(C_*(\widetilde{X}),\pi_1G)$
, where
$\mathbb{Z}\pi=\mathbb{Z}[\pi_1X]$
is the group ring of
$\pi_1X$
and
$C_*(\widetilde{X})$
is the
$\mathbb{Z}\pi$
-module of chains on the universal cover
$\widetilde X$
of X.
Note now that
$\Psi(-)_*$
in (2.2) induces, by composition, a
$\pi_0G$
-action on the
$\mathbb{Z}\pi$
-module
$C^2_{\mathbb{Z}[\pi_1X]}(\widetilde{X},\pi_1G)$
. Explicitly,
$a\in \pi_0G$
acts on a 2-cochain
$\tau\in C^2_{\mathbb{Z}[\pi_1X]}(\widetilde{X},\pi_1G)$
as:
\begin{equation}a\cdot\tau=\Psi(a)_*\circ\tau.\end{equation}
Since
$\widetilde{X}$
has dimension 2, every 2-cochain is a cocycle hence, passing to the quotient, (2.4) yields a
$\pi_0G$
-action on
$H^2(X,\pi_1\mathcal{G}_{\mu_1})$
. Let
$$H^2(X,\pi_1\mathcal{G}_{\mu_1})/\pi_0G,$$
be the corresponding quotient set.
We are now ready to state the result concerning the topological classification of principal G-bundles over X.
Theorem 2.2. Let G be a Lie group with
$\pi_0G$
abelian and let X be a two-dimensional connected CW-complex. There is a bijection between the set of isomorphism classes of continuous principal G-bundles over X with invariant
$\mu_1\in H^1(X,\pi_0G)$
and the (non-empty) quotient set
$H^2(X,\pi_1\mathcal{G}_{\mu_1})/\pi_0G$
.
This means that the map:
$$\chi\,{:}\,[X,BG]\to H^1(X,\pi_0G),$$
defined in (2.1) is such that there is bijection of sets
$\chi^{-1}(\mu_1)\simeq H^2(X,\pi_1\mathcal{G}_{\mu_1})/\pi_0G$
.
Remark 2.3. Of course if one has a topological space M which is homotopically equivalent to a finite two-dimensional CW-complex X, then
$[M,BG]\cong[X,BG]$
, so the above theorem also applies for the classification of principal G-bundles over M. For instance, M could be the complement of a finite number of points in a compact three-dimensional manifold.
Remark 2.4. Using different methods, Theorem 2.2 has actually been proved before in [Reference Oliveira14], in the particular case X is a closed oriented surface.
We will prove the theorem in Section 5. In the next sections, we will briefly recall some notions (of obstruction theory and of Postnikov sections) which will be required for it. Before that, let us now consider some explicit examples (most of them quite classical) of applications of this theorem.
Example 2.5. Let X be any finite connected two-dimensional CW-complex and G a Lie group with
$\pi_0G$
abelian.
-
(1) If G is connected, then G-bundles over X are classified by:
as it is well known (for surfaces, see for example [15], Proposition
$$[X,BG]\cong H^2(X,\pi_1G),$$
$5.1$
).
-
(2) If
$\pi_0G$
acts trivially on
$\pi_1G$
, then G-bundles over X are classified by: Because
$$[X,BG]\cong H^1(X,\pi_0G)\times H^2(X,\pi_1G).$$
$\pi_0G$
is abelian, this case yields when X is a closed (i.e., compact and without boundary) oriented surface of genus g, and yields
$$[X,BG]\cong\pi_0G^{2g}\times\pi_1G,$$
when X is a closed non-orientable surface which is a connected sum of k copies of the projective plane
$$[X,BG]\cong(\pi_0G)_2\times\pi_0G^{k-1}\times\pi_1G/2\pi_1G,$$
$\mathbb{R}\mathbb{P}^2$
. Here,
$(\pi_0G)_2$
denotes the 2-torsion subgroup of
$\pi_0G$
.
-
(3) When
$G=\textrm{O}(n)$
, the group of orthogonal transformations of
$\mathbb{R}^n$
, with
$n\geqslant 3$
, then we are in the situation of the previous item and the classification is given by the first and second Stiefel–Whitney classes
$w_1,w_2$
. -
(4) If X is simply connected, then principal G-bundles over X are classified by:
In particular, this holds for the 2-sphere
$$[X,BG]\cong H^2(X,\pi_1G)/\pi_0G.$$
$S^2$
and gives
$[S^2,BG]\cong \pi_1G/\pi_0G$
. Again this is quite classical, see [Reference Steenrod20], Section 18.
-
(5) Here is another classical example, in which
$\pi_0G$
acts nontrivially on
$\pi_1G$
, and so which we can deduce from the above theorem. Consider
$G=\textrm{O}(2)$
, the group of orthogonal transformations of
$\mathbb{R}^2$
.Then
$\pi_0\textrm{O}(2)=\mathbb{Z}_2$
acts nontrivially on
$\pi_1\textrm{O}(2)=\mathbb{Z}$
, by changing the sign of the generator. Indeed, a generator can be represented by the loop
$\gamma(\theta)=\left (\begin{smallmatrix}\cos(2\pi\theta) &\sin(2\pi\theta) \\ -\sin(2\pi\theta) & \cos(2\pi\theta)\end{smallmatrix}\right)$
, with
$\theta\in[0,1]$
, and the nontrivial element of
$\pi_0\textrm{O}(2)$
, which we can represent by
$\left (\begin{smallmatrix}1 & 0 \\ 0 & -1\end{smallmatrix}\right)$
, takes it to the inverse loop
$\gamma(-\theta)$
.-
(a) Suppose X is a closed oriented surface of genus g. Then, we have the isomorphism
$H^2(X,\mathbb{Z})\cong\mathbb{Z}$
by cap product with the fundamental class. Since the action of
$\pi_0\textrm{O}(2)=\mathbb{Z}_2$
on
$H^2(X,\mathbb{Z})$
by (2.4) is by post-composition on the coefficients, the isomorphism
$H^2(X,\mathbb{Z})\cong\mathbb{Z}$
is
$\pi_0\textrm{O}(2)$
-equivariant with the action on the right-hand side given by (2.2). Note that this argument always applies for any coefficients
$\pi_1G$
, and hence applies generally and not just for
$G=\textrm{O}(2)$
.Hence,
$\textrm{O}(2)$
-bundles over X with
$\mu_1=0$
, that is,
$w_1=0$
(hence which reduce to
$\textrm{SO}(2)\cong S^1$
-bundles), are classified by
$H^2(X,\mathbb{Z})/\mathbb{Z}_2\cong\mathbb{Z}/\mathbb{Z}_2\cong\mathbb{Z}_{\geqslant 0}$
.Consider now
$\textrm{O}(2)$
-bundles over X with first Stiefel–Whitney class
$w_1=\mu_1\neq 0$
(so non-orientable rank 2 orthogonal bundles on X). These are hence classified by
$H^2(X,\mathbb{Z}_{w_1})/\mathbb{Z}_2$
. Then, by Poincaré duality with local coefficients (see [Reference Spanier18], Theorem 10.4) and by [Reference Davis and Kirk4, Proposition 5.14 (1)] (or [Reference Whitehead22, Theorem 3.2, VI]), (2.5)where
\begin{equation}H^2(X,\mathbb{Z}_{w_1})\cong H_0(X,\mathbb{Z}_{w_1})\cong\mathbb{Z}/H_{w_1}=\pi_1\textrm{O}(2)/H_{w_1},\end{equation}
(2.6)and
\begin{equation}H_{w_1}=\langle x-\gamma\cdot x\,|\, x\in\pi_1\textrm{O}(2), \gamma\in\pi_1X\rangle,\end{equation}
$\gamma\cdot x$
is the action of
$\gamma$
on x determined by
$w_1$
and by (2.3). From the calculation at the beginning of the example,
$H_{w_1}\cong 2\mathbb{Z}$
, so
$H^2(X,\mathbb{Z}_{w_1})\cong\mathbb{Z}_2$
. Now we have to look at the action of
$\mathbb{Z}_2$
on the set
$H^2(X,\mathbb{Z}_{w_1})$
induced by (2.4). As above, the isomorphism
$H^2(X,\mathbb{Z}_{w_1})\cong\mathbb{Z}_2=\{0,1\}$
is equivariant with respect to the
$\pi_0\textrm{O}(2)$
-actions (2.4) and (2.2), because duality is also given by cap product and also because the isomorphism of [Reference Davis and Kirk4] Proposition 5.14 (1) is
$\pi_0G$
-equivariant. Again this holds in general and not just for
$G=\textrm{O}(2)$
. But the
$\mathbb{Z}_2=\pi_0\textrm{O}(2)$
-action on
$\mathbb{Z}_2=\{0,1\}$
changes the sign of the generator, hence preserves the parity, thus is trivial. So
$H^2(X,\mathbb{Z}_{w_1})/\mathbb{Z}_2\cong\mathbb{Z}_2$
.
We conclude then the following common knowledge fact: rank 2 orthogonal bundles over a closed oriented surface X of genus g are topologically classified by the characteristic classes in
where
\begin{align*}(\mu_1,\mu_2)\in(\{0\}\times\mathbb{Z}_{\geqslant 0})\cup ((\mathbb{Z}_2)^{2g}\smallsetminus\{0\})\times\mathbb{Z}_2,\\[-10pt]\end{align*}
$\mu_1$
is the first Stiefel–Whitney class and
$\mu_2$
is the (nonnegative) degree when
$\mu_1=0$
and the second Stiefel–Whitney class when
$\mu_1\neq 0$
.
-
(b) Suppose now that X a closed but non-orientable surface. Then
$H^2(X,\mathbb{Z})\cong \mathbb{Z}/2\mathbb{Z}\cong\mathbb{Z}_2$
, and we have to see how
$\mathbb{Z}_2=\pi_0\textrm{O}(2)$
acts via (2.4) on
$H^2(X,\mathbb{Z})$
. This is the same as considering the action (2.2) of
$\mathbb{Z}_2=\pi_0\textrm{O}(2)$
on
$\mathbb{Z}/2\mathbb{Z}\cong\mathbb{Z}_2$
because the isomorphism
$H^2(X,\mathbb{Z})\cong \mathbb{Z}/2\mathbb{Z}$
is equivariant by arguments similar to the orientable case (just take instead the fundamental class of X in homology with local coefficients, cf. [Reference Hatcher7], Example 3H.3); this holds in general and not only for
$\textrm{O}(2)$
. From above, such action changes the sign of the generator, hence preserves the parity. So
$H^2(X,\mathbb{Z})/\mathbb{Z}_2\cong(\mathbb{Z}/2\mathbb{Z})/\mathbb{Z}_2\cong\mathbb{Z}/2\mathbb{Z}\cong\mathbb{Z}_2$
.Suppose now that
$\mu_1=w_1\neq 0$
. Write (2.7)for the corresponding nontrivial orientation character associated with the oriented double cover (this is really the first Stiefel–Whitney class of X, i.e., of its tangent bundle), and
\begin{equation}w_X\,{:}\,\pi_1X\to\operatorname{Aut}(\mathbb{Z})\cong\mathbb{Z}_2,\end{equation}
$\mathbb{Z}_{w_X}$
for the associated local system on X. Then, as above, using Poincaré duality (see [Reference Spanier18, Theorem 10.4]), and [Reference Davis and Kirk4, Proposition 5.14 (1)], we find that (2.8)where
\begin{equation}H^2(X,\mathbb{Z}_{w_1})\cong H_0(X,\mathbb{Z}_{w_X}\otimes_{\mathbb{Z}[\pi_1X]}\mathbb{Z}_{w_1})\cong(\mathbb{Z}/H_{w_X}\otimes_{\mathbb{Z}}\mathbb{Z}/H_{w_1})\cong \mathbb{Z}_2\otimes_{\mathbb{Z}}\mathbb{Z}_2\cong\mathbb{Z}_2,\end{equation}
$H_{w_1}$
is given analogously to (2.6) and
$H_{w_X}=\langle x-\gamma\cdot x\,|\, x\in\mathbb{Z}, \gamma\in\pi_1X\rangle$
with
$\pi_1X$
acting by the nontrivial orientation character
$w_X$
in (2.7) (thus so that
$H_{w_X}\cong 2\mathbb{Z}$
). Here we used again that the two first isomorphisms are
$\pi_0G$
-equivariant with respect to (2.4) and (2.2) (and this is true for any group, not just
$\textrm{O}(2)$
).
Concluding, rank 2 orthogonal bundles over a non-orientable surface X which is a connected sum of k copies of
$\mathbb{R}\mathbb{P}^2$
, are topologically classified by:
\begin{align*}(\mu_1,\mu_2)\in(\{0\}\times\mathbb{Z}_2)\cup (\mathbb{Z}_2^k\smallsetminus\{0\}\times\mathbb{Z}_2)=\mathbb{Z}_2^k\times\mathbb{Z}_2.\end{align*}
-
-
(6) Let us see now a perhaps slightly less known case. We will use, without reference, some of the results we used in the previous example, which hold in general, such as the various versions of Poincaré duality and the
$\pi_0G$
-equivariance of the isomorphisms from the various
$H^2$
under the actions (2.2) and (2.4).Let
$n\geqslant 4$
be even and consider the projective orthogonal group
$\textrm{PO}(n)=\textrm{O}(n)/\mathbb{Z}_2$
, where
$\mathbb{Z}_2=\{\pm I_n\}$
is the center of
$\textrm{O}(n)$
. (If n is odd
$\textrm{PO}(n)$
is connected.) Since n is even,
$\pi_0\textrm{PO}(n)\cong\mathbb{Z}_2$
and More precisely, the universal cover of
$$\pi_1\textrm{PO}(n)=\begin{cases} \mathbb{Z}_2\times\mathbb{Z}_2 & \text{if } n=0\ \text{mod}\ 4 \\[3pt] \mathbb{Z}_4 & \text{if } n=2\ \text{mod}\ 4. \end{cases}$$
$\textrm{PO}(n)$
is the
$\textrm{Pin}(n)$
and, if
$p\,{:}\,\textrm{Pin}(n)\to\textrm{PO}(n)$
is the covering projection, then, as a set (and using the abelian notation)
$\ker(p)=\{0,1,\omega_n,-\omega_n\}$
where
$\omega_n=e_1\cdots e_n$
is the oriented volume element of
$\textrm{Pin}(n)$
in the standard construction of this group via the Clifford algebra
$\textrm{Cl}(n)$
(see, e.g., [Reference Lawson and Michelsohn10]). So, if
$n=0 \ \text{mod}\ 4$
,
$\pm\omega_n$
are elements of order 2, while if
$n=2 \ \text{mod}\ 4$
,
$\pm\omega_n$
have order 4. It turns out that
$\pi_0\textrm{PO}(n)$
acts on
$\pi_1\textrm{PO}(n)$
by leaving 0 and 1 fixed and identifying
$\pm\omega_n$
. More precisely, recall that
$\textrm{Pin}(n)$
is a group with two connected components,
$\textrm{Pin}(n)^-$
and
$\textrm{Spin}(n)$
, where
$\textrm{Pin}(n)^-$
denotes the component which does not contain the identity. We have that
$\pm\omega_n$
do not lie in the center of
$\textrm{Pin}(n)$
(which equals to
$\{0,1\}$
). In fact,
$\omega_n$
commutes with elements in
$\text{Spin}(n)$
and anti-commutes with elements in
$\textrm{Pin}(n)^-$
. This explains that
$\pi_1\textrm{PO}(n)/\pi_0\textrm{PO}(n)=\{0,1,[\omega_n]\}$
where we
$[\omega_n]$
denotes the class of
$\omega_n\in\pi_1\textrm{PO}(n)$
in
$\pi_1\textrm{PO}(n)/\pi_0\textrm{PO}(n)$
, consisting by
$\pm\omega$
.-
(a) Suppose now that X is a closed oriented surface of genus g.
Hence,
$\textrm{PO}(n)$
-bundles on X which reduce to
$\textrm{PSO}(n)$
(so with
$\mu_1=0$
) are classified by:
$$H^2(X,\pi_1\textrm{PO}(n))/\mathbb{Z}_2\cong\pi_1\textrm{PO}(n)/\mathbb{Z}_2\cong\{0,1,[\omega_n]\}.$$
If
$\mu_1\neq 0$
, then reasoning in a similar manner to the
$\textrm{O}(2)$
case in (2.5), one shows that
$H^2(X,(\mathbb{Z}_4)_{\mu_1})\cong\{[0],[\omega_n]\}\cong\mathbb{Z}_2$
if
$n=2\text{ mod }4$
. So 0 and 1 are identified in this twisted cohomology. In addition, 0 and
$\omega_n$
are not in the same orbit under the
$\pi_0\textrm{PO}(n)$
-action, so the action of
$\mathbb{Z}_2=\pi_0\textrm{PO}(n)$
in
$\mathbb{Z}_2=H^2(X,(\mathbb{Z}_4)_{\mu_1})$
, induced by (2.4), is trivial. So
$H^2(X,(\mathbb{Z}_4)_{\mu_1})/\mathbb{Z}_2\cong\mathbb{Z}_2$
for
$\mu_1\neq 0$
and
$n=2\text{ mod }4$
. The same argument gives the same result for n multiple of 4. Concluding, if
$n\geqslant 4$
is even,
$\textrm{PO}(n)$
-bundles over the surface X are classified by characteristic classes: So we see that, when
$$(\mu_1,\mu_2)\in\left(\{0\}\times\{0,1,[\omega_n]\}\right)\cup\left((\mathbb{Z}_2^{2g}\smallsetminus\{0\})\times\mathbb{Z}_2\right).$$
$n\geqslant 4$
is even, there are precisely
$2^{2g+1}+1$
isomorphism classes of topological
$\textrm{PO}(n)$
-bundles over such surface. These invariants have interpretations in terms of obstruction theory of bundles [Reference Oliveira14, Proposition 3.2]. Namely, a
$\textrm{PO}(n)$
-bundle with
$\mu_1=0$
(so actually a
$\textrm{PSO}(n)$
-bundle) lifts to
$\textrm{SO}(n)$
-bundle if and only if
$\mu_2=0,1$
and lifts to
$\textrm{Spin}(n)$
-bundle if and only if
$\mu_2=0$
. A
$\textrm{PO}(n)$
-bundle with
$\mu_1\neq 0$
lifts to
$\textrm{O}(n)$
-bundle if and only it lifts to a
$\textrm{Pin}(n)$
-bundle and this happens if and only if
$\mu_2=0$
. Indeed, if a
$\textrm{PO}(n)$
-bundle with
$\mu_1\neq 0$
lifts to
$\textrm{O}(n)$
, then one can always choose such a lift to have vanishing second Stiefel–Whitney class; see Remark 3.6 of [Reference Oliveira14].
-
(b) Suppose now that X is closed and non-orientable. Then
Here,
$$H^2(X,\pi_1\textrm{PO}(n))\cong\pi_1\textrm{PO}(n)/2\pi_1\textrm{PO}(n).$$
$2\pi_1\textrm{PO}(n)=\{0\}$
, if
$n=0\ \text{mod}\ 4$
, while
$2\pi_1\textrm{PO}(n)=\{0,1\}$
for
$n=2\ \text{mod}\ 4$
, so By acting further by
$$H^2(X,\pi_1\textrm{PO}(n))\cong\begin{cases} \mathbb{Z}_2\times\mathbb{Z}_2 & \text{if } n=0\ \text{mod}\ 4 \\[3pt] \{[0],[\omega_n]\}\cong\mathbb{Z}_2 & \text{if } n=2\ \text{mod}\ 4. \end{cases}$$
$\mathbb{Z}_2=\pi_0\textrm{PO}(n)$
as above, we see that
$\textrm{PO}(n)$
-bundles on the non-orientable surface X which reduce to
$\textrm{PSO}(n)$
, so with
$\mu_1=0$
, are classified by: Consider now
$$H^2(X,\pi_1\textrm{PO}(n))/\mathbb{Z}_2\cong\begin{cases} \{0,1,[\omega_n]\} & \text{if } n=0\ \text{mod}\ 4 \\[3pt] \{[0],[\omega_n]\}\cong\mathbb{Z}_2 & \text{if } n=2\ \text{mod}\ 4. \end{cases}$$
$\mu_1\neq 0$
and, as above, let
$w_X\,{:}\,\pi_1X\to\operatorname{Aut}(\mathbb{Z})\cong\mathbb{Z}_2$
be the nontrivial orientation character, with
$\mathbb{Z}_{w_X}$
the corresponding local system on X. Then, as in (2.8) and in Example 5(a), independently of the residue of n modulo 4. The next action of
\begin{equation*}\begin{split}H^2(X,\pi_1\textrm{PO}(n)_{\mu_1})&\cong H_0(X,\mathbb{Z}_{w_X}\otimes_{\mathbb{Z}[\pi_1X]}\pi_1\textrm{PO}(n)_{\mu_1})\\[3pt] &\cong\mathbb{Z}_2\otimes_{\mathbb{Z}}\{[0],[\omega_n]\}\cong\mathbb{Z}_2\otimes_{\mathbb{Z}}\mathbb{Z}_2\cong\mathbb{Z}_2,\end{split}\end{equation*}
$\mathbb{Z}_2=\pi_0\textrm{PO}(n)$
in
$\mathbb{Z}_2\cong H^2(X,\pi_1\textrm{PO}(n)_{\mu_1})$
is trivial as in Example 5(a).
Concluding, projective orthogonal bundles of rank
$n\geqslant 4$
even, over a non-orientable surface X which is a connected sum of k copies of
$\mathbb{R}\mathbb{P}^2$
, are topologically classified by:
$$(\mu_1,\mu_2)\in\begin{cases}(\{0\}\times\{0,1,[\omega_n]\})\cup (\mathbb{Z}_2^k\smallsetminus\{0\}\times\mathbb{Z}_2) & \text{if } n=0\ \text{mod}\ 4 \\ \\[-7pt] \mathbb{Z}_2^k\times\mathbb{Z}_2 & \text{if } n=2\ \text{mod}\ 4. \\\end{cases}$$
-
Remark 2.6. The explicit examples (3), (5), and (6) are valid not only for the stated groups but also for any group which is homotopically equivalent to it. For example, respectively,
$G=\textrm{GL}(n,\mathbb{R})$
,
$n\geqslant 3$
,
$G=\textrm{GL}(2,\mathbb{R})$
and
$G=\textrm{PGL}(n,\mathbb{R})$
, with
$n\geqslant 4$
even.
3. Reminder of obstruction theory in fibrations
Here, we briefly sketch the theory of obstructions in fibrations which will be used in the proof of Theorem 2.2. Some good references, among several others, on this material are [Reference Davis and Kirk4,Reference Steenrod20,Reference Whitehead22]. We always take based spaces.
Consider a Hurewicz (or Serre) fibration
$p\,{:}\,E\to Y$
with fibre F and let
$f\,{:}\,X\to Y$
be a continuous map. The group
$\pi_1F$
acts on
$\pi_kF$
(cf. Section 6.16 of [Reference Davis and Kirk4] or Section 4A of [Reference Hatcher7]) through free homotopies of based maps
$S^k\to F$
and the quotient
$\pi_kF/\pi_1F$
is
$[S^k,F]$
. Assume that F is simple, meaning that the action of
$\pi_1F$
on
$\pi_kF$
is trivial for every k (in the course of the proof of Theorem 2.2, we will be in this case). Hence,
$[S^k,F]=\pi_kF$
, for all k.
3.1 Obstruction to extending a partial lift
Let
$X_1$
be the 1-skeleton of our two-dimensional CW-complex X and let
$$g\,{:}\,X_1\longrightarrow E,$$
be a partial lift of f:
Recall the cochain complex
$C^*_{\mathbb{Z}[\pi_1X]}(\widetilde{X},\pi_1F)=\textrm{Hom}_{\mathbb{Z}[\pi_1X]}(C_*(\widetilde{X}),\pi_1F)$
, with
$\mathbb{Z}[\pi_1X]$
being the group ring of
$\pi_1X$
and
$C_*(\widetilde{X})$
the
$\mathbb{Z}\pi$
-module of chains on the universal cover
$\pi\,{:}\,\widetilde X\to X$
. The obstruction to extending the partial lift
$g\,{:}\,X_1\to E$
to a lift
$\tilde{f}\,{:}\,X\to E$
is given by a 2-cochain, not in
$C^*_{\mathbb{Z}[\pi_1X]}(\widetilde{X},\pi_1F)$
but rather in
$C^*_{\mathbb{Z}[\pi_1X]}(\widetilde{X},\pi_1\mathcal F_{\alpha_1})$
, where
$\pi_1\mathcal F_{\alpha_1}$
is a local system where
$\pi_1F$
is given the
$\mathbb{Z}[\pi_1X]$
-module via
\begin{equation}\alpha_1\,{:}\,\pi_1X\stackrel{f_*}{\longrightarrow}\pi_1Y\longrightarrow\operatorname{Aut}(\pi_1F),\end{equation}
with
$\pi_1Y\to\operatorname{Aut}(\pi_1F)$
induced by the monodromy representation
$\pi_1Y\to\operatorname{Aut}^h_*(F)$
, where
$\operatorname{Aut}^h_*(F)$
denotes the space of based homotopy self-equivalences of F; see [Reference Davis and Kirk4, Proposition 6.62] (here one uses again that F is simple). We will just give an idea of the definition of the mentioned 2-cochain. For details, see Section 7.10 of [Reference Davis and Kirk4].
Consider a 2-cell
$\tilde{e}_i^2\in C_*(\widetilde{X})$
of
$\widetilde{X}$
and let
$h_i\,{:}\,\mathbb D\to\widetilde X$
be the corresponding characteristic map (
$\mathbb D\subset\mathbb{R}^2$
denotes the closed unit disk), with
$\varphi_i=h_i|_{S^1}\,{:}\,S^1\to\widetilde{X}_1$
the attaching map. The composite
$p\circ g\circ\pi\circ\varphi_i\,{:}\,S^1\to Y$
is null-homotopic because it equals to
$f\circ\pi\circ\varphi_i$
which extends to
$\mathbb D\to Y$
. By lifting this null-homotopy (p is a fibration), we obtain a homotopy between
$g\circ\pi\circ\varphi_i$
and a map
$S^1\to F$
. So
$[g\circ\pi\circ\varphi_i]\in [S^1,F]=\pi_1F$
because F is simple. This element of
$\pi_1F$
depends however on the null-homotopy of
$f\circ\pi\circ\varphi_i$
. To remove this dependence, one has to consider the local system
$\pi_1\mathcal{F}_{\alpha_1}$
.
So consider the 2-cochain
\begin{equation}c^2(g)\in C^2_{\mathbb{Z}[\pi_1X]}(\widetilde{X},\pi_1\mathcal F_{\alpha_1}),\end{equation}
whose value on 2-cells
$\tilde{e}_i^2$
is
$$c^2(g)(\tilde{e}_i^2)=[g\circ\pi\circ\varphi_i]\in\pi_1\mathcal{F}_{\alpha_1},$$
and then extend linearly. It is an obstruction 2-cochain, since g extends to a lift
$\tilde f\,{:}\,X\to E$
of f if and only if
$c^2(g)=0$
; cf. Theorem 7.37 (and also Theorem 7.1) of [Reference Davis and Kirk4]. In particular if F is simply connected, the existence of such lift
$\tilde f$
is granted.
Remark 3.1. Even though we will not need this fact here, the cochain
$c^2(g)$
is in fact a cocycle so represents a class in
$H^2(X,\pi_1\mathcal{F}_{\alpha_1})$
. It turns out that such class vanishes if and only if g can be redefined (relative to the 0-skeleton) in such a way that it can then be extended to a lift
$\tilde f\,{:}\,X\to E$
of f.
Similarly, if one has
$g'\,{:}\,X_0\to E$
defined on the 0-skeleton of X such that
$p\circ g=f|_{X_0}$
(obviously, this is always possible), then there is an obstruction 1-cochain:
\begin{equation}c^1(g')\in C^1_{{\mathbb{Z}[\pi_1X]}}(\widetilde{X},\pi_0\mathcal{F}_{\alpha_0}),\end{equation}
analogously defined, with
$\alpha_0\,{:}\,\pi_1X\stackrel{f_*}{\longrightarrow}\pi_1Y\longrightarrow\operatorname{Aut}(\pi_0F)$
defined analogously to
$\alpha_1$
. Again, it vanishes precisely when g
$^{\prime}$
extends to a partial lift
$g\,{:}\,X_1\to E$
of f. In particular, this holds if F is connected.
3.2 Obstruction to the existence of vertical homotopies
As usual, write
$I=[0,1]$
.
Definition 3.2. Let
$p\,{:}\,E\to Y$
be a fibration and
$f\,{:}\,X\to Y$
a map. Two lifts
$f_0,f_1\,{:}\,X\to E$
of f are vertically homotopic if there is a vertical homotopy between them, that is, a homotopy
$K\,{:}\,X\times I\to E$
between
$f_0$
and
$f_1$
such that
$p\circ K\,{:}\,X\times I\to Y$
is the constant homotopy of f.
In other words, the homotopy K preserves the fibres of p. This is a stronger relation than simply being homotopic: two lifts of f may be homotopic but not vertically homotopic.
Let
$f_0$
and
$f_1$
be two lifts of
$f\,{:}\,X\to Y$
and let
$K_1$
be a vertical homotopy between them on
$X_1$
, that is, between their restrictions
$f_0|_{X_1}$
and
$f_1|_{X_1}$
. We can ask whether
$f_0$
and
$f_1$
are vertically homotopic, that is, if we can extend
$K_1$
to a vertical homotopy on X. There is indeed an obstruction to the existence of such a vertical homotopy K, called the difference 2-cochain:
\begin{equation}d^2(f_0,K_1,f_1)\in C^2_{{\mathbb{Z}[\pi_1X]}}(\widetilde{X},\pi_2\mathcal{F}_{\alpha_2}),\end{equation}
where
\begin{equation}\alpha_2\,{:}\,\pi_1X\stackrel{f_*}{\longrightarrow}\pi_1Y\longrightarrow\operatorname{Aut}(\pi_2F),\end{equation}
is defined as
$\alpha_1$
in (3.1).
$d^2(f_0,K_1,f_1)$
is nothing but a slight modification (an increase of dimension) of the obstruction 2-cochain defined in (3.2), since it is an obstruction cochain to extend to
$X\times I$
the map on the 2-skeleton of
$X\times I$
:
$$T=f_0\cup K_1\cup f_1\,{:}\,X\times\{0\}\cup X_1\times I\cup X\times\{1\}\longrightarrow E,$$
lifting the constant homotopy
$H_f\,{:}\,X\times I\to Y$
,
$H_f(x,t)=f(x)$
.
To define
$d^2(f_0,K_1,f_1)$
more explicitly, take any 2-cell
$e_i^2$
of X, so that
$e_i^2\times I$
is a 3-cell of
$X\times I$
. Consider a cell
$\tilde{e}_i^2\times I$
of
$\widetilde{X}\times I$
mapping to
$e_i^2\times I$
by the covering map
$\pi\times 1\,{:}\,\widetilde{X}\times I\to X\times I$
, and take the corresponding attaching
$\varphi_i\,{:}\,S^2\to\widetilde{X}\times\{0\}\cup\widetilde{X}_1\times I\cup\widetilde{X}\times\{1\}$
be the attaching map. Then
\begin{equation}d^2(f_0,K_1,f_1)(e_i^2)=c^3(T)(\tilde{e}_i^2\times I)=[T\circ(\pi\times 1)\circ\varphi_i]\in\pi_2\mathcal{F}_{\alpha_2},\end{equation}
where
$c^3(T)$
is the obstruction cochain analogous to (3.2) but in dimension 3. We then have that the partial vertical homotopy T extends to a vertical homotopy
$X\times I\to E$
if and only if the 2-cochain
$d^2(f_0,K_1,f_1)$
vanishes.
Note finally that, since X has dimension 2,
$d^2(f_0,K_1,f_1)$
is actually a cocycle, therefore defines cohomology class:
\begin{equation}\delta^2(f_0,K_1,f_1)\in H^2(X,\pi_2\mathcal{F}_{\alpha_2}).\end{equation}
Again, there is also a similar difference 1-cochain in dimension 1,
\begin{equation}d^1(f^{\prime}_0,K_0,f^{\prime}_1)\in C^1_{{\mathbb{Z}[\pi_1X]}}(\widetilde{X},\pi_1\mathcal{F}_{\alpha_1}),\end{equation}
which is the obstruction to the existence of vertical homotopies of lifts
$f_0^{\prime},f_1^{\prime}\,{:}\,X_1\to E$
of
$f|_{X_1}$
, when we are given a partial homotopy, over the 0-skeleton
$X_0$
of X,
$K_0\,{:}\,X_0\times I\to E$
between
$f_0^{\prime}|_{X_0}$
and
$f_1^{\prime}|_{X_0}$
. So
$d^1(f^{\prime}_0,K_0,f^{\prime}_1)=0$
if and only if
$T'=f^{\prime}_0\cup K_0\cup f^{\prime}_1\,{:}\,X\times\{0\}\cup X_0\times I\cup X\times\{1\}\longrightarrow E$
can be extended to a vertical homotopy
$X_1\times I\to E$
between
$f_0^{\prime},f_1^{\prime}$
. In particular, this is always possible if F is simply connected.
4. A reminder of Postnikov sections
The material in this section is also well known. We provide references in due course.
4.1 Universal fibrations of Eilenberg–Maclane spaces
We work within the category of compactly generated based spaces. Let A be an abelian group and, for
$n\geqslant 1$
, let K(A, n) be the corresponding Eilenberg–MacLane space.
There is a specific model for K(A, n) which is a topological abelian group. It is constructed by taking the geometrical realization of the simplicial abelian group associated, via the Dold–Kan correspondence [Reference Goerss and Jardine6], to the chain complex
$A[-n]$
which has A in dimension n and 0 elsewhere. In all that follows we use this model for K(A, n) and we choose for base point the zero of its group structure.
Consider the space
$\textrm{Map}(X,K(A,n))$
of all continuous maps from X to K(A, n), with the topology determined by the compact-open topology, and so that
$\textrm{Map}(X,K(A,n))$
is compactly generated (see Definition 6.2 and Section 6.1.3 of [Reference Davis and Kirk4]). For the given model of K(A, n),
$\textrm{Map}(X,K(A,n))$
is a topological abelian group.
A group-like monoid is a topological monoid such that the monoid of its path connected components is a group (the difference from a topological group is the possible nonexistence of inverses).
Let
$\operatorname{Aut}^h(K(A,n))$
denote the group-like monoid of all self-homotopy equivalences of K(A, n). The model of K(A, n) is functorial, thus a group homomorphism
$A\to B$
induces a continuous map
$K(A,n)\to K(B,n)$
which is also a group homomorphism. It follows that an automorphism of A induces an automorphism of the topological abelian group K(A, n). Hence,
$\operatorname{Aut}(A)$
acts on K(A, n) by group automorphisms, so we can take their semidirect product
$\operatorname{Aut}(A)\ltimes K(A,n)$
. This produces an inclusion:
\begin{equation}\operatorname{Aut}(A)\subset\operatorname{Aut}^h(K(A,n)),\end{equation}
given by the composite
$\operatorname{Aut}(A)\hookrightarrow \operatorname{Aut}(A)\ltimes K(A,n)\hookrightarrow \operatorname{Aut}^h(K(A,n))$
where the second map is the inclusion:
\begin{equation} \nu:\operatorname{Aut}(A)\ltimes K(A,n)\hookrightarrow \operatorname{Aut}^h(K(A,n)),\ \ \ \nu(\varphi,x)(z)=\varphi(z)+x,\end{equation}
with
$+$
denoting the group operation in A. It turns out that the inclusion (4.2) is a weak homotopy equivalence.
Now, there exists [Reference May11,Reference Stasheff19] a unique (up to homotopy equivalence) CW-complex
$B\operatorname{Aut}^h(K(A,n))$
which is a classifying space for fibre homotopy equivalence classes of fibrations over X, with fibre homotopically equivalent to K(A, n). So there is a corresponding universal fibration
$\operatorname{Aut}^h(K(A,n))\to E\operatorname{Aut}^h(K(A,n))\to B\operatorname{Aut}^h(K(A,n))$
, which has similar properties to the classifying space BG and to the universal G-bundle
$EG\to BG$
, for a topological group G. In particular, the set of equivalence classes of the above-mentioned fibrations is in bijection with the set of free (i.e., non-based) homotopy classes of maps
$X\to B\operatorname{Aut}^h(K(A,n))$
, that is,
$[X,B\operatorname{Aut}^h(K(A,n))]$
.
Since (4.2) is a weak homotopy equivalence, and since both
$B\operatorname{Aut}^h(K(A,n))$
and
$B(\operatorname{Aut}(A)\ltimes K(A,n))$
are CW-complexes, it follows that
$B\operatorname{Aut}^h(K(A,n))$
is homotopically equivalent to
$B(\operatorname{Aut}(A)\ltimes K(A,n))$
. In other words,
$B(\operatorname{Aut}(A)\ltimes K(A,n))$
is a model for
$B\operatorname{Aut}^h(K(A,n))$
.
4.2 Postnikov sections
Write
$$P_kBG,$$
for the
$k^{th}$
Postnikov section of BG. By definition (see e.g., [Reference Hatcher7] Chapter 4) these CW-complexes fit in a commutative diagram as below, called the Postnikov tower of BG:
where the vertical maps are fibrations and such that the maps
$BG\to P_kBG$
induce isomorphisms
$\pi_iBG\cong\pi_iP_kBG$
if
$i\leqslant k$
and, for
$i>k$
,
$\pi_iP_kBG=0$
. For each k, the homotopy fibre of the fibrations
$P_kBG\to P_{k-1}BG$
is the Eilenberg–Maclane space
$K(\pi_{k-1}G,k)$
.
Again, each Postnikov section
$P_kBG$
is unique up to homotopy equivalence, hence so is the Postnikov tower. In particular,
$P_1BG= B\pi_0G=K(\pi_0G,1)$
.
Regarding the second Postnikov section
$P_2BG$
, there is [Reference Robinson16] a model for
$P_2BG\to B\pi_0G$
which is a fibre bundle with structure group
$\pi_0G$
. To briefly see this, consider the group-like monoid
$\operatorname{Aut}^h(K(\pi_1G,2))$
of self-homotopy equivalences of
$K(\pi_1G,2)$
. Consider the universal fibration:
$$\operatorname{Aut}^h(K(\pi_1G,2))\longrightarrow E\operatorname{Aut}^h(K(\pi_1G,2))\longrightarrow B\operatorname{Aut}^h(K(\pi_1G,2)),$$
as defined in the previous section. Recall that
$B(\operatorname{Aut}(\pi_1G)\ltimes K(\pi_1G,2))$
is a model for the classifying space
$B\operatorname{Aut}^h(K(\pi_1G,2))$
. Let
\begin{equation}\mathcal{U}=E\operatorname{Aut}^h(K(\pi_1G,2))\times_{\operatorname{Aut}^h(K(\pi_1G,2))}K(\pi_1G,2)\longrightarrow B(\operatorname{Aut}(\pi_1G)\ltimes K(\pi_1G,2))\end{equation}
be the
$K(\pi_1G,2)$
-fibration obtained from the above universal fibration.
The splitting
$$\operatorname{Aut}(\pi_1G)\to \operatorname{Aut}(\pi_1G)\ltimes K(\pi_1G,2),\ \ \varphi\mapsto(\varphi,0),$$
of the exact sequence
$K(\pi_1G,2)\hookrightarrow \operatorname{Aut}(\pi_1G)\ltimes K(\pi_1G,2)\to\operatorname{Aut}(\pi_1G)$
yields a section
$$e\,{:}\,B\operatorname{Aut}(\pi_1G)\to B(\operatorname{Aut}(\pi_1G)\ltimes K(\pi_1G,2)),$$
of the fibration
$ B(\operatorname{Aut}(\pi_1G)\ltimes K(\pi_1G,2))\to B\operatorname{Aut}(\pi_1G)$
induced by the above exact sequence.
Hence, the pullback of
$\mathcal{U}$
in (4.3) under the composition:
$$B\pi_0G\to B\operatorname{Aut}(\pi_1G)\xrightarrow{\ e\ } B(\operatorname{Aut}(\pi_1G)\ltimes K(\pi_1G,2)),$$
is the fibre bundle:
$$E\pi_0G\times_{\pi_0G}K(\pi_1G,2)\to B\pi_0G,$$
with fibre
$K(\pi_1G,2)$
, structure group
$\pi_0G$
and where
$E\pi_0G\to B\pi_0G$
is the universal
$\pi_0G$
-principal bundle. Here,
$\pi_0G$
acts on the
$K(\pi_1G,2)$
-factor via the composition:
\begin{equation}\pi_0G\xrightarrow{\Psi(-)_*}\operatorname{Aut}(\pi_1G)\hookrightarrow\operatorname{Aut}^h(K(\pi_1G,2)).\end{equation}
Thus, we use the functorial construction of the Eilenberg–Maclane space
$K(\pi_1G,2)$
explained in the preceding section. On the other hand, the
$\pi_0G$
-action on the
$E\pi_0G$
-factor is by the monodromy action of
$\pi_0G=\pi_1(B\pi_0G)$
(based on the base point of
$B\pi_0G=K(\pi_0G,1)$
). So, if
$\gamma\,{:}\,S^1\to B\pi_0G$
is a loop representing a class in
$\pi_0G$
and
$v\in E\pi_0G$
, then
$\gamma\cdot v=v+\tilde\gamma(1)$
where
$\tilde\gamma$
is the lift of
$\gamma$
through v and
$+$
is the group operation on
$E\pi_0G$
(recall that
$E\pi_0G$
is an abelian group because
$B\pi_0G$
is so).
Concluding, using (4.4), if
$[a,b]\in E\pi_0G\times_{\pi_0G}K(\pi_1G,2)$
and
$g=\gamma\in\pi_0G=\pi_1(B\pi_0G)$
, then
\begin{equation}[a,b]=[a+\tilde\gamma(1),\Psi_*(-g)(b)].\end{equation}
This is the model for
$P_2BG$
we will use
\begin{equation}P_2BG=E\pi_0G\times_{\pi_0G}K(\pi_1G,2)\to B\pi_0G.\end{equation}
5. The proof
Now that we have provided the necessary background, we prove the classification Theorem 2.2. This will be done by a sequence of lemmas.
5.1 Replacement of BG by
$\boldsymbol{P}_{\boldsymbol{2}}\boldsymbol{BG}$
Note that the map
$BG\to P_1BG=B\pi_0G$
is
$p_{0,*}$
as defined in (2.1). The homotopy fibre of the fibration
$P_2BG\to P_1BG$
is
$K(\pi_1G,2)$
, that is, we obtain the fibration:
\begin{equation}K(\pi_1G,2)\longrightarrow P_2BG\stackrel{p}{\longrightarrow}B\pi_0G,\end{equation}
and the commutative diagram:
Since the second homotopy group of any Lie group vanishes (cf. [Reference Mimura and Toda12] Chapter VI, Theorem 4.17), we have
$\pi_3BG=0=\pi_3P_2BG$
so actually the map
$BG\to P_2BG$
induces isomorphisms
$\pi_iBG\cong\pi_iP_2BG$
, for
$i\leqslant 3$
, that is, it is a 3-equivalence. Since
$\dim X=2<3$
, we conclude by [Reference Whitehead22], Chapter IV, Theorem
$7.16$
, that
$BG\to P_2BG$
induces a bijection:
\begin{equation} [X,BG]\simeq[X,P_2BG].\end{equation}
Hence, in order to classify G-bundles over X, it suffices to consider the set:
$$[X,P_2BG],$$
instead of [X, BG].
As we have seen above, obtaining the classification of G-bundles with fixed invariant
$\mu_1\in [X,B\pi_0G]$
is equivalent to describing the fibre over
$\mu_1$
of the map
$\chi\,{:}\,[X,BG]\to[X,B\pi_0G]$
defined in (2.1).
Now, consider the map induced by the fibration p in (5.1):
\begin{equation}\chi'\,{:}|,[X,P_2BG]\longrightarrow [X,B\pi_0G], \ \ \ \chi'([h])=[p\circ h].\end{equation}
From (5.2) and the previous diagram, we have the commutative diagram:
so the next lemma follows immediately.
Lemma 5.1. There is a bijection between the set of isomorphism classes of continuous principal G-bundles over X with invariant
$\mu_1\in [X,B\pi_0G]$
and the fibre over
$\mu_1$
of
$\chi'$
.
Let us now begin applying the obstruction theory sketched in Section 3 to our situation, thus to the fibration (5.1) and to the next diagram:
where f is a representative of a class
$\mu_1\in[X,B\pi_0G]$
.
We want to analyze the fibre
$\chi'^{-1}(\mu_1)$
and a first question is if it is non-empty. Being non-empty means that we can lift f to
$P_2BG$
. To see this, first notice that, since
$K(\pi_1G,2)$
is connected, we can always find a partial lift f
$^{\prime}$
of f over the 1-skeleton, that is, a lift of
$f|_{X_1}$
, because (3.3) vanishes. In addition, as
$K(\pi_1G,2)$
is simply connected, then the obstruction 2-cochain (3.2) is again zero and hence we can lift f to a map
$X\to P_2BG$
. So:
Lemma 5.2. The map
$\chi'$
is surjective.
5.2 Homotopy classes of lifts and vertical homotopy classes of lifts
Our next task is then to describe the fibre of
$\chi'$
over the class
$\mu_1\in[X,B\pi_0G]$
. This fibre is in general just a set, namely the set of homotopy classes in
$[X,B\pi_0G]$
which project to a representative of the class
$\mu_1$
, hence to a map homotopic to
$f\,{:}\,X\to B\pi_0G$
. We will describe all such homotopy classes of lifts of f in terms of vertical homotopy classes of lifts of f. Denote the latter set by
$$[X,P_2BG]_f.$$
First note that if
$g\,{:}\,X\to B\pi_0G$
is another representative of the class
$\mu_1$
, then by lifting a homotopy between f and g, we obtain a bijection
$[X,P_2BG]_f\cong [X,P_2BG]_g$
. So we loose nothing by choosing any representative f of
$\mu_1$
.
Consider the fundamental group
$\pi_1(\textrm{Map}(X,B\pi_0G),f)$
, which we regard as the group of homotopy classes of self-homotopies of f. It acts on
$[X,P_2BG]_f$
also by lifting these self-homotopies, that is, if
$f_0\in [X,P_2BG]_f$
is a lift of f, and
$H\in\pi_1(\textrm{Map}(X,B\pi_0G),f)$
is a self-homotopy of f, then H acts on
$f_0$
as
$H\cdot f_0=\tilde H(-,1)$
, where
$\tilde H\,{:}\,X\times I\to P_2BG$
is a lift of H such that
$\tilde H(-,0)=f_0$
. If another lift
$\tilde H'$
of H is taken so that
$\tilde H'(-,0)=f_0$
, then
$\tilde H'(-,1)$
is vertically homotopic to
$\tilde H(-,1)$
, so the action is well defined.
Since
$\pi_0G$
is abelian,
$B\pi_0G=K(\pi_0G,1)$
is a topological abelian group, hence so is
$\textrm{Map}(X,B\pi_0G)$
. It follows that
$\pi_1(\textrm{Map}(X,B\pi_0G),f)$
is also independent of f.
So the orbit space:
$$[X,P_2BG]_f/\pi_1(\textrm{Map}(X,B\pi_0G),f),$$
is independent on the choice of the representative f of
$\mu_1$
.
Lemma 5.3. Given
$\mu_1\in [X,B\pi_0G]$
, there is a bijection of sets
$$\chi'^{-1}(\mu_1)\cong[X,P_2BG]_f/\pi_1(\textrm{Map}(X,B\pi_0G),f),$$
with
$f\,{:}\,X\to B\pi_0G$
representing
$\mu_1$
.
Proof. By definition,
$\chi'^{-1}(\mu_1)\subset [X,P_2BG]$
. Consider the natural map:
$$[X,P_2BG]_f\to \chi'^{-1}(\mu_1),$$
which sends a vertical homotopy class of a lift
$g\,{:}\,X\to P_2BG$
of f to its (not necessarily vertical) homotopy class. This is clearly surjective.
Take two homotopic lifts
$f_0$
and
$f_1$
of f, hence representing the same point in
$\chi'^{-1}(\mu_1)$
. Projecting the homotopy through
$p\,{:}\,P_2BG\to B\pi_0G$
yields a self-homotopy of f, which lifts to the homotopy between
$f_0$
and
$f_1$
we started with. Hence,
$f_0$
and
$f_1$
represent classes in
$[X,P_2BG]_f$
which lie in the same orbit of
$\pi_1(\textrm{Map}(X,B\pi_0G),f)$
; note that
$f_0$
and
$f_1$
are vertically homotopic precisely if the induced self-homotopy is homotopically trivial. Conversely, by the definition of the action of
$\pi_1(\textrm{Map}(X,B\pi_0G),f)$
by lifting self-homotopies of f, we identify the lifts of f which are homotopic. This shows that the above map induces an injective map:
$$[X,P_2BG]_f/\pi_1(\textrm{Map}(X,B\pi_0G),f)\to \chi'^{-1}(\mu_1).$$
Since
$[X,P_2BG]_f\to \chi'^{-1}(\mu_1)$
is surjective, then so is the induced map, and we are done.
Now we use the model (4.6) for
$P_2BG$
, so that we have the next diagram:
The remaining part of the paper will always refer to the above diagram.
Let
$\pi_0G=\pi_1(B\pi_0G)$
act on the set
$[X,E\pi_0G\times_{\pi_0G}K(\pi_1G,2)]_f$
of vertical homotopy classes of lifts of f as in (4.4), so via the inclusion
$\operatorname{Aut}(\pi_1G)\subset\operatorname{Aut}(K(\pi_1G,2))$
. More precisely, a lift
$f_0$
of f representing a class in
$[X,E\pi_0G\times_{\pi_0G}K(\pi_1G,2)]_f$
can be written as
$f_0(x)=[h_1(x),h_2(x)]\in E\pi_0G\times_{\pi_0G}K(\pi_1G,2)$
, where the
$h_i$
are defined up to the simultaneous
$\pi_0G$
-action on both factors as in (4.5). Then
$g\in\pi_0G$
acts on the representative
$f_0$
as:
\begin{equation} (g\cdot f_0)(x)= [h_1(x),\Psi(g)_*(h_2(x))],\end{equation}
for
$x\in X$
and this induces an action on the homotopy classes of lifts of f. Indeed
$g\cdot f_0$
is another lift of f since
$[h_1(x),\Psi(g)_*(h_2(x))]$
and
$[h_1(x),h_2(x)]$
lie in the same fibre of p.
The next lemma shows that the fibre that we are studying is in bijection with the quotient set for the action (5.5).
Lemma 5.4. Let
$[X,E\pi_0G\times_{\pi_0G}K(\pi_1G,2)]_f$
denote the set of vertical homotopy classes of lifts of f in diagram (5.4), together with the
$\pi_0G$
-action (5.5). Then there is a bijection:
$$\chi'^{-1}(\mu_1)\simeq [X,E\pi_0G\times_{\pi_0G}K(\pi_1G,2)]_f/\pi_0G.$$
Proof. Using our model
$P_2BG=E\pi_0G\times_{\pi_0G}K(\pi_1G,2)$
, we know from Lemma 5.3 that
\begin{equation}\chi'^{-1}(\mu_1)\simeq [X,E\pi_0G\times_{\pi_0G}K(\pi_1G,2)]_f/\pi_1(\textrm{Map}(X,B\pi_0G),f),\end{equation}
where the group
$\pi_1(\textrm{Map}(X,B\pi_0G),f)$
acts by lifting self-homotopies of f in (5.4).
Now we compute
$\pi_1(\textrm{Map}(X,B\pi_0G),f)$
. As we said before, this is independent of f, because
$\textrm{Map}(X,B\pi_0G)$
is a topological abelian group. So we compute
$\pi_1\textrm{Map}(X,B\pi_0G)$
taking for base point the constant map:
$$\text{const}\in\textrm{Map}(X,B\pi_0G),$$
equal to the base point of
$B\pi_0G=K(\pi_0G,1)$
. In this case,
\begin{align}\pi_1(\textrm{Map}(X,B\pi_0G),\text{const})&=[(X\times S^1)/(X\times 1),B\pi_0G]\nonumber\\[3pt] &=[SX\vee S^1,B\pi_0G]\nonumber\\[3pt] &=[S^1,B\pi_0G]\nonumber\\[3pt] &=\pi_0G.\end{align}
Here,
$SX=(X\times I)/(X\times 0\cup X\times 1)$
is the unreduced suspension of X, which is simply connected because X is connected, and
$\vee$
is the wedge sum. Notice that in (5.7) is not relevant to distinguish classes of based or unbased maps because
$B\pi_0G$
is a simple space (it is 1-simple since
$\pi_0G$
is abelian). Moreover, the third equality holds since a homotopy class of a (based) map
$f\,{:}\,SX\vee S^1\to B\pi_0G$
is defined by two homotopy classes of (based) maps
$f_1\,{:}\,SX\to B\pi_0G$
and
$f_2\,{:}\,S^1\to B\pi_0G$
, but
$[SX,B\pi_0G]=[SX,K(\pi_0G,1)]=H^1(SX,\pi_0G)=0$
because
$\pi_1SX=0$
.
Denote by
$+$
the group operation on
$B\pi_0G=K(\pi_0G,1)$
and let
$$g\in\pi_0G\cong\pi_1(B\pi_0G).$$
If we represent g by a loop
$$\gamma\,{:}\,S^1\longrightarrow B\pi_0G,$$
then the self-homotopy of f associated with g is
$H\,{:}\,X\times S^1\to B\pi_0G$
defined by:
\begin{equation}H(x,t)=f(x)+\gamma(t).\end{equation}
Here, the operation of summing f is the homeomorphism which identifies the component of the constant map
$\text{const}\,{:}\,X\to B\pi_0G$
in
$\textrm{Map}(X,B\pi_0G)$
with that of f. Now we use diagram (5.4). The element
$g\in\pi_0G$
acts on the class of
$f_1$
by lifting the self-homotopy H of f given in (5.8) to
$E\pi_0G\times_{\pi_0G}K(\pi_1G,2)$
and taking its final value. As
$B\pi_0G$
is an abelian group, then
$E\pi_0G$
is also an abelian group and we denote again the operation by
$+$
. A lift of H is given by:
$$\tilde{H}(x,t)=[h_1(x)+\tilde\gamma(t),h_2(x)],$$
where
$\tilde\gamma$
is a lift of
$\gamma$
. So, by (4.5),
$$\tilde{H}(x,1)=[h_1(x)+\tilde\gamma(1),h_2(x)]=[h_1(x),\Psi(g)_*(h_2(x))].$$
Hence, the action of
$\pi_1(\textrm{Map}(X,B\pi_0G),f)$
by lifting self-homotopies is compatible with the action (5.5) of
$\pi_0G$
and with the identification
$\pi_1(\textrm{Map}(X,B\pi_0G),f)\cong\pi_1(\textrm{Map}(X,B\pi_0G),\text{const})\cong\pi_0G$
in (5.7). This, together with (5.6), completes the proof of the lemma.
5.3 Bijection with twisted cohomology
Consider the fibration p in (5.4). The corresponding difference cochain (3.8) is zero, so there are always vertical homotopies between lifts of f on
$X_1$
. Thus, given two lifts
$f_0$
and
$f_1$
of f, we can suppose that
$f_0|_{X_1}=f_1|_{X_1}$
and that
$K_1$
is the constant homotopy between them. We will hence write
$$\delta^2(f_0,f_1),$$
instead of
$\delta^2(f_0,K_1,f_1)$
for the cocycle (3.7) determined by the difference cochain (3.4). Moreover, the action
$\alpha_2$
defined in (3.5) becomes
$$\alpha_2\,{:}\,\pi_1X\xrightarrow{f_*}\pi_1B\pi_0G\longrightarrow\operatorname{Aut}(\pi_2(K(\pi_1G,2))),$$
that is
$$\alpha_2\,{:}\,\pi_1X\xrightarrow{f_*}\pi_0G\longrightarrow\operatorname{Aut}(\pi_1G).$$
But p is a fibre bundle with
$\pi_0G$
as the structure group, with
$\pi_0G$
acting on the fibre
$K(\pi_1G,2)$
as in (4.4), so via
$\Psi(-)_*$
. Hence, the action
$\alpha_2$
coincides with
$\Psi(-)_*\circ \mu_{1*}$
in (2.3). Hence, we have that
$$\delta^2(f_0,f_1)\in H^2(X,\pi_1\mathcal{G}_{\mu_1}),$$
with
$\pi_1\mathcal{G}_{\mu_1}$
being the local system determined by (2.3).
The following result (Corollary 6.16 of Chapter VI of [Reference Whitehead22]) shows that there is a close relation between
$[X,E\pi_0G\times_{\pi_0G}K(\pi_1G,2)]_f$
and
$H^2(X,\pi_1\mathcal{G}_{\mu_1})$
.
Proposition 5.5. Let
$f_0\,{:}\,X\to E\pi_0G\times_{\pi_0G}K(\pi_1G,2)$
be any lift of
$f\,{:}\,X\to B\pi_0G$
. Then the map
$$\phi\,{:}\,[X,E\pi_0G\times_{\pi_0G}K(\pi_1G,2)]_f\longrightarrow H^2(X,\pi_1\mathcal{G}_{\mu_1}),\ \ \ \ \phi(f_1)=\delta^2(f_0,f_1)$$
is a bijection.
Now we want to see the
$\pi_0G$
-quotient of Lemma 5.4 on the side of twisted cohomology
$H^2(X,\pi_1\mathcal{G}_{\mu_1})$
, via the correspondence of the previous proposition and via the action of
$\pi_0G$
in
$H^2(X,\pi_1\mathcal{G}_{\mu_1})$
induced from the action in
$C^2_{\mathbb{Z}[\pi_1X]}(\widetilde X,\pi_1G)$
defined in (2.4).
This is the content of the next and final lemma in the proof of Theorem 2.2.
Lemma 5.6. The bijection between
$[X,E\pi_0G\times_{\pi_0G}K(\pi_1G,2)]_f$
. and
$H^2(X,\pi_1\mathcal{G}_{\mu_1})$
is
$\pi_0G$
-equivariant with respect to (5.5) and (2.4), respectively. Hence, it induces a bijection on the sets of
$\pi_0G$
-orbits:
$$[X,E\pi_0G\times_{\pi_0G}K(\pi_1G,2)]_f/\pi_0G\simeq H^2(X,\pi_1\mathcal{G}_{\mu_1})/\pi_0G.$$
Proof. Recall that we are always dealing with the situation represented by diagram (5.4). For the correspondence in Proposition 5.5, one has a choice of a lift
$f_0$
of f and the natural one is to choose the zero map, that is,
$f_0(x)=[g_1(x),0]$
, with
$g_1(x)$
such that
$p([g_1(x),0])=f(x)$
.
Given another lift
$f_1$
of f, we have already seen that we can suppose that
$f_1|_{X_1}=f_0|_{X_1}=0$
. With these choices, the cocycle
$\delta^2(f_0,f_1)$
is given by (3.4) and (3.6), with
$T=f_1$
, because
$f_0$
is the zero map and
$f_1|_{X_1}=f_0|_{X_1}=0$
(so
$K_1$
is the constant homotopy equal to zero), so that we can collapse
$\partial \tilde{e}_i^2\times I\cup\tilde{e}_i^2\times 0$
to one point:
$$\delta^2(f_1)(e_i^2)=[f_1\circ\pi\circ\varphi_i]\in\pi_2K(\pi_1G,2)\cong\pi_1G.$$
On the other hand, by the definition of the action of
$\pi_0G$
in
$C^2_{\mathbb{Z}[\pi_1X]}(\widetilde{X},\pi_1G)$
in (2.4), we have that, for
$g\in\pi_0G$
,
\begin{equation} (g\cdot \delta^2(f_1))(e_i^2)=\Psi(g)_*([f_1\circ\pi\circ\varphi_i])\in\pi_1G\cong\pi_2(K(\pi_1G,2)).\end{equation}
But by (4.4), if we write
$f_1(x)=[h_1(x),h_2(x)]$
, we conclude that
\begin{equation} \Psi(g)_*([f_1\circ\pi\circ\varphi_i])=[f^{\prime}_1\circ\pi\circ\varphi_i]\end{equation}
where
$f^{\prime}_1(x)=[h_1(x),\Psi(g)_*(h_2(x))]$
.
By (5.5), (5.9), and (5.10), we have that
$$g\cdot \delta^2(f_1)=\delta^2(g\cdot f_1).$$
We conclude that the bijection stated in Proposition 5.5 is
$\pi_0G$
-equivariant and this completes the proof.
Finally, the proof Theorem 2.2 follows from Lemmas 5.1, 5.2, 5.4, and 5.6.
