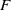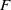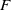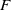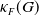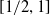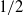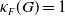1. Introduction
Let
![]() $\mathscr{G}= \{ (G_n,{\textrm{dist}}_n) \}_{n \ge 1 }$
be a family of groups, each equipped with a bi-invariant bounded metric. Bi-invariance means that for every
$\mathscr{G}= \{ (G_n,{\textrm{dist}}_n) \}_{n \ge 1 }$
be a family of groups, each equipped with a bi-invariant bounded metric. Bi-invariance means that for every
![]() $x,y, g_1, g_2 \in G_n$
, we have the equality:
$x,y, g_1, g_2 \in G_n$
, we have the equality:
A
![]() $\mathscr{G}$
-approximation of a countable group
$\mathscr{G}$
-approximation of a countable group
![]() $G$
consists of an increasing sequence
$G$
consists of an increasing sequence
![]() $(n_k)_{k \ge 1}$
of positive integers and a sequence
$(n_k)_{k \ge 1}$
of positive integers and a sequence
![]() $(\phi _k)_{k \ge 1}$
of maps:
$(\phi _k)_{k \ge 1}$
of maps:
satisfying the following two properties:
-
1. (Asymptotic homomorphism) For all
 $g, h \in G$
, one has
$g, h \in G$
, one has \begin{align*} \lim _{k \to \infty } {\textrm {dist}}_{n_k} \!\left(\phi _k( gh), \phi _k(g) \phi _k(h) \right)=0.\end{align*}
\begin{align*} \lim _{k \to \infty } {\textrm {dist}}_{n_k} \!\left(\phi _k( gh), \phi _k(g) \phi _k(h) \right)=0.\end{align*}
-
2. (Uniform injectivity) There exists
 $\kappa \gt 0$
such that for all
$\kappa \gt 0$
such that for all
 $g \in G \setminus \{ e_\Gamma \}$
,
$g \in G \setminus \{ e_\Gamma \}$
, \begin{align*} \limsup _{k \to \infty } {\textrm {dist}}_{n_k} \!\left( \phi _k ( g), e_{_{G_{n_k} }}\right) \ge \kappa .\end{align*}
\begin{align*} \limsup _{k \to \infty } {\textrm {dist}}_{n_k} \!\left( \phi _k ( g), e_{_{G_{n_k} }}\right) \ge \kappa .\end{align*}
We will then also say that
![]() $G$
is
$G$
is
![]() $\kappa$
-approximable by
$\kappa$
-approximable by
![]() $\mathscr{G}$
. Perhaps the most prominent and well-studied classes of approximable groups are the sofic and hyperlinear groups, which correspond, respectively, to approximation by the family of symmetric groups equipped with the normalized Hamming distance and the family of unitary groups equipped with normalized Hilbert–Schmidt distance. The class of sofic groups was introduced by Gromov in connection with the so-called Gottschalk surjunctivity conjecture [Reference Gromov11], while the terminology is due to Weiss [Reference Weiss23]. Hyperlinear groups first appeared in the context of Conne’s embedding conjecture. The term hyperlinear was coined by Rădulescu [Reference Rădulescu21]. Sofic groups are shown to be hyperlinear [[Reference Elek and Szabó8], Theorem 2], It is unknown whether every group is sofic, or even hyperlinear.
$\mathscr{G}$
. Perhaps the most prominent and well-studied classes of approximable groups are the sofic and hyperlinear groups, which correspond, respectively, to approximation by the family of symmetric groups equipped with the normalized Hamming distance and the family of unitary groups equipped with normalized Hilbert–Schmidt distance. The class of sofic groups was introduced by Gromov in connection with the so-called Gottschalk surjunctivity conjecture [Reference Gromov11], while the terminology is due to Weiss [Reference Weiss23]. Hyperlinear groups first appeared in the context of Conne’s embedding conjecture. The term hyperlinear was coined by Rădulescu [Reference Rădulescu21]. Sofic groups are shown to be hyperlinear [[Reference Elek and Szabó8], Theorem 2], It is unknown whether every group is sofic, or even hyperlinear.
The class of linear sofic groups over an arbitrary field was introduced by Arzhantseva and Păunescu [[Reference Arzhantseva and Păunescu3], Definition 4.1 and the paragraph following Definition 4.2] who proved fundamental results about this class of groups. This mode of approximation defining linear sofic groups uses general linear groups (over a general field
![]() $F$
fixed in the discussion) as target groups, while the metric is defined using the normalized rank. In this regards, linear sofic groups provide a hybrid form of approximation.
$F$
fixed in the discussion) as target groups, while the metric is defined using the normalized rank. In this regards, linear sofic groups provide a hybrid form of approximation.
In order to define this metric, let
![]() $F$
be a field. For
$F$
be a field. For
![]() $d \times d$
matrices
$d \times d$
matrices
![]() $A, B \in \textrm{GL}_d(F)$
, we define
$A, B \in \textrm{GL}_d(F)$
, we define
The following definition of linear sofic groups will be more convenient for our purpose. The equivalence of two definitions is proven in [[Reference Arzhantseva and Păunescu3], Proposition 4.4].
Definition 1.1.
Let
![]() $F$
be a field,
$F$
be a field,
![]() $G$
a countable group and
$G$
a countable group and
![]() $0 \lt \kappa \le 1$
. We say that
$0 \lt \kappa \le 1$
. We say that
![]() $G$
is
$G$
is
![]() $\kappa$
-linear sofic over
$\kappa$
-linear sofic over
![]() $F$
if for every finite set
$F$
if for every finite set
![]() $S \subseteq G$
and every
$S \subseteq G$
and every
![]() $ \delta \gt 0$
and every
$ \delta \gt 0$
and every
![]() $0 \le \kappa ^{\prime} \lt \kappa$
, there exists
$0 \le \kappa ^{\prime} \lt \kappa$
, there exists
![]() $d \ge 1$
and a map
$d \ge 1$
and a map
![]() $\phi \,:\, S \to \textrm{GL}_d(F)$
satisfying the following two properties:
$\phi \,:\, S \to \textrm{GL}_d(F)$
satisfying the following two properties:
-
(AH) For all
 $g, h, gh \in S$
, one has
$g, h, gh \in S$
, one has
 $ \rho _d ( \phi ( gh), \phi (g) \phi (h) )\lt \delta$
.
$ \rho _d ( \phi ( gh), \phi (g) \phi (h) )\lt \delta$
. -
(D) For all
 $g \in S \setminus \{ e \}$
,
$g \in S \setminus \{ e \}$
,
 $\rho _d ( \phi ( g),{\textrm{Id}} ) \ge \kappa ^{\prime}$
.
$\rho _d ( \phi ( g),{\textrm{Id}} ) \ge \kappa ^{\prime}$
.
Such a map is called an
![]() $(S, \delta, \kappa ^{\prime})$
-map. Roughly speaking, (AH) guarantees that
$(S, \delta, \kappa ^{\prime})$
-map. Roughly speaking, (AH) guarantees that
![]() $\phi$
is almost a homomorphism, while (D) shows that distinct elements are separated out. Following [Reference Arzhantseva and Păunescu3], we say that
$\phi$
is almost a homomorphism, while (D) shows that distinct elements are separated out. Following [Reference Arzhantseva and Păunescu3], we say that
![]() $G$
is linear sofic over
$G$
is linear sofic over
![]() $F$
if it is
$F$
if it is
![]() $\kappa$
-linear sofic for some
$\kappa$
-linear sofic for some
![]() $\kappa \gt 0$
. It is clear that if
$\kappa \gt 0$
. It is clear that if
![]() $\kappa _1\lt \kappa _2$
, then every
$\kappa _1\lt \kappa _2$
, then every
![]() $\kappa _2$
-linear sofic group is
$\kappa _2$
-linear sofic group is
![]() $\kappa _1$
-linear sofic. For a countable group
$\kappa _1$
-linear sofic. For a countable group
![]() $G$
, we write
$G$
, we write
Note that whenever
![]() $G$
is not
$G$
is not
![]() $\kappa$
-linear sofic over
$\kappa$
-linear sofic over
![]() $F$
for any
$F$
for any
![]() $ \kappa \gt 0$
, we define
$ \kappa \gt 0$
, we define
![]() $\kappa _F(G)$
to be zero.
$\kappa _F(G)$
to be zero.
Remark 1.2. The notion of metric approximation can also be defined using the notion of metric ultraproducts. This alternative definition allows one to avoid limiting processes that require passing to subsequences and thereby simplifies certain arguments, see [Reference Arzhantseva and Păunescu3] for examples. Since this point of view will not provide us with any special advantages, we will not use this definition.
1.1. The amplification argument
Let
![]() $\mathscr{G}= \{ (G_n,{\textrm{dist}}_n) \}_{n \ge 1 }$
be as above, and assume that the diameter of
$\mathscr{G}= \{ (G_n,{\textrm{dist}}_n) \}_{n \ge 1 }$
be as above, and assume that the diameter of
![]() $G_n$
with respect to
$G_n$
with respect to
![]() ${\textrm{dist}}_n$
is normalized to be
${\textrm{dist}}_n$
is normalized to be
![]() $1$
. It is natural to ask whether a
$1$
. It is natural to ask whether a
![]() $\kappa$
-approximable group for some
$\kappa$
-approximable group for some
![]() $\kappa \gt 0$
is always
$\kappa \gt 0$
is always
![]() $1$
-approximable. Elek and Szabó [Reference Elek and Szabó8] proved that this is the case for sofic groups. A similar statement (with a modified proof) holds for hyperlinear groups. Note that this implies that analogously defined
$1$
-approximable. Elek and Szabó [Reference Elek and Szabó8] proved that this is the case for sofic groups. A similar statement (with a modified proof) holds for hyperlinear groups. Note that this implies that analogously defined
![]() $\kappa _{\textrm{sofic} }$
and
$\kappa _{\textrm{sofic} }$
and
![]() $\kappa _{\textrm{hyperlinear} }$
can only take values in the set
$\kappa _{\textrm{hyperlinear} }$
can only take values in the set
![]() $\{ 0, 1 \}$
, and the long-standing open question asking whether all groups are sofic is equivalent to
$\{ 0, 1 \}$
, and the long-standing open question asking whether all groups are sofic is equivalent to
![]() $\kappa _{\textrm{sofic}} (G)=1$
for all groups
$\kappa _{\textrm{sofic}} (G)=1$
for all groups
![]() $G$
.
$G$
.
Let us recall that both proofs are based on a basic tool, often referred to as amplification, which uses the identity:
for matrices
![]() $a$
and
$a$
and
![]() $b$
. This identity allows one to show that there exists a function
$b$
. This identity allows one to show that there exists a function
![]() $f\,:\, (0,1) \to (0,1)$
such that if one starts with a map
$f\,:\, (0,1) \to (0,1)$
such that if one starts with a map
![]() $\phi \,:\, S \to{\mathsf{S}}_n$
with
$\phi \,:\, S \to{\mathsf{S}}_n$
with
![]() ${\textrm{dist}}_{\textrm{Hamm}} ( \phi ( g), e ) \ge \beta$
, then the tensor power
${\textrm{dist}}_{\textrm{Hamm}} ( \phi ( g), e ) \ge \beta$
, then the tensor power
![]() $\phi ^{\otimes 2}\,:\, S \to{\mathsf{S}}_{n \times n}$
defined by
$\phi ^{\otimes 2}\,:\, S \to{\mathsf{S}}_{n \times n}$
defined by
![]() $\phi ^{\otimes 2}(g)(i,j)= (\phi (g)(i), \phi (g)j)$
satisfies
$\phi ^{\otimes 2}(g)(i,j)= (\phi (g)(i), \phi (g)j)$
satisfies
![]() ${\textrm{dist}}_{\textrm{Hamm}} ( \phi ^{\otimes 2}(g), e ) \ge f(\beta )$
. Moreover, starting from any
${\textrm{dist}}_{\textrm{Hamm}} ( \phi ^{\otimes 2}(g), e ) \ge f(\beta )$
. Moreover, starting from any
![]() $\beta$
, the sequence of iterates
$\beta$
, the sequence of iterates
![]() $f^{(n)}(\beta )$
converges to
$f^{(n)}(\beta )$
converges to
![]() $1$
. Hence, by iterating the tensor power operation, one can arrive at arbitrarily well sofic approximation. The case of hyperlinear groups is dealt with in a similar fashion. As it was observed in [Reference Arzhantseva and Păunescu3], (1.1) does not have an analog for linear sofic approximations. In [Reference Arzhantseva and Păunescu3], Arzhantseva and Păunescu invented a new amplification argument to prove that every linear sofic group is
$1$
. Hence, by iterating the tensor power operation, one can arrive at arbitrarily well sofic approximation. The case of hyperlinear groups is dealt with in a similar fashion. As it was observed in [Reference Arzhantseva and Păunescu3], (1.1) does not have an analog for linear sofic approximations. In [Reference Arzhantseva and Păunescu3], Arzhantseva and Păunescu invented a new amplification argument to prove that every linear sofic group is
![]() $1/4$
-linear sofic. A particularly innovative aspect of this argument is that it tracks two different quantities that when coupled together can be used to control the distance to the identity. Then using clever properties of ranks of tensor powers, they prove that this amplification argument works. The question of whether the constant
$1/4$
-linear sofic. A particularly innovative aspect of this argument is that it tracks two different quantities that when coupled together can be used to control the distance to the identity. Then using clever properties of ranks of tensor powers, they prove that this amplification argument works. The question of whether the constant
![]() $1/4$
can be improved is left open in [Reference Arzhantseva and Păunescu3]. We will build upon their work to answer this question in the case of fields of characteristic zero.
$1/4$
can be improved is left open in [Reference Arzhantseva and Păunescu3]. We will build upon their work to answer this question in the case of fields of characteristic zero.
1.2. Statement of results
In this paper, we will address the question of optimality of linear sofic approximations. The main results of this paper is the theorem below.
Theorem A.
Let
![]() $G$
be a countable linear sofic group over
$G$
be a countable linear sofic group over
![]() $\mathbb{C}$
. Then
$\mathbb{C}$
. Then
-
1. If
 $G$
is torsion-free, then
$G$
is torsion-free, then
 $G$
is
$G$
is
 $1$
-linear sofic over
$1$
-linear sofic over
 $\mathbb{C}$
.
$\mathbb{C}$
. -
2. Unconditionally,
 $G$
is
$G$
is
 $1/2$
-linear sofic over
$1/2$
-linear sofic over
 $\mathbb{C}$
. Moreover, the constant
$\mathbb{C}$
. Moreover, the constant
 $1/2$
cannot be improved.
$1/2$
cannot be improved.
Note that the assertion in TheoremA is in stark contrast with the case of sofic and hyperlinear groups. An interesting observation in [Reference Arzhantseva and Păunescu3] (see the paragraph before Proposition 5.12) is that the amplification argument does not see the interaction between group elements and will equally work for a subset of a group. TheoremA, however, shows that the optimal constant does indeed depend on the group structure and can even change by passing to a subgroup of finite index.
Remark 1.3.
Although we stated Theorem A over
![]() $\mathbb{C}$
, one can easily see that it implies the same statement over all fields of characteristic zero; see Remark 5.1. However, an important part of the argument that is based on Lemma 4.2 does not work when
$\mathbb{C}$
, one can easily see that it implies the same statement over all fields of characteristic zero; see Remark 5.1. However, an important part of the argument that is based on Lemma 4.2 does not work when
![]() $F$
has positive characteristic. See Remark 5.2 for more details. Henceforth, we write
$F$
has positive characteristic. See Remark 5.2 for more details. Henceforth, we write
![]() $\kappa$
instead of
$\kappa$
instead of
![]() $\kappa _{\mathbb{C}}$
.
$\kappa _{\mathbb{C}}$
.
We briefly outline the proof of TheoremA, which is following the main strategy of [Reference Arzhantseva and Păunescu3]. Given a finite subset
![]() $S \subseteq G$
and
$S \subseteq G$
and
![]() $ \delta _0 \gt 0$
, we start with an
$ \delta _0 \gt 0$
, we start with an
![]() $(S, \delta _0, 0.24)$
-map
$(S, \delta _0, 0.24)$
-map
![]() $\phi _0$
(in the sense of Definition1.1) provided by [Reference Arzhantseva and Păunescu3]. Using a sequence of functorial operations (see 2.1 for definitions), we replace
$\phi _0$
(in the sense of Definition1.1) provided by [Reference Arzhantseva and Păunescu3]. Using a sequence of functorial operations (see 2.1 for definitions), we replace
![]() $\phi _0$
with an
$\phi _0$
with an
![]() $(S, \delta _0, 0.23)$
-map which has the additional property that for every
$(S, \delta _0, 0.23)$
-map which has the additional property that for every
![]() $g \in S$
, at least
$g \in S$
, at least
![]() $1/100$
of eigenvalues of matrix
$1/100$
of eigenvalues of matrix
![]() $\phi (g)$
are
$\phi (g)$
are
![]() $1$
. We will then show that the rank of tensor powers of
$1$
. We will then show that the rank of tensor powers of
![]() $\phi (g)$
are controlled by the return probability of a certain random walk on a finitely generated subgroup of
$\phi (g)$
are controlled by the return probability of a certain random walk on a finitely generated subgroup of
![]() ${\mathbb{C}}^{\ast }$
. We will establish required effective non-concentration estimates in Theorem3.9. This part of proof uses a variety of tools ranging from Fourier analysis to additive combinatorics. Let us note that the effectiveness of these bounds is a key element of the proof: as the asymptotic homomorphism condition (AH) deteriorates after every iteration of tensor power, we need to know in advance the number of required iterations so that we can start with an appropriate
${\mathbb{C}}^{\ast }$
. We will establish required effective non-concentration estimates in Theorem3.9. This part of proof uses a variety of tools ranging from Fourier analysis to additive combinatorics. Let us note that the effectiveness of these bounds is a key element of the proof: as the asymptotic homomorphism condition (AH) deteriorates after every iteration of tensor power, we need to know in advance the number of required iterations so that we can start with an appropriate
![]() $ \delta _0$
. The counter-intuitive move of adding ones as eigenvalues is needed for this purpose. When
$ \delta _0$
. The counter-intuitive move of adding ones as eigenvalues is needed for this purpose. When
![]() $\phi _0(g)$
is close to unipotent, this argument completely breaks down. In this case, again using the method of [Reference Arzhantseva and Păunescu3], we will instead show the normalized number of Jordan block of tensor powers tends to zero with an effective bound for speed. This is carried out in Theorem4.1 by translating the problem to estimating integrals of certain trigonometric sums. In summary, our proof can be viewed as a version of amplification argument where we use additional functors in the process.
$\phi _0(g)$
is close to unipotent, this argument completely breaks down. In this case, again using the method of [Reference Arzhantseva and Păunescu3], we will instead show the normalized number of Jordan block of tensor powers tends to zero with an effective bound for speed. This is carried out in Theorem4.1 by translating the problem to estimating integrals of certain trigonometric sums. In summary, our proof can be viewed as a version of amplification argument where we use additional functors in the process.
Another result of this paper involves determining
![]() $\kappa (G)$
for finite groups.
$\kappa (G)$
for finite groups.
Theorem B.
Let
![]() $G$
be a finite group.
$G$
be a finite group.
-
1. There exists a finite-dimensional linear representation
 $\psi \,:\, G \to \textrm{GL}_d({\mathbb{C}})$
of
$\psi \,:\, G \to \textrm{GL}_d({\mathbb{C}})$
of
 $G$
such that
In particular,
$G$
such that
In particular, \begin{align*} \kappa (G)= \min _{g \in G} \rho _d( \psi (g), {\textrm {Id}}). \end{align*}
\begin{align*} \kappa (G)= \min _{g \in G} \rho _d( \psi (g), {\textrm {Id}}). \end{align*}
 $\kappa (G)$
is a rational number.
$\kappa (G)$
is a rational number.
-
2.
 $\kappa (G)=1$
iff
$\kappa (G)=1$
iff
 $G$
has a fixed-point free complex representation.
$G$
has a fixed-point free complex representation.
-
3. Let
 ${\mathbb{Z}}_p$
denote the cyclic group of order
${\mathbb{Z}}_p$
denote the cyclic group of order
 $p$
. For prime
$p$
. For prime
 $p$
and
$p$
and
 $n \ge 2$
, we have
In particular,
$n \ge 2$
, we have
In particular, \begin{align*}\kappa ({\mathbb {Z}}_p^n)= \frac {p^n - p^{n-1}}{p^n-1}. \end{align*}
\begin{align*}\kappa ({\mathbb {Z}}_p^n)= \frac {p^n - p^{n-1}}{p^n-1}. \end{align*}
 $\kappa ({\mathbb{Z}}_2^n) \to 1/2$
as
$\kappa ({\mathbb{Z}}_2^n) \to 1/2$
as
 $n \to \infty$
.
$n \to \infty$
.
One of the main ingredients in the proof of TheoremB is the notion of stability. Broadly described, stability of a group in a mode of metric approximation demands that almost representations be small deformations of exact representations. Finite groups are easily seen to enjoy this property with respect to linear sofic approximations, see Proposition6.2. Once this is established, the problem reduces to representation theory of finite groups. Proof of Part (a) of TheoremB is based on the simplex method in linear programming. Part (3) implements this for groups
![]() ${\mathbb{Z}}_p^n$
,
${\mathbb{Z}}_p^n$
,
![]() $n \ge 2$
. We finally remark that all finite groups to which (2) of TheoremA applies have been classified by Joseph Wolf [Reference Wolf24]. They include groups such as
$n \ge 2$
. We finally remark that all finite groups to which (2) of TheoremA applies have been classified by Joseph Wolf [Reference Wolf24]. They include groups such as
![]() $\textrm{PSL}_2({\mathbb{F}}_5)$
. The next result establishes the value of
$\textrm{PSL}_2({\mathbb{F}}_5)$
. The next result establishes the value of
![]() $\kappa _F(G)$
for certain classes of groups over fields of positive characteristic.
$\kappa _F(G)$
for certain classes of groups over fields of positive characteristic.
Theorem C.
Let
![]() $F$
be a field of characteristic
$F$
be a field of characteristic
![]() $p$
, and let
$p$
, and let
![]() $G$
be a finite group such that
$G$
be a finite group such that
![]() $p$
is the smallest prime dividing
$p$
is the smallest prime dividing
![]() $|G|$
. Then
$|G|$
. Then
One of the problems posed in [Reference Arzhantseva and Păunescu3] is whether the notions of linear sofic approximation over
![]() $\mathbb{C}$
and
$\mathbb{C}$
and
![]() ${\mathbb{F}}_p$
are equivalent. TheoremB and TheoremC together show that in general the values of
${\mathbb{F}}_p$
are equivalent. TheoremB and TheoremC together show that in general the values of
![]() $\kappa _{\mathbb{C}}(G)$
and
$\kappa _{\mathbb{C}}(G)$
and
![]() $\kappa _{{\mathbb{F}}_p}(G)$
need not coincide for a finite group
$\kappa _{{\mathbb{F}}_p}(G)$
need not coincide for a finite group
![]() $G$
. This may be viewed as a quantitative reason for the difficulty of the problem of equivalence. We note that quantitative approaches to other metric approximations have also been considered before, see [Reference Arzhantseva and Cherix1].
$G$
. This may be viewed as a quantitative reason for the difficulty of the problem of equivalence. We note that quantitative approaches to other metric approximations have also been considered before, see [Reference Arzhantseva and Cherix1].
This paper is organized as follows: in Section 2, we will collect basic facts related to the rank metric, and basic theory of random walks on abelian groups and explain how they relate to our question. In Section 3, we prove various non-concentration estimates for random walks on abelian groups. Section 4 contains the proof of Theorem4.1, involving matrices in Jordan canonical form. These ingredients are put together in Section 5 to prove TheoremA, except for the optimality claim. The optimality, as well as the proof of TheoremsB and C, are discussed in Section 6.
2. Preliminaries and notation
In this section, we will set some notation and gather a number of basic facts needed in the rest of the paper. We will denote the group of invertible
![]() $d \times d$
matrices over the field
$d \times d$
matrices over the field
![]() $\mathbb{C}$
by
$\mathbb{C}$
by
![]() $\textrm{GL}_d({\mathbb{C}})$
. This space can be turned into a metric space by defining for
$\textrm{GL}_d({\mathbb{C}})$
. This space can be turned into a metric space by defining for
![]() $A, B \in \textrm{GL}_d({\mathbb{C}})$
:
$A, B \in \textrm{GL}_d({\mathbb{C}})$
:
We will often suppress the subscript
![]() $d$
and simply write
$d$
and simply write
![]() $\rho (A, B)$
. Every
$\rho (A, B)$
. Every
![]() $A \in \textrm{GL}_d({\mathbb{C}})$
has
$A \in \textrm{GL}_d({\mathbb{C}})$
has
![]() $d$
eigenvalues
$d$
eigenvalues
![]() $ \lambda _1, \dots, \lambda _d$
, each counted with multiplicity. We write
$ \lambda _1, \dots, \lambda _d$
, each counted with multiplicity. We write
For
![]() $j \ge 1$
, let us denote by
$j \ge 1$
, let us denote by
![]() $W_j$
the set of all
$W_j$
the set of all
![]() $j$
-th roots of unity in
$j$
-th roots of unity in
![]() $\mathbb{C}$
. It will later be convenient to consider the following quantity:
$\mathbb{C}$
. It will later be convenient to consider the following quantity:
 \begin{align*} {\textbf {m}}^{\le r}(A)=\frac {1}{d} \# \! \left\{ 1 \le i \le d \,:\, \lambda _i \in \bigcup _{ j=1}^{ r} W_j \right \}. \end{align*}
\begin{align*} {\textbf {m}}^{\le r}(A)=\frac {1}{d} \# \! \left\{ 1 \le i \le d \,:\, \lambda _i \in \bigcup _{ j=1}^{ r} W_j \right \}. \end{align*}
The number of Jordan blocks of
![]() $A$
(in its Jordan canonical form) will be denoted by
$A$
(in its Jordan canonical form) will be denoted by
![]() ${\textbf{j}}(A)$
. The number of Jordan blocks corresponding with
${\textbf{j}}(A)$
. The number of Jordan blocks corresponding with
![]() $1$
on the diagonal will be denoted by
$1$
on the diagonal will be denoted by
![]() ${\textbf{j}}_1(A)$
. Note that
${\textbf{j}}_1(A)$
. Note that
The following lemma plays a key role in the arguments used in [Reference Arzhantseva and Păunescu3]:
Lemma 2.1 ([Reference Arzhantseva and Păunescu3]). For every
![]() $A \in \textrm{GL}_d({\mathbb{C}})$
, we have
$A \in \textrm{GL}_d({\mathbb{C}})$
, we have
The next lemma will be essential for tracking the multiplicity of eigenvalue
![]() $1$
in tensor powers of a matrix
$1$
in tensor powers of a matrix
![]() $A$
:
$A$
:
Lemma 2.2 ([Reference Arzhantseva and Păunescu3], Lemma 5.1). Suppose that
![]() $\{ \lambda _1, \dots, \lambda _d \}$
is the set of eigenvalues of a
$\{ \lambda _1, \dots, \lambda _d \}$
is the set of eigenvalues of a
![]() $d \times d$
complex matrix
$d \times d$
complex matrix
![]() $A$
, each counted with multiplicity. Then, for
$A$
, each counted with multiplicity. Then, for
![]() $k \ge 1$
the set of eigenvalues of
$k \ge 1$
the set of eigenvalues of
![]() $A^{\otimes k}$
counted with multiplicity is given by:
$A^{\otimes k}$
counted with multiplicity is given by:
Proof. There exists
![]() $P \in \textrm{GL}_d({\mathbb{C}})$
such that
$P \in \textrm{GL}_d({\mathbb{C}})$
such that
![]() $P^{-1}AP$
is upper-triangular. Hence, without loss of generality, we can assume that
$P^{-1}AP$
is upper-triangular. Hence, without loss of generality, we can assume that
![]() $A$
is upper-triangular with diagonal entries
$A$
is upper-triangular with diagonal entries
![]() $ \lambda _1, \dots, \lambda _d$
. It is easy to see that
$ \lambda _1, \dots, \lambda _d$
. It is easy to see that
![]() $A^{\otimes k}$
will be upper-triangular in an appropriate ordering of the bases, with diagonal entries given by the list above. Special case
$A^{\otimes k}$
will be upper-triangular in an appropriate ordering of the bases, with diagonal entries given by the list above. Special case
![]() $k=2$
is dealt with in Lemma 5.1 of [Reference Arzhantseva and Păunescu3].
$k=2$
is dealt with in Lemma 5.1 of [Reference Arzhantseva and Păunescu3].
2.1. Three functorial operations
Let us now consider three functorial operations that can be applied to a family of matrices in
![]() $\textrm{GL}_d({\mathbb{C}})$
. These will be used to replace an
$\textrm{GL}_d({\mathbb{C}})$
. These will be used to replace an
![]() $(S, \delta, \kappa )$
-map by an
$(S, \delta, \kappa )$
-map by an
![]() $(S, \delta ^{\prime}, \kappa ^{\prime})$
-map, which has some better properties. An alternative point of view is that each operation can be viewed as post-composition of the initial map by a representation of
$(S, \delta ^{\prime}, \kappa ^{\prime})$
-map, which has some better properties. An alternative point of view is that each operation can be viewed as post-composition of the initial map by a representation of
![]() $\textrm{GL}_n$
.
$\textrm{GL}_n$
.
-
1. (Tensors) Consider the representations
where \begin{align*}\Psi _{T,m}\,:\, \textrm {GL}_d({\mathbb {C}}) \to \textrm {GL}_{d^m}({\mathbb {C}}), \quad A \mapsto A \otimes \cdots \otimes A,\end{align*}
\begin{align*}\Psi _{T,m}\,:\, \textrm {GL}_d({\mathbb {C}}) \to \textrm {GL}_{d^m}({\mathbb {C}}), \quad A \mapsto A \otimes \cdots \otimes A,\end{align*}
 $m$
denotes the number of tensors. We will denote
$m$
denotes the number of tensors. We will denote
 $\Psi _{T,m}(A)$
by
$\Psi _{T,m}(A)$
by
 ${\mathsf{T}}^m A$
.
${\mathsf{T}}^m A$
.
-
2. (Direct sums) For
 $ m \ge 1$
, letwhere the number of summands is
$ m \ge 1$
, letwhere the number of summands is \begin{align*}\Psi _{S,m}\,:\, \textrm {GL}_d({\mathbb {C}}) \to \textrm {GL}_{md}({\mathbb {C}}), \quad A \mapsto A \oplus \cdots \oplus A,\end{align*}
\begin{align*}\Psi _{S,m}\,:\, \textrm {GL}_d({\mathbb {C}}) \to \textrm {GL}_{md}({\mathbb {C}}), \quad A \mapsto A \oplus \cdots \oplus A,\end{align*}
 $m$
. Instead of
$m$
. Instead of
 $\Psi _{S,m}(A)$
, we write
$\Psi _{S,m}(A)$
, we write
 ${\mathsf{S}}^m A$
.
${\mathsf{S}}^m A$
.
-
3. (Adding Identity) For
 $m \ge 0$
, consider the representationwhere
$m \ge 0$
, consider the representationwhere \begin{align*} \Psi _{I, m} \,:\, \textrm {GL}_d({\mathbb {C}}) \to \textrm {GL}_{m+d}({\mathbb {C}}), \quad A \mapsto A \oplus {\textrm {Id}}_m,\end{align*}
\begin{align*} \Psi _{I, m} \,:\, \textrm {GL}_d({\mathbb {C}}) \to \textrm {GL}_{m+d}({\mathbb {C}}), \quad A \mapsto A \oplus {\textrm {Id}}_m,\end{align*}
 ${\textrm{Id}}_m$
is the identity matrix of size
${\textrm{Id}}_m$
is the identity matrix of size
 $m$
. We write
$m$
. We write
 ${\mathsf{I}}^m A$
for
${\mathsf{I}}^m A$
for
 $ \Psi _{I, m} (A)$
.
$ \Psi _{I, m} (A)$
.
Lemma 2.3.
Let
![]() $A$
and
$A$
and
![]() $B$
be
$B$
be
![]() $d \times d$
matrices. Then for
$d \times d$
matrices. Then for
![]() $m,n \ge 1$
we have
$m,n \ge 1$
we have
-
1.
 ${\textbf{m}}_1({\mathsf{I}}^{md}{\mathsf{S}}^n A)={\textbf{m}}_1(A)+ \frac{m}{n}.$
${\textbf{m}}_1({\mathsf{I}}^{md}{\mathsf{S}}^n A)={\textbf{m}}_1(A)+ \frac{m}{n}.$
-
2.
 $\rho ({\mathsf{I}}^{md}{\mathsf{S}}^n A,{\mathsf{I}}^{md}{\mathsf{S}}^n B) \le \rho (A, B).$
$\rho ({\mathsf{I}}^{md}{\mathsf{S}}^n A,{\mathsf{I}}^{md}{\mathsf{S}}^n B) \le \rho (A, B).$
-
3.
 $\rho ({\mathsf{I}}^{md}{\mathsf{S}}^n A,{\textrm{Id}}) = \frac{n}{n+m} \rho (A,{\textrm{Id}}).$
$\rho ({\mathsf{I}}^{md}{\mathsf{S}}^n A,{\textrm{Id}}) = \frac{n}{n+m} \rho (A,{\textrm{Id}}).$
Proof. Parts (1) and (2) are straightforward computations. For (3) note that
The claim follows by a simple computation.
Proposition 2.4.
Let
![]() $G$
be a linear sofic group. Then for every finite
$G$
be a linear sofic group. Then for every finite
![]() $S \subseteq G$
,
$S \subseteq G$
,
![]() $ \delta \gt 0$
, and
$ \delta \gt 0$
, and
![]() $\kappa \lt 0.24$
, there exists an
$\kappa \lt 0.24$
, there exists an
![]() $( S, \delta, \kappa )$
-map
$( S, \delta, \kappa )$
-map
![]() $\phi$
such that
$\phi$
such that
![]() ${\textbf{m}}_1( \phi (g) ) \ge 0.01$
for all
${\textbf{m}}_1( \phi (g) ) \ge 0.01$
for all
![]() $g \in S \setminus \{ e \}$
.
$g \in S \setminus \{ e \}$
.
Proof. We know from [Reference Arzhantseva and Păunescu3] that
![]() $\kappa (G) \ge 1/4$
. Since
$\kappa (G) \ge 1/4$
. Since
![]() $ \kappa + 0.01 \lt 0.25 \le \kappa (G)$
, there exists a
$ \kappa + 0.01 \lt 0.25 \le \kappa (G)$
, there exists a
![]() $( S, \epsilon, 0.01+\kappa )$
-map, which we denote by
$( S, \epsilon, 0.01+\kappa )$
-map, which we denote by
![]() $\phi _0$
. Set
$\phi _0$
. Set
![]() $\phi ={\mathsf{I}}^{d}{\mathsf{S}}^{100} \phi _0$
. By Lemma2.3, we have
$\phi ={\mathsf{I}}^{d}{\mathsf{S}}^{100} \phi _0$
. By Lemma2.3, we have
![]() ${\textbf{m}}_1( \phi (g)) \ge 0.01$
. Moreover, for every
${\textbf{m}}_1( \phi (g)) \ge 0.01$
. Moreover, for every
![]() $g \in S \setminus \{ e \}$
we have
$g \in S \setminus \{ e \}$
we have
Lemma 2.5.
Let
![]() $A$
and
$A$
and
![]() $B$
be
$B$
be
![]() $d \times d$
matrices. Then
$d \times d$
matrices. Then
![]() $\rho ({\mathsf{T}}^n A,{\mathsf{T}}^n B) \le n \rho (A, B)$
.
$\rho ({\mathsf{T}}^n A,{\mathsf{T}}^n B) \le n \rho (A, B)$
.
Proof. For
![]() $n=2$
, we have
$n=2$
, we have
![]() $A \otimes A - B \otimes B= A \otimes (A- B)+ ( A -B) \otimes B.$
The claim follows from [[Reference Arzhantseva and Păunescu3], Proposition 5] and the triangle inequality. The general case follows by a simple inductive argument.
$A \otimes A - B \otimes B= A \otimes (A- B)+ ( A -B) \otimes B.$
The claim follows from [[Reference Arzhantseva and Păunescu3], Proposition 5] and the triangle inequality. The general case follows by a simple inductive argument.
2.2. Preliminaries from probability theory
It will be convenient to reinterpret Lemma2.2 in a probabilistic language. Let
![]() $(\Lambda, +)$
be a countable abelian group with the neutral element denoted by
$(\Lambda, +)$
be a countable abelian group with the neutral element denoted by
![]() $0$
. By a probability measure on
$0$
. By a probability measure on
![]() $\Lambda$
, we mean a map
$\Lambda$
, we mean a map
![]() $\mu \,:\, \Lambda \to [0,1]$
such that
$\mu \,:\, \Lambda \to [0,1]$
such that
![]() $ \sum _{ a \in \Lambda }\mu (a)=1$
. We will then write
$ \sum _{ a \in \Lambda }\mu (a)=1$
. We will then write
![]() $\mu = \sum _{ a \in \Lambda } \mu (a) \delta _a$
. For
$\mu = \sum _{ a \in \Lambda } \mu (a) \delta _a$
. For
![]() $B \subseteq \Lambda$
, we define
$B \subseteq \Lambda$
, we define
![]() $\mu (B)= \sum _{ a \in B} \mu (a)$
. We say that
$\mu (B)= \sum _{ a \in B} \mu (a)$
. We say that
![]() $\mu$
is finitely supported if there exists a finite set
$\mu$
is finitely supported if there exists a finite set
![]() $B \subseteq \Lambda$
such that
$B \subseteq \Lambda$
such that
![]() $\mu (B)=1$
. The smallest set with this property is called the support of
$\mu (B)=1$
. The smallest set with this property is called the support of
![]() $\mu$
. Probability measures considered in this paper are finitely supported.
$\mu$
. Probability measures considered in this paper are finitely supported.
The convolution of probability measures measures
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
on
$\mu _2$
on
![]() $\Lambda$
is the probability measure defined by:
$\Lambda$
is the probability measure defined by:
One can see that the convolution is commutative and associative. The
![]() $k$
-th convolution power of
$k$
-th convolution power of
![]() $\mu$
will be denoted by
$\mu$
will be denoted by
![]() $\mu ^{(k)}$
. Given a probability measure
$\mu ^{(k)}$
. Given a probability measure
![]() $\mu$
on the group
$\mu$
on the group
![]() $A$
, the
$A$
, the
![]() $\mu$
-random walk on
$\mu$
-random walk on
![]() $\Lambda$
(or the random walk governed by
$\Lambda$
(or the random walk governed by
![]() $\mu$
) is the random process defined as follows. Let
$\mu$
) is the random process defined as follows. Let
![]() $(X_k)_{k \ge 1}$
be a sequence of independent random variables, where the law of
$(X_k)_{k \ge 1}$
be a sequence of independent random variables, where the law of
![]() $X_i$
is
$X_i$
is
![]() $\mu$
. Define the process
$\mu$
. Define the process
![]() $(S_k)_{k \ge 0}$
by
$(S_k)_{k \ge 0}$
by
![]() $S_0=0$
and
$S_0=0$
and
![]() $S_k= X_1+ \cdots + X_k$
. It is easy to see that the law of
$S_k= X_1+ \cdots + X_k$
. It is easy to see that the law of
![]() $X_k$
is
$X_k$
is
![]() $\mu ^{(k)}$
. We will use the notation
$\mu ^{(k)}$
. We will use the notation
![]() $\textbf{P} \left [ E \right ]$
to denote the probability of an event
$\textbf{P} \left [ E \right ]$
to denote the probability of an event
![]() $E$
. Similarly,
$E$
. Similarly,
![]() $\textbf{E}[X]$
denotes the expected value of a random variable
$\textbf{E}[X]$
denotes the expected value of a random variable
![]() $X$
.
$X$
.
Given
![]() $A \in \textrm{GL}_d({\mathbb{C}})$
with eigenvalues
$A \in \textrm{GL}_d({\mathbb{C}})$
with eigenvalues
![]() $ \lambda _1, \dots, \lambda _d$
, define the probability measure on
$ \lambda _1, \dots, \lambda _d$
, define the probability measure on
![]() $\mathbb{C}$
:
$\mathbb{C}$
:
Proposition 2.6.
Let
![]() $A$
be a
$A$
be a
![]() $d \times d$
invertible complex matrix. Then
$d \times d$
invertible complex matrix. Then
-
1.
 $ \xi _A$
is a finitely supported probability measure on the multiplicative group
$ \xi _A$
is a finitely supported probability measure on the multiplicative group
 ${\mathbb{C}}^{\ast }\,:\!=\,{\mathbb{C}} \setminus \{ 0 \}$
.
${\mathbb{C}}^{\ast }\,:\!=\,{\mathbb{C}} \setminus \{ 0 \}$
. -
2.
 $\xi _A( 1) ={\textbf{m}}_1(A).$
$\xi _A( 1) ={\textbf{m}}_1(A).$
-
3. For all integer
 $k \ge 1$
, we have
$k \ge 1$
, we have
 \begin{align*} \xi _{ {\mathsf {T}}^k(A) } = (\xi _A)^{ ( k)}. \end{align*}
\begin{align*} \xi _{ {\mathsf {T}}^k(A) } = (\xi _A)^{ ( k)}. \end{align*}
Proof. Parts (1) and (2) follow from the definition of
![]() $\xi _A$
. Part (3) is an immediate corollary of Lemma2.2.
$\xi _A$
. Part (3) is an immediate corollary of Lemma2.2.
3. Effective non-concentration bounds on abelian groups
This section is devoted to proving effective non-concentration bounds for random walks on abelian groups. We will use the additive notation in most of this section. However, we will eventually apply these results to subgroups of the multiplicative group of nonzero complex numbers. Let
![]() $\nu$
be a finitely supported probability measure on a finitely generated abelian group
$\nu$
be a finitely supported probability measure on a finitely generated abelian group
![]() $\Lambda$
. Our goal is to prove effective upper bounds for the return probability
$\Lambda$
. Our goal is to prove effective upper bounds for the return probability
![]() $\nu ^{(n)} (0)$
.
$\nu ^{(n)} (0)$
.
Lemma 3.1.
Let
![]() $\nu$
be a finitely supported probability measure on
$\nu$
be a finitely supported probability measure on
![]() ${\mathbb{Z}}^d$
such that
${\mathbb{Z}}^d$
such that
![]() $\beta \le \nu (0) \le 1- \beta$
for some
$\beta \le \nu (0) \le 1- \beta$
for some
![]() $0\lt \beta \lt 1/2$
. Then
$0\lt \beta \lt 1/2$
. Then
where
![]() $C$
is an absolute constant.
$C$
is an absolute constant.
Note that the key aspect of Lemma3.1 is that the decay rate is controlled only by
![]() $\beta$
without no further assumption on the distribution of
$\beta$
without no further assumption on the distribution of
![]() $\nu$
. This fact will be crucial in our application. The proof of Lemma3.1 is based on a non-concentration estimate in classical probability theory. Before stating the theorem, we need a few definitions. The concentration function
$\nu$
. This fact will be crucial in our application. The proof of Lemma3.1 is based on a non-concentration estimate in classical probability theory. Before stating the theorem, we need a few definitions. The concentration function
![]() $Q(X, \lambda )$
of a random variable
$Q(X, \lambda )$
of a random variable
![]() $X$
is defined by:
$X$
is defined by:
We will use a theorem of Rogozin [Reference Rogozin20], which generalizes a special case due to Kolmogorov[Reference Kolmogorov13]. Our statement of the theorem is taken from [[Reference Esseen9], Theorem 1], where a new proof using Fourier analysis is given. A variation of this proof can also be found in [[Reference Petrov19], Chapter].
Theorem 3.2 (Rogozin). Suppose
![]() $X_1, \dots, X_n$
are independent random variables and
$X_1, \dots, X_n$
are independent random variables and
![]() $S_n= X_1+ \cdots +X_n$
. Then for every nonnegative
$S_n= X_1+ \cdots +X_n$
. Then for every nonnegative
![]() $ \lambda _1, \dots, \lambda _n \le L$
, we have
$ \lambda _1, \dots, \lambda _n \le L$
, we have
 \begin{align*} Q(S_n, L) \le C \, L \left ( \sum _{ k =1}^{n} \lambda _k^2 (1- Q( X_k, \lambda _k) ) \right )^{-1/2}, \end{align*}
\begin{align*} Q(S_n, L) \le C \, L \left ( \sum _{ k =1}^{n} \lambda _k^2 (1- Q( X_k, \lambda _k) ) \right )^{-1/2}, \end{align*}
where
![]() $C$
is an absolute constant.
$C$
is an absolute constant.
Proof of Lemma 3.1. Let
![]() $\iota \,:\,{\mathbb{Z}}^d \to{\mathbb{R}}$
denote an embedding of
$\iota \,:\,{\mathbb{Z}}^d \to{\mathbb{R}}$
denote an embedding of
![]() ${\mathbb{Z}}^d$
into
${\mathbb{Z}}^d$
into
![]() $\mathbb{R}$
as an abelian group. Let
$\mathbb{R}$
as an abelian group. Let
![]() $\nu ^{\prime}$
denote the push-forward of
$\nu ^{\prime}$
denote the push-forward of
![]() $\nu$
which is a finitely supported probability measure defined by
$\nu$
which is a finitely supported probability measure defined by
![]() $\nu ^{\prime}(x) = \nu ( \iota ^{-1} (x) )$
for every
$\nu ^{\prime}(x) = \nu ( \iota ^{-1} (x) )$
for every
![]() $x \in{\mathbb{R}}$
. Let
$x \in{\mathbb{R}}$
. Let
![]() $X_1, \dots, X_n$
be independent identically distributed random variables with distribution
$X_1, \dots, X_n$
be independent identically distributed random variables with distribution
![]() $\nu ^{\prime}$
. Then by choosing all
$\nu ^{\prime}$
. Then by choosing all
![]() $ \lambda _i$
equal to
$ \lambda _i$
equal to
![]() $ \lambda \gt 0$
, we obtain
$ \lambda \gt 0$
, we obtain
Letting
![]() $ \lambda \to 0$
we obtain
$ \lambda \to 0$
we obtain
![]() $\nu ^{\prime(n)}(0)= \textbf{P} \left [ S_n =0 \right ] \le C ( n(1-q ))^{-1/2}$
where
$\nu ^{\prime(n)}(0)= \textbf{P} \left [ S_n =0 \right ] \le C ( n(1-q ))^{-1/2}$
where
![]() $q= \max _{x \in{\mathbb{R}}} \textbf{P} \left [ X_i=x \right ]$
. Since
$q= \max _{x \in{\mathbb{R}}} \textbf{P} \left [ X_i=x \right ]$
. Since
![]() $\nu^{\prime}(0)=\nu (0) \ge \beta$
, we have
$\nu^{\prime}(0)=\nu (0) \ge \beta$
, we have
![]() $\nu ^{\prime}(x) \le 1- \beta$
for all
$\nu ^{\prime}(x) \le 1- \beta$
for all
![]() $x \in{\mathbb{R}} \setminus \{ 0 \}$
. Since
$x \in{\mathbb{R}} \setminus \{ 0 \}$
. Since
![]() $\nu (0) \le 1-\beta$
, we have
$\nu (0) \le 1-\beta$
, we have
![]() $q \le 1- \beta$
. The claim follows by noticing that
$q \le 1- \beta$
. The claim follows by noticing that
![]() $\nu ^{(n)}(0_{{\mathbb{Z}}_d})= \nu ^{\prime(n)} (0_{{\mathbb{R}}})$
.
$\nu ^{(n)}(0_{{\mathbb{Z}}_d})= \nu ^{\prime(n)} (0_{{\mathbb{R}}})$
.
Remark 3.3.
It might be tempting to expect a similar upper bound for
![]() $\nu ^{(n)} (0)$
under the weaker assumption that
$\nu ^{(n)} (0)$
under the weaker assumption that
![]() $ \nu (0) \le 1- \beta$
. This is, however, not true. To see this, consider the probability measure
$ \nu (0) \le 1- \beta$
. This is, however, not true. To see this, consider the probability measure
![]() $\nu _k$
with
$\nu _k$
with
![]() $\nu _k(1)= 1- \frac{1}{k}$
and
$\nu _k(1)= 1- \frac{1}{k}$
and
![]() $\nu _k({-}k)= \frac{1}{k}$
. Although
$\nu _k({-}k)= \frac{1}{k}$
. Although
![]() $\nu _k(0)=0$
, we have for all
$\nu _k(0)=0$
, we have for all
![]() $k \ge 1$
$k \ge 1$
![]() $\nu _k^{(k+1)}(0)= \frac{k+1}{k} ( 1- \frac{1}{k})^k \approx 1/e$
.
$\nu _k^{(k+1)}(0)= \frac{k+1}{k} ( 1- \frac{1}{k})^k \approx 1/e$
.
We will now consider a variant of Lemma3.1 for finite cyclic groups
![]() ${\mathbb{Z}}_N$
. In this case, the uniform measure is the stationary measure and hence
${\mathbb{Z}}_N$
. In this case, the uniform measure is the stationary measure and hence
![]() $\nu ^n(0)$
(under irreducibility assumptions) will converge to
$\nu ^n(0)$
(under irreducibility assumptions) will converge to
![]() $1/N$
as
$1/N$
as
![]() $n \to \infty$
. Note, however, that the random walk and its frequency of visits to zero can be bounded by how much the measure is supported on small subgroups. The next lemma provides an effective upper bound for
$n \to \infty$
. Note, however, that the random walk and its frequency of visits to zero can be bounded by how much the measure is supported on small subgroups. The next lemma provides an effective upper bound for
![]() $\nu ^{(n)} (0)$
only depending on the mass given to elements of small order.
$\nu ^{(n)} (0)$
only depending on the mass given to elements of small order.
Lemma 3.4 (Non-concentration for random walks on cyclic groups). Let
![]() $\nu$
be a probability measure on
$\nu$
be a probability measure on
![]() ${\mathbb{Z}}_N$
. Further, suppose that for some
${\mathbb{Z}}_N$
. Further, suppose that for some
![]() $0\lt \beta \le 1/2$
and positive integer
$0\lt \beta \le 1/2$
and positive integer
![]() $r\gt 1$
the following hold:
$r\gt 1$
the following hold:
-
1.
 $\beta \le \nu (0) \le 1- \beta$
.
$\beta \le \nu (0) \le 1- \beta$
. -
2. For every subgroup
 $H \le{\mathbb{Z}}_N$
with
$H \le{\mathbb{Z}}_N$
with
 $|H| \le r$
, we have
$|H| \le r$
, we have
 $ \nu (H) \le 1- \beta$
.
$ \nu (H) \le 1- \beta$
.
Then for all
![]() $n \ge 1$
, we have
$n \ge 1$
, we have
where
![]() $C^{\prime}$
is an absolute constant.
$C^{\prime}$
is an absolute constant.
The following proof is an adaptation of the proof of Littlewood-Offord estimate [[Reference Nguyen and Wood18], Theorem 6.3]. This theorem is proven under different conditions, where instead of condition (2), a stronger assumption on the measure of all subgroups is imposed.
The proof uses the Fourier transform of measure and some of Let
![]() $\nu$
be a probability measure on
$\nu$
be a probability measure on
![]() ${\mathbb{Z}}_N$
. Write
${\mathbb{Z}}_N$
. Write
![]() $e_N(x)= \exp ( 2 \pi i x/ N)$
for
$e_N(x)= \exp ( 2 \pi i x/ N)$
for
![]() $x \in{\mathbb{Z}}_N$
. The following basic property of
$x \in{\mathbb{Z}}_N$
. The following basic property of
![]() $e_N$
is used several times in the sequel. For each
$e_N$
is used several times in the sequel. For each
![]() $a \in{\mathbb{Z}}_n$
, we have
$a \in{\mathbb{Z}}_n$
, we have
![]() $\sum _{x \in{\mathbb{Z}}_n} e_N(ax)$
. We will define the (Fourier) transform
$\sum _{x \in{\mathbb{Z}}_n} e_N(ax)$
. We will define the (Fourier) transform
![]() $ \widehat{\nu }:{\mathbb{Z}}_N \to{\mathbb{C}}$
by:
$ \widehat{\nu }:{\mathbb{Z}}_N \to{\mathbb{C}}$
by:
Lemma 3.5.
Let
![]() $\nu$
be a probability measure on
$\nu$
be a probability measure on
![]() ${\mathbb{Z}}_N$
. Then we have
${\mathbb{Z}}_N$
. Then we have
-
1.
 $ \widehat{\nu }(0)=1$
.
$ \widehat{\nu }(0)=1$
. -
2. For all
 $n \ge 1$
, we have
$n \ge 1$
, we have
 $ \widehat{\nu ^{(n)}} = (\widehat{\nu })^n$
.
$ \widehat{\nu ^{(n)}} = (\widehat{\nu })^n$
. -
3.
 $\nu (0)= \frac{1}{N} \sum _{t \in{\mathbb{Z}}_N} \widehat{\nu }(t).$
$\nu (0)= \frac{1}{N} \sum _{t \in{\mathbb{Z}}_N} \widehat{\nu }(t).$
Proof. Part (1) is clear. For (2), suppose that
![]() $\nu _1$
and
$\nu _1$
and
![]() $\nu _2$
are two probability measures on
$\nu _2$
are two probability measures on
![]() ${\mathbb{Z}}_N$
. Then we have
${\mathbb{Z}}_N$
. Then we have
 \begin{equation} \begin{split} \widehat{ \nu _1 \ast \nu _2} (t) &= \sum _{ a \in{\mathbb{Z}}_N} (\nu _1 \ast \nu _2)(a) e_N(at) \\ &= \sum _{ a \in{\mathbb{Z}}_N} \sum _{ a_1+ a_2=a } \nu _1 (a_1) \nu _2(a_2) e_N(a_1t) e_N(a_2t) \\ &= \sum _{ a_1 \in{\mathbb{Z}}_N} \nu _1 (a_1) e_N(a_1t) \sum _{ a_2 \in{\mathbb{Z}}_N} \nu _2 (a_2) e_N(a_2t) = \widehat{ \nu _1} (t) \widehat{\nu _2} (t). \end{split} \end{equation}
\begin{equation} \begin{split} \widehat{ \nu _1 \ast \nu _2} (t) &= \sum _{ a \in{\mathbb{Z}}_N} (\nu _1 \ast \nu _2)(a) e_N(at) \\ &= \sum _{ a \in{\mathbb{Z}}_N} \sum _{ a_1+ a_2=a } \nu _1 (a_1) \nu _2(a_2) e_N(a_1t) e_N(a_2t) \\ &= \sum _{ a_1 \in{\mathbb{Z}}_N} \nu _1 (a_1) e_N(a_1t) \sum _{ a_2 \in{\mathbb{Z}}_N} \nu _2 (a_2) e_N(a_2t) = \widehat{ \nu _1} (t) \widehat{\nu _2} (t). \end{split} \end{equation}
Now, (2) follows by induction. For (3) note that
 \begin{equation} \begin{split} \frac{1}{N} \sum _{t \in{\mathbb{Z}}_N} \widehat{\nu }(t) &= \frac{1}{N} \sum _{t \in{\mathbb{Z}}_N} \sum _{ a \in{\mathbb{Z}}_N } \nu (a) e_N( at) \\ & = \frac{1}{N} \sum _{a \in{\mathbb{Z}}_N} \nu (a) \sum _{ t \in{\mathbb{Z}}_N } e_N( a) = \nu (0), \end{split} \end{equation}
\begin{equation} \begin{split} \frac{1}{N} \sum _{t \in{\mathbb{Z}}_N} \widehat{\nu }(t) &= \frac{1}{N} \sum _{t \in{\mathbb{Z}}_N} \sum _{ a \in{\mathbb{Z}}_N } \nu (a) e_N( at) \\ & = \frac{1}{N} \sum _{a \in{\mathbb{Z}}_N} \nu (a) \sum _{ t \in{\mathbb{Z}}_N } e_N( a) = \nu (0), \end{split} \end{equation}
where the last equality follows from the fact that for every
![]() $a \in{\mathbb{Z}}_N$
, we have
$a \in{\mathbb{Z}}_N$
, we have
![]() $ \sum _{ t \in{\mathbb{Z}}_N } e_N( at)=0$
unless
$ \sum _{ t \in{\mathbb{Z}}_N } e_N( at)=0$
unless
![]() $a=0$
, in which case it is equal to
$a=0$
, in which case it is equal to
![]() $N$
.
$N$
.
We can now start with the proof of Lemma3.4.
Proof of Lemma 3.4. Using parts (2) and (3) of Lemma3.5, we have
Applying riangle inequality, we deduce
Writing
![]() $\psi (t)= 1- | \widehat{\nu }(t)|^2$
and using the inequality
$\psi (t)= 1- | \widehat{\nu }(t)|^2$
and using the inequality
![]() $ |x| \le \exp \left ( - \frac{1-x^2}{2 } \right )$
that holds for all
$ |x| \le \exp \left ( - \frac{1-x^2}{2 } \right )$
that holds for all
![]() $x \in{\mathbb{R}}$
, we obtain
$x \in{\mathbb{R}}$
, we obtain
Set
![]() $f(t)= n \psi (t)$
and define
$f(t)= n \psi (t)$
and define
![]() $ T(w)= \{ t\,:\, f(t) \le w \}$
. Note that since
$ T(w)= \{ t\,:\, f(t) \le w \}$
. Note that since
![]() $f(0)=n \psi (0)=0$
, hence
$f(0)=n \psi (0)=0$
, hence
![]() $0 \in T(w)$
for all
$0 \in T(w)$
for all
![]() $w \ge 0$
.
$w \ge 0$
.
By separating the sum into level sets, we obtain the following inequality:
For an integer
![]() $k \ge 1$
, and subsets
$k \ge 1$
, and subsets
![]() $A_1, \dots, A_k \subseteq{\mathbb{Z}}_N$
, we write
$A_1, \dots, A_k \subseteq{\mathbb{Z}}_N$
, we write
We use the shorthand
![]() $kA$
for
$kA$
for
![]() $A+ \cdots +A$
, where
$A+ \cdots +A$
, where
![]() $k$
is the number of summands. The following lemma is proven in [[Reference Maples15], Proposition 3.5] for all finite fields. A simple verification shows that it applies verbatim to all finite cyclic groups. For reader’s convenience, we will sketch the modification needed in the proof.
$k$
is the number of summands. The following lemma is proven in [[Reference Maples15], Proposition 3.5] for all finite fields. A simple verification shows that it applies verbatim to all finite cyclic groups. For reader’s convenience, we will sketch the modification needed in the proof.
Lemma 3.6.
For any
![]() $w\gt 0$
and integer
$w\gt 0$
and integer
![]() $k \ge 1$
, we have
$k \ge 1$
, we have
Proof. It suffices to show that for all
![]() $ \beta _1, \dots, \beta _k \in{\mathbb{Z}}_N$
, we have
$ \beta _1, \dots, \beta _k \in{\mathbb{Z}}_N$
, we have
This, in turn can be rewritten as:
 \begin{align*} 1- \sum _{ a,b \in {\mathbb {Z}}_N} \mu (a) \mu (b) \cos \!\left( \frac {2\pi }{N}(a-b)( \beta _1+ \cdots + \beta _k) \right) \le k^2- k \sum _{j=1}^k \sum _{ a, b \in {\mathbb {Z}}_N} \mu (a) \mu (b) \cos \!\left ( \frac {2\pi }{N} (a-b) \beta _j \right). \end{align*}
\begin{align*} 1- \sum _{ a,b \in {\mathbb {Z}}_N} \mu (a) \mu (b) \cos \!\left( \frac {2\pi }{N}(a-b)( \beta _1+ \cdots + \beta _k) \right) \le k^2- k \sum _{j=1}^k \sum _{ a, b \in {\mathbb {Z}}_N} \mu (a) \mu (b) \cos \!\left ( \frac {2\pi }{N} (a-b) \beta _j \right). \end{align*}
This follows from the trigonometric inequality proven in [[Reference Maples15], Proposition 3.1].
We will also need a lemma from additive combinatorics. Define the set of symmetries of a set
![]() $A \subseteq{\mathbb{Z}}_N$
by
$A \subseteq{\mathbb{Z}}_N$
by
![]() $\textrm{Sym} A\,:\!=\, \{ h \in{\mathbb{Z}}_N\,:\, h+ A = A \}$
. Note that
$\textrm{Sym} A\,:\!=\, \{ h \in{\mathbb{Z}}_N\,:\, h+ A = A \}$
. Note that
![]() $\textrm{Sym} A$
is a subgroup of
$\textrm{Sym} A$
is a subgroup of
![]() ${\mathbb{Z}}_N$
and if
${\mathbb{Z}}_N$
and if
![]() $0 \in A$
then
$0 \in A$
then
![]() $ \textrm{Sym} (A) \subseteq A$
. The lemma follows by a simple inductive argument from [[Reference Tao and Van22], Theorem 5.5].
$ \textrm{Sym} (A) \subseteq A$
. The lemma follows by a simple inductive argument from [[Reference Tao and Van22], Theorem 5.5].
Lemma 3.7 (Kneser’s bound). Let
![]() $Z$
be an abelian group and
$Z$
be an abelian group and
![]() $A_1, \dots, A_k \subseteq Z$
are finite subsets. Then we have
$A_1, \dots, A_k \subseteq Z$
are finite subsets. Then we have
In particular, for any finite
![]() $A$
we have
$A$
we have
where
![]() $kA= A+ \cdots +A$
, with the sum containing
$kA= A+ \cdots +A$
, with the sum containing
![]() $k$
copies of
$k$
copies of
![]() $A$
.
$A$
.
We will now claim that if
![]() $H$
is a subgroup of
$H$
is a subgroup of
![]() ${\mathbb{Z}}_N$
with
${\mathbb{Z}}_N$
with
![]() $|H| \ge \frac{N}{r}$
, then there exists
$|H| \ge \frac{N}{r}$
, then there exists
![]() $t \in H$
with
$t \in H$
with
![]() $f(t) \ge n \beta$
. To prove this note that
$f(t) \ge n \beta$
. To prove this note that
Expanding the definition of
![]() $ \widehat{\nu }$
in
$ \widehat{\nu }$
in
![]() $| \widehat{\nu }(t)|^2= \widehat{\nu }(t) \cdot \overline{ \widehat{\nu }(t)}$
, and summing for
$| \widehat{\nu }(t)|^2= \widehat{\nu }(t) \cdot \overline{ \widehat{\nu }(t)}$
, and summing for
![]() $t \in H$
we obtain
$t \in H$
we obtain
 \begin{equation} \begin{split} \sum _{ t \in H } | \widehat{\nu } ( t)|^2 & =\sum _{ t \in H } \sum _{ \theta _1 \in{\mathbb{Z}}_n } \nu (\theta _1) e_N(\theta _1 t) \sum _{ \theta _2 \in{\mathbb{Z}}_n } \nu (\theta _2) e_N({-}\theta _2t) \\ &= \sum _{ t \in H } \sum _{ \theta _1, \theta _2 \in{\mathbb{Z}}_n } \nu (\theta _1) \nu (\theta _2) e_N( ( \theta _1-\theta _2)t) = |H| \cdot \sum _{ \theta _1, \theta _2 \in{\mathbb{Z}}_N} \nu ( \theta _1) \nu (\theta _2){\textbf{1}}_{ H^\perp } ( \theta _1- \theta _2) \\ & = |H| \cdot \sum _{ \theta _1 \in{\mathbb{Z}}_N} \nu ( \theta _1) \nu ( \theta _1+ H^\perp ). \end{split} \end{equation}
\begin{equation} \begin{split} \sum _{ t \in H } | \widehat{\nu } ( t)|^2 & =\sum _{ t \in H } \sum _{ \theta _1 \in{\mathbb{Z}}_n } \nu (\theta _1) e_N(\theta _1 t) \sum _{ \theta _2 \in{\mathbb{Z}}_n } \nu (\theta _2) e_N({-}\theta _2t) \\ &= \sum _{ t \in H } \sum _{ \theta _1, \theta _2 \in{\mathbb{Z}}_n } \nu (\theta _1) \nu (\theta _2) e_N( ( \theta _1-\theta _2)t) = |H| \cdot \sum _{ \theta _1, \theta _2 \in{\mathbb{Z}}_N} \nu ( \theta _1) \nu (\theta _2){\textbf{1}}_{ H^\perp } ( \theta _1- \theta _2) \\ & = |H| \cdot \sum _{ \theta _1 \in{\mathbb{Z}}_N} \nu ( \theta _1) \nu ( \theta _1+ H^\perp ). \end{split} \end{equation}
Here,
![]() $H^\perp$
denotes the dual of
$H^\perp$
denotes the dual of
![]() $H$
, consisting of
$H$
, consisting of
![]() $x \in{\mathbb{Z}}_N$
such that
$x \in{\mathbb{Z}}_N$
such that
![]() $e_N( hx)=1$
for all
$e_N( hx)=1$
for all
![]() $h \in H$
. Note that
$h \in H$
. Note that
![]() $H^\perp$
is a subgroup of
$H^\perp$
is a subgroup of
![]() ${\mathbb{Z}}_N$
. If
${\mathbb{Z}}_N$
. If
![]() $\theta _1 \not \in H^\perp$
, then
$\theta _1 \not \in H^\perp$
, then
![]() $ 0 \not \in \theta _1+ H^\perp$
and hence
$ 0 \not \in \theta _1+ H^\perp$
and hence
![]() $\nu ( \theta _1+ H^\perp ) \le 1- \nu (0) \le 1- \beta$
. If
$\nu ( \theta _1+ H^\perp ) \le 1- \nu (0) \le 1- \beta$
. If
![]() $\theta _1 \in H^\perp$
, then
$\theta _1 \in H^\perp$
, then
![]() $ \theta _1+ H^\perp = H^\perp$
. Since
$ \theta _1+ H^\perp = H^\perp$
. Since
![]() $|H^\perp | \le r$
, we have
$|H^\perp | \le r$
, we have
![]() $ \nu (\theta _1+ H^\perp ) \le 1- \beta$
in this case as well. This implies that
$ \nu (\theta _1+ H^\perp ) \le 1- \beta$
in this case as well. This implies that
![]() $ \sum _{ t \in H } | \widehat{\nu } ( t)|^2 \le 1- \beta$
. This shows that
$ \sum _{ t \in H } | \widehat{\nu } ( t)|^2 \le 1- \beta$
. This shows that
![]() $ \frac{1}{|H|} \sum _{ t \in H } f(t) \ge n \beta, $
implying that there exists
$ \frac{1}{|H|} \sum _{ t \in H } f(t) \ge n \beta, $
implying that there exists
![]() $t \in H$
such that
$t \in H$
such that
![]() $f(t) \ge n \beta$
.
$f(t) \ge n \beta$
.
Let us now suppose
![]() $ w \lt n \beta$
. Let
$ w \lt n \beta$
. Let
![]() $k$
be the largest positive integer with
$k$
be the largest positive integer with
![]() $k^2 w\lt n \beta$
. We claim that
$k^2 w\lt n \beta$
. We claim that
![]() $| \textrm{Sym} ( k T( w)) | \le \frac{N}{r}$
. In fact, if this is not the case, using Lemma3.6 we have
$| \textrm{Sym} ( k T( w)) | \le \frac{N}{r}$
. In fact, if this is not the case, using Lemma3.6 we have
it follows that
![]() $T(k^2 w)$
contains a subgroup
$T(k^2 w)$
contains a subgroup
![]() $H$
with more than
$H$
with more than
![]() $N/r$
elements. We will then have
$N/r$
elements. We will then have
which contradicts that claim proved above. It follows from Lemma3.7 that for all
![]() $w \lt n \beta$
, we have
$w \lt n \beta$
, we have
By the choice of
![]() $k \ge 1$
, we have
$k \ge 1$
, we have
implying that
![]() $k \ge \sqrt{ \frac{n\beta }{4w}}$
. Putting all these together we obtain
$k \ge \sqrt{ \frac{n\beta }{4w}}$
. Putting all these together we obtain
 \begin{align*} |T(w)| \le \sqrt { \frac {4w}{n \beta }} N + \frac {N}{r}. \end{align*}
\begin{align*} |T(w)| \le \sqrt { \frac {4w}{n \beta }} N + \frac {N}{r}. \end{align*}
Inserting the latter bound in the range
![]() $w\lt n \beta$
and the trivial bound
$w\lt n \beta$
and the trivial bound
![]() $|T(w)| \le N$
for
$|T(w)| \le N$
for
![]() $w \gt n \beta$
into (3.3), we arrive at
$w \gt n \beta$
into (3.3), we arrive at
 \begin{equation} \begin{split} \nu ^{(n)}(0) & \le \frac{1}{2N} \int _0^{ n \beta } \left(\sqrt{ \frac{4w}{n \beta }} N + \frac{N}{r} \right) e^{-w/2} dw+ \frac{1}{2N} \int _{n\beta }^{ \infty } Ne^{-w/2} dw \\ & \le \frac{C}{ \sqrt{ n \beta } } \int _0^{ \infty } \sqrt{ w} e^{-w/2} dw + \frac{1}{r}+ \frac{1}{2} \int _{n\beta }^{ \infty } e^{- w/2} dw \\ & \le \frac{1}{r}+ \frac{C^{\prime}}{ \sqrt{ n \beta } }+ e ^{-n\beta /2} \end{split} \end{equation}
\begin{equation} \begin{split} \nu ^{(n)}(0) & \le \frac{1}{2N} \int _0^{ n \beta } \left(\sqrt{ \frac{4w}{n \beta }} N + \frac{N}{r} \right) e^{-w/2} dw+ \frac{1}{2N} \int _{n\beta }^{ \infty } Ne^{-w/2} dw \\ & \le \frac{C}{ \sqrt{ n \beta } } \int _0^{ \infty } \sqrt{ w} e^{-w/2} dw + \frac{1}{r}+ \frac{1}{2} \int _{n\beta }^{ \infty } e^{- w/2} dw \\ & \le \frac{1}{r}+ \frac{C^{\prime}}{ \sqrt{ n \beta } }+ e ^{-n\beta /2} \end{split} \end{equation}
This ends the proof of Lemma3.4.
Lemma 3.8.
Let
![]() $\nu$
be a probability measure on
$\nu$
be a probability measure on
![]() ${\mathbb{Z}}_N$
and
${\mathbb{Z}}_N$
and
![]() $0\lt \beta \lt 1/2$
such that
$0\lt \beta \lt 1/2$
such that
![]() $\beta \le \nu (0) \le 1- \beta$
. Then for some constant
$\beta \le \nu (0) \le 1- \beta$
. Then for some constant
![]() $C^{\prime}$
and all
$C^{\prime}$
and all
![]() $n \ge 1$
, we have
$n \ge 1$
, we have
Proof. This is proven is similar to the proof of Lemma3.4. As before we write
We now claim that for all
![]() $ w\lt n \beta$
we have
$ w\lt n \beta$
we have
 \begin{align*} |T(w)| \le \sqrt { \frac {4w}{n \beta }} N + \frac {N}{2}. \end{align*}
\begin{align*} |T(w)| \le \sqrt { \frac {4w}{n \beta }} N + \frac {N}{2}. \end{align*}
To show this, for
![]() $ w \lt n \beta$
denote by
$ w \lt n \beta$
denote by
![]() $k$
the largest positive integer with
$k$
the largest positive integer with
![]() $k^2 w\lt n \beta$
. We claim that
$k^2 w\lt n \beta$
. We claim that
![]() $| \textrm{Sym} ( T( w)+ \cdots + T(w)) | \le \frac{N}{2}$
. Suppose that this is not the case. Recall that
$| \textrm{Sym} ( T( w)+ \cdots + T(w)) | \le \frac{N}{2}$
. Suppose that this is not the case. Recall that
![]() $ T(w)= \{ t: f(t) \le w \}$
, where
$ T(w)= \{ t: f(t) \le w \}$
, where
![]() $f(t)= n \left ( 1- | \widehat{\nu } (t)|^2 \right )$
. Since
$f(t)= n \left ( 1- | \widehat{\nu } (t)|^2 \right )$
. Since
![]() $ \widehat{\nu }(0)=1$
, we have
$ \widehat{\nu }(0)=1$
, we have
![]() $f(0)=0$
. Since
$f(0)=0$
. Since
![]() $w\gt 0$
, we have
$w\gt 0$
, we have
![]() $0 \in T(w)$
. This implies that
$0 \in T(w)$
. This implies that
it follows that
![]() $T(k^2 w)$
contains a subgroup with more than
$T(k^2 w)$
contains a subgroup with more than
![]() $N/2$
elements, hence has to be equal to
$N/2$
elements, hence has to be equal to
![]() ${\mathbb{Z}}_N$
, from which it follows that
${\mathbb{Z}}_N$
, from which it follows that
![]() $T( n \beta )={\mathbb{Z}}_N$
. On the other hand, using the Plancherel formula we have
$T( n \beta )={\mathbb{Z}}_N$
. On the other hand, using the Plancherel formula we have
where the second inequality follows from
![]() $ (1- \beta )- (1-\beta )^2 - \beta ^2 = \beta ( 1-2 \beta )\gt 0$
. This implies that
$ (1- \beta )- (1-\beta )^2 - \beta ^2 = \beta ( 1-2 \beta )\gt 0$
. This implies that
![]() $ \frac{1}{N} \sum _{t \in{\mathbb{Z}}_N} (1- | \widehat{\nu }(t)|^2) \ge \beta$
. Hence, there exists
$ \frac{1}{N} \sum _{t \in{\mathbb{Z}}_N} (1- | \widehat{\nu }(t)|^2) \ge \beta$
. Hence, there exists
![]() $t \in{\mathbb{Z}}_N$
such that
$t \in{\mathbb{Z}}_N$
such that
![]() $f(t) \ge n \beta$
. A similar argument as above finishes the proof.
$f(t) \ge n \beta$
. A similar argument as above finishes the proof.
We will now combine Lemmas3.1, 3.4, 3.8 to prove a non-concentration theorem for random walks on abelian groups with cyclic torsion component. Let
![]() $\Lambda \,:\!=\, \Lambda _1 \times \Lambda _2$
where
$\Lambda \,:\!=\, \Lambda _1 \times \Lambda _2$
where
![]() $\Lambda _1 \sim{\mathbb{Z}}^s$
and
$\Lambda _1 \sim{\mathbb{Z}}^s$
and
![]() $\Lambda _2 \simeq{\mathbb{Z}}_N$
are free and torsion components of
$\Lambda _2 \simeq{\mathbb{Z}}_N$
are free and torsion components of
![]() $\Lambda$
. For
$\Lambda$
. For
![]() $i=1,2$
, denote the projection from
$i=1,2$
, denote the projection from
![]() $\Lambda$
onto
$\Lambda$
onto
![]() $\Lambda _i$
by
$\Lambda _i$
by
![]() $\pi _i$
, and for probability measure
$\pi _i$
, and for probability measure
![]() $\nu$
on
$\nu$
on
![]() $\Lambda$
, we write
$\Lambda$
, we write
![]() $\nu _i\,:\!=\,(\pi _i)_{\ast } \nu$
for the push-forward of
$\nu _i\,:\!=\,(\pi _i)_{\ast } \nu$
for the push-forward of
![]() $\nu$
under
$\nu$
under
![]() $\pi _i$
.
$\pi _i$
.
Theorem 3.9 (Non-concentration for random walks on abelian groups). Let
![]() $\Lambda$
be a finitely generated abelian group with a cyclic torsion subgroup and
$\Lambda$
be a finitely generated abelian group with a cyclic torsion subgroup and
![]() $\nu$
a finitely supported probability measure on
$\nu$
a finitely supported probability measure on
![]() $\Lambda$
. Let
$\Lambda$
. Let
![]() $ 0\lt \beta \lt 1/2$
and
$ 0\lt \beta \lt 1/2$
and
![]() $r \ge 1$
be a positive integer. Assume that
$r \ge 1$
be a positive integer. Assume that
-
1.
 $ \beta \le \nu (0) \le 1- \beta$
.
$ \beta \le \nu (0) \le 1- \beta$
. -
2.
 $\nu (\Lambda ^{{\tiny{\le r}}}) \le 1 - \beta$
, where
$\nu (\Lambda ^{{\tiny{\le r}}}) \le 1 - \beta$
, where
 $\Lambda ^{\le r}$
is the subset of
$\Lambda ^{\le r}$
is the subset of
 $ \Lambda$
consisting of elements of order at most
$ \Lambda$
consisting of elements of order at most
 $r$
.
$r$
.
Then for all
![]() $n \ge 1$
, we have
$n \ge 1$
, we have
where
![]() $C^{\prime\prime}$
is an absolute constant. Moreover, only under assumption (1) above, we have
$C^{\prime\prime}$
is an absolute constant. Moreover, only under assumption (1) above, we have
Proof. Clearly, we have
Moreover, the inequality
![]() $\beta \le \nu _j(0)$
is satisfied for both
$\beta \le \nu _j(0)$
is satisfied for both
![]() $j=1,2$
. We consider two cases: if
$j=1,2$
. We consider two cases: if
![]() $ \nu _1(0) \le 1- \frac{\beta }{4}$
, then it follows from Lemma3.1 that
$ \nu _1(0) \le 1- \frac{\beta }{4}$
, then it follows from Lemma3.1 that
Hence, suppose that
![]() $ \nu _1(0) \gt 1- \frac{\beta }{4}$
. We claim that in this case we must have
$ \nu _1(0) \gt 1- \frac{\beta }{4}$
. We claim that in this case we must have
![]() $ \nu _2(0) \le 1- \frac{\beta }{2}$
. If this is not the case, then
$ \nu _2(0) \le 1- \frac{\beta }{2}$
. If this is not the case, then
![]() $\nu _2(0) \ge 1 - \frac{1}{2} \beta$
which contradicts assumption (2). We will now verify condition (2) of Lemma3.4 by finding an upper bound on the measure (under
$\nu _2(0) \ge 1 - \frac{1}{2} \beta$
which contradicts assumption (2). We will now verify condition (2) of Lemma3.4 by finding an upper bound on the measure (under
![]() $\nu _2$
) of the set of elements of order at most
$\nu _2$
) of the set of elements of order at most
![]() $r$
in
$r$
in
![]() $\Lambda _2$
:
$\Lambda _2$
:
 \begin{equation} \begin{split} \nu _2 \!\left\{ z \in \Lambda _2\,:\,{\textrm{ord}}_{\Lambda _2}(z) \le r \right \} & = \nu \!\left\{ z= (z_1, z_2) \in \Lambda \,:\,{\textrm{ord}}_{\Lambda _2} ( z_2) \le r \right\} \\ & \le \nu \!\left( \left\{ z= (0, z_2) \in \Lambda \,:\,{\textrm{ord}} ( z) \le r \right \} \right ) + \nu \!\left( \left \{ z= (z_1, z_2) \in \Lambda \,:\, z_1 \neq 0 \right \} \right) \\ & \le 1- \beta + \frac{\beta }{4} \lt 1- \frac{\beta }{2}. \end{split} \end{equation}
\begin{equation} \begin{split} \nu _2 \!\left\{ z \in \Lambda _2\,:\,{\textrm{ord}}_{\Lambda _2}(z) \le r \right \} & = \nu \!\left\{ z= (z_1, z_2) \in \Lambda \,:\,{\textrm{ord}}_{\Lambda _2} ( z_2) \le r \right\} \\ & \le \nu \!\left( \left\{ z= (0, z_2) \in \Lambda \,:\,{\textrm{ord}} ( z) \le r \right \} \right ) + \nu \!\left( \left \{ z= (z_1, z_2) \in \Lambda \,:\, z_1 \neq 0 \right \} \right) \\ & \le 1- \beta + \frac{\beta }{4} \lt 1- \frac{\beta }{2}. \end{split} \end{equation}
In particular, if
![]() $H$
is a subgroup with
$H$
is a subgroup with
![]() $|H| \le r$
, then the order of every element of
$|H| \le r$
, then the order of every element of
![]() $H$
is at most
$H$
is at most
![]() $r$
, and hence
$r$
, and hence
![]() $\nu _2(H) \le 1 - \frac{\beta }{2}$
. We can now apply Lemma3.4 and Lemma3.8 (with
$\nu _2(H) \le 1 - \frac{\beta }{2}$
. We can now apply Lemma3.4 and Lemma3.8 (with
![]() $\beta /2$
instead of
$\beta /2$
instead of
![]() $\beta$
) to obtain the result.
$\beta$
) to obtain the result.
Corollary 3.10.
Let
![]() $A$
be a matrix in
$A$
be a matrix in
![]() $\textrm{GL}_d({\mathbb{C}})$
and
$\textrm{GL}_d({\mathbb{C}})$
and
![]() $\beta \gt 0$
. Assume that
$\beta \gt 0$
. Assume that
-
1.
 $\beta \le{\textbf{m}}_1(A) \le 1-\beta$
.
$\beta \le{\textbf{m}}_1(A) \le 1-\beta$
. -
2.
 ${\textbf{m}}^{\le r}(A) \le (1- \beta )$
${\textbf{m}}^{\le r}(A) \le (1- \beta )$
Then for every
![]() $ \eta \gt 0$
there exists
$ \eta \gt 0$
there exists
![]() $M\,:\!=\,M(\beta, r, \eta )$
such that for all
$M\,:\!=\,M(\beta, r, \eta )$
such that for all
![]() $n \ge M$
, we have
$n \ge M$
, we have
Moreover, only under assumption (1), for every
![]() $ \eta \gt 0$
there exists
$ \eta \gt 0$
there exists
![]() $M^{\prime}\,:\!=\,M^{\prime}(\beta, \eta )$
such that, for all
$M^{\prime}\,:\!=\,M^{\prime}(\beta, \eta )$
such that, for all
![]() $n \ge M^{\prime}$
we have
$n \ge M^{\prime}$
we have
Proof. Denote by
![]() $ \Lambda$
the subgroup of
$ \Lambda$
the subgroup of
![]() ${\mathbb{C}}^{\ast }$
generated by the eigenvalues of
${\mathbb{C}}^{\ast }$
generated by the eigenvalues of
![]() $A$
. Denote the subgroup of torsion elements in
$A$
. Denote the subgroup of torsion elements in
![]() $\Lambda$
by
$\Lambda$
by
![]() $\Lambda _2$
and let
$\Lambda _2$
and let
![]() $\Lambda _1 \simeq{\mathbb{Z}}^s$
be a subgroup of
$\Lambda _1 \simeq{\mathbb{Z}}^s$
be a subgroup of
![]() $ \Lambda$
such that
$ \Lambda$
such that
![]() $ \Lambda = \Lambda _1 \times \Lambda _2$
. First suppose that conditions (1) and (2) hold. These guarantee that
$ \Lambda = \Lambda _1 \times \Lambda _2$
. First suppose that conditions (1) and (2) hold. These guarantee that
![]() $\xi _A$
satisfies (1) and (2) of Theorem3.9. It follows that for all
$\xi _A$
satisfies (1) and (2) of Theorem3.9. It follows that for all
![]() $n \ge 1$
we have
$n \ge 1$
we have
Given
![]() $\eta \gt 0$
, we can find
$\eta \gt 0$
, we can find
![]() $M=M(\beta, \eta )$
such that for all
$M=M(\beta, \eta )$
such that for all
![]() $n \ge M$
we have
$n \ge M$
we have
This inequality together with the bound
![]() ${\textbf{m}}_1({\mathsf{T}}^n A) = \xi _A^{(n)}(1)$
establishes the claim. The second part of the statement (involving only assumption (1)) follows by a similar argument.
${\textbf{m}}_1({\mathsf{T}}^n A) = \xi _A^{(n)}(1)$
establishes the claim. The second part of the statement (involving only assumption (1)) follows by a similar argument.
4. Dynamics of the number of Jordan blocks under tensor powers
In this section, we will study the effect of amplification on matrices
![]() $A$
with
$A$
with
![]() ${\textbf{m}}_1(A)$
close to
${\textbf{m}}_1(A)$
close to
![]() $1$
. If
$1$
. If
![]() $A$
is such a matrix, for
$A$
is such a matrix, for
![]() $\rho (A-{\textrm{Id}})$
to be away from zero, a definite proportion of its Jordan blocks have to be of size at least
$\rho (A-{\textrm{Id}})$
to be away from zero, a definite proportion of its Jordan blocks have to be of size at least
![]() $2$
. We will show that under this condition, the proportion of the number of Jordan blocks to the size of matrix tends to zero. Moreover, we will give an effective bound for the number of iterations required to reduce this ratio below any given positive
$2$
. We will show that under this condition, the proportion of the number of Jordan blocks to the size of matrix tends to zero. Moreover, we will give an effective bound for the number of iterations required to reduce this ratio below any given positive
![]() $\epsilon$
.
$\epsilon$
.
We will denote by
![]() $J(\alpha, s)$
a Jordan block of size
$J(\alpha, s)$
a Jordan block of size
![]() $s$
with eigenvalue
$s$
with eigenvalue
![]() $ \alpha$
. Let
$ \alpha$
. Let
![]() $A$
be a
$A$
be a
![]() $d \times d$
complex matrix. We denote by
$d \times d$
complex matrix. We denote by
![]() ${\textbf{j}}(A)$
the number of Jordan blocks in the Jordan decomposition of
${\textbf{j}}(A)$
the number of Jordan blocks in the Jordan decomposition of
![]() $A$
divided by
$A$
divided by
![]() $d$
, hence
$d$
, hence
![]() $0 \le{\textbf{j}}(A) \le 1$
, with
$0 \le{\textbf{j}}(A) \le 1$
, with
![]() ${\textbf{j}}(A)=1$
iff
${\textbf{j}}(A)=1$
iff
![]() $A$
is diagonalizable. Define a sequence of matrices by setting
$A$
is diagonalizable. Define a sequence of matrices by setting
The main result of this section is the following theorem:
Theorem 4.1.
For every
![]() $ \gamma \gt 0$
and every
$ \gamma \gt 0$
and every
![]() $\eta \gt 0$
, there exists
$\eta \gt 0$
, there exists
![]() $N(\gamma, \eta )$
such that if
$N(\gamma, \eta )$
such that if
![]() ${\textbf{j}}(A) \le 1- \gamma$
and
${\textbf{j}}(A) \le 1- \gamma$
and
![]() $m\gt N(\gamma, \eta )$
then
$m\gt N(\gamma, \eta )$
then
![]() ${\textbf{j}}(A_m)\lt \eta$
, where
${\textbf{j}}(A_m)\lt \eta$
, where
![]() $A_m$
is defined by (4.1).
$A_m$
is defined by (4.1).
The proof of this theorem will involve estimating certain trigonometric integrals. Before reformulating the problem, we will recall some elementary facts.
Lemma 4.2 ([Reference Arzhantseva and Păunescu3, Reference Iima and Iwamatsu12], Lemma 5.7). For
![]() $m,n \in \mathbb{N}$
and
$m,n \in \mathbb{N}$
and
![]() $\alpha, \beta \in{\mathbb{C}}$
, we have
$\alpha, \beta \in{\mathbb{C}}$
, we have
Remark 4.3.
It follows from this lemma that the number of Jordan blocks of a given size in tensor powers of
![]() $A$
only depends on the size of Jordan blocks in
$A$
only depends on the size of Jordan blocks in
![]() $A$
and not on the corresponding eigenvalues. We will use this simple fact later.
$A$
and not on the corresponding eigenvalues. We will use this simple fact later.
In order to study the asymptotic behavior of the number of Jordan blocks in tensor powers of
![]() $A$
, it will be convenient to set up some algebraic framework. Let us denote by
$A$
, it will be convenient to set up some algebraic framework. Let us denote by
![]() $\mathcal{A}$
the set of all
$\mathcal{A}$
the set of all
![]() $n \times n$
matrices in the Jordan normal form with eigenvalue
$n \times n$
matrices in the Jordan normal form with eigenvalue
![]() $1$
on the diagonal, where
$1$
on the diagonal, where
![]() $n \ge 1$
varies over the set of all natural numbers. Note that if
$n \ge 1$
varies over the set of all natural numbers. Note that if
![]() $A \in{\mathcal{A}}$
, then
$A \in{\mathcal{A}}$
, then
![]() $A \otimes A \in{\mathcal{A}}$
. We will denote by
$A \otimes A \in{\mathcal{A}}$
. We will denote by
![]() $\mathcal{E}$
the set of all formal linear combinations
$\mathcal{E}$
the set of all formal linear combinations
![]() $ \sum _{ n \ge 1 } c_n \delta _n$
, where
$ \sum _{ n \ge 1 } c_n \delta _n$
, where
![]() $c_n \ge 0$
are integers and
$c_n \ge 0$
are integers and
![]() $c_n=0$
for all but finitely many values of
$c_n=0$
for all but finitely many values of
![]() $n$
. We equip
$n$
. We equip
![]() $\mathcal{E}$
with a binary operation defined by:
$\mathcal{E}$
with a binary operation defined by:
and extended linearly to
![]() ${\mathcal{T}}$
. Finally, for
${\mathcal{T}}$
. Finally, for
![]() $n \ge 1$
, consider the Laurent polynomial
$n \ge 1$
, consider the Laurent polynomial
and denote by
![]() $\mathcal{T}$
the set of all (finite) integer linear combinations of
$\mathcal{T}$
the set of all (finite) integer linear combinations of
![]() $\{ T_n(x)\}_{n \ge 1}$
. Note that since
$\{ T_n(x)\}_{n \ge 1}$
. Note that since
![]() $T_n$
have different degrees, they do form a basis for the
$T_n$
have different degrees, they do form a basis for the
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() $\mathcal{T}$
.
$\mathcal{T}$
.
Now we will construct natural maps between these objects that will allow us to encode the number and size of Jordan blocks in tensor powers of a matrix using polynomials
![]() $T_n(x)$
. First, define the map
$T_n(x)$
. First, define the map
![]() $\Delta \,:\,{\mathcal{A}} \to{\mathcal{E}}$
as follows. Let
$\Delta \,:\,{\mathcal{A}} \to{\mathcal{E}}$
as follows. Let
![]() $A \in{\mathcal{A}}$
be a matrix with
$A \in{\mathcal{A}}$
be a matrix with
![]() $c_i$
blocks of size
$c_i$
blocks of size
![]() $i$
for
$i$
for
![]() $i \ge 1$
. Then define
$i \ge 1$
. Then define
Note that
![]() $\Delta$
is a bijection. We now define
$\Delta$
is a bijection. We now define
![]() ${\Theta}\,:\,{\mathcal{E}} \to {\mathcal{T}}$
by
${\Theta}\,:\,{\mathcal{E}} \to {\mathcal{T}}$
by
 \begin{align*} {\Theta} \left ( \sum _{ n \ge 1 } c_n \delta _n \right ) = \sum _{ n \ge 1} c_n T_n(x). \end{align*}
\begin{align*} {\Theta} \left ( \sum _{ n \ge 1 } c_n \delta _n \right ) = \sum _{ n \ge 1} c_n T_n(x). \end{align*}
Lemma 4.4. The following hold:
-
1. For all
 $A_1, A_2 \in{\mathcal{A}}$
, we have
$A_1, A_2 \in{\mathcal{A}}$
, we have
 $\Delta (A_1 \otimes A_2)= \Delta (A_1) \ast \Delta (A_2).$
$\Delta (A_1 \otimes A_2)= \Delta (A_1) \ast \Delta (A_2).$
-
2. For all
 $x_1, x_2 \in{\mathcal{E}}$
, we have
$x_1, x_2 \in{\mathcal{E}}$
, we have
 ${\Theta} (x_1 \ast x_2)={\Theta}(x_1){\Theta}(x_2).$
${\Theta} (x_1 \ast x_2)={\Theta}(x_1){\Theta}(x_2).$
Proof. For (1), note that when
![]() $A_1$
consists of one block of size
$A_1$
consists of one block of size
![]() $m$
and
$m$
and
![]() $A_2$
is a block of size
$A_2$
is a block of size
![]() $n$
, this is a restatement of Lemma4.2. In this case, we have
$n$
, this is a restatement of Lemma4.2. In this case, we have
![]() $\Delta (A_1)= \delta _m$
and
$\Delta (A_1)= \delta _m$
and
![]() $\Delta (A_2)= \delta _n$
and
$\Delta (A_2)= \delta _n$
and
![]() $\Delta (A_1 \otimes A_2)$
is precisely the expression defined by
$\Delta (A_1 \otimes A_2)$
is precisely the expression defined by
![]() $\delta _m \ast \delta _n$
. It follows immediately from the definition of tensor product of matrices that the equality extends to all linear combinations with nonnegative integer coefficients. This establishes (1).
$\delta _m \ast \delta _n$
. It follows immediately from the definition of tensor product of matrices that the equality extends to all linear combinations with nonnegative integer coefficients. This establishes (1).
In order to prove (2), we will show that For
![]() $m,n \in \mathbb{N}$
, the following identity holds:
$m,n \in \mathbb{N}$
, the following identity holds:
Without loss of generality, assume that
![]() $m \le n$
. We will proceed by calculating the coefficient of
$m \le n$
. We will proceed by calculating the coefficient of
![]() $x^{r}$
for
$x^{r}$
for
![]() $ r \in{\mathbb{Z}}$
on both sides. Note that
$ r \in{\mathbb{Z}}$
on both sides. Note that
![]() $x^r$
appears on either the right-hand side or the left-hand side if and only if
$x^r$
appears on either the right-hand side or the left-hand side if and only if
![]() $ r = m+n - 2j$
for some
$ r = m+n - 2j$
for some
![]() $1 \le j \le m + n - 1$
. Since the coefficients of
$1 \le j \le m + n - 1$
. Since the coefficients of
![]() $x^j$
and
$x^j$
and
![]() $x^{-j}$
are equal, it suffices to consider the coefficient of
$x^{-j}$
are equal, it suffices to consider the coefficient of
![]() $x^r$
for nonnegative values of
$x^r$
for nonnegative values of
![]() $r$
, which correspond to
$r$
, which correspond to
![]() $0 \le j \le \frac{m+n}{2}$
. Fix
$0 \le j \le \frac{m+n}{2}$
. Fix
![]() $j$
in this range. It follows from the definition that
$j$
in this range. It follows from the definition that
![]() $x^{m+n - 2j}$
appears in
$x^{m+n - 2j}$
appears in
![]() $T_{m+n + 1 - 2k}$
if and only if
$T_{m+n + 1 - 2k}$
if and only if
![]() $m+n - 2k \ge m+n- 2j$
, or, equivalently if
$m+n - 2k \ge m+n- 2j$
, or, equivalently if
![]() $k \le j$
. Since we have
$k \le j$
. Since we have
![]() $ 1 \le k \le m$
, the term
$ 1 \le k \le m$
, the term
![]() $x^{m+n - 2j}$
appears exactly
$x^{m+n - 2j}$
appears exactly
![]() $\min ( j, m)$
times on the right-hand side. We now show that the coefficient of
$\min ( j, m)$
times on the right-hand side. We now show that the coefficient of
![]() $x^{m+n - 2j}$
on the left-hand side is the same. Note that the coefficient of the term
$x^{m+n - 2j}$
on the left-hand side is the same. Note that the coefficient of the term
![]() $x^r$
with
$x^r$
with
![]() $r=m+n-2j$
in
$r=m+n-2j$
in
![]() $T_m T_n$
is equal to the number of pairs
$T_m T_n$
is equal to the number of pairs
![]() $(j_1, j_2)$
such that
$(j_1, j_2)$
such that
![]() $x^{m + 1 - 2j_1}$
appears in
$x^{m + 1 - 2j_1}$
appears in
![]() $T_m$
and
$T_m$
and
![]() $x^{n + 1 - 2j_2}$
appears in
$x^{n + 1 - 2j_2}$
appears in
![]() $T_n$
where
$T_n$
where
![]() $(m+1-2j_1)+(n+1-2j_2)= m+n - 2j$
. These conditions can be reformulated as below:
$(m+1-2j_1)+(n+1-2j_2)= m+n - 2j$
. These conditions can be reformulated as below:
Let us distinguish two cases: first suppose that
![]() $j \le m$
. In this case, we choose
$j \le m$
. In this case, we choose
![]() $1 \le j_1 \le j$
and any such choice determines
$1 \le j_1 \le j$
and any such choice determines
![]() $j_2= j+1-j_1$
uniquely. Hence, the number of solutions to (4.2) is
$j_2= j+1-j_1$
uniquely. Hence, the number of solutions to (4.2) is
![]() $j$
. When
$j$
. When
![]() $j\gt m$
, then
$j\gt m$
, then
![]() $j_1$
is allowed to vary in the range
$j_1$
is allowed to vary in the range
![]() $1 \le j_1 \le m$
, and since
$1 \le j_1 \le m$
, and since
![]() $j \le \frac{m +n}{2}$
,
$j \le \frac{m +n}{2}$
,
![]() $j_2\,:\!=\,j+1-j_1$
will automatically satisfy the inequality
$j_2\,:\!=\,j+1-j_1$
will automatically satisfy the inequality
![]() $1 \le j_2 \le n$
. In conclusion, the coefficient of
$1 \le j_2 \le n$
. In conclusion, the coefficient of
![]() $x^{m+n-2j}$
on the left-hand side equals
$x^{m+n-2j}$
on the left-hand side equals
![]() $\min (j,m)$
as well. This proves the claim. It thus follows that
$\min (j,m)$
as well. This proves the claim. It thus follows that
![]() ${\Theta} (x_1 \ast x_2)={\Theta}(x_1){\Theta}(x_2)$
holds for
${\Theta} (x_1 \ast x_2)={\Theta}(x_1){\Theta}(x_2)$
holds for
![]() $x_1= \delta _m$
and
$x_1= \delta _m$
and
![]() $x_2= \delta _n$
. Since
$x_2= \delta _n$
. Since
![]() ${\Theta}$
is extended to
${\Theta}$
is extended to
![]() ${\mathcal{E}}$
by linearity, the general case follows immediately.
${\mathcal{E}}$
by linearity, the general case follows immediately.
Corollary 4.5.
Let
![]() $A$
be a
$A$
be a
![]() $d \times d$
invertible complex matrix. Let
$d \times d$
invertible complex matrix. Let
![]() $a_n^{(k)}$
be the multiplicity of Jordan blocks of size
$a_n^{(k)}$
be the multiplicity of Jordan blocks of size
![]() $n$
in the Jordan decomposition of
$n$
in the Jordan decomposition of
![]() $A_k$
:
$A_k$
:
 \begin{align*} \left ( \sum _{n \ge 1}a_n^{(1)}T_n(x) \right ) ^{2^{k-1}} = \sum _{n \ge 1} a_n^{(k)}T_n(x)\end{align*}
\begin{align*} \left ( \sum _{n \ge 1}a_n^{(1)}T_n(x) \right ) ^{2^{k-1}} = \sum _{n \ge 1} a_n^{(k)}T_n(x)\end{align*}
Proof. Using Remark 4.3, we can assume that all eigenvalues are equal to
![]() $1$
, or
$1$
, or
![]() $A \in{\mathcal{A}}$
. It is clear that
$A \in{\mathcal{A}}$
. It is clear that
![]() $\Delta (A)= \sum _{n \ge 1} a_n^{(1)} \delta _n$
. Part (1) of Lemma4.4 implies that
$\Delta (A)= \sum _{n \ge 1} a_n^{(1)} \delta _n$
. Part (1) of Lemma4.4 implies that
Since
![]() $\Delta (A_m)= \sum _{n \ge 1} a_n^{(m)} \delta _n$
, applying
$\Delta (A_m)= \sum _{n \ge 1} a_n^{(m)} \delta _n$
, applying
![]() ${\Theta}$
to the previous equation and using part (2) of Lemma4.4 give
${\Theta}$
to the previous equation and using part (2) of Lemma4.4 give
 \begin{align*} \sum _{n \ge 1} a_n^{(m)}T_n(x)= \left ( \sum _{n \ge 1} a_n^{(m-1)}T_n(x) \right )^2. \end{align*}
\begin{align*} \sum _{n \ge 1} a_n^{(m)}T_n(x)= \left ( \sum _{n \ge 1} a_n^{(m-1)}T_n(x) \right )^2. \end{align*}
The claim follows by induction on
![]() $m$
.
$m$
.
It will be more convenient to work with a trigonometric generating function. This is carried out in the next lemma.
Corollary 4.6. With the same notation as in Corollary 4.5 , set
For all
![]() $k \ge 1$
, we have
$k \ge 1$
, we have
Proof. Substituting
![]() $x = e^{i\theta }$
into
$x = e^{i\theta }$
into
![]() $T_n(x)$
yields
$T_n(x)$
yields
By applying Corollary4.5, we obtain
 \begin{align*} \left ( \underset {n \ge 1}{\sum } a_n^{(1)} \frac {\sin (n \theta )}{\sin (\theta )} \right ) ^{2^k} =\underset {n \ge 1}{\sum } a_n^{(k)} \frac {\sin (n \theta )}{\sin (\theta )}.\end{align*}
\begin{align*} \left ( \underset {n \ge 1}{\sum } a_n^{(1)} \frac {\sin (n \theta )}{\sin (\theta )} \right ) ^{2^k} =\underset {n \ge 1}{\sum } a_n^{(k)} \frac {\sin (n \theta )}{\sin (\theta )}.\end{align*}
Lemma 4.7.
Let
![]() $ 0 \le \epsilon \le 2$
and
$ 0 \le \epsilon \le 2$
and
![]() $2 \le n \in \mathbb{N}$
. For any real number
$2 \le n \in \mathbb{N}$
. For any real number
![]() $\theta$
such that
$\theta$
such that
![]() $|\cos (\theta )| \le 1 - \frac{\epsilon }{2}$
, we have
$|\cos (\theta )| \le 1 - \frac{\epsilon }{2}$
, we have
In particular,
![]() $|\frac{\sin (n\theta )}{\sin (\theta )}| \le n$
holds for all
$|\frac{\sin (n\theta )}{\sin (\theta )}| \le n$
holds for all
![]() $\theta \in \mathbb{R}$
.
$\theta \in \mathbb{R}$
.
Proof. We will proceed by induction on
![]() $n$
. For
$n$
. For
![]() $n = 2$
, the required inequality is obvious. Assume that it also holds for
$n = 2$
, the required inequality is obvious. Assume that it also holds for
![]() $n$
. One can write:
$n$
. One can write:
Thus, the required inequality holds for
![]() $n+1$
as well and we are done.
$n+1$
as well and we are done.
Corollary 4.8.
For all
![]() $\theta \in{\mathbb{R}}$
, we have
$\theta \in{\mathbb{R}}$
, we have
![]() $|P_1(\theta )| \le 1$
.
$|P_1(\theta )| \le 1$
.
Proof. This follows immediately from Lemma4.7 and the equality
![]() $ \sum _{ n \ge 1} n a_{n}^{(1)} = d$
.
$ \sum _{ n \ge 1} n a_{n}^{(1)} = d$
.
For a measurable subset
![]() $ B \subseteq{\mathbb{R}}$
, we denote by
$ B \subseteq{\mathbb{R}}$
, we denote by
![]() $\mu (B)$
is the Lebesgue measure of
$\mu (B)$
is the Lebesgue measure of
![]() $B$
. We will also denote the number of Jordan blocks of size
$B$
. We will also denote the number of Jordan blocks of size
![]() $1$
in
$1$
in
![]() $A$
by
$A$
by
![]() ${\textbf{j}}_1(A)$
.
${\textbf{j}}_1(A)$
.
Lemma 4.9.
Suppose that
![]() $A \in \textrm{GL}_d(\mathbb{C})$
is in the Jordan normal form. For
$A \in \textrm{GL}_d(\mathbb{C})$
is in the Jordan normal form. For
![]() $ \epsilon \gt 0$
, set
$ \epsilon \gt 0$
, set
Then
Proof. If all Jordan blocks are of size
![]() $1$
, then
$1$
, then
![]() ${\textbf{j}}_1(A)={\textbf{j}}(A)$
and the claim follow Corollary4.8. More generally, suppose
${\textbf{j}}_1(A)={\textbf{j}}(A)$
and the claim follow Corollary4.8. More generally, suppose
![]() $\cos (\theta ) \le 1 - \frac{\epsilon }{2}$
. Then it follows from Lemma4.7 that
$\cos (\theta ) \le 1 - \frac{\epsilon }{2}$
. Then it follows from Lemma4.7 that
This implies that
![]() $\theta \in B_{\epsilon }$
. Hence,
$\theta \in B_{\epsilon }$
. Hence,
where one can easily verify the last inequality for all
![]() $ \epsilon \in (0,1)$
.
$ \epsilon \in (0,1)$
.
Lemma 4.10.
Suppose
![]() $A \in \textrm{GL}_d({\mathbb{C}})$
is not unipotent, that is,
$A \in \textrm{GL}_d({\mathbb{C}})$
is not unipotent, that is,
![]() ${\textbf{j}}(A) \lt 1$
. Then we have
${\textbf{j}}(A) \lt 1$
. Then we have
![]() ${\textbf{j}}_1(A \otimes A ) \le{\textbf{j}}(A)^2$
.
${\textbf{j}}_1(A \otimes A ) \le{\textbf{j}}(A)^2$
.
Proof. First, notice that
![]() $J(\alpha, s) \bigotimes J(\beta, t)$
generates a Jordan block of size 1 if and only if the equation
$J(\alpha, s) \bigotimes J(\beta, t)$
generates a Jordan block of size 1 if and only if the equation
![]() $s+t + 1 - 2i = 1$
holds for some
$s+t + 1 - 2i = 1$
holds for some
![]() $1 \le i \le \min (s,t)$
. Equivalently
$1 \le i \le \min (s,t)$
. Equivalently
![]() $s+t = 2i$
for
$s+t = 2i$
for
![]() $1 \le i \le \min (s,t)$
. This equation has a solution if and only if
$1 \le i \le \min (s,t)$
. This equation has a solution if and only if
![]() $s = t$
. Therefore, we have
$s = t$
. Therefore, we have
Lemma 4.11.
For
![]() $a,b \in \mathbb{R}$
, define
$a,b \in \mathbb{R}$
, define
![]() $I_n(a,b) = \int _a^b \frac{\sin (n\theta )}{\sin (\theta )}d\theta$
. Then for all
$I_n(a,b) = \int _a^b \frac{\sin (n\theta )}{\sin (\theta )}d\theta$
. Then for all
![]() $n\in \mathbb{Z}$
we have
$n\in \mathbb{Z}$
we have
Proof. As
![]() $a, b$
are fixed during this proof, we write
$a, b$
are fixed during this proof, we write
![]() $I_n$
instead of
$I_n$
instead of
![]() $I_n(a,b)$
. First note that
$I_n(a,b)$
. First note that
Using
![]() $\cos (2\theta ) = \cos ^2(\theta ) - \sin ^2(\theta ) = 1 - 2 \sin ^2(\theta )$
, we can write
$\cos (2\theta ) = \cos ^2(\theta ) - \sin ^2(\theta ) = 1 - 2 \sin ^2(\theta )$
, we can write
 \begin{align*} I_{n+2} = &\int _a^b \frac{\sin (n\theta )(1 - 2 \sin ^2(\theta ))}{\sin (\theta )}d\theta + 2\int _a^b \cos (\theta ) \cos (n\theta ) d\theta \\ = & \int _a^b \frac{\sin (n\theta )}{\sin (\theta )}d\theta - 2 \int _a^b \sin (\theta )\sin (n\theta )d\theta + 2 \int _a^b \cos (\theta )\cos (n\theta ) d\theta \\ =& I_n +2 \int _a^b ({\cos} (n\theta )\cos (\theta ) - \sin (n\theta )\sin (\theta ) d\theta \\ =& I_n +2 \int _a^b \cos ((n+1)\theta )d\theta = I_n + \frac{2}{n+1}(\sin ((n+1)b)-\sin ((n+1)a). \end{align*}
\begin{align*} I_{n+2} = &\int _a^b \frac{\sin (n\theta )(1 - 2 \sin ^2(\theta ))}{\sin (\theta )}d\theta + 2\int _a^b \cos (\theta ) \cos (n\theta ) d\theta \\ = & \int _a^b \frac{\sin (n\theta )}{\sin (\theta )}d\theta - 2 \int _a^b \sin (\theta )\sin (n\theta )d\theta + 2 \int _a^b \cos (\theta )\cos (n\theta ) d\theta \\ =& I_n +2 \int _a^b ({\cos} (n\theta )\cos (\theta ) - \sin (n\theta )\sin (\theta ) d\theta \\ =& I_n +2 \int _a^b \cos ((n+1)\theta )d\theta = I_n + \frac{2}{n+1}(\sin ((n+1)b)-\sin ((n+1)a). \end{align*}
Corollary 4.12.
-
1. For all odd integers
 $n$
, we have
$n$
, we have
 \begin{align*}I_n(0, 2 \pi ) = 2\pi, \quad I_n( \frac {\pi }{2}, \frac {3\pi }{2}) = \pi .\end{align*}
\begin{align*}I_n(0, 2 \pi ) = 2\pi, \quad I_n( \frac {\pi }{2}, \frac {3\pi }{2}) = \pi .\end{align*}
-
2. For all even integers
 $n$
, we have
$n$
, we have
 \begin{align*} I_n(0, 2 \pi ) = 0, \quad I_n( \frac {\pi }{2}, \frac {3\pi }{2}) \ge 3. \end{align*}
\begin{align*} I_n(0, 2 \pi ) = 0, \quad I_n( \frac {\pi }{2}, \frac {3\pi }{2}) \ge 3. \end{align*}
Proof. A direct computation shows that
![]() $I_2(0, 2 \pi ) = 0$
and
$I_2(0, 2 \pi ) = 0$
and
![]() $I_1 (0, 2 \pi ) = 2\pi$
. Repeated application of Lemma4.11 extends this to all integers
$I_1 (0, 2 \pi ) = 2\pi$
. Repeated application of Lemma4.11 extends this to all integers
![]() $n$
. In a similar fashion, checking that
$n$
. In a similar fashion, checking that
![]() $I_1( \pi /2, 3 \pi /2) = \pi$
together with
$I_1( \pi /2, 3 \pi /2) = \pi$
together with
![]() $\sin ((n+1)\frac{\pi }{2})= \sin (3(n+1)\frac{\pi }{2}) = 0$
implies the claim for all odd values of
$\sin ((n+1)\frac{\pi }{2})= \sin (3(n+1)\frac{\pi }{2}) = 0$
implies the claim for all odd values of
![]() $n$
. The last inequality is easy to check for
$n$
. The last inequality is easy to check for
![]() $ n = 2, 4$
. For
$ n = 2, 4$
. For
![]() $ n \overset{4}{\equiv } 0$
, we have
$ n \overset{4}{\equiv } 0$
, we have
and for
![]() $n \overset{4}{\equiv } 2$
we can write
$n \overset{4}{\equiv } 2$
we can write
Corollary 4.13.
Let
![]() $A \in \textrm{GL}_d({\mathbb{C}})$
and
$A \in \textrm{GL}_d({\mathbb{C}})$
and
![]() $P_k(\theta )$
be defined as above. Then we have
$P_k(\theta )$
be defined as above. Then we have
Proof. Using Corollary4.6 and Corollary4.12, we can write
 \begin{align*} \int _0^{2 \pi }P_1(\theta )^{2^k} d\theta & \ge \int _{\frac{\pi }{2}}^{\frac{3\pi }{2}}P_1(\theta )^{2^k} d\theta = \sum _{n \ge 1} \frac{a_n^{(k)}}{d^{2^k}} \int _{\frac{\pi }{2}}^{\frac{3\pi }{2}} \frac{\sin (n\theta )}{\sin (\theta )}d\theta \\ & \ge 3 \sum _{n\ge 1}\frac{a_{2n}^{(k)}}{d^{2^k}} + 2 \pi \sum _{n\ge 1}\frac{a_{2n-1}^{(k)}}{d^{2^k}} \ge 3{\textbf{j}}(A_k). \end{align*}
\begin{align*} \int _0^{2 \pi }P_1(\theta )^{2^k} d\theta & \ge \int _{\frac{\pi }{2}}^{\frac{3\pi }{2}}P_1(\theta )^{2^k} d\theta = \sum _{n \ge 1} \frac{a_n^{(k)}}{d^{2^k}} \int _{\frac{\pi }{2}}^{\frac{3\pi }{2}} \frac{\sin (n\theta )}{\sin (\theta )}d\theta \\ & \ge 3 \sum _{n\ge 1}\frac{a_{2n}^{(k)}}{d^{2^k}} + 2 \pi \sum _{n\ge 1}\frac{a_{2n-1}^{(k)}}{d^{2^k}} \ge 3{\textbf{j}}(A_k). \end{align*}
Proof of Theorem 4.1. Let
![]() $A \in \textrm{GL}_d(\mathbb{C})$
be such that
$A \in \textrm{GL}_d(\mathbb{C})$
be such that
![]() ${\textbf{j}}(A) \le \frac{1}{t}$
, where
${\textbf{j}}(A) \le \frac{1}{t}$
, where
![]() $ t= (1-\gamma )^{-1}\gt 1$
. Let
$ t= (1-\gamma )^{-1}\gt 1$
. Let
![]() $\tau \lt \frac{1}{2} (\gamma /(1-\gamma ) )^2$
. We will find a function
$\tau \lt \frac{1}{2} (\gamma /(1-\gamma ) )^2$
. We will find a function
![]() $N_0(\gamma )$
such that for all
$N_0(\gamma )$
such that for all
![]() $m \ge N_0(\gamma )$
we have
$m \ge N_0(\gamma )$
we have
![]() ${\textbf{j}}(A_m) \le \frac{1}{t+\tau }$
. By repeating this process, we see that for all
${\textbf{j}}(A_m) \le \frac{1}{t+\tau }$
. By repeating this process, we see that for all
![]() $\ell \ge 1$
and all
$\ell \ge 1$
and all
![]() $m\ge \ell N_0(\gamma )$
we have
$m\ge \ell N_0(\gamma )$
we have
![]() ${\textbf{j}}(A_m) \le \frac{1}{t+ \ell \tau }$
. Let
${\textbf{j}}(A_m) \le \frac{1}{t+ \ell \tau }$
. Let
![]() $k$
be defined by
$k$
be defined by
![]() $k=\left \lceil ( \eta \tau )^{-1} \right \rceil +1$
so that
$k=\left \lceil ( \eta \tau )^{-1} \right \rceil +1$
so that
![]() $k\tau \gt \eta ^{-1}$
. It is clear that
$k\tau \gt \eta ^{-1}$
. It is clear that
will satisfy the required property.
If we have
![]() ${\textbf{j}}(A \otimes A) \le \frac{1}{t+\tau }$
we set
${\textbf{j}}(A \otimes A) \le \frac{1}{t+\tau }$
we set
![]() $m=2$
, and we are done. Note that Proposition 5.8. of [Reference Arzhantseva and Păunescu3], we have
$m=2$
, and we are done. Note that Proposition 5.8. of [Reference Arzhantseva and Păunescu3], we have
![]() ${\textbf{j}}(B \otimes B) \le{\textbf{j}}(B)$
for any matrix
${\textbf{j}}(B \otimes B) \le{\textbf{j}}(B)$
for any matrix
![]() $B$
. Since
$B$
. Since
![]() $A_{m+1} = A_m \otimes A_m$
, it follows that if we once the inequality holds for
$A_{m+1} = A_m \otimes A_m$
, it follows that if we once the inequality holds for
![]() $m=2$
then the same inequality will continue to hold for all
$m=2$
then the same inequality will continue to hold for all
![]() $m \ge 2$
. Set let us assume that
$m \ge 2$
. Set let us assume that
![]() ${\textbf{j}}(A \otimes A) \gt \frac{1}{t+\tau }$
. Then, we have
${\textbf{j}}(A \otimes A) \gt \frac{1}{t+\tau }$
. Then, we have
 \begin{align*} \int _0^{2\pi } P_1(\theta )^{2^k}d\theta =& \int _{B_{\epsilon }} |P_1(\theta )|^{2^k}d\theta + \int _{[0,2\pi ] \setminus B_{\epsilon }} |P_1(\theta )|^{2^k} d\theta \\ \le & \int _{B_{\epsilon }} (1 - \epsilon ({\textbf{j}}(A) -{\textbf{j}}_1(A)))^{2^k}d\theta + \int _{[0,2\pi ] \setminus B_{\epsilon }} d\theta \\ \le & 2\pi (1 - \epsilon ({\textbf{j}}(A) -{\textbf{j}}_1(A)))^{2^k} + \mu ([0,2\pi ]\setminus B_{\epsilon }) \\ \le & 2\pi \left ( 1 - \frac{1}{t+\tau }\epsilon + \frac{1}{t^2}\epsilon \right ) ^{2^k} + 8 \sqrt{ \epsilon } \end{align*}
\begin{align*} \int _0^{2\pi } P_1(\theta )^{2^k}d\theta =& \int _{B_{\epsilon }} |P_1(\theta )|^{2^k}d\theta + \int _{[0,2\pi ] \setminus B_{\epsilon }} |P_1(\theta )|^{2^k} d\theta \\ \le & \int _{B_{\epsilon }} (1 - \epsilon ({\textbf{j}}(A) -{\textbf{j}}_1(A)))^{2^k}d\theta + \int _{[0,2\pi ] \setminus B_{\epsilon }} d\theta \\ \le & 2\pi (1 - \epsilon ({\textbf{j}}(A) -{\textbf{j}}_1(A)))^{2^k} + \mu ([0,2\pi ]\setminus B_{\epsilon }) \\ \le & 2\pi \left ( 1 - \frac{1}{t+\tau }\epsilon + \frac{1}{t^2}\epsilon \right ) ^{2^k} + 8 \sqrt{ \epsilon } \end{align*}
It follows from the choice of
![]() $\tau$
that
$\tau$
that
![]() $ \frac{1}{t+ \tau }\gt \frac{2}{t^2}$
. This implies that
$ \frac{1}{t+ \tau }\gt \frac{2}{t^2}$
. This implies that
Set
![]() $ \epsilon = \frac{1}{2^{8}(t+\tau )^2}\lt \frac{1}{2t^2}$
so that the second term is bounded by
$ \epsilon = \frac{1}{2^{8}(t+\tau )^2}\lt \frac{1}{2t^2}$
so that the second term is bounded by
![]() $ \frac{1}{2(t+\tau )}$
. Now, let
$ \frac{1}{2(t+\tau )}$
. Now, let
![]() $N_0(\gamma )$
be the smallest positive integer
$N_0(\gamma )$
be the smallest positive integer
![]() $m$
such that
$m$
such that
It is clear that for this value of
![]() $m$
, we have
$m$
, we have
The claim will now follow from Corollary4.13.
5. Proof of TheoremA
In this section, we will prove parts (1) and (2) of TheoremA. The proof crucially depends on the inequality
from Lemma2.1. Let
![]() $G$
be a torsion-free group and
$G$
be a torsion-free group and
![]() $S$
a finite subset of
$S$
a finite subset of
![]() $G$
with
$G$
with
![]() $e \not \in S$
. We will show that for every
$e \not \in S$
. We will show that for every
![]() $ \epsilon \gt 0$
and
$ \epsilon \gt 0$
and
![]() $\delta \gt 0$
an
$\delta \gt 0$
an
![]() $(S, \delta, 1- \epsilon )$
-map into
$(S, \delta, 1- \epsilon )$
-map into
![]() $\textrm{GL}_D({\mathbb{C}})$
exists. Let
$\textrm{GL}_D({\mathbb{C}})$
exists. Let
![]() $r= \lfloor 2/ \epsilon \rfloor +1$
and set
$r= \lfloor 2/ \epsilon \rfloor +1$
and set
![]() $ \overline{S} = \{ g^{n}\,:\, g \in S, 1 \le n \le r! \}$
. By Lemma2.4, there exists an
$ \overline{S} = \{ g^{n}\,:\, g \in S, 1 \le n \le r! \}$
. By Lemma2.4, there exists an
![]() $(\overline{S}, \delta _0, 0.23)$
-map
$(\overline{S}, \delta _0, 0.23)$
-map
![]() $\phi _0$
such that
$\phi _0$
such that
for all
![]() $g \in \overline{S}$
. Here,
$g \in \overline{S}$
. Here,
![]() $\delta _0$
is a small quantity whose values will be determined later. We will find
$\delta _0$
is a small quantity whose values will be determined later. We will find
![]() $N$
such that for
$N$
such that for
![]() $n \gt N$
, the tensor power
$n \gt N$
, the tensor power
![]() ${\mathsf{T}}^{2^n} \phi _0$
is an
${\mathsf{T}}^{2^n} \phi _0$
is an
![]() $(S, \delta, 1- \epsilon )$
-map. Fix some
$(S, \delta, 1- \epsilon )$
-map. Fix some
![]() $g \in S$
. We will consider two different cases.
$g \in S$
. We will consider two different cases.
Case (1): Suppose that
![]() ${\textbf{j}}(\phi _0(g^{r!}))\lt 0.99$
. Then it follows from Lemma2.5 and Theorem4.1 that for
${\textbf{j}}(\phi _0(g^{r!}))\lt 0.99$
. Then it follows from Lemma2.5 and Theorem4.1 that for
![]() $m = N(0.01, \epsilon /2)$
we have
$m = N(0.01, \epsilon /2)$
we have
![]() ${\textbf{j}}({\mathsf{T}}^{2^m}\phi _0(g^{r!})) \le \epsilon$
. This implies that
${\textbf{j}}({\mathsf{T}}^{2^m}\phi _0(g^{r!})) \le \epsilon$
. This implies that
On the other hand, using Lemma2.5, we have
as soon as
![]() $\delta _0 \lt \epsilon / 2^{m+1}r!$
. From here, we have by the triangle inequality that
$\delta _0 \lt \epsilon / 2^{m+1}r!$
. From here, we have by the triangle inequality that
Note that if
![]() $B$
is any matrix and
$B$
is any matrix and
![]() $m\ge 1$
, then
$m\ge 1$
, then
![]() $\ker (B-I) \subseteq \ker (B^m-I)$
. In other words, we have
$\ker (B-I) \subseteq \ker (B^m-I)$
. In other words, we have
![]() $\rho (B, I) \ge \rho (B^m, I)$
. This implies that
$\rho (B, I) \ge \rho (B^m, I)$
. This implies that
![]() $\rho ({\mathsf{T}}^{2^m}\phi _0(g),{\textrm{Id}}) \ge 1- \epsilon .$
$\rho ({\mathsf{T}}^{2^m}\phi _0(g),{\textrm{Id}}) \ge 1- \epsilon .$
Case (2): Suppose that
![]() ${\textbf{j}}(\phi _0(g^{r!})) \ge 0.99$
. The proportion of blocks corresponding to eigenvalue
${\textbf{j}}(\phi _0(g^{r!})) \ge 0.99$
. The proportion of blocks corresponding to eigenvalue
![]() $1$
is
$1$
is
![]() ${\textbf{j}}_1(\phi _0(g^{r!}))$
, and the proportion of other blocks is at most
${\textbf{j}}_1(\phi _0(g^{r!}))$
, and the proportion of other blocks is at most
![]() $ 1- \xi _{ \phi _0(g^{r!})}(1).$
This implies that
$ 1- \xi _{ \phi _0(g^{r!})}(1).$
This implies that
Since
![]() ${\textbf{j}}_1(\phi _0(g^{r!}) ) = 1- \rho ( \phi _0(g^{r!}),{\textrm{Id}}) \le 1-0.23= 0.77$
, we obtain
${\textbf{j}}_1(\phi _0(g^{r!}) ) = 1- \rho ( \phi _0(g^{r!}),{\textrm{Id}}) \le 1-0.23= 0.77$
, we obtain
Also note that
It thus follows that
as long as
![]() $\delta _0\lt \frac{1}{100 \, r!}$
. If
$\delta _0\lt \frac{1}{100 \, r!}$
. If
![]() $D$
denotes the size of the matrix
$D$
denotes the size of the matrix
![]() $\phi _0(g)^{r!}$
, then we know that
$\phi _0(g)^{r!}$
, then we know that
![]() $\phi _0(g)^{r!}$
has at least
$\phi _0(g)^{r!}$
has at least
![]() $0.99D$
Jordan blocks. If
$0.99D$
Jordan blocks. If
![]() $k$
denotes the number of blocks corresponding to the eigenvalue
$k$
denotes the number of blocks corresponding to the eigenvalue
![]() $1$
, then noting that each such block contributes a one-dimensional subspace to
$1$
, then noting that each such block contributes a one-dimensional subspace to
![]() $\ker (\phi _0(g)^{r!}-I)$
, we deduce that
$\ker (\phi _0(g)^{r!}-I)$
, we deduce that
![]() $k \le 0.21D$
. Note that by the assumption
$k \le 0.21D$
. Note that by the assumption
![]() ${\textbf{j}}(\phi _0(g^{r!})) \ge 0.99$
, that is,
${\textbf{j}}(\phi _0(g^{r!})) \ge 0.99$
, that is,
![]() $\phi _0(g^{r!})$
has at least
$\phi _0(g^{r!})$
has at least
![]() $ 0.99D$
Jordan blocks. This means that the total number of eigenvalues (with multiplicity) coming from blocks of size at least
$ 0.99D$
Jordan blocks. This means that the total number of eigenvalues (with multiplicity) coming from blocks of size at least
![]() $2$
is at most
$2$
is at most
![]() $0.01D$
. Hence, the multiplicity of
$0.01D$
. Hence, the multiplicity of
![]() $1$
as an eigenvalue of
$1$
as an eigenvalue of
![]() $ \phi _0(g^{r!})$
is at most
$ \phi _0(g^{r!})$
is at most
![]() $ 0.23D$
.
$ 0.23D$
.
Note that if
![]() $ ( \lambda _i)_{1 \le i \le d}$
are eigenvalues of
$ ( \lambda _i)_{1 \le i \le d}$
are eigenvalues of
![]() $\rho (g)$
, then
$\rho (g)$
, then
![]() $ ( \lambda _i^{r!})$
are eigenvalues of
$ ( \lambda _i^{r!})$
are eigenvalues of
![]() $\rho (g)^{r!}$
. If
$\rho (g)^{r!}$
. If
![]() $ \lambda _i^k=1$
for some
$ \lambda _i^k=1$
for some
![]() $ 1 \le k \le r$
, then
$ 1 \le k \le r$
, then
![]() $ \lambda _i^{r!}=1$
. This implies that
$ \lambda _i^{r!}=1$
. This implies that
for
![]() $\beta = 0.23$
. Applying Lemma3.10 it follows that for
$\beta = 0.23$
. Applying Lemma3.10 it follows that for
![]() $m\gt M(\beta, r, 1/r)$
, we have
$m\gt M(\beta, r, 1/r)$
, we have
It follows that
![]() $ \rho ({\mathsf{T}}^m \phi _0(g)),{\textrm{Id}} ) \ge 1- \epsilon$
. In conclusion, for
$ \rho ({\mathsf{T}}^m \phi _0(g)),{\textrm{Id}} ) \ge 1- \epsilon$
. In conclusion, for
![]() $m\gt \max ( M(\beta, r, 1/r), N(0.01, \epsilon ))$
, we have
$m\gt \max ( M(\beta, r, 1/r), N(0.01, \epsilon ))$
, we have
for all
![]() $g \in S$
. Note, however, that
$g \in S$
. Note, however, that
Hence, we need to choose
![]() $\delta _0\lt \min\!\left ( \frac{1}{100 \, r!}, \frac{\delta }{2^N}, \frac{\epsilon }{2^{m+1}r!}\right)$
with
$\delta _0\lt \min\!\left ( \frac{1}{100 \, r!}, \frac{\delta }{2^N}, \frac{\epsilon }{2^{m+1}r!}\right)$
with
![]() $N= \max ( M(\beta, r, 1/r), N(0.01, \epsilon ))$
for the desired inequality to hold. The proof of (2) is similar and somewhat simpler. This time, we work directly with
$N= \max ( M(\beta, r, 1/r), N(0.01, \epsilon ))$
for the desired inequality to hold. The proof of (2) is similar and somewhat simpler. This time, we work directly with
![]() $S$
(and not
$S$
(and not
![]() $ \overline{S}$
) and apply part (2) of Corollary3.10.
$ \overline{S}$
) and apply part (2) of Corollary3.10.
Remark 5.1.
One can deduce from Theorem A the more general version in which the field of complex numbers is replaced by an arbitrary field of characteristic zero
![]() $F$
. In order to see this, suppose that
$F$
. In order to see this, suppose that
![]() $G$
is
$G$
is
![]() $\kappa$
-linear sofic over
$\kappa$
-linear sofic over
![]() $F$
. This implies that for every finite set
$F$
. This implies that for every finite set
![]() $S \subseteq G$
and every
$S \subseteq G$
and every
![]() $ \delta \gt 0$
and every
$ \delta \gt 0$
and every
![]() $0 \le \kappa ^{\prime} \lt \kappa$
, there exists
$0 \le \kappa ^{\prime} \lt \kappa$
, there exists
![]() $d \ge 1$
and a map
$d \ge 1$
and a map
![]() $\phi \,:\, S \to \textrm{GL}_d(F)$
that satisfies properties
$\phi \,:\, S \to \textrm{GL}_d(F)$
that satisfies properties
![]() $(AH)$
and
$(AH)$
and
![]() $(D)$
of Definition 1.1. Since
$(D)$
of Definition 1.1. Since
![]() $S$
is finite, one can replace
$S$
is finite, one can replace
![]() $F$
by a finitely generated subfield
$F$
by a finitely generated subfield
![]() $F^{\prime}$
of
$F^{\prime}$
of
![]() $F$
(depending on
$F$
(depending on
![]() $S$
). However, every such field is isomorphic to a subfield of
$S$
). However, every such field is isomorphic to a subfield of
![]() $\mathbb{C}$
. This implies that the arguments given above show that one can amplify
$\mathbb{C}$
. This implies that the arguments given above show that one can amplify
![]() $\phi$
. Now, note that all the amplifications are constructed via the functorial operations describe in 2.1. This implies that the image remains in
$\phi$
. Now, note that all the amplifications are constructed via the functorial operations describe in 2.1. This implies that the image remains in
![]() $\textrm{GL}_m(F)$
for some
$\textrm{GL}_m(F)$
for some
![]() $m \ge 1$
, from which the claim follows.
$m \ge 1$
, from which the claim follows.
6. Stability and the proof of TheoremsB and C
In this section, we will prove TheoremB. Along the way, we will also address the more general question of determining
![]() $\kappa (G)$
when
$\kappa (G)$
when
![]() $G$
is an arbitrary finite group. As a byproduct, we will show that the bound
$G$
is an arbitrary finite group. As a byproduct, we will show that the bound
![]() $\kappa (G) \ge 1/2$
cannot be improved for finite groups. This will be carried out through computation of
$\kappa (G) \ge 1/2$
cannot be improved for finite groups. This will be carried out through computation of
![]() $\kappa ({\mathbb{Z}}_p^n)$
, from which it will follow that as
$\kappa ({\mathbb{Z}}_p^n)$
, from which it will follow that as
![]() $n \to \infty$
$n \to \infty$
The special case of
![]() $p=2$
will then prove the claim. One ingredient of the proof is the notion of stability for linear sofic representations. Studying stability for different modes of metric approximation has been an active area of research in the last decade. Stability of finite groups for sofic approximation was proved by Glebsky and Rivera [Reference Glebsky and Rivera10]. Arzhantseva and Păunescu [Reference Arzhantseva and Paunescu2] showed that abelian groups are stable for sofic approximation. This result was generalized by Becker, Lubotzky, and Thom [Reference Becker, Lubotzky and Thom5] who established a criterion in terms of invariant random subgroups for (sofic) stability in the class of amenable groups. For other related results, see for instance [Reference Arzhantseva and Paunescu2, Reference De Chiffre, Glebsky, Lubotzky and Thom6, Reference Becker, Lubotzky and Thom5, Reference Becker and Lubotzky4] and references therein. Some progress toward proving the stability of
$p=2$
will then prove the claim. One ingredient of the proof is the notion of stability for linear sofic representations. Studying stability for different modes of metric approximation has been an active area of research in the last decade. Stability of finite groups for sofic approximation was proved by Glebsky and Rivera [Reference Glebsky and Rivera10]. Arzhantseva and Păunescu [Reference Arzhantseva and Paunescu2] showed that abelian groups are stable for sofic approximation. This result was generalized by Becker, Lubotzky, and Thom [Reference Becker, Lubotzky and Thom5] who established a criterion in terms of invariant random subgroups for (sofic) stability in the class of amenable groups. For other related results, see for instance [Reference Arzhantseva and Paunescu2, Reference De Chiffre, Glebsky, Lubotzky and Thom6, Reference Becker, Lubotzky and Thom5, Reference Becker and Lubotzky4] and references therein. Some progress toward proving the stability of
![]() ${\mathbb{Z}}^2$
in linear sofic approximation has been made in [Reference Elek and Grabowski7]. Our first theorem establishes the stability of finite groups in the normalized rank metric. Before stating and proving this result, we will need a simple fact from linear algebra.
${\mathbb{Z}}^2$
in linear sofic approximation has been made in [Reference Elek and Grabowski7]. Our first theorem establishes the stability of finite groups in the normalized rank metric. Before stating and proving this result, we will need a simple fact from linear algebra.
Lemma 6.1.
Suppose that
![]() $W_1, \dots, W_i$
are subspaces of
$W_1, \dots, W_i$
are subspaces of
![]() ${\mathbb{C}}^d$
with
${\mathbb{C}}^d$
with
![]() $\dim (W_r) \ge d( 1- \epsilon )$
, for
$\dim (W_r) \ge d( 1- \epsilon )$
, for
![]() $ 1 \le i \le r$
. Then, we have
$ 1 \le i \le r$
. Then, we have
![]() $\dim (\cap _{i=1}^r W_{i} )\ge d(1- r \epsilon )$
.
$\dim (\cap _{i=1}^r W_{i} )\ge d(1- r \epsilon )$
.
Proof. We will proceed by induction on
![]() $r$
. For
$r$
. For
![]() $r=1$
there is nothing to prove. Assume that the claim is shown for
$r=1$
there is nothing to prove. Assume that the claim is shown for
![]() $r-1$
. Then, using the induction hypothesis, one can write
$r-1$
. Then, using the induction hypothesis, one can write
 \begin{align*} \dim (\cap _{i=1}^r W_{i} ) &= \dim ( \cap _{i=1}^{r-1} W_{i} ) + \dim (W_{r}) - \dim (\cap _{i=1}^{k-1} W_{i} + W_{r}) \\ & \ge d ( 1 - (r-1) \epsilon ) + d ( 1 - \epsilon ) - d \\ & = d(1 - r \epsilon ) \end{align*}
\begin{align*} \dim (\cap _{i=1}^r W_{i} ) &= \dim ( \cap _{i=1}^{r-1} W_{i} ) + \dim (W_{r}) - \dim (\cap _{i=1}^{k-1} W_{i} + W_{r}) \\ & \ge d ( 1 - (r-1) \epsilon ) + d ( 1 - \epsilon ) - d \\ & = d(1 - r \epsilon ) \end{align*}
Proposition 6.2.
Let
![]() $G$
be a finite group,
$G$
be a finite group,
![]() $ \epsilon \gt 0$
and
$ \epsilon \gt 0$
and
![]() $\varphi \,:\, G \to \textrm{GL}_d(\mathbb{C})$
is such that for all
$\varphi \,:\, G \to \textrm{GL}_d(\mathbb{C})$
is such that for all
![]() $g,h \in G$
we have
$g,h \in G$
we have
Then there exists a representation
![]() $\psi \,:\, G \to \textrm{GL}_d(\mathbb{C})$
such that for every
$\psi \,:\, G \to \textrm{GL}_d(\mathbb{C})$
such that for every
![]() $g \in G$
we have
$g \in G$
we have
Proof. For
![]() $g, h \in G$
, consider the subspace defined by
$g, h \in G$
, consider the subspace defined by
and set
![]() $W = \cap _{g,h \in G} W_{g,h}$
. We claim that
$W = \cap _{g,h \in G} W_{g,h}$
. We claim that
![]() $W$
is a
$W$
is a
![]() $G$
-invariant subspace of
$G$
-invariant subspace of
![]() ${\mathbb{C}}^d$
. Assume that
${\mathbb{C}}^d$
. Assume that
![]() $w_1$
is an arbitrary element of
$w_1$
is an arbitrary element of
![]() $W$
. It suffices to prove that for any
$W$
. It suffices to prove that for any
![]() $k \in G$
,
$k \in G$
,
![]() $\varphi (k)w_1$
is an element of
$\varphi (k)w_1$
is an element of
![]() $W$
as well. Since
$W$
as well. Since
![]() $w_1 \in W$
, we can write
$w_1 \in W$
, we can write
 \begin{align*} \varphi (g)\varphi (h)\big (\varphi (k)w_1\big ) = & \varphi (g) \big ( \varphi (h)\varphi (k)w_1\big ) \\ = &\varphi (g)\varphi (hk)w_1 = \varphi (ghk)w_1 \\ = & \varphi (gh)(\varphi (k) w_1) \end{align*}
\begin{align*} \varphi (g)\varphi (h)\big (\varphi (k)w_1\big ) = & \varphi (g) \big ( \varphi (h)\varphi (k)w_1\big ) \\ = &\varphi (g)\varphi (hk)w_1 = \varphi (ghk)w_1 \\ = & \varphi (gh)(\varphi (k) w_1) \end{align*}
This implies that
![]() $ \varphi (k)w_1 \in W_{g,h}$
, proving the claim. In summary,
$ \varphi (k)w_1 \in W_{g,h}$
, proving the claim. In summary,
![]() $W \le{\mathbb{C}}^d$
is a
$W \le{\mathbb{C}}^d$
is a
![]() $G$
-invariant subspace with the property that the restriction of
$G$
-invariant subspace with the property that the restriction of
![]() $\psi (g)$
to
$\psi (g)$
to
![]() $W$
is a representation of
$W$
is a representation of
![]() $G$
. Let
$G$
. Let
![]() $W^{\perp }$
be a subspace complement of
$W^{\perp }$
be a subspace complement of
![]() $W$
. For
$W$
. For
![]() $g \in G$
, define
$g \in G$
, define
![]() $\psi (g) \in \textrm{GL}_d({\mathbb{C}})$
to be the linear transformation that acts on
$\psi (g) \in \textrm{GL}_d({\mathbb{C}})$
to be the linear transformation that acts on
![]() $W$
via
$W$
via
![]() $\varphi$
and on
$\varphi$
and on
![]() $W^{\perp }$
by identity. It is clear that
$W^{\perp }$
by identity. It is clear that
![]() $\psi$
defined in this way is a
$\psi$
defined in this way is a
![]() $G$
-representations. Finally, for every
$G$
-representations. Finally, for every
![]() $g \in G$
we have
$g \in G$
we have
This finishes the proof.
Remark 6.3.
It is noteworthy that our proof establishes stability with a linear estimate. However, the constant depends on
![]() $|G|$
. It would be interesting to see if this dependency can be relaxed for certain families of groups.
$|G|$
. It would be interesting to see if this dependency can be relaxed for certain families of groups.
We will start by providing a simple description of irreducible representations of the group
![]() $G={\mathbb{Z}}_p^n$
. We start by setting some notation. Recall that
$G={\mathbb{Z}}_p^n$
. We start by setting some notation. Recall that
![]() $\textrm{e}_p\,:\,{\mathbb{Z}}_p \to{\mathbb{C}}^\ast$
denotes the character
$\textrm{e}_p\,:\,{\mathbb{Z}}_p \to{\mathbb{C}}^\ast$
denotes the character
![]() $\textrm{e}_p(x)= \exp (2\pi i x/p)$
. Also, for
$\textrm{e}_p(x)= \exp (2\pi i x/p)$
. Also, for
![]() $x= (x_1, \dots, x_n ), y= ( y_1, \dots, y_n) \in{\mathbb{Z}}_p^n$
, we write
$x= (x_1, \dots, x_n ), y= ( y_1, \dots, y_n) \in{\mathbb{Z}}_p^n$
, we write
![]() $x \cdot y = \sum _{ i =1}^{n} x_i y_i$
. For each
$x \cdot y = \sum _{ i =1}^{n} x_i y_i$
. For each
![]() $a \in{\mathbb{Z}}_p^n$
, define
$a \in{\mathbb{Z}}_p^n$
, define
![]() $\phi _a\,:\,{\mathbb{Z}}_p^n \to{\mathbb{C}}^\ast$
by
$\phi _a\,:\,{\mathbb{Z}}_p^n \to{\mathbb{C}}^\ast$
by
![]() $\phi _a(x)= \textrm{e}_p( a \cdot x)$
. It is a well known [Reference Luong14] fact that
$\phi _a(x)= \textrm{e}_p( a \cdot x)$
. It is a well known [Reference Luong14] fact that
![]() $\phi _a$
, as
$\phi _a$
, as
![]() $a \in{\mathbb{Z}}_p^n$
constitute all irreducible representations of
$a \in{\mathbb{Z}}_p^n$
constitute all irreducible representations of
![]() ${\mathbb{Z}}_p^n$
.
${\mathbb{Z}}_p^n$
.
Proposition 6.4.
For
![]() $n\ge 2$
, we have
$n\ge 2$
, we have
Proof. Let
denote the direct sum of all
![]() $\phi _a$
other than the trivial representation
$\phi _a$
other than the trivial representation
![]() $\phi _0$
. One can regard
$\phi _0$
. One can regard
![]() $\phi (x)$
as a diagonal matrix of size
$\phi (x)$
as a diagonal matrix of size
![]() $p^n-1$
with diagonal entries
$p^n-1$
with diagonal entries
![]() $\phi _a(x)$
for nonzero
$\phi _a(x)$
for nonzero
![]() $a \in{\mathbb{Z}}_p^n$
. We claim that for every
$a \in{\mathbb{Z}}_p^n$
. We claim that for every
![]() $x \neq 0$
, the set of
$x \neq 0$
, the set of
![]() $\{ a \in{\mathbb{Z}}_p^n \setminus \{ 0 \}\,:\, \phi _a(x)=1 \}$
has cardinality
$\{ a \in{\mathbb{Z}}_p^n \setminus \{ 0 \}\,:\, \phi _a(x)=1 \}$
has cardinality
![]() $p^{n-1}$
. In fact, the condition
$p^{n-1}$
. In fact, the condition
![]() $\phi _a(x)=1$
corresponds to the equation
$\phi _a(x)=1$
corresponds to the equation
![]() $ \sum _{ i =1}^{n } a_i x_i=0$
for
$ \sum _{ i =1}^{n } a_i x_i=0$
for
![]() $a$
which has exactly
$a$
which has exactly
![]() $p^{n-1}-1$
nonzero solutions. Hence,
$p^{n-1}-1$
nonzero solutions. Hence,
![]() $ \textrm{rank} \phi (x)= p^n-p^{n-1}$
, from which it follows that
$ \textrm{rank} \phi (x)= p^n-p^{n-1}$
, from which it follows that
To prove the reverse inequality, we first suppose
![]() $\psi$
is a
$\psi$
is a
![]() $d$
-dimensional representation of
$d$
-dimensional representation of
![]() $G$
. Decompose
$G$
. Decompose
![]() $\psi$
into a direct sum of irreducible representations
$\psi$
into a direct sum of irreducible representations
![]() $ \phi _a$
and denote the multiplicity of
$ \phi _a$
and denote the multiplicity of
![]() $\phi _a$
by
$\phi _a$
by
![]() $c_a$
:
$c_a$
:
Set
and write
![]() $B(x)= \{ a \in{\mathbb{Z}}_p^n\,:\, \phi _a(x) \neq 1\}$
. This implies that for every nonzero
$B(x)= \{ a \in{\mathbb{Z}}_p^n\,:\, \phi _a(x) \neq 1\}$
. This implies that for every nonzero
![]() $x\in{\mathbb{Z}}_p^n$
, we have
$x\in{\mathbb{Z}}_p^n$
, we have
Without loss of generality, we can assume that
![]() $c_0=0$
, since by removing the trivial representation the value of
$c_0=0$
, since by removing the trivial representation the value of
![]() $\beta$
can only increase. Note also that for every
$\beta$
can only increase. Note also that for every
![]() $a \neq 0$
, there are exactly
$a \neq 0$
, there are exactly
![]() $p^{n} - p^{n-1}$
elements
$p^{n} - p^{n-1}$
elements
![]() $x \in{\mathbb{Z}}_p^n$
with
$x \in{\mathbb{Z}}_p^n$
with
![]() $a \in B(x)$
. This implies that
$a \in B(x)$
. This implies that
This together with (6.1) implies that
![]() $ \beta \le \frac{p^n- p^{n-1}}{p^n-1}$
.
$ \beta \le \frac{p^n- p^{n-1}}{p^n-1}$
.
Now, to finish the proof assume that
![]() $\beta \,:\!=\, \kappa ({\mathbb{Z}}_p^n)\gt \frac{p^n- p^{n-1}}{p^n-1}.$
Choose
$\beta \,:\!=\, \kappa ({\mathbb{Z}}_p^n)\gt \frac{p^n- p^{n-1}}{p^n-1}.$
Choose
![]() $ \epsilon \gt 0$
such that
$ \epsilon \gt 0$
such that
![]() $ p^{2n} \epsilon \lt \beta - \frac{p^n- p^{n-1}}{p^n-1}$
. Let
$ p^{2n} \epsilon \lt \beta - \frac{p^n- p^{n-1}}{p^n-1}$
. Let
![]() $ \varphi \,:\,{\mathbb{Z}}_p^n \to \textrm{GL}_d({\mathbb{C}})$
be such that
$ \varphi \,:\,{\mathbb{Z}}_p^n \to \textrm{GL}_d({\mathbb{C}})$
be such that
holds for all
![]() $x, y \in{\mathbb{Z}}_p^n$
. Use Lemma6.2 to find a representation
$x, y \in{\mathbb{Z}}_p^n$
. Use Lemma6.2 to find a representation
![]() $\psi \,:\,{\mathbb{Z}}_p^n \to \textrm{GL}_d({\mathbb{C}})$
such that
$\psi \,:\,{\mathbb{Z}}_p^n \to \textrm{GL}_d({\mathbb{C}})$
such that
![]() $ \rho ( \varphi (x), \psi (x) ) \lt p^{2n} \epsilon$
. Since
$ \rho ( \varphi (x), \psi (x) ) \lt p^{2n} \epsilon$
. Since
![]() $ \rho ( \varphi (x),{\textrm{Id}}) \ge \beta$
for all nonzero
$ \rho ( \varphi (x),{\textrm{Id}}) \ge \beta$
for all nonzero
![]() $x \in{\mathbb{Z}}_p^n$
, it follows that for all
$x \in{\mathbb{Z}}_p^n$
, it follows that for all
![]() $x \neq 0$
$x \neq 0$
This is a contradiction.
Corollary 6.5.
The best constant for the class of all groups is
![]() $1/2$
.
$1/2$
.
6.1. The value of
 $\kappa (G)$
for finite groups
$\kappa (G)$
for finite groups
Let
![]() $G$
be an arbitrary finite group. Note that it follows from Proposition6.2 that
$G$
be an arbitrary finite group. Note that it follows from Proposition6.2 that
where
![]() $\psi$
ranges over all finite-dimensional representations of
$\psi$
ranges over all finite-dimensional representations of
![]() $G$
. The first observation is that the supremum can be upgraded to a maximum.
$G$
. The first observation is that the supremum can be upgraded to a maximum.
Proposition 6.6.
Let
![]() $G$
be a finite group. Then there exists a finite-dimensional representation
$G$
be a finite group. Then there exists a finite-dimensional representation
![]() $\psi \,:\, G \to \textrm{GL}_d({\mathbb{C}})$
of
$\psi \,:\, G \to \textrm{GL}_d({\mathbb{C}})$
of
![]() $G$
such that
$G$
such that
In particular,
![]() $\kappa (G)$
is a rational number.
$\kappa (G)$
is a rational number.
Proof. Denote by
![]() $R= \{ \psi _0, \dots, \psi _{c-1} \}$
the set of all irreducible representations of
$R= \{ \psi _0, \dots, \psi _{c-1} \}$
the set of all irreducible representations of
![]() $G$
up to isomorphism. Pick
$G$
up to isomorphism. Pick
![]() $C= \{ g_0, \dots, g_{c-1} \}$
to be a set of representatives for all conjugacy classes of
$C= \{ g_0, \dots, g_{c-1} \}$
to be a set of representatives for all conjugacy classes of
![]() $G$
. We will assume that
$G$
. We will assume that
![]() $\psi _0$
is the trivial representation and
$\psi _0$
is the trivial representation and
![]() $g_0\,:\!=\,e$
is the identity element of
$g_0\,:\!=\,e$
is the identity element of
![]() $G$
. Consider the
$G$
. Consider the
![]() $(c-1) \times (c-1)$
matrix
$(c-1) \times (c-1)$
matrix
![]() $K$
where
$K$
where
Note that
![]() $K_{ij}$
does not depend on the choice of the representative
$K_{ij}$
does not depend on the choice of the representative
![]() $g_i$
. Set
$g_i$
. Set
![]() $ \beta = \kappa (G)$
, and write
$ \beta = \kappa (G)$
, and write
 \begin{align*} \Delta = \left\{ (x_1, \dots, x_{c-1}): x_i \ge 0, \sum _{ 1 \le i \le c-1 } x_i =1 \right \}. \end{align*}
\begin{align*} \Delta = \left\{ (x_1, \dots, x_{c-1}): x_i \ge 0, \sum _{ 1 \le i \le c-1 } x_i =1 \right \}. \end{align*}
For each representation
![]() $ \psi \,:\, G \to \textrm{GL}_d({\mathbb{C}})$
which does not contain the trivial representation, we can decompose
$ \psi \,:\, G \to \textrm{GL}_d({\mathbb{C}})$
which does not contain the trivial representation, we can decompose
![]() $\rho$
as
$\rho$
as
![]() $ \rho = \oplus _{j=1}^{c-1} n_i \psi _i$
, and define
$ \rho = \oplus _{j=1}^{c-1} n_i \psi _i$
, and define
![]() $\delta ( \psi ) \in \Delta$
to be the column vector:
$\delta ( \psi ) \in \Delta$
to be the column vector:
of normalized multiplicities of irreducible representations of
![]() $G$
. It is easy to see that
$G$
. It is easy to see that
![]() $ \min _{g \in G} \rho ( \psi (g),{\textrm{Id}}) \ge \alpha$
holds iff for all
$ \min _{g \in G} \rho ( \psi (g),{\textrm{Id}}) \ge \alpha$
holds iff for all
![]() $g \in G$
$g \in G$
These conditions can be more succinctly expressed as:
where we write
![]() $x \le y$
for two vectors
$x \le y$
for two vectors
![]() $x, y$
if every entry of
$x, y$
if every entry of
![]() $y-x$
is nonnegative. By assumption, for every
$y-x$
is nonnegative. By assumption, for every
![]() $ m \ge 1$
, there exists a representation
$ m \ge 1$
, there exists a representation
![]() $ \psi _m$
such that
$ \psi _m$
such that
![]() $ K \delta (\psi _m) \le (1- \beta + \frac{1}{m}) (1,1, \dots, 1)^t$
holds. In other words, the set
$ K \delta (\psi _m) \le (1- \beta + \frac{1}{m}) (1,1, \dots, 1)^t$
holds. In other words, the set
is nonempty. By compactness of
![]() $ \Delta$
, it follows that there exists a point
$ \Delta$
, it follows that there exists a point
![]() $x \in \Delta$
such that
$x \in \Delta$
such that
![]() $K x \le (1- \beta ) (1,1, \dots, 1)^t$
. Note that these constitute a system of inequalities involving
$K x \le (1- \beta ) (1,1, \dots, 1)^t$
. Note that these constitute a system of inequalities involving
![]() $x_1, \dots, x_{c-1}$
and
$x_1, \dots, x_{c-1}$
and
![]() $\beta$
with rational coefficients. Now using the fact the the set of solutions to this system is a rational polytope (or equivalently using the proof of Farkas’ lemma [Reference Matousek16]), we deduce that both
$\beta$
with rational coefficients. Now using the fact the the set of solutions to this system is a rational polytope (or equivalently using the proof of Farkas’ lemma [Reference Matousek16]), we deduce that both
![]() $\beta$
and
$\beta$
and
![]() $(x_1, \dots, x_{c-1})$
are rational. This proves the claim.
$(x_1, \dots, x_{c-1})$
are rational. This proves the claim.
Remark 6.7.
There are noncyclic finite groups
![]() $F$
for which
$F$
for which
![]() $\kappa (F)=1$
. For instance, let
$\kappa (F)=1$
. For instance, let
![]() $F$
be a finite subgroup of
$F$
be a finite subgroup of
![]() $\textrm{{SU}}_2({\mathbb{C}})$
. Such groups are cyclic of odd order and double covers of finite subgroups of
$\textrm{{SU}}_2({\mathbb{C}})$
. Such groups are cyclic of odd order and double covers of finite subgroups of
![]() ${\textrm{SO}}_3({\mathbb{R}})$
, which include the alternating groups of
${\textrm{SO}}_3({\mathbb{R}})$
, which include the alternating groups of
![]() $4,5$
letters, and the symmetric group on
$4,5$
letters, and the symmetric group on
![]() $4$
letters. We claim that the natural representation
$4$
letters. We claim that the natural representation
![]() $\rho$
of
$\rho$
of
![]() $F$
in
$F$
in
![]() $\textrm{GL}_2({\mathbb{C}})$
has the property that for
$\textrm{GL}_2({\mathbb{C}})$
has the property that for
![]() $ g \neq e$
the eigenvalues of
$ g \neq e$
the eigenvalues of
![]() $\rho (g)$
are not
$\rho (g)$
are not
![]() $1$
. This is clear since if one eigenvalue is
$1$
. This is clear since if one eigenvalue is
![]() $1$
, then the other has to be
$1$
, then the other has to be
![]() $1$
as well, contradicting the faithfulness of
$1$
as well, contradicting the faithfulness of
![]() $ \rho$
. These groups include, for instance,
$ \rho$
. These groups include, for instance,
![]() $\textrm{SL}_2({\mathbb{F}}_5)$
.
$\textrm{SL}_2({\mathbb{F}}_5)$
.
Proposition 6.8.
Let
![]() $G$
be a finite group. Then
$G$
be a finite group. Then
![]() $\kappa (G)=1$
iff
$\kappa (G)=1$
iff
![]() $G$
has a fixed-point free complex representation.
$G$
has a fixed-point free complex representation.
These groups have been classified by Joseph A. Wolf. The classification is rather complicated. We refer the reader to [Reference Wolf24] for proofs and to [[Reference Nakaoka17], Theorem (1.7)] for a concise statement and the table listing these groups. The difficulty of classifying finite groups
![]() $G$
with
$G$
with
![]() $\kappa (G)=1$
suggests that the problem of determining
$\kappa (G)=1$
suggests that the problem of determining
![]() $\kappa (G)$
in terms of
$\kappa (G)$
in terms of
![]() $G$
may be a challenging one.
$G$
may be a challenging one.
Remark 6.9.
Given a field
![]() $F$
, one can also study the notion of linear sofic approximation over
$F$
, one can also study the notion of linear sofic approximation over
![]() $F$
. It is not known whether linear sofic groups over
$F$
. It is not known whether linear sofic groups over
![]() $\mathbb{C}$
and other fields coincide. However, one can show that
$\mathbb{C}$
and other fields coincide. However, one can show that
![]() $\kappa _{{\mathbb{C}}}(G)$
and
$\kappa _{{\mathbb{C}}}(G)$
and
![]() $\kappa _F(G)$
do not need to coincide. This will be seen in the next subsection.
$\kappa _F(G)$
do not need to coincide. This will be seen in the next subsection.
6.2. Optimal linear sofic approximation over fields of positive characteristic
In this subsection, we will prove TheoremC
Proof of Theorem C. Let
![]() $F$
be a field of characteristic
$F$
be a field of characteristic
![]() $p$
. It is easy to see that the proof of Proposition6.2 works over
$p$
. It is easy to see that the proof of Proposition6.2 works over
![]() $F$
without any changes. Hence, for any finite group
$F$
without any changes. Hence, for any finite group
![]() $G$
we have
$G$
we have
where
![]() $\psi$
runs over all representations
$\psi$
runs over all representations
![]() $\psi \,:\, G \to \textrm{GL}_d(F).$
$\psi \,:\, G \to \textrm{GL}_d(F).$
Suppose
![]() $\rho :G \to \textrm{GL}_d(F)$
is a linear representation. Let
$\rho :G \to \textrm{GL}_d(F)$
is a linear representation. Let
![]() $g$
be an element of order
$g$
be an element of order
![]() $p$
in
$p$
in
![]() $G$
. Write
$G$
. Write
![]() $\psi (g)={\textrm{Id}}+ \tau (g)$
where
$\psi (g)={\textrm{Id}}+ \tau (g)$
where
![]() $\tau (g)$
is a
$\tau (g)$
is a
![]() $d \times d$
matrix over
$d \times d$
matrix over
![]() $F$
. From
$F$
. From
![]() $ \psi (g)^p={\textrm{Id}}$
, and
$ \psi (g)^p={\textrm{Id}}$
, and
![]() $F$
has characteristic
$F$
has characteristic
![]() $p$
, it follows that
$p$
, it follows that
![]() $\tau (g)^p=0$
. Let
$\tau (g)^p=0$
. Let
![]() $J$
denote the Jordan canonical form of
$J$
denote the Jordan canonical form of
![]() $\tau (g)$
, consisting of
$\tau (g)$
, consisting of
![]() $k$
blocks. It follows from
$k$
blocks. It follows from
![]() $\tau (g)^p=0$
that each block in
$\tau (g)^p=0$
that each block in
![]() $J$
is a nilpotent block of size at most
$J$
is a nilpotent block of size at most
![]() $p$
, implying
$p$
, implying
![]() $kp \ge d$
. Since
$kp \ge d$
. Since
![]() $k=\dim \ker \tau (g)$
, we have
$k=\dim \ker \tau (g)$
, we have
This shows that
![]() $\kappa (G) \le 1- \frac{1}{p}$
. To prove the reverse inequality, let
$\kappa (G) \le 1- \frac{1}{p}$
. To prove the reverse inequality, let
![]() $V$
denote the vector space consisting of all functions
$V$
denote the vector space consisting of all functions
![]() $f\,:\, G \to F$
. Clearly,
$f\,:\, G \to F$
. Clearly,
![]() $d\,:\!=\, \dim V= |G|$
. Consider the left regular representation of
$d\,:\!=\, \dim V= |G|$
. Consider the left regular representation of
![]() $G$
on
$G$
on
![]() $V$
defined by:
$V$
defined by:
Let
![]() $g \in G \setminus \{ e \}$
, and consider the subspace
$g \in G \setminus \{ e \}$
, and consider the subspace
Any
![]() $f \in W(g)$
is invariant from the left by the subgroup
$f \in W(g)$
is invariant from the left by the subgroup
![]() $ \langle g \rangle$
generated by
$ \langle g \rangle$
generated by
![]() $g$
. It follows that
$g$
. It follows that
Hence,
proving the claim.
Acknowledgment
The authors would like to thank Goulnara Arzhantseva for helpful comments and suggestions on an earlier version of this paper. We also thank the anonymous referee for a careful reading of the paper and numerous remarks that significantly improved the exposition of this paper. Special thanks are due to Iosif Pinelis for providing the reference to Theorem3.2.