Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-12T06:58:30.766Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the rational homological dimension of lattices in positive characteristic

Part of: Special aspects of infinite or finite groups Connections with homological algebra and category theory

Published online by Cambridge University Press:  10 June 2022

Sam Hughes Open the ORCID record for Sam Hughes [Opens in a new window]
Sam Hughes*
Affiliation:
Mathematical Institute, Andrew Wiles Building, University of Oxford, Oxford OX2 6GG, UK E-mail: sam.hughes@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We show via 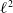$\ell^2$ -homology that the rational homological dimension of a lattice in a product of simple simply connected Chevalley groups over global function fields is equal to the rational cohomological dimension and to the dimension of the associated Bruhat–Tits building.

MSC classification

Primary: 20J06: Cohomology of groups
Secondary: 20F67: Hyperbolic groups and nonpositively curved groups
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 65 , Issue 1 , January 2023 , pp. 138 - 140
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Davis, M. W. et al., Weighted L2-cohomology of Coxeter groups, Geom. Topol. 11 (2007), 47–138. ISSN: 1465-3060. doi: 10.2140/gt.2007.11.47.Google Scholar
Dymara, J., L2-cohomology of buildings with fundamental class, Proc. Amer. Math. Soc. 132(6) (2004), 1839–1843. ISSN: 0002-9939. doi: 10.1090/S0002-9939-03-07234-4.CrossRefGoogle Scholar
Dymara, J., Thin buildings, Geom. Topol. 10 (2006), 667–694. ISSN: 1465-3060. doi: 10.2140/gt.2006.10.667.CrossRefGoogle Scholar
Gaboriau, D., Invariants l2 de relations d’Équivalence et de groupes, Publ. Math. Inst. Hautes Études Sci. 95 (2002), 93–150. ISSN: 0073-8301. doi: 10.1007/s102400200002.Google Scholar
Gandini, G., Bounding the homological finiteness length, Bull. London Math. Soc. 44(6) (2012), 1209–1214. ISSN: 0024-6093. doi: 10.1112/blms/bds047.Google Scholar
Gromov, M., Asymptotic invariants of infinite groups, in Geometric group theory, Vol. 2 (Sussex, 1991), London Mathematical Society Lecture Note Series, vol. 182 (Cambridge University Press, Cambridge, 1993), 1–295.Google Scholar
Hughes, S., Equivariant cohomology, lattices, and trees, PhD Thesis (School of Mathematical Sciences, University of Southampton, 2021).Google Scholar
Hughes, S., Graphs and complexes of lattices (2021). arXiv:2104.13728 [math.GR].Google Scholar
Hughes, S., Lattices in a product of trees, hierarchically hyperbolic groups, and virtual torsion-freeness, Bull. London Math. Soc. doi: 10.1112/blms.12637 CrossRefGoogle Scholar
Hughes, S., Irreducible lattices fibring over the circle (2022). arXiv:2201.06525 [math.GR].Google Scholar
Hughes, S. and Valiunas, M., Commensurating HNN-extensions: hierarchical hyperbolicity and biautomaticity (2021). arXiv: 2203.11996 [math.GR].Google Scholar
Lück, W., $\textit{L}^{2}$ -invariants: theory and applications to geometry and K-theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. ${3}^{rd}$ Series. A Series of Modern Surveys in Mathematics], vol. 44 (Springer-Verlag, Berlin, 2002), xvi+595. iSBN: 3-540-43566-2. doi: 10.1007/978-3-662-04687-6.Google Scholar
Petersen, H. D., Sauer, R. and Thom, A., $\textit{L}^{2}$ -Betti numbers of totally disconnected groups and their approximation by Betti numbers of lattices, J. Topol. 11(1) (2018), 257–282. ISSN: 1753–8416. doi: 10.1112/topo.12056.Google Scholar