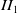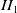1. Introduction
Right from the early days of the evolution of the theory of operator algebras, the methods of crossed product constructions and fixed point subalgebras with respect to actions by various algebraic objects on operator algebras have served extremely well to provide numerous examples with specific properties as well as to be considered as suitable candidates for structure results under certain given hypotheses. One of the first such structure results (thanks to Ocneanu, Jones, Sutherland, Popa, Kosaki, and Hong) states that every irreducible regular inclusion of factors of type
$II_1$
with finite Jones index is a group subfactor of the form
$N \subset N\rtimes G$
, with respect to an outer action of a finite group G on N. In particular, every such subfactor has depth 2. Further, it has also been established (in a series of papers by Ocneanu, David, Szymański, and Nikshych-Vainerman) that every finite index inclusion of type
$II_1$
factors of depth 2 is of the form
$N \subset N \rtimes H$
, with respect to a minimal action of some biconnected weak Hopf
$C^*$
-algebra H – see [Reference David7, Reference Longo12, Reference Nikshych and Vainerman13, Reference Ocneanu16, Reference Szymański23]. More recently, Popa, Shlyakhtenko and Vaes, in [Reference Popa, Shlyakhtenko and Vaes22], among various interesting results, classified regular subalgebras B of the hyperfinite
$II_1$
-factor R with
$B'\cap R = \mathcal{Z}(B)$
. However, they do not provide any structure for nonirreducible regular inclusions of factors of type
$II_1$
. This short note is a first naive attempt in this direction, in which we prove the following:
Theorem 4.6. Let
$N\subset M$
be a finite index regular inclusion of
$II_1$
-factors with commutative relative commutant
$N^{\prime}\cap M$
. Then, there exists a biconnected weak Kac algebra K and a minimal action of K on N such that
$N\subset M$
is isomorphic to
$N\subset N\rtimes K$
.
It must be mentioned here that Ceccherini-Silberstein (in [Reference Ceccherini-Silberstein6]) claimed to have proved that every finite index regular subfactor is a crossed product subfactor with respect to an outer action of a finite dimensional Hopf
$C^*$
-algebra. However, his assertion is incorrect, and there is an obvious oversight in his proof as is pointed out in Remark 4.1.
Theorem 4.6 is achieved by first proving that any finite index regular inclusion of
$II_1$
-factors with commutative first relative commutant has depth 2 and then an appropriate application of Nikshych–Vainerman’s characterization of depth 2 subfactors yields the desired structure. In order to take care of the first part, we utilize the notion of unitary orthonormal basis by Popa to show (in Theorem 4.3) that any regular subfactor with simple or commutative relative commutant is of depth at most 2. It fits well to mention here that, in fact, Popa had recently asked (in [Reference Popa21]) whether every integer index irreducible inclusion of
$II_1$
-factors admits a unitary orthonormal basis or not. It seems to be a difficult question to answer in full generality. In fact, the question can be asked for nonirreducible inclusions as well, and we provide a partial answer in:
Theorem 3.21. Let
$N\subset M$
be a finite index regular inclusion of factors of type
$II_1$
. If
$N^{\prime}\cap M$
is either commutative or simple, then M admits a unitary orthonormal basis over N.
Then, the second part of Theorem 4.6 is taken care of by a suitable application of the notion of two-sided basis for inclusions of finite von Neumann algebras. In fact, somewhat related to Popa’s question, and equally fundamental in nature, is the question related to the existence of a two-sided Pimsner–Popa basis for any extremal inclusion of
$II_1$
-factors, which was asked by Vaughan Jones around a decade back at various places. This question too has tasted too little success. In [Reference Bakshi and Gupta2], we had shown that every finite index regular inclusion of
$II_1$
-factors admits a two-sided Pimsner–Popa basis, and we have suitably adopted the idea of its proof in proving Theorem 3.21. We move one more step closer toward answering Jones’ question by proving the following:
Theorem 3.14. Let
$N\subset M$
be a finite index inclusion of type
$II_1$
-factors of depth 2 with simple relative commutant
$N^{\prime}\cap M$
. Then,
$M_2$
admits a two-sided Pimsner–Popa basis over
$M_1$
. Furthermore, M also admits a two-sided basis over N.
The flow of the article is in the reverse order in the sense that, after some preliminaries in Section 2, we first make an attempt to partially answer Jones’ question regarding existence of two-sided basis in the first half of Section 3 and then move toward Popa’s question regarding existence of unitary orthonormal basis in the second half of the same section. Finally, in Section 4, we establish that any regular subfactor with commutative first relative commutant is given by crossed product by a weak Kac algebra.
2. Preliminaries
Since there are slightly varying (though equivalent) definitions available in literature, in order to avoid any possible confusion, we quickly recall the definition that we shall be using here. For further details, we refer the reader to [Reference Böhm, Nill and Szlachányi5, Reference Nikshych and Vainerman13–Reference Nill, Szlachanyi and Wiesbrock15] and the references therein.
Definition 2.1 [Reference Böhm, Nill and Szlachányi5, Reference Nill, Szlachanyi and Wiesbrock15].
-
(1) A weak bialgebra is a quintuple
$(A,m,\eta,\Delta,\varepsilon)$
so that
$(A,m,\eta)$
is an algebra,
$(A,\Delta,\varepsilon)$
is a coalgebra and the tuple satisfies the following compatibility conditions between algebra and coalgebra structures:-
(a)
$\Delta$
is an algebra homomorphism. -
(b)
$\varepsilon(xyz)=\varepsilon(xy_1)\varepsilon(y_2z)$
and
$\varepsilon(xyz)=\varepsilon(xy_2)\varepsilon(y_1z)$
for all
$x,y, z\in A$
. -
(c)
${\Delta}^2(1)=(\Delta(1)\otimes 1)(1\otimes \Delta(1))=(1\otimes \Delta(1))(\Delta(1)\otimes 1).$
-
-
(2) A weak Hopf algebra (or a quantum groupoid) is a weak bialgebra
$(A,m,\eta,\Delta,\varepsilon)$
along with a k-linear map
$S\;:\;A\rightarrow A$
, called an antipode, satisfying the following antipode axioms:-
(a)
$x_1S(x_2)=\varepsilon(1_1x)1_2$
, -
(b)
$S(x_1)x_2=1_1\varepsilon(x1_2)$
and -
(c)
$S(x_1)x_2 S(x_3)=S(x).$
-
-
(3) A weak Hopf algebra
$(A,m,\eta,\Delta,\varepsilon)$
is said to be a weak Hopf
$C^*$
-algebra if A is a finite dimensional
$C^*$
-algebra and the comultiplication map is
$*$
-preserving, i.e.,
$\Delta(x^*)={\Delta(x)}^*.$
As in the preceding definition, throughout this paper, we shall use the Sweedler’s notation, i.e.,
$\Delta(x) = x_{(1)} \otimes x_{(2)}$
and
$(\Delta \otimes \mathrm{Id})\Delta (x) = x_{(1)} \otimes x_{(2)} \otimes x_{(3)} = ( \mathrm{Id}\otimes \Delta )\Delta (x)$
for all
$x \in A$
.
Definition 2.2 [Reference Böhm, Nill and Szlachányi5]. A weak Kac algebra is a weak Hopf
$C^*$
-algebra
$(A,m,\eta,\Delta,\varepsilon, S)$
such that
$S^2=\mathrm{Id}_A$
and S is
$*$
-preserving.
Remark 2.3.
-
(1) A weak Hopf algebra is a Hopf algebra if and only if the comultiplication is unit-preserving if and only if the counit is a homomorphism of algebras. In particular, every Kac algebra is a weak Kac algebra.
-
(2) The dual of a weak Kac algebra also admits a canonical weak Kac algebra.
Example 2.4. Given a finite groupoid
$\mathcal{G}$
, the associated groupoid algebra
$\mathbb{C}[\mathcal{G}]$
inherits a canonical weak Kac algebra structure with respect to the comultiplication
$\Delta$
, the counit
$\varepsilon$
, and the antipode S satisfying
\begin{align*}\Delta(g) = g \otimes g, \varepsilon(g) = 1, S(g) = g^{-1}\ \;\textrm{for}\ g \in \mathcal{G}.\end{align*}
It is easily seen that
$\mathbb{C}[\mathcal{G}]$
(resp.,
$\mathbb{C}[\mathcal{G}]^*$
) is a cocommutative (resp., commutative) weak Kac algebra. And, conversely, it was proved by Yamanouchi that for every cocommutative weak Kac algebra H there exists a finite groupoid
$\mathcal{G}$
such that H is isomorphic to
$\mathbb{C}[\mathcal{G}]$
.
Given any weak Kac algebra A, the target (resp., source) counital map
$\varepsilon^t$
(resp.,
$\varepsilon^s$
) on A, is given by
$\varepsilon^t(x)=\varepsilon(1_{(1)}x)1_{(2)}$
(resp.,
$\varepsilon^s(x)=1_{(1)}\varepsilon(x1_{(2)}))$
for
$x\in A$
, where
$\Delta(1) = 1_{(1)}\otimes 1_{(2)}$
in Sweedler’s notation. These maps are idempotent, i.e.,
$\varepsilon^t \circ \varepsilon^t = \varepsilon^t$
,
$\varepsilon^s \circ \varepsilon^s = \varepsilon^s$
, and their images are unital
$C^*$
-subalgebras (called the Cartan subalgebras) of A:
\begin{equation*} A_t\;:\!=\;\{x\in A\;:\;\varepsilon^t(x)=x\}\ \;\textrm{and}\; \ A_s\;:\!=\;\{x\in A\;:\;\varepsilon^s(x)=x\}. \end{equation*}
A is said to be connected if the inclusion
$A_t\subset A$
is connected (see [Reference Goodman, de la Harpe and Jones8] for definition). And, A is said to be biconnected if both A and its dual are connected.
Remark 2.5. Given a finite groupoid
$\mathcal{G}$
, the groupoid algebra
$\mathbb{C}[\mathcal{G}]$
is biconnected if and only if
$\mathcal{G}$
is a group.
2.1. Crossed product construction
We now briefly recall the notion of the crossed product construction via an action of a weak Hopf
$C^*$
-algebra, as in [Reference Nill, Szlachanyi and Wiesbrock15] (also see [Reference Nikshych and Vainerman13, Reference Nikshych and Vainerman14]).
Definition 2.6.
-
(1) By a (left) action of a weak Hopf
$C^*$
-algebra A on a von Neumann algebra M, we mean a linear map which defines a (left) module structure on M and satisfies the conditions
\begin{equation*} A\otimes M\ni a\otimes x \mapsto (a\vartriangleright x)\in M \end{equation*}
-
(a)
$a\vartriangleright xy=(a_{(1)}\vartriangleright x)(a_{(2)}\vartriangleright y)$
, -
(b)
$(a\vartriangleright x)^*=S(a)^*\vartriangleright x^*,$
and -
(c)
$a\vartriangleright 1=\varepsilon^t(a)\vartriangleright 1$
and
$a \vartriangleright 1=0$
iff
$\varepsilon^t(a)=0$
for
$a \in A$
,
$x, y \in M$
. -
(2) Under such a (left) action, the crossed product algebra
$M\rtimes A$
is defined as follows: As a
$\mathbb{C}$
-vector space it is the relative tensor product
$M\otimes_{A_t} A$
, where A (resp., M) admits a canonical left (resp., right)
$A_t$
-module structure so that
$ x (z\vartriangleright 1)\otimes a \sim x \otimes za, $
for all
$x\in M, a\in A,z\in A_t.$
For each
$(a, x) \in A \times M$
,
$[x\otimes a]$
denotes the class of the element
$x\otimes a$
and a natural
$*$
-algebra structure on
$M\otimes_{A_t} A$
is given by
\begin{equation*} [x\otimes a][y\otimes b]=[x(a_{(1)}\vartriangleright y)\otimes a_{(2)}b], \end{equation*}
for all
\begin{equation*} [x\otimes a]^*=[(a_{(1)}^*\vartriangleright x^*)\otimes a_{(2)}^*],\end{equation*}
$x,y\in M$
and
$a,b\in A$
.
-
(3) The action is said to be minimal if
$A^{\prime}\cap (M\rtimes A)=A_s.$
Remark 2.7 [Reference Nikshych and Vainerman13–Reference Nill, Szlachanyi and Wiesbrock15].
-
(1)
$M\rtimes A$
can be realized as a von Neumann algebra. -
(2) If M is a
$II_1$
-factor and A is a weak Hopf
$C^*$
-algebra acting minimally on M, then
$M \rtimes A$
is also a
$II_1$
-factor.
Our interest in actions of weak Hopf
$C^*$
-algebras stems from the following beautiful characterization of depth 2 subfactors by Nikshych and Vainerman. Before stating them, it would be appropriate to recall the following definition.
Definition 2.8. Consider a finite index inclusion
$N\subset M$
of
$II_1$
-factors and suppose
$N\subset M\subset M_1\subset \cdots \subset M_k\subset \cdots $
is its tower of Jones’ basic construction. Then, the inclusion
$N\subset M$
is said to have finite depth if there exists a k such that
$N^{\prime}\cap M_{k-2}\subset N^{\prime}\cap M_{k-1}\subset N^{\prime}\cap M_{k}$
is an instance of basic construction. The least such k is defined as the depth of the inclusion.
We urge the reader to see [Reference Goodman, de la Harpe and Jones8] for various other equivalent formulations of the notion of depth.
For any finite index irreducible inclusion
$N\subset M$
of
$II_1$
-factors, i.e.,
$N^{\prime}\cap M=\mathbb{C}$
, it was announced by Ocneanu (in [Reference Ocneanu16]) and proved later, separately, by Szymański, David and Longo—see [Reference David7, Reference Longo12, Reference Szymański23] —that if
$N \subset M$
is of depth 2, then there exists a Kac algebra K and a minimal action of K on
$M_1$
such that
$M_2\cong M_1\rtimes K$
and
$M = M_1^H$
. More generally, Nikshych and Vainerman obtained the following characterization:
Theorem 2.9 [Reference Böhm, Nill and Szlachányi5, Reference Nikshych and Vainerman13]. A finite index inclusion
$N\subset M$
of
$II_1$
-factors is of depth 2 if and only if there exists a biconnected weak Hopf
$C^*$
-algebra H and a minimal action of H on
$M_1$
such that
$M_2\cong M_1\rtimes H$
and
$M = M_1^H$
.
3. Pimsner–Popa bases
Let
$\mathcal{N}\subset \mathcal{M}$
be a unital inclusion of von Neumann algebras equipped with a faithful normal conditional expectation
$\mathcal{E}$
from
$\mathcal{M}$
onto
$\mathcal{N}$
. Then, a finite set
$\mathcal{B}\;:\!=\;\{\lambda_1,\ldots,\lambda_n\}\subset\mathcal{M}$
is called a left (resp., right) Pimsner–Popa basis for
$\mathcal{M}$
over
$\mathcal{N}$
via
$\mathcal{E}$
if every
$x\in \mathcal{M}$
can be expressed as
$x=\sum_{i=1}^n\mathcal{E}(x\lambda^*_i)\lambda_i$
(resp.,
$x=\sum_{j\;=\;1}^n\lambda_j\mathcal{E}(\lambda^*_jx)$
. Further, such a basis
$\{\lambda_i\}$
is said to be orthonormal if
$\mathcal{E}(\lambda_i \lambda_j^*)= \delta_{i,j}$
for all i, j. And, a collection
$\mathcal{B}$
is said to be a two-sided basis if it is simultaneously a left and a right Pimsner–Popa basis.
In this article, when we do not use the adjectives left or right, by a basis we shall always mean a right Pimsner–Popa basis (and not a two-sided basis).
3.1. Two-sided basis
About a decade back, Vaughan Jones asked the following question at various places.Footnote 1
Question 3.1 (Vaughan Jones). Let N be a
$II_1$
-factor and
$N\subset M$
be an extremal subfactor of finite index. Then, does there always exist a two-sided Pimsner–Popa basis for M over N?
Example 3.2. Given a finite group G and a subgroup H, by Hall’s Marriage Theorem, we can obtain a set of coset representatives which acts simultaneously as representatives of left and right cosetsFootnote 2 of H in G. Therefore, if G acts outerly on a
$II_1$
-factor N, then
$N\rtimes G$
always possesses a two-sided unitary orthonormal basis over
$N\rtimes H$
.
This observation, therefore, allows us to think about the existence of a two-sided basis as a subfactor analogue of Hall’s Marriage Theorem.
Definition 3.3. An inclusion
$\mathcal{Q} \subset \mathcal{P}$
of von Neumann algebras is said to be regular if its group of normalizers
$\mathcal{N}_{\mathcal{P}}(\mathcal{Q})\;:\!=\;\{u\in\mathcal{U}(\mathcal{P})\;:\;u\mathcal{Q}u^*=\mathcal{Q}\}$
generates
$\mathcal{P}$
as von Neumann algebra, i.e.,
$\mathcal{N}_{\mathcal{P}}(\mathcal{Q})'' = \mathcal{P}$
.
Remark 3.4. To the best of our knowledge, till date, too little progress has been made in answering Questions 3.1.
-
(1) If
$N\subset M$
is a regular irreducible subfactor of type
$II_1$
of finite index, then (from some works of Ocneanu, Jones, Sutherland, Popa, Kosaki) it is a well-known fact that it is isomorphic to
$N\subset N\rtimes G$
, for some outer action of a finite group G on N—see [Reference Hong9], for a precise statement. In particular, M has a two-sided basis over N. -
(2) In [Reference Bakshi and Gupta2], we could drop the irreducibility condition and showed, without depending upon any structure result, that every finite index regular subfactor
$N \subset M$
of type
$II_1$
admits a two-sided basis. A little thought should convince the reader that the two-sided basis we constructed in [Reference Bakshi and Gupta2] is in fact orthonormal.
A comment pertaining to an application of the notion of two-sided basis fits in well here:
Remark 3.5. It is a known fact to the experts that any regular subfactor of type
$II_1$
has integer index – see [Reference Goodman, de la Harpe and Jones8, p. 150]. However, there was no explicit proof easily accessible in literature until Ceccherini-Silberstein [Reference Ceccherini-Silberstein6] suggested having one. Though, the argument provided in [Reference Ceccherini-Silberstein6, Theorem 4.5] seems incomplete as is indicated in Remark 3.19.
To our satisfaction, we could do a little better (in [Reference Bakshi and Gupta2]) by exhibiting that, for any finite index regular subfactor
$N \subset M$
of type
$II_1$
, its index is given explicitly by
\begin{equation}[M\;:\;N] =|G|\, \mathrm{dim}(N'\cap M),\end{equation}
where G denotes the generalized Weyl group of the inclusion
$N\subset M$
, which is defined as the quotient group
$\frac{\mathcal{N}_M(N)}{\mathcal{U}(N) \mathcal{U}(N'\cap M)}$
.
Depending upon the structure result of irreducible depth 2 subfactors by Szymański and a result by Kac which determines when a Kac algebra is a group algebra, Nikshych and Vainermann deduced (in [Reference Nikshych and Vainerman13, Corollary 4.19]) that a depth 2 subfactor of type
$II_1$
with prime index p is necessarily a group subfactor with respect to an outer action of the cyclic group
$\mathbb Z/p\mathbb Z$
. Interestingly, it turns out that the formula in equation (3.1) has the following analogous consequence.
Proposition 3.6. Let
$N \subset M$
be a finite index regular inclusion of
$II_1$
-factors. If
$[M\;:\;N]=p$
is prime, then
$N\subset M$
is irreducible.
In particular, the cyclic group
$G\;:\!=\;\mathbb Z/p\mathbb Z$
acts outerly on N and
$N \subset M$
is isomorphic to
$N \subset N \rtimes G$
.
Proof. Suppose, on contrary, that
$N\subset M$
is not irreducible. Then, from equation (3.1), it follows that
\begin{equation*}[M\;:\;N]= \mathrm{dim}_{\mathbb{C}}(N'\cap M). \end{equation*}
Note that, if
$\Lambda$
denotes the inclusion matrix of the inclusion
$\mathbb{C} \subset N'\cap M$
, then
$\|\Lambda\|^2 = \mathrm{dim}_{\mathbb{C}}(N'\cap M)$
. In particular,
$\|\Lambda\|^2 = [M\;:\;N]$
, which then implies that
$\mathbb{C} \subset N'\cap M \subset N'\cap M_1$
is an instance of basic construction - see [Reference Goodman, de la Harpe and Jones8, Theorem 4.6.3 (vii)]. Thus,
$N'\cap M \cong M_n(\mathbb{C})$
for some
$n \geq2$
; so that
$[M\;:\;N]= n^2$
. This contradicts the hypothesis that
$[M\;:\;N]$
is a prime number. Hence,
$N \subset M$
must be irreducible.
The asserted structure of
$N \subset M$
is then well known.
Further, employing appropriate two-sided bases for the inclusions
$N \subset N \vee (N'\cap M)$
and
$N \vee (N'\cap M)\subset M$
, the following useful observation was proved explicitly in the first two paragraphs of the proof of [Reference Bakshi and Gupta2, Theorem 3.12]. We will be using it crucially in the proof of Theorem 4.6 and shall not repeat the details here.
Proposition 3.7 [Reference Bakshi and Gupta2]. Let
$N \subset M$
be a finite index regular inclusion of
$II_1$
-factors. Then, the Watatani index of the restriction of
$\mathrm{tr}_M$
to
$N'\cap M$
is a scalar.
Adding to the list, we shall provide, in the next section, an yet another application of the notion of two-sided basis for regular inclusions.
3.1.1 One more step toward Jones’ question
Note that, any irreducible regular factorial inclusion of type
$II_1$
, being isomorphic to a crossed product subfactor by a group, must be of depth 2 (see [Reference Goodman, de la Harpe and Jones8] or Definition 2.8 for definition). Thus, it is natural to ask the following question:
Question 3.8. Let
$N\subset M$
be a depth 2 subfactor of type
$II_1$
of finite index. Then, does
$M/N$
always have a two-sided basis?
We do not know the answer yet in this generality. However, we provide a partial answer in Theorem 3.14, for which we require some preparation.
First, we need (a mild generalization of) a useful result of Popa [Reference Popa20, Section 1.1.5]. Popa had proved it for any (left or right) orthonormal basis, and it is easy to see that it holds for any (left or right) Pimsner–Popa basis as well. Recall that a commuting square
$(D,C, B, A)$
of von Neumann algebras is said to be nondegenerate if
\begin{equation*}\overline{\mathrm{span}[CB]}^{\mathrm{S.O.T.}} = A = \overline{\mathrm{span}[BC]}^{\mathrm{S.O.T.}}.\end{equation*}
Lemma 3.9 (Popa). Let
$\mathcal{M}$
be a finite von Neumann algebra with a faithful normal tracial state and
$(\mathcal{N},\mathcal{K},\mathcal{L},\mathcal{M})$
be a nondegenerate commuting square of von Neumann subalgebras of
$\mathcal{M}$
. Then, any right basis for
$\mathcal{K}/\mathcal{N}$
is also a right basis for
$\mathcal{M}/\mathcal{L}.$
Proof. Suppose
$\{\lambda_i\;:\;i\in I\}$
is a right basis for
$\mathcal{K}/\mathcal{N}$
. Then,
$\sum_i\lambda_i e^{\mathcal{K}}_{\mathcal{N}}\lambda^*_i=1$
, where
$e^{\mathcal{K}}_{\mathcal{N}}$
denotes the Jones projection corresponding to the inclusion
$\mathcal{N}\subset \mathcal{K}$
. Let
$\Omega$
denote the canonical cyclic vector for
$L^2(\mathcal{M})$
. Then, for any
$x\in \mathcal{L}$
and
$y\in \mathcal{K}$
, we have
\begin{align*} \sum_i \lambda_i e^{\mathcal{M}}_{\mathcal{L}} \lambda^*_i(yx\Omega) &= \sum_i \lambda_i E^{\mathcal{M}}_{\mathcal{L}}(\lambda^*_iyx)\Omega\\ &= \sum_i \lambda_i E^{\mathcal{M}}_{\mathcal{L}}(\lambda^*_iy)x\Omega\\ &= \sum_i \lambda_i E^{\mathcal{K}}_{\mathcal{N}}(\lambda^*_iy)x\Omega \qquad \textrm{[by commuting square condition]}\\ &= yx\Omega. \end{align*}
As the commuting square is nondegenerate, we have
$\overline{\mathrm{span}\, \mathcal{L}\mathcal{K}}^{\mathrm{SOT}}=\mathcal{M}=\overline{\mathrm{span}\, \mathcal{K}\mathcal{L}}^{\mathrm{SOT}}$
. In particular,
$\overline{[\mathrm{span}\, \mathcal{L}\mathcal{K}] \Omega}^{\|\cdot\|_2}=L^2(\mathcal{M})=\overline{[\mathrm{span}\, \mathcal{K}\mathcal{L}]\Omega }^{\|\cdot\|_2}$
. Therefore, we conclude that
$\sum_i\lambda_ie^{\mathcal{M}}_{\mathcal{L}}\lambda^*_i=1$
and the proof is complete.
Some specific conditions guarantee nondegeneracy of some commuting squares.
Lemma 3.10. Let
$\mathcal{M}$
be a finite von Neumann algebra with a faithful normal tracial state and
$(\mathcal{N}, \mathcal{P}, \mathcal{Q}, \mathcal{M})$
be a commuting square consisting of von Neumann subalgebras of
$\mathcal{M}$
. If, either
-
(1)
$\mathcal{Q}\subset \mathcal{M}$
is an inclusion of
$II_1$
-factors with finite index and
$\mathcal{N}\subset \mathcal{P}$
is a connected inclusion of finite dimensional
$C^*$
-algebras with
$ [\mathcal{M}\;:\;\mathcal{Q}] =\|\Lambda\|^2$
, where
$\Lambda$
denotes the inclusion matrix of
$\mathcal{N}\subset \mathcal{P}$
; or -
(2) both
$\mathcal{N}\subset \mathcal{P}$
and
$\mathcal{Q}\subset \mathcal{M}$
are connected inclusions of finite dimensional
$C^*$
-algebras with
$ \|\Lambda\|^2=\|\Gamma\|^2$
, where
$\Lambda$
and
$\Gamma$
denote the respective inclusion matrices.
Then
$(\mathcal{N}, \mathcal{P}, \mathcal{Q}, \mathcal{M})$
is nondegenerate.
Proof. A proof can be obtained on similar lines as that of [Reference Bakshi and Kodiyalam3, Lemma 18] based on the characterization of a basis illustrated in [Reference Bakshi1, Theorem 2.2].
The next useful observation is a straight forward adaptation of [Reference Bakshi and Gupta2, Proposition 3.3], which uses the notion of path algebras associated to inclusions of finite dimensional
$C^*$
-algebras by Sunder and Ocneanu. We skip the details.
Lemma 3.11 [Reference Bakshi and Gupta2]. Let A be a finite dimensional
$C^*$
-algebra and tr be a faithful tracial state on A. Then, A has a two-sided orthonormal basis over
$\mathbb{C}$
with respect to tr.
The following interesting observation is a folklore.
Proposition 3.12. Let
$N\subset M$
be a finite index depth 2 subfactor of type
$II_1$
and
$M \supset N \supset N_{-1}\supset N_{-2}\supset \cdots \supset N_{-k} \supset \cdots$
be a tunnel construction for
$N \subset M$
. Then,
$N_{-2k}\subset N_{-2k +1}$
has depth 2 for all
$k \geq 1$
.
Moreover,
$M_{2k-1} \subset M_{2k}$
is also of depth 2 for all
$ k\geq 1$
.
Proof. For the tunnel part, it suffices to show that
$N_{-2}\subset N_{-1}$
has depth 2.
Let
$\Gamma$
and
$\Omega$
denote the inclusion matrices for the inclusions
$(N'_{\!\!-2}\cap N_{-1} \subset N'_{\!\!-2}\cap N )$
and
$(N'_{\!\!-2}\cap N \subset N'_{\!\!-2}\cap M )$
, respectively. Then, by [Reference Goodman, de la Harpe and Jones8, Theorem 4.6.3], it will follow that
$N_{-2} \subset N_{-1}$
has depth 2 if we can show that
$\|\Gamma\|^2 < [N_{-1}\;:\;N_{-2}] =\|\Omega\|^2 $
.
Consider the Jones’ basic construction tower
\begin{equation*}N_{-2} \subset N_{-1} \subset N \subset M \subset M_1 \subset M_2 \subset M_3 \cdots \subset M_k \subset \cdots.\end{equation*}
By [Reference Bisch4, Theorem 2.13], there exists a
$*$
-isomorphism (the shift operator)
$\varphi\;:\;N'_{\!\!-2} \cap M \rightarrow N'\cap M_2$
such that
$\varphi(N'_{\!\!-2}\cap N) = N'\cap M_1 $
and
$\varphi(N'_{\!\!-2}\cap N_{-1}) = N'\cap M $
. Thus, the truncated towers
$ [N'_{\!\!-2}\cap N_{-1} \subset N'_{\!\!-2}\cap N \subset N'_{\!\!-2}\cap M ] $
and
$[N'\cap M \subset N'\cap M_1 \subset N'\cap M_2] $
are isomorphic. In particular, if
$\Lambda_i$
denotes the inclusion matrix for the inclusion
$(N'\cap M_i \subset N'\cap M_{i+1} )$
, then
$\Lambda_0 =\Gamma$
and
$\Lambda_1 = \Omega$
; so, by [Reference Goodman, de la Harpe and Jones8, Theorem 4.6.3], we obtain
$ \|\Omega\|^2 = \|\Lambda_1\|^2 = [M\;:\;N]= [N_{-1}\;:\;N_{-2}] $
and
$ \|\Gamma\|^2 = \|\Lambda_0\|^2 < [M\;:\;N] = [N_{-1}\;:\;N_{-2}] $
.
For the basic construction part, it suffices to show that
$M_1\subset M_2$
has depth 2. The shift operator
$\psi\;:\;N'\cap M_2 \rightarrow M_1'\cap M_{4}$
does the job as above.
Corollary 3.13. Let
$N\subset M$
be a finite index depth 2 subfactor of type
$II_1$
. Then,
$M_k \subset M_{k+1}$
also has depth 2 for all
$k \geq 0$
.
In particular,
$N_{-k}\subset N_{-k +1}$
has depth 2 for all
$k \geq 1$
, for any tunnel construction
$M \supset N \supset N_{-1}\supset N_{-2}\supset \cdots \supset N_{-k} \supset \cdots$
of
$N \subset M$
.
Proof. It suffices to show that
$M \subset M_1$
is of depth 2.
Fix a 2-step downward basic construction
$N_{-2}\subset N_{-1}\subset N$
of
$N \subset M$
. Then, by the preceding proposition,
$N_{-2} \subset N_{-1}$
is also of depth 2. So, by [Reference Nikshych and Vainerman13], there exists a biconnected weak Hopf
$C^*$
-algebra H with a minimal action on N such that
$(N^H \subset N)\cong (N_{-1} \subset N)$
. Thus,
$N_{-1} \subset N$
is also of depth 2, by [Reference Böhm, Nill and Szlachányi5] (also see [Reference Nikshych and Vainerman14, Section 8.1]). Thus, by Proposition 3.12 again,
$M\subset M_1$
is also of depth 2.
We are now all set for the theorem of this subsection.
Theorem 3.14. Let
$N\subset M$
be a finite index inclusion of type
$II_1$
-factors of depth 2 with simple relative commutant
$N^{\prime}\cap M$
. Then,
$M_2$
admits a two-sided orthonormal basis over
$M_1$
.
Furthermore, M also admits a two-sided orthonormal basis over N.
Proof. Although some of the arguments below are well known (see [Reference Popa20]), we provide sufficient details for the sake of self-containment and convenience of the reader.
Step I: Any (left/right) basis for
$M^{\prime}\cap M_2$
over
$M^{\prime}\cap M_1$
is also a (left/right) basis for
$M_2$
over
$M_1$
.
Note that, by Lemma 3.9, it suffices to show that the quadruple
\begin{equation*}\begin{matrix} M_1\;\;\;\;\; &\subset\;\;\;\;\; & M_2 \\[3pt] \cup\;\;\;\;\; &\ \;\;\;\;\; &\cup \\[3pt] M^{\prime}\cap M_1\;\;\;\;\; &\subset\;\;\;\;\; & M^{\prime}\cap M_2\end{matrix}\end{equation*}
is a nondegenerate commuting square. Toward this direction, first, recall that the quadruple
\begin{equation*}\mathcal{G}_1 \;:\!=\; \begin{matrix} M\;\;\;\;\; &\subset\;\;\;\;\; & M_1 \\[3pt] \cup\;\;\;\;\; &\ \;\;\;\;\; &\cup\\[3pt] N^{\prime}\cap M\;\;\;\;\; &\subset\;\;\;\;\; & N^{\prime}\cap M_1\end{matrix}\end{equation*}
is a commuting square—see, for instance, [Reference Goodman, de la Harpe and Jones8, Proposition 4.2.7], wherein the bottom inclusion is connected.
Let
$\Lambda$
denote the inclusion matrix for the inclusion
$N^{\prime}\cap M\subset N^{\prime}\cap M_1$
. Since
$N\subset M$
is of depth 2, as was recalled in Proposition 3.12, we have
$[M_1\;:\;M]=[M\;:\;N]= {\lVert \Lambda\Vert}^2.$
Therefore, by Lemma 3.10, the quadruple
$\mathcal{G}_1$
is a nondegenerate commuting square. Thus, its extension (as defined in [Reference Popa20, Section 1.1.6]) is given by the quadruple
\begin{equation*}\mathcal{G}_2\;:\!=\;\begin{matrix} M_1\;\;\;\;\; &\subset\;\;\;\;\; & M_2 \\[3pt] \cup\;\;\;\;\; &\ \;\;\;\;\; &\cup\\[3pt] N^{\prime}\cap M_1\;\;\;\;\; &\subset\;\;\;\;\; & N^{\prime}\cap M_2\end{matrix};\end{equation*}
and, by the proposition in Section 1.1.6 of [Reference Popa20],
$\mathcal{G}_2$
is a nondegenerate commuting square as well. On the other hand, note that if
$\Gamma$
denotes the inclusion matrix for
$M'\cap M_1 \subset M^{\prime}\cap M_2$
, then since
$M \subset M_1$
is also of depth 2 (see Corollary 3.13), we have
$\|\Gamma\|^2 = [M_1\;:\;M]= [M\;:\;N]=\|\Lambda^T\|^2$
; so, the commuting square
\begin{equation*}\mathcal{G}_3\;:\!=\;\begin{matrix} N^{\prime}\cap M_1\;\;\;\;\; &\stackrel{\Lambda^T}{\subset}\;\;\;\;\; &N^{\prime}\cap M_2 \\[3pt] \cup\;\;\;\;\; &\ \;\;\;\;\; &\cup\\[3pt] M^{\prime}\cap M_1\;\;\;\;\; &\stackrel{\Gamma}{\subset}\;\;\;\;\; &M^{\prime}\cap M_2\end{matrix}\end{equation*}
is also nondegenerate, by Lemma 3.10. In particular, concatenating
$\mathcal{G}_2$
and
$\mathcal{G}_3$
, we deduce from [Reference Popa20, Section 1.1.5] that the quadruple
\begin{equation*}\begin{matrix} M_1\;\;\;\;\; &\subset\;\;\;\;\; & M_2 \\[3pt] \cup\;\;\;\;\; &\ \;\;\;\;\; &\cup\\[3pt] M^{\prime}\cap M_1\;\;\;\;\; &\subset\;\;\;\;\; & M^{\prime}\cap M_2\end{matrix}\end{equation*}
is a nondegenerate commuting square.
Step II:
$M^{\prime}\cap M_2$
has a two-sided orthonormal basis over
$M^{\prime}\cap M_1$
.
We assert that
$( M'\cap M_1 \subset M^{\prime}\cap M_2)$
is isomorphic to
$( M'\cap M_1 \subset (M^{\prime}\cap M_1) \otimes Q)$
for some unital
$*$
-subalgebra Q of
$(M'\cap M_1)' \cap(M'\cap M_3)$
. Once this is established, we can then readily deduce from Lemma 3.11 that
$M^{\prime}\cap M_2$
has a two-sided orthonormal basis over
$M^{\prime}\cap M_1$
.
Since
$N'\cap M \ni x \mapsto Jx^*J \in M'\cap M_1$
is an anti-isomorphism and
$N'\cap M$
is simple, so is
$M^{\prime}\cap M_1$
. Again, since
$M \subset M_1$
is also of depth 2, the tower
\begin{equation*}M'\cap M_1 \subset M'\cap M_2 \subset M'\cap M_3 \end{equation*}
is an instance of basic construction. So,
$M^{\prime}\cap M_3$
is also simple. Thus, it follows from [Reference Goodman, de la Harpe and Jones8, Lemma 2.2.2] that
$(M^{\prime}\cap M_1)^{\prime}\cap (M^{\prime}\cap M_3)$
is simple and that
\begin{equation*}M^{\prime}\cap M_3 \cong (M^{\prime}\cap M_1)\otimes [(M^{\prime}\cap M_1)^{\prime}\cap (M^{\prime}\cap M_3)].\end{equation*}
Suppose that
$M^{\prime}\cap M_1\cong M_n(\mathbb{C})$
and that
$M^{\prime}\cap M_3\cong M_n(\mathbb{C})\otimes M_k(\mathbb{C}).$
Denote the intermediate subalgebra corresponding to
$M^{\prime}\cap M_2$
by P. It is well known that P is of the form
$M_n(\mathbb{C})\otimes Q$
, where Q is some unital
$*$
-subalgebra of
$M_k(\mathbb{C})$
. We provide the details for the convenience of the reader. By [Reference Goodman, de la Harpe and Jones8, Proposition 4.2.7] again, the quadruple
\begin{equation*} \mathcal{G}_4\;:\!=\;\begin{matrix} P\;\;\;\;\; &\subset\;\;\;\;\; & M_n(\mathbb{C})\otimes M_k(\mathbb{C})\;\;\;\;\; \\ \cup\;\;\;\;\; &\ \;\;\;\;\; &\cup \\ {(M_n(\mathbb{C}) \otimes 1)}^{\prime}\cap P\;\;\;\;\; &\subset\;\;\;\;\; & 1\otimes M_k(\mathbb{C}). \end{matrix} \end{equation*}
is also a commuting square. Note that, there exists a unital
$*$
-subalgebra Q of
$M_k(\mathbb{C})$
such that
${(M_n(\mathbb{C}) \otimes 1)}^{\prime}\cap P=1\otimes Q$
. Clearly,
$M_n(\mathbb{C})\otimes Q\subseteq P$
. To see the reverse inclusion, consider
$x = \sum_ia_i\otimes b_i \in P \subset M_n(\mathbb{C})\otimes M_k(\mathbb{C}).$
Then, we have
$x= \sum(a_i\otimes 1) E_P(1\otimes b_i)$
. Since
$\mathcal{G}_4$
is a commuting square, we immediately see that
$E_P(1\otimes b_i)\in1\otimes Q$
and hence
$x\in M_n(\mathbb{C})\otimes Q.$
In conclusion, we have
$P=M_n(\mathbb{C})\otimes Q$
, as was asserted.
Thus, from Steps I and II, we deduce that
$M_2$
has a two-sided orthonormal basis over
$M_1$
.
Finally, fix any 2-step downward basic construction
$N_{-2}\subset N_{-1}\subset N\subset M$
for
$N\subset M$
. Then, by Proposition 3.12,
$N_{-2}\subset N_{-1}$
also has depth 2. Further, as seen in Proposition 3.12,
$N'_{\!\!-2}\cap N_{-1} \cong N'\cap M$
is simple. Hence, we readily deduce from the preceding discussion that M must admit a two-sided orthonormal basis over N.
As an immediate consequence we deduce the following
Corollary 3.15. Every finite index irreducible inclusion of
$II_1$
factors of depth 2 admits a two-sided orthonormal basis.
Remark 3.16. Note that a subfactor as in Theorem 3.14 need not be regular. For instance, any Kac algebra K, which is not a group algebra, acts outerly on the hyperfinite factor R and yields a nonregular irreducible depth 2 subfactor.
3.2 Unitary orthonormal basis
We now move toward unitary orthonormal bases and touch upon another fundamental question asked recently by Sorin Popa in [Reference Popa21, Section 3.5].
Question 3.17 (Sorin Popa). Does there always exist an orthonormal basis consisting of n many unitaries for an integer index (
$=n$
) irreducible inclusion of
$II_1$
-factors?
Example 3.18. Let H be a subgroup of a finite group G. If G acts outerly on a
$II_1$
-factor N, then
$N \rtimes G$
has a unitary orthonormal basis over
$N\rtimes H$
. In particular, every irreducible regular subfactor, being isomorphic to a group subfactor, admits a unitary orthonormal basis.
In view of the preceding example, it is natural to ask whether we can drop the irreducibility condition or not. The following remarks fall in place here:
Remark 3.19.
-
(1) The question of existence of unitary orthonormal basis for a general finite index regular subfactor which is not necessarily irreducible (thus modifying Question 3.17) was discussed by Ceccherini-Silberstein [Reference Ceccherini-Silberstein6]. In fact, he asserted (in [Reference Ceccherini-Silberstein6, Theorem 4.5]) that if
$N\subset M$
is a regular subfactor with finite index, then
$M/N$
has a unitary orthonormal basis. However, his proof depends on a technique of Popa ([Reference Popa19, Theorem 2.3]) which holds for Cartan subalgebras. Since Popa’s proof depends crucially on maximal abelian-ness of the subalgebra, it is not clear whether it holds, more generally, for regular subalgebras or not. So, the proof of [Reference Ceccherini-Silberstein6, Theorem 4.5] seems to be incomplete, although the statement may still be true, which we rephrase in Conjecture 3.20. -
(2) Furthermore, Ceccherini-Silberstein (in [Reference Ceccherini-Silberstein6, Theorem 4.7]) had also asserted that if
$M/N$
has a unitary orthonormal basis, then the subfactor
$M_1\subset M_2$
is of the form
$M_1 \subset M_1 \rtimes H$
and hence has depth 2 (see for instance [Reference Nikshych and Vainerman13]), which then implies that
$N \subset M$
is also of depth 2—see Proposition 3.12. However, this is well known to be incorrect as every group-subgroup subfactor
$(R\times H)\subset (R\rtimes G)$
always has a unitary orthonormal basis (see Example 3.18) whereas it is not necessarily of depth 2. -
(3) Though not directly related to the present discussion, the characterization of index 3 subfactors provided in Corollary 3.19 of [Reference Ceccherini-Silberstein6] is known to be incorrect.
Conjecture 3.20. Let
$N\subset M$
be a finite index regular inclusion of factors of type
$II_1$
. Then,
$M/N$
has a unitary orthonormal basis.
As a partial progress in the resolution of this conjecture, we prove the following:
Theorem 3.21. Let
$N\subset M$
be a finite index regular inclusion of factors of type
$II_1$
. If
$N^{\prime}\cap M$
is either commutative or simple, then M admits a unitary orthonormal basis over N.
We will need the following couple of results to achieve this. Recall that, for a unital inclusion
$B \subset A$
of finite dimensional
$C^*$
-algebras with inclusion matrix
$\Lambda$
, a tracial state tr on A is said to be a Markov trace for
$B \subset A$
if
\begin{equation*}\Lambda^t \Lambda \bar{t} = \|\Lambda\|^2 \bar{t},\end{equation*}
where
$\bar{t}$
denotes the trace vector of the tracial state tr. For more on Markov trace, see [Reference Goodman, de la Harpe and Jones8, Reference Jones and Sunder11].
Lemma 3.22. Let
$A\;:\!=\;\mathbb{C} \oplus \mathbb{C} \oplus\cdots \oplus \mathbb{C}$
(n-copies).
-
(1) The Markov trace
$\mathrm{tr}\;:\;A \rightarrow \mathbb{C}$
for the unital inclusion
$\mathbb{C} \subset A$
is given by
\begin{equation*} \mathrm{tr}((z_1, \ldots, z_n)) = \frac{1}{n} \sum_i z_i. \end{equation*}
-
(2) There exists a unitary orthonormal basis for A over
$\mathbb{C}$
with respect to the Markov trace if and only if there exists a unitary matrix
$U=[u_{ij}]\in M_n(\mathbb{C})$
such that
$|u_{ij}| = \frac{1}{\sqrt{n}}$
for all
$1 \leq i, j \leq n$
.
Proof. (1) This follows easily from [Reference Goodman, de la Harpe and Jones8, Proposition 2.7.2].
(2):
$(\!\Rightarrow\!)$
Let
$\{\lambda_i=(z_i^{(1)}, z_i^{(2)}, \ldots, z_i^{(n)})\;:\;1 \leq i \leq n\}$
be a unitary orthonormal basis for A over
$\mathbb{C}$
. Consider the matrix
$ U =[u_{ij}] \in M_n $
whose entries are given by
$ u_{ij}= \frac{1}{\sqrt{n}}z_{i}^{(j)} $
, i.e., whose i-th column constitutes of the complex entries in
$\lambda_i$
. Then,
$|u_{ij}|=\frac{1}{\sqrt{n}}$
for all
$1 \leq i, j \leq n$
and
\begin{equation*}U^*U= \begin{bmatrix}\mathrm{tr}(\lambda_1^*\lambda_1)\;\;\;\;\; & \mathrm{tr}(\lambda_1^*\lambda_2)\;\;\;\;\; & \cdots\;\;\;\;\; & \mathrm{tr}(\lambda_1^*\lambda_n)\\[3pt] \mathrm{tr}(\lambda_2^*\lambda_1)\;\;\;\;\; & \mathrm{tr}(\lambda_2^*\lambda_2)\;\;\;\;\; & \cdots\;\;\;\;\; & \mathrm{tr}(\lambda_2^*\lambda_n)\\[3pt] \vdots\;\;\;\;\; & \vdots\;\;\;\;\; & \ddots\;\;\;\;\; & \vdots\;\;\;\;\; \\[3pt] \mathrm{tr}(\lambda_n^*\lambda_1)\;\;\;\;\; & \mathrm{tr}(\lambda_n^*\lambda_2)\;\;\;\;\; & \cdots\;\;\;\;\; & \mathrm{tr}(\lambda_n^*\lambda_n)\\ \end{bmatrix}= I_n.\end{equation*}
$(\!\Leftarrow)$
Let
$U=[u_{ij}]\in U(n)$
be such that
$|u_{ij}| = \frac{1}{\sqrt{n}}$
for all
$1 \leq i, j \leq n$
. Consider
\begin{equation*}\lambda_i \;:\!=\; \sqrt{n}\, (u_{1i}, u_{2i}, \ldots, u_{ni}) \in A,\ i =1 , 2, \ldots, n.\end{equation*}
Since
$|u_{ij}| = \frac{1}{\sqrt{n}}$
for all
$1 \leq i , j \leq n$
, it follows that
$\lambda_i^*\lambda_i=(1, 1, \ldots, 1)$
for all
$1 \leq i \leq n$
, i.e., each
$\lambda_i$
is a unitary in A. Further, note that
\begin{equation*}I_n= U^*U = [u_{ij}]^*[u_{ij}] =\begin{bmatrix}\mathrm{tr}(\lambda_1^*\lambda_1)\;\;\;\;\; & \mathrm{tr}(\lambda_1^*\lambda_2)\;\;\;\;\; & \cdots\;\;\;\;\; & \mathrm{tr}(\lambda_1^*\lambda_n)\\[3pt] \mathrm{tr}(\lambda_2^*\lambda_1)\;\;\;\;\; & \mathrm{tr}(\lambda_2^*\lambda_2)\;\;\;\;\; & \cdots\;\;\;\;\; & \mathrm{tr}(\lambda_2^*\lambda_n)\\[3pt] \vdots\;\;\;\;\; & \vdots\;\;\;\;\; & \ddots\;\;\;\;\; & \vdots\;\;\;\;\; \\[3pt] \mathrm{tr}(\lambda_n^*\lambda_1)\;\;\;\;\; & \mathrm{tr}(\lambda_n^*\lambda_2)\;\;\;\;\; & \cdots\;\;\;\;\; & \mathrm{tr}(\lambda_n^*\lambda_n)\\ \end{bmatrix}.\end{equation*}
Hence,
$\mathrm{tr}(\lambda_i^*\lambda_j) = \delta_{i,j}$
for all
$ 1 \leq i,j \leq n$
, which implies that
$\{\lambda_1, \ldots, \lambda_n\}$
forms a unitary orthonormal basis for A over
$\mathbb{C}$
with respect to above tracial state.
Recall that a unitary error basis for a matrix algebra
$M_n(\mathbb{C})$
is a Hamel basis that is orthogonal with respect to the inner product induced by the canonical trace of
$M_n(\mathbb{C})$
. Little is known about their structure. There are two popular methods of construction of unitary error bases. One is algebraic in nature (due to Knill) and the other combinatorial (due to Werner).
Proposition 3.23. Let A be a finite dimensional
$C^*$
-algebra which is either simple or commutative. Then,
$A/\mathbb{C}$
has a unitary orthonormal basis with respect to the Markov trace for the unital inclusion
$\mathbb{C} \subset A$
.
Proof. Suppose first that
$A=M_n(\mathbb{C})$
for some
$n \geq 2$
. The existence of a unitary orthonormal basis follows from the known construction of a unitary error basis. We include the details for the reader’s convenience.
We first recall such a basis for
$n=2$
(because of its importance and popularity in quantum information theory). The Pauli spin matrices (unitary error bases in dimension 2) are defined as follows:
\begin{equation*}\sigma_x=\begin{bmatrix} 0\;\;\;\;\; & 1\\[3pt] 1\;\;\;\;\; & 0 \end{bmatrix}, \sigma_y=\begin{bmatrix} 0\;\;\;\;\; & -i\\ i\;\;\;\;\; & 0 \end{bmatrix}, \sigma_z=\begin{bmatrix} 1\;\;\;\;\; & 0\\ 0\;\;\;\;\; & -1 \end{bmatrix}.\end{equation*}
It is an amazing fact that the set
$\{\mathrm{I}_2,\sigma_x,\sigma_y,\sigma_z\}$
forms an orthonormal basis consisting of unitaries for
$M_2(\mathbb{C}).$
For higher dimensions, consider the following two important matrices due to Sylvester and Weyl:
\begin{equation*} U= \begin{bmatrix} 1\;\;\;\;\; & 0\;\;\;\;\; & 0\;\;\;\;\; & \cdots\;\;\;\;\; & 0\\[3pt] 0\;\;\;\;\; & \omega\;\;\;\;\; & 0\;\;\;\;\; & \cdots\;\;\;\;\; & 0\\[3pt] 0\;\;\;\;\; & 0\;\;\;\;\; & {\omega}^2\;\;\;\;\; & \cdots\;\;\;\;\; & 0\\[3pt] \vdots\;\;\;\;\; & \vdots\;\;\;\;\; & \vdots\;\;\;\;\; & \ddots\;\;\;\;\; & \vdots\\[3pt] 0\;\;\;\;\; & 0\;\;\;\;\; & 0\;\;\;\;\; & \cdots\;\;\;\;\; & {\omega}^{n-1} \end{bmatrix}\end{equation*}
and
\begin{equation*}V=\begin{bmatrix}0\;\;\;\;\; & 0\;\;\;\;\; & 0\;\;\;\;\; & \cdots\;\;\;\;\; & 0\;\;\;\;\; & 1\\[3pt] 1\;\;\;\;\; & 0\;\;\;\;\; & 0\;\;\;\;\; & \cdots\;\;\;\;\; & 0\;\;\;\;\; & 0 \\[3pt] 0\;\;\;\;\; & 1\;\;\;\;\; & 0\;\;\;\;\; & \cdots\;\;\;\;\; & 0\;\;\;\;\; & 0\\[3pt] 0\;\;\;\;\; & 0 \;\;\;\;\;& 1\;\;\;\;\; & \cdots\;\;\;\;\; & 0\;\;\;\;\; & 0\\[3pt] \vdots\;\;\;\;\; & \vdots\;\;\;\;\; & \vdots\;\;\;\;\; & \ddots\;\;\;\;\; & \vdots\;\;\;\;\; & \vdots\\[3pt] 0\;\;\;\;\; & 0\;\;\;\;\; & 0\;\;\;\;\; & \cdots\;\;\;\;\; & 1\;\;\;\;\; & 0 \end{bmatrix},\end{equation*}
where
$\omega \;:\!=\; e^{-2\pi i /n}$
(a primitive root of unity). Then, it is known that the set
$\{U^iV^j\;:\;1\leq i,j\leq n\}$
forms a unitary error basis (in fact, a nice error basis) for
$M_n(\mathbb{C})$
. These matrices also appeared in a work of Popa ([Reference Popa18]) (see also [Reference Ceccherini-Silberstein6]). This proves that
$A/\mathbb{C}$
has unitary orthonormal basis whenever A is simple.
Next, let A be isomorphic to
$\mathbb{C}\oplus \mathbb{C} \oplus \cdots \oplus \mathbb{C}$
(n-copies). Now, for a primitive root of unity
$\omega$
as above, consider the well-known unitary DFT matrix
\begin{equation*} U \;:\!=\; \frac{1}{\sqrt{n}} \begin{bmatrix}1\;\;\;\;\; & 1\;\;\;\;\; & 1\;\;\;\;\; & 1\;\;\;\;\;& \cdots\;\;\;\;\; & 1\\[3pt] 1\;\;\;\;\; & \omega\;\;\;\;\; & \omega^2\;\;\;\;\; & \omega^3\;\;\;\;\; & \cdots\;\;\;\;\; & \omega^{n-1} \\[3pt] 1\;\;\;\;\; & \omega^2\;\;\;\;\; & \omega^4\;\;\;\;\; & \omega^6\;\;\;\;\; & \cdots\;\;\;\;\; & \omega^{2(n-1)}\\[3pt] 1\;\;\;\;\; & \omega^3\;\;\;\;\; & \omega^6\;\;\;\;\; & \omega^9\;\;\;\;\; & \cdots\;\;\;\;\; & \omega^{3(n-1)}\\[3pt] \vdots\;\;\;\;\; & \vdots\;\;\;\;\; & \vdots\;\;\;\;\; & \vdots\;\;\;\;\; & \ddots\;\;\;\;\; & \vdots\\[3pt] 1\;\;\;\;\; & \omega^{n-1}\;\;\;\;\; & \omega^{2(n-1)}\;\;\;\;\; & \omega^{3(n-1)}\;\;\;\;\; & \cdots\;\;\;\;\; & \omega^{(-1)(n-1)} \end{bmatrix}. \end{equation*}
Clearly, each entry of U has modulus
$1/\sqrt{n}$
. So, by Proposition 3.23, there exists a unitary orthonormal basis for
$A/\mathbb{C}$
with respect to the Markov trace.
The preceding observation will prove to be very crucial in the next section. Thus, it seems it is worthwhile to investigate in detail the existence of unitary basis of the finite dimensional inclusions
$B\subset A$
, which, in turn, may prove to be useful in answering the question of Popa for hyperfinite irreducible subfactors.
Lemma 3.24. Let
$N \subset M$
be a finite index regular subfactor of type
$II_1$
. Then,
${\mathrm{tr}_M}_{|_{N'\cap M}}$
is the Markov trace for the inclusion
$\mathbb{C} \subset N'\cap M$
.
Proof. As pointed out in Proposition 3.7, it can be extracted from the proof of [Reference Bakshi and Gupta2, Theorem 3.12] that the Watatani index ([Reference Watatani25]) of
$\textrm{Ind}(\mathrm{tr}_M)$
is a scalar. Thus, it follows from [Reference Watatani25, Corollary 2.4.3] and [Reference Jones and Sunder11, Proposition 3.2.3] that
${\mathrm{tr}_M}_{|_{N'\cap M}}$
is indeed the Markov trace for the inclusion
$\mathbb{C}\subset N^{\prime}\cap M$
.
Proof of Theorem 3.21: Consider the intermediate von Neumann subalgebra
$\mathcal{R}\;:\!=\;N\vee(N^{\prime}\cap M)$
. Then, as in the proof of [Reference Bakshi and Gupta2, Lemma 3.4], we see that
$(\mathbb{C},N^{\prime}\cap M, N,\mathcal{R})$
is a nondegenerate commuting square. By Lemma 3.24,
$\mathrm{tr}_M|_{N'\cap M}$
is the Markov trace for
$\mathbb{C} \subset N'\cap M$
; so, by Proposition 3.23, there exists a unitary orthonormal basis, say,
$\{u_i\;:\;i\in I\}$
for
$N^{\prime}\cap M$
over
$\mathbb{C}$
. Then, by Lemma 3.9,
$\{ u_i\;:\;i \in I\}$
is a unitary orthonormal basis for
$\mathcal{R}/N$
as well.
On the other hand, since
$N \subset M$
is regular, from [Reference Bakshi and Gupta2, Proposition 3.7], we know that
$M/\mathcal{R}$
also has a unitary orthonormal basis, say,
$\{v_j\;:\;j\in J\}$
. We assert that
$\{v_ju_i\;:\;i\in I, j\in J\}$
is a unitary orthonormal basis for
$M/N$
. It is easy to see that
$\{v_ju_i\;:\;i\in I\;\textrm{and}\;j\in J\}$
is a Pimsner–Popa basis for
$M/N$
. Also,
\begin{equation*}E^M_N(u^*_i v_j^*v_ku_l)=E^{\mathcal{R}}_N\circ E^M_{\mathcal{R}}(u^*_iv_j^*v_ku_l)=E^{\mathcal{R}}_N\big(u^*_iE^M_{\mathcal{R}}(v^*_jv_k)u_l\big)=\delta_{j,k}\delta_{i,l}.\end{equation*}
Thus,
$\{v_ju_i\;:\;i\in I\;\textrm{and}\;j\in J\}$
is a unitary orthonormal basis for
$M/N$
.
3.3 Two-sided basis versus unitary orthonormal basis
Some preliminary observations suggest that the above questions of Jones (Question 3.1) and Popa (Question 3.17) may be intimately interrelated in the case of integer index (extremal) subfactors. Below, we illustrate some such connections.
The following fact is implicit in [Reference Ceccherini-Silberstein6].
Lemma 3.25 [Reference Ceccherini-Silberstein6]. Let
$N\subset M$
be a subfactor of finite index. If
$M/N$
has a unitary orthonormal basis, then
$M_1/M$
admits a two-sided unitary orthonormal basis.
In particular,
$N \subset M$
is extremal.
Proof. This proof is extracted verbatim from [Reference Ceccherini-Silberstein6]. Suppose
$\{\lambda_i\;:\;1 \leq i \leq n\}$
is a unitary orthonormal basis for
$M/N$
. Thus,
$\sum_i \lambda_ie_1\lambda^*_i=1.$
Now, put
\begin{equation*}v_k=\sum_{i=0}^{n-1} {\omega}^{ki} \lambda_ie_1\lambda^*_i, 0 \leq k\leq n-1,\end{equation*}
where
$\omega$
is an nth root of unity. In [Reference Ceccherini-Silberstein6, Proposition 3.24], it has been shown that
$\{v_k\}$
is a unitary orthonormal basis for
$M_1/M$
. Clearly, this is two sided.
Next, recall that
$N\subset M$
is extremal if and only if
$M\subset M_1$
is extremal—see, for instance, [Reference Popa20]. Since
$M_1/M$
has a two-sided basis, it is easily seen (see [Reference Bakshi and Gupta2]) that it is extremal.
Proposition 3.26. Let
$N \subset M$
be a finite index hyperfinite subfactor of type
$II_1$
with finite depth. If
$M/N$
has a unitary orthonormal basis, then it also has a two-sided unitary orthonormal basis.
Proof. By Lemma 3.25, it follows that
$M_1/M$
, and hence,
$M_2/M_1$
has a two-sided unitary orthonormal basis. It is known that the standard invariants of the extremal subfactors
$N \subset M$
and
$M_1 \subset M_2$
are isomorphic. Thus, by Popa’s classification result (see [Reference Popa20]),
$N \subset M$
and
$M_1 \subset M_2$
, both being hyperfinite, are isomorphic. Hence,
$N \subset M$
has a two-sided basis. This completes the proof.
It will be good to know an answer of the following natural question.
Question 3.27. If
$N\subset M$
is a finite depth integer index subfactor of type
$II_1$
, then is it true that
$M/N$
has a unitary orthonormal basis if and only if
$M/N$
has a two-sided Pimsner–Popa basis?
Remark 3.28. Note that even if it can be shown that a finite index subfactor with a two-sided basis also admits a unitary orthonormal basis, then in view of [Reference Bakshi and Gupta2], it will follow that Conjecture 3.20 holds true.
4. Regular subfactors and weak Kac algebras
As recalled in the introduction, a finite index irreducible regular inclusion of
$II_1$
-factors is always of the form
$N \subset N \rtimes G$
with respect to an outer action of a finite group G. It is then natural to ask what happens if we drop the irreducibility condition.
Remark 4.1. Employing Szymański’s characterization of depth 2 (irreducible) subfactors, Ceccherini-Silberstein (in [Reference Ceccherini-Silberstein6, Theorem 4.6]) asserted that every finite index regular subfactor
$N \subset M$
of type
$II_1$
is of the form
$N \subset N \rtimes H$
with respect to an outer action of a finite dimensional Hopf
$*$
-algebra H on N. However, it had the following obvious oversight:
If his assertion is true, then it will automatically force
$N\subset M$
to be irreducible, whereas he has claimed to have characterized regular subfactors sans irreducibility.
In fact, Ceccherini–Silberstein’s oversight stems from an incomplete proof of an assertion made in [Reference Ceccherini-Silberstein6, Theorem 4.5], as explained later:
In the proof of [Reference Ceccherini-Silberstein6, Theorem 4.6], in view of [Reference Ceccherini-Silberstein6, Theorem 4.5], a unitary orthonormal basis
$\{\lambda_i\}$
is chosen for
$M/N$
and then it is deduced that
\begin{equation*} N^{\prime}\cap M_1=\textrm{Alg}\{\lambda_ie_1\lambda^*_i\;:\;i\in I\}.\end{equation*}
Note that, the family
$\{\lambda_ie_1\lambda^*_i\}$
consists of mutually orthogonal projections with
$\sum_i \lambda_ie_1\lambda^*_i= 1$
. Thus, if
$N\subset M$
is regular with finite index, then according to [Reference Ceccherini-Silberstein6, Theorem 4.6],
$N^{\prime}\cap M_1$
is always commutative. However, this is known to be untrue. For instance, taking an irreducible regular subfactor
$K\subset L$
and putting
$N=\mathbb{C}\otimes K$
and
$M=M_n(\mathbb C)\otimes L$
, it can be seen that
$N\subset M$
is regular (see Lemma 4.2) with integer index and
$N^{\prime}\cap M \cong M_n(\mathbb C)$
; so that
$N'\cap M_1$
is not commutative.
So, the question of characterizing (finite index) regular subfactors of type
$II_1$
is still unresolved.
Lemma 4.2. Let
$N\subset M$
be a regular inclusion of von Neumann algebras. Then,
$\mathbb{C} \otimes N\subset M_n \otimes M$
is also regular.
Proof. Note that
$\{ u \otimes v\;:\;u \in U(n), v \in \mathcal{N}_M(N)\}\subseteq \mathcal{N}_{M_n \otimes M}(\mathbb{C} \otimes N)$
. Thus,
\begin{equation*}[*\textrm{-alg}\, U(n)] \otimes [*\textrm{-alg}\, \mathcal{N}_M(N) ] \subseteq*\textrm{-alg}\, \mathcal{N}_{M_n \otimes M} (\mathbb{C} \otimes N).\end{equation*}
It is enough to show that
\begin{equation*}\{ u \otimes z\;:\;u \in U(n), z \in M\}\subset \mathcal{N}_{M_n \otimes M} (\mathbb{C} \otimes N)''.\end{equation*}
Let
$z \in M$
and
$u \in U(n)$
. Then, there exists a net
$\{x_i\}$
in
$*\textrm{-alg}\, \mathcal{N}_M(N)$
such that
$x_i\stackrel{\mathrm{WOT}}{\longrightarrow} z$
. Thus,
$\{u \otimes x_i\}$
is a net in
$ [*\textrm{-AC}\, U(n)] \otimes [*\textrm{-alg}\, \mathcal{N}_M(N)]$
, which is a
$*$
-subalgebra of
$*\textrm{-alg}\, \mathcal{N}_{M_n \otimes M} (\mathbb{C} \otimes N)$
. Also,
$u \otimes x_i\stackrel{\mathrm{WOT}}{\longrightarrow} u \otimes z$
. Hence,
$u\otimes z \in \left(*\textrm{-alg}\, \mathcal{N}_{M_n \otimes M} (\mathbb{C}\otimes N)\right)''$
.
Theorem 4.3. Let
$N\subset M$
be a finite index regular inclusion of type
$II_1$
-factors such that
$N^{\prime}\cap M$
is either simple or commutative. Then,
$N\subset M$
is of depth at most 2.
Proof. Note that, by Theorem 3.21, M admits a unitary orthonormal basis over N. More precisely, taking
$\mathcal{R}\;:\!=\;N \vee (N'\cap M)$
, we saw that
$\mathcal{R}/N$
admits a unitary orthonormal basis, say,
$\{u_i\;:\;i\in I\}\subset \mathcal{U}(N^{\prime}\cap M)\subset \mathcal{N}_M(N)$
;
$M/\mathcal{R}$
admits a unitary orthonormal basis
$\{v_j\;:\;j\in J\}\subset \mathcal{N}_M(N)$
; and then, taking
$w_{i,j}=v_ju_i$
we saw that
$\{w_{i,j}\;:\;i\in I, j\in J\}$
is a unitary orthonormal basis for
$M/N$
and
$\{w_{i,j}\;:\;(i, j) \in I \times J\}\subset \mathcal{N}_M(N).$
In particular, we have
$\sum_{i,j} w_{i,j}e_1w^*_{i,j}=1.$
Now, note that for any unitary
$u\in N$
we have
$w^*_{i,j}uw_{i,j}=v_{i,j}$
for some unitary
$v_{i,j}\in N$
. Thus,
\begin{equation*} u(w_{i,j}e_1w^*_{i,j})u^*=w_{i,j}v_{i,j}e_1v^*_{i,j}w^*_{i,j}= w_{i,j}e_1w^*_{i,j}. \end{equation*}
This implies that
$w_{i,j}e_1w^*_{i,j}\in N^{\prime}\cap M_1$
for all
$(i,j)\in I\times J$
. Further, we readily see that
\begin{equation*} (w_{i,j}e_1w^*_{i,j})e_2(w_{i,j}e_1w^*_{i,j})=\tau w_{i,j}e_1w^*_{i,j} \ \forall\ (i, j) \in I \times J. \end{equation*}
Hence,
$w_{i,j}e_1w^*_{i,j}\in (N^{\prime}\cap M_1)e_2 (N^{\prime}\cap M_1)$
for every
$(i,j)\in I\times J$
. Now, since
$1=\sum_{i,j} w_{i,j}e_1w^*_{i,j}$
and that
$(N^{\prime}\cap M_1)e_2(N^{\prime}\cap M_1)$
is an ideal in
$N^{\prime}\cap M_2$
, it follows that
$(N^{\prime}\cap M_1)e_2 (N^{\prime}\cap M_1)=N^{\prime}\cap M_2.$
Thus, in view of [Reference Goodman, de la Harpe and Jones8, Theorem 4.6.3],
$N \subset M$
has depth at most 2.
Corollary 4.4. If
$N\subset M$
is a finite index regular inclusion of type
$II_1$
factors such that
$N^{\prime}\cap M$
is commutative, then it has depth 2.
Few remarks are in order which tell that the converse of the above result need not be true.
Remark 4.5.
-
(1) A depth 2 subfactor having commutative first relative commutant need not be regular. For example, consider a finite dimensional Hopf
$C^*$
-algebra (that is, a Kac algebra) K, which is not a group algebra, acting minimally on a type
$II_1$
factor N. Then,
$N\subset N\rtimes K$
is a depth 2 subfactor. Being irreducible, this subfactor is not regular. -
(2) Notice that a depth 2 regular subfactor
$N\subset M$
may have a noncommutative first relative commutant. As an example, one may look at the subfactor illustrated in Remark 4.1.
Theorem 4.6. Let
$N\subset M$
be a finite index regular inclusion of
$II_1$
-factors with commutative relative commutant
$N^{\prime}\cap M$
. Then, there exists a biconnected weak Kac algebra K and a minimal action of K on N such that
$N\subset M$
is isomorphic to
$N\subset N\rtimes K$
.
Proof. By Theorem 4.3 and Corollary 4.4, we observe that
$N \subset M$
has depth 2. Choose a 2-step downward basic construction
$N_{-2}\subset N_{-1}\subset N\subset M$
. Then,
$N_{-2}\subset N_{-1}$
is also of depth two – see Corollary 3.13. Let
$K\;:\!=\;N'_{\!\!-1}\cap M$
. From [Reference Nikshych and Vainerman13], it will follow that K admits a biconnected weak Kac algebra structure (with an appropriate action on N) provided the Watatani index of
${\mathrm{tr}_N}_{|_{N'_{\!\!-1}\cap N}}$
is a scalar.
By Proposition 3.7, we know that
$\textrm{Ind}({\mathrm{tr}_M}_{|_{N^{\prime}\cap M}})$
is a scalar. Let
$J\;:\;L^2(N) \rightarrow L^2(N)$
denote the modular conjugation operator. Since
$N_{-1} \subset N \subset M$
is an instance of basic construction, the map
$B(L^2(N)) \ni x \mapsto JxJ \in B(L^2(N))$
is an anti-isomorphism that maps
$N'_{\!\!-1}$
onto M and
$\mathrm{tr}_M = \mathrm{tr}_{N'_{\!\!-1}}\circ [J(\cdot) J]$
; so that
$ {\mathrm{tr}_M}_{|_{N'\cap M}} = {\big({\mathrm{tr}_{N'_{\!\!-1}}}\circ [J (\cdot) J]\big)}_{|_{N'\cap M}}.$
Also,
$J(N'\cap M) = N'_{\!\!-1}\cap N$
; so that,
$N'_{\!\!-1}\cap N$
is commutative and
$(\mathbb{C} \subset N'\cap M) \cong (\mathbb{C} \subset N'_{\!\!-1}\cap N)$
. Further, since
$N_{-1}\subset N$
is extremal (being of depth 2), we have
\begin{equation*}{\mathrm{tr}_N}_{|_{N'_{\!\!-1}\cap N }} = {\mathrm{tr}_{N'_{\!\!-1}}}_{|_{N'_{\!\!-1}\cap N }}.\end{equation*}
Thus,
${\mathrm{tr}_M}_{|_{N'\cap M}}$
and
${\mathrm{tr}_N}_{|_{N'_{\!\!-1}\cap N }}$
have same trace vectors and hence
\begin{equation*} \mathrm{Ind}({\mathrm{tr}_N}_{|_{N'_{\!\!-1}\cap N}}) = \textrm{Ind}({\mathrm{tr}_M}_{|_{N^{\prime}\cap M}}) ,\end{equation*}
which is a scalar. Thus, by [Reference Nikshych and Vainerman13, Corollary 4.7 and Theorem 4.17], K admits a weak Kac algebra structure, which is also biconnected, by [Reference Nikshych and Vainerman13, Remark 5.8 (ii)]. Further, by [Reference Nikshych and Vainerman13, Propositions 6.1 and 6.3, and Remark 6.4 (i)], K acts minimally on N such that
$N \subset M$
is isomorphic to
$N \subset N\rtimes K$
. This completes the proof.
We end our discussion with a few well-known classes of reducible regular subfactors.
Example 4.7.
-
(1) If a finite group G acts innerly on a
$II_1$
factor N in such a way that
$M= N\rtimes G$
is a
$II_1$
factor, then the inclusion
$N\subset M$
is regular and
$N^{\prime}\cap M$
is nontrivial.Footnote 3
-
(2) Suppose N is a type
$II_1$
factor. Then, the depth 1 subfactor
$\mathbb{C}\otimes N\subset M_n(\mathbb{C})\otimes N$
is an example of a regular subfactor with simple first relative commutant (
$\cong M_n(\mathbb{C})$
). -
(3) Let P be a
$II_1$
-factor and
$\alpha \in \textrm{Aut}(P)$
. Consider the diagonal inclusion which is well known to be a subfactor of type
\begin{equation*} N\;:\!=\;\left\{\begin{pmatrix}x\;\;\;\;\; & 0\;\;\;\;\; \\ 0\;\;\;\;\; & \alpha(x) \end{pmatrix} \;:\; x \in P\right\} \subset M\;:\!=\;P \otimes M_2(\mathbb{C}), \end{equation*}
$II_1$
with
$[M\;:\;N]= 4$
. If
$\alpha$
is an outer automorphism, then it is well known and can be easily seen that Next, recall the Connes’ outer conjugacy invariants
\begin{equation*} N'\cap M =\{\mathrm{diag}(\lambda,\mu)\;:\;\lambda, \mu \in \mathbb{C} \}. \end{equation*}
$p_0(\alpha)\in \mathbb N$
and
$\gamma (\alpha)\in \mathbb{C}$
given by
$\{ n \in \mathbb Z\;:\;\alpha^n \in \mathrm{Inn}(P)\} = p_0(\alpha) \mathbb Z$
and
$\alpha (u) = \gamma (\alpha) u$
for some
$u \in \mathcal{U}(P)$
with
$\alpha^{p_0(\alpha)}=\mathrm{Ad}_u$
. Note that, if
$p_0(\alpha) = 2$
(in particular,
$\alpha$
is outer) and
$\gamma(\alpha) \neq 1$
, then it is known that
$N \subset M$
has depth 2 - see [Reference Nikshych and Vainerman13, Section 7]. We show that
$N \subset M$
is regular as well, i.e.,
${\mathcal{N}_M(N)}^{\prime \prime}=M$
.
Let
$Q\;:\!=\; {\mathcal{N}_M(N)}^{\prime \prime}$
and fix a
$1\neq u\in\mathcal{U}(P)$
such that
${\alpha}^2=\mathrm{Ad}_u$
. Since it is clear that
\begin{equation*}\{\mathrm{diag}(1,c)\;:\; c \in \mathbb{T}\setminus \{1\} \} \subseteq {\mathcal{N}}_M(N)\setminus N, \end{equation*}
$Q\neq N$
. In view of the fact that
$N\subset M$
is a maximal subfactor (see, for instance, [Reference Teruya and Watatani24, Theorem 5.4]), it is sufficient to show that Q is a factor. To this end, we show that
$Q^{\prime}\cap Q\neq \{\mathrm{diag}(\lambda, \mu) \;:\; \lambda, \mu \in \mathbb{C}\}$
; this will then prove that Q is a factor as
$Q^{\prime}\cap Q\subseteq N^{\prime}\cap M \cong \mathbb{C}\oplus \mathbb{C}$
.
Suppose, on the contrary, that
$Q^{\prime}\cap Q = \{\mathrm{diag}(\lambda , \mu)\;:\;\lambda, \mu \in \mathbb{C}\}$
. Then, we see that the projection
$p\;:\!=\; \begin{pmatrix} 1& 0 \\ 0 & 0 \end{pmatrix}$
belongs (to
$Q'\cap Q$
and hence) to Q; thus, We assert that the diagonal subalgebra
\begin{equation*} \{\mathrm{diag}(x,y)\;:\;x,y \in P\}= pMp\oplus (1-p)M(1-p)=pNp\oplus (1-p)N(1-p)\subseteq Q. \end{equation*}
$ D \;:\!=\; \{\mathrm{diag}(x,y)\;:\;x,y \in P\}$
is a maximal von Neumann subalgebra of M, i.e.,
$\{ D, a\}''=M$
for any
$a \in M \setminus D$
. Assuming this assertion, if we consider
$x\;:\!=\; \begin{pmatrix} 0 & 1 \\ u & 0 \end{pmatrix}\in M$
, then
$x\notin D$
and a simple calculation shows that
$x \in \mathcal{N}_M(N)\subset Q$
; so, by the maximality of D in M, it follows that
$Q = M$
(a factor), which contradicts the assumption that
$Q'\cap Q \cong \mathbb{C} \oplus \mathbb{C}$
. Hence, it just remains to prove the maximality of D in M. Let
$y \in M\setminus D$
. Without loss of generality, we can assume that
$y=\begin{pmatrix}0 & w \\ z & 0 \end{pmatrix} $
with
$(w,z) \neq (0,0)$
. Further, we can assume that
$w \neq 0$
. Since P is a
$II_1$
-factor, it is algebraically simple; so, we have
$PwP =P$
. Thus, for each
$0 \neq a\in P$
, we have
$a= \sum_{i} x_i w y_i$
for a finite collection
$\{x_i, y_i\;:\;1 \leq i \leq n\}$
in P. Thus, Likewise,
\begin{equation*}\begin{pmatrix} 0\;\;\;\;\; & a \\ 0\;\;\;\;\; & 0 \end{pmatrix} = \sum_i \begin{pmatrix} x_i\;\;\;\;\; & 0 \\ 0\;\;\;\;\; & 0 \end{pmatrix}\begin{pmatrix} 0\;\;\;\;\; & w \\ z\;\;\;\;\; & 0 \end{pmatrix} \begin{pmatrix} 0 & 0 \\ 0 & y_i \end{pmatrix}\in \{D, y\}''.\end{equation*}
$\begin{pmatrix} 0 & 0 \\ a & 0 \end{pmatrix} \in \{D,y\}''$
. Hence,
$\begin{pmatrix} 0 & a \\ b & 0 \end{pmatrix} \in \{D,y\}''$
for all
$a, b \in P$
, which then implies that
$\{D, y\}''= M$
, i.e., D is maximal in M.
Acknowledgements
The authors would like to thank Yongle Jiang for bringing last-Example 4.7(3) to our notice and Vijay Kodiyalam, Sebastien Palcoux and Leonid Vainerman for many fruitful exchanges. The authors would also like to mark their note of appreciation to T. Ceccherini-Silberstein for acknowledging our concerns related to the oversights in some of his proofs (from [Reference Ceccherini-Silberstein6]).
