Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-15T01:38:59.758Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE AND CONCENTRATION OF SOLUTION FOR A NON-LOCAL REGIONAL SCHRÖDINGER EQUATION WITH COMPETING POTENTIALS

Published online by Cambridge University Press:  25 July 2018

CLAUDIANOR O. ALVES  and
CÉSAR E. TORRES LEDESMA
CLAUDIANOR O. ALVES
Affiliation:
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, CEP: 58429-900 Campina Grande, PB, Brazil E-mail: coalves@mat.ufcg.edu.br
CÉSAR E. TORRES LEDESMA
Affiliation:
Departamento de Matemáticas, Universidad Nacional de Trujillo, Av. Juan Pablo II s/n. Trujillo-Perú, Peru E-mail: ctl_576@yahoo.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the existence and concentration phenomena of solutions for the following non-local regional Schrödinger equation

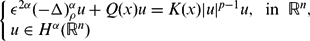$$\begin{equation*} \left\{ \begin{array}{l} \epsilon^{2\alpha}(-\Delta)_\rho^{\alpha} u + Q(x)u = K(x)|u|^{p-1}u,\;\;\mbox{in}\;\; \mathbb{R}^n,\\ u\in H^{\alpha}(\mathbb{R}^n) \end{array} \right. \end{equation*}$$
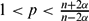where ϵ is a positive parameter, 0 < α < 1, $1<p<\frac{n+2\alpha}{n-2\alpha}$, n > 2α; (−Δ)ρα is a variational version of the regional fractional Laplacian, whose range of scope is a ball with radius ρ(x) > 0, ρ, Q, K are competing functions.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 61 , Issue 2 , May 2019 , pp. 441 - 460
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

References

REFERENCES

1. Cheng, M., Bound state for the fractional Schrödinger equation with unbounded potential, J. Math. Phys. 53 (2012), 043507.Google Scholar
2. Chen, G. and Zheng, Y., Concentration phenomenon for fractional nonlinear Schrödinger equations, Comm. Pure Appl. Anal. 13 (6) (2014), 2359–2376.Google Scholar
3. Dávila, J., Del Pino, M. and Wei, J., Concentrating standing waves for the fractional nonlinear Schrödinger equation, J. Differ. Equ. 256 (2014), 858–892.Google Scholar
4. Dipierro, S., Palatucci, G. and Valdinoci, E. Valdinoci, Existence and symmetry results for a Schrödinger type problem involving the fractional Laplacian, Matematiche 68 (2013), 201–216.Google Scholar
5. Felmer, P., Quaas, A. and Tan, J., Positive solutions of nonlinear Schrödinger equation with the fractional laplacian, Proc. Edinburgh: Sect. A Math. 142 (6) (2012), 1237–1262.Google Scholar
6. Felmer, P. and Torres, C., Non-linear Schrödinger equation with non-local regional diffusion, Calc. Var. Partial Diff. Equ. 54 (2015), 75–98.Google Scholar
7. Felmer, P. and Torres, C., Radial symmetry of ground states for a regional fractional nonlinear Schrödinger equation, Comm. Pure Appl. Anal. 13 (2014), 2395–2406.Google Scholar
8. Guan, Q.-Y., Integration by parts formula for regional fractional Laplacian, Commun. Math. Phys. 266 (2006), 289–329.Google Scholar
9. Guan, Q.-Y. and Ma, Z. M., The reflected α-symmetric stable processes and regional fractional Laplacian. Probab. Theory Relat. Fields 134 (2006), 649–694.Google Scholar
10. Ishii, H. and Nakamura, G., A class of integral equations and approximation of p-Laplace equations, Calc. Var. 37 (2010), 485–522.Google Scholar
11. Secchi, S., Ground state solutions for nonlinear fractional Schrödinger equations in ℝn, J. Math. Phys. 54 (2013), 031501.Google Scholar
12. Shang, X. and Zhang, J., Concentrating solutions of nonlinear fractional Schrödinger equation with potentials, J. Differ. Equ. 258 (2015), 1106–1128.Google Scholar
13. Shang, X. and Zhang, J., Existence and multiplicity solutions of fractional Schrödinger equation with competing potential functions, Complex Variables Elliptic Equ. 61 (2016), 1435–1463.Google Scholar
14. Torres, C., Symmetric ground state solution for a non-linear Schrödinger equation with non-local regional diffusion, Complex Variables Elliptic Equ., http://dx.doi.org/10.1080/17476933.2016.1178730 (2016)Google Scholar
15. Torres, C., Multiplicity and symmetry results for a nonlinear Schrödinger equation with non-local regional diffusion, Math. Meth. Appl. Sci. 39 (2016), 2808–2820.Google Scholar
16. Torres, C., Nonlinear Dirichlet problem with non local regional diffusion, Fract. Cal. Appl. Anal. 19 (2) (2016), 379–393.Google Scholar
17. Willem, M., Minimax theorems (Birkhäuser, Boston, Basel, Berlin, 1996).Google Scholar