No CrossRef data available.
Article contents
Hausdorff dimension of sets defined by almost convergent binary expansion sequences
Published online by Cambridge University Press: 13 March 2023
Abstract
In this paper, we study the Hausdorff dimension of sets defined by almost convergent binary expansion sequences. More precisely, the Hausdorff dimension of the following set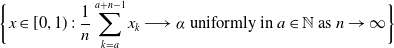 \begin{align*} \bigg\{x\in[0,1)\;:\;\frac{1}{n}\sum_{k=a}^{a+n-1}x_{k}\longrightarrow\alpha\textrm{ uniformly in }a\in\mathbb{N}\textrm{ as }n\rightarrow\infty\bigg\} \end{align*}
\begin{align*} \bigg\{x\in[0,1)\;:\;\frac{1}{n}\sum_{k=a}^{a+n-1}x_{k}\longrightarrow\alpha\textrm{ uniformly in }a\in\mathbb{N}\textrm{ as }n\rightarrow\infty\bigg\} \end{align*} $ \alpha\in[0,1] $. This completes a question considered by Usachev [Glasg. Math. J. 64 (2022), 691–697] where only the dimension for rational
$ \alpha\in[0,1] $. This completes a question considered by Usachev [Glasg. Math. J. 64 (2022), 691–697] where only the dimension for rational  $ \alpha $ is given.
$ \alpha $ is given.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust



