Hostname: page-component-6dbcb7884d-64ff6 Total loading time: 0 Render date: 2025-02-14T02:53:25.709Z Has data issue: false hasContentIssue false
  • English
  • Français

A QUOTIENT OF THE LUBIN–TATE TOWER

Part of: Algebraic number theory: local and $p$-adic fields Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  27 July 2017

JUDITH LUDWIG
JUDITH LUDWIG*
Affiliation:
Max Planck Institute for Mathematics, Vivatsgasse 7, 53111 Bonn, Germany; ludwig@mpim-bonn.mpg.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article we show that the quotient 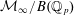${\mathcal{M}}_{\infty }/B(\mathbb{Q}_{p})$ of the Lubin–Tate space at infinite level 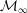${\mathcal{M}}_{\infty }$ by the Borel subgroup of upper triangular matrices 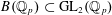$B(\mathbb{Q}_{p})\subset \operatorname{GL}_{2}(\mathbb{Q}_{p})$ exists as a perfectoid space. As an application we show that Scholze’s functor 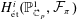$H_{\acute{\text{e}}\text{t}}^{i}(\mathbb{P}_{\mathbb{C}_{p}}^{1},{\mathcal{F}}_{\unicode[STIX]{x1D70B}})$ is concentrated in degree one whenever $\unicode[STIX]{x1D70B}$ is an irreducible principal series representation or a twist of the Steinberg representation of 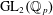$\operatorname{GL}_{2}(\mathbb{Q}_{p})$.

MSC classification

Primary: 11S37: Langlands-Weil conjectures, nonabelian class field theory
Secondary: 14G22: Rigid analytic geometry
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e17
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2017

References

Artin, M., Grothendieck, A. and Verdier, J.-L., Theorie de Topos et Cohomologie Etale des Schemas I, II, III, Lecture Notes in Mathematics, 269, 270, 305 (Springer, New York, 1971).Google Scholar
Breuil, C., ‘The emerging p-adic Langlands programme’, inProceedings of the International Congress of Mathematicians, Vol. II (Hindustan Book Agency, New Delhi, 2010), 203–230.Google Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., ‘Patching and the $p$ -adic local Langlands program for $\text{GL}(2,\mathbb{Q}_{p})$ ’, Preprint, 2016, arXiv:1609.06902v1.Google Scholar
Caraiani, A. and Scholze, P., ‘On the generic part of the cohomology of compact unitary Shimura varieties’, Ann. of Math. (2) to appear, Preprint, 2015, arXiv:1511.02418v1.Google Scholar
Gee, T. and Kisin, M., ‘The Breuil–Mézard conjecture for potentially Barsotti–Tate representations’, Forum Math. Pi 2 (2014), e1, 56.CrossRefGoogle Scholar
Hansen, D., ‘Quotients of adic spaces’, Math. Res. Lett., (2016) to appear, http://www.math.columbia.edu/∼hansen/overcon.pdf.Google Scholar
Huber, R., ‘A generalization of formal schemes and rigid analytic varieties’, Math. Z. 217(4) (1994), 513–551.CrossRefGoogle Scholar
Huber, R., Étale Cohomology of Rigid Analytic Varieties and Adic Spaces, Aspects of Mathematics, E30 (Friedr. Vieweg & Sohn, Braunschweig, 1996).Google Scholar
de Jong, J. and van der Put, M., ‘Étale cohomology of rigid analytic spaces’, Doc. Math. 1(01) (1996), 1–56 (electronic).Google Scholar
Rapoport, M. and Zink, Th., Period Spaces for p-divisible Groups, Annals of Mathematics Studies, 141 (Princeton University Press, Princeton, NJ, 1996).Google Scholar
Scholze, P., ‘On torsion in the cohomology of locally symmetric spaces’, Ann. of Math. (2) 182(3) (2015), 945–1066.Google Scholar
Scholze, P., ‘ p-adic Hodge theory for rigid-analytic varieties’, Forum Math. Pi 1 (2013), e1, 77 pp.CrossRefGoogle Scholar
Scholze, P., ‘On the p-adic cohomology of the Lubin–Tate tower’, Preprint, 2015, arXiv:1506.04022.Google Scholar
Scholze, P. and Weinstein, J., ‘Moduli of p-divisible groups’, Camb. J. Math. 1(2) (2013), 145–237.Google Scholar
Weinstein, J., ‘Peter Scholze’s lectures on $p$ -adic geometry’, (2015), http://math.bu.edu/people/jsweinst/Math274/ScholzeLectures.pdf.Google Scholar
Weinstein, J., ‘Semistable models for modular curves of arbitrary level’, Invent. Math. 205(2) (2016), 459–526.Google Scholar