Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-10T11:13:29.710Z Has data issue: false hasContentIssue false
  • English
  • Français

THE EXPECTED JAGGEDNESS OF ORDER IDEALS

Part of: Ordered sets Computational aspects in algebraic geometry Algebraic combinatorics

Published online by Cambridge University Press:  15 March 2017

MELODY CHAN ,
SHAHRZAD HADDADAN ,
SAM HOPKINS  and
LUCA MOCI
MELODY CHAN
Affiliation:
Department of Mathematics, Brown University, Providence, RI, USA; mtchan@math.brown.edu
SHAHRZAD HADDADAN
Affiliation:
Dipartimento di Informatica, Sapienza University of Rome, Rome, Italy; Shahrzad.Haddadan@gmail.com
SAM HOPKINS
Affiliation:
Department of Mathematics, MIT, Cambridge, MA, USA; shopkins@mit.edu
LUCA MOCI
Affiliation:
IMJ-PRG, Université Paris 7, Paris, France; lucamoci@hotmail.com

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The jaggedness of an order ideal 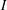$I$ in a poset 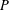$P$ is the number of maximal elements in 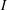$I$ plus the number of minimal elements of 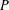$P$ not in 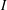$I$. A probability distribution on the set of order ideals of 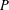$P$ is toggle-symmetric if for every 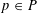$p\in P$, the probability that 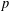$p$ is maximal in 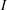$I$ equals the probability that 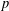$p$ is minimal not in 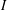$I$. In this paper, we prove a formula for the expected jaggedness of an order ideal of 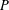$P$ under any toggle-symmetric probability distribution when 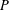$P$ is the poset of boxes in a skew Young diagram. Our result extends the main combinatorial theorem of Chan–López–Pflueger–Teixidor [Trans. Amer. Math. Soc., forthcoming. 2015, arXiv:1506.00516], who used an expected jaggedness computation as a key ingredient to prove an algebro-geometric formula; and it has applications to homomesies, in the sense of Propp–Roby, of the antichain cardinality statistic for order ideals in partially ordered sets.

MSC classification

Primary: 05E18: Group actions on combinatorial structures 06A07: Combinatorics of partially ordered sets
Secondary: 14Q05: Curves
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e9
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Aitken, A. C., ‘The monomial expansion of determinantal symmetric functions’, Proc. Roy. Soc. Edinburgh. Sect. A 61 (1943), 300–310.Google Scholar
Ayyer, A., Schilling, A. and Thiéry, N. M., ‘Spectral gap for random-to-random shuffling on linear extensions’, Exp. Math. 26(1) (2017), 22–30.Google Scholar
Bloom, J., Pechenik, O. and Saracino, D., ‘Proofs and generalizations of a homomesy conjecture of Propp and Roby’, Discrete Math. 339(1) (2016), 194–206.Google Scholar
Brouwer, A. E. and Schrijver, A., On the period of an operator, defined on antichains. Mathematisch Centrum, Amsterdam, 1974. Mathematisch Centrum Afdeling Zuivere Wiskunde ZW 24/74.Google Scholar
Cameron, P. J. and Fon-Der-Flaass, D. G., ‘Orbits of antichains revisited’, European J. Combin. 16(6) (1995), 545–554.Google Scholar
Chan, M., López Martín, A., Pflueger, N. and Teixidor i Bigas, M., ‘Genera of Brill-Noether curves and staircase paths in Young tableaux’, Trans. Amer. Math. Soc., forthcoming. 2015, arXiv:1506.00516.Google Scholar
Einstein, D., Farber, M., Gunawan, E., Joseph, M., Macauley, M., Propp, J. and Rubinstein-Salzedo, S., ‘Noncrossing partitions, toggles, and homomesies’, Preprint, 2015, arXiv:1510.06362.Google Scholar
Eisenbud, D. and Harris, J., ‘Limit linear series: basic theory’, Invent. Math. 85(2) (1986), 337–371.Google Scholar
Gessel, I. M., ‘A historical survey of P-partitions’, inThe Mathematical Legacy of Richard P. Stanley (eds. Hersh, P., Lam, T., Pylyavskyy, P. and Reiner, V.) (American Mathematical Society, Providence, RI, 2016), 169–188.Google Scholar
Kreweras, G., ‘Sur une classe de problèmes de dénombrement liés au treillis des partitions des entiers’, Cah. BURO 6 (1965), 9–107.Google Scholar
MacMahon, P. A., Combinatory Analysis, Dover Phoenix Editions, Vol. I, II (bound in one volume) (Dover Publications, Inc., Mineola, NY, 2004), Reprint of An Introduction to Combinatory Analysis (1920) and Combinatory Analysis. Vol. I, II (1915, 1916).Google Scholar
Propp, J. and Roby, T., ‘Homomesy in the product of two chains’, Electron. J. Combin. 22(3) (2015), Paper 3, 4.Google Scholar
Reiner, V., Stanton, D. and White, D., ‘What is … cyclic sieving?’, Notices Amer. Math. Soc. 61(2) (2014), 169–171.CrossRefGoogle Scholar
Roby, T., ‘Dynamical algebraic combinatorics and the homomesy phenomenon’, inRecent Trends in Combinatorics, The IMA Volumes in Mathematics and its Applications, 159 (Springer International Publishing Switzerland, 2016), 619–652. [Cham].Google Scholar
Stanley, R. P., Enumerative Combinatorics, Vol. 2, Cambridge Studies in Advanced Mathematics, 62 (Cambridge University Press, Cambridge, 1999).Google Scholar
Stanley, R. P., Enumerative Combinatorics, 2nd edn, Vol. 1, Cambridge Studies in Advanced Mathematics, 49 (Cambridge University Press, Cambridge, 2012).Google Scholar
Striker, J., ‘The toggle group, homomesy, and the Razumov–Stroganov correspondence’, Electron. J. Combin. 22(2) (2015), Paper 2, 57.Google Scholar
Striker, J. and Williams, N., ‘Promotion and rowmotion’, European J. Combin. 33(8) (2012), 1919–1942.Google Scholar