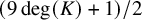1. Introduction
1.1. Average analytic ranks of elliptic curves
Let E be an elliptic curve over a number field K. The Mordell–Weil theorem states that the set of K-rational points
![]() $E(K)$
of E forms a finitely generated abelian group
$E(K)$
of E forms a finitely generated abelian group
![]() $E(K)\cong E(K)_{\text {tor}}\oplus {\mathbb Z}^r$
, where
$E(K)\cong E(K)_{\text {tor}}\oplus {\mathbb Z}^r$
, where
![]() $E(K)_{\text {tor}}$
is the finite torsion subgroup and
$E(K)_{\text {tor}}$
is the finite torsion subgroup and
![]() $r\in {\mathbb Z}_{\geq 0}$
is the rank. The study of ranks of elliptic curves has become a central topic in number theory. Despite this attention, ranks remain a mystery in many ways.
$r\in {\mathbb Z}_{\geq 0}$
is the rank. The study of ranks of elliptic curves has become a central topic in number theory. Despite this attention, ranks remain a mystery in many ways.
Birch and Swinnerton-Dyer [Reference Birch and Swinnerton-DyerBSD65] famously conjectured that the rank of an elliptic curve equals its analytic rank (i.e., the order of vanishing of its L-function at
![]() $s=1$
).
$s=1$
).
To get an understanding of ranks of elliptic curves in general, one can hope to determine the average rank of elliptic curves. As there are infinitely many elliptic curves, in order to make sense of this average, one must order elliptic curves in some way. Throughout this article, we order elliptic curves by their naive height, as defined at the end of Section 2. The average analytic rank of elliptic curves over the rational numbers was first bounded by Brumer [Reference BrumerBru92], who gave an upper bound of
![]() $2.3$
under the assumption of the Generalized Riemann Hypothesis for elliptic L-functions.Footnote
1
Under the same conditions, this bound was improved to
$2.3$
under the assumption of the Generalized Riemann Hypothesis for elliptic L-functions.Footnote
1
Under the same conditions, this bound was improved to
![]() $2$
by Heath-Brown [Reference Heath-BrownHB04], and then to
$2$
by Heath-Brown [Reference Heath-BrownHB04], and then to
![]() $25/14\approx 1.8$
by Young [Reference YoungYou06]. In a remarkable series of papers [Reference Bhargava and ShankarBS15a, Reference Bhargava and ShankarBS15b, Reference Bhargava and ShankarBS13a, Reference Bhargava and ShankarBS13b], Bhargava and Shankar bounded the average size of
$25/14\approx 1.8$
by Young [Reference YoungYou06]. In a remarkable series of papers [Reference Bhargava and ShankarBS15a, Reference Bhargava and ShankarBS15b, Reference Bhargava and ShankarBS13a, Reference Bhargava and ShankarBS13b], Bhargava and Shankar bounded the average size of
![]() $2$
-,
$2$
-,
![]() $3$
-,
$3$
-,
![]() $4$
- and
$4$
- and
![]() $5$
-Selmer groups of elliptic curves, leading to an unconditional upper bound of
$5$
-Selmer groups of elliptic curves, leading to an unconditional upper bound of
![]() $0.885$
for the average rank of elliptic curves over
$0.885$
for the average rank of elliptic curves over
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
Surprisingly little is known about average ranks of elliptic curves over number fields beyond
![]() ${\mathbb Q}$
. In Shankar’s doctoral thesis [Reference ShankarSha13], he extends his work with Bhargava on bounding
${\mathbb Q}$
. In Shankar’s doctoral thesis [Reference ShankarSha13], he extends his work with Bhargava on bounding
![]() $2$
-Selmer groups to show that the average rank of elliptic curves over number fields is bounded above by
$2$
-Selmer groups to show that the average rank of elliptic curves over number fields is bounded above by
![]() $1.5$
. However, Shankar’s result counts reduced Weierstrass equations, which differs from counting isomorphism classes. In particular, counting reduced Weierstrass equations coincides with counting isomorphism classes of elliptic curves only for the finitely many number fields with unit group
$1.5$
. However, Shankar’s result counts reduced Weierstrass equations, which differs from counting isomorphism classes. In particular, counting reduced Weierstrass equations coincides with counting isomorphism classes of elliptic curves only for the finitely many number fields with unit group
![]() $\{\pm 1\}$
and class number
$\{\pm 1\}$
and class number
![]() $1$
– namely,
$1$
– namely,
![]() ${\mathbb Q}$
and the imaginary quadratic extensions
${\mathbb Q}$
and the imaginary quadratic extensions
![]() ${\mathbb Q}(\sqrt {-d})$
for
${\mathbb Q}(\sqrt {-d})$
for
![]() $d\in \{2, 7, 11, 19, 43, 67, 163\}$
. Outside of these cases, there can be multiple reduced Weierstrass equations within the same isomorphism class of elliptic curves.
$d\in \{2, 7, 11, 19, 43, 67, 163\}$
. Outside of these cases, there can be multiple reduced Weierstrass equations within the same isomorphism class of elliptic curves.
In this article, we prove a conditional bound for the average analytic rank of isomorphism classes of elliptic curves over an arbitrary number field. This appears to be the first known bound on average ranks of isomorphism classes of elliptic curves over arbitrary number fields, as well as the first bound for average analytic ranks of elliptic curves over number fields other than
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
Theorem 1.1.1. Let K be a number field of degree d. Assume that all elliptic curves over K are modular and that their L-functions satisfy the Generalized Riemann Hypothesis. Then, the average analytic rank of isomorphism classes of elliptic curves over K, when ordered by naive height, is bounded above by
![]() $(9d+1)/2$
.
$(9d+1)/2$
.
One of the main difficulties in extending methods for counting elliptic curves over the rational numbers to elliptic curves over more general number fields is that one may no longer have a bijection between reduced short Weierstrass models and isomorphism classes of elliptic curves. We overcome this difficulty by exploiting the geometry of the moduli stack of elliptic curves. In particular, the (compactified) moduli stack of elliptic curves is isomorphic to the weighted projective stack
![]() ${\mathcal P}(4,6)$
. From this perspective, questions about counting elliptic curves of bounded height turn into questions about counting points of bounded height on weighted projective stacks. Such questions can then be studied using various tools from Diophantine geometry.
${\mathcal P}(4,6)$
. From this perspective, questions about counting elliptic curves of bounded height turn into questions about counting points of bounded height on weighted projective stacks. Such questions can then be studied using various tools from Diophantine geometry.
One of the key ingredients in the proof of Theorem 1.1.1 is estimating the number of elliptic curves with prescribed local conditions over number fields. To state our results on counting elliptic curves, we introduce some notation. Let K be a number field with ring of integers
![]() ${\mathcal O}_K$
, discriminant
${\mathcal O}_K$
, discriminant
![]() $\Delta _K$
, class number
$\Delta _K$
, class number
![]() $h_K$
, regulator
$h_K$
, regulator
![]() $R_K$
, and which contains
$R_K$
, and which contains
![]() $\varpi _K$
roots of unity. Let
$\varpi _K$
roots of unity. Let
![]() $\text {Val}(K)$
denote the set of places of K, let
$\text {Val}(K)$
denote the set of places of K, let
![]() $\text {Val}_0(K)$
denote the set of finite places, and let
$\text {Val}_0(K)$
denote the set of finite places, and let
![]() $\text {Val}_\infty (K)$
denote the set of infinite places. Let
$\text {Val}_\infty (K)$
denote the set of infinite places. Let
![]() $\zeta _K$
denote the Dedekind zeta function of K. Let
$\zeta _K$
denote the Dedekind zeta function of K. Let
![]() $H(\cdot )$
denote the Hurwitz-Kronecker class number (see Subsection 5.1 for the definition). For a prime
$H(\cdot )$
denote the Hurwitz-Kronecker class number (see Subsection 5.1 for the definition). For a prime
![]() ${\mathfrak p}\subset {\mathcal O}_K$
, above a rational prime
${\mathfrak p}\subset {\mathcal O}_K$
, above a rational prime
![]() $p\in {\mathbb Z}$
, we will write
$p\in {\mathbb Z}$
, we will write
![]() $\deg ({\mathfrak p})$
for the index of fields
$\deg ({\mathfrak p})$
for the index of fields
![]() $[{\mathcal O}_K/{\mathfrak p}:{\mathbb Z}/p]$
, which we will refer to as the degree of
$[{\mathcal O}_K/{\mathfrak p}:{\mathbb Z}/p]$
, which we will refer to as the degree of
![]() ${\mathfrak p}$
.
${\mathfrak p}$
.
Theorem 1.1.2. Let K be a degree d number field, and let
![]() ${\mathfrak p}$
be a prime ideal of
${\mathfrak p}$
be a prime ideal of
![]() ${\mathcal O}_K$
of norm q such that
${\mathcal O}_K$
of norm q such that
![]() $2\nmid q$
and
$2\nmid q$
and
![]() $3\nmid q$
. Let
$3\nmid q$
. Let
![]() ${\mathscr L}$
be one of the local conditions listed in Table 1. Then the number of elliptic curves over K with naive height less than B, and which satisfy the local condition
${\mathscr L}$
be one of the local conditions listed in Table 1. Then the number of elliptic curves over K with naive height less than B, and which satisfy the local condition
![]() ${\mathscr L}$
at
${\mathscr L}$
at
![]() ${\mathfrak p}$
, is
${\mathfrak p}$
, is
where
 $$\begin{align*}\kappa=\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{2}R_K10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_{K} |\Delta_K|\zeta_K(10)}, \end{align*}$$
$$\begin{align*}\kappa=\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{2}R_K10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_{K} |\Delta_K|\zeta_K(10)}, \end{align*}$$
and where
![]() $\kappa _{\mathscr L}$
and
$\kappa _{\mathscr L}$
and
![]() $\epsilon _{\mathscr L}$
are as in Table 1.
$\epsilon _{\mathscr L}$
are as in Table 1.
Table 1 Local conditions.

We also give asymptotics for counting elliptic curves with a prescribed trace of Frobenius:
Theorem 1.1.3. Let K be a degree d number field, and let
![]() ${\mathfrak p}$
be a degree n prime ideal of
${\mathfrak p}$
be a degree n prime ideal of
![]() ${\mathcal O}_K$
above a rational prime
${\mathcal O}_K$
above a rational prime
![]() $p>3$
. Set
$p>3$
. Set
![]() $q=N_{K/{\mathbb Q}}({\mathfrak p})=p^n$
, the norm of
$q=N_{K/{\mathbb Q}}({\mathfrak p})=p^n$
, the norm of
![]() ${\mathfrak p}$
. Let
${\mathfrak p}$
. Let
![]() $a\in {\mathbb Z}$
be an integer satisfying
$a\in {\mathbb Z}$
be an integer satisfying
![]() $|a|\leq 2\sqrt {q}$
. Then, the number of elliptic curves over K with naive height less than B, good reduction at
$|a|\leq 2\sqrt {q}$
. Then, the number of elliptic curves over K with naive height less than B, good reduction at
![]() ${\mathfrak p}$
, and which have trace of Frobenius a at
${\mathfrak p}$
, and which have trace of Frobenius a at
![]() ${\mathfrak p}$
, is
${\mathfrak p}$
, is
where
 $$\begin{align*}\kappa=\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{2}R_K10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_{K} |\Delta_K|\zeta_K(10)}, \end{align*}$$
$$\begin{align*}\kappa=\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{2}R_K10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_{K} |\Delta_K|\zeta_K(10)}, \end{align*}$$
and where
![]() $\kappa _{n,a}$
and
$\kappa _{n,a}$
and
![]() $\epsilon _{n,a}$
are as in Table 2.
$\epsilon _{n,a}$
are as in Table 2.
Table 2 Constants for Theorem 1.1.3.

Theorem 1.1.2 and Theorem 1.1.3 generalize a result of Cho and Jeong [Reference Cho and JeongCJ23b, Theorem 1.4] for elliptic curves over
![]() ${\mathbb Q}$
to elliptic curves over arbitrary number fields. For more results on counting elliptic curves with prescribed local conditions, see the work of Cremona and Sadek [Reference Cremona and SadekCS23].
${\mathbb Q}$
to elliptic curves over arbitrary number fields. For more results on counting elliptic curves with prescribed local conditions, see the work of Cremona and Sadek [Reference Cremona and SadekCS23].
1.2. Counting points on weighted projective stacks
Our results for counting isomorphism classes of elliptic curves are special cases of a more general theorem for counting points of bounded height on weighted projective stacks.
In [Reference SchanuelSch79], Schanuel proved an asymptotic for the number of rational points of bounded height on projective spaces over number fields. This was generalized to weighted projective stacks by Deng [Reference DengDen98] (see also the work of Darda [Reference DardaDar21], which gives a proof using height zeta functions). In this paper, we extend these results to count points of bounded height which satisfy finitely many prescribed local conditions (see Theorem 4.0.5).
Remark 1.2.1. Let us briefly mention some additional results related to counting points of bounded height on weighted projective stacks. Recently, Bruin and Manterola Ayala [Reference AyalaMA21, Reference Bruin and AyalaBMA23] have generalized Deng’s result to count points whose images, with respect to a morphism of weighted projective stacks, are of bounded height. Using the geometric sieve, Bright, Browning and Loughran [Reference Bright, Browning and LoughranBBL16] have proven a generalization of Schanuel’s theorem which allows one to impose infinitely many local conditions on the points of projective space being counted. In [Reference PhillipsPhi22], the author combines these results to count points whose images, with respect to a morphism of weighted projective stacks, are of bounded height and satisfy prescribed local conditions. Such a result has applications to counting elliptic curves with certain prescribed level structures and local conditions. Building from this result, Cho, Jeong and Park [Reference Cho, Jeong and ParkCJP23] have given a conditional bound for average analytic ranks of isomorphism classes of elliptic curves over number fields with a prescribed level structure.
1.3. Asymptotic notation
Let
![]() $f:{\mathbb R}_{>0}\to {\mathbb R}$
and
$f:{\mathbb R}_{>0}\to {\mathbb R}$
and
![]() $g:{\mathbb R}_{>0}\to {\mathbb R}$
be real valued functions. Throughout the article, we will write
$g:{\mathbb R}_{>0}\to {\mathbb R}$
be real valued functions. Throughout the article, we will write
![]() $f=O(g)$
(or
$f=O(g)$
(or
![]() $f\ll g$
) if there exist constants
$f\ll g$
) if there exist constants
![]() $C,D\in {\mathbb R}_{>0}$
such that for all
$C,D\in {\mathbb R}_{>0}$
such that for all
![]() $x\geq D$
, we have
$x\geq D$
, we have
![]() $|f(x)|\leq C\cdot g(x)$
. We refer to any such C as the implied constant. If the implied constant depends on a parameter t, then we will write
$|f(x)|\leq C\cdot g(x)$
. We refer to any such C as the implied constant. If the implied constant depends on a parameter t, then we will write
![]() $f=O_t(g)$
(or
$f=O_t(g)$
(or
![]() $f\ll _t g$
).
$f\ll _t g$
).
1.4. Organization
In Section 2, we cover basic facts about weighted projective stacks and heights defined on weighted projective stacks. In Section 3, we prove a result for counting points of bounded height satisfying prescribed local conditions on affine spaces over number fields. In Section 4, we prove our main result for counting points of bounded height on weighted projective stacks (Theorem 4.0.5). In Section 5, we apply Theorem 4.0.5 to count elliptic curves with prescribed local conditions. This is where we prove Theorem 1.1.2 and Theorem 1.1.3. Finally, in Section 6, we use the explicit formula for L-functions, together with our results for counting elliptic curves with prescribed local conditions, to bound the average analytic rank of elliptic curves over number fields. This is where we prove Theorem 1.1.1.
2. Preliminaries on weighted projective stacks
In this section, we recall basic facts about weighted projective stacks with an emphasis on heights.
2.1. Heights on weighted projective stacks
Given an
![]() $(n+1)$
-tuple of positive integers
$(n+1)$
-tuple of positive integers
![]() ${\textbf {w}}=(w_0,\dots ,w_n)$
, the weighted projective stack
${\textbf {w}}=(w_0,\dots ,w_n)$
, the weighted projective stack
![]() ${\mathcal P}({\textbf {w}})$
is the quotient stack
${\mathcal P}({\textbf {w}})$
is the quotient stack
where the multiplicative group scheme,
![]() $\mathbb {G}_m$
, acts on the punctured affine space,
$\mathbb {G}_m$
, acts on the punctured affine space,
![]() ${\mathbb A}^{n+1}-\{0\}$
, as follows:
${\mathbb A}^{n+1}-\{0\}$
, as follows:
 $$ \begin{align*} \mathbb{G}_m\times({\mathbb A}^{n+1}-\{0\}) &\to ({\mathbb A}^{n+1}-\{0\})\\ (\lambda,(x_0,\dots,x_n)) &\mapsto \lambda\ast_{\textbf{w}} (x_0,\dots,x_n)\stackrel{\mathrm{def}}{=}(\lambda^{w_0}x_0,\dots, \lambda^{w_n}x_n). \end{align*} $$
$$ \begin{align*} \mathbb{G}_m\times({\mathbb A}^{n+1}-\{0\}) &\to ({\mathbb A}^{n+1}-\{0\})\\ (\lambda,(x_0,\dots,x_n)) &\mapsto \lambda\ast_{\textbf{w}} (x_0,\dots,x_n)\stackrel{\mathrm{def}}{=}(\lambda^{w_0}x_0,\dots, \lambda^{w_n}x_n). \end{align*} $$
In the special case when
![]() ${\textbf {w}}=(1,\dots ,1)$
, this recovers the usual projective space
${\textbf {w}}=(1,\dots ,1)$
, this recovers the usual projective space
![]() ${\mathbb P}^n$
.
${\mathbb P}^n$
.
The point
![]() $[(a_0,\dots ,a_n)]\in {\mathcal P}(w_0,\dots ,w_n)$
has stabilizer
$[(a_0,\dots ,a_n)]\in {\mathcal P}(w_0,\dots ,w_n)$
has stabilizer
![]() $\mu _m$
, where
$\mu _m$
, where
![]() $m=\gcd (w_i : a_i\neq 0)$
. When K is a field of characteristic zero, we have that
$m=\gcd (w_i : a_i\neq 0)$
. When K is a field of characteristic zero, we have that
![]() $\mu _m$
is finite and reduced over K. It follows that, over fields of characteristic zero,
$\mu _m$
is finite and reduced over K. It follows that, over fields of characteristic zero,
![]() ${\mathcal P}(w_0,\dots ,w_n)$
is a Deligne–Mumford stack.
${\mathcal P}(w_0,\dots ,w_n)$
is a Deligne–Mumford stack.
For any field F, let
![]() ${\mathcal P}({\textbf {w}})(F)$
denote the set of isomorphism classes of the groupoid of F-points of
${\mathcal P}({\textbf {w}})(F)$
denote the set of isomorphism classes of the groupoid of F-points of
![]() ${\mathcal P}({\textbf {w}})$
. More concretely,
${\mathcal P}({\textbf {w}})$
. More concretely,
![]() ${\mathcal P}({\textbf {w}})(F)$
is in canonical bijection with the quotient
${\mathcal P}({\textbf {w}})(F)$
is in canonical bijection with the quotient
where
![]() $F^\times $
acts on
$F^\times $
acts on
![]() $F^{n+1}-\{0\}$
by the weighted action
$F^{n+1}-\{0\}$
by the weighted action
 $$ \begin{align*} F^\times \times (F^{n+1}-\{0\}) &\to (F^{n+1}-\{0\})\\ (\lambda, (a_0,\dots,a_n)) &\mapsto (\lambda^{w_0}a_0,\dots,\lambda^{w_n}a_n). \end{align*} $$
$$ \begin{align*} F^\times \times (F^{n+1}-\{0\}) &\to (F^{n+1}-\{0\})\\ (\lambda, (a_0,\dots,a_n)) &\mapsto (\lambda^{w_0}a_0,\dots,\lambda^{w_n}a_n). \end{align*} $$
Throughout this article, unless otherwise stated, we assume all weighted projective stacks
![]() ${\mathcal P}({\textbf {w}})$
are defined over a number field K.
${\mathcal P}({\textbf {w}})$
are defined over a number field K.
For each finite place
![]() $v\in \text {Val}_0(K)$
, let
$v\in \text {Val}_0(K)$
, let
![]() ${\mathfrak p}_v$
be the corresponding prime ideal, and let
${\mathfrak p}_v$
be the corresponding prime ideal, and let
![]() $\pi _v$
be a uniformizer for the completion
$\pi _v$
be a uniformizer for the completion
![]() $K_v$
of K at v. For
$K_v$
of K at v. For
![]() $x=(x_0,\dots ,x_n)\in K^{n+1}-\{0\}$
, set
$x=(x_0,\dots ,x_n)\in K^{n+1}-\{0\}$
, set
![]() $|x_i|_{{\textbf {w}},v}\stackrel {\mathrm{def}}{=}|\pi _v|_v^{\lfloor v(x_i)/w_i\rfloor }$
, and set
$|x_i|_{{\textbf {w}},v}\stackrel {\mathrm{def}}{=}|\pi _v|_v^{\lfloor v(x_i)/w_i\rfloor }$
, and set
 $$\begin{align*}|x|_{{{\textbf{w}}},v}\stackrel{\mathrm{def}}{=}\begin{cases} \max_i\{|x_i|_{{\textbf{w}},v}\} & \text{ if } v\in \text{Val}_0(K)\\ \max_i\{|x_i|_v^{1/w_i}\} & \text{ if } v\in \text{Val}_\infty(K). \end{cases} \end{align*}$$
$$\begin{align*}|x|_{{{\textbf{w}}},v}\stackrel{\mathrm{def}}{=}\begin{cases} \max_i\{|x_i|_{{\textbf{w}},v}\} & \text{ if } v\in \text{Val}_0(K)\\ \max_i\{|x_i|_v^{1/w_i}\} & \text{ if } v\in \text{Val}_\infty(K). \end{cases} \end{align*}$$
Definition 2.1.1 (Height).
The (exponential) height of a point
![]() $x=[x_0:\cdots :x_n]\in {\mathcal P}({\textbf {w}})(K)$
is defined as
$x=[x_0:\cdots :x_n]\in {\mathcal P}({\textbf {w}})(K)$
is defined as
 $$\begin{align*}\text{Ht}_{\textbf{w}}(x)\stackrel{\mathrm{def}}{=}\prod_{v\in \text{Val}(K)} |(x_0,\dots,x_n)|_{{\textbf{w}},v}. \end{align*}$$
$$\begin{align*}\text{Ht}_{\textbf{w}}(x)\stackrel{\mathrm{def}}{=}\prod_{v\in \text{Val}(K)} |(x_0,\dots,x_n)|_{{\textbf{w}},v}. \end{align*}$$
It is straightforward to check that this height function does not depend on the choice of representative of x.
Definition 2.1.2 (Scaling ideal).
Define the scaling ideal
![]() ${\mathfrak I}_{{\textbf {w}}}(x)$
of
${\mathfrak I}_{{\textbf {w}}}(x)$
of
![]() $x=(x_0,\dots ,x_n)\in K^{n+1}-\{0\}$
to be the fractional ideal
$x=(x_0,\dots ,x_n)\in K^{n+1}-\{0\}$
to be the fractional ideal
 $$\begin{align*}{\mathfrak I}_{{\textbf{w}}}(x)\stackrel{\mathrm{def}}{=}\prod_{v\in \text{Val}_0(K)} {\mathfrak p}_v^{\min_i\{\lfloor v(x_i)/w_i\rfloor\}}. \end{align*}$$
$$\begin{align*}{\mathfrak I}_{{\textbf{w}}}(x)\stackrel{\mathrm{def}}{=}\prod_{v\in \text{Val}_0(K)} {\mathfrak p}_v^{\min_i\{\lfloor v(x_i)/w_i\rfloor\}}. \end{align*}$$
The scaling ideal
![]() ${\mathfrak I}_{{\textbf {w}}}(x)$
can be characterized as the intersection of all fractional ideals
${\mathfrak I}_{{\textbf {w}}}(x)$
can be characterized as the intersection of all fractional ideals
![]() ${\mathfrak a}$
of
${\mathfrak a}$
of
![]() ${\mathcal O}_K$
such that
${\mathcal O}_K$
such that
![]() $x\in {\mathfrak a}^{w_0}\times \cdots \times {\mathfrak a}^{w_n}\subseteq K^{n+1}$
. It has the property that
$x\in {\mathfrak a}^{w_0}\times \cdots \times {\mathfrak a}^{w_n}\subseteq K^{n+1}$
. It has the property that
The height can be written in terms of the scaling ideal as follows:
 $$\begin{align*}\text{Ht}_{\textbf{w}}([x_0:\dots:x_n])=\frac{1}{N_{K/{\mathbb Q}}({\mathfrak I}_{\textbf{w}}(x))}\prod_{v\in \text{Val}_\infty(K)} \max_i\{|x_i|_v^{1/w_i}\}. \end{align*}$$
$$\begin{align*}\text{Ht}_{\textbf{w}}([x_0:\dots:x_n])=\frac{1}{N_{K/{\mathbb Q}}({\mathfrak I}_{\textbf{w}}(x))}\prod_{v\in \text{Val}_\infty(K)} \max_i\{|x_i|_v^{1/w_i}\}. \end{align*}$$
It is straightforward to check that this agrees with the height from Definition 2.1.1.
Remark 2.1.3. The height
![]() $\text {Ht}_{\textbf {w}}$
was first defined by Deng [Reference DengDen98]. In the case of projective spaces,
$\text {Ht}_{\textbf {w}}$
was first defined by Deng [Reference DengDen98]. In the case of projective spaces,
![]() ${\mathbb P}^n={\mathcal P}(1,\dots ,1)$
, this height corresponds to the usual Weil height. In more geometric terms, this height on weighted projective stacks can be viewed as the ‘stacky height’ associated to the tautological bundle of
${\mathbb P}^n={\mathcal P}(1,\dots ,1)$
, this height corresponds to the usual Weil height. In more geometric terms, this height on weighted projective stacks can be viewed as the ‘stacky height’ associated to the tautological bundle of
![]() ${\mathcal P}({\textbf {w}})$
(see [Reference Ellenberg, Satriano and Zureick-BrownESZB23, §3.3] for this and much more about heights on stacks).
${\mathcal P}({\textbf {w}})$
(see [Reference Ellenberg, Satriano and Zureick-BrownESZB23, §3.3] for this and much more about heights on stacks).
The (compactified) moduli stack of elliptic curves,
![]() ${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
, is isomorphic to the weighted projective stack
${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
, is isomorphic to the weighted projective stack
![]() ${\mathcal P}(4,6)$
. This isomorphism can be given explicitly as
${\mathcal P}(4,6)$
. This isomorphism can be given explicitly as
 $$ \begin{align*} {\mathcal X}_{\text{GL}_2({\mathbb Z})} &\xrightarrow{\sim} {\mathcal P}(4,6)\\ y^2=x^3+Ax+B & \mapsto [A:B]. \end{align*} $$
$$ \begin{align*} {\mathcal X}_{\text{GL}_2({\mathbb Z})} &\xrightarrow{\sim} {\mathcal P}(4,6)\\ y^2=x^3+Ax+B & \mapsto [A:B]. \end{align*} $$
Under this isomorphism, the tautological bundle on
![]() ${\mathcal P}(4,6)$
corresponds to the Hodge bundle on
${\mathcal P}(4,6)$
corresponds to the Hodge bundle on
![]() ${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
. The usual naive height of an elliptic curve E over K with a reduced integral short Weierstrass equation
${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
. The usual naive height of an elliptic curve E over K with a reduced integral short Weierstrass equation
![]() $y^2=x^3+Ax+B$
is defined as
$y^2=x^3+Ax+B$
is defined as
 $$\begin{align*}\text{Ht}(E)\stackrel{\mathrm{def}}{=}\prod_{v\in \text{Val}_\infty(K)} \max\{|A|_v^3,|B|_v^2\}. \end{align*}$$
$$\begin{align*}\text{Ht}(E)\stackrel{\mathrm{def}}{=}\prod_{v\in \text{Val}_\infty(K)} \max\{|A|_v^3,|B|_v^2\}. \end{align*}$$
One can show that this naive height is the same as the stacky height on
![]() ${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
with respect to the twelfth power of the Hodge bundle [Reference Ellenberg, Satriano and Zureick-BrownESZB23, §3.3]. For any short Weierstrass equation
${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
with respect to the twelfth power of the Hodge bundle [Reference Ellenberg, Satriano and Zureick-BrownESZB23, §3.3]. For any short Weierstrass equation
![]() $y^2=x^3+ax+b$
of E, the naive height is given by
$y^2=x^3+ax+b$
of E, the naive height is given by
3. Weighted geometry of numbers over number fields
Let K be a number field. In this section, we prove asymptotics for the number of K-rational points of bounded height with prescribed local conditions on affine spaces with respect to a weighting. For these asymptotics, we give a power savings error term which is independent of the local conditions.
3.1. O-minimal geometry
We briefly cover the basics of o-minimal geometry which will be needed in this article. A general reference for this subsection is [Reference van den DriesvdD98, §1]. Let
![]() $m_L$
denote Lebesgue measure on
$m_L$
denote Lebesgue measure on
![]() ${\mathbb R}^n$
.
${\mathbb R}^n$
.
Definition 3.1.1 (Semi-algebraic set).
A (real) semi-algebraic subset of
![]() ${\mathbb R}^n$
is a finite union of sets of the form
${\mathbb R}^n$
is a finite union of sets of the form
where
![]() $f_1,\dots ,f_k,g_1,\dots ,g_l\in {\mathbb R}[X_1,\dots ,X_n]$
.
$f_1,\dots ,f_k,g_1,\dots ,g_l\in {\mathbb R}[X_1,\dots ,X_n]$
.
Definition 3.1.2 (Structure).
A structure is a sequence,
![]() ${\mathcal S}=({\mathcal S}_n)_{n\in {\mathbb Z}_{>0}}$
, where each
${\mathcal S}=({\mathcal S}_n)_{n\in {\mathbb Z}_{>0}}$
, where each
![]() ${\mathcal S}_n$
is a set of subsets of
${\mathcal S}_n$
is a set of subsets of
![]() ${\mathbb R}^n$
with the following properties:
${\mathbb R}^n$
with the following properties:
-
(i) If
 $A,B\in {\mathcal S}_n$
, then
$A,B\in {\mathcal S}_n$
, then
 $A\cup B\in {\mathcal S}_n$
and
$A\cup B\in {\mathcal S}_n$
and
 ${\mathbb R}^n - A\in {\mathcal S}_n$
(i.e.,
${\mathbb R}^n - A\in {\mathcal S}_n$
(i.e.,
 ${\mathcal S}_n$
is a Boolean algebra).
${\mathcal S}_n$
is a Boolean algebra). -
(ii) If
 $A\in {\mathcal S}_m$
and
$A\in {\mathcal S}_m$
and
 $B\in {\mathcal S}_n$
, then
$B\in {\mathcal S}_n$
, then
 $A\times B\in {\mathcal S}_{n+m}$
.
$A\times B\in {\mathcal S}_{n+m}$
. -
(iii) If
 $\pi :{\mathbb R}^n\to {\mathbb R}^m$
is the projection to m distinct coordinates and
$\pi :{\mathbb R}^n\to {\mathbb R}^m$
is the projection to m distinct coordinates and
 $A\in {\mathcal S}_n$
, then
$A\in {\mathcal S}_n$
, then
 $\pi (A)\in {\mathcal S}_m$
.
$\pi (A)\in {\mathcal S}_m$
. -
(iv) All real semi-algebraic subsets of
 ${\mathbb R}^n$
are in
${\mathbb R}^n$
are in
 ${\mathcal S}_n$
.
${\mathcal S}_n$
.
A subset is definable in
![]() ${\mathcal S}$
if it is contained in some
${\mathcal S}$
if it is contained in some
![]() ${\mathcal S}_n$
. Let
${\mathcal S}_n$
. Let
![]() $D\subseteq S_n$
. A function
$D\subseteq S_n$
. A function
![]() $f\colon D\to {\mathbb R}^m$
is said to be definable in
$f\colon D\to {\mathbb R}^m$
is said to be definable in
![]() ${\mathcal S}$
if its graph,
${\mathcal S}$
if its graph,
![]() $\Gamma (f)\stackrel {\mathrm{def}}{=}\{(x,f(x)):x\in D\}\subseteq {\mathbb R}^{m+n}$
, is definable in
$\Gamma (f)\stackrel {\mathrm{def}}{=}\{(x,f(x)):x\in D\}\subseteq {\mathbb R}^{m+n}$
, is definable in
![]() ${\mathcal S}$
.
${\mathcal S}$
.
Note that the intersection of definable sets is definable by property (i).
Definition 3.1.3 (O-minimal structure).
An o-minimal structure is a structure in which the following additional property holds:
-
(v) The boundary of each set in
 ${\mathcal S}_1$
is a finite set of points.
${\mathcal S}_1$
is a finite set of points.
The class of semialgebraic sets is an example of an o-minimal structure (see, for example, [Reference van den DriesvdD98, §2]). The main structure we will use is
![]() ${\mathbb R}_{\exp }$
, which is defined to be the smallest structure in which the real exponential function,
${\mathbb R}_{\exp }$
, which is defined to be the smallest structure in which the real exponential function,
![]() $\exp \colon {\mathbb R}\to {\mathbb R}$
, is definable. Observe that the function
$\exp \colon {\mathbb R}\to {\mathbb R}$
, is definable. Observe that the function
![]() $\log (x)$
is definable in
$\log (x)$
is definable in
![]() ${\mathbb R}_{\exp }$
since its graph,
${\mathbb R}_{\exp }$
since its graph,
is clearly definable in
![]() ${\mathbb R}_{\exp }$
.
${\mathbb R}_{\exp }$
.
Theorem 3.1.4 [Reference WilkieWil96].
The structure
![]() ${\mathbb R}_{\exp }$
is o-minimal.
${\mathbb R}_{\exp }$
is o-minimal.
From now on, we will call a subset of
![]() ${\mathbb R}^n$
definable if it is definable in some o-minimal structure.
${\mathbb R}^n$
definable if it is definable in some o-minimal structure.
3.2. Weighted geometry-of-numbers
The following proposition is a version of the Principle of Lipschitz, which gives estimates for the number of lattice points in a weighted homogeneous space.
Proposition 3.2.1. Let
![]() $R\subset {\mathbb R}^{n}$
be a bounded set definable in an o-minimal structure. Let
$R\subset {\mathbb R}^{n}$
be a bounded set definable in an o-minimal structure. Let
![]() $\Lambda \subset {\mathbb R}^n$
be a rank n lattice with successive minima
$\Lambda \subset {\mathbb R}^n$
be a rank n lattice with successive minima
![]() $\lambda _1,\dots ,\lambda _n$
(with respect to the origin-centered unit ball in
$\lambda _1,\dots ,\lambda _n$
(with respect to the origin-centered unit ball in
![]() ${\mathbb R}^n$
). Set
${\mathbb R}^n$
). Set
Then, for sufficiently largeFootnote 2 B,
where the implied constant depends only on R and
![]() ${\textbf {w}}$
.
${\textbf {w}}$
.
Proof. This will follow from a general version of the Principle of Lipschitz due to Barroero and Widmer [Reference Barroero and WidmerBW14, Theorem 1.3]. Since
![]() $m_L(R(B))=B^{|{\textbf {w}}|} m_L(R)$
, [Reference Barroero and WidmerBW14, Theorem 1.3] gives the desired leading term. Let
$m_L(R(B))=B^{|{\textbf {w}}|} m_L(R)$
, [Reference Barroero and WidmerBW14, Theorem 1.3] gives the desired leading term. Let
![]() $V_j(R(B))$
denote the sum of the j-dimensional volumes of the orthogonal projections of
$V_j(R(B))$
denote the sum of the j-dimensional volumes of the orthogonal projections of
![]() $R(B)$
onto each j-dimensional coordinate subspace of
$R(B)$
onto each j-dimensional coordinate subspace of
![]() ${\mathbb R}^n$
. The error term given in [Reference Barroero and WidmerBW14, Theorem 1.3] is
${\mathbb R}^n$
. The error term given in [Reference Barroero and WidmerBW14, Theorem 1.3] is
 $$ \begin{align} O\,\left(1+\sum_{j=1}^{n-1} \frac{V_j(R(B))}{\lambda_1\cdots \lambda_j}\right), \end{align} $$
$$ \begin{align} O\,\left(1+\sum_{j=1}^{n-1} \frac{V_j(R(B))}{\lambda_1\cdots \lambda_j}\right), \end{align} $$
where the implied constant depends only on R. In our case, one observes that
![]() $V_i(R(B))=O(V_{j}(R(B)))$
for all
$V_i(R(B))=O(V_{j}(R(B)))$
for all
![]() $i\leq j$
. Moreover,
$i\leq j$
. Moreover,
![]() $V_{n-1}(R(B))=O(\sum _{i\leq n} B^{|{\textbf {w}}|-w_i})=O(B^{|{\textbf {w}}|-w_{\min }})$
, where the implied constant depends only on R and
$V_{n-1}(R(B))=O(\sum _{i\leq n} B^{|{\textbf {w}}|-w_i})=O(B^{|{\textbf {w}}|-w_{\min }})$
, where the implied constant depends only on R and
![]() ${\textbf {w}}$
. By dimension considerations, we see that if
${\textbf {w}}$
. By dimension considerations, we see that if
![]() $B^{|{\textbf {w}}|-w_{\min }}=O(V_i(R(B)))$
, then we must have
$B^{|{\textbf {w}}|-w_{\min }}=O(V_i(R(B)))$
, then we must have
![]() $i\geq n-1$
. From these observations, it follows that
$i\geq n-1$
. From these observations, it follows that
 $$\begin{align*}O\,\left(1+\sum_{j=1}^{n-1} \frac{V_j(R(B))}{\lambda_1\cdots \lambda_j}\right)=O\,\left(\frac{V_{n-1}(R(B))}{\lambda_1\cdots\lambda_{n-1}}\right). \end{align*}$$
$$\begin{align*}O\,\left(1+\sum_{j=1}^{n-1} \frac{V_j(R(B))}{\lambda_1\cdots \lambda_j}\right)=O\,\left(\frac{V_{n-1}(R(B))}{\lambda_1\cdots\lambda_{n-1}}\right). \end{align*}$$
By Minkowski’s second theorem [Reference Minkowski and ApproximationenMin07] (for a more modern reference see, for example, [Reference CasselsCas59, p. 203]),
where
![]() $\mathscr {B}_n$
is the unit ball in
$\mathscr {B}_n$
is the unit ball in
![]() ${\mathbb R}^n$
. From this, we obtain the desired expression for the error term,
${\mathbb R}^n$
. From this, we obtain the desired expression for the error term,
 $$\begin{align*}O\,\left(\frac{V_{n-1}(R(B))}{\lambda_1\cdots\lambda_{n-1}}\right)=O\,\left(\frac{\lambda_n B^{|{\textbf{w}}|-w_{\min}}}{\det(\Lambda)}\right).\\[-44pt] \end{align*}$$
$$\begin{align*}O\,\left(\frac{V_{n-1}(R(B))}{\lambda_1\cdots\lambda_{n-1}}\right)=O\,\left(\frac{\lambda_n B^{|{\textbf{w}}|-w_{\min}}}{\det(\Lambda)}\right).\\[-44pt] \end{align*}$$
Definition 3.2.2 (Boxes).
A (
![]() $\mathbf {{\mathbb Z}_p^n}$
)-box is a subset
$\mathbf {{\mathbb Z}_p^n}$
)-box is a subset
![]() ${\mathcal B}_p\subset {\mathbb Z}_p^n$
for which there exist closed balls
${\mathcal B}_p\subset {\mathbb Z}_p^n$
for which there exist closed balls
where
![]() $a_j\in {\mathbb Z}_p$
and
$a_j\in {\mathbb Z}_p$
and
![]() $b_{p,j}\in \{p^{-k}: k\in {\mathbb Z}_{\geq 0}\}$
, such that
$b_{p,j}\in \{p^{-k}: k\in {\mathbb Z}_{\geq 0}\}$
, such that
![]() ${\mathcal B}_p$
equals the Cartesian product
${\mathcal B}_p$
equals the Cartesian product
![]() $\prod _{j=1}^n {\mathcal B}_{p,j}$
. Let S be a finite set of primes. An S-box is a subset
$\prod _{j=1}^n {\mathcal B}_{p,j}$
. Let S be a finite set of primes. An S-box is a subset
![]() ${\mathcal B}\subset \prod _{p\in S} {\mathbb Z}_p^n$
for which there exist
${\mathcal B}\subset \prod _{p\in S} {\mathbb Z}_p^n$
for which there exist
![]() ${\mathbb Z}_p^n$
-boxes
${\mathbb Z}_p^n$
-boxes
![]() ${\mathcal B}_p$
such that
${\mathcal B}_p$
such that
 $$\begin{align*}{\mathcal B}=\prod_{p\in S} {\mathcal B}_{p}=\prod_{p\in S}\prod_{j=1}^n {\mathcal B}_{p,j}. \end{align*}$$
$$\begin{align*}{\mathcal B}=\prod_{p\in S} {\mathcal B}_{p}=\prod_{p\in S}\prod_{j=1}^n {\mathcal B}_{p,j}. \end{align*}$$
Lemma 3.2.3 (Box Lemma).
Let
![]() $\Omega _\infty \subset {\mathbb R}^n$
be a bounded subset definable in an o-minimal structure. Let S be a finite set of primes and
$\Omega _\infty \subset {\mathbb R}^n$
be a bounded subset definable in an o-minimal structure. Let S be a finite set of primes and
![]() ${\mathcal B}=\prod _{p\in S} {\mathcal B}_p$
an S-box. Then, for each
${\mathcal B}=\prod _{p\in S} {\mathcal B}_p$
an S-box. Then, for each
![]() $B\in {\mathbb R}_{>0}$
, we have
$B\in {\mathbb R}_{>0}$
, we have
 $$ \begin{align*} &\#\left\{x\in {\mathbb Z}^n \cap \left(B\ast_{\textbf{w}} \Omega_\infty\right): x\in \prod_{p\in S} \mathcal{B}_p \right\}\\ &\hspace{1cm}=\left(m_L(\Omega_\infty)\prod_{p\in S} m_p(\mathcal{B}_p)\right)B^{|{\textbf{w}}|} + O\,\left(\max_j\left\{\prod_{p\in S} b_{p,j}^{-1}\right\}\left(\prod_{p \in S} m_p(\mathcal{B}_p)\right)B^{|{\textbf{w}}|-w_{\min}} \right), \end{align*} $$
$$ \begin{align*} &\#\left\{x\in {\mathbb Z}^n \cap \left(B\ast_{\textbf{w}} \Omega_\infty\right): x\in \prod_{p\in S} \mathcal{B}_p \right\}\\ &\hspace{1cm}=\left(m_L(\Omega_\infty)\prod_{p\in S} m_p(\mathcal{B}_p)\right)B^{|{\textbf{w}}|} + O\,\left(\max_j\left\{\prod_{p\in S} b_{p,j}^{-1}\right\}\left(\prod_{p \in S} m_p(\mathcal{B}_p)\right)B^{|{\textbf{w}}|-w_{\min}} \right), \end{align*} $$
where the implied constant depends only on
![]() $\Omega _\infty $
and
$\Omega _\infty $
and
![]() ${\textbf {w}}$
.
${\textbf {w}}$
.
Proof. We have that
![]() $\mathcal {B}_p=\prod _{j=1}^n \mathcal {B}_{p,j}$
with
$\mathcal {B}_p=\prod _{j=1}^n \mathcal {B}_{p,j}$
with
![]() $\mathcal {B}_{p,j}=\{x\in {\mathbb Z}_p : |x-a_j|_p\leq b_{p,j}\}$
, where
$\mathcal {B}_{p,j}=\{x\in {\mathbb Z}_p : |x-a_j|_p\leq b_{p,j}\}$
, where
![]() $a_j\in {\mathbb Z}_p$
and
$a_j\in {\mathbb Z}_p$
and
![]() $b_{p,j}\in \{p^{-k} : k\in {\mathbb Z}_{\geq 0}\}$
. Observe that for each
$b_{p,j}\in \{p^{-k} : k\in {\mathbb Z}_{\geq 0}\}$
. Observe that for each
![]() $j\in \{1,\dots ,n\}$
, the set
$j\in \{1,\dots ,n\}$
, the set
![]() ${\mathbb Z}\cap \mathcal {B}_{p,j}$
is a translate of the sublattice
${\mathbb Z}\cap \mathcal {B}_{p,j}$
is a translate of the sublattice
![]() $\langle b_{p,j}^{-1}\rangle \subseteq {\mathbb Z}$
. By the Chinese Remainder Theorem, the set
$\langle b_{p,j}^{-1}\rangle \subseteq {\mathbb Z}$
. By the Chinese Remainder Theorem, the set
![]() ${\mathbb Z}\cap \prod _{p\in S} \mathcal {B}_{p,j}$
is a translate of the sublattice
${\mathbb Z}\cap \prod _{p\in S} \mathcal {B}_{p,j}$
is a translate of the sublattice
![]() $\left \langle \prod _{p\in S} b_{p,j}^{-1}\right \rangle \subseteq {\mathbb Z}$
. Taking a Cartesian product, we find that the set
$\left \langle \prod _{p\in S} b_{p,j}^{-1}\right \rangle \subseteq {\mathbb Z}$
. Taking a Cartesian product, we find that the set
 $$\begin{align*}\prod_{j=1}^n\left( {\mathbb Z}\cap \prod_{p\in S} \mathcal{B}_{p,j}\right)={\mathbb Z}^n\cap \prod_{p\in S} \mathcal{B}_p \end{align*}$$
$$\begin{align*}\prod_{j=1}^n\left( {\mathbb Z}\cap \prod_{p\in S} \mathcal{B}_{p,j}\right)={\mathbb Z}^n\cap \prod_{p\in S} \mathcal{B}_p \end{align*}$$
is a translate of a sub-lattice of
![]() ${\mathbb Z}^n$
whose successive minima are
${\mathbb Z}^n$
whose successive minima are
![]() $\prod _{p\in S} b_{p,j}^{-1}$
. In particular, the n-th successive minimum of the sublattice is
$\prod _{p\in S} b_{p,j}^{-1}$
. In particular, the n-th successive minimum of the sublattice is
 $$\begin{align*}\max_j\left\{\prod_{p\in S} b_{p,j}^{-1}\right\}, \end{align*}$$
$$\begin{align*}\max_j\left\{\prod_{p\in S} b_{p,j}^{-1}\right\}, \end{align*}$$
and the determinant of the sublattice is
 $$\begin{align*}\prod_{j=1}^n\prod_{p\in S} b_{p,j}^{-1}=\prod_{p\in S}m_p(\mathcal{B}_p)^{-1}. \end{align*}$$
$$\begin{align*}\prod_{j=1}^n\prod_{p\in S} b_{p,j}^{-1}=\prod_{p\in S}m_p(\mathcal{B}_p)^{-1}. \end{align*}$$
The lemma then follows from Proposition 3.2.1.
Let
![]() $\Lambda $
be a free
$\Lambda $
be a free
![]() ${\mathbb Z}$
-module of finite rank n. Set
${\mathbb Z}$
-module of finite rank n. Set
![]() $\Lambda _\infty =\Lambda \otimes _{\mathbb Z} {\mathbb R}$
and
$\Lambda _\infty =\Lambda \otimes _{\mathbb Z} {\mathbb R}$
and
![]() $\Lambda _p=\Lambda \otimes _{\mathbb Z} {\mathbb Z}_p$
. Equip
$\Lambda _p=\Lambda \otimes _{\mathbb Z} {\mathbb Z}_p$
. Equip
![]() $\Lambda _\infty $
and
$\Lambda _\infty $
and
![]() $\Lambda _p$
with Haar measures
$\Lambda _p$
with Haar measures
![]() $m_\infty $
and
$m_\infty $
and
![]() $m_p$
, respectively, normalized so that
$m_p$
, respectively, normalized so that
![]() $m_p(\Lambda _p)=1$
for all but finitely many primes p. As
$m_p(\Lambda _p)=1$
for all but finitely many primes p. As
![]() $\Lambda _p\cong {\mathbb Z}_p^n$
, we define a (
$\Lambda _p\cong {\mathbb Z}_p^n$
, we define a (
![]() $\mathbf {\Lambda _p)}$
-box to be a subset of
$\mathbf {\Lambda _p)}$
-box to be a subset of
![]() $\Lambda _p$
isomorphic to a
$\Lambda _p$
isomorphic to a
![]() $({\mathbb Z}_p^n)$
-box.
$({\mathbb Z}_p^n)$
-box.
Lemma 3.2.4. Let
![]() $\Lambda $
be a free
$\Lambda $
be a free
![]() ${\mathbb Z}$
-module of finite rank n, let
${\mathbb Z}$
-module of finite rank n, let
![]() $\Omega _\infty \subset \Lambda _\infty $
be a bounded definable subset, and, for each prime p in a finite subset S, let
$\Omega _\infty \subset \Lambda _\infty $
be a bounded definable subset, and, for each prime p in a finite subset S, let
![]() $\Omega _p=\prod _j \{x\in {\mathbb Z}_p : |x-a_{p,j}|_p\leq \omega _{p,j}\}\subset \Lambda _p$
be a
$\Omega _p=\prod _j \{x\in {\mathbb Z}_p : |x-a_{p,j}|_p\leq \omega _{p,j}\}\subset \Lambda _p$
be a
![]() $(\Lambda _p)$
-box. Let
$(\Lambda _p)$
-box. Let
![]() ${\textbf {w}}=(w_1,\dots ,w_n)$
be an n-tuple of positive integers. Then,
${\textbf {w}}=(w_1,\dots ,w_n)$
be an n-tuple of positive integers. Then,
 $$ \begin{align*} &\#\{x\in \Lambda\cap \left(B \ast_{\textbf{w}} \Omega_\infty\right): x\in \Omega_p \text{ for all primes } p\in S\}\\ &\hspace{1cm}= \left(\frac{m_\infty(\Omega_\infty)}{m_\infty(\Lambda_\infty/\Lambda)}\prod_{p\in S} \frac{m_p(\Omega_p)}{m_p(\Lambda_p)}\right)B^{|{\textbf{w}}|} + O\,\left(\max_j\left\{\prod_{p\in S} \omega_{p,j}^{-1}\right\}\left(\prod_{p\in S} \frac{m_p(\Omega_p)}{m_p(\Lambda_p)}\right)B^{|{\textbf{w}}|-w_{\min}}\right), \end{align*} $$
$$ \begin{align*} &\#\{x\in \Lambda\cap \left(B \ast_{\textbf{w}} \Omega_\infty\right): x\in \Omega_p \text{ for all primes } p\in S\}\\ &\hspace{1cm}= \left(\frac{m_\infty(\Omega_\infty)}{m_\infty(\Lambda_\infty/\Lambda)}\prod_{p\in S} \frac{m_p(\Omega_p)}{m_p(\Lambda_p)}\right)B^{|{\textbf{w}}|} + O\,\left(\max_j\left\{\prod_{p\in S} \omega_{p,j}^{-1}\right\}\left(\prod_{p\in S} \frac{m_p(\Omega_p)}{m_p(\Lambda_p)}\right)B^{|{\textbf{w}}|-w_{\min}}\right), \end{align*} $$
where the implied constant depends only on
![]() $\Lambda $
,
$\Lambda $
,
![]() $\Omega _\infty $
, and
$\Omega _\infty $
, and
![]() ${\textbf {w}}$
.
${\textbf {w}}$
.
Proof. Fix an isomorphism
![]() $\Lambda \cong {\mathbb Z}^n$
. The measures
$\Lambda \cong {\mathbb Z}^n$
. The measures
![]() $m_\infty $
and
$m_\infty $
and
![]() $m_p$
on
$m_p$
on
![]() $\Lambda _\infty $
and
$\Lambda _\infty $
and
![]() $\Lambda _p$
induce measures on
$\Lambda _p$
induce measures on
![]() ${\mathbb R}^n$
and
${\mathbb R}^n$
and
![]() ${\mathbb Z}_p^n$
which differ from the usual Haar measures by
${\mathbb Z}_p^n$
which differ from the usual Haar measures by
![]() $m_\infty (\Lambda _\infty /\Lambda )$
and
$m_\infty (\Lambda _\infty /\Lambda )$
and
![]() $m_p(\Lambda _p)$
, respectively. It therefore suffices to prove the result in the case
$m_p(\Lambda _p)$
, respectively. It therefore suffices to prove the result in the case
![]() $\Lambda ={\mathbb Z}^n$
, and
$\Lambda ={\mathbb Z}^n$
, and
![]() $m_\infty =m_L$
and
$m_\infty =m_L$
and
![]() $m_p$
are the usual Haar measures; but this case is precisely the Box Lemma (Lemma 3.2.3).
$m_p$
are the usual Haar measures; but this case is precisely the Box Lemma (Lemma 3.2.3).
If K is a number field of degree d over
![]() ${\mathbb Q}$
with discriminant
${\mathbb Q}$
with discriminant
![]() $\Delta _K$
, then its ring of integers
$\Delta _K$
, then its ring of integers
![]() ${\mathcal O}_K$
may naturally be viewed as a rank d lattice in
${\mathcal O}_K$
may naturally be viewed as a rank d lattice in
![]() $K_\infty \stackrel {\mathrm{def}}{=}{\mathcal O}_K\otimes _{{\mathbb Z}} {\mathbb R}=\prod _{v|\infty } K_v$
. This lattice has covolume
$K_\infty \stackrel {\mathrm{def}}{=}{\mathcal O}_K\otimes _{{\mathbb Z}} {\mathbb R}=\prod _{v|\infty } K_v$
. This lattice has covolume
![]() $|\Delta _K|^{1/2}$
with respect to the usual Haar measure
$|\Delta _K|^{1/2}$
with respect to the usual Haar measure
![]() $m_\infty $
on
$m_\infty $
on
![]() $K_\infty $
(which differs from Lebesgue measure on
$K_\infty $
(which differs from Lebesgue measure on
![]() $K_\infty \cong {\mathbb R}^{r_1+2r_2}$
by a factor of
$K_\infty \cong {\mathbb R}^{r_1+2r_2}$
by a factor of
![]() $2^{r_2}$
) [Reference NeukirchNeu99, Chapter I Proposition 5.2]. More generally, any nonzero integral ideal
$2^{r_2}$
) [Reference NeukirchNeu99, Chapter I Proposition 5.2]. More generally, any nonzero integral ideal
![]() ${\mathfrak a}\subseteq {\mathcal O}_K$
may be viewed as a lattice in
${\mathfrak a}\subseteq {\mathcal O}_K$
may be viewed as a lattice in
![]() $K_\infty $
with covolume
$K_\infty $
with covolume
![]() $N_{K/{\mathbb Q}}({\mathfrak a})|\Delta _K|^{1/2}$
. For an n-tuple of positive integers
$N_{K/{\mathbb Q}}({\mathfrak a})|\Delta _K|^{1/2}$
. For an n-tuple of positive integers
![]() ${\textbf {w}}=(w_1,\dots ,w_n)$
, define the lattice
${\textbf {w}}=(w_1,\dots ,w_n)$
, define the lattice
where we view each
![]() ${\mathfrak a}^{w_i}$
as a subset of
${\mathfrak a}^{w_i}$
as a subset of
![]() $K_\infty $
. This lattice has covolume
$K_\infty $
. This lattice has covolume
![]() $N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf {w}}|}|\Delta _K|^{n/2}$
. For example, in the case that
$N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf {w}}|}|\Delta _K|^{n/2}$
. For example, in the case that
![]() ${\mathfrak a}={\mathcal O}_K$
and
${\mathfrak a}={\mathcal O}_K$
and
![]() $w_i=1$
for all i, one has the lattice
$w_i=1$
for all i, one has the lattice
![]() ${\mathfrak a}^{\textbf {w}}={\mathcal O}_K^{n}$
of covolume
${\mathfrak a}^{\textbf {w}}={\mathcal O}_K^{n}$
of covolume
![]() $|\Delta _K|^{n/2}$
.
$|\Delta _K|^{n/2}$
.
For any rational prime p, we have
![]() ${\mathcal O}_K\otimes _{{\mathbb Z}} {\mathbb Z}_p=\prod _{{\mathfrak p}|p} {\mathcal O}_{K,{\mathfrak p}}$
. Equip each
${\mathcal O}_K\otimes _{{\mathbb Z}} {\mathbb Z}_p=\prod _{{\mathfrak p}|p} {\mathcal O}_{K,{\mathfrak p}}$
. Equip each
![]() ${\mathcal O}_{K,{\mathfrak p}}$
with the Haar measure
${\mathcal O}_{K,{\mathfrak p}}$
with the Haar measure
![]() $m_{\mathfrak p}$
, normalized so that
$m_{\mathfrak p}$
, normalized so that
![]() $m_{\mathfrak p}({\mathcal O}_{K,{\mathfrak p}})=1$
. This measure induces a measure on
$m_{\mathfrak p}({\mathcal O}_{K,{\mathfrak p}})=1$
. This measure induces a measure on
![]() ${\mathcal O}_{K,{\mathfrak p}}^n$
, which we will also denote by
${\mathcal O}_{K,{\mathfrak p}}^n$
, which we will also denote by
![]() $m_{\mathfrak p}$
. Similarly, the measure
$m_{\mathfrak p}$
. Similarly, the measure
![]() $m_\infty $
on
$m_\infty $
on
![]() $K_\infty $
induces a measure on
$K_\infty $
induces a measure on
![]() $K_\infty ^n$
, which we will denote by
$K_\infty ^n$
, which we will denote by
![]() $m_\infty $
.
$m_\infty $
.
For
![]() $v\in \text {Val}_0(K)$
a finite place, let
$v\in \text {Val}_0(K)$
a finite place, let
![]() $q_v$
denote the size of the residue field
$q_v$
denote the size of the residue field
![]() ${\mathcal O}_{K}/{\mathfrak p}_v$
. Let
${\mathcal O}_{K}/{\mathfrak p}_v$
. Let
![]() ${\mathfrak a}_{\mathfrak p}$
denote the image of
${\mathfrak a}_{\mathfrak p}$
denote the image of
![]() ${\mathfrak a}$
in
${\mathfrak a}$
in
![]() ${\mathcal O}_{K,{\mathfrak p}}$
.
${\mathcal O}_{K,{\mathfrak p}}$
.
Definition 3.2.5 (Local condition).
An (affine) local condition at a finite place
![]() $v\in \text {Val}_0(K)$
will refer to a subset
$v\in \text {Val}_0(K)$
will refer to a subset
![]() $\Omega _v\subseteq {\mathcal O}_{K,{\mathfrak p}_v}^n$
. We call a local condition
$\Omega _v\subseteq {\mathcal O}_{K,{\mathfrak p}_v}^n$
. We call a local condition
![]() $\Omega _v$
irreducible if it is an (
$\Omega _v$
irreducible if it is an (
![]() ${\mathcal O}_{K,{\mathfrak p}_v}^n$
)-box – that is, if there exist
${\mathcal O}_{K,{\mathfrak p}_v}^n$
)-box – that is, if there exist
![]() $a_{j}\in {\mathcal O}_{K,{\mathfrak p}_v}$
and
$a_{j}\in {\mathcal O}_{K,{\mathfrak p}_v}$
and
![]() $\omega _{j}\in \{q_v^{-k} : k\in {\mathbb Z}_{\geq 0}\}$
such that
$\omega _{j}\in \{q_v^{-k} : k\in {\mathbb Z}_{\geq 0}\}$
such that
![]() $\Omega _v=\prod _j \{ x\in {\mathcal O}_{K,{\mathfrak p}_v} : |x-a_j|_v\leq \omega _j\}\subset {\mathcal O}_{K,{\mathfrak p}_v}^n$
.
$\Omega _v=\prod _j \{ x\in {\mathcal O}_{K,{\mathfrak p}_v} : |x-a_j|_v\leq \omega _j\}\subset {\mathcal O}_{K,{\mathfrak p}_v}^n$
.
Remark 3.2.6. Though our results will mostly concern irreducible local conditions, by taking unions and complements, one can easily extend these results to many other local conditions.
We now apply Lemma 3.2.4 to the rank
![]() $nd$
lattice
$nd$
lattice
![]() ${\mathfrak a}^{\textbf {w}}$
, and with the
${\mathfrak a}^{\textbf {w}}$
, and with the
![]() $(nd)$
-tuple of weights
$(nd)$
-tuple of weights
![]() $\tilde {{\textbf {w}}}=(w_1,\dots ,w_1,w_2,\dots ,w_2,\dots ,w_n,\dots ,w_n)$
, obtained by repeating each of the weights in the n-tuple
$\tilde {{\textbf {w}}}=(w_1,\dots ,w_1,w_2,\dots ,w_2,\dots ,w_n,\dots ,w_n)$
, obtained by repeating each of the weights in the n-tuple
![]() ${\textbf {w}}$
exactly d times. Observing that
${\textbf {w}}$
exactly d times. Observing that
![]() $|\tilde {{\textbf {w}}}|=d|{\textbf {w}}|$
and
$|\tilde {{\textbf {w}}}|=d|{\textbf {w}}|$
and
![]() $\tilde {w}_{\min }=w_{\min }$
, we obtain the following proposition:
$\tilde {w}_{\min }=w_{\min }$
, we obtain the following proposition:
Proposition 3.2.7. Let
![]() $\Omega _\infty \subset K_\infty ^{n}$
be a bounded definable subset. Let S be a finite set of prime ideals of
$\Omega _\infty \subset K_\infty ^{n}$
be a bounded definable subset. Let S be a finite set of prime ideals of
![]() ${\mathcal O}_K$
. For each
${\mathcal O}_K$
. For each
![]() ${\mathfrak p}\in S$
, let
${\mathfrak p}\in S$
, let
![]() $\Omega _{\mathfrak p}=\prod _j \{x\in {\mathcal O}_{K,{\mathfrak p}} : |x-a_{{\mathfrak p},j}|_{\mathfrak p}\leq \omega _{{\mathfrak p},j}\}\subset {\mathcal O}_{K,{\mathfrak p}}^n$
be an irreducible local condition. Then,
$\Omega _{\mathfrak p}=\prod _j \{x\in {\mathcal O}_{K,{\mathfrak p}} : |x-a_{{\mathfrak p},j}|_{\mathfrak p}\leq \omega _{{\mathfrak p},j}\}\subset {\mathcal O}_{K,{\mathfrak p}}^n$
be an irreducible local condition. Then,
where
 $$ \begin{align*} \kappa&=\frac{m_\infty(\Omega_\infty)}{N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf{w}}|}|\Delta_K|^{n/2}} \left(\prod_{{\mathfrak p}\in S} \frac{m_{\mathfrak p}(\Omega_{\mathfrak p}\cap {\mathfrak a}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak a}_{\mathfrak p}^{\textbf{w}})}\right),\\ \epsilon&=\max_j\left\{\prod_{{\mathfrak p}\in S} \omega_{{\mathfrak p},j}^{-1}\right\}\left(\prod_{{\mathfrak p}\in S} \frac{m_{\mathfrak p}(\Omega_{\mathfrak p}\cap {\mathfrak a}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak a}_{\mathfrak p}^{\textbf{w}})}\right), \end{align*} $$
$$ \begin{align*} \kappa&=\frac{m_\infty(\Omega_\infty)}{N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf{w}}|}|\Delta_K|^{n/2}} \left(\prod_{{\mathfrak p}\in S} \frac{m_{\mathfrak p}(\Omega_{\mathfrak p}\cap {\mathfrak a}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak a}_{\mathfrak p}^{\textbf{w}})}\right),\\ \epsilon&=\max_j\left\{\prod_{{\mathfrak p}\in S} \omega_{{\mathfrak p},j}^{-1}\right\}\left(\prod_{{\mathfrak p}\in S} \frac{m_{\mathfrak p}(\Omega_{\mathfrak p}\cap {\mathfrak a}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak a}_{\mathfrak p}^{\textbf{w}})}\right), \end{align*} $$
and where the implied constant depends only on K,
![]() $\Omega _\infty $
and
$\Omega _\infty $
and
![]() ${\textbf {w}}$
.
${\textbf {w}}$
.
4. Counting points on weighted projective stacks
In this section, we prove our results for counting points of bounded height on weighted projective stacks.
Definition 4.0.1 (Local condition).
A (projective) local condition at a place
![]() $v\in \text {Val}(K)$
will refer to a subset
$v\in \text {Val}(K)$
will refer to a subset
![]() $\Omega _v\subseteq \mathcal {P}({\textbf {w}})(K_v)$
.
$\Omega _v\subseteq \mathcal {P}({\textbf {w}})(K_v)$
.
For a projective local condition
![]() $\Omega _v\subseteq {\mathcal P}({\textbf {w}})(K_v)$
, we denote the affine cone of
$\Omega _v\subseteq {\mathcal P}({\textbf {w}})(K_v)$
, we denote the affine cone of
![]() $\Omega _v$
by
$\Omega _v$
by
![]() $\Omega _v^{\mathrm{aff}}\subseteq ({\mathbb A}^{n+1}-\{0\})(K_v)$
(i.e.,
$\Omega _v^{\mathrm{aff}}\subseteq ({\mathbb A}^{n+1}-\{0\})(K_v)$
(i.e.,
![]() $\Omega _v^{\mathrm{aff}}$
is the preimage of
$\Omega _v^{\mathrm{aff}}$
is the preimage of
![]() $\Omega $
with respect to the map
$\Omega $
with respect to the map
![]() $({\mathbb A}^{n+1}-\{0\})\to {\mathcal P}({\textbf {w}})$
). For
$({\mathbb A}^{n+1}-\{0\})\to {\mathcal P}({\textbf {w}})$
). For
![]() $v\in \text {Val}_0(K)$
, the set
$v\in \text {Val}_0(K)$
, the set
![]() $\Omega _v^{\mathrm{aff}}\cap {\mathcal O}_{K,{\mathfrak p}_v}^{n+1}$
is an affine local condition, but not an irreducible affine local condition (see Definition 3.2.5).
$\Omega _v^{\mathrm{aff}}\cap {\mathcal O}_{K,{\mathfrak p}_v}^{n+1}$
is an affine local condition, but not an irreducible affine local condition (see Definition 3.2.5).
Example 4.0.2. Let
![]() $v\in \text {Val}_0(K)$
be a finite place. Consider the projective local condition
$v\in \text {Val}_0(K)$
be a finite place. Consider the projective local condition
Then,
Though this is not an irreducible affine local condition, it contains the irreducible affine local condition
Letting
![]() $\pi _v$
be a uniformizer of
$\pi _v$
be a uniformizer of
![]() ${\mathcal O}_{K,v}$
, we have
${\mathcal O}_{K,v}$
, we have
where
![]() $\pi _v^t \ast _{(1,1)} \Omega _{v,0}^{\mathrm{aff}}$
is an irreducible affine local condition for each t.
$\pi _v^t \ast _{(1,1)} \Omega _{v,0}^{\mathrm{aff}}$
is an irreducible affine local condition for each t.
This example motivates the following definition:
Definition 4.0.3 (Irreducible projective local condition).
A projective local condition
![]() $\Omega _v\subseteq {\mathcal P}({\textbf {w}})(K_v)$
is said to be irreducible if there exists an irreducible affine local condition
$\Omega _v\subseteq {\mathcal P}({\textbf {w}})(K_v)$
is said to be irreducible if there exists an irreducible affine local condition
![]() $\Omega _{v,0}^{\mathrm{aff}}$
such that
$\Omega _{v,0}^{\mathrm{aff}}$
such that
In analogy to the archimedean setting, for any ideal
![]() ${\mathfrak a}_v\subseteq {\mathcal O}_{K,v}$
, set
${\mathfrak a}_v\subseteq {\mathcal O}_{K,v}$
, set
Proposition 4.0.4. Let
![]() $\Omega _v\subsetneq {\mathcal P}({\textbf {w}})(K_v)$
be a nontrivial irreducible projective local condition with
$\Omega _v\subsetneq {\mathcal P}({\textbf {w}})(K_v)$
be a nontrivial irreducible projective local condition with
 $$\begin{align*}\Omega^{\mathrm{aff}}_{v,0}=\prod_{j=0}^n\{x\in{\mathcal O}_{K,v} : |x-a_{j}|_v\leq \omega_j\}. \end{align*}$$
$$\begin{align*}\Omega^{\mathrm{aff}}_{v,0}=\prod_{j=0}^n\{x\in{\mathcal O}_{K,v} : |x-a_{j}|_v\leq \omega_j\}. \end{align*}$$
For
![]() $t\in {\mathbb Z}_{\geq 0}$
, set
$t\in {\mathbb Z}_{\geq 0}$
, set
![]() $\Omega ^{\mathrm{aff}}_{v,t}=\pi _v^t\ast _{\textbf {w}} \Omega ^{\mathrm{aff}}_{v,0}$
. Then we have the following:
$\Omega ^{\mathrm{aff}}_{v,t}=\pi _v^t\ast _{\textbf {w}} \Omega ^{\mathrm{aff}}_{v,0}$
. Then we have the following:
-
(a) There exists a j for which
 $|a_j|_v> \omega _j$
.
$|a_j|_v> \omega _j$
. -
(b) For
 $t\neq s$
, we have
$t\neq s$
, we have
 $\Omega ^{\mathrm{aff}}_{v,t}\cap \Omega ^{\mathrm{aff}}_{v,s}=\emptyset $
.
$\Omega ^{\mathrm{aff}}_{v,t}\cap \Omega ^{\mathrm{aff}}_{v,s}=\emptyset $
. -
(c) For
 $s,t\in {\mathbb Z}_{\geq 0}$
with
$s,t\in {\mathbb Z}_{\geq 0}$
with
 $s<t$
, we have
$s<t$
, we have
 $\Omega _{v,s}^{\mathrm{aff}}\cap (\pi _v^{t})^{{\textbf {w}}}=\emptyset $
.
$\Omega _{v,s}^{\mathrm{aff}}\cap (\pi _v^{t})^{{\textbf {w}}}=\emptyset $
.
Proof. (a) We first prove the contrapositive of part (a). Suppose that
![]() $|a_j|_v\leq \omega _j$
for all j. If each
$|a_j|_v\leq \omega _j$
for all j. If each
![]() $\omega _j=1$
, then
$\omega _j=1$
, then
![]() $\Omega ^{\mathrm{aff}}_{v,0}={\mathcal O}_{K,v}^{n+1}=\Omega _{v}^{\mathrm{aff}}\cap {\mathcal O}_{K,v}^{n+1}$
, but then
$\Omega ^{\mathrm{aff}}_{v,0}={\mathcal O}_{K,v}^{n+1}=\Omega _{v}^{\mathrm{aff}}\cap {\mathcal O}_{K,v}^{n+1}$
, but then
![]() $\Omega _v={\mathcal P}({\textbf {w}})(K_v)$
would be the trivial projective local condition. Therefore, there must exist an index j for which
$\Omega _v={\mathcal P}({\textbf {w}})(K_v)$
would be the trivial projective local condition. Therefore, there must exist an index j for which
![]() $\omega _j\neq 1$
. By possibly reordering, we may assume
$\omega _j\neq 1$
. By possibly reordering, we may assume
![]() $\omega _1\neq 1$
. As
$\omega _1\neq 1$
. As
![]() $|a_1|_v\leq \omega _1<1$
, we have that
$|a_1|_v\leq \omega _1<1$
, we have that
![]() $|1-a_1|_v=1>\omega _1$
(by the ultrametric triangle inequality). Let
$|1-a_1|_v=1>\omega _1$
(by the ultrametric triangle inequality). Let
![]() $b\in {\mathcal O}_{K,v}-\{0\}$
be such that
$b\in {\mathcal O}_{K,v}-\{0\}$
be such that
![]() $|b-a_1|_v\leq \omega _1$
. Then
$|b-a_1|_v\leq \omega _1$
. Then
![]() $(b,0,\dots ,0)$
and
$(b,0,\dots ,0)$
and
![]() $(1,0,\dots ,0)$
are points in the affine cone
$(1,0,\dots ,0)$
are points in the affine cone
![]() $K_v^{n+1}-\{0\}$
of
$K_v^{n+1}-\{0\}$
of
![]() ${\mathcal P}({\textbf {w}})(K_v)$
, each above the point
${\mathcal P}({\textbf {w}})(K_v)$
, each above the point
![]() $[1:0:\cdots :0]\in {\mathcal P}({\textbf {w}})(K_v)$
, but only one is contained in
$[1:0:\cdots :0]\in {\mathcal P}({\textbf {w}})(K_v)$
, but only one is contained in
![]() $\Omega _v^{\mathrm{aff}}$
. We conclude that
$\Omega _v^{\mathrm{aff}}$
. We conclude that
![]() $\Omega _v^{\mathrm{aff}}$
cannot be the entire subset of the affine cone above a projective local condition.
$\Omega _v^{\mathrm{aff}}$
cannot be the entire subset of the affine cone above a projective local condition.
(b) We now show that if
![]() $|a_j|_v> \omega _j$
for some j, then for
$|a_j|_v> \omega _j$
for some j, then for
![]() $t\neq s$
, we have
$t\neq s$
, we have
![]() $\Omega ^{\mathrm{aff}}_{v,t}\cap \Omega ^{\mathrm{aff}}_{v,s}=\emptyset $
. Observe that
$\Omega ^{\mathrm{aff}}_{v,t}\cap \Omega ^{\mathrm{aff}}_{v,s}=\emptyset $
. Observe that
 $$\begin{align*}\Omega^{\mathrm{aff}}_{v,t}=\prod_{j=0}^n \{x\in {\mathcal O}_{K,v} : |x-\pi_v^{tw_j} a_j|_v\leq q_v^{-tw_j}\omega_j\} \end{align*}$$
$$\begin{align*}\Omega^{\mathrm{aff}}_{v,t}=\prod_{j=0}^n \{x\in {\mathcal O}_{K,v} : |x-\pi_v^{tw_j} a_j|_v\leq q_v^{-tw_j}\omega_j\} \end{align*}$$
is a product of v-adic balls centered at
![]() $\pi _v^{tw_j}a_j$
with radius
$\pi _v^{tw_j}a_j$
with radius
![]() $q_v^{-tw_j}\omega _j$
. Without loss of generality, we may assume
$q_v^{-tw_j}\omega _j$
. Without loss of generality, we may assume
![]() $s< t$
. Using
$s< t$
. Using
![]() $|a_j|_v>\omega _j$
, we have that
$|a_j|_v>\omega _j$
, we have that
In particular, the distance between the centers of the balls
is larger than either of the radii, and thus, the balls must be disjoint (since we are in an ultrametric space).
(c) We will show that if
![]() $\Omega _{v,s}^{\mathrm{aff}}\cap (\pi _v^{t})^{{\textbf {w}}}$
is nonempty, then
$\Omega _{v,s}^{\mathrm{aff}}\cap (\pi _v^{t})^{{\textbf {w}}}$
is nonempty, then
![]() $\Omega _v$
is not a projective local condition. Let
$\Omega _v$
is not a projective local condition. Let
![]() $y=(y_0,\dots ,y_n)\in \Omega _{v,s}^{\mathrm{aff}}\cap (\pi _v^{t})^{{\textbf {w}}}$
and let
$y=(y_0,\dots ,y_n)\in \Omega _{v,s}^{\mathrm{aff}}\cap (\pi _v^{t})^{{\textbf {w}}}$
and let
![]() $y'=(y^{\prime }_0,\dots ,y^{\prime }_n)\in {\mathcal O}_{K,v}^{n+1}$
be such that
$y'=(y^{\prime }_0,\dots ,y^{\prime }_n)\in {\mathcal O}_{K,v}^{n+1}$
be such that
![]() $y=\pi _v^t\ast _{\textbf {w}} y'$
. It will suffice to show that
$y=\pi _v^t\ast _{\textbf {w}} y'$
. It will suffice to show that
![]() $y'$
is not in
$y'$
is not in
![]() $\Omega ^{\mathrm{aff}}_v$
.
$\Omega ^{\mathrm{aff}}_v$
.
By part (a), we may choose j to be such that
![]() $|a_j|_v>\omega _j$
. From this, together with the fact that
$|a_j|_v>\omega _j$
. From this, together with the fact that
![]() $y_j\in \pi _v^{t w_j}$
satisfies
$y_j\in \pi _v^{t w_j}$
satisfies
![]() $|y_j-\pi _v^{sw_j} a_j|_v\leq q_v^{-sw_j}\omega _j$
, implies that we must have
$|y_j-\pi _v^{sw_j} a_j|_v\leq q_v^{-sw_j}\omega _j$
, implies that we must have
![]() $|y_j|_v=q_v^{-sw_j}|a_j|_v$
. Therefore,
$|y_j|_v=q_v^{-sw_j}|a_j|_v$
. Therefore,
![]() $|y^{\prime }_j|_v=q_v^{(t-s)w_j}|a_j|_v$
. Since
$|y^{\prime }_j|_v=q_v^{(t-s)w_j}|a_j|_v$
. Since
![]() $s<t$
, this implies that
$s<t$
, this implies that
![]() $|y^{\prime }_j|_v\neq |\pi _v^{rw_j}a_j|_v$
for any
$|y^{\prime }_j|_v\neq |\pi _v^{rw_j}a_j|_v$
for any
![]() $r\in {\mathbb Z}_{\geq 0}$
, and thus,
$r\in {\mathbb Z}_{\geq 0}$
, and thus,
![]() $y'$
is not contained in
$y'$
is not contained in
![]() $\Omega ^{\mathrm{aff}}_v\cap {\mathcal O}_{K,v}^{n+1}=\bigcup _t \Omega ^{\mathrm{aff}}_{v,t}$
.
$\Omega ^{\mathrm{aff}}_v\cap {\mathcal O}_{K,v}^{n+1}=\bigcup _t \Omega ^{\mathrm{aff}}_{v,t}$
.
For any set of projective local conditions
![]() $(\Omega _v)_{v}$
, define the sets
$(\Omega _v)_{v}$
, define the sets
 $$ \begin{align*} \Omega&\stackrel{\mathrm{def}}{=}\{x\in {\mathcal P}({\textbf{w}})(K) : x\in \Omega_v \text{ for all } v\in \text{Val}(K)\} ,\\ \Omega_\infty&\stackrel{\mathrm{def}}{=}\{x\in {\mathcal P}({\textbf{w}})(K) : x\in \Omega_v \text{ for all } v\in \text{Val}_\infty(K)\},\\ \Omega_0&\stackrel{\mathrm{def}}{=}\{x\in {\mathcal P}({\textbf{w}})(K) : x\in \Omega_v \text{ for all } v\in \text{Val}_0(K)\}. \end{align*} $$
$$ \begin{align*} \Omega&\stackrel{\mathrm{def}}{=}\{x\in {\mathcal P}({\textbf{w}})(K) : x\in \Omega_v \text{ for all } v\in \text{Val}(K)\} ,\\ \Omega_\infty&\stackrel{\mathrm{def}}{=}\{x\in {\mathcal P}({\textbf{w}})(K) : x\in \Omega_v \text{ for all } v\in \text{Val}_\infty(K)\},\\ \Omega_0&\stackrel{\mathrm{def}}{=}\{x\in {\mathcal P}({\textbf{w}})(K) : x\in \Omega_v \text{ for all } v\in \text{Val}_0(K)\}. \end{align*} $$
Set
![]() $\varpi _{K,{\textbf {w}}}\stackrel {\mathrm{def}}{=} \varpi _K/\gcd (\varpi _K,w_0,\dots ,w_n)$
, where we recall that
$\varpi _{K,{\textbf {w}}}\stackrel {\mathrm{def}}{=} \varpi _K/\gcd (\varpi _K,w_0,\dots ,w_n)$
, where we recall that
![]() $\varpi _K$
is the number of roots of unity in K.
$\varpi _K$
is the number of roots of unity in K.
Theorem 4.0.5. Let K be a degree d number field over
![]() ${\mathbb Q}$
. Let
${\mathbb Q}$
. Let
![]() $S\subset \text {Val}_0(K)$
be a finite set of finite places. For each
$S\subset \text {Val}_0(K)$
be a finite set of finite places. For each
![]() $v\in \text {Val}_\infty (K)\cup S$
, let
$v\in \text {Val}_\infty (K)\cup S$
, let
![]() $\Omega _v\subset {\mathcal P}({\textbf {w}})(K_v)$
be a projective local condition. Suppose that
$\Omega _v\subset {\mathcal P}({\textbf {w}})(K_v)$
be a projective local condition. Suppose that
![]() $\Omega ^{\mathrm{aff}}_\infty $
is a bounded definable subset of
$\Omega ^{\mathrm{aff}}_\infty $
is a bounded definable subset of
![]() $K_\infty ^{n+1}$
and that
$K_\infty ^{n+1}$
and that
![]() $\Omega _v$
is irreducible for all
$\Omega _v$
is irreducible for all
![]() $v\in S$
with
$v\in S$
with
 $$\begin{align*}\Omega_{v,0}^{\mathrm{aff}}=\prod_{j=0}^n\{x\in {\mathcal O}_{K,v}: |x-a_{v,j}|_v\leq \omega_{v,j}\}, \end{align*}$$
$$\begin{align*}\Omega_{v,0}^{\mathrm{aff}}=\prod_{j=0}^n\{x\in {\mathcal O}_{K,v}: |x-a_{v,j}|_v\leq \omega_{v,j}\}, \end{align*}$$
where
![]() $a_{v,j}\in {\mathcal O}_{K,v}$
and
$a_{v,j}\in {\mathcal O}_{K,v}$
and
![]() $\omega _{v,j}\in \{q_v^{-k}:k\in {\mathbb Z}_{\geq 0}\}$
(see Definitions 4.0.3 and 3.2.5). Then,
$\omega _{v,j}\in \{q_v^{-k}:k\in {\mathbb Z}_{\geq 0}\}$
(see Definitions 4.0.3 and 3.2.5). Then,
 $$ \begin{align*} \#\{x\in {\mathcal P}({\textbf{w}})(K): \text{Ht}_{{\textbf{w}}}(x)\leq B, x\in \Omega\} = \kappa B^{|{\textbf{w}}|} + \begin{cases} O\,\left(\epsilon_\Omega B\log(B)\right) & {\substack{\text{ if } {\textbf{w}}=(1,1)\\ \text{and}\ K={\mathbb Q},}}\\ O\,\left(\epsilon_\Omega B^{\frac{d|{\textbf{w}}|-w_{\min}}{d}}\right) & \text{ else, } \end{cases} \end{align*} $$
$$ \begin{align*} \#\{x\in {\mathcal P}({\textbf{w}})(K): \text{Ht}_{{\textbf{w}}}(x)\leq B, x\in \Omega\} = \kappa B^{|{\textbf{w}}|} + \begin{cases} O\,\left(\epsilon_\Omega B\log(B)\right) & {\substack{\text{ if } {\textbf{w}}=(1,1)\\ \text{and}\ K={\mathbb Q},}}\\ O\,\left(\epsilon_\Omega B^{\frac{d|{\textbf{w}}|-w_{\min}}{d}}\right) & \text{ else, } \end{cases} \end{align*} $$
where the leading coefficient is
 $$\begin{align*}\kappa=\kappa_\Omega\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{n+1}R_K|{\textbf{w}}|^{r_1+r_2-1}}{\varpi_{K,{\textbf{w}}}|\Delta_K|^{(n+1)/2}\zeta_K(|{\textbf{w}}|)}, \end{align*}$$
$$\begin{align*}\kappa=\kappa_\Omega\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{n+1}R_K|{\textbf{w}}|^{r_1+r_2-1}}{\varpi_{K,{\textbf{w}}}|\Delta_K|^{(n+1)/2}\zeta_K(|{\textbf{w}}|)}, \end{align*}$$
where
 $$\begin{align*}\kappa_\Omega=\prod_{v|\infty} \frac{m_v(\{x\in \Omega_v^{\mathrm{aff}} : \text{Ht}_{{\textbf{w}},v}(x)\leq 1\})}{m_v(\{x\in K_v^{n+1}: \text{Ht}_{{\textbf{w}},v}(x)\leq 1\})} \prod_{v\in S} m_v(\Omega_v^{\mathrm{aff}}\cap {\mathcal O}_{K,v}^{n+1}), \end{align*}$$
$$\begin{align*}\kappa_\Omega=\prod_{v|\infty} \frac{m_v(\{x\in \Omega_v^{\mathrm{aff}} : \text{Ht}_{{\textbf{w}},v}(x)\leq 1\})}{m_v(\{x\in K_v^{n+1}: \text{Ht}_{{\textbf{w}},v}(x)\leq 1\})} \prod_{v\in S} m_v(\Omega_v^{\mathrm{aff}}\cap {\mathcal O}_{K,v}^{n+1}), \end{align*}$$
where the factor in the error term is
 $$\begin{align*}\epsilon_{\Omega}=\sum_{t=0}^\infty \max\limits_j\left\{\prod\limits_{v\in S} \frac{N_{K/{\mathbb Q}}({\mathfrak p}_v)^{tw_j}}{\omega_{v,j}}\right\}\frac{1}{N_{K/{\mathbb Q}}({\mathfrak p}_v)^{t|{\textbf{w}}|}}\prod\limits_{v\in S} m_v(\Omega_{v,0}^{\mathrm{aff}}), \end{align*}$$
$$\begin{align*}\epsilon_{\Omega}=\sum_{t=0}^\infty \max\limits_j\left\{\prod\limits_{v\in S} \frac{N_{K/{\mathbb Q}}({\mathfrak p}_v)^{tw_j}}{\omega_{v,j}}\right\}\frac{1}{N_{K/{\mathbb Q}}({\mathfrak p}_v)^{t|{\textbf{w}}|}}\prod\limits_{v\in S} m_v(\Omega_{v,0}^{\mathrm{aff}}), \end{align*}$$
and where the implied constant is independent of the local conditions
![]() $\Omega _{v}$
with
$\Omega _{v}$
with
![]() $v\in S$
.
$v\in S$
.
Proof. Let
![]() ${\mathfrak c}_1,\dots ,{\mathfrak c}_h$
be a set of integral ideal representatives of the ideal class group of K. Then, we get the following partition of
${\mathfrak c}_1,\dots ,{\mathfrak c}_h$
be a set of integral ideal representatives of the ideal class group of K. Then, we get the following partition of
![]() ${\mathcal P}({\textbf {w}})(K)$
into points whose scaling ideals are in the same ideal class:
${\mathcal P}({\textbf {w}})(K)$
into points whose scaling ideals are in the same ideal class:
 $$\begin{align*}{\mathcal P}({\textbf{w}})(K)=\bigsqcup_{i=1}^h \{x\in {\mathcal P}({\textbf{w}})(K): [{\mathfrak I}_{\textbf{w}}(x)]=[{\mathfrak c}_i]\}. \end{align*}$$
$$\begin{align*}{\mathcal P}({\textbf{w}})(K)=\bigsqcup_{i=1}^h \{x\in {\mathcal P}({\textbf{w}})(K): [{\mathfrak I}_{\textbf{w}}(x)]=[{\mathfrak c}_i]\}. \end{align*}$$
This is well defined since the ideal class of a scaling ideal
![]() $[{\mathfrak I}_{\textbf {w}}(x)]$
does not depend on the representative of x [Reference DengDen98, Proposition 3.3].
$[{\mathfrak I}_{\textbf {w}}(x)]$
does not depend on the representative of x [Reference DengDen98, Proposition 3.3].
For each
![]() ${\mathfrak c}\in \{{\mathfrak c}_1,\dots ,{\mathfrak c}_h\}$
, consider the counting function
${\mathfrak c}\in \{{\mathfrak c}_1,\dots ,{\mathfrak c}_h\}$
, consider the counting function
Note that
 $$\begin{align*}\#\{x\in {\mathcal P}({\textbf{w}})(K): \text{Ht}_{{\textbf{w}}}(x)\leq B, x\in \Omega\}=\sum_{i=1}^{h} M(\Omega,{\mathfrak c}_i,B). \end{align*}$$
$$\begin{align*}\#\{x\in {\mathcal P}({\textbf{w}})(K): \text{Ht}_{{\textbf{w}}}(x)\leq B, x\in \Omega\}=\sum_{i=1}^{h} M(\Omega,{\mathfrak c}_i,B). \end{align*}$$
Following Schanuel [Reference SchanuelSch79], we shall find an asymptotic for
![]() $M(\Omega ,{\mathfrak c},B)$
by counting integral points in affine space and then moding out by an action of the unit group, followed by an action of principal ideals.
$M(\Omega ,{\mathfrak c},B)$
by counting integral points in affine space and then moding out by an action of the unit group, followed by an action of principal ideals.
Consider the (weighted) action of the unit group
![]() ${\mathcal O}_K^\times $
on
${\mathcal O}_K^\times $
on
![]() $K^{n+1}-\{0\}$
given by
$K^{n+1}-\{0\}$
given by
and let
![]() $(K^{n+1}-\{0\})/{\mathcal O}_K^\times $
denote the corresponding set of orbits. Let
$(K^{n+1}-\{0\})/{\mathcal O}_K^\times $
denote the corresponding set of orbits. Let
![]() $\Omega ^{\mathrm{aff}}$
be the affine cone of
$\Omega ^{\mathrm{aff}}$
be the affine cone of
![]() $\Omega $
. We may describe
$\Omega $
. We may describe
![]() $M(\Omega ,{\mathfrak c},B)$
in terms of
$M(\Omega ,{\mathfrak c},B)$
in terms of
![]() ${\mathcal O}_K^\times $
-orbits of an affine cone. In particular, there is a bijection between
${\mathcal O}_K^\times $
-orbits of an affine cone. In particular, there is a bijection between
and
 $$\begin{align*}\left\{[(x_0,\dots,x_n)]\in (K^{n+1}-\{0\})/{\mathcal O}_K^\times : \frac{\text{Ht}_{{\textbf{w}},\infty}(x)}{N_{K/{\mathbb Q}}({\mathfrak c})}\leq B,\ {\mathfrak I}_{\textbf{w}}(x)={\mathfrak c},\ x\in \Omega^{\mathrm{aff}}\right\} \end{align*}$$
$$\begin{align*}\left\{[(x_0,\dots,x_n)]\in (K^{n+1}-\{0\})/{\mathcal O}_K^\times : \frac{\text{Ht}_{{\textbf{w}},\infty}(x)}{N_{K/{\mathbb Q}}({\mathfrak c})}\leq B,\ {\mathfrak I}_{\textbf{w}}(x)={\mathfrak c},\ x\in \Omega^{\mathrm{aff}}\right\} \end{align*}$$
given by
and therefore,
 $$\begin{align*}M(\Omega,{\mathfrak c},B)=\#\left\{x\in (K^{n+1}-\{0\})/{\mathcal O}_K^\times : \frac{\text{Ht}_{{\textbf{w}},\infty}(x)}{N_{K/{\mathbb Q}}({\mathfrak c})}\leq B,\ {\mathfrak I}_{\textbf{w}}(x)={\mathfrak c},\ x\in \Omega^{\mathrm{aff}}\right\}. \end{align*}$$
$$\begin{align*}M(\Omega,{\mathfrak c},B)=\#\left\{x\in (K^{n+1}-\{0\})/{\mathcal O}_K^\times : \frac{\text{Ht}_{{\textbf{w}},\infty}(x)}{N_{K/{\mathbb Q}}({\mathfrak c})}\leq B,\ {\mathfrak I}_{\textbf{w}}(x)={\mathfrak c},\ x\in \Omega^{\mathrm{aff}}\right\}. \end{align*}$$
Our general strategy will be to first find an asymptotic for the counting function
 $$\begin{align*}M'(\Omega,{\mathfrak c},B)\stackrel{\mathrm{def}}{=}\#\left\{x\in (K^{n+1}-\{0\})/{\mathcal O}_K^\times : \frac{\text{Ht}_{{\textbf{w}},\infty}(x)}{N_{K/{\mathbb Q}}({\mathfrak c})}\leq B,\ {\mathfrak I}_{\textbf{w}}(x)\subseteq{\mathfrak c},\ x\in \Omega^{\mathrm{aff}}\right\} \end{align*}$$
$$\begin{align*}M'(\Omega,{\mathfrak c},B)\stackrel{\mathrm{def}}{=}\#\left\{x\in (K^{n+1}-\{0\})/{\mathcal O}_K^\times : \frac{\text{Ht}_{{\textbf{w}},\infty}(x)}{N_{K/{\mathbb Q}}({\mathfrak c})}\leq B,\ {\mathfrak I}_{\textbf{w}}(x)\subseteq{\mathfrak c},\ x\in \Omega^{\mathrm{aff}}\right\} \end{align*}$$
and then use Möbius inversion to obtain an asymptotic formula for
![]() $M(\Omega ,{\mathfrak c},B)$
.
$M(\Omega ,{\mathfrak c},B)$
.
We are now going to construct a fundamental domain for the (
![]() ${\textbf {w}}$
-weighted) action of the unit group
${\textbf {w}}$
-weighted) action of the unit group
![]() ${\mathcal O}_K^{\times }$
on
${\mathcal O}_K^{\times }$
on
![]() $K_\infty ^{n+1}-\{0\}$
. This will be done using Dirichlet’s Unit Theorem. Let
$K_\infty ^{n+1}-\{0\}$
. This will be done using Dirichlet’s Unit Theorem. Let
![]() $\varpi (K)$
denote the set of roots of unity in K.
$\varpi (K)$
denote the set of roots of unity in K.
Theorem 4.0.6 (Dirichlet’s Unit Theorem).
The image
![]() $\Lambda $
of the map
$\Lambda $
of the map
 $$ \begin{align*} \lambda\colon {\mathcal O}_K^\times &\to {\mathbb R}^{r_1+r_2}\\ u &\mapsto (\log |u|_v)_{v\in \text{Val}_\infty(K)} \end{align*} $$
$$ \begin{align*} \lambda\colon {\mathcal O}_K^\times &\to {\mathbb R}^{r_1+r_2}\\ u &\mapsto (\log |u|_v)_{v\in \text{Val}_\infty(K)} \end{align*} $$
is a rank
![]() $r\stackrel {\mathrm{def}}{=} r_1+r_2-1$
lattice in the hyperplane H defined by
$r\stackrel {\mathrm{def}}{=} r_1+r_2-1$
lattice in the hyperplane H defined by
![]() $\sum _{v\in \text {Val}_\infty (K)} x_v=0$
and
$\sum _{v\in \text {Val}_\infty (K)} x_v=0$
and
![]() $\ker (\lambda )=\varpi (K)$
.
$\ker (\lambda )=\varpi (K)$
.
For each
![]() $v\in \text {Val}_\infty (K)$
, define a map
$v\in \text {Val}_\infty (K)$
, define a map
 $$ \begin{align*} \eta_v\colon K_v^{n+1}-\{0\} &\to {\mathbb R} \\ (x_0,\dots,x_n) &\mapsto \log\max_i |x_i|_v^{1/w_i}. \end{align*} $$
$$ \begin{align*} \eta_v\colon K_v^{n+1}-\{0\} &\to {\mathbb R} \\ (x_0,\dots,x_n) &\mapsto \log\max_i |x_i|_v^{1/w_i}. \end{align*} $$
Combine these maps to obtain a single map
 $$ \begin{align*} \eta\colon \prod_{v\in \text{Val}_\infty(K)} (K_v^{n+1}-\{0\}) &\to {\mathbb R}^{r_1+r_2}\\ x & \mapsto (\eta_v(x_v)). \end{align*} $$
$$ \begin{align*} \eta\colon \prod_{v\in \text{Val}_\infty(K)} (K_v^{n+1}-\{0\}) &\to {\mathbb R}^{r_1+r_2}\\ x & \mapsto (\eta_v(x_v)). \end{align*} $$
Let H be the hyperplane in Dirichlet’s unit theorem, and let
be the projection along the vector
![]() $(d_v)_{v\in \text {Val}_\infty (K)}$
, where
$(d_v)_{v\in \text {Val}_\infty (K)}$
, where
![]() $d_v=1$
if v is real and
$d_v=1$
if v is real and
![]() $d_v=2$
if v is complex. More explicitly,
$d_v=2$
if v is complex. More explicitly,
 $$\begin{align*}(\text{pr}(x))_v = x_v-\left(\frac{1}{d}\sum_{v'\in\text{Val}_\infty(K)} x_{v'}\right) d_v. \end{align*}$$
$$\begin{align*}(\text{pr}(x))_v = x_v-\left(\frac{1}{d}\sum_{v'\in\text{Val}_\infty(K)} x_{v'}\right) d_v. \end{align*}$$
The reason for choosing this projection is to ensure that a certain expanding region (which we are about to construct) will be weighted homogeneous (see Lemma 4.0.7).
Let
![]() $\{u_1,\dots ,u_r\}$
be a basis for the image of
$\{u_1,\dots ,u_r\}$
be a basis for the image of
![]() ${\mathcal O}_K^\times $
in the hyperplane H, and let
${\mathcal O}_K^\times $
in the hyperplane H, and let
![]() $\{\check {u}_1,\dots ,\check {u_r}\}$
be the dual basis. Then the set
$\{\check {u}_1,\dots ,\check {u_r}\}$
be the dual basis. Then the set
is a fundamental domain for H modulo
![]() $\Lambda $
, and
$\Lambda $
, and
![]() ${\mathcal F}\stackrel {\mathrm{def}}{=}(\text {pr}\circ \eta )^{-1}\tilde {{\mathcal F}}$
is a fundamental domain for the (
${\mathcal F}\stackrel {\mathrm{def}}{=}(\text {pr}\circ \eta )^{-1}\tilde {{\mathcal F}}$
is a fundamental domain for the (
![]() ${\textbf {w}}$
-weighted) action of
${\textbf {w}}$
-weighted) action of
![]() ${\mathcal O}_K^\times $
on
${\mathcal O}_K^\times $
on
![]() $\prod _{v\in \text {Val}_\infty (K)}(K_v^{n+1}-\{0\})$
.
$\prod _{v\in \text {Val}_\infty (K)}(K_v^{n+1}-\{0\})$
.
Define the sets
 $$\begin{align*}{\mathcal D}(B)\stackrel{\mathrm{def}}{=}\left\{x\in \prod_{v\in \text{Val}_\infty(K)} (K_v^{n+1}-\{0\}) : \text{Ht}_{{\textbf{w}},\infty}(x) \leq B\right\} \end{align*}$$
$$\begin{align*}{\mathcal D}(B)\stackrel{\mathrm{def}}{=}\left\{x\in \prod_{v\in \text{Val}_\infty(K)} (K_v^{n+1}-\{0\}) : \text{Ht}_{{\textbf{w}},\infty}(x) \leq B\right\} \end{align*}$$
and
![]() ${\mathcal F}(B)\stackrel {\mathrm{def}}{=}{\mathcal F}\cap {\mathcal D}(B)$
. The sets
${\mathcal F}(B)\stackrel {\mathrm{def}}{=}{\mathcal F}\cap {\mathcal D}(B)$
. The sets
![]() ${\mathcal D}(B)$
are
${\mathcal D}(B)$
are
![]() ${\mathcal O}_K^\times $
-stable, in the sense that if
${\mathcal O}_K^\times $
-stable, in the sense that if
![]() $u\in {\mathcal O}_K^{\times }$
and
$u\in {\mathcal O}_K^{\times }$
and
![]() $x\in {\mathcal D}(B)$
, then
$x\in {\mathcal D}(B)$
, then
![]() $u\ast _{{\textbf {w}}} x\in {\mathcal D}(B)$
; this can be seen by the following computation:
$u\ast _{{\textbf {w}}} x\in {\mathcal D}(B)$
; this can be seen by the following computation:
 $$ \begin{align*} \text{Ht}_{{\textbf{w}},\infty}(u\ast_{\textbf{w}} x)&=\prod_{v|\infty} \max_i |u^{w_i}x_{v,i}|_v^{1/w_i}\\ &=\prod_{v|\infty} |u|_v \prod_{v|\infty}\max_i |x_{v,i}|_v^{1/w_i}\\ &=\prod_{v|\infty}\max_i |x_{v,i}|_v^{1/w_i}\\ &=\text{Ht}_{{\textbf{w}},\infty}(x). \end{align*} $$
$$ \begin{align*} \text{Ht}_{{\textbf{w}},\infty}(u\ast_{\textbf{w}} x)&=\prod_{v|\infty} \max_i |u^{w_i}x_{v,i}|_v^{1/w_i}\\ &=\prod_{v|\infty} |u|_v \prod_{v|\infty}\max_i |x_{v,i}|_v^{1/w_i}\\ &=\prod_{v|\infty}\max_i |x_{v,i}|_v^{1/w_i}\\ &=\text{Ht}_{{\textbf{w}},\infty}(x). \end{align*} $$
Similarly, for any
![]() $t\in {\mathbb R}$
, we have that
$t\in {\mathbb R}$
, we have that
This shows that
![]() ${\mathcal D}(B)=B^{1/d}{\mathcal D}(1)$
for all
${\mathcal D}(B)=B^{1/d}{\mathcal D}(1)$
for all
![]() $B>0$
.
$B>0$
.
However,
![]() ${\mathcal F}$
is stable under the weighted action of
${\mathcal F}$
is stable under the weighted action of
![]() $t\in {\mathbb R}^\times $
, in the sense that
$t\in {\mathbb R}^\times $
, in the sense that
![]() $t\ast _{{\textbf {w}}} {\mathcal F}={\mathcal F}$
. To see this, note that for any
$t\ast _{{\textbf {w}}} {\mathcal F}={\mathcal F}$
. To see this, note that for any
![]() $x\in \prod _{v|\infty } (K_v^{n+1}-\{0\})$
,
$x\in \prod _{v|\infty } (K_v^{n+1}-\{0\})$
,
Since the projection
![]() $\text {pr}$
is linear and annihilates the vector
$\text {pr}$
is linear and annihilates the vector
![]() $(d_v)_{v|\infty }$
, we have that
$(d_v)_{v|\infty }$
, we have that
as desired. From our observations, we obtain the following lemma:
Lemma 4.0.7. The regions
![]() ${\mathcal F}(B)$
are weighted homogeneous, in the sense that
${\mathcal F}(B)$
are weighted homogeneous, in the sense that
![]() ${\mathcal F}(B)=B^{1/d}\ast _{{\textbf {w}}} {\mathcal F}(1)$
for all
${\mathcal F}(B)=B^{1/d}\ast _{{\textbf {w}}} {\mathcal F}(1)$
for all
![]() $B>0$
.
$B>0$
.
We are now going to count lattice points in
![]() ${\mathcal F}(B)$
. In [Reference SchanuelSch79], this is done by using the classical Principle of Lipschitz [Reference DavenportDav51] (see also [Reference LangLan94, VI §2 Theorem 2]). One of the cruxes of Schanuel’s argument is verifying that a fundamental domain (analogous to our
${\mathcal F}(B)$
. In [Reference SchanuelSch79], this is done by using the classical Principle of Lipschitz [Reference DavenportDav51] (see also [Reference LangLan94, VI §2 Theorem 2]). One of the cruxes of Schanuel’s argument is verifying that a fundamental domain (analogous to our
![]() ${\mathcal F}(1)$
) has Lipschitz parameterizable boundary, so that he can apply the Principle of Lipschitz. Though one can modify this part of Schanuel’s argument to work in our case, we will instead take a slightly different route, using an o-minimal version of the Principle of Lipschitz (Proposition 3.2.1). This allows one to give a more streamlined proof of this part of Schanuel’s argument, which may be useful in future generalizations.
${\mathcal F}(1)$
) has Lipschitz parameterizable boundary, so that he can apply the Principle of Lipschitz. Though one can modify this part of Schanuel’s argument to work in our case, we will instead take a slightly different route, using an o-minimal version of the Principle of Lipschitz (Proposition 3.2.1). This allows one to give a more streamlined proof of this part of Schanuel’s argument, which may be useful in future generalizations.
Lemma 4.0.8. The set
![]() ${\mathcal F}(1)$
is bounded.
${\mathcal F}(1)$
is bounded.
Proof. Let
![]() $\tilde {H}\subset \prod _{v|\infty } {\mathbb R}_v$
be the subset defined by
$\tilde {H}\subset \prod _{v|\infty } {\mathbb R}_v$
be the subset defined by
![]() $\sum _{v|\infty } x_v\leq 0$
. Note that
$\sum _{v|\infty } x_v\leq 0$
. Note that
![]() ${\mathcal F}(1)=\eta ^{-1}(\tilde {H} \cap \text {pr}^{-1}(\tilde {{\mathcal F}}))$
. It follows from the definition of
${\mathcal F}(1)=\eta ^{-1}(\tilde {H} \cap \text {pr}^{-1}(\tilde {{\mathcal F}}))$
. It follows from the definition of
![]() $\eta $
that, in order to show
$\eta $
that, in order to show
![]() ${\mathcal F}(1)$
is bounded, it suffices to show that the set
${\mathcal F}(1)$
is bounded, it suffices to show that the set
is bounded above (i.e., there exist constants
![]() $c_1,\dots ,c_{r_1+r_2}$
such that for each
$c_1,\dots ,c_{r_1+r_2}$
such that for each
we have
![]() $x_i\leq c_i$
for all i). For this, note that any
$x_i\leq c_i$
for all i). For this, note that any
![]() $x\in S$
can be written as
$x\in S$
can be written as
 $$\begin{align*}x=\text{pr}(x) + (d_v)_v \frac{1}{d} \sum_{v'|\infty} x_{v'}, \end{align*}$$
$$\begin{align*}x=\text{pr}(x) + (d_v)_v \frac{1}{d} \sum_{v'|\infty} x_{v'}, \end{align*}$$
and thus, the components of S are bounded above, noting that the first term,
![]() $\text {pr}(x)$
, has components bounded above, and the second term has negative components.
$\text {pr}(x)$
, has components bounded above, and the second term has negative components.
Lemma 4.0.9. The set
![]() ${\mathcal F}(1)$
is definable in
${\mathcal F}(1)$
is definable in
![]() ${\mathbb R}_{\exp {}}$
.
${\mathbb R}_{\exp {}}$
.
Proof. We make the following straightforward observations:
-
○ The product
 $\prod _{v|\infty } (K_v^{n+1}-\{0\})$
, viewed as a subset of
$\prod _{v|\infty } (K_v^{n+1}-\{0\})$
, viewed as a subset of
 ${\mathbb R}^{(r_1+2r_2)(n+1)}$
, is semi-algebraic since it is clearly the complement of a semi-algebraic set.
${\mathbb R}^{(r_1+2r_2)(n+1)}$
, is semi-algebraic since it is clearly the complement of a semi-algebraic set. -
○ The set
 ${\mathcal D}(1)$
is semi-algebraic.
${\mathcal D}(1)$
is semi-algebraic. -
○ The set
is definable in $$ \begin{align*} {\mathcal F}&=\{x\in \prod_{v|\infty} (K_v^{n+1}-\{0\}) : \text{pr}\circ\eta(x)\in \tilde{{\mathcal F}}\}\\ &=\left\{x\in \prod_{v|\infty} (K_v^{n+1}-\{0\}) : 0\leq \check{u}_j \left(\log(\max_i |x_i|_v^{1/w_i})-d_v\left(\frac{1}{d} \sum_{v|\infty}\log(\max_i |x_i|_{v'}^{1/w_i})\right)\right)_v <1 \forall j\right\} \end{align*} $$
$$ \begin{align*} {\mathcal F}&=\{x\in \prod_{v|\infty} (K_v^{n+1}-\{0\}) : \text{pr}\circ\eta(x)\in \tilde{{\mathcal F}}\}\\ &=\left\{x\in \prod_{v|\infty} (K_v^{n+1}-\{0\}) : 0\leq \check{u}_j \left(\log(\max_i |x_i|_v^{1/w_i})-d_v\left(\frac{1}{d} \sum_{v|\infty}\log(\max_i |x_i|_{v'}^{1/w_i})\right)\right)_v <1 \forall j\right\} \end{align*} $$
 ${\mathbb R}_{\exp }$
since it can be described in terms of polynomials and
${\mathbb R}_{\exp }$
since it can be described in terms of polynomials and
 $\log $
, and
$\log $
, and
 $\log $
is definable in
$\log $
is definable in
 ${\mathbb R}_{\exp }$
(as observed in Subsection 3.1).
${\mathbb R}_{\exp }$
(as observed in Subsection 3.1).
It follows that the intersection
![]() ${\mathcal F}(1)={\mathcal F}\cap {\mathcal D}(1)$
is definable in
${\mathcal F}(1)={\mathcal F}\cap {\mathcal D}(1)$
is definable in
![]() ${\mathbb R}_{\exp }$
.
${\mathbb R}_{\exp }$
.
We now analyze
![]() $M'(\Omega ,{\mathfrak c},B)$
. Note that if
$M'(\Omega ,{\mathfrak c},B)$
. Note that if
![]() ${\mathfrak I}_{\textbf {w}}(x)\subseteq {\mathfrak c}$
, then we must have that x is contained in the lattice
${\mathfrak I}_{\textbf {w}}(x)\subseteq {\mathfrak c}$
, then we must have that x is contained in the lattice
Therefore, we can write
![]() $M'(\Omega ,{\mathfrak c},B)$
as
$M'(\Omega ,{\mathfrak c},B)$
as
 $$\begin{align*}M'(\Omega,{\mathfrak c},B)=\#\left\{x\in ({\mathfrak c}^{\textbf{w}}-\{0\})/{\mathcal O}_K^\times : \frac{\text{Ht}_{{\textbf{w}},\infty}(x)}{N_{K/{\mathbb Q}}({\mathfrak c})}\leq B,\ x\in \Omega^{\mathrm{aff}}\right\}. \end{align*}$$
$$\begin{align*}M'(\Omega,{\mathfrak c},B)=\#\left\{x\in ({\mathfrak c}^{\textbf{w}}-\{0\})/{\mathcal O}_K^\times : \frac{\text{Ht}_{{\textbf{w}},\infty}(x)}{N_{K/{\mathbb Q}}({\mathfrak c})}\leq B,\ x\in \Omega^{\mathrm{aff}}\right\}. \end{align*}$$
We now stratify
![]() $\Omega $
. For each
$\Omega $
. For each
![]() $t\in {\mathbb Z}_{\geq 0}$
, set
$t\in {\mathbb Z}_{\geq 0}$
, set
 $$\begin{align*}\Omega_{v,t}^{\mathrm{aff}}=\pi_v^t\ast_{\textbf{w}} \Omega_{v,0}^{\mathrm{aff}}=\prod_{j=0}^n \{x\in {\mathcal O}_{K,v} : |x- \pi_v^{w_j t} a_{v,j}|_v\leq q_v^{-w_j t}\omega_{v,j}\}. \end{align*}$$
$$\begin{align*}\Omega_{v,t}^{\mathrm{aff}}=\pi_v^t\ast_{\textbf{w}} \Omega_{v,0}^{\mathrm{aff}}=\prod_{j=0}^n \{x\in {\mathcal O}_{K,v} : |x- \pi_v^{w_j t} a_{v,j}|_v\leq q_v^{-w_j t}\omega_{v,j}\}. \end{align*}$$
For
![]() ${ {\textbf {t}}}=(t_v)_{v\in S} \in {\mathbb Z}_{\geq 0}^{\# S}$
, set
${ {\textbf {t}}}=(t_v)_{v\in S} \in {\mathbb Z}_{\geq 0}^{\# S}$
, set
Since each
![]() $\Omega _v$
is irreducible, we have
$\Omega _v$
is irreducible, we have
 $$\begin{align*}\Omega^{\mathrm{aff}} \cap {\mathcal O}_{K,v}^{n+1} = \bigsqcup_{{{\textbf{t}}}\in {\mathbb Z}^{\# S}_{\geq 0}} \Omega_{{\textbf{t}}}^{\mathrm{aff}}. \end{align*}$$
$$\begin{align*}\Omega^{\mathrm{aff}} \cap {\mathcal O}_{K,v}^{n+1} = \bigsqcup_{{{\textbf{t}}}\in {\mathbb Z}^{\# S}_{\geq 0}} \Omega_{{\textbf{t}}}^{\mathrm{aff}}. \end{align*}$$
Set
 $$\begin{align*}\epsilon_{{{\textbf{t}}}}=\max_j\left\{\prod_{{\mathfrak p}\in S} q_v^{t_vw_j}\omega_{v,j}^{-1}\right\}\left(\prod_{{\mathfrak p}\in S} \frac{m_{\mathfrak p}(\Omega_{v,t_v}^{\mathrm{aff}}\cap {\mathfrak c}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{\textbf{w}})}\right). \end{align*}$$
$$\begin{align*}\epsilon_{{{\textbf{t}}}}=\max_j\left\{\prod_{{\mathfrak p}\in S} q_v^{t_vw_j}\omega_{v,j}^{-1}\right\}\left(\prod_{{\mathfrak p}\in S} \frac{m_{\mathfrak p}(\Omega_{v,t_v}^{\mathrm{aff}}\cap {\mathfrak c}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{\textbf{w}})}\right). \end{align*}$$
Note that each
![]() $\varpi (K)$
-orbit (with respect to the
$\varpi (K)$
-orbit (with respect to the
![]() ${\textbf {w}}$
-weighted action) of an element of
${\textbf {w}}$
-weighted action) of an element of
![]() $(K-\{0\})^{n+1}$
contains
$(K-\{0\})^{n+1}$
contains
![]() $\varpi _{K,{\textbf {w}}}$
elements. Thus,
$\varpi _{K,{\textbf {w}}}$
elements. Thus,
 $$ \begin{align} M'(\Omega, {\mathfrak c}, B) =\sum_{{{\textbf{t}}}\in {\mathbb Z}^{\# S}_{\geq 0}} \left(\frac{\# \left\{ \Omega^{\mathrm{aff}}_{{{\textbf{t}}}} \cap {\mathcal F}\left(N_{K/{\mathbb Q}}({\mathfrak c}) B\right)\cap {\mathfrak c}^{\textbf{w}}\right\}}{\varpi_{K,{\textbf{w}}}} + O\,\left(\epsilon_{{\textbf{t}}} B^{|{\textbf{w}}|-w_{\min}/d}\right)\right), \end{align} $$
$$ \begin{align} M'(\Omega, {\mathfrak c}, B) =\sum_{{{\textbf{t}}}\in {\mathbb Z}^{\# S}_{\geq 0}} \left(\frac{\# \left\{ \Omega^{\mathrm{aff}}_{{{\textbf{t}}}} \cap {\mathcal F}\left(N_{K/{\mathbb Q}}({\mathfrak c}) B\right)\cap {\mathfrak c}^{\textbf{w}}\right\}}{\varpi_{K,{\textbf{w}}}} + O\,\left(\epsilon_{{\textbf{t}}} B^{|{\textbf{w}}|-w_{\min}/d}\right)\right), \end{align} $$
where each error term accounts for the points of
![]() $M'(\Omega ,{\mathfrak c}, B)$
contained in the intersection of
$M'(\Omega ,{\mathfrak c}, B)$
contained in the intersection of
![]() $\Omega _{ {\textbf {t}}}^{\mathrm{aff}}$
and the subvariety of the affine cone of
$\Omega _{ {\textbf {t}}}^{\mathrm{aff}}$
and the subvariety of the affine cone of
![]() ${\mathcal P}({\textbf {w}})(K)$
consisting of points with at least one coordinate equal to zero; by Proposition 3.2.7, this error is at most
${\mathcal P}({\textbf {w}})(K)$
consisting of points with at least one coordinate equal to zero; by Proposition 3.2.7, this error is at most
![]() $O\left (\epsilon _{ {\textbf {t}}} \left (B^{1/d}\right )^{d|{\textbf {w}}|-w_{\min }}\right )$
.
$O\left (\epsilon _{ {\textbf {t}}} \left (B^{1/d}\right )^{d|{\textbf {w}}|-w_{\min }}\right )$
.
By Lemma 4.0.8 and Lemma 4.0.9, we may apply Proposition 3.2.7, with
![]() ${\mathfrak a}={\mathfrak c}$
and the local conditions
${\mathfrak a}={\mathfrak c}$
and the local conditions
![]() $\Omega ^{\mathrm{aff}}_v\cap {\mathcal F}(1)$
for
$\Omega ^{\mathrm{aff}}_v\cap {\mathcal F}(1)$
for
![]() $v|\infty $
and
$v|\infty $
and
![]() $\Omega ^{\mathrm{aff}}_{v,t}$
for
$\Omega ^{\mathrm{aff}}_{v,t}$
for
![]() $v\in S$
. Doing so, we have
$v\in S$
. Doing so, we have
 $$\begin{align*}\#\{\Omega_{{{\textbf{t}}}}^{\mathrm{aff}}\cap {\mathcal F}(N_{K/{\mathbb Q}}({\mathfrak c})B)\cap {\mathfrak c}^{{\textbf{w}}}\}=\frac{m_\infty(\Omega^{\mathrm{aff}}_\infty\cap {\mathcal F}(1))}{|\Delta_K|^{(n+1)/2}} \left(\prod_{{\mathfrak p}\in S} \frac{m_{\mathfrak p}(\Omega^{\mathrm{aff}}_{v,t_v}\cap{\mathfrak c}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{\textbf{w}})}\right)B^{|{\textbf{w}}|} + O\,\left(\epsilon_{{{\textbf{t}}}} B^{|{\textbf{w}}|-\frac{w_{\min}}{d}}\right). \end{align*}$$
$$\begin{align*}\#\{\Omega_{{{\textbf{t}}}}^{\mathrm{aff}}\cap {\mathcal F}(N_{K/{\mathbb Q}}({\mathfrak c})B)\cap {\mathfrak c}^{{\textbf{w}}}\}=\frac{m_\infty(\Omega^{\mathrm{aff}}_\infty\cap {\mathcal F}(1))}{|\Delta_K|^{(n+1)/2}} \left(\prod_{{\mathfrak p}\in S} \frac{m_{\mathfrak p}(\Omega^{\mathrm{aff}}_{v,t_v}\cap{\mathfrak c}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{\textbf{w}})}\right)B^{|{\textbf{w}}|} + O\,\left(\epsilon_{{{\textbf{t}}}} B^{|{\textbf{w}}|-\frac{w_{\min}}{d}}\right). \end{align*}$$
Let
![]() $v({\mathfrak c})$
denote the v-adic valuation of the ideal
$v({\mathfrak c})$
denote the v-adic valuation of the ideal
![]() ${\mathfrak c}\subseteq {\mathcal O}_K$
(i.e., the valuation of any (and all) embeddings of
${\mathfrak c}\subseteq {\mathcal O}_K$
(i.e., the valuation of any (and all) embeddings of
![]() ${\mathfrak c}$
into
${\mathfrak c}$
into
![]() ${\mathcal O}_{K,v}$
). By Proposition 4.0.4(c), if
${\mathcal O}_{K,v}$
). By Proposition 4.0.4(c), if
![]() $t< v({\mathfrak c})$
, then
$t< v({\mathfrak c})$
, then
![]() $m_{\mathfrak p}(\Omega ^{\mathrm{aff}}_{v,t}\cap {\mathfrak c}_{\mathfrak p}^{\textbf {w}})=0$
. However, when
$m_{\mathfrak p}(\Omega ^{\mathrm{aff}}_{v,t}\cap {\mathfrak c}_{\mathfrak p}^{\textbf {w}})=0$
. However, when
![]() $t\geq v({\mathfrak c})$
, we compute
$t\geq v({\mathfrak c})$
, we compute
 $$ \begin{align*} \frac{m_{\mathfrak p}(\Omega^{\mathrm{aff}}_{v,t}\cap{\mathfrak c}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{{\textbf{w}}})} &=\frac{1}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{\textbf{w}})} m_{\mathfrak p}\left(\prod_{j=0}^n \{x\in {\mathfrak c}_{\mathfrak p}^{w_j} : |x-\pi_v^{tw_j}a_j|_v\leq q_v^{-tw_j}\omega_j\}\right)\\ &=\frac{1}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{\textbf{w}})} m_{\mathfrak p}\left(\prod_{j=0}^n \{x\in {\mathcal O}_{K,{\mathfrak p}} : |\pi_v^{v({\mathfrak c})w_j}x-\pi_v^{tw_j}a_j|_v\leq q_v^{-tw_j}\omega_j\}\right)\\ &=m_{\mathfrak p}\left(\Omega^{\mathrm{aff}}_{v,t-v({\mathfrak c})}\right). \end{align*} $$
$$ \begin{align*} \frac{m_{\mathfrak p}(\Omega^{\mathrm{aff}}_{v,t}\cap{\mathfrak c}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{{\textbf{w}}})} &=\frac{1}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{\textbf{w}})} m_{\mathfrak p}\left(\prod_{j=0}^n \{x\in {\mathfrak c}_{\mathfrak p}^{w_j} : |x-\pi_v^{tw_j}a_j|_v\leq q_v^{-tw_j}\omega_j\}\right)\\ &=\frac{1}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{\textbf{w}})} m_{\mathfrak p}\left(\prod_{j=0}^n \{x\in {\mathcal O}_{K,{\mathfrak p}} : |\pi_v^{v({\mathfrak c})w_j}x-\pi_v^{tw_j}a_j|_v\leq q_v^{-tw_j}\omega_j\}\right)\\ &=m_{\mathfrak p}\left(\Omega^{\mathrm{aff}}_{v,t-v({\mathfrak c})}\right). \end{align*} $$
By Proposition 4.0.4, we know that the
![]() $\Omega _{v,t}^{\mathrm{aff}}$
are disjoint for distinct values of t. Therefore, summing over all
$\Omega _{v,t}^{\mathrm{aff}}$
are disjoint for distinct values of t. Therefore, summing over all
![]() $t\in {\mathbb Z}_{\geq 0}$
, it follows that
$t\in {\mathbb Z}_{\geq 0}$
, it follows that
 $$\begin{align*}\sum_{t\geq 0} \frac{m_{\mathfrak p}(\Omega^{\mathrm{aff}}_{v,t}\cap{\mathfrak c}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{{\textbf{w}}})}=\sum_{s\geq 0} m_{\mathfrak p}(\Omega_{v,s}^{\mathrm{aff}})=m_{\mathfrak p}(\Omega_v^{\mathrm{aff}}\cap {\mathcal O}_{K,v}^{n+1}), \end{align*}$$
$$\begin{align*}\sum_{t\geq 0} \frac{m_{\mathfrak p}(\Omega^{\mathrm{aff}}_{v,t}\cap{\mathfrak c}_{\mathfrak p}^{\textbf{w}})}{m_{\mathfrak p}({\mathfrak c}_{\mathfrak p}^{{\textbf{w}}})}=\sum_{s\geq 0} m_{\mathfrak p}(\Omega_{v,s}^{\mathrm{aff}})=m_{\mathfrak p}(\Omega_v^{\mathrm{aff}}\cap {\mathcal O}_{K,v}^{n+1}), \end{align*}$$
and we obtain the asymptotic
 $$ \begin{align} M'(\Omega,{\mathfrak c},B)=\frac{m_\infty(\Omega^{\mathrm{aff}}_\infty\cap {\mathcal F}(1))}{\varpi_{K,{\textbf{w}}}|\Delta_K|^{(n+1)/2}} \left(\prod_{{\mathfrak p}\in S} m_{\mathfrak p}(\Omega^{\mathrm{aff}}_{v}\cap{\mathcal O}_{K,v}^{n+1})\right)B^{|{\textbf{w}}|}+ O\,\left(\epsilon_\Omega B^{|{\textbf{w}}|-w_{\min}/d}\right). \end{align} $$
$$ \begin{align} M'(\Omega,{\mathfrak c},B)=\frac{m_\infty(\Omega^{\mathrm{aff}}_\infty\cap {\mathcal F}(1))}{\varpi_{K,{\textbf{w}}}|\Delta_K|^{(n+1)/2}} \left(\prod_{{\mathfrak p}\in S} m_{\mathfrak p}(\Omega^{\mathrm{aff}}_{v}\cap{\mathcal O}_{K,v}^{n+1})\right)B^{|{\textbf{w}}|}+ O\,\left(\epsilon_\Omega B^{|{\textbf{w}}|-w_{\min}/d}\right). \end{align} $$
Note that as
![]() $m_\infty $
is the product of measures
$m_\infty $
is the product of measures
![]() $(m_v)_{v|\infty }$
, one has
$(m_v)_{v|\infty }$
, one has
 $$\begin{align*}\frac{m_\infty(\Omega_\infty^{\mathrm{aff}}\cap {\mathcal F}(1))}{m_\infty({\mathcal F}(1))}=\prod_{v|\infty}\frac{m_v(\{x\in \Omega_v^{\mathrm{aff}} : \text{Ht}_v(x)\leq 1\})}{m_v(\{x\in K_v^{n+1} : \text{Ht}_v(x)\leq 1\})}, \end{align*}$$
$$\begin{align*}\frac{m_\infty(\Omega_\infty^{\mathrm{aff}}\cap {\mathcal F}(1))}{m_\infty({\mathcal F}(1))}=\prod_{v|\infty}\frac{m_v(\{x\in \Omega_v^{\mathrm{aff}} : \text{Ht}_v(x)\leq 1\})}{m_v(\{x\in K_v^{n+1} : \text{Ht}_v(x)\leq 1\})}, \end{align*}$$
and thus,
 $$ \begin{align} m_\infty(\Omega_\infty^{\mathrm{aff}}\cap {\mathcal F}(1))=m_\infty({\mathcal F}(1))\prod_{v|\infty}\frac{m_v(\{x\in \Omega_v^{\mathrm{aff}} : \text{Ht}_v(x)\leq 1\})}{m_v(\{x\in K_v^{n+1} : \text{Ht}_v(x)\leq 1\})}. \end{align} $$
$$ \begin{align} m_\infty(\Omega_\infty^{\mathrm{aff}}\cap {\mathcal F}(1))=m_\infty({\mathcal F}(1))\prod_{v|\infty}\frac{m_v(\{x\in \Omega_v^{\mathrm{aff}} : \text{Ht}_v(x)\leq 1\})}{m_v(\{x\in K_v^{n+1} : \text{Ht}_v(x)\leq 1\})}. \end{align} $$
Computing the volume of
![]() ${\mathcal F}(1)$
as in [Reference DengDen98, Proposition 5.3], we obtain
${\mathcal F}(1)$
as in [Reference DengDen98, Proposition 5.3], we obtain
This differs by a factor of
![]() $2^{(n+1)r_2}$
from Deng’s result since we are using the usual Haar measure on
$2^{(n+1)r_2}$
from Deng’s result since we are using the usual Haar measure on
![]() $K_\infty $
, rather than the Lebesgue measure.
$K_\infty $
, rather than the Lebesgue measure.
Observe that the leading cofficient of the asymptotic (3) equals
![]() $\zeta _K(|{\textbf {w}}|)\kappa /h_K$
, where
$\zeta _K(|{\textbf {w}}|)\kappa /h_K$
, where
![]() $\kappa $
is as in the statement of Theorem 4.0.5.
$\kappa $
is as in the statement of Theorem 4.0.5.
Note that for
![]() $x\in {\mathfrak c}^{\textbf {w}}$
,
$x\in {\mathfrak c}^{\textbf {w}}$
,
![]() ${\mathfrak I}_{\textbf {w}}(x)={\mathfrak a}{\mathfrak c}$
for some ideal
${\mathfrak I}_{\textbf {w}}(x)={\mathfrak a}{\mathfrak c}$
for some ideal
![]() ${\mathfrak a}\subseteq {\mathcal O}_K$
. Then,
${\mathfrak a}\subseteq {\mathcal O}_K$
. Then,
![]() $\text {Ht}_{\textbf {w}}(x)=\text {Ht}_{{\textbf {w}},\infty }(x)/N_{K/{\mathbb Q}}({\mathfrak a}{\mathfrak c})$
. Therefore,
$\text {Ht}_{\textbf {w}}(x)=\text {Ht}_{{\textbf {w}},\infty }(x)/N_{K/{\mathbb Q}}({\mathfrak a}{\mathfrak c})$
. Therefore,
 $$\begin{align*}M'(\Omega,{\mathfrak c},B)=\sum_{{\mathfrak a}\subseteq {\mathcal O}_K} M(\Omega,{\mathfrak a}{\mathfrak c}, B/N_{K/{\mathbb Q}}({\mathfrak a}))=\sum_{\substack{{\mathfrak a}\subseteq {\mathcal O}_K \\ N_{K/{\mathbb Q}}({\mathfrak a})\leq B}} M(\Omega,{\mathfrak a}{\mathfrak c}, B/N_{K/{\mathbb Q}}({\mathfrak a})), \end{align*}$$
$$\begin{align*}M'(\Omega,{\mathfrak c},B)=\sum_{{\mathfrak a}\subseteq {\mathcal O}_K} M(\Omega,{\mathfrak a}{\mathfrak c}, B/N_{K/{\mathbb Q}}({\mathfrak a}))=\sum_{\substack{{\mathfrak a}\subseteq {\mathcal O}_K \\ N_{K/{\mathbb Q}}({\mathfrak a})\leq B}} M(\Omega,{\mathfrak a}{\mathfrak c}, B/N_{K/{\mathbb Q}}({\mathfrak a})), \end{align*}$$
where the inequality
![]() $N_{K/{\mathbb Q}}({\mathfrak a})\leq B$
comes from the fact that
$N_{K/{\mathbb Q}}({\mathfrak a})\leq B$
comes from the fact that
![]() $M(\Omega ,{\mathfrak c},B)=0$
if
$M(\Omega ,{\mathfrak c},B)=0$
if
![]() $B<1$
, since all points have height greater than or equal to
$B<1$
, since all points have height greater than or equal to
![]() $1$
.
$1$
.
Since the ideals of
![]() ${\mathcal O}_K$
form a poset (ordered by inclusion), we may use Möbius inversion (see, for example, [Reference StanleySta97, §3.7] for details about Möbius inversion for posets). Applying Möbius inversion, and using our asymptotic (3) for
${\mathcal O}_K$
form a poset (ordered by inclusion), we may use Möbius inversion (see, for example, [Reference StanleySta97, §3.7] for details about Möbius inversion for posets). Applying Möbius inversion, and using our asymptotic (3) for
![]() $M'(\Omega ,{\mathfrak c},B)$
, we have that
$M'(\Omega ,{\mathfrak c},B)$
, we have that
 $$ \begin{align*} M(\Omega,{\mathfrak c},B) &=\sum_{\substack{{\mathfrak a}\subseteq {\mathcal O}_K\\ N_{K/{\mathbb Q}}({\mathfrak a})\leq B}} \mu({\mathfrak a})\left(\frac{\zeta_K(|{\textbf{w}}|)\kappa}{h_K}\left(\frac{B}{N_{K/{\mathbb Q}}({\mathfrak a})}\right)^{|{\textbf{w}}|}+ O\,\left(\epsilon_\Omega\left(\frac{B}{N_{K/{\mathbb Q}}({\mathfrak a})}\right)^{|{\textbf{w}}|-w_{\min}/d}\right)\right)\\&=\frac{\zeta_K(|{\textbf{w}}|)\kappa}{h_K} B^{|{\textbf{w}}|}\left(\sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \mu({\mathfrak a})\frac{1}{N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf{w}}|}} - \sum_{\substack{{\mathfrak a}\subseteq {\mathcal O}_K\\ N_{K/{\mathbb Q}}({\mathfrak a})> B}}\mu({\mathfrak a})\frac{1}{N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf{w}}|}}\right)\\& \quad +O\,\left(\epsilon_\Omega B^{|{\textbf{w}}|-w_{\min}/d} \sum_{\substack{{\mathfrak a}\subseteq {\mathcal O}_K\\ N_{K/{\mathbb Q}}({\mathfrak a})\leq B}}\frac{1}{N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf{w}}|-w_{\min}/d}}\right)\\&=\frac{\zeta_K(|{\textbf{w}}|)\kappa}{h_K} B^{|{\textbf{w}}|}\left(\frac{1}{\zeta_K(|{\textbf{w}}|)} - O\,\left(B^{-|{\textbf{w}}|+1}\right)\right) + \begin{cases} O\,\left(\epsilon_\Omega B\log(B)\right) & {\substack{\text{ if } {\textbf{w}}=(1,1)\\ \text{and}\ K={\mathbb Q},}}\\ O\,\left(\epsilon_\Omega B^{|{\textbf{w}}|-w_{\min}/d}\right) & \text{ else, } \end{cases}\\&= \frac{\kappa}{h_K} B^{|{\textbf{w}}|} + \begin{cases} O\,\left(\epsilon_\Omega B\log(B)\right) & \text{ if } {\textbf{w}}=(1,1) \text{ and } K={\mathbb Q},\\ O\,\left(\epsilon_\Omega B^{|{\textbf{w}}|-w_{\min}/d}\right) & \text{ else. } \end{cases} \end{align*} $$
$$ \begin{align*} M(\Omega,{\mathfrak c},B) &=\sum_{\substack{{\mathfrak a}\subseteq {\mathcal O}_K\\ N_{K/{\mathbb Q}}({\mathfrak a})\leq B}} \mu({\mathfrak a})\left(\frac{\zeta_K(|{\textbf{w}}|)\kappa}{h_K}\left(\frac{B}{N_{K/{\mathbb Q}}({\mathfrak a})}\right)^{|{\textbf{w}}|}+ O\,\left(\epsilon_\Omega\left(\frac{B}{N_{K/{\mathbb Q}}({\mathfrak a})}\right)^{|{\textbf{w}}|-w_{\min}/d}\right)\right)\\&=\frac{\zeta_K(|{\textbf{w}}|)\kappa}{h_K} B^{|{\textbf{w}}|}\left(\sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \mu({\mathfrak a})\frac{1}{N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf{w}}|}} - \sum_{\substack{{\mathfrak a}\subseteq {\mathcal O}_K\\ N_{K/{\mathbb Q}}({\mathfrak a})> B}}\mu({\mathfrak a})\frac{1}{N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf{w}}|}}\right)\\& \quad +O\,\left(\epsilon_\Omega B^{|{\textbf{w}}|-w_{\min}/d} \sum_{\substack{{\mathfrak a}\subseteq {\mathcal O}_K\\ N_{K/{\mathbb Q}}({\mathfrak a})\leq B}}\frac{1}{N_{K/{\mathbb Q}}({\mathfrak a})^{|{\textbf{w}}|-w_{\min}/d}}\right)\\&=\frac{\zeta_K(|{\textbf{w}}|)\kappa}{h_K} B^{|{\textbf{w}}|}\left(\frac{1}{\zeta_K(|{\textbf{w}}|)} - O\,\left(B^{-|{\textbf{w}}|+1}\right)\right) + \begin{cases} O\,\left(\epsilon_\Omega B\log(B)\right) & {\substack{\text{ if } {\textbf{w}}=(1,1)\\ \text{and}\ K={\mathbb Q},}}\\ O\,\left(\epsilon_\Omega B^{|{\textbf{w}}|-w_{\min}/d}\right) & \text{ else, } \end{cases}\\&= \frac{\kappa}{h_K} B^{|{\textbf{w}}|} + \begin{cases} O\,\left(\epsilon_\Omega B\log(B)\right) & \text{ if } {\textbf{w}}=(1,1) \text{ and } K={\mathbb Q},\\ O\,\left(\epsilon_\Omega B^{|{\textbf{w}}|-w_{\min}/d}\right) & \text{ else. } \end{cases} \end{align*} $$
Summing over the
![]() $h_K$
ideal class representatives
$h_K$
ideal class representatives
![]() ${\mathfrak c}_i$
, we arrive at Theorem 4.0.5.
${\mathfrak c}_i$
, we arrive at Theorem 4.0.5.
5. Counting elliptic curves
In this section, we apply Theorem 4.0.5 to the moduli stack of elliptic curves.
5.1. Counting elliptic curves with a prescribed local condition
An application of Theorem 4.0.5 gives the following result:
Corollary 5.1.1. Let
![]() ${\mathcal E}_K(B)$
denote the set of isomorphism classes of elliptic curves over K with height less than B. Then,
${\mathcal E}_K(B)$
denote the set of isomorphism classes of elliptic curves over K with height less than B. Then,
where
 $$\begin{align*}\kappa=\frac{h_K (2^{r_1+r_2}\pi^{r_2})^{2} R_K 10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_K |\Delta_K| \zeta_K(10)}. \end{align*}$$
$$\begin{align*}\kappa=\frac{h_K (2^{r_1+r_2}\pi^{r_2})^{2} R_K 10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_K |\Delta_K| \zeta_K(10)}. \end{align*}$$
Proof. Recall that the moduli stack of elliptic curves,
![]() ${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
, is isomorphic to the weighted projective stack
${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
, is isomorphic to the weighted projective stack
![]() ${\mathcal P}(4,6)$
. Also recall that the naive height on
${\mathcal P}(4,6)$
. Also recall that the naive height on
![]() ${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
corresponds to the twelfth power of the height on
${\mathcal X}_{\text {GL}_2({\mathbb Z})}$
corresponds to the twelfth power of the height on
![]() ${\mathcal P}(4,6)$
with respect to the tautological bundle (i.e., the height
${\mathcal P}(4,6)$
with respect to the tautological bundle (i.e., the height
![]() $\text {Ht}_{(4,6)}$
). Therefore, the desired result follows from applying Theorem 4.0.5 to
$\text {Ht}_{(4,6)}$
). Therefore, the desired result follows from applying Theorem 4.0.5 to
![]() ${\mathcal P}(4,6)$
with trivial local conditions (i.e.,
${\mathcal P}(4,6)$
with trivial local conditions (i.e.,
![]() $S=\emptyset $
).
$S=\emptyset $
).
We now use Theorem 4.0.5 to count elliptic curves with a prescribed local condition.
Theorem 1.1.2.
Let K be a degree d number field, and let
![]() ${\mathfrak p}\subset {\mathcal O}_K$
be a prime ideal of norm q such that
${\mathfrak p}\subset {\mathcal O}_K$
be a prime ideal of norm q such that
![]() $2\nmid q$
and
$2\nmid q$
and
![]() $3\nmid q$
. Let
$3\nmid q$
. Let
![]() ${\mathscr L}$
be one of the local conditions listed in Table 1. Then the number of elliptic curves over K with naive height less than B and which satisfy the local condition
${\mathscr L}$
be one of the local conditions listed in Table 1. Then the number of elliptic curves over K with naive height less than B and which satisfy the local condition
![]() ${\mathscr L}$
at
${\mathscr L}$
at
![]() ${\mathfrak p}$
is
${\mathfrak p}$
is
where
 $$\begin{align*}\kappa=\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{2}R_K10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_{K} |\Delta_K|\zeta_K(10)}, \end{align*}$$
$$\begin{align*}\kappa=\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{2}R_K10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_{K} |\Delta_K|\zeta_K(10)}, \end{align*}$$
and where
![]() $\kappa _{\mathscr L}$
and
$\kappa _{\mathscr L}$
and
![]() $\epsilon _{\mathscr L}$
are as in Table 1.
$\epsilon _{\mathscr L}$
are as in Table 1.
Proof.
Good reduction case. Note that the number of elliptic curves over
![]() ${\mathbb F}_q$
with good reduction is
${\mathbb F}_q$
with good reduction is
For each pair
![]() $(a,b)$
in the above set, fix a lift in
$(a,b)$
in the above set, fix a lift in
![]() ${\mathcal O}_{K,v}^2$
, which, by an abuse of notation, we will also denote
${\mathcal O}_{K,v}^2$
, which, by an abuse of notation, we will also denote
![]() $(a,b)$
. Then, consider the irreducible local condition
$(a,b)$
. Then, consider the irreducible local condition
 $$\begin{align*}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(a,b)\stackrel{\mathrm{def}}{=}\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-a|_v\leq \frac{1}{q},\ |x_1-b|_v\leq \frac{1}{q}\right\}. \end{align*}$$
$$\begin{align*}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(a,b)\stackrel{\mathrm{def}}{=}\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-a|_v\leq \frac{1}{q},\ |x_1-b|_v\leq \frac{1}{q}\right\}. \end{align*}$$
We find the
![]() ${\mathfrak p}$
-adic measure
${\mathfrak p}$
-adic measure
For
![]() $t\in {\mathbb Z}_{\geq 0}$
, the sets
$t\in {\mathbb Z}_{\geq 0}$
, the sets
 $$\begin{align*}\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b)=\pi_v^t\ast_{(4,6)}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(a,b)=\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-q^{4t}a|_v\leq \frac{1}{q^{4t+1}},\ |x_1-q^{6t}b|_v\leq \frac{1}{q^{6t+1}}\right\} \end{align*}$$
$$\begin{align*}\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b)=\pi_v^t\ast_{(4,6)}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(a,b)=\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-q^{4t}a|_v\leq \frac{1}{q^{4t+1}},\ |x_1-q^{6t}b|_v\leq \frac{1}{q^{6t+1}}\right\} \end{align*}$$
each have
![]() ${\mathfrak p}$
-adic measure
${\mathfrak p}$
-adic measure
Applying Theorem 4.0.5 to each
![]() $\Omega _{{\mathfrak p},0}^{\mathrm{aff}}(a,b)$
, and summing over all the
$\Omega _{{\mathfrak p},0}^{\mathrm{aff}}(a,b)$
, and summing over all the
![]() $q^2-q$
possible
$q^2-q$
possible
![]() $(a,b)$
pairs, it follows that the number of elliptic curves of bounded height over K with good reduction at
$(a,b)$
pairs, it follows that the number of elliptic curves of bounded height over K with good reduction at
![]() ${\mathfrak p}$
is
${\mathfrak p}$
is
where
 $$\begin{align*}\kappa_{\mathscr L}=\sum_{(a,b)}\sum_{t=0}^\infty m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b))=(q^2-q)\sum_{t=0}^\infty \frac{1}{q^{10t+2}}=(q^2-q)\frac{1}{q^2}\frac{q^{10}}{q^{10}-1}= \frac{q-1}{q}\frac{q^{10}}{q^{10}-1}, \end{align*}$$
$$\begin{align*}\kappa_{\mathscr L}=\sum_{(a,b)}\sum_{t=0}^\infty m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b))=(q^2-q)\sum_{t=0}^\infty \frac{1}{q^{10t+2}}=(q^2-q)\frac{1}{q^2}\frac{q^{10}}{q^{10}-1}= \frac{q-1}{q}\frac{q^{10}}{q^{10}-1}, \end{align*}$$
and
 $$\begin{align*}\epsilon=\sum_{(a,b)}\sum_{t=0}^\infty\max\{q^{4t+1},q^{6t+1}\}m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b)) =(q^2-q)\sum_{t=0}^\infty \frac{q^{6t+1}}{q^{10t+2}} =\frac{q^5-q^4}{q^4-1}. \end{align*}$$
$$\begin{align*}\epsilon=\sum_{(a,b)}\sum_{t=0}^\infty\max\{q^{4t+1},q^{6t+1}\}m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b)) =(q^2-q)\sum_{t=0}^\infty \frac{q^{6t+1}}{q^{10t+2}} =\frac{q^5-q^4}{q^4-1}. \end{align*}$$
As the error term can be rewritten as
![]() $O(q B^{\frac {5}{6}-\frac {1}{3d}})$
, we may replace the coefficient
$O(q B^{\frac {5}{6}-\frac {1}{3d}})$
, we may replace the coefficient
![]() $\epsilon $
in the asymptotic (5) with
$\epsilon $
in the asymptotic (5) with
![]() $\epsilon _{\mathscr L}=q$
.
$\epsilon _{\mathscr L}=q$
.
Kodaira type III* case. By Tate’s algorithm [Reference TateTat75], an elliptic curve over
![]() $K_{\mathfrak p}$
given in short Weierstrass form,
$K_{\mathfrak p}$
given in short Weierstrass form,
![]() $E:y^2=x^3+ax+b$
, has type III* reduction if and only if
$E:y^2=x^3+ax+b$
, has type III* reduction if and only if
![]() $v_{\mathfrak p}(a)=3$
and
$v_{\mathfrak p}(a)=3$
and
![]() $v_{\mathfrak p}(b)\geq 5$
. Observe that
$v_{\mathfrak p}(b)\geq 5$
. Observe that
For each pair
![]() $(a,b)$
in the above set, fix a lift in
$(a,b)$
in the above set, fix a lift in
![]() ${\mathcal O}_{K,v}^2$
, which, by an abuse of notation, we will also denote
${\mathcal O}_{K,v}^2$
, which, by an abuse of notation, we will also denote
![]() $(a,b)$
. Then, consider the irreducible local condition
$(a,b)$
. Then, consider the irreducible local condition
 $$\begin{align*}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(a,b)\stackrel{\mathrm{def}}{=} \left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-a|_v\leq \frac{1}{q^5},\ |x_1-b|_v\leq \frac{1}{q^5}\right\}. \end{align*}$$
$$\begin{align*}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(a,b)\stackrel{\mathrm{def}}{=} \left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-a|_v\leq \frac{1}{q^5},\ |x_1-b|_v\leq \frac{1}{q^5}\right\}. \end{align*}$$
We find that the
![]() ${\mathfrak p}$
-adic measure of this set is
${\mathfrak p}$
-adic measure of this set is
The sets
 $$\begin{align*}\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b)= \pi_v^t\ast_{(4,6)}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(a,b)=\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-q^{4t}a|_v\leq \frac{1}{q^{4t+5}},\ |x_1-q^{6t}b|_v\leq \frac{1}{q^{6t+5}}\right\} \end{align*}$$
$$\begin{align*}\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b)= \pi_v^t\ast_{(4,6)}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(a,b)=\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-q^{4t}a|_v\leq \frac{1}{q^{4t+5}},\ |x_1-q^{6t}b|_v\leq \frac{1}{q^{6t+5}}\right\} \end{align*}$$
each have
![]() ${\mathfrak p}$
-adic measure
${\mathfrak p}$
-adic measure
Applying Theorem 4.0.5 to each
![]() $\Omega _{{\mathfrak p},0}^{\mathrm{aff}}(a,b)$
, and summing over all pairs
$\Omega _{{\mathfrak p},0}^{\mathrm{aff}}(a,b)$
, and summing over all pairs
![]() $(a,b)$
, yields the following asymptotic for the number of elliptic curves of bounded height over K with reduction of Kodaira type III* at
$(a,b)$
, yields the following asymptotic for the number of elliptic curves of bounded height over K with reduction of Kodaira type III* at
![]() ${\mathfrak p}$
:
${\mathfrak p}$
:
where
 $$\begin{align*}\kappa_{\mathscr L} =\sum_{(a,b)}\sum_{t=0}^\infty m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b))=q(q-1)\sum_{t=0}^\infty \frac{1}{q^{10t+10}}=(q^2-q)\frac{1}{q^{10}}\frac{q^{10}}{q^{10}-1}=\frac{q-1}{q^9}\frac{q^{10}}{q^{10}-1}, \end{align*}$$
$$\begin{align*}\kappa_{\mathscr L} =\sum_{(a,b)}\sum_{t=0}^\infty m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b))=q(q-1)\sum_{t=0}^\infty \frac{1}{q^{10t+10}}=(q^2-q)\frac{1}{q^{10}}\frac{q^{10}}{q^{10}-1}=\frac{q-1}{q^9}\frac{q^{10}}{q^{10}-1}, \end{align*}$$
and
 $$\begin{align*}\epsilon=\sum_{(a,b)}\sum_{t=0}^\infty\max\{q^{4t+5},q^{6t+5}\}m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b)) =(q^2-q)\sum_{t=0}^\infty \frac{q^{6t+5}}{q^{10t+10}} =\frac{q-1}{q^{4}-1}. \end{align*}$$
$$\begin{align*}\epsilon=\sum_{(a,b)}\sum_{t=0}^\infty\max\{q^{4t+5},q^{6t+5}\}m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(a,b)) =(q^2-q)\sum_{t=0}^\infty \frac{q^{6t+5}}{q^{10t+10}} =\frac{q-1}{q^{4}-1}. \end{align*}$$
As the error term can be rewritten as
![]() $O(q^{-3}B^{\frac {5}{6}-\frac {1}{3d}})$
, we may replace the coefficient
$O(q^{-3}B^{\frac {5}{6}-\frac {1}{3d}})$
, we may replace the coefficient
![]() $\epsilon $
in the asymptotic (6) with
$\epsilon $
in the asymptotic (6) with
![]() $\epsilon _{\mathscr L}=1/q^{3}$
.
$\epsilon _{\mathscr L}=1/q^{3}$
.
The other cases can be proven similarly to those given above.
We now turn to estimating the number of elliptic curves with a prescribed trace of Frobenius. For
![]() $b,c\in {\mathbb F}_q$
, let
$b,c\in {\mathbb F}_q$
, let
![]() $E_{b,c}$
denote the short Weierstrass model
$E_{b,c}$
denote the short Weierstrass model
![]() $y^2=x^3+bx+c$
, with disciminant
$y^2=x^3+bx+c$
, with disciminant
![]() $\Delta (b,c)=-16(4b^3+27c^2)$
and trace of Frobenius
$\Delta (b,c)=-16(4b^3+27c^2)$
and trace of Frobenius
![]() $a_q(E_{b,c})$
. We study the counting function
$a_q(E_{b,c})$
. We study the counting function
This function is closely related to Hurwitz-Kronecker class numbers, which we now recall. Let K be an imaginary quadratic field with ring of integers
![]() ${\mathcal O}_K$
, and let
${\mathcal O}_K$
, and let
![]() ${\mathcal O}$
be an order in K with class number
${\mathcal O}$
be an order in K with class number
![]() $h({\mathcal O})$
. The Hurwitz-Kronecker class number of
$h({\mathcal O})$
. The Hurwitz-Kronecker class number of
![]() ${\mathcal O}$
, denoted
${\mathcal O}$
, denoted
![]() $H(\text {disc}({\mathcal O}))$
, is defined as
$H(\text {disc}({\mathcal O}))$
, is defined as
 $$ \begin{align} H(\text{disc}({\mathcal O}))\stackrel{\mathrm{def}}{=}\sum_{{\mathcal O}\subset {\mathcal O}' \subset {\mathcal O}_K} \frac{h({\mathcal O}')}{\# {\mathcal O}^{\prime\times}}. \end{align} $$
$$ \begin{align} H(\text{disc}({\mathcal O}))\stackrel{\mathrm{def}}{=}\sum_{{\mathcal O}\subset {\mathcal O}' \subset {\mathcal O}_K} \frac{h({\mathcal O}')}{\# {\mathcal O}^{\prime\times}}. \end{align} $$
This definition of the Hurwitz-Kronecker class number agrees with the definition given in [Reference LenstraLen87] but is half as large as it is sometimes defined (such as in [Reference CoxCox89]). Let
![]() $q=p^n$
be a power of a prime
$q=p^n$
be a power of a prime
![]() $p>3$
. Then, a beautiful result, following largely from work of Deuring [Reference DeuringDeu41], expresses the number of elliptic curves over a finite field
$p>3$
. Then, a beautiful result, following largely from work of Deuring [Reference DeuringDeu41], expresses the number of elliptic curves over a finite field
![]() ${\mathbb F}_q$
with a prescribed trace of Frobenius in terms of Hurwitz-Kronecker class numbers:
${\mathbb F}_q$
with a prescribed trace of Frobenius in terms of Hurwitz-Kronecker class numbers:
 $$ \begin{align} \begin{aligned} H(a,q)=\begin{cases} (q-1) H(a^2-4q) & \text{ if } |a|<2\sqrt{q} \text{ and } p\nmid a\\ (q-1)H(-4p) & \text{ if } n \text{ is odd and } a=0\\ \frac{q-1}{12}\left(p+6-4\genfrac{(}{)}{}{}{-3}{p}-3\genfrac{(}{)}{}{}{-4}{p}\right) & \text{ if } n \text{ is even and } a^2=4q\\ (q-1)\left(1-\genfrac{(}{)}{}{}{-3}{p}\right) & \text{ if } n \text{ is even and } a^2=q\\ (q-1)\left(1-\genfrac{(}{)}{}{}{-4}{p}\right) & \text{ if } n \text{ is even and } a=0\\ 0 & \text{ otherwise.} \end{cases} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} H(a,q)=\begin{cases} (q-1) H(a^2-4q) & \text{ if } |a|<2\sqrt{q} \text{ and } p\nmid a\\ (q-1)H(-4p) & \text{ if } n \text{ is odd and } a=0\\ \frac{q-1}{12}\left(p+6-4\genfrac{(}{)}{}{}{-3}{p}-3\genfrac{(}{)}{}{}{-4}{p}\right) & \text{ if } n \text{ is even and } a^2=4q\\ (q-1)\left(1-\genfrac{(}{)}{}{}{-3}{p}\right) & \text{ if } n \text{ is even and } a^2=q\\ (q-1)\left(1-\genfrac{(}{)}{}{}{-4}{p}\right) & \text{ if } n \text{ is even and } a=0\\ 0 & \text{ otherwise.} \end{cases} \end{aligned} \end{align} $$
This formula can be derived from [Reference SchoofSch87, Theorem 4.6], which counts the number of isomorphism classes of elliptic curves over
![]() ${\mathbb F}_q$
with a prescribed trace of Frobenius. From this, one can deduce formula (9) by noting that the isomorphism class of each
${\mathbb F}_q$
with a prescribed trace of Frobenius. From this, one can deduce formula (9) by noting that the isomorphism class of each
![]() $E_{b,c}$
contains exactly
$E_{b,c}$
contains exactly
![]() $q-1$
elliptic curves. To see that each isomorphism class contains exactly
$q-1$
elliptic curves. To see that each isomorphism class contains exactly
![]() $q-1$
elliptic curves, note that
$q-1$
elliptic curves, note that
![]() $E_{b,c}\cong E_{d,e}$
if and only if
$E_{b,c}\cong E_{d,e}$
if and only if
![]() $(d,e)=(\lambda ^4b, \lambda ^6c)$
for some
$(d,e)=(\lambda ^4b, \lambda ^6c)$
for some
![]() $\lambda \in {\mathbb F}_q^\times $
, and since
$\lambda \in {\mathbb F}_q^\times $
, and since
![]() $p>3$
, the pairs
$p>3$
, the pairs
![]() $(\lambda ^4b, \lambda ^6c)$
will be distinct for distinct
$(\lambda ^4b, \lambda ^6c)$
will be distinct for distinct
![]() $\lambda \in {\mathbb F}_q^\times $
. (See [Reference CoxCox89, Theorem 14.18] for a proof of formula (9) in the case that
$\lambda \in {\mathbb F}_q^\times $
. (See [Reference CoxCox89, Theorem 14.18] for a proof of formula (9) in the case that
![]() $q=p$
is a prime.)
$q=p$
is a prime.)
Theorem 1.1.3.
Let K be a degree d number field, and let
![]() ${\mathfrak p}$
be a prime ideal of
${\mathfrak p}$
be a prime ideal of
![]() ${\mathcal O}_K$
of degree n above a rational prime
${\mathcal O}_K$
of degree n above a rational prime
![]() $p>3$
. Set
$p>3$
. Set
![]() $q=p^n$
. Let
$q=p^n$
. Let
![]() $a\in {\mathbb Z}$
be an integer satisfying
$a\in {\mathbb Z}$
be an integer satisfying
![]() $|a|\leq 2\sqrt {q}$
. Then, the number of elliptic curves over K with naive height less than B, good reduction at
$|a|\leq 2\sqrt {q}$
. Then, the number of elliptic curves over K with naive height less than B, good reduction at
![]() ${\mathfrak p}$
, and which have trace of Frobenius a at
${\mathfrak p}$
, and which have trace of Frobenius a at
![]() ${\mathfrak p}$
is
${\mathfrak p}$
is
where
 $$\begin{align*}\kappa=\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{2}R_K10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_{K} |\Delta_K|\zeta_K(10)}, \end{align*}$$
$$\begin{align*}\kappa=\frac{h_K \left(2^{r_1+r_2}\pi^{r_2}\right)^{2}R_K10^{r_1+r_2-1}\gcd(2,\varpi_K)}{\varpi_{K} |\Delta_K|\zeta_K(10)}, \end{align*}$$
and where
![]() $\kappa _{n,a}$
and
$\kappa _{n,a}$
and
![]() $\epsilon _{n,a}$
are as in Table 2.
$\epsilon _{n,a}$
are as in Table 2.
Proof. For each of the
![]() $H(a,q)$
pairs
$H(a,q)$
pairs
![]() $(b,c)$
in the set
$(b,c)$
in the set
fix a lift in
![]() ${\mathcal O}_{K,v}^2$
, which, by an abuse of notation, we will also denote
${\mathcal O}_{K,v}^2$
, which, by an abuse of notation, we will also denote
![]() $(b,c)$
. Then consider the irreducible local condition
$(b,c)$
. Then consider the irreducible local condition
 $$\begin{align*}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(b,c)\stackrel{\mathrm{def}}{=}\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-b|_v\leq \frac{1}{q},\ |x_1-c|_v\leq \frac{1}{q}\right\}. \end{align*}$$
$$\begin{align*}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(b,c)\stackrel{\mathrm{def}}{=}\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-b|_v\leq \frac{1}{q},\ |x_1-c|_v\leq \frac{1}{q}\right\}. \end{align*}$$
We find that the
![]() ${\mathfrak p}$
-adic measure of each of these local conditions is
${\mathfrak p}$
-adic measure of each of these local conditions is
More generally, for
![]() $t\in {\mathbb Z}_{\geq 0}$
, the sets
$t\in {\mathbb Z}_{\geq 0}$
, the sets
 $$\begin{align*}\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(b,c)=\pi_v^t\ast_{(4,6)}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(b,c)=\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-q^{4t}b|_v\leq \frac{1}{q^{4t+1}},\ |x_1-q^{6t}c|_v\leq \frac{1}{q^{6t+1}}\right\} \end{align*}$$
$$\begin{align*}\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(b,c)=\pi_v^t\ast_{(4,6)}\Omega_{{\mathfrak p},0}^{\mathrm{aff}}(b,c)=\left\{(x_0,x_1)\in {\mathcal O}_{K,v}^{2} : |x_0-q^{4t}b|_v\leq \frac{1}{q^{4t+1}},\ |x_1-q^{6t}c|_v\leq \frac{1}{q^{6t+1}}\right\} \end{align*}$$
each have
![]() ${\mathfrak p}$
-adic measure
${\mathfrak p}$
-adic measure
Applying Theorem 4.0.5 to each
![]() $\Omega _{{\mathfrak p},0}^{\mathrm{aff}}(b,c)$
, and summing over all the
$\Omega _{{\mathfrak p},0}^{\mathrm{aff}}(b,c)$
, and summing over all the
![]() $H(a,q)$
possible
$H(a,q)$
possible
![]() $(b,c)$
pairs, it follows that the number of elliptic curves of bounded height over K with good reduction at
$(b,c)$
pairs, it follows that the number of elliptic curves of bounded height over K with good reduction at
![]() ${\mathfrak p}$
and trace of Frobenius a at
${\mathfrak p}$
and trace of Frobenius a at
![]() ${\mathfrak p}$
is
${\mathfrak p}$
is
where
 $$\begin{align*}\kappa'=\sum_{(b,c)}\sum_{t=0}^\infty m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(b,c))=H(a,q)\sum_{t=0}^\infty \frac{1}{q^{10t+2}}=H(a,q)\frac{1}{q^2}\frac{q^{10}}{q^{10}-1}, \end{align*}$$
$$\begin{align*}\kappa'=\sum_{(b,c)}\sum_{t=0}^\infty m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(b,c))=H(a,q)\sum_{t=0}^\infty \frac{1}{q^{10t+2}}=H(a,q)\frac{1}{q^2}\frac{q^{10}}{q^{10}-1}, \end{align*}$$
and
 $$\begin{align*}\epsilon=\sum_{(b,c)}\sum_{t=0}^\infty\max\{q^{4t+1},q^{6t+1}\}m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(b,c)) =H(a,q)\sum_{t=0}^\infty \frac{q^{6t+1}}{q^{10t+2}} =H(a,q)\frac{q^3}{q^4-1}. \end{align*}$$
$$\begin{align*}\epsilon=\sum_{(b,c)}\sum_{t=0}^\infty\max\{q^{4t+1},q^{6t+1}\}m_{{\mathfrak p}}(\Omega_{{\mathfrak p},t}^{\mathrm{aff}}(b,c)) =H(a,q)\sum_{t=0}^\infty \frac{q^{6t+1}}{q^{10t+2}} =H(a,q)\frac{q^3}{q^4-1}. \end{align*}$$
From this, the desired asymptotics can now be derived using (9).
For example, in the case that a is an integer satisfying
![]() $|a|< 2\sqrt {q}$
and
$|a|< 2\sqrt {q}$
and
![]() $p\nmid a$
, we have that
$p\nmid a$
, we have that
![]() $H(a,q)=(q-1)H(a^2-4q)$
. Thus,
$H(a,q)=(q-1)H(a^2-4q)$
. Thus,
 $$\begin{align*}\kappa'=\frac{H(a,q)}{q^2}\frac{q^{10}}{q^{10}-1}=\frac{(q-1)H(a^2-4q)}{q^2}\frac{q^{10}}{q^{10}-1}=\kappa_{n,a} \end{align*}$$
$$\begin{align*}\kappa'=\frac{H(a,q)}{q^2}\frac{q^{10}}{q^{10}-1}=\frac{(q-1)H(a^2-4q)}{q^2}\frac{q^{10}}{q^{10}-1}=\kappa_{n,a} \end{align*}$$
and
 $$\begin{align*}\epsilon=(q-1)H(a^2-4q)\frac{q^3}{q^4-1}. \end{align*}$$
$$\begin{align*}\epsilon=(q-1)H(a^2-4q)\frac{q^3}{q^4-1}. \end{align*}$$
As the error term can be rewritten as
![]() $O\left (H(a^2-4q)B^{\frac {5}{6}-\frac {1}{3d}}\right )$
, we may replace the coefficient
$O\left (H(a^2-4q)B^{\frac {5}{6}-\frac {1}{3d}}\right )$
, we may replace the coefficient
![]() $\epsilon $
in the asymptotic (10) with
$\epsilon $
in the asymptotic (10) with
![]() $\epsilon _{n,a}=H(a^2-4q)$
.
$\epsilon _{n,a}=H(a^2-4q)$
.
6. Average analytic ranks
In this section, we use our results from the previous section on counting elliptic curves with prescribed local conditions in order to give a bound for the average analytic rank of elliptic curves over number fields. Our strategy will mainly follow that of Cho and Jeong [Reference Cho and JeongCJ23b, Reference Cho and JeongCJ23a] and is related to Brumer’s strategy (see Remark 6.1.3).
6.1. L-functions of elliptic curves
In this subsection, we recall basic facts about L-functions of elliptic curves. Our exposition mostly follows [Reference MillerMil02, Appendix A].
Let E be an elliptic curve of discriminant
![]() $\Delta _E$
over a number field K. For each finite place
$\Delta _E$
over a number field K. For each finite place
![]() $v\in \text {Val}_0(K)$
, let
$v\in \text {Val}_0(K)$
, let
![]() $E_v$
denote the reduction of E at v, let
$E_v$
denote the reduction of E at v, let
![]() $q_v$
be the order of the residue field
$q_v$
be the order of the residue field
![]() $k_v$
of K at v, let
$k_v$
of K at v, let
![]() $N_v=\# E_v({\mathbb F}_{q_v})$
, and let
$N_v=\# E_v({\mathbb F}_{q_v})$
, and let
![]() $a_v=q_v+1-N_v$
. If E has bad reduction at v, set
$a_v=q_v+1-N_v$
. If E has bad reduction at v, set
 $$\begin{align*}b_v\stackrel{\mathrm{def}}{=} \begin{cases} 1 & \text{ if }E\text{ has split multiplicative reduction at }v,\\ -1 & \text{ if }E\text{ has nonsplit multiplicative reduction at }v,\\ 0 & \text{ if }E\text{ has additive reduction at }v. \end{cases} \end{align*}$$
$$\begin{align*}b_v\stackrel{\mathrm{def}}{=} \begin{cases} 1 & \text{ if }E\text{ has split multiplicative reduction at }v,\\ -1 & \text{ if }E\text{ has nonsplit multiplicative reduction at }v,\\ 0 & \text{ if }E\text{ has additive reduction at }v. \end{cases} \end{align*}$$
For each
![]() $v\in \text {Val}_0(K)$
, define a polynomial
$v\in \text {Val}_0(K)$
, define a polynomial
![]() $L_v(E/K,T)$
by
$L_v(E/K,T)$
by
 $$\begin{align*}L_v(E/K,T)\stackrel{\mathrm{def}}{=}\begin{cases} 1-a_v T+ q_v T^2 & \text{ if }E\text{ has good reduction at }v,\\ 1-b_vT & \text{ if }E\text{ has bad reduction at }v. \end{cases} \end{align*}$$
$$\begin{align*}L_v(E/K,T)\stackrel{\mathrm{def}}{=}\begin{cases} 1-a_v T+ q_v T^2 & \text{ if }E\text{ has good reduction at }v,\\ 1-b_vT & \text{ if }E\text{ has bad reduction at }v. \end{cases} \end{align*}$$
The Hasse–Weil
![]() $\mathbf {L}$
-function
$\mathbf {L}$
-function
![]() $L(E/K,s)$
of E over K is defined as the Euler product
$L(E/K,s)$
of E over K is defined as the Euler product
 $$\begin{align*}L(E/K,s)\stackrel{\mathrm{def}}{=} \prod_{v\in \text{Val}_0(K)} L_v(E/K, q_v^{-s})^{-1}. \end{align*}$$
$$\begin{align*}L(E/K,s)\stackrel{\mathrm{def}}{=} \prod_{v\in \text{Val}_0(K)} L_v(E/K, q_v^{-s})^{-1}. \end{align*}$$
The logarithmic derivative of
![]() $L(E/K,s)$
is
$L(E/K,s)$
is
 $$\begin{align*}\frac{L'}{L}(E/K,s)=-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \frac{d}{ds}\left(\log(1-b_v q_v^{-s})\right)-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)=0}} \frac{d}{ds}\left(\log(1-a_v q_v^{-s}+q_v^{1-2s})\right). \end{align*}$$
$$\begin{align*}\frac{L'}{L}(E/K,s)=-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \frac{d}{ds}\left(\log(1-b_v q_v^{-s})\right)-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)=0}} \frac{d}{ds}\left(\log(1-a_v q_v^{-s}+q_v^{1-2s})\right). \end{align*}$$
The first sum can be rewritten as
 $$\begin{align*}-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \frac{d}{ds}\left(\log(1-b_v q_v^{-s})\right)=\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \frac{d}{ds}\left(\sum_{k=1}^\infty \frac{b_v^k}{k q_v^{ks}}\right)=-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \sum_{k=1}^\infty \frac{b_v^k \log(q_v)}{q_v^{ks}}. \end{align*}$$
$$\begin{align*}-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \frac{d}{ds}\left(\log(1-b_v q_v^{-s})\right)=\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \frac{d}{ds}\left(\sum_{k=1}^\infty \frac{b_v^k}{k q_v^{ks}}\right)=-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \sum_{k=1}^\infty \frac{b_v^k \log(q_v)}{q_v^{ks}}. \end{align*}$$
For the second sum, factor
![]() $1-a_v T+q_v T^2$
as
$1-a_v T+q_v T^2$
as
![]() $(1-\alpha _v T)(1-\beta _v T)$
, where
$(1-\alpha _v T)(1-\beta _v T)$
, where
![]() $\alpha _v+\beta _v=a_v$
and
$\alpha _v+\beta _v=a_v$
and
![]() $\alpha _v\beta _v=q_v$
. Then,
$\alpha _v\beta _v=q_v$
. Then,
 $$\begin{align*}-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)=0}} \frac{d}{ds}\left(\log(1-a_v q_v^{-s}+q_v^{1-2s})\right)=-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)=0}} \sum_{k=1}^\infty \frac{(\alpha_v^k+\beta_v^k) \log(q_v)}{q_v^{ks}}. \end{align*}$$
$$\begin{align*}-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)=0}} \frac{d}{ds}\left(\log(1-a_v q_v^{-s}+q_v^{1-2s})\right)=-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)=0}} \sum_{k=1}^\infty \frac{(\alpha_v^k+\beta_v^k) \log(q_v)}{q_v^{ks}}. \end{align*}$$
We thus obtain the following expression for the logarithmic derivative of
![]() $L(E/K,s)$
:
$L(E/K,s)$
:
 $$ \begin{align*} \frac{L'}{L}(E/K,s)=-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \sum_{k=1}^\infty \frac{b_v^k \log(q_v)}{q_v^{ks}}-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)=0}} \sum_{k=1}^\infty \frac{(\alpha_v^k+\beta_v^k) \log(q_v)}{q_v^{ks}}. \end{align*} $$
$$ \begin{align*} \frac{L'}{L}(E/K,s)=-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)>0}} \sum_{k=1}^\infty \frac{b_v^k \log(q_v)}{q_v^{ks}}-\sum_{\substack{v\in \text{Val}_0(K)\\ v(\Delta_E)=0}} \sum_{k=1}^\infty \frac{(\alpha_v^k+\beta_v^k) \log(q_v)}{q_v^{ks}}. \end{align*} $$
Define the von Mangoldt function on integral ideals
![]() ${\mathfrak a}\subseteq {\mathcal O}_K$
as
${\mathfrak a}\subseteq {\mathcal O}_K$
as
 $$\begin{align*}\Lambda_K({\mathfrak a})\stackrel{\mathrm{def}}{=} \begin{cases} \log(q_v) & \text{ if } {\mathfrak a}={\mathfrak p}_v^k \text{ for some } k,\\ 0 & \text{ otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\Lambda_K({\mathfrak a})\stackrel{\mathrm{def}}{=} \begin{cases} \log(q_v) & \text{ if } {\mathfrak a}={\mathfrak p}_v^k \text{ for some } k,\\ 0 & \text{ otherwise.} \end{cases} \end{align*}$$
For prime powers, set
 $$\begin{align*}\widehat{a_E}({\mathfrak p}_v^k)=\begin{cases} \alpha_v^k+\beta_v^k & \text{ if }E\text{ has good reduction at }{\mathfrak p}_v,\\ b_v^k & \text{ if }E\text{ has bad reduction at }{\mathfrak p}_v, \end{cases} \end{align*}$$
$$\begin{align*}\widehat{a_E}({\mathfrak p}_v^k)=\begin{cases} \alpha_v^k+\beta_v^k & \text{ if }E\text{ has good reduction at }{\mathfrak p}_v,\\ b_v^k & \text{ if }E\text{ has bad reduction at }{\mathfrak p}_v, \end{cases} \end{align*}$$
and for
![]() ${\mathfrak a}$
not a power of a prime, set
${\mathfrak a}$
not a power of a prime, set
![]() $\widehat {a_E}({\mathfrak a})=0$
. Then our expression for the logarithmic derivative of
$\widehat {a_E}({\mathfrak a})=0$
. Then our expression for the logarithmic derivative of
![]() $L(E/K,s)$
becomes
$L(E/K,s)$
becomes
 $$ \begin{align} \frac{L'}{L}(E/K,s)=-\sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{\widehat{a_E}({\mathfrak a})\Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})^s}, \end{align} $$
$$ \begin{align} \frac{L'}{L}(E/K,s)=-\sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{\widehat{a_E}({\mathfrak a})\Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})^s}, \end{align} $$
where the sum is over the nonzero integral ideals of
![]() ${\mathcal O}_K$
.
${\mathcal O}_K$
.
Let
![]() $\Gamma (s)\stackrel {\mathrm{def}}{=}\int _0^\infty t^{s-1}e^{-t} dt$
be the usual gamma function. Let
$\Gamma (s)\stackrel {\mathrm{def}}{=}\int _0^\infty t^{s-1}e^{-t} dt$
be the usual gamma function. Let
![]() $\Gamma _K(s)$
be the gamma factor
$\Gamma _K(s)$
be the gamma factor
Let
![]() $\mathfrak {f}_{E/K}$
be the conductor of E over K, and define a constant
$\mathfrak {f}_{E/K}$
be the conductor of E over K, and define a constant
Define the completed Hasse–Weil
![]() $\mathbf {L}$
-function,
$\mathbf {L}$
-function,
![]() $\Lambda (E/K, s)$
, as
$\Lambda (E/K, s)$
, as
We now assume that our elliptic curve E is modular over K, so that the L-function
![]() $L(E/K,s)$
is automorphic. This implies that the Hasse–Weil conjecture holds true for E, and thus,
$L(E/K,s)$
is automorphic. This implies that the Hasse–Weil conjecture holds true for E, and thus,
where
![]() $\epsilon (E)\in \{\pm 1\}$
is the root number. We see that the logarithmic derivative of
$\epsilon (E)\in \{\pm 1\}$
is the root number. We see that the logarithmic derivative of
![]() $\Lambda (E/K, s)$
is
$\Lambda (E/K, s)$
is
We now state the explicit formula for L-functions of elliptic curves over number fields:
Proposition 6.1.1 (Explicit Formula).
Let
![]() $\phi \colon {\mathbb C}\to {\mathbb C}$
be a partial function that is even and analytic in the strip
$\phi \colon {\mathbb C}\to {\mathbb C}$
be a partial function that is even and analytic in the strip
![]() $|\operatorname {Im}(s)|\leq \frac {1}{2}+\epsilon $
for some
$|\operatorname {Im}(s)|\leq \frac {1}{2}+\epsilon $
for some
![]() $\epsilon>0$
, and assume that on this strip
$\epsilon>0$
, and assume that on this strip
![]() $|\phi (s)|\ll (1+|s|)^{-(1+\delta )}$
for some
$|\phi (s)|\ll (1+|s|)^{-(1+\delta )}$
for some
![]() $\delta>0$
as
$\delta>0$
as
![]() $|\text {Re}(s)|\to \infty $
. For
$|\text {Re}(s)|\to \infty $
. For
![]() $x\in {\mathbb R}$
, assume that
$x\in {\mathbb R}$
, assume that
![]() $\phi (x)\in {\mathbb R}$
, and set
$\phi (x)\in {\mathbb R}$
, and set
the Fourier transform. Let E be a modular elliptic curve over a number field K. Suppose that the L-function
![]() $L(E/K,s)$
associated to E satisfies the Generalized Riemann Hypothesis, so that all nontrivial zeros
$L(E/K,s)$
associated to E satisfies the Generalized Riemann Hypothesis, so that all nontrivial zeros
![]() $\rho _j$
of
$\rho _j$
of
![]() $L(E/K,s)$
are of the form
$L(E/K,s)$
are of the form
Let
![]() $r(E)\stackrel {\mathrm{def}}{=}\text {ord}_{s=1}(L(E/K,s))$
be the analytic rank of E. Then, we have
$r(E)\stackrel {\mathrm{def}}{=}\text {ord}_{s=1}(L(E/K,s))$
be the analytic rank of E. Then, we have
 $$ \begin{align*} &r(E)\phi(0)+\sum_{\rho_j\neq 1} \phi(\gamma_j)\\ &\hspace{5mm} =\frac{\widehat{\phi}(0)}{2\pi}\log(A_{E/K})+\frac{1}{\pi}\int_{{\mathbb R}}\frac{\Gamma_K'}{\Gamma_K}(1+iy) \phi(y) dy -\frac{1}{\pi} \sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{2\pi}\right), \end{align*} $$
$$ \begin{align*} &r(E)\phi(0)+\sum_{\rho_j\neq 1} \phi(\gamma_j)\\ &\hspace{5mm} =\frac{\widehat{\phi}(0)}{2\pi}\log(A_{E/K})+\frac{1}{\pi}\int_{{\mathbb R}}\frac{\Gamma_K'}{\Gamma_K}(1+iy) \phi(y) dy -\frac{1}{\pi} \sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{2\pi}\right), \end{align*} $$
where the sum on the left-hand side is over the zeros
![]() $\rho _j\neq 1$
with relevant multiplicity.
$\rho _j\neq 1$
with relevant multiplicity.
Proposition 6.1.1 is a slight generalization of [Reference Iwaniec and KowalskiIK04, Theorem 5.12] (see also [Reference MestreMes86] and [Reference MillerMil02, Appendix A] for the specific case of L-functions of elliptic curves). In [Reference Iwaniec and KowalskiIK04], the condition on the test function
![]() $\phi $
is that it is a Schwartz function. However, as observed in [Reference Goldston and GonekGG07, Lemma 1], the proof of [Reference Iwaniec and KowalskiIK04, Theorem 5.12] can be adapted to work for the set of functions
$\phi $
is that it is a Schwartz function. However, as observed in [Reference Goldston and GonekGG07, Lemma 1], the proof of [Reference Iwaniec and KowalskiIK04, Theorem 5.12] can be adapted to work for the set of functions
![]() $\phi $
satisfying the conditions in Proposition 6.1.1. We will use the following modified version of the explicit formula:
$\phi $
satisfying the conditions in Proposition 6.1.1. We will use the following modified version of the explicit formula:
Corollary 6.1.2 (Modified Explicit Formula).
Maintaining the notation from Proposition 6.1.1 and letting X be a parameter, we have that
 $$ \begin{align} \begin{split} &r(E)\phi(0)+\sum_{\gamma_j\neq 0} \phi\left(\gamma_j\frac{\log(X)}{2\pi}\right) \\ &\hspace{1mm}= \frac{\widehat{\phi}(0) \log(A_{E/K})}{\log(X)} -\frac{2}{\log(X)} \sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{\log(X)}\right)+O\,\left(\frac{1}{\log(X)}\right). \end{split} \end{align} $$
$$ \begin{align} \begin{split} &r(E)\phi(0)+\sum_{\gamma_j\neq 0} \phi\left(\gamma_j\frac{\log(X)}{2\pi}\right) \\ &\hspace{1mm}= \frac{\widehat{\phi}(0) \log(A_{E/K})}{\log(X)} -\frac{2}{\log(X)} \sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{\log(X)}\right)+O\,\left(\frac{1}{\log(X)}\right). \end{split} \end{align} $$
Proof. From the explicit formula (Proposition 6.1.1), it follows that
 $$ \begin{align} r(E)\phi(0)+\sum_{\gamma_j\neq 0} \phi\left(\gamma_j\frac{\log(X)}{2\pi}\right) &= \frac{\widehat{\phi}(0) \log(A_{E/K})}{\log(X)}+\frac{1}{\pi}\int_{{\mathbb R}}\frac{\Gamma_K'}{\Gamma_K}(1+iy) \phi\left(y\frac{\log(X)}{2\pi}\right) dy \nonumber\\& \quad -\frac{2}{\log(X)} \sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{\log(X)}\right). \end{align} $$
$$ \begin{align} r(E)\phi(0)+\sum_{\gamma_j\neq 0} \phi\left(\gamma_j\frac{\log(X)}{2\pi}\right) &= \frac{\widehat{\phi}(0) \log(A_{E/K})}{\log(X)}+\frac{1}{\pi}\int_{{\mathbb R}}\frac{\Gamma_K'}{\Gamma_K}(1+iy) \phi\left(y\frac{\log(X)}{2\pi}\right) dy \nonumber\\& \quad -\frac{2}{\log(X)} \sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{\log(X)}\right). \end{align} $$
A classical estimate for the logarithmic derivative of the gamma function is
 $$\begin{align*}\left| \frac{\Gamma'}{\Gamma}(1+iy)\right|=O(\log(|y|+2)). \end{align*}$$
$$\begin{align*}\left| \frac{\Gamma'}{\Gamma}(1+iy)\right|=O(\log(|y|+2)). \end{align*}$$
From this, and the fact that
![]() $\phi $
is absolutely integrable (since
$\phi $
is absolutely integrable (since
![]() $|\phi (s)|\ll (1+|s|)^{-(1+\delta )}$
), it follows that
$|\phi (s)|\ll (1+|s|)^{-(1+\delta )}$
), it follows that
 $$\begin{align*}\int_{{\mathbb R}}\frac{\Gamma_K'}{\Gamma_K}(1+iy) \phi\left(y\frac{\log(X)}{2\pi}\right) dy=O\,\left(\frac{1}{\log(X)}\right). \end{align*}$$
$$\begin{align*}\int_{{\mathbb R}}\frac{\Gamma_K'}{\Gamma_K}(1+iy) \phi\left(y\frac{\log(X)}{2\pi}\right) dy=O\,\left(\frac{1}{\log(X)}\right). \end{align*}$$
Substituting this into (14) gives the modified explicit formula.
We now use the modified explicit formula to obtain an expression that bounds the analytic rank. Let E be an elliptic curve with minimal discriminant
![]() ${\mathfrak D}_{E/K}$
and of height less than or equal to X. For each such E, we have that
${\mathfrak D}_{E/K}$
and of height less than or equal to X. For each such E, we have that
![]() $N_{K/{\mathbb Q}}({\mathfrak D}_{E/K})\ll X$
, and therefore,
$N_{K/{\mathbb Q}}({\mathfrak D}_{E/K})\ll X$
, and therefore,
But since the conductor
![]() ${\mathfrak f}_{E/K}$
divides the minimal discriminant
${\mathfrak f}_{E/K}$
divides the minimal discriminant
![]() ${\mathfrak D}_{E/K}$
, one has
${\mathfrak D}_{E/K}$
, one has
![]() $N_{K/{\mathbb Q}}({\mathfrak f}_{E/K})\leq N_{K/{\mathbb Q}}({\mathfrak D}_{E/K})$
, and thus,
$N_{K/{\mathbb Q}}({\mathfrak f}_{E/K})\leq N_{K/{\mathbb Q}}({\mathfrak D}_{E/K})$
, and thus,
It follows that
![]() $\log (A_{E/K})/\log (X)\leq 1+O(1/\log X)$
. By Corollary 6.1.2, this observation gives the inequality
$\log (A_{E/K})/\log (X)\leq 1+O(1/\log X)$
. By Corollary 6.1.2, this observation gives the inequality
 $$ \begin{align*} &r(E)\phi(0)+\sum_{\gamma_j\neq 0} \phi\left(\gamma_j\frac{\log(X)}{2\pi}\right)\\ &\hspace{1cm}\leq \widehat{\phi}(0)-\frac{2}{\log(X)} \sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{\log(X)}\right) +O\,\left(\frac{1}{\log X}\right). \end{align*} $$
$$ \begin{align*} &r(E)\phi(0)+\sum_{\gamma_j\neq 0} \phi\left(\gamma_j\frac{\log(X)}{2\pi}\right)\\ &\hspace{1cm}\leq \widehat{\phi}(0)-\frac{2}{\log(X)} \sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{\log(X)}\right) +O\,\left(\frac{1}{\log X}\right). \end{align*} $$
We further simplify by rewriting the sum on the right-hand side as
 $$\begin{align*}\sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{\log(X)}\right) =\sum_{v\in \text{Val}_0(K)} \sum_{k\geq 1} \frac{ \widehat{a_E}({\mathfrak p}_v^k) \log(q_v)}{q_v^k}\cdot\widehat{\phi}\left(\frac{k \log(q_v)}{\log(X)}\right). \end{align*}$$
$$\begin{align*}\sum_{{\mathfrak a}\subseteq {\mathcal O}_K} \frac{ \widehat{a_E}({\mathfrak a}) \Lambda_K({\mathfrak a})}{N_{K/{\mathbb Q}}({\mathfrak a})}\cdot\widehat{\phi}\left(\frac{\log(N_{K/{\mathbb Q}}({\mathfrak a}))}{\log(X)}\right) =\sum_{v\in \text{Val}_0(K)} \sum_{k\geq 1} \frac{ \widehat{a_E}({\mathfrak p}_v^k) \log(q_v)}{q_v^k}\cdot\widehat{\phi}\left(\frac{k \log(q_v)}{\log(X)}\right). \end{align*}$$
By the Weil Conjectures for Elliptic curves,
![]() $|\alpha _v|=|\beta _v|=\sqrt {q_v}$
(see, for example, [Reference SilvermanSil09, §V Theorem 2.3.1(a)]). From this, and the fact that
$|\alpha _v|=|\beta _v|=\sqrt {q_v}$
(see, for example, [Reference SilvermanSil09, §V Theorem 2.3.1(a)]). From this, and the fact that
![]() $|b_v|\leq 1$
, we have
$|b_v|\leq 1$
, we have
![]() $|\widehat {a_E}({\mathfrak p}_v^k)|\leq 2q_v^{k/2}$
. Using this, we bound the
$|\widehat {a_E}({\mathfrak p}_v^k)|\leq 2q_v^{k/2}$
. Using this, we bound the
![]() $k\geq 3$
part of the sum:
$k\geq 3$
part of the sum:
 $$ \begin{align*} \sum_{v\in \text{Val}_0(K)} \sum_{k\geq 3} \frac{ \widehat{a_E}({\mathfrak p}_v^k) \log(q_v)}{q_v^k}\cdot\widehat{\phi}\left(\frac{k \log(q_v)}{\log(X)}\right) & \leq \sum_{v\in \text{Val}_0(K)} \sum_{k\geq 3} \frac{ 2 \log(q_v)}{q_v^{k/2}} ||\widehat{\phi}||_\infty\\ &\leq \sum_{v\in \text{Val}_0(K)} \frac{ 2 \log(q_v)}{q_v^{3/2} (1-q_v^{-1/2})} ||\widehat{\phi}||_\infty\\ &=O(1), \end{align*} $$
$$ \begin{align*} \sum_{v\in \text{Val}_0(K)} \sum_{k\geq 3} \frac{ \widehat{a_E}({\mathfrak p}_v^k) \log(q_v)}{q_v^k}\cdot\widehat{\phi}\left(\frac{k \log(q_v)}{\log(X)}\right) & \leq \sum_{v\in \text{Val}_0(K)} \sum_{k\geq 3} \frac{ 2 \log(q_v)}{q_v^{k/2}} ||\widehat{\phi}||_\infty\\ &\leq \sum_{v\in \text{Val}_0(K)} \frac{ 2 \log(q_v)}{q_v^{3/2} (1-q_v^{-1/2})} ||\widehat{\phi}||_\infty\\ &=O(1), \end{align*} $$
where
![]() $||f||_\infty $
is the usual
$||f||_\infty $
is the usual
![]() $L^\infty $
-norm defined as
$L^\infty $
-norm defined as
where
![]() $m_L$
is the Lebesgue measure on
$m_L$
is the Lebesgue measure on
![]() ${\mathbb R}$
. Also note that for any finite set of places
${\mathbb R}$
. Also note that for any finite set of places
![]() $S\subset \text {Val}_0(K)$
, we clearly have
$S\subset \text {Val}_0(K)$
, we clearly have
 $$\begin{align*}\sum_{v\in S} \sum_{k=1}^2 \frac{ \widehat{a_E}({\mathfrak p}_v^k) \log(q_v)}{q_v^k}\cdot\widehat{\phi}\left(\frac{k \log(q_v)}{\log(X)}\right)=O(1). \end{align*}$$
$$\begin{align*}\sum_{v\in S} \sum_{k=1}^2 \frac{ \widehat{a_E}({\mathfrak p}_v^k) \log(q_v)}{q_v^k}\cdot\widehat{\phi}\left(\frac{k \log(q_v)}{\log(X)}\right)=O(1). \end{align*}$$
Therefore, setting
 $$\begin{align*}U_{k}(E,\phi, X)\stackrel{\mathrm{def}}{=} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\widehat{a_E}({\mathfrak p}_v^k)\log(q_v)}{q_v^k} \cdot \widehat{\phi}\left( \frac{k\log(q_v)}{\log(X)}\right), \end{align*}$$
$$\begin{align*}U_{k}(E,\phi, X)\stackrel{\mathrm{def}}{=} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\widehat{a_E}({\mathfrak p}_v^k)\log(q_v)}{q_v^k} \cdot \widehat{\phi}\left( \frac{k\log(q_v)}{\log(X)}\right), \end{align*}$$
we have
 $$\begin{align*}r(E)\phi(0)+\sum_{\gamma_j\neq 0} \phi\left(\gamma_j\frac{\log(X)}{2\pi}\right) \leq \widehat{\phi}(0)-\frac{2}{\log(X)} ( U_1(E,\phi ,X)+U_2(E,\phi,X)) +O\,\left(\frac{1}{\log X}\right). \end{align*}$$
$$\begin{align*}r(E)\phi(0)+\sum_{\gamma_j\neq 0} \phi\left(\gamma_j\frac{\log(X)}{2\pi}\right) \leq \widehat{\phi}(0)-\frac{2}{\log(X)} ( U_1(E,\phi ,X)+U_2(E,\phi,X)) +O\,\left(\frac{1}{\log X}\right). \end{align*}$$
We now average over isomorphism classes of elliptic curves. For each elliptic curve E, let
![]() $\rho _{E,j}=1+i\gamma _{E,j}$
be the nontrivial zeros of the L-function
$\rho _{E,j}=1+i\gamma _{E,j}$
be the nontrivial zeros of the L-function
![]() $L(E/K,s)$
. Let
$L(E/K,s)$
. Let
![]() ${\mathcal E}_K(B)$
denote the set of isomorphism classes of elliptic curves over K with height bounded by B. Setting
${\mathcal E}_K(B)$
denote the set of isomorphism classes of elliptic curves over K with height bounded by B. Setting
 $$ \begin{align*} S_k(\phi,B) &\stackrel{\mathrm{def}}{=} \frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{E\in {\mathcal E}_{K}(B)} U_k(E,\phi,B)\\ &=\frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v^k} \cdot \widehat{\phi}\left( \frac{k\log(q_v)}{\log(B)}\right)\sum_{E\in{\mathcal E}_{K}(B)} \widehat{a_E}({\mathfrak p}_v^k), \end{align*} $$
$$ \begin{align*} S_k(\phi,B) &\stackrel{\mathrm{def}}{=} \frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{E\in {\mathcal E}_{K}(B)} U_k(E,\phi,B)\\ &=\frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v^k} \cdot \widehat{\phi}\left( \frac{k\log(q_v)}{\log(B)}\right)\sum_{E\in{\mathcal E}_{K}(B)} \widehat{a_E}({\mathfrak p}_v^k), \end{align*} $$
we have that
 $$ \begin{align} \begin{split} &\phi(0) \frac{1}{\#\mathcal{E}_{K}(B)} \sum_{E\in {\mathcal E}_{K}(B)} r(E)+\frac{1}{\# {\mathcal E}_{K}(B)} \sum_{E\in{\mathcal E}_{K}(B)}\sum_{\gamma_{E,j}\neq 0}\phi\left(\gamma_{E,j}\frac{\log(B)}{2\pi}\right)\\& \quad \leq \widehat{\phi}(0)-S_1(\phi,B)-S_2(\phi,B)+O\,\left(\frac{1}{\log(B)}\right). \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\phi(0) \frac{1}{\#\mathcal{E}_{K}(B)} \sum_{E\in {\mathcal E}_{K}(B)} r(E)+\frac{1}{\# {\mathcal E}_{K}(B)} \sum_{E\in{\mathcal E}_{K}(B)}\sum_{\gamma_{E,j}\neq 0}\phi\left(\gamma_{E,j}\frac{\log(B)}{2\pi}\right)\\& \quad \leq \widehat{\phi}(0)-S_1(\phi,B)-S_2(\phi,B)+O\,\left(\frac{1}{\log(B)}\right). \end{split} \end{align} $$
Remark 6.1.3. So far, we have followed the same strategy as Brumer [Reference BrumerBru92]. The main difficulty in estimating the
![]() $S_k(\phi ,B)$
is estimating the sums of the
$S_k(\phi ,B)$
is estimating the sums of the
![]() $\widehat {a_E}({\mathfrak p}_v^k)$
. Brumer does this by relating the sums to certain exponential sums. Following Cho and Jeong [Reference Cho and JeongCJ23b, Reference Cho and JeongCJ23a], we will take a slightly different approach, instead estimating the sums using our estimates for the number of elliptic curves with a prescribed trace of Frobenius (Theorem 1.1.3).
$\widehat {a_E}({\mathfrak p}_v^k)$
. Brumer does this by relating the sums to certain exponential sums. Following Cho and Jeong [Reference Cho and JeongCJ23b, Reference Cho and JeongCJ23a], we will take a slightly different approach, instead estimating the sums using our estimates for the number of elliptic curves with a prescribed trace of Frobenius (Theorem 1.1.3).
For our applications, we shall use the test function
 $$\begin{align*}\phi(y)=\begin{cases} \left(\frac{\sin(\pi \nu y)}{2\pi y}\right)^2 & \text{ if } y\neq 0,\\ \nu^2/4 & \text{ if }y=0, \end{cases} \end{align*}$$
$$\begin{align*}\phi(y)=\begin{cases} \left(\frac{\sin(\pi \nu y)}{2\pi y}\right)^2 & \text{ if } y\neq 0,\\ \nu^2/4 & \text{ if }y=0, \end{cases} \end{align*}$$
whose Fourier transform is
 $$\begin{align*}\widehat{\phi}(t)=\begin{cases} \frac{1}{2}\left(\frac{\nu}{2}-\frac{|t|}{2}\right) &\text{ for } |t|\leq \nu\\ 0 &\text{ for } |t|>\nu. \end{cases} \end{align*}$$
$$\begin{align*}\widehat{\phi}(t)=\begin{cases} \frac{1}{2}\left(\frac{\nu}{2}-\frac{|t|}{2}\right) &\text{ for } |t|\leq \nu\\ 0 &\text{ for } |t|>\nu. \end{cases} \end{align*}$$
Observe that this test function satisfies the conditions of Proposition 6.1.1 (despite not being a Schwartz function).
Our strategy will be to show that
This will imply the following upper bound for the average analytic rank of elliptic curves over the number field K:
 $$\begin{align*}\frac{\widehat{\phi}(0)}{\phi(0)}+\frac{1}{2} = \frac{1}{\nu}+\frac{1}{2}. \end{align*}$$
$$\begin{align*}\frac{\widehat{\phi}(0)}{\phi(0)}+\frac{1}{2} = \frac{1}{\nu}+\frac{1}{2}. \end{align*}$$
6.2. Class number estimates
In this subsection, we give some estimates for the counting functions
![]() $H(a,q)$
, which were defined in Subsection 5.1 equation (7). These results will be used in the next subsection.
$H(a,q)$
, which were defined in Subsection 5.1 equation (7). These results will be used in the next subsection.
Proposition 6.2.1. For any
![]() $a\in {\mathbb Z}$
, we have
$a\in {\mathbb Z}$
, we have
as a function of q for any
![]() $\epsilon>0$
.
$\epsilon>0$
.
Proof. By formula (9) for
![]() $H(a,q)$
, it suffices to show
$H(a,q)$
, it suffices to show
![]() $H(a^2-4q)\ll _{\epsilon } q^{1/2+\epsilon }$
and
$H(a^2-4q)\ll _{\epsilon } q^{1/2+\epsilon }$
and
![]() $H(-4p)\ll _{\epsilon } q^{1/2+\epsilon }$
, and for this, it will suffice to show that for all possible n, we have
$H(-4p)\ll _{\epsilon } q^{1/2+\epsilon }$
, and for this, it will suffice to show that for all possible n, we have
![]() $H(n)\ll _{\epsilon } |n|^{1/2+\epsilon }$
. As n must be the discriminant of an order in an imaginary quadratic field, it must be negative, non-square and congruent to
$H(n)\ll _{\epsilon } |n|^{1/2+\epsilon }$
. As n must be the discriminant of an order in an imaginary quadratic field, it must be negative, non-square and congruent to
![]() $0$
or
$0$
or
![]() $1$
modulo
$1$
modulo
![]() $4$
.
$4$
.
Let
![]() $\text {sqf}(n)$
denote the squarefree part of n (e.g.,
$\text {sqf}(n)$
denote the squarefree part of n (e.g.,
![]() $\text {sqf}(12)=3$
), and let
$\text {sqf}(12)=3$
), and let
![]() $\text {sq}(n)$
be such that
$\text {sq}(n)$
be such that
![]() $n=\text {sqf}(n)\cdot \text {sq}(n)^2$
(e.g.,
$n=\text {sqf}(n)\cdot \text {sq}(n)^2$
(e.g.,
![]() $\text {sq}(12)=2$
). For non-square negative integers D that are congruent to
$\text {sq}(12)=2$
). For non-square negative integers D that are congruent to
![]() $0$
or
$0$
or
![]() $1$
modulo
$1$
modulo
![]() $4$
, let
$4$
, let
![]() ${\mathcal O}_{D}$
denote the imaginary quadratic order of discriminant D. We can rewrite equation (8) as
${\mathcal O}_{D}$
denote the imaginary quadratic order of discriminant D. We can rewrite equation (8) as
 $$\begin{align*}H(n)=\sum_{\substack{d|\text{sq}(n)\\ n/d^2\equiv 0,1\quad\pmod{4}}} \frac{h({\mathcal O}_{n/d^2})}{\#{\mathcal O}_{n/d^2}^{\times}}. \end{align*}$$
$$\begin{align*}H(n)=\sum_{\substack{d|\text{sq}(n)\\ n/d^2\equiv 0,1\quad\pmod{4}}} \frac{h({\mathcal O}_{n/d^2})}{\#{\mathcal O}_{n/d^2}^{\times}}. \end{align*}$$
Define a quadratic character
 $$ \begin{align*} \chi_D:{\mathbb Z}&\to {\mathbb C}^{\times}\\ m & \mapsto \genfrac{(}{)}{}{}{D}{m}. \end{align*} $$
$$ \begin{align*} \chi_D:{\mathbb Z}&\to {\mathbb C}^{\times}\\ m & \mapsto \genfrac{(}{)}{}{}{D}{m}. \end{align*} $$
Observe that
 $$ \begin{align} \lim_{s\to 1}(s-1)\zeta_{{\mathcal O}_D}(s) = \sum_{m=1}^\infty \frac{\chi_D(m)}{m} =\sum_{m=1}^\infty \chi_D(m) \int_m^{\infty}\frac{1}{x^2}dx. \end{align} $$
$$ \begin{align} \lim_{s\to 1}(s-1)\zeta_{{\mathcal O}_D}(s) = \sum_{m=1}^\infty \frac{\chi_D(m)}{m} =\sum_{m=1}^\infty \chi_D(m) \int_m^{\infty}\frac{1}{x^2}dx. \end{align} $$
For any positive integer
![]() $r\in {\mathbb Z}_{\geq 1}$
, the Pólya–Vinogradov inequality gives
$r\in {\mathbb Z}_{\geq 1}$
, the Pólya–Vinogradov inequality gives
 $$\begin{align*}\left|\sum_{m=1}^r \chi_D(m)\right|\leq 2\sqrt{|D|} \log(|D|). \end{align*}$$
$$\begin{align*}\left|\sum_{m=1}^r \chi_D(m)\right|\leq 2\sqrt{|D|} \log(|D|). \end{align*}$$
In particular, the functions
![]() $f_r(x)=\sum _{m=1}^r \chi _D(m)/x^2$
are dominated by
$f_r(x)=\sum _{m=1}^r \chi _D(m)/x^2$
are dominated by
![]() $2\sqrt {|D|}\log (|D|)/x^{2}$
on
$2\sqrt {|D|}\log (|D|)/x^{2}$
on
![]() ${\mathbb R}_{\geq 1}$
. Therefore, by the dominated convergence theorem, we may switch the sum and integral in (16), so that
${\mathbb R}_{\geq 1}$
. Therefore, by the dominated convergence theorem, we may switch the sum and integral in (16), so that
 $$ \begin{align*} \sum_{m=1}^\infty \chi_D(m) \int_m^{\infty}\frac{1}{x^2}dx=\int_1^{\infty} \left(\sum_{m=1}^x \chi_D(m)\right) \frac{1}{x^2} dx. \end{align*} $$
$$ \begin{align*} \sum_{m=1}^\infty \chi_D(m) \int_m^{\infty}\frac{1}{x^2}dx=\int_1^{\infty} \left(\sum_{m=1}^x \chi_D(m)\right) \frac{1}{x^2} dx. \end{align*} $$
Splitting this integral and again applying the Pólya–Vinogradov inequality, we find that for any
![]() $\epsilon>0$
,
$\epsilon>0$
,
 $$ \begin{align*} \lim_{s\to 1}(s-1)\zeta_{{\mathcal O}_D}(s) &= \int_1^{\sqrt{|D|}} \left(\sum_{m=1}^x \chi_D(m)\right) \frac{1}{x^2} dx + \int_{\sqrt{|D|}}^{\infty} \left(\sum_{m=1}^x \chi_D(m)\right) \frac{1}{x^2} dx \\ &\ll \int_1^{\sqrt{|D|}} \frac{x}{x^2} dx + \int_{\sqrt{|D|}}^{\infty} \frac{\sqrt{|D|}\log(|D|)}{x^2} dx \\ &\ll \log(|D|) + \log(|D|) \\ &\ll |D|^{\epsilon}. \end{align*} $$
$$ \begin{align*} \lim_{s\to 1}(s-1)\zeta_{{\mathcal O}_D}(s) &= \int_1^{\sqrt{|D|}} \left(\sum_{m=1}^x \chi_D(m)\right) \frac{1}{x^2} dx + \int_{\sqrt{|D|}}^{\infty} \left(\sum_{m=1}^x \chi_D(m)\right) \frac{1}{x^2} dx \\ &\ll \int_1^{\sqrt{|D|}} \frac{x}{x^2} dx + \int_{\sqrt{|D|}}^{\infty} \frac{\sqrt{|D|}\log(|D|)}{x^2} dx \\ &\ll \log(|D|) + \log(|D|) \\ &\ll |D|^{\epsilon}. \end{align*} $$
From this and the analytic class number formula [Reference Jordan and PoonenJP20, Theorem 1.1], we have the following upper bound for class numbers of orders in imaginary quadratic fields:
Let
![]() $\tau (n)$
denote the number of divisors of n, and recall that
$\tau (n)$
denote the number of divisors of n, and recall that
![]() $\tau (n)\ll _{\epsilon } |n|^{\epsilon }$
for any
$\tau (n)\ll _{\epsilon } |n|^{\epsilon }$
for any
![]() $\epsilon>0$
. Combining the above observations, we have
$\epsilon>0$
. Combining the above observations, we have
 $$\begin{align*}H(n)\leq \sum_{\substack{d|\text{sq}(n)\\ n/d^2\equiv 0,1\quad\pmod{4}}} h({\mathcal O}_{n/d^2})\ll \tau(\text{sq}(n)) |n|^{1/2+\epsilon}\ll_{\epsilon} |n|^{1/2+\epsilon}.\\[-58pt] \end{align*}$$
$$\begin{align*}H(n)\leq \sum_{\substack{d|\text{sq}(n)\\ n/d^2\equiv 0,1\quad\pmod{4}}} h({\mathcal O}_{n/d^2})\ll \tau(\text{sq}(n)) |n|^{1/2+\epsilon}\ll_{\epsilon} |n|^{1/2+\epsilon}.\\[-58pt] \end{align*}$$
The next proposition gives estimates for certain sums involving
![]() $H(a,q)$
.
$H(a,q)$
.
Proposition 6.2.2. Let q be a power of a prime
![]() $p>3$
. For any
$p>3$
. For any
![]() $\epsilon>0$
, we have the following estimates:
$\epsilon>0$
, we have the following estimates:
 $$ \begin{align*} &\sum_{|a|\leq 2\sqrt{q}} H(a,q)= q^2-q,\\ &\sum_{|a|\leq 2\sqrt{q}} aH(a,q)=0,\\ &\sum_{|a|\leq 2\sqrt{q}} a^2 H(a,q)=q^3+O\,\left(q^{\frac{5}{2}+\epsilon}\right). \end{align*} $$
$$ \begin{align*} &\sum_{|a|\leq 2\sqrt{q}} H(a,q)= q^2-q,\\ &\sum_{|a|\leq 2\sqrt{q}} aH(a,q)=0,\\ &\sum_{|a|\leq 2\sqrt{q}} a^2 H(a,q)=q^3+O\,\left(q^{\frac{5}{2}+\epsilon}\right). \end{align*} $$
Proof. The first sum: We have that
 $$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} H(a,q)=\#\{(b,c)\in {\mathbb F}_q\times{\mathbb F}_q : \Delta(b,c)\neq 0\}=q^2-q. \end{align*}$$
$$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} H(a,q)=\#\{(b,c)\in {\mathbb F}_q\times{\mathbb F}_q : \Delta(b,c)\neq 0\}=q^2-q. \end{align*}$$
The second sum: Pairing positive and negative terms, we have that
 $$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} a H(a,q)=\sum_{0<a \leq 2\sqrt{q}} \left(a H(a,q)-a H(a,q)\right)= 0, \end{align*}$$
$$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} a H(a,q)=\sum_{0<a \leq 2\sqrt{q}} \left(a H(a,q)-a H(a,q)\right)= 0, \end{align*}$$
where we have used that
![]() $H(a,q)=H(-a,q)$
.
$H(a,q)=H(-a,q)$
.
The third sum: This sum is the most subtle. As observed in Subsection 5.1, each isomorphism class of elliptic curves over
![]() ${\mathbb F}_q$
contains exactly
${\mathbb F}_q$
contains exactly
![]() $q-1$
elliptic curves, which can be thought of as the size of the orbit of an elliptic curve E with respect to the weighted
$q-1$
elliptic curves, which can be thought of as the size of the orbit of an elliptic curve E with respect to the weighted
![]() ${\mathbb G}_m({\mathbb F}_q)$
action, with weights
${\mathbb G}_m({\mathbb F}_q)$
action, with weights
![]() $4$
and
$4$
and
![]() $6$
. Let
$6$
. Let
![]() ${\mathcal E}_{{\mathbb F}_q}$
denote the set of isomorphism classes of elliptic curves over
${\mathcal E}_{{\mathbb F}_q}$
denote the set of isomorphism classes of elliptic curves over
![]() ${\mathbb F}_q$
. By the orbit stabilizer theorem,
${\mathbb F}_q$
. By the orbit stabilizer theorem,
 $$\begin{align*}H(a,q)=\sum_{\substack{E\in {\mathcal E}_{{\mathbb F}_q}\\ a_q(E)=a}}\frac{q-1}{\#\text{Aut}_{{\mathbb F}_q}(E)}. \end{align*}$$
$$\begin{align*}H(a,q)=\sum_{\substack{E\in {\mathcal E}_{{\mathbb F}_q}\\ a_q(E)=a}}\frac{q-1}{\#\text{Aut}_{{\mathbb F}_q}(E)}. \end{align*}$$
Therefore, we can rewrite the third sum as
 $$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} a^2 H(a,q) =(q-1)\sum_{|a|\leq 2\sqrt{q}}\sum_{{\substack{E\in {\mathcal E}_{{\mathbb F}_q}\\ a_q(E)=a}}} \frac{a^2}{\#\text{Aut}_{{\mathbb F}_q}(E)} =(q-1)\sum_{E\in {\mathcal E}_{{\mathbb F}_q}} \frac{a_q(E)^2}{\#\text{Aut}_{{\mathbb F}_q}(E)}. \end{align*}$$
$$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} a^2 H(a,q) =(q-1)\sum_{|a|\leq 2\sqrt{q}}\sum_{{\substack{E\in {\mathcal E}_{{\mathbb F}_q}\\ a_q(E)=a}}} \frac{a^2}{\#\text{Aut}_{{\mathbb F}_q}(E)} =(q-1)\sum_{E\in {\mathcal E}_{{\mathbb F}_q}} \frac{a_q(E)^2}{\#\text{Aut}_{{\mathbb F}_q}(E)}. \end{align*}$$
The final sum can be estimated using work of Birch [Reference BirchBir68] and Ihara [Reference IharaIha67], as we now explain. Write
![]() $q=p^r$
. Define an indicator function
$q=p^r$
. Define an indicator function
 $$\begin{align*}\delta_{2{\mathbb Z}}(r)=\begin{cases} 1 & \text{ if }r\text{ is even}\\ 0 & \text{ if }r\text{ is odd}. \end{cases} \end{align*}$$
$$\begin{align*}\delta_{2{\mathbb Z}}(r)=\begin{cases} 1 & \text{ if }r\text{ is even}\\ 0 & \text{ if }r\text{ is odd}. \end{cases} \end{align*}$$
Let
![]() $T_k(m)$
be the m-th Hecke operator on the space of weight k cusp forms of level 1, and let
$T_k(m)$
be the m-th Hecke operator on the space of weight k cusp forms of level 1, and let
![]() $\text {Tr}(T_k(m))$
denote the trace of
$\text {Tr}(T_k(m))$
denote the trace of
![]() $T_k(m)$
.
$T_k(m)$
.
The following result is due to Birch (in the
![]() $r=1$
case) [Reference BirchBir68] and Ihara (for
$r=1$
case) [Reference BirchBir68] and Ihara (for
![]() $r>1$
) [Reference IharaIha67] (see [Reference Kaplan and PetrowKP17, Theorem 2]):
$r>1$
) [Reference IharaIha67] (see [Reference Kaplan and PetrowKP17, Theorem 2]):
Theorem 6.2.3 (Birch-Ihara).
With notation as above, we have that
 $$ \begin{align*} \frac{1}{q}\sum_{E\in {\mathcal E}_{{\mathbb F}_q}} \frac{a_q(E)^2}{\#\text{Aut}_{{\mathbb F}_q}(E)} \end{align*} $$
$$ \begin{align*} \frac{1}{q}\sum_{E\in {\mathcal E}_{{\mathbb F}_q}} \frac{a_q(E)^2}{\#\text{Aut}_{{\mathbb F}_q}(E)} \end{align*} $$
equals
 $$ \begin{align*} &\frac{1}{q}\left(p^3\text{Tr}(T_4(p^{r-2}))-\text{Tr}(T_4(q)) +\frac{1}{2}\left( p^3 \sum_{i=0}^{r-2} \min\{p^i,p^{r-2-i}\}^3-\sum_{i=0}^{r} \min\{p^i, p^{r-i}\}^3\right)\right)\\& \quad + p \text{Tr}(T_2(p^{r-2})) - \text{Tr}(T_2(q)) + \frac{1}{2}\left(p \sum_{i=0}^{r-2} \min\{p^i,p^{r-2-i}\} - \sum_{i=0}^r \min\{p^i,p^{r-i}\} \right) \\& \quad + \sum_{i=0}^r p^i-p\sum_{i=0}^{r-2}p^i. \end{align*} $$
$$ \begin{align*} &\frac{1}{q}\left(p^3\text{Tr}(T_4(p^{r-2}))-\text{Tr}(T_4(q)) +\frac{1}{2}\left( p^3 \sum_{i=0}^{r-2} \min\{p^i,p^{r-2-i}\}^3-\sum_{i=0}^{r} \min\{p^i, p^{r-i}\}^3\right)\right)\\& \quad + p \text{Tr}(T_2(p^{r-2})) - \text{Tr}(T_2(q)) + \frac{1}{2}\left(p \sum_{i=0}^{r-2} \min\{p^i,p^{r-2-i}\} - \sum_{i=0}^r \min\{p^i,p^{r-i}\} \right) \\& \quad + \sum_{i=0}^r p^i-p\sum_{i=0}^{r-2}p^i. \end{align*} $$
We now show that for any
![]() $\epsilon>0$
,
$\epsilon>0$
,
 $$ \begin{align*} \sum_{E\in {\mathcal E}_{{\mathbb F}_q}} \frac{a_q(E)^2}{\#\text{Aut}_{{\mathbb F}_q}(E)} = q^2 + O(q^{3/2+\epsilon}). \end{align*} $$
$$ \begin{align*} \sum_{E\in {\mathcal E}_{{\mathbb F}_q}} \frac{a_q(E)^2}{\#\text{Aut}_{{\mathbb F}_q}(E)} = q^2 + O(q^{3/2+\epsilon}). \end{align*} $$
Using the Ramanujan–Peterson–Deligne bound for Hecke eigenvalues [Reference DeligneDel74], one can show that for any prime power
![]() $p^s$
and any
$p^s$
and any
![]() $\epsilon>0$
,
$\epsilon>0$
,
(see, for example, the introduction of [Reference PetrowPet18]). In particular,
and
We now estimate the sums in Theorem 6.2.3. As a function of q, the sum
![]() $\sum _{i=0}^{r} \min \{p^i, p^{r-i}\}^3$
has on the order of
$\sum _{i=0}^{r} \min \{p^i, p^{r-i}\}^3$
has on the order of
![]() $\log (q)$
terms, and each term is bounded above by
$\log (q)$
terms, and each term is bounded above by
![]() $\left (p^{r/2}\right )^3=q^{3/2}$
. Therefore,
$\left (p^{r/2}\right )^3=q^{3/2}$
. Therefore,
 $$ \begin{align*} \sum_{i=0}^{r} \min\{p^i, p^{r-i}\}^3\ll q^{3/2}\log(q)\ll q^{3/2+\epsilon}. \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{r} \min\{p^i, p^{r-i}\}^3\ll q^{3/2}\log(q)\ll q^{3/2+\epsilon}. \end{align*} $$
Similar reasoning shows that
 $$ \begin{align*} p^3 \sum_{i=0}^{r-2} \min\{p^i,p^{r-2-i}\}^3\ll p^3\log(q)p^{3(r-2)/2}\ll q^{3/2+\epsilon}. \end{align*} $$
$$ \begin{align*} p^3 \sum_{i=0}^{r-2} \min\{p^i,p^{r-2-i}\}^3\ll p^3\log(q)p^{3(r-2)/2}\ll q^{3/2+\epsilon}. \end{align*} $$
We also compute
 $$ \begin{align*} p \sum_{i=0}^{r-2} \min\{p^i,p^{r-2-i}\} - \sum_{i=0}^r \min\{p^i,p^{r-i}\} =-\sum_{i\in\{0,r\}} \min\{p^i,p^{r-i}\} =-2, \end{align*} $$
$$ \begin{align*} p \sum_{i=0}^{r-2} \min\{p^i,p^{r-2-i}\} - \sum_{i=0}^r \min\{p^i,p^{r-i}\} =-\sum_{i\in\{0,r\}} \min\{p^i,p^{r-i}\} =-2, \end{align*} $$
and
 $$ \begin{align*} \sum_{i=0}^r p^i-p\sum_{i=0}^{r-2}p^i=\sum_{i\in \{0,r\}} p^i = 1 + q. \end{align*} $$
$$ \begin{align*} \sum_{i=0}^r p^i-p\sum_{i=0}^{r-2}p^i=\sum_{i\in \{0,r\}} p^i = 1 + q. \end{align*} $$
Combining the above estimates, we find that
 $$ \begin{align*} \frac{1}{q}\sum_{E\in {\mathcal E}_{{\mathbb F}_q}} \frac{a_q(E)^2}{\#\text{Aut}_{{\mathbb F}_q}(E)} &= {\mathcal O}\left(\frac{q^{3/2+\epsilon}}{q}\right) + O(q^{1/2+\epsilon})-\frac{2}{2}+(1+q)= q + O(q^{1/2+\epsilon}). \end{align*} $$
$$ \begin{align*} \frac{1}{q}\sum_{E\in {\mathcal E}_{{\mathbb F}_q}} \frac{a_q(E)^2}{\#\text{Aut}_{{\mathbb F}_q}(E)} &= {\mathcal O}\left(\frac{q^{3/2+\epsilon}}{q}\right) + O(q^{1/2+\epsilon})-\frac{2}{2}+(1+q)= q + O(q^{1/2+\epsilon}). \end{align*} $$
From this, we obtain
 $$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} a^2 H(a,q)=(q-1)\left(q^2 + O(q^{3/2+\epsilon})\right)=q^3+O(q^{5/2+\epsilon}).\\[-51pt] \end{align*}$$
$$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} a^2 H(a,q)=(q-1)\left(q^2 + O(q^{3/2+\epsilon})\right)=q^3+O(q^{5/2+\epsilon}).\\[-51pt] \end{align*}$$
6.3. Estimating
 $S_1(\phi ,B)$
and
$S_1(\phi ,B)$
and
 $S_2(\phi ,B)$
$S_2(\phi ,B)$
Lemma 6.3.1. Let
![]() ${\mathfrak p}\subset {\mathcal O}_K$
be a prime ideal of norm
${\mathfrak p}\subset {\mathcal O}_K$
be a prime ideal of norm
![]() $N_{K/{\mathbb Q}}({\mathfrak p})=q$
such that
$N_{K/{\mathbb Q}}({\mathfrak p})=q$
such that
![]() $2\nmid q$
and
$2\nmid q$
and
![]() $3\nmid q$
. Then, for any
$3\nmid q$
. Then, for any
![]() $\epsilon>0$
, we have the following upper bound:
$\epsilon>0$
, we have the following upper bound:
 $$\begin{align*}\sum_{E\in {\mathcal E}_K(B)} \widehat{a_E}({\mathfrak p})\ll_{\epsilon} \frac{1}{q} B^{5/6}+q^{3/2+\epsilon} B^{5/6-1/3d}. \end{align*}$$
$$\begin{align*}\sum_{E\in {\mathcal E}_K(B)} \widehat{a_E}({\mathfrak p})\ll_{\epsilon} \frac{1}{q} B^{5/6}+q^{3/2+\epsilon} B^{5/6-1/3d}. \end{align*}$$
Proof. Let
![]() ${\mathcal E}_K^{\text {mult}}(B)$
denote the set of elliptic curves over K of naive height bounded by B and multiplicative reduction at
${\mathcal E}_K^{\text {mult}}(B)$
denote the set of elliptic curves over K of naive height bounded by B and multiplicative reduction at
![]() ${\mathfrak p}$
. Then, we have
${\mathfrak p}$
. Then, we have
 $$\begin{align*}\sum_{E\in {\mathcal E}_K(B)}\widehat{a_E}({\mathfrak p})=\sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K(B)\\ a_{\mathfrak p}(E)=a}} \widehat{a_E}({\mathfrak p}) + \sum_{E\in {\mathcal E}_K^{\text{mult}}(B)} \widehat{a_E}({\mathfrak p}). \end{align*}$$
$$\begin{align*}\sum_{E\in {\mathcal E}_K(B)}\widehat{a_E}({\mathfrak p})=\sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K(B)\\ a_{\mathfrak p}(E)=a}} \widehat{a_E}({\mathfrak p}) + \sum_{E\in {\mathcal E}_K^{\text{mult}}(B)} \widehat{a_E}({\mathfrak p}). \end{align*}$$
By Theorem 1.1.2, we have that
 $$ \begin{align} \left|\sum_{E\in {\mathcal E}_K^{\text{mult}}(B)} \widehat{a_E}({\mathfrak p})\right|\ll \#{\mathcal E}_K^{\text{mult}}(B) \ll \frac{1}{q}B^{5/6}+B^{5/6-1/3d}. \end{align} $$
$$ \begin{align} \left|\sum_{E\in {\mathcal E}_K^{\text{mult}}(B)} \widehat{a_E}({\mathfrak p})\right|\ll \#{\mathcal E}_K^{\text{mult}}(B) \ll \frac{1}{q}B^{5/6}+B^{5/6-1/3d}. \end{align} $$
By Proposition 6.2.2, Proposition 6.2.1 and the proof of Theorem 1.1.3, we have that
 $$ \begin{align*} \sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K(B)\\ a_{\mathfrak p}(E)=a}} \widehat{a_E}({\mathfrak p}) &=\sum_{|a|\leq 2\sqrt{q}} a\left(\kappa\frac{H(a,q)}{q^2}\frac{q^{10}}{q^{10}-1}B^{5/6}+O\,\left(q^{-1}H(a,q)B^{5/6-1/3d}\right)\right)\\ &=0+\sum_{|a|\leq 2\sqrt{q}} O\,\left(a q^{-1}H(a,q)B^{5/6-1/3d}\right)\\ &\ll \max_{|a|\leq 2\sqrt{q}}\{H(a,q)\} B^{5/6-1/3d}\\ &\ll_{\epsilon} q^{3/2+\epsilon} B^{5/6-1/3d}. \end{align*} $$
$$ \begin{align*} \sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K(B)\\ a_{\mathfrak p}(E)=a}} \widehat{a_E}({\mathfrak p}) &=\sum_{|a|\leq 2\sqrt{q}} a\left(\kappa\frac{H(a,q)}{q^2}\frac{q^{10}}{q^{10}-1}B^{5/6}+O\,\left(q^{-1}H(a,q)B^{5/6-1/3d}\right)\right)\\ &=0+\sum_{|a|\leq 2\sqrt{q}} O\,\left(a q^{-1}H(a,q)B^{5/6-1/3d}\right)\\ &\ll \max_{|a|\leq 2\sqrt{q}}\{H(a,q)\} B^{5/6-1/3d}\\ &\ll_{\epsilon} q^{3/2+\epsilon} B^{5/6-1/3d}. \end{align*} $$
This, together with the bound (17), implies the lemma.
Lemma 6.3.2. Let
![]() ${\mathfrak p}\subset {\mathcal O}_K$
be a prime ideal with norm
${\mathfrak p}\subset {\mathcal O}_K$
be a prime ideal with norm
![]() $N_{K/{\mathbb Q}}({\mathfrak p})=q$
such that
$N_{K/{\mathbb Q}}({\mathfrak p})=q$
such that
![]() $2\nmid q$
and
$2\nmid q$
and
![]() $3\nmid q$
. Then, we have the following estimate:
$3\nmid q$
. Then, we have the following estimate:
 $$\begin{align*}\sum_{E\in {\mathcal E}_K(B)} \widehat{a_E}({\mathfrak p}^2)=-\kappa q B^{5/6}+O\,\left(q^{1/2+\epsilon}B^{\frac{5}{6}}+q^2 B^{\frac{5}{6}-\frac{1}{3d}}\right), \end{align*}$$
$$\begin{align*}\sum_{E\in {\mathcal E}_K(B)} \widehat{a_E}({\mathfrak p}^2)=-\kappa q B^{5/6}+O\,\left(q^{1/2+\epsilon}B^{\frac{5}{6}}+q^2 B^{\frac{5}{6}-\frac{1}{3d}}\right), \end{align*}$$
where the implied constant does not depend on q.
Proof. Let
![]() ${\mathcal E}_K^{good}(B)$
(resp.
${\mathcal E}_K^{good}(B)$
(resp.
![]() ${\mathcal E}_K^{\text {mult}}(B)$
) denote the set of elliptic curves over K with good reduction (resp. multiplicative reduction) at
${\mathcal E}_K^{\text {mult}}(B)$
) denote the set of elliptic curves over K with good reduction (resp. multiplicative reduction) at
![]() ${\mathfrak p}$
and height bounded by B. In this case, we have that
${\mathfrak p}$
and height bounded by B. In this case, we have that
 $$\begin{align*}\sum_{E\in {\mathcal E}_K(B)} \widehat{a_E}({\mathfrak p}^2)=\sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K^{good}(B)\\ a_{\mathfrak p}(E)=a}} \widehat{a_E}({\mathfrak p}^2) + \sum_{E\in {\mathcal E}_K^{\text{mult}}(B)} \widehat{a_E}({\mathfrak p}^2). \end{align*}$$
$$\begin{align*}\sum_{E\in {\mathcal E}_K(B)} \widehat{a_E}({\mathfrak p}^2)=\sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K^{good}(B)\\ a_{\mathfrak p}(E)=a}} \widehat{a_E}({\mathfrak p}^2) + \sum_{E\in {\mathcal E}_K^{\text{mult}}(B)} \widehat{a_E}({\mathfrak p}^2). \end{align*}$$
Since
![]() $\widehat {a_E}({\mathfrak p}^2)=\widehat {a_E}({\mathfrak p})^2=1$
for all
$\widehat {a_E}({\mathfrak p}^2)=\widehat {a_E}({\mathfrak p})^2=1$
for all
![]() $E\in {\mathcal E}_K^{\text {mult}}(B)$
, we have, by Theorem 1.1.2, that
$E\in {\mathcal E}_K^{\text {mult}}(B)$
, we have, by Theorem 1.1.2, that
 $$ \begin{align} \left|\sum_{E\in {\mathcal E}_K^{\text{mult}}(B)} \widehat{a_E}({\mathfrak p}^2)\right|=\#{\mathcal E}_K^{\text{mult}}(B)=\kappa \frac{q-1}{q^2}\frac{q^{10}}{q^{10}-1} B^{5/6}+O(B^{5/6-1/3d})=O\,\left(B^{5/6}\right). \end{align} $$
$$ \begin{align} \left|\sum_{E\in {\mathcal E}_K^{\text{mult}}(B)} \widehat{a_E}({\mathfrak p}^2)\right|=\#{\mathcal E}_K^{\text{mult}}(B)=\kappa \frac{q-1}{q^2}\frac{q^{10}}{q^{10}-1} B^{5/6}+O(B^{5/6-1/3d})=O\,\left(B^{5/6}\right). \end{align} $$
In the case that E has good reduction at
![]() ${\mathfrak p}$
, a straightforward computation shows that
${\mathfrak p}$
, a straightforward computation shows that
![]() $\widehat {a_E}({\mathfrak p}^2)$
equals
$\widehat {a_E}({\mathfrak p}^2)$
equals
![]() $a_{\mathfrak p}(E)^2-2q$
. Therefore, by Proposition 6.2.2 and the proof of Theorem 1.1.3, we have that
$a_{\mathfrak p}(E)^2-2q$
. Therefore, by Proposition 6.2.2 and the proof of Theorem 1.1.3, we have that
 $$ \begin{align*} \sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K^{good}(B)\\ a_{\mathfrak p}(E)=a}} \widehat{a_E}({\mathfrak p}^2) &=\sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K^{good}(B)\\ a_{\mathfrak p}(E)=a}} (a_{\mathfrak p}(E)^2-2q)\\&=\sum_{|a|\leq 2\sqrt{q}} (a^2-2q)\left(\kappa\frac{H(a,q)}{q^2}\frac{q^{10}}{q^{10}-1}B^{5/6}+O\,\left(q^{-1}H(a,q)B^{5/6-1/3d}\right)\right)\\&=\frac{\kappa q^{8}}{q^{10}-1}\left(\sum_{|a|\leq 2\sqrt{q}} a^2 H(a,q)-2q\sum_{|a|\leq 2\sqrt{q}} H(a,q)\right) B^{\frac{5}{6}}+O\,\left(q^2 B^{\frac{5}{6}-\frac{1}{3d}}\right)\\&=\frac{-\kappa q^{11}}{q^{10}-1} B^{5/6}+O\,\left(q^{1/2+\epsilon}B^{\frac{5}{6}}+q^2 B^{\frac{5}{6}-\frac{1}{3d}}\right). \end{align*} $$
$$ \begin{align*} \sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K^{good}(B)\\ a_{\mathfrak p}(E)=a}} \widehat{a_E}({\mathfrak p}^2) &=\sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K^{good}(B)\\ a_{\mathfrak p}(E)=a}} (a_{\mathfrak p}(E)^2-2q)\\&=\sum_{|a|\leq 2\sqrt{q}} (a^2-2q)\left(\kappa\frac{H(a,q)}{q^2}\frac{q^{10}}{q^{10}-1}B^{5/6}+O\,\left(q^{-1}H(a,q)B^{5/6-1/3d}\right)\right)\\&=\frac{\kappa q^{8}}{q^{10}-1}\left(\sum_{|a|\leq 2\sqrt{q}} a^2 H(a,q)-2q\sum_{|a|\leq 2\sqrt{q}} H(a,q)\right) B^{\frac{5}{6}}+O\,\left(q^2 B^{\frac{5}{6}-\frac{1}{3d}}\right)\\&=\frac{-\kappa q^{11}}{q^{10}-1} B^{5/6}+O\,\left(q^{1/2+\epsilon}B^{\frac{5}{6}}+q^2 B^{\frac{5}{6}-\frac{1}{3d}}\right). \end{align*} $$
Observe that
 $$\begin{align*}\frac{q^{10}}{q^{10}-1}=\sum_{k=0}^{\infty} q^{-10k}=1+O(q^{-10}). \end{align*}$$
$$\begin{align*}\frac{q^{10}}{q^{10}-1}=\sum_{k=0}^{\infty} q^{-10k}=1+O(q^{-10}). \end{align*}$$
Therefore,
 $$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K^{good}(B)\\ a_{\mathfrak p}(E)=a}}\widehat{a_E}({\mathfrak p}^2)=-\kappa q B^{5/6}+O\,\left(q^{1/2+\epsilon}B^{\frac{5}{6}}+q^2 B^{\frac{5}{6}-\frac{1}{3d}}\right). \end{align*}$$
$$\begin{align*}\sum_{|a|\leq 2\sqrt{q}} \sum_{\substack{E\in{\mathcal E}_K^{good}(B)\\ a_{\mathfrak p}(E)=a}}\widehat{a_E}({\mathfrak p}^2)=-\kappa q B^{5/6}+O\,\left(q^{1/2+\epsilon}B^{\frac{5}{6}}+q^2 B^{\frac{5}{6}-\frac{1}{3d}}\right). \end{align*}$$
This, together with the bound (18), implies the lemma.
6.4. Bounding the average analytic rank of elliptic curves
We now prove our main result.
Theorem 1.1.1.
Let K be a number field of degree d. Assume that all elliptic curves over K are modular and that their L-functions satisfy the Riemann-Hypothesis. Then the average analytic rank of isomorphism classes of elliptic curves over K, when ordered by naive height, is bounded above by
![]() $(9d+1)/2$
.
$(9d+1)/2$
.
Proof. By Lemma 6.3.1 and the observation that
![]() $\widehat {\phi }$
is supported on the interval
$\widehat {\phi }$
is supported on the interval
![]() $[-\nu ,\nu ]$
, we have that
$[-\nu ,\nu ]$
, we have that
 $$ \begin{align*} S_1(\phi,B)&=\frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{ v\in \text{Val}_0(K)\\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \cdot \widehat{\phi}\left( \frac{\log(q_v)}{\log(B)}\right)\sum_{E\in{\mathcal E}_{K}(B)} \widehat{a_E}({\mathfrak p}_v)\\ &\ll_{\epsilon} \frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K)\\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \cdot \widehat{\phi}\left( \frac{\log(q_v)}{\log(B)}\right)\left(\frac{1}{q_v} B^{5/6}+q_v^{3/2+\epsilon}B^{5/6-1/3d}\right)\\ &\ll \frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ q_v\leq B^\nu \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \left(\frac{1}{q_v} B^{5/6}+q_v^{3/2+\epsilon}B^{5/6-1/3d}\right). \end{align*} $$
$$ \begin{align*} S_1(\phi,B)&=\frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{ v\in \text{Val}_0(K)\\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \cdot \widehat{\phi}\left( \frac{\log(q_v)}{\log(B)}\right)\sum_{E\in{\mathcal E}_{K}(B)} \widehat{a_E}({\mathfrak p}_v)\\ &\ll_{\epsilon} \frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K)\\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \cdot \widehat{\phi}\left( \frac{\log(q_v)}{\log(B)}\right)\left(\frac{1}{q_v} B^{5/6}+q_v^{3/2+\epsilon}B^{5/6-1/3d}\right)\\ &\ll \frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ q_v\leq B^\nu \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \left(\frac{1}{q_v} B^{5/6}+q_v^{3/2+\epsilon}B^{5/6-1/3d}\right). \end{align*} $$
By Corollary 5.1.1, we know that
![]() $\#{\mathcal E}_K(B)=\kappa B^{5/6}+O(B^{5/6-1/3d})$
. Using this and the prime ideal theorem, we have that
$\#{\mathcal E}_K(B)=\kappa B^{5/6}+O(B^{5/6-1/3d})$
. Using this and the prime ideal theorem, we have that
 $$ \begin{align} S_1(\phi,B) \ll_{\epsilon} \frac{2}{\log(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ q_v\leq B^\nu \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \left(\frac{1}{q_v}+q_v^{3/2+\epsilon}B^{-1/3d}\right) \ll\frac{1+B^{(3/2+\epsilon)\nu-1/3d}}{\log(B)}. \end{align} $$
$$ \begin{align} S_1(\phi,B) \ll_{\epsilon} \frac{2}{\log(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ q_v\leq B^\nu \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \left(\frac{1}{q_v}+q_v^{3/2+\epsilon}B^{-1/3d}\right) \ll\frac{1+B^{(3/2+\epsilon)\nu-1/3d}}{\log(B)}. \end{align} $$
By Lemma 6.3.2, we have
 $$ \begin{align*} S_2(\phi,B) &=\frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v^2} \cdot \widehat{\phi}\left(\frac{2\log(q_v)}{\log(B)}\right)\sum_{E\in{\mathcal E}_{K}(B)} \widehat{a_E}({\mathfrak p}_v^2)\\&=\frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v^2} \cdot \widehat{\phi}\left(\frac{2\log(q_v)}{\log(B)}\right)\left(-\kappa q_v B^{\frac{5}{6}}+O(q_v^{\frac{1}{2}+\epsilon}B^{\frac{5}{6}}+q_v^2 B^{\frac{5}{6}-\frac{1}{3d}})\right). \end{align*} $$
$$ \begin{align*} S_2(\phi,B) &=\frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v^2} \cdot \widehat{\phi}\left(\frac{2\log(q_v)}{\log(B)}\right)\sum_{E\in{\mathcal E}_{K}(B)} \widehat{a_E}({\mathfrak p}_v^2)\\&=\frac{2}{\log(B) \#{\mathcal E}_{K}(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v^2} \cdot \widehat{\phi}\left(\frac{2\log(q_v)}{\log(B)}\right)\left(-\kappa q_v B^{\frac{5}{6}}+O(q_v^{\frac{1}{2}+\epsilon}B^{\frac{5}{6}}+q_v^2 B^{\frac{5}{6}-\frac{1}{3d}})\right). \end{align*} $$
Assuming
![]() $\epsilon <1/4$
and using
$\epsilon <1/4$
and using
![]() $\#{\mathcal E}_K(B)=\kappa B^{5/6}+O(B^{5/6-1/3d})$
, we have
$\#{\mathcal E}_K(B)=\kappa B^{5/6}+O(B^{5/6-1/3d})$
, we have
 $$ \begin{align*} S_2(\phi,B) &=\frac{2}{\log(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v^2} \cdot \widehat{\phi}\left( \frac{2\log(q_v)}{\log(B)}\right)\left(-q_v +O(q_v^{1/2+\epsilon}+q_v^2 B^{-1/3d})\right)\\&=\frac{-2}{\log(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \cdot \widehat{\phi}\left( \frac{2\log(q_v)}{\log(B)}\right) +O\,\left(\frac{1}{\log{B}}\sum_{\substack{v\in \text{Val}_0(K) \\ q_v\leq B^{\nu/2}}}\left(\frac{1}{q_v^{3/2-\epsilon}}+\log(q_v)B^{-1/3d}\right)\right)\\ &=\frac{-1}{\log(B)} \sum_{\substack{ v\in \text{Val}_0(K) \\ q_v\leq B^{\nu/2} \\ 2\nmid q_v,\ 3\nmid q_v}} \left(\frac{\nu \log(q_v)}{2q_v} - \frac{\log(q_v)^2}{q_v\log(B)}\right) +O\,\left(\frac{1+B^{\nu/2-1/3d}}{\log(B)}\right). \end{align*} $$
$$ \begin{align*} S_2(\phi,B) &=\frac{2}{\log(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v^2} \cdot \widehat{\phi}\left( \frac{2\log(q_v)}{\log(B)}\right)\left(-q_v +O(q_v^{1/2+\epsilon}+q_v^2 B^{-1/3d})\right)\\&=\frac{-2}{\log(B)} \sum_{\substack{v\in \text{Val}_0(K) \\ 2\nmid q_v,\ 3\nmid q_v}} \frac{\log(q_v)}{q_v} \cdot \widehat{\phi}\left( \frac{2\log(q_v)}{\log(B)}\right) +O\,\left(\frac{1}{\log{B}}\sum_{\substack{v\in \text{Val}_0(K) \\ q_v\leq B^{\nu/2}}}\left(\frac{1}{q_v^{3/2-\epsilon}}+\log(q_v)B^{-1/3d}\right)\right)\\ &=\frac{-1}{\log(B)} \sum_{\substack{ v\in \text{Val}_0(K) \\ q_v\leq B^{\nu/2} \\ 2\nmid q_v,\ 3\nmid q_v}} \left(\frac{\nu \log(q_v)}{2q_v} - \frac{\log(q_v)^2}{q_v\log(B)}\right) +O\,\left(\frac{1+B^{\nu/2-1/3d}}{\log(B)}\right). \end{align*} $$
Arguments using the prime ideal theorem show that
 $$\begin{align*}\sum_{\substack{ v\in \text{Val}_0(K) \\ q_v\leq X}} \frac{\log(q_v)}{q_v}=\log(X)+O(1) \end{align*}$$
$$\begin{align*}\sum_{\substack{ v\in \text{Val}_0(K) \\ q_v\leq X}} \frac{\log(q_v)}{q_v}=\log(X)+O(1) \end{align*}$$
and
 $$\begin{align*}\sum_{\substack{ v\in \text{Val}_0(K) \\ q_v\leq X}} \frac{\log(q_v)^2}{q_v}=\frac{\log(X)^2}{2}+O(\log\log(X)). \end{align*}$$
$$\begin{align*}\sum_{\substack{ v\in \text{Val}_0(K) \\ q_v\leq X}} \frac{\log(q_v)^2}{q_v}=\frac{\log(X)^2}{2}+O(\log\log(X)). \end{align*}$$
From this, it follows that
 $$ \begin{align*} &\sum_{\substack{ v\in \text{Val}_0(K) \\ q_v\leq B^{\nu/2} \\ 2\nmid q_v,\ 3\nmid q_v}} \left(\frac{\nu \log(q_v)}{2q_v} - \frac{\log(q_v)^2}{q_v\log(B)}\right)\\& \quad = \frac{\nu}{2} \left(\log(B^{\nu/2})+O(1)\right)-\frac{1}{\log(B)}\left(\frac{\log(B^{\nu/2})^2}{2}+O(\log\log(B^{\nu/2}))\right) \\& \quad =\left(\frac{\nu^2}{4}\log(B)+O(1)\right)-\left(\frac{\nu^2}{8}\log(B)+O(1)\right)\\& \quad =\frac{\nu^2}{8}\log(B)+O(1). \end{align*} $$
$$ \begin{align*} &\sum_{\substack{ v\in \text{Val}_0(K) \\ q_v\leq B^{\nu/2} \\ 2\nmid q_v,\ 3\nmid q_v}} \left(\frac{\nu \log(q_v)}{2q_v} - \frac{\log(q_v)^2}{q_v\log(B)}\right)\\& \quad = \frac{\nu}{2} \left(\log(B^{\nu/2})+O(1)\right)-\frac{1}{\log(B)}\left(\frac{\log(B^{\nu/2})^2}{2}+O(\log\log(B^{\nu/2}))\right) \\& \quad =\left(\frac{\nu^2}{4}\log(B)+O(1)\right)-\left(\frac{\nu^2}{8}\log(B)+O(1)\right)\\& \quad =\frac{\nu^2}{8}\log(B)+O(1). \end{align*} $$
Therefore,
 $$\begin{align*}S_2(\phi,B)=\frac{-\phi(0)}{2}+O\,\left(\frac{1+B^{\nu/2-1/3d}}{\log(B)}\right). \end{align*}$$
$$\begin{align*}S_2(\phi,B)=\frac{-\phi(0)}{2}+O\,\left(\frac{1+B^{\nu/2-1/3d}}{\log(B)}\right). \end{align*}$$
Taking
![]() $\nu =(3d(3/2+\epsilon ))^{-1}$
and combining the above estimate for
$\nu =(3d(3/2+\epsilon ))^{-1}$
and combining the above estimate for
![]() $S_2$
with our bound (19) for
$S_2$
with our bound (19) for
![]() $S_1$
, we obtain
$S_1$
, we obtain
Substituting this into (15) and taking the limit superior as B goes to infinity gives the following upper bound for the average analytic rank of elliptic curves over K:
for any
![]() $0<\epsilon <1/4$
. Since the limit superior exists, and since
$0<\epsilon <1/4$
. Since the limit superior exists, and since
![]() $\epsilon $
can be taken arbitrarily small, we obtain the bound
$\epsilon $
can be taken arbitrarily small, we obtain the bound
![]() $(9d+1)/2$
.
$(9d+1)/2$
.
Acknowledgements
The author thanks Brandon Alberts, Peter Bruin, Peter Cho, Jordan Ellenberg, Ben Kane, Irati Manterola Ayala, Steven Miller, Grant Molnar, Filip Najman, Junyeong Park, John Voight and David Zureick-Brown for helpful conversations and comments on this work. Special thanks to Bryden Cais and Doug Ulmer for their encouragement throughout this project. The author is especially grateful to Keunyoung Jeong for providing thoughtful feedback and corrections. Finally, a huge thank you to the anonymous referee for thoroughly reading this article multiple times and pointing out countless corrections and suggestions that greatly improved the accuracy and readability of the article.
Competing interest
The authors have no competing interest to declare.
Funding statement
During the completion of this work, the author was supported by the National Science Foundation, via grant DMS-2303011.