Hostname: page-component-6dbcb7884d-64ff6 Total loading time: 0 Render date: 2025-02-14T07:44:42.492Z Has data issue: false hasContentIssue false
  • English
  • Français

Deligne-Beilinson cohomology of the universal K3 surface

Part of: Cycles and subschemes Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  15 August 2022

Zhiyuan Li  and
Xun Zhang
Zhiyuan Li
Affiliation:
Shanghai Center for Mathematical Sciences, Fudan University, 220 Handan Road, Shanghai, 200433 China; E-mail: zhiyuan_li@fudan.edu.cn
Xun Zhang
Affiliation:
Math Department, Fudan University, 220 Handan Road, Shanghai, 200433 China; E-mail: 18110180041@fudan.edu.cn
Get access

Abstract

O’Grady’s generalised Franchetta conjecture (GFC) is concerned with codimension 2 algebraic cycles on universal polarised K3 surfaces. In [4], this conjecture has been studied in the Betti cohomology groups. Following a suggestion of Voisin, we investigate this problem in the Deligne-Beilinson (DB) cohomology groups. In this paper, we develop the theory of Deligne-Beilinson cohomology groups on (smooth) Deligne-Mumford stacks. Using the automorphic cohomology group and Noether-Lefschetz theory, we compute the 4th DB-cohomology group of universal oriented polarised K3 surfaces with at worst an 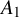$A_1$ -singularity and show that GFC for such family holds in DB-cohomology. In particular, this confirms O’Grady’s original conjecture in DB cohomology.

MSC classification

Primary: 14J28: $K3$ surfaces and Enriques surfaces
Secondary: 14C25: Algebraic cycles
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Sigma , Volume 10 , 2022 , e64
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beauville, Arnaud. A remark on the generalized Franchetta conjecture for K3 surfaces. Mathematische Zeitschrift, 2021.Google Scholar
Beauville, Arnaud and Voisin, Claire. On the Chow ring of a K3 surface. J. Algebraic Geom., 13(3):417–426, 2004.CrossRefGoogle Scholar
Behrend, Kai. Cohomology of stacks. Intersection theory and moduli, ICTP Lect. Notes, 19:249–294, 2004.Google Scholar
Bergeron, Nicolas and Li, Zhiyuan. Tautological classes on moduli spaces of hyper-Kähler manifolds. Duke Math. J., 168(7):1179–1230, 2019.CrossRefGoogle Scholar
Beĭlinson, A. A.. Higher regulators and values of L-functions . In Current problems in mathematics, Vol. 24, Itogi Nauki i Tekhniki, pages 181–238. Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1984.Google Scholar
Bloch, Spencer. Algebraic cycles and the Beĭlinson conjectures. In The Lefschetz centennial conference, Part I (Mexico City, 1984), volume 58 of Contemp. Math., pages 65–79. Amer. Math. Soc., Providence, RI, 1986.Google Scholar
Burns, Dan Jr. and Rapoport, Michael. On the Torelli problem for kählerian K-3 surfaces. Ann. Sci. École Norm. Sup. (4), 8(2):235–273, 1975.CrossRefGoogle Scholar
Debarre, Olivier. Hyperkähler manifolds. arXiv:1810.02087, 2018.Google Scholar
Deligne, P.. Théorème de Lefschetz et critères de dégénérescence de suites spectrales. Inst. Hautes Études Sci. Publ. Math., (35):259–278, 1968.CrossRefGoogle Scholar
Deligne, P.. Théorie de Hodge, III. Inst. Hautes Études Sci. Publ. Math., (44):5–78, 1974.CrossRefGoogle Scholar
Dolgachev, I. V.. Mirror symmetry for lattice polarized K3 surfaces. J. Math. Sci., 81(3):2599–2630, 1996. Algebraic geometry, 4.CrossRefGoogle Scholar
Eisenbud, David and Harris, Joe. 3264 and all that—a second course in algebraic geometry. Cambridge University Press, Cambridge, 2016.CrossRefGoogle Scholar
Esnault, Hélène and Viehweg, Eckart. Deligne-Beĭlinson cohomology. In Beĭlinson’s conjectures on special values of $L$ -functions, volume 4 of Perspect. Math., pages 43–91. Academic Press, Boston, MA, 1988.Google Scholar
Lie, Fu and Robert Laterveer. Special cubic fourfolds, K3 surfaces and the Franchetta property. arXiv:2112.02437, 2021.Google Scholar
Lie, Fu, Robert Laterveer, and Charles Vial. The generalized Franchetta conjecture for some hyper-Kähler varieties. J. Math. Pures Appl. (9), 130:1–35, 2019. With an appendix by the authors and Mingmin Shen. Google Scholar
Lie, Fu, Laterveer, Robert, and Vial, Charles. The generalized Franchetta conjecture for some hyper-Kähler varieties, II. J. Éc. polytech. Math., 8:1065–1097, 2021.Google Scholar
Fulton, William. Intersection Theory. Springer, New York, NY, second edition, 1998.CrossRefGoogle Scholar
Gillet, Henri. Intersection theory on algebraic stacks and $Q$ -varieties. In Proceedings of the Luminy conference on algebraic $K$ -theory (Luminy, 1983), volume 34, pages 193–240, 1984.CrossRefGoogle Scholar
Gritsenko, V., Hulek, K., and Sankaran, G. K.. Moduli spaces of irreducible symplectic manifolds. Compos. Math., 146(2):404–434, 2010.CrossRefGoogle Scholar
Gritsenko, V.A., Hulek, Klaus, and Sankaran, G.K.. The Kodaira dimension of the moduli of K3 surfaces. Inventiones Mathematicae, 169:519–567, 01 2007.CrossRefGoogle Scholar
Huybrechts, Daniel. A global Torelli theorem for hyperkähler manifolds [after M. Verbitsky]. Astérisque, (348):Exp. No. 1040, x, 375–403, 2012. Séminaire Bourbaki: Vol. 2010/2011. Exposés 1027–1042.Google Scholar
Jannsen, Uwe. Deligne homology, Hodge-D-conjecture and motives, Beılinson’s conjectures on special values of L-functions, 305–372. Perspec. Math, 4, 1988.Google Scholar
Joshua, Roy. Higher intersection theory on algebraic stacks. I. $K$ -Theory, 27(2):133–195, 2002.CrossRefGoogle Scholar
Kazarian, Maxim. Multisingularities, cobordisms, and enumerative geometry. Russian Mathematical Surveys, 58(4):665–724, 2003.CrossRefGoogle Scholar
Kazarian, Maxim. Thom polynomials for Lagrange, Legendre, and critical point function singularities. Proceedings of The London Mathematical Society, 86(3):707–734, 2003.CrossRefGoogle Scholar
Kohrita, Tohru. Deligne-Beilinson cycle maps for Lichtenbaum cohomology. Homology Homotopy Appl., 21(1):187–212, 2019.CrossRefGoogle Scholar
Kudla, Stephen S.. Algebraic cycles on Shimura varieties of orthogonal type. Duke Math. J., 86(1):39–78, 1997.CrossRefGoogle Scholar
Laterveer, Robert. The generalized Franchetta conjecture for some hyperkähler fourfolds. Publ. Res. Inst. Math. Sci., 55(4):859–893, 2019.CrossRefGoogle Scholar
Laumon, G. and Moret-Bailly, L.. Champs alébriques, volume 39 of Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern Surveys in Mathematics. Springer-Verlag Berlin Heidelberg, 2000.CrossRefGoogle Scholar
Laza, Radu and O’Grady, Kieran. Birational geometry of the moduli space of quartic K3 surfaces. Compositio Mathematica, 155(9):1655–1710, 2019.CrossRefGoogle Scholar
Matsusaka, T. and Mumford, D.. Two fundamental theorems on deformations of polarized varieties. Amer. J. Math., 86:668–684, 1964.CrossRefGoogle Scholar
Maulik, Davesh and Pandharipande, Rahul. Gromov-Witten theory and Noether-Lefschetz theory. In A celebration of algebraic geometry, volume 18 of Clay Math. Proc., pages 469–507. Amer. Math. Soc., Providence, RI, 2013.Google Scholar
Mazza, Carlo, Voevodsky, Vladimir, and Weibel, Charles. Lecture notes on motivic cohomology, volume 2 of Clay Mathematics Monographs. American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA, 2006.Google Scholar
Miranda, Rick. The moduli of Weierstrass fibrations over ${\mathsf{P}}^1$ . Math. Ann., 255(3):379–394, 1981.CrossRefGoogle Scholar
Miranda, Rick. The basic theory of elliptic surfaces, volume 1 of Pubblicazioni del Dipartimento di matematica dell’Universita’ di Pisa. ETS Editrice Pisa, 1989.Google Scholar
Nikulin, V. V.. Integer symmetric bilinear forms and some of their geometric applications. Izv. Akad. Nauk SSSR Ser. Mat., 43(1):111–177, 238, 1979.Google Scholar
Oberdieck, Georg and Pixton, Aaron. Holomorphic anomaly equations and the Igusa cusp form conjecture. Invent. Math., 213(2):507–587, 2018.CrossRefGoogle Scholar
Odaka, Yuji and Oshima, Yoshiki. Collapsing K3 surfaces, tropical geometry and moduli compactifications of Satake, Morgan-Shalen type, volume 40 of MSJ Memoirs. Mathematical Society of Japan, Tokyo, 2021.CrossRefGoogle Scholar
O’Grady, Kieran G.. Moduli of sheaves and the Chow group of $K3$ surfaces. J. Math. Pures Appl. (9), 100(5):701–718, 2013.CrossRefGoogle Scholar
Olsson, Martin. Algebraic spaces and stacks, volume 62 of Colloquium Publications. American Mathematical Society, 2016.Google Scholar
Pavic, N., Shen, J., and Yin, Q.. On O’Grady’s generalized Franchetta conjecture. ArXiv e-prints, April 2016.CrossRefGoogle Scholar
Vistoli, Angelo. Intersection theory on algebraic stacks and on their moduli spaces. Invent. Math., 97(3):613–670, 1989.CrossRefGoogle Scholar
Voisin, Claire. Hodge theory and complex algebraic geometry. II, volume 77 of Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge, English edition, 2007. Translated from the French by Schneps, Leila.Google Scholar