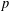Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-11T08:56:58.870Z Has data issue: false hasContentIssue false
  • English
  • Français

$p$-ADIC 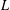$L$-FUNCTIONS FOR UNITARY GROUPS

Part of: Arithmetic problems. Diophantine geometry Algebraic number theory: global fields Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  06 May 2020

ELLEN EISCHEN ,
MICHAEL HARRIS ,
JIANSHU LI  and
CHRISTOPHER SKINNER
ELLEN EISCHEN
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403, USA; eeischen@uoregon.edu
MICHAEL HARRIS
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, USA; harris@math.columbia.edu
JIANSHU LI
Affiliation:
Institute for Advanced Study in Mathematics, Zhejiang University, Hangzhou, China; matom@ust.hk, jianshu@sjtu.edu.cn
CHRISTOPHER SKINNER
Affiliation:
Department of Mathematics, Princeton University, Fine Hall, Washington Road, Princeton, NJ 08544-1000, USA; cmcls@math.princeton.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

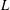This paper completes the construction of $p$-adic $L$-functions for unitary groups. More precisely, in Harris, Li and Skinner [‘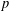$p$-adic 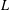$L$-functions for unitary Shimura varieties. I. Construction of the Eisenstein measure’, Doc. Math.Extra Vol. (2006), 393–464 (electronic)], three of the authors proposed an approach to constructing such 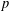$p$-adic 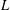$L$-functions (Part I). Building on more recent results, including the first named author’s construction of Eisenstein measures and 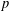$p$-adic differential operators [Eischen, ‘A $p$-adic Eisenstein measure for unitary groups’, J. Reine Angew. Math.699 (2015), 111–142; ‘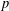$p$-adic differential operators on automorphic forms on unitary groups’, Ann. Inst. Fourier (Grenoble)62(1) (2012), 177–243], Part II of the present paper provides the calculations of local $\unicode[STIX]{x1D701}$-integrals occurring in the Euler product (including at 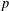$p$). Part III of the present paper develops the formalism needed to pair Eisenstein measures with Hida families in the setting of the doubling method.

MSC classification

Primary: 11F85: $p$-adic theory, local fields 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture) 11F55: Other groups and their modular and automorphic forms (several variables)
Secondary: 11R23: Iwasawa theory 14G35: Modular and Shimura varieties 11G10: Abelian varieties of dimension $> 1$ 11F03: Modular and automorphic functions
Type
Number Theory
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e9
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Blasius, D., Harris, M. and Ramakrishnan, D., ‘Coherent cohomology, limits of discrete series, and Galois conjugation’, Duke Math. J. 73(3) (1994), 647–685.CrossRefGoogle Scholar
Caraiani, A., Eischen, E., Fintzen, J., Mantovan, E. and Varma, I., ‘p-adic q-expansion principles on unitary shimura varieties’, inDirections in Number Theory, Vol. 3 (Springer, Cham, 2016), 197–243.CrossRefGoogle Scholar
Casselman, W., ‘Introduction to the theory of admissible representations of $p$-adic reductive groups’, Unpublished manuscript, 1995, https://www.math.ubc.ca/∼cass/research/pdf/p-adic-book.pdf.Google Scholar
Chai, C.-L., Conrad, B. and Oort, F., Complex Multiplication and Lifting Problems, Mathematical Surveys and Monographs, 195 (American Mathematical Society, Providence, RI, 2014).Google Scholar
Chenevier, G., ‘Familles p-adiques de formes automorphes pour GLn’, J. Reine Angew. Math. 570 (2004), 143–217.Google Scholar
Clozel, L., Harris, M. and Taylor, R., ‘Automorphy for some l-adic lifts of automorphic mod l Galois representations’, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181. With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras.CrossRefGoogle Scholar
Coates, J., ‘On p-adic L-functions attached to motives over Q . II’, Bol. Soc. Brasil. Mat. (N.S.) 20(1) (1989), 101–112.CrossRefGoogle Scholar
Coates, J. and Perrin-Riou, B., ‘On p-adic L-functions attached to motives over Q’, inAlgebraic Number Theory, Advanced Studies in Pure Mathematics, 17 (Academic Press, Boston, MA, 1989), 23–54.Google Scholar
Deligne, P., ‘Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques’, inAutomorphic Forms, Representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proceedings of Symposia in Pure Mathematics, XXXIII (American Mathematical Society, Providence, RI, 1979), 247–289.Google Scholar
Eischen, E., Fintzen, J., Mantovan, E. and Varma, I., ‘Differential operators and families of automorphic forms on unitary groups of arbitrary signature’, Doc. Math. 23 (2018), 445–495.Google Scholar
Eischen, E. E., ‘p-adic differential operators on automorphic forms on unitary groups’, Ann. Inst. Fourier (Grenoble) 62(1) (2012), 177–243.CrossRefGoogle Scholar
Eischen, E., ‘A p-adic Eisenstein measure for vector-weight automorphic forms’, Algebra Number Theory 8(10) (2014), 2433–2469.CrossRefGoogle Scholar
Eischen, E. E., ‘A p-adic Eisenstein measure for unitary groups’, J. Reine Angew. Math. 699 (2015), 111–142.Google Scholar
Eischen, E. E., ‘Differential operators, pullbacks, and families of automorphic forms on unitary groups’, Ann. Math. Qué. 40(1) (2016), 55–82.CrossRefGoogle Scholar
Eischen, E. and Mantovan, E., ‘p-adic families of automorphic forms in the 𝜇-ordinary setting’, Amer. J. Math. (2019), Accepted for publication.Google Scholar
Garrett, P. B., ‘Pullbacks of Eisenstein series; applications’, inAutomorphic Forms of Several Variables (Katata, 1983), Progress in Mathematics, 46 (Birkhäuser Boston, Boston, MA, 1984), 114–137.Google Scholar
Garrett, P., ‘Values of Archimedean zeta integrals for unitary groups’, inEisenstein Series and Applications, Progress in Mathematics, 258 (Birkhäuser, Boston, Boston, MA, 2008), 125–148.CrossRefGoogle Scholar
Gelbart, S., Piatetski-Shapiro, I. and Rallis, S., Explicit Constructions of Automorphic L-functions, Lecture Notes in Mathematics, 1254 (Springer, Berlin, 1987).CrossRefGoogle Scholar
Goodman, R. and Wallach, N. R., Symmetry, Representations, and Invariants, Graduate Texts in Mathematics, 255 (Springer, Dordrecht, 2009).CrossRefGoogle Scholar
Harris, M., ‘Arithmetic vector bundles and automorphic forms on Shimura varieties. II’, Compositio Math. 60(3) (1986), 323–378.Google Scholar
Harris, M., ‘Functorial properties of toroidal compactifications of locally symmetric varieties’, Proc. Lond. Math. Soc. (3) 59(1) (1989), 1–22.CrossRefGoogle Scholar
Harris, M., ‘Automorphic forms of ∂ -cohomology type as coherent cohomology classes’, J. Differential Geom. 32(1) (1990), 1–63.CrossRefGoogle Scholar
Harris, M., ‘L-functions and periods of polarized regular motives’, J. Reine Angew. Math. 483 (1997), 75–161.Google Scholar
Harris, M., ‘A simple proof of rationality of Siegel–Weil Eisenstein series’, inEisenstein Series and Applications, Progress in Mathematics, 258 (Birkhäuser, Boston, MA, 2008), 149–185.CrossRefGoogle Scholar
Harris, M., ‘Beilinson–Bernstein localization over ℚ and periods of automorphic forms’, Int. Math. Res. Not. IMRN 9 (2013), 2000–2053.CrossRefGoogle Scholar
Harris, M., ‘The Taylor–Wiles method for coherent cohomology’, J. Reine Angew. Math. 679 (2013), 125–153.CrossRefGoogle Scholar
Harris, M., Kudla, S. S. and Sweet, W. J., ‘Theta dichotomy for unitary groups’, J. Amer. Math. Soc. 9(4) (1996), 941–1004.CrossRefGoogle Scholar
Harris, M., Li, J.-S. and Skinner, C. M., ‘The Rallis inner product formula and p-adic L-functions’, inAutomorphic Representations, L-functions and Applications: Progress and Prospects, Ohio State Univ. Math. Res. Inst. Publ., 11 (de Gruyter, Berlin, 2005), 225–255.Google Scholar
Harris, M., Li, J.-S. and Skinner, C. M., ‘p-adic L-functions for unitary Shimura varieties. I. Construction of the Eisenstein Measure’, Doc. Math. Extra Vol. (2006), 393–464 (electronic).Google Scholar
Hida, H., ‘A p-adic measure attached to the zeta functions associated with two elliptic modular forms. II’, Ann. Inst. Fourier (Grenoble) 38(3) (1988), 1–83.CrossRefGoogle Scholar
Hida, H., ‘On the search of genuine p-adic modular L-functions for GL(n)’, Mém. Soc. Math. Fr. (N.S.) 67 (1996), vi+110, With a correction to: ‘On $p$-adic $L$-functions of $\text{GL}(2)\times \text{GL}(2)$ over totally real fields’ Ann. Inst. Fourier (Grenoble) 41(2) (1991), 311–391.Google Scholar
Hida, H., ‘Automorphic induction and Leopoldt type conjectures for GL(n)’, Asian J. Math. 2(4) (1998), 667–710. Mikio Sato: a great Japanese mathematician of the twentieth century.CrossRefGoogle Scholar
Hida, H., ‘Control theorems of coherent sheaves on Shimura varieties of PEL type’, J. Inst. Math. Jussieu 1(1) (2002), 1–76.CrossRefGoogle Scholar
Hida, H., p-adic Automorphic Forms on Shimura Varieties, Springer Monographs in Mathematics (Springer, New York, 2004).CrossRefGoogle Scholar
Jacquet, H., ‘Principal L-functions of the linear group’, inAutomorphic Forms, Representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proceedings of Symposia in Applied Mathematics, XXXIII (American Mathematical Society, Providence, RI, 1979), 63–86.Google Scholar
Kaletha, T., Minguez, A., Shin, S. W. and White, P.-J., ‘Endoscopic classification of representations: Inner forms of unitary groups’, Preprint, 2014,arXiv:1409.3731.pdf.Google Scholar
Katz, N. M., ‘p-adic L-functions for CM fields’, Invent. Math. 49(3) (1978), 199–297.CrossRefGoogle Scholar
Kottwitz, R. E., ‘Points on some Shimura varieties over finite fields’, J. Amer. Math. Soc. 5(2) (1992), 373–444.CrossRefGoogle Scholar
Labesse, J.-P., ‘Changement de base CM et séries discrètes’, inOn the Stabilization of the Trace Formula, Stab. Trace Formula Shimura Var. Arith. Appl., 1 (Int. Press, Somerville, MA, 2011), 429–470.Google Scholar
Lan, K.-W., ‘Comparison between analytic and algebraic constructions of toroidal compactifications of PEL-type Shimura varieties’, J. Reine Angew. Math. 664 (2012), 163–228.Google Scholar
Lan, K.-W., Arithmetic Compactifications of PEL-type Shimura Varieties, London Mathematical Society Monographs, 36 (Princeton University Press, Princeton, NJ, 2013).Google Scholar
Lan, K.-W., ‘Higher Koecher’s principle’, Math. Res. Lett. 23(1) (2016), 163–199.CrossRefGoogle Scholar
Lan, K.-W., ‘Integral models of toroidal compactifications with projective cone decompositions’, Int. Math. Res. Not. IMRN 11 (2017), 3237–3280.Google Scholar
Lan, K.-W., Compactifications of PEL-type Shimura Varieties and Kuga Families with Ordinary Loci, (World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2018).Google Scholar
Lan, K.-W. and Suh, J., ‘Vanishing theorems for torsion automorphic sheaves on general PEL-type Shimura varieties’, Adv. Math. 242 (2013), 228–286.CrossRefGoogle Scholar
Li, J.-S., ‘Nonvanishing theorems for the cohomology of certain arithmetic quotients’, J. Reine Angew. Math. 428 (1992), 177–217.Google Scholar
Liu, Z., ‘The doubling Archimedean zeta integrals for p-adic interpolation’, Math. Res. Lett. (2019), Accepted for publication. Preprint available at arXiv:1904.07121.Google Scholar
Liu, Z., ‘p-adic L-functions for ordinary families on symplectic groups’, J. Inst. Math. Jussieu (2019), 1–61.Google Scholar
Mœglin, C., Vignéras, M.-F. and Waldspurger, J.-L., Correspondances de Howe sur un corps p-adique, Lecture Notes in Mathematics, 1291 (Springer, Berlin, 1987).CrossRefGoogle Scholar
Mok, C. P., ‘Endoscopic classification of representations of quasi-split unitary groups’, Mem. Amer. Math. Soc. 235(1108) (2015), vi+248.Google Scholar
Moonen, B., ‘Serre–Tate theory for moduli spaces of PEL type’, Ann. Sci. Éc. Norm. Supér. (4) 37(2) (2004), 223–269.CrossRefGoogle Scholar
Panchishkin, A. A., ‘Motives over totally real fields and p-adic L-functions’, Ann. Inst. Fourier (Grenoble) 44(4) (1994), 989–1023.CrossRefGoogle Scholar
Pilloni, V., ‘Prolongement analytique sur les variétés de Siegel’, Duke Math. J. 157(1) (2011), 167–222.CrossRefGoogle Scholar
Shimura, G., Euler Products and Eisenstein Series, CBMS Regional Conference Series in Mathematics, 93 (Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1997).CrossRefGoogle Scholar
Shimura, G., Arithmeticity in the Theory of Automorphic Forms, Mathematical Surveys and Monographs, 82 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Skinner, C. and Urban, E., ‘Sur les déformations p-adiques des formes de Saito–Kurokawa’, C. R. Math. Acad. Sci. Paris 335(7) (2002), 581–586.CrossRefGoogle Scholar
Skinner, C. and Urban, E., ‘The Iwasawa main conjectures for GL2’, Invent. Math. 195(1) (2014), 1–277.CrossRefGoogle Scholar
Wan, X., ‘Families of nearly ordinary Eisenstein series on unitary groups’, Algebra Number Theory 9(9) (2015), 1955–2054. With an appendix by Kai-Wen Lan.CrossRefGoogle Scholar
Wedhorn, T., ‘Ordinariness in good reductions of Shimura varieties of PEL-type’, Ann. Sci. Éc. Norm. Supér. (4) 32(5) (1999), 575–618.CrossRefGoogle Scholar