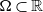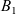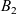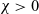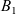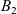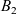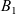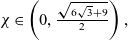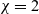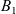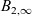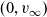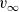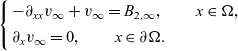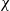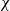1 Introduction
Driven by the need to understand the spatio-temporal dynamics of crime hotspots, which are regions in space that have a disproportionately high level of crime, Short and collaborators introduced a reaction–advection–diffusion system to describe the evolution of urban crime in [Reference Short, D’Orsogna, Pasour, Tita, Brantingham, Bertozzi and Chayes40]. When posed in spatial one-dimensional domains
![]() $\Omega$
, this system read
$\Omega$
, this system read
 \begin{equation} \left\{ \begin{array}{ll} u_t = u_{xx} - \chi \big(\frac{u}{v} v_x\big)_x - uv +B_1(x,t), \qquad & x\in \Omega, \ t>0, \\[1mm] v_t = v_{xx} +uv - v + B_2(x,t), \qquad & x\in \Omega, \ t>0, \end{array} \right.\end{equation}
\begin{equation} \left\{ \begin{array}{ll} u_t = u_{xx} - \chi \big(\frac{u}{v} v_x\big)_x - uv +B_1(x,t), \qquad & x\in \Omega, \ t>0, \\[1mm] v_t = v_{xx} +uv - v + B_2(x,t), \qquad & x\in \Omega, \ t>0, \end{array} \right.\end{equation}
with the parameter
![]() $\chi$
fixed as:
$\chi$
fixed as:
and with given source functions
![]() $B_1$
and
$B_1$
and
![]() $B_2$
. In (1.1), u(x,t) represents the density of criminal agents and v(x,t) the attractiveness value, which provides a measure of how susceptible a certain location x is to crime at time t. System (1.1) was derived from an agent-based model rooted on the assumption of ‘routine activity theory’, a criminology theory stating that opportunity is the most important factor leading to crime [Reference Cohen and Felson11, Reference Felson14]. The system models two sociological effects: the ‘repeat and near-repeat victimization’ effect and the ‘broken-windows theory’. The former has been observed in residential burglary data and alludes to the fact that the burglarisation of a house increases the probability of that same house, as well as neighbouring houses, to be burgled again within a short period of time following the original burglary [Reference Johnson, Bowers and Hirschfield21, Reference Short, D’Orsogna, Brantingham and Tita39]. The latter is the theory that, in a sense, crime is self-exciting – crime tends to lead to more crime [Reference Kelling and Wilson23].
$B_2$
. In (1.1), u(x,t) represents the density of criminal agents and v(x,t) the attractiveness value, which provides a measure of how susceptible a certain location x is to crime at time t. System (1.1) was derived from an agent-based model rooted on the assumption of ‘routine activity theory’, a criminology theory stating that opportunity is the most important factor leading to crime [Reference Cohen and Felson11, Reference Felson14]. The system models two sociological effects: the ‘repeat and near-repeat victimization’ effect and the ‘broken-windows theory’. The former has been observed in residential burglary data and alludes to the fact that the burglarisation of a house increases the probability of that same house, as well as neighbouring houses, to be burgled again within a short period of time following the original burglary [Reference Johnson, Bowers and Hirschfield21, Reference Short, D’Orsogna, Brantingham and Tita39]. The latter is the theory that, in a sense, crime is self-exciting – crime tends to lead to more crime [Reference Kelling and Wilson23].
From the first equation in (1.1), we see that criminal agents move according to a combination of conditional and unconditional diffusion. The conditional diffusion is a biased movement towards high concentrations of the attractiveness value, which leads to the taxis term seen in the first equation. We stress that the coefficient
![]() $\chi = 2$
in front of the taxis term, which we shall see adds a challenge, comes from the first principles derivation of system (1.1) and thus it is important that our theory cover this case – see [Reference Short, D’Orsogna, Pasour, Tita, Brantingham, Bertozzi and Chayes40] for more details. The assumption that criminal agents abstain from committing the second crime leads to decay term
$\chi = 2$
in front of the taxis term, which we shall see adds a challenge, comes from the first principles derivation of system (1.1) and thus it is important that our theory cover this case – see [Reference Short, D’Orsogna, Pasour, Tita, Brantingham, Bertozzi and Chayes40] for more details. The assumption that criminal agents abstain from committing the second crime leads to decay term
![]() $-uv.$
Indeed, roughly speaking, the expected number of crime is given by uv and so the expected number of criminal agents removed is uv. The prescribed non-negative term
$-uv.$
Indeed, roughly speaking, the expected number of crime is given by uv and so the expected number of criminal agents removed is uv. The prescribed non-negative term
![]() $B_1(x)$
describes the introduction of criminal agents into the system. Furthermore, the repeat victimisation effect assumes that each criminal activity increases the attractiveness value leading to the
$B_1(x)$
describes the introduction of criminal agents into the system. Furthermore, the repeat victimisation effect assumes that each criminal activity increases the attractiveness value leading to the
![]() $+uv$
term in the second equation of (1.1), while the near-repeat victimisation effect leads to the unconditional diffusion also observed in that equation. Finally, the assumption that certain neighbourhoods tend to be more crime-prone than others, whatever these reasons may be, is included in the prescribed non-negative term
$+uv$
term in the second equation of (1.1), while the near-repeat victimisation effect leads to the unconditional diffusion also observed in that equation. Finally, the assumption that certain neighbourhoods tend to be more crime-prone than others, whatever these reasons may be, is included in the prescribed non-negative term
![]() $B_2(x).$
$B_2(x).$
The introduction of system (1.1) has generated a great deal of activity related to the analysis of (1.1), which have contributed to the mathematical theory as well as to the understanding of crime dynamics. For example, the emergence and suppression of hotspots was studied by Short et al. in [Reference Short, Bertozzi and Brantingham38], providing insight into the effectiveness of hotspot policing. The existence and stability of localised patterns representing hotspots has been studied in various works – see [Reference Berestycki, Wei and Winter7, Reference Cantrell, Cosner and Manásevich9, Reference Gu, Wang and Guangzeng16, Reference Kolokolnikiv, Ward and Wei24, Reference Tse and Ward46]. A more general class of systems was proposed for the dynamics of criminal activity by Berestycki and Nadal in [Reference Berestycki and Nadal5] – see also [Reference Berestycki, Rodríguez and Ryzhik6] for an analysis of these models. The system (1.1) has also been generalised in various directions. For example, the incorporation of law enforcement has been proposed and analysed in [Reference Jones, Brantingham and Chayes22, Reference Ricketson33, Reference Zipkin, Short and Bertozzi56]; the movement of commuter criminal agents was modelled in [Reference Chaturapruek, Breslau, Yazidi, Kolokolnikiv and McCalla10] through the use of LÉvy flights. The dynamics of crime has also be studied with the use of dynamics systems, we refer the readers to [Reference McMillon, Simon and Morenoff28, Reference Nuño, Herrero and Primicerio31]. It is also important to note that the work in [Reference Short, D’Orsogna, Pasour, Tita, Brantingham, Bertozzi and Chayes40] has been the impetus for the use of PDE-type models to gain insight into various other social phenomena – see for example [Reference Barbaro, Chayes and D’Orsogna3, Reference Rodríguez and Ryzhik36, Reference Smith, Bertozzi, Brantingham, Tita and Valasik41]. Interested readers are referred to the comprehensive review of mathematical models and theory for criminal activity in [Reference D’Orsogna and Perc12].
From a perspective of mathematical analysis, (1.1) shares essential ingredients with the celebrated Keller–Segel model for chemotaxis processes in biology, which in its simplest form can be obtained on considering the constant sensitivity function
![]() $S\equiv 1$
in
$S\equiv 1$
in
 \begin{equation} \left\{ \begin{array}{ll} u_t = \Delta u - \nabla \cdot (uS(v)\nabla v), \qquad & \;\;\;\;\;\;x\in \Omega, \ t>0, \\[1mm] v_t = \Delta v - v + u, \qquad & \;\;\;\;\;\;x\in \Omega, \ t>0. \end{array} \right.\end{equation}
\begin{equation} \left\{ \begin{array}{ll} u_t = \Delta u - \nabla \cdot (uS(v)\nabla v), \qquad & \;\;\;\;\;\;x\in \Omega, \ t>0, \\[1mm] v_t = \Delta v - v + u, \qquad & \;\;\;\;\;\;x\in \Omega, \ t>0. \end{array} \right.\end{equation}
Here, the interplay of such cross-diffusive terms with the linear production mechanism expressed in the second equation is known to have a strongly destabilising potential in multi-dimensional situations: when posed under no-flux boundary conditions in bounded domains
![]() $\Omega\subset\mathbb{R}^n$
,
$\Omega\subset\mathbb{R}^n$
,
![]() $n\ge 1$
, (1.3) is globally well posed in the case
$n\ge 1$
, (1.3) is globally well posed in the case
![]() $n=1$
([Reference Osaki and Yagi32]), whereas some solutions may blow up in finite time when either
$n=1$
([Reference Osaki and Yagi32]), whereas some solutions may blow up in finite time when either
![]() $n= 2$
and the conserved quantity
$n= 2$
and the conserved quantity
![]() $\int_\Omega u(\cdot,t)$
is suitably large ([Reference Herrero and VelÁzquez18]), or when
$\int_\Omega u(\cdot,t)$
is suitably large ([Reference Herrero and VelÁzquez18]), or when
![]() $n\ge 3$
([Reference Winkler52]; cf. also the surveys [Reference Bellomo, Bellouquid, Tao and Winkler4, Reference Nagai and Senaba30]).
$n\ge 3$
([Reference Winkler52]; cf. also the surveys [Reference Bellomo, Bellouquid, Tao and Winkler4, Reference Nagai and Senaba30]).
That, in contrast to this, decaying sensitivities may exert a substantial regularising effect is indicated by the fact that if, for example,
![]() $S(v)=\frac{a}{(1+bv)^\alpha}$
for all
$S(v)=\frac{a}{(1+bv)^\alpha}$
for all
![]() $v\ge 0$
and some
$v\ge 0$
and some
![]() $a>0$
,
$a>0$
,
![]() $b>0$
and
$b>0$
and
![]() $\alpha>1$
, then actually for arbitrary
$\alpha>1$
, then actually for arbitrary
![]() $n\ge 1$
global bounded solutions to (1.3) always exist ([Reference Winkler49]). However, in the particular case of the so-called logarithmic sensitivity given by
$n\ge 1$
global bounded solutions to (1.3) always exist ([Reference Winkler49]). However, in the particular case of the so-called logarithmic sensitivity given by
![]() $S(v)=\frac{\chi}{v}$
for
$S(v)=\frac{\chi}{v}$
for
![]() $v>0$
with
$v>0$
with
![]() $\chi>0$
, as present in (1.1), the situation seems less clear in that global bounded solutions so far have been constructed only under smallness conditions of the form
$\chi>0$
, as present in (1.1), the situation seems less clear in that global bounded solutions so far have been constructed only under smallness conditions of the form
![]() $\chi<\sqrt{\frac{2}{n}}$
([Reference Biler8, Reference Winkler51]), with a slight extension up to the weaker condition
$\chi<\sqrt{\frac{2}{n}}$
([Reference Biler8, Reference Winkler51]), with a slight extension up to the weaker condition
![]() $\chi<\chi_0$
with some
$\chi<\chi_0$
with some
![]() $\chi_0\in (1.015,2)$
possible when
$\chi_0\in (1.015,2)$
possible when
![]() $n=2$
([Reference Lankeit25]); for larger values of
$n=2$
([Reference Lankeit25]); for larger values of
![]() $\chi$
including the choice in (1.2), in the case
$\chi$
including the choice in (1.2), in the case
![]() $n\ge 2$
only certain global weak solutions to (1.3), possibly becoming unbounded in finite time, are known to exist in various generalised frameworks ([Reference Lankeit and Winkler26, Reference Stinner and Winkler42, Reference Winkler51]), and even some examples of exploding solutions have been found to exist ([Reference Nagai and Senaba29]).
$n\ge 2$
only certain global weak solutions to (1.3), possibly becoming unbounded in finite time, are known to exist in various generalised frameworks ([Reference Lankeit and Winkler26, Reference Stinner and Winkler42, Reference Winkler51]), and even some examples of exploding solutions have been found to exist ([Reference Nagai and Senaba29]).
With regard to issues of regularity and boundedness, the situation in (1.1) seems yet more delicate than in the latter version of (1.3): In (1.1), namely, the production of the attractiveness value occurs in a non-linear manner, which in comparison to (1.3) may further stimulate the self-enhanced generation of large cross-diffusive gradients, and it seems far from obvious to which extent such mechanisms can be compensated by the supplementary absorptive term
![]() $-uv$
in the first equation of (1.1). Accordingly, the literature on initial-value problems for (1.1) is still at an early stage and limited to first finding on local existence and uniqueness achieved in [Reference Rodríguez and Bertozzi35], and some results on global solvability either addressing certain modified versions which contain additional regularising ingredients ([Reference Manásevich, Phan and Souplet27, Reference Rodríguez34, Reference Rodrguez and Winkler37]), or restricted to constant parameter functions
$-uv$
in the first equation of (1.1). Accordingly, the literature on initial-value problems for (1.1) is still at an early stage and limited to first finding on local existence and uniqueness achieved in [Reference Rodríguez and Bertozzi35], and some results on global solvability either addressing certain modified versions which contain additional regularising ingredients ([Reference Manásevich, Phan and Souplet27, Reference Rodríguez34, Reference Rodrguez and Winkler37]), or restricted to constant parameter functions
![]() $B_1$
and
$B_1$
and
![]() $B_2$
([Reference Wang, Wang and Feng47]). Statements on global existence in the fully general model (1.1) have been obtained only under appropriate smallness conditions on the initial data in two-dimensional boundary value problems ([Reference Ahn, Kang and Lee1, Reference Tao and Winkler45]) or operate in frameworks of radially symmetric but possibly unbounded renormalised solutions ([Reference Winkler55]).
$B_2$
([Reference Wang, Wang and Feng47]). Statements on global existence in the fully general model (1.1) have been obtained only under appropriate smallness conditions on the initial data in two-dimensional boundary value problems ([Reference Ahn, Kang and Lee1, Reference Tao and Winkler45]) or operate in frameworks of radially symmetric but possibly unbounded renormalised solutions ([Reference Winkler55]).
Main results. In the present work, we attempt to undertake the first step into a qualitative theory for the full original model from [Reference Short, D’Orsogna, Pasour, Tita, Brantingham, Bertozzi and Chayes40] by developing an approach capable of analysing the spatially one-dimensional system (1.1) in a range of parameters including the choice given in (1.2). Here, we will first concentrate be on establishing a result on global existence of classical solutions under mild assumptions on
![]() $\chi$
,
$\chi$
,
![]() $B_1$
and
$B_1$
and
![]() $B_2$
. Our second focus will be on the derivation of qualitative solution properties under additional assumptions.
$B_2$
. Our second focus will be on the derivation of qualitative solution properties under additional assumptions.
In order to specify the set-up for our analysis, for a given parameter
![]() $\chi>0$
, let us consider (1.1) along with the boundary conditions:
$\chi>0$
, let us consider (1.1) along with the boundary conditions:
and the initial conditions:
in a bounded open interval
![]() $\Omega\subset \mathbb{R}$
. We assume throughout the sequel that
$\Omega\subset \mathbb{R}$
. We assume throughout the sequel that
and that
 \begin{equation} \left\{ \begin{array}{ll} u_0\in C^0(\overline{\Omega}),& \quad \mbox{with } u_0\ge 0 \mbox{ in } \Omega, \\[1mm] v_0\in W^{1,\infty}(\Omega),& \quad \mbox{with } v_0> 0 \mbox{ in } \overline{\Omega}. \end{array} \right.\end{equation}
\begin{equation} \left\{ \begin{array}{ll} u_0\in C^0(\overline{\Omega}),& \quad \mbox{with } u_0\ge 0 \mbox{ in } \Omega, \\[1mm] v_0\in W^{1,\infty}(\Omega),& \quad \mbox{with } v_0> 0 \mbox{ in } \overline{\Omega}. \end{array} \right.\end{equation}
In this general framework, we shall see that in fact for arbitrary
![]() $\chi>0$
, the problem (1.1), (1.4), (1.5) is globally well posed in the following sense.
$\chi>0$
, the problem (1.1), (1.4), (1.5) is globally well posed in the following sense.
Theorem 1.1 Let
![]() $\chi>0$
and suppose that
$\chi>0$
and suppose that
![]() $B_1$
and
$B_1$
and
![]() $B_2$
satisfy (1.6). Then for any choice of
$B_2$
satisfy (1.6). Then for any choice of
![]() $u_0$
and
$u_0$
and
![]() $v_0$
fulfilling (1.7), the problems (1.1), (1.4), (1.5) possess a global classical solution, for each
$v_0$
fulfilling (1.7), the problems (1.1), (1.4), (1.5) possess a global classical solution, for each
![]() $r>1$
uniquely determined by the inclusions:
$r>1$
uniquely determined by the inclusions:
 \begin{equation} \left\{ \begin{array}{l} u\in C^0(\overline{\Omega}\times [0,\infty)) \cap C^{2,1}(\overline{\Omega}\times (0,\infty)), \\[1mm] v\in C^0([0,\infty);W^{1,r}(\Omega)) \cap C^{2,1}(\overline{\Omega}\times (0,\infty)), \end{array} \right. \end{equation}
\begin{equation} \left\{ \begin{array}{l} u\in C^0(\overline{\Omega}\times [0,\infty)) \cap C^{2,1}(\overline{\Omega}\times (0,\infty)), \\[1mm] v\in C^0([0,\infty);W^{1,r}(\Omega)) \cap C^{2,1}(\overline{\Omega}\times (0,\infty)), \end{array} \right. \end{equation}
for which
![]() $u,v>0$
in
$u,v>0$
in
![]() $\overline{\Omega}\times (0,\infty)$
.
$\overline{\Omega}\times (0,\infty)$
.
The qualitative behaviour of these solutions, especially on large timescales, will evidently depend on respective asymptotic properties of the parameter functions
![]() $B_1$
and
$B_1$
and
![]() $B_2$
. Our efforts in this direction will particularly make use of either suitable assumptions on large-time decay of
$B_2$
. Our efforts in this direction will particularly make use of either suitable assumptions on large-time decay of
![]() $B_1$
or of certain weak but temporally uniform positivity properties of
$B_1$
or of certain weak but temporally uniform positivity properties of
![]() $B_2$
. Specifically, in our analysis, we will alternately refer to the hypotheses:
$B_2$
. Specifically, in our analysis, we will alternately refer to the hypotheses:
 \begin{equation} \int_0^\infty \int_\Omega B_1 < \infty, \end{equation}
\begin{equation} \int_0^\infty \int_\Omega B_1 < \infty, \end{equation}
and, in a weaker form:
on decay of
![]() $B_1$
, and
$B_1$
, and
 \begin{equation} \inf_{t>0} \int_\Omega B_2(x,t)dx > 0, \end{equation}
\begin{equation} \inf_{t>0} \int_\Omega B_2(x,t)dx > 0, \end{equation}
on the positivity of
![]() $B_2$
. In some places, we will also assume that
$B_2$
. In some places, we will also assume that
![]() $B_2$
stabilises in the sense that
$B_2$
stabilises in the sense that
 \begin{equation} \int_t^{t+1} \int_\Omega \Big(B_2(x,s)-B_{2,\infty}(x)\Big)^2 dxds \to 0 \qquad \mbox{as } t\to\infty, \end{equation}
\begin{equation} \int_t^{t+1} \int_\Omega \Big(B_2(x,s)-B_{2,\infty}(x)\Big)^2 dxds \to 0 \qquad \mbox{as } t\to\infty, \end{equation}
holds with some
![]() $B_{2,\infty}\in L^2(\Omega)$
.
$B_{2,\infty}\in L^2(\Omega)$
.
Indeed, the assumption (H2) implies boundedness of both solution components, and under the additional requirement that (H1’) be valid, u must even decay in the large time limit.
Theorem 1.2 Let
![]() $\chi>0$
and suppose that (1.6) and (1.7) are fulfilled. If moreover (1.7) holds, then there exists
$\chi>0$
and suppose that (1.6) and (1.7) are fulfilled. If moreover (1.7) holds, then there exists
![]() $C>0$
with the property that the solution (u,v) of (1.1), (1.4), (H2) satisfies
$C>0$
with the property that the solution (u,v) of (1.1), (1.4), (H2) satisfies
and
If additionally (H1’) is valid, then
We shall secondly see that for all
![]() $\chi$
within an appropriate range, including the relevant value
$\chi$
within an appropriate range, including the relevant value
![]() $\chi=2$
, also the mere assumption (H1) is sufficient for boundedness, at least of the second solution component, and that moreover the latter even stabilises when additionally (H3) is satisfied.
$\chi=2$
, also the mere assumption (H1) is sufficient for boundedness, at least of the second solution component, and that moreover the latter even stabilises when additionally (H3) is satisfied.
Theorem 1.3 Let
![]() $\chi>0$
be such that
$\chi>0$
be such that
and let
![]() $B_1$
and
$B_1$
and
![]() $B_2$
be such that besides (1.6), also (H1) holds. Then for each pair
$B_2$
be such that besides (1.6), also (H1) holds. Then for each pair
![]() $(u_0,v_0)$
fulfilling (1.7), one can find
$(u_0,v_0)$
fulfilling (1.7), one can find
![]() $C>0$
such that the solution (u,v) of (1.1), (1.4), (1.5) satisfies
$C>0$
such that the solution (u,v) of (1.1), (1.4), (1.5) satisfies
Furthermore, if (H3) is valid with some
![]() $B_{2,\infty}\in L^2(\Omega)$
, then
$B_{2,\infty}\in L^2(\Omega)$
, then
where
![]() $v_\infty$
denotes the solution to the boundary value problem:
$v_\infty$
denotes the solution to the boundary value problem:
 \begin{equation} \left\{ \begin{array}{l} -\partial_{xx}v_\infty + v_\infty = B_{2,\infty}, \qquad x\in \Omega, \\[1mm] \partial_xv_{\infty}=0, \qquad x\in\partial\Omega. \end{array} \right. \end{equation}
\begin{equation} \left\{ \begin{array}{l} -\partial_{xx}v_\infty + v_\infty = B_{2,\infty}, \qquad x\in \Omega, \\[1mm] \partial_xv_{\infty}=0, \qquad x\in\partial\Omega. \end{array} \right. \end{equation}
Let us finally state an essentially immediate consequence of Theorem 1.2 and Theorem 1.3 under slightly sharper but yet quite practicable assumptions.
Corollary 1.4 Let
![]() $\chi\in (0,\frac{\sqrt{6\sqrt{3}+9}}{2})$
, and suppose that the functions
$\chi\in (0,\frac{\sqrt{6\sqrt{3}+9}}{2})$
, and suppose that the functions
![]() $B_1$
and
$B_1$
and
![]() $B_2$
are such that beyond (1.6) and (H1), we have
$B_2$
are such that beyond (1.6) and (H1), we have
with some
![]() $0\not\equiv B_{2,\infty} \in L^1(\Omega)$
. Then for each
$0\not\equiv B_{2,\infty} \in L^1(\Omega)$
. Then for each
![]() $u_0$
and
$u_0$
and
![]() $v_0$
satisfying (1.7), the corresponding solution (u,v) of (1.1), (1.4), (1.5) has the properties that
$v_0$
satisfying (1.7), the corresponding solution (u,v) of (1.1), (1.4), (1.5) has the properties that
and
where
![]() $v_\infty$
solves (1.15).
$v_\infty$
solves (1.15).
Proof. In view of the dominated convergence theorem, (1.16) along with the boundedness of
![]() $B_2$
entails that actually
$B_2$
entails that actually
![]() $B_{2,\infty}\in L^\infty(\Omega)$
, that (H3) holds and that moreover
$B_{2,\infty}\in L^\infty(\Omega)$
, that (H3) holds and that moreover
![]() $\int_\Omega B_2(\cdot,t)\to \int_\Omega B_{2,\infty}\ne 0$
as
$\int_\Omega B_2(\cdot,t)\to \int_\Omega B_{2,\infty}\ne 0$
as
![]() $t\to\infty$
, whence for some
$t\to\infty$
, whence for some
![]() $t_0>0$
we have
$t_0>0$
we have
![]() $\inf_{t>t_0} \int_\Omega B_2(\cdot,t)>0$
. The claim therefore results on applying Theorem 1.2 and Theorem 1.3 with
$\inf_{t>t_0} \int_\Omega B_2(\cdot,t)>0$
. The claim therefore results on applying Theorem 1.2 and Theorem 1.3 with
![]() $(u,v,B_1,B_2)(x,t)$
replaced by
$(u,v,B_1,B_2)(x,t)$
replaced by
![]() $(u,v,B_1,B_2)(x,t_0+t)$
for
$(u,v,B_1,B_2)(x,t_0+t)$
for
![]() $(x,t)\in\overline{\Omega}\times [0,\infty)$
.
$(x,t)\in\overline{\Omega}\times [0,\infty)$
.
Outline. After asserting local existence of solutions and some of their basic features in Section 2, in Section 3 we will derive some fundamental estimates resulting from an analysis of the coupled functional
![]() $\int_\Omega u^p v^q$
which indeed enjoys a certain entropy-type property if, in dependence on the size of
$\int_\Omega u^p v^q$
which indeed enjoys a certain entropy-type property if, in dependence on the size of
![]() $\chi$
, the crucial exponent p therein is small enough and q belongs to an appropriate range. Accordingly implied consequences on regularity features will thereafter enable us to verify Theorem 1.1 and Theorem 1.2 in Section 4. Finally, Section 5 will contain our proof of Theorem 1.3, where we highlight already here that particular challenges will be linked to the derivation of
$\chi$
, the crucial exponent p therein is small enough and q belongs to an appropriate range. Accordingly implied consequences on regularity features will thereafter enable us to verify Theorem 1.1 and Theorem 1.2 in Section 4. Finally, Section 5 will contain our proof of Theorem 1.3, where we highlight already here that particular challenges will be linked to the derivation of
![]() $L^\infty$
bounds for v, and that these will be accomplished on the basis of a recursive argument available under the assumption (1.12).
$L^\infty$
bounds for v, and that these will be accomplished on the basis of a recursive argument available under the assumption (1.12).
2 Local existence and basic estimates
Let us first make sure that our overall assumptions warrant local-in-time solvability of (1.1), (1.4), (1.5), along with a convenient extensibility criterion.
Lemma 2.1 Under the assumptions of Theorem 1.1, there exist
![]() $T_{max}\in (0,\infty]$
and a uniquely determined pair (u,v) of functions:
$T_{max}\in (0,\infty]$
and a uniquely determined pair (u,v) of functions:
 \begin{eqnarray*} \left\{ \begin{array}{l} u \in C^0(\overline{\Omega}\times [0,T_{max})) \cap C^{2,1}(\overline{\Omega}\times (0,T_{max})), \\[1mm] v \in \bigcap\limits_{r>1} C^0([0,T_{max}); W^{1,r}(\Omega)) \cap C^{2,1}(\overline{\Omega}\times (0,T_{max})), \end{array} \right. \end{eqnarray*}
\begin{eqnarray*} \left\{ \begin{array}{l} u \in C^0(\overline{\Omega}\times [0,T_{max})) \cap C^{2,1}(\overline{\Omega}\times (0,T_{max})), \\[1mm] v \in \bigcap\limits_{r>1} C^0([0,T_{max}); W^{1,r}(\Omega)) \cap C^{2,1}(\overline{\Omega}\times (0,T_{max})), \end{array} \right. \end{eqnarray*}
which solve (1.1), (1.4), (1.5) classically in
![]() $\overline{\Omega}\times [0,T_{max}).$
Moreover,
$\overline{\Omega}\times [0,T_{max}).$
Moreover,
![]() $u>0$
and
$u>0$
and
![]() $v>0$
in
$v>0$
in
![]() $\overline{\Omega}\times (0,T_{max})$
and
$\overline{\Omega}\times (0,T_{max})$
and
 \begin{align} & \mbox{either $T_{max}=\infty$, or} \nonumber\\ & \limsup_{t\nearrow T_{max}} \Big\{ \|u(\cdot,t)\|_{L^\infty(\Omega)} + \Big\|\frac{1}{v(\cdot,t)}\Big\|_{L^\infty(\Omega)} + \|v_x(\cdot,t)\|_{L^r(\Omega)} \Big\} = \infty \quad \mbox{for all } r>1. \end{align}
\begin{align} & \mbox{either $T_{max}=\infty$, or} \nonumber\\ & \limsup_{t\nearrow T_{max}} \Big\{ \|u(\cdot,t)\|_{L^\infty(\Omega)} + \Big\|\frac{1}{v(\cdot,t)}\Big\|_{L^\infty(\Omega)} + \|v_x(\cdot,t)\|_{L^r(\Omega)} \Big\} = \infty \quad \mbox{for all } r>1. \end{align}
Proof. The results is a straightforward application of well-established techniques from the theory of tridiagonal cross-diffusive systems ([Reference Amann2], specifically applied to chemotaxis systems [Reference Horstmann and Winkler20]).
Throughout the sequel, without explicit further mentioning, we shall assume the requirements of Theorem 1.1 to be met, and let u, v and
![]() $T_{max}$
be as provided by Lemma 2.1.
$T_{max}$
be as provided by Lemma 2.1.
In order to derive some basic features of this solution, let us recall the following well-known pointwise positivity property of the Neumann heat semigroup
![]() $(e^{t\Delta})_{t\ge 0}$
on the bounded real interval
$(e^{t\Delta})_{t\ge 0}$
on the bounded real interval
![]() $\Omega$
(cf. e.g. [Reference Hillen, Painter and Winkler19, Lemma 3.1]).
$\Omega$
(cf. e.g. [Reference Hillen, Painter and Winkler19, Lemma 3.1]).
Lemma 2.2 Let
![]() $\tau>0$
. Then there exists a constant
$\tau>0$
. Then there exists a constant
![]() $C>0$
such that for all non-negative
$C>0$
such that for all non-negative
![]() $\varphi\in C^0(\overline{\Omega})$
,
$\varphi\in C^0(\overline{\Omega})$
,
Using the previous lemma along with a parabolic comparison argument, we obtain a basic but important pointwise lower estimate for the second solution component. This lower bound is local-in-time for arbitrary
![]() $B_1$
and
$B_1$
and
![]() $B_2$
and global-in-time when (H2) is satisfied.
$B_2$
and global-in-time when (H2) is satisfied.
Lemma 2.3 For all
![]() $T>0$
there exists
$T>0$
there exists
![]() $C(T)>0$
such that with
$C(T)>0$
such that with
![]() $T_{max}$
from Lemma 2.1, for
$T_{max}$
from Lemma 2.1, for
![]() $\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
, we have
$\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
, we have
with
Proof. We represent v according to
and observe that here by the comparison principle for the Neumann problem associated with the heat equation, the second summand on the right is non-negative, whereas
To gain a pointwise lower estimate for the rightmost integral in (2.4), we invoke Lemma 2.2 to find
![]() $c_1>0$
such that with
$c_1>0$
such that with
![]() $\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
, for any non-negative
$\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
, for any non-negative
![]() $\varphi\in C^0(\overline{\Omega})$
, we have
$\varphi\in C^0(\overline{\Omega})$
, we have
which implies that
 \begin{align*} \int_0^t e^{(t-s)(\Delta-1)} B_2(\cdot,s) ds &\ge \int_0^{t-\frac{\tau}{2}} e^{-(t-s)} e^{(t-s)\Delta} B_2(\cdot,s) ds \\ &\ge \int_0^{t-\frac{\tau}{2}} e^{-(t-s)} \cdot \Big\{ c_1 \int_\Omega B_2(\cdot,s) \Big\} ds \\ \end{align*}
\begin{align*} \int_0^t e^{(t-s)(\Delta-1)} B_2(\cdot,s) ds &\ge \int_0^{t-\frac{\tau}{2}} e^{-(t-s)} e^{(t-s)\Delta} B_2(\cdot,s) ds \\ &\ge \int_0^{t-\frac{\tau}{2}} e^{-(t-s)} \cdot \Big\{ c_1 \int_\Omega B_2(\cdot,s) \Big\} ds \\ \end{align*}
 \begin{align*} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; &\ge c_1 c_2 \int_0^{t-\frac{\tau}{2}} e^{-(t-s)} ds\\ &= c_1 c_2 \cdot \Big(e^{-\frac{\tau}{2}} - e^{-t}\Big) \\ &\ge c_3\;:=\; c_1 c_2 \cdot \Big( e^{-\frac{\tau}{2}} - e^{-\tau}\Big) \qquad \mbox{for all } t>\tau \end{align*}
\begin{align*} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; &\ge c_1 c_2 \int_0^{t-\frac{\tau}{2}} e^{-(t-s)} ds\\ &= c_1 c_2 \cdot \Big(e^{-\frac{\tau}{2}} - e^{-t}\Big) \\ &\ge c_3\;:=\; c_1 c_2 \cdot \Big( e^{-\frac{\tau}{2}} - e^{-\tau}\Big) \qquad \mbox{for all } t>\tau \end{align*}
with
![]() $c_2\;:=\;\inf_{t>0} \int_\Omega B_2(\cdot,t) \ge 0$
. Together with (2.5) and (2.4), this entails that
$c_2\;:=\;\inf_{t>0} \int_\Omega B_2(\cdot,t) \ge 0$
. Together with (2.5) and (2.4), this entails that
and that
and thereby establishes both (2.2) and (2.3).
Further fundamental properties of (1.1) are connected to the evolution of the total mass
![]() $\int_\Omega u$
and the associated total absorption rate
$\int_\Omega u$
and the associated total absorption rate
![]() $\int_\Omega uv$
. We formulate these properties in such a way that important dependences of the appearing constants are accounted for in order to provide statements that will be useful for our asymptotic analysis in Theorem 1.2 and Theorem 1.3.
$\int_\Omega uv$
. We formulate these properties in such a way that important dependences of the appearing constants are accounted for in order to provide statements that will be useful for our asymptotic analysis in Theorem 1.2 and Theorem 1.3.
Lemma 2.4 For all
![]() $T>0$
, there exists
$T>0$
, there exists
![]() $C(T)>0$
such that with
$C(T)>0$
such that with
![]() $\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
,
$\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
,
where
Moreover, for all
![]() $T>0$
and each
$T>0$
and each
![]() $\xi\in (0,T)$
, there exists
$\xi\in (0,T)$
, there exists
![]() $K(T,\xi)>0$
with the properties that
$K(T,\xi)>0$
with the properties that
and
as well as
Proof. Integrating the first equation in (1.1) yields
and hence
as well as
 \begin{align} & \int_t^{t+\xi} \int_\Omega uv \le \int_\Omega u(\cdot,t) + \int_t^{t+\xi} \int_\Omega B_1 \le c_1(T) + c_1(2T) \nonumber \\ & \qquad \mbox{for all $t \in (0,\widehat{T}_{max}-\xi)$ and any } \xi \in (0,T). \end{align}
\begin{align} & \int_t^{t+\xi} \int_\Omega uv \le \int_\Omega u(\cdot,t) + \int_t^{t+\xi} \int_\Omega B_1 \le c_1(T) + c_1(2T) \nonumber \\ & \qquad \mbox{for all $t \in (0,\widehat{T}_{max}-\xi)$ and any } \xi \in (0,T). \end{align}
For general
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, (2.12) and (2.13) directly imply (2.6) and (2.8) with
$B_2$
, (2.12) and (2.13) directly imply (2.6) and (2.8) with
![]() $C(T)\;:=\;c_1(T)$
and
$C(T)\;:=\;c_1(T)$
and
![]() $K(T,\xi)\;:=\;c_1(T)+c_1(2T)$
for
$K(T,\xi)\;:=\;c_1(T)+c_1(2T)$
for
![]() $T>0$
and
$T>0$
and
![]() $\xi\in (0,T)$
, and if in addition (H1) holds, then
$\xi\in (0,T)$
, and if in addition (H1) holds, then
![]() $c_1(T)\le c_2\;:=\;\int_{\Omega}u_0+\int_0^\infty \int_\Omega B_1$
for all
$c_1(T)\le c_2\;:=\;\int_{\Omega}u_0+\int_0^\infty \int_\Omega B_1$
for all
![]() $T>0$
and thus (2.12) and (2.13) moreover show that
$T>0$
and thus (2.12) and (2.13) moreover show that
![]() $C(T)\le c_2$
in this case.
$C(T)\le c_2$
in this case.
Assuming the hypothesis (H2) henceforth, we recall that thanks to the latter, Lemma 2.3 implies the existence of
![]() $c_3>0$
fulfilling
$c_3>0$
fulfilling
![]() $v\ge c_3$
in
$v\ge c_3$
in
![]() $\Omega\times (0,T_{max})$
, whence going back to (2.11) we see that then
$\Omega\times (0,T_{max})$
, whence going back to (2.11) we see that then
with
![]() $c_4\;:=\;|\Omega|\cdot\|B_1\|_{L^\infty(\Omega\times (0,\infty))}$
. By an ODE comparison, this firstly ensures that
$c_4\;:=\;|\Omega|\cdot\|B_1\|_{L^\infty(\Omega\times (0,\infty))}$
. By an ODE comparison, this firstly ensures that
whereupon an integration in (2.14) shows that furthermore
and that hence indeed the estimates in (2.6) and (2.8) can actually be achieved to be independent of T also when (H2) holds.
The previous lemma has the following consequence for the time evolution of
![]() $\int_\Omega v$
.
$\int_\Omega v$
.
Lemma 2.5 For all
![]() $T>0$
, there exists
$T>0$
, there exists
![]() $C(T)>0$
such that with
$C(T)>0$
such that with
![]() $\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
$\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
![]() $\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
we have
$\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
we have
and
Proof. From the second equation in (1.1), we obtain that
Here, we only need to observe that thanks to Lemma 2.4 and the boundedness of
![]() $B_2$
we can find
$B_2$
we can find
![]() $c_1(T)>0$
such that for
$c_1(T)>0$
such that for
![]() $h(t)\;:=\;\int_\Omega u(\cdot,t)v(\cdot,t) + \int_\Omega B_2(\cdot,t)$
,
$h(t)\;:=\;\int_\Omega u(\cdot,t)v(\cdot,t) + \int_\Omega B_2(\cdot,t)$
,
![]() $t\in (0,T_{max})$
, we have
$t\in (0,T_{max})$
, we have
and that
Therefore, extending h by zero to all of
![]() $(0,\infty)$
, we may apply Lemma 7.1 from the appendix below so as to derive (2.15) and (2.16) from (2.17).
$(0,\infty)$
, we may apply Lemma 7.1 from the appendix below so as to derive (2.15) and (2.16) from (2.17).
3 Fundamental estimates resulting from an analysis of
 $\int_\Omega u^p v^q$
$\int_\Omega u^p v^q$
The main goal of this section consists of deriving spatio-temporal
![]() $L^2$
bounds for both
$L^2$
bounds for both
![]() $u_x$
and
$u_x$
and
![]() $v_x$
with appropriate solution-dependent weight functions. This will be accomplished in Lemma 3.3 through an analysis of the functional
$v_x$
with appropriate solution-dependent weight functions. This will be accomplished in Lemma 3.3 through an analysis of the functional
![]() $\int_\Omega u^p v^q$
for adequately small
$\int_\Omega u^p v^q$
for adequately small
![]() $p\in (0,1)$
and certain positive
$p\in (0,1)$
and certain positive
![]() $q<1-p$
taken from a suitable interval. Entropy-like properties of functionals containing multiplicative couplings of both solution components have played important roles in the analysis of several chemotaxis problems at various stages of existence and regularity theory, but in most precedent cases the respective dependence on the unknown is either of strictly convex type with respect to both solution components separately ([Reference Tao43, Reference Tao and Winkler44, Reference Winkler49, Reference Winkler53]) or at least exhibits some superlinear growth with respect to the full solution couple when viewed as a whole ([Reference Biler8, Reference Manásevich, Phan and Souplet27]). In addition, contrary to related situations addressing singular sensitivities of the form in (1.1) ([Reference Stinner and Winkler42, Reference Winkler51]), the additional zero-order non-linearities uv appearing in the present context of (1.1) will require adequately coping with respectively occurring superlinear terms (cf. e.g. (3.21) below). In preparation to a corresponding testing procedure, we will therefore independently derive a regularity property of v by using a quasi-entropy property of the functional
$q<1-p$
taken from a suitable interval. Entropy-like properties of functionals containing multiplicative couplings of both solution components have played important roles in the analysis of several chemotaxis problems at various stages of existence and regularity theory, but in most precedent cases the respective dependence on the unknown is either of strictly convex type with respect to both solution components separately ([Reference Tao43, Reference Tao and Winkler44, Reference Winkler49, Reference Winkler53]) or at least exhibits some superlinear growth with respect to the full solution couple when viewed as a whole ([Reference Biler8, Reference Manásevich, Phan and Souplet27]). In addition, contrary to related situations addressing singular sensitivities of the form in (1.1) ([Reference Stinner and Winkler42, Reference Winkler51]), the additional zero-order non-linearities uv appearing in the present context of (1.1) will require adequately coping with respectively occurring superlinear terms (cf. e.g. (3.21) below). In preparation to a corresponding testing procedure, we will therefore independently derive a regularity property of v by using a quasi-entropy property of the functional
![]() $-\int_\Omega v^q$
for arbitrary
$-\int_\Omega v^q$
for arbitrary
![]() $q\in (0,1)$
.
$q\in (0,1)$
.
3.1 A spatio-temporal bound for v in
 $\textbf{L}^{\textbf{r}}$
for
$\textbf{L}^{\textbf{r}}$
for
 $\textbf{r < 3}$
$\textbf{r < 3}$
By means of a standard testing procedure solely involving the second equation in (1.1), thanks to Lemma 2.5 and the non-negativity of
![]() $B_2$
we can derive the following.
$B_2$
we can derive the following.
Lemma 3.1 Let
![]() $q\in (0,1)$
. Then for each
$q\in (0,1)$
. Then for each
![]() $T>0$
, one can find
$T>0$
, one can find
![]() $C(T)>0$
with the properties that
$C(T)>0$
with the properties that
and that
where again
![]() $\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
$\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
![]() $\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
.
$\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
.
Proof. As
![]() $v>0$
in
$v>0$
in
![]() $\overline{\Omega}\times [0,T_{max})$
by Lemma 2.3, we may test the second equation in (1.1) by
$\overline{\Omega}\times [0,T_{max})$
by Lemma 2.3, we may test the second equation in (1.1) by
![]() $v^{q-1}$
to see that
$v^{q-1}$
to see that
 \begin{eqnarray*} \frac{1}{q} \frac{d}{dt} \int_\Omega v^q &=& (1-q) \int_\Omega v^{q-2} v_x^2 + \int_\Omega uv^q - \int_\Omega v^q + \int_\Omega B_2 v^{q-1} \\ &\ge& (1-q)\int_\Omega v^{q-2} v_x^2 - \int_\Omega v^q \qquad \mbox{for all } t\in (0,T_{max}), \end{eqnarray*}
\begin{eqnarray*} \frac{1}{q} \frac{d}{dt} \int_\Omega v^q &=& (1-q) \int_\Omega v^{q-2} v_x^2 + \int_\Omega uv^q - \int_\Omega v^q + \int_\Omega B_2 v^{q-1} \\ &\ge& (1-q)\int_\Omega v^{q-2} v_x^2 - \int_\Omega v^q \qquad \mbox{for all } t\in (0,T_{max}), \end{eqnarray*}
which on further integration yields that
Since with
![]() $c_1\;:=\;|\Omega|^{1-q}$
, we have
$c_1\;:=\;|\Omega|^{1-q}$
, we have
by the Hölder inequality, from (3.3) we thus obtain that
which in view of Lemma 2.5 implies (3.1) and (3.2).
Thanks to the fact that the considered spatial setting is one-dimensional, an interpolation of the above result with the outcome of Lemma 2.5 has a natural consequence on space-time integrability of v.
Lemma 3.2 Given
![]() $r\in (1,3)$
, for any
$r\in (1,3)$
, for any
![]() $T>0$
one can fix
$T>0$
one can fix
![]() $C(T)>0$
such that
$C(T)>0$
such that
and that
where
![]() $\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
$\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
![]() $\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
.
$\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
.
Proof. We may assume that
![]() $r\in (2,3)$
and then let
$r\in (2,3)$
and then let
![]() $q\;:=\;r-2\in (0,1)$
to obtain from Lemma 3.1 that there exists
$q\;:=\;r-2\in (0,1)$
to obtain from Lemma 3.1 that there exists
![]() $c_1(T)>0$
such that
$c_1(T)>0$
such that
while Lemma 2.5 provides
![]() $c_2(T)>0$
fulfilling
$c_2(T)>0$
fulfilling
where
Now, from the Gagliardo–Nirenberg inequality, we know that there exists
![]() $c_3>0$
satisfying
$c_3>0$
satisfying
 \begin{eqnarray*} \int_t^{t+\tau} \int_\Omega v^r &=& \int_t^{t+\tau} \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2r}{q}(\Omega)}^\frac{2r}{q} ds \\[5pt] &\le& c_3 \int_t^{t+\tau} \bigg\{ \Big\| (v^\frac{q}{2})_x(\cdot,s) \Big\|_{L^2(\Omega)}^\frac{2(r-1)}{q+1} \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2}{q}(\Omega)}^\frac{2(q+r)}{q(q+1)} + \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2}{q}(\Omega)}^\frac{2r}{q} \bigg\} ds \end{eqnarray*}
\begin{eqnarray*} \int_t^{t+\tau} \int_\Omega v^r &=& \int_t^{t+\tau} \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2r}{q}(\Omega)}^\frac{2r}{q} ds \\[5pt] &\le& c_3 \int_t^{t+\tau} \bigg\{ \Big\| (v^\frac{q}{2})_x(\cdot,s) \Big\|_{L^2(\Omega)}^\frac{2(r-1)}{q+1} \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2}{q}(\Omega)}^\frac{2(q+r)}{q(q+1)} + \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2}{q}(\Omega)}^\frac{2r}{q} \bigg\} ds \end{eqnarray*}
for all
![]() $t\in (0,\widehat{T}_{max}-\tau)$
, so that since
$t\in (0,\widehat{T}_{max}-\tau)$
, so that since
due to our choice of q we obtain from (3.6) and (3.7) that
 \begin{eqnarray*} \int_t^{t+\tau} \int_\Omega v^r &\le& c_3 \int_t^{t+\tau} \bigg\{ \Big\|(v^\frac{q}{2})_x(\cdot,s)\Big\|_{L^2(\Omega)}^2 \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2}{q}(\Omega)}^\frac{4}{q} + \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2}{q}(\Omega)}^\frac{2r}{q} \bigg\} ds \\[5pt] &\le& c_3 \cdot \Big\{ c_1(T) c_2^2(T) + c_2^r(T) \Big\} \qquad \mbox{for all } t\in (0,\widehat{T}_{max}-\tau), \end{eqnarray*}
\begin{eqnarray*} \int_t^{t+\tau} \int_\Omega v^r &\le& c_3 \int_t^{t+\tau} \bigg\{ \Big\|(v^\frac{q}{2})_x(\cdot,s)\Big\|_{L^2(\Omega)}^2 \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2}{q}(\Omega)}^\frac{4}{q} + \|v^\frac{q}{2}(\cdot,s)\|_{L^\frac{2}{q}(\Omega)}^\frac{2r}{q} \bigg\} ds \\[5pt] &\le& c_3 \cdot \Big\{ c_1(T) c_2^2(T) + c_2^r(T) \Big\} \qquad \mbox{for all } t\in (0,\widehat{T}_{max}-\tau), \end{eqnarray*}
3.2 Analysis of the functional
 $\int_\Omega u^p v^q$
for small positive p and certain
$\int_\Omega u^p v^q$
for small positive p and certain
 $\textbf{q}\textbf{\;>\;0}$
$\textbf{q}\textbf{\;>\;0}$
We can now proceed to the following lemma which provides some regularity information that will be fundamental for our subsequent analysis.
Lemma 3.3 Let
![]() $p\in (0,1)$
be such that
$p\in (0,1)$
be such that
![]() $p<\frac{1}{\chi^2}$
and suppose that
$p<\frac{1}{\chi^2}$
and suppose that
![]() $q\in (q^-(p),q^+(p))$
, where
$q\in (q^-(p),q^+(p))$
, where
Then for all
![]() $T>0$
there exists
$T>0$
there exists
![]() $C(T)>0$
such that with
$C(T)>0$
such that with
![]() $\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
$\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
![]() $\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
we have
$\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
we have
as well as
and
Proof. Using that u and v are both positive in
![]() $\overline{\Omega}\times (0,T_{max})$
, on the basis of (1.1) and several integrations by parts we compute
$\overline{\Omega}\times (0,T_{max})$
, on the basis of (1.1) and several integrations by parts we compute
 \begin{eqnarray} \frac{d}{dt} \int_\Omega u^p v^q &=& p \int_\Omega u^{p-1} v^q \cdot \Big\{ u_{xx} - \chi \Big(\frac{u}{v} v_x\Big)_x - uv + B_1 \Big\} + q\int_\Omega u^p v^{q-1} \cdot \Big\{ v_{xx} + uv - v + B_2\Big\} \nonumber\\[5pt] &=& p(1-p) \int_\Omega u^{p-2} v^q u_x^2 - pq \int_\Omega u^{p-1} v^{q-1} u_x v_x \nonumber\\[5pt] & & - p(1-p)\chi \int_\Omega u^{p-1} v^{q-1} u_x v_x + pq\chi \int_\Omega u^p v^{q-2} v_x^2 \nonumber\\[5pt] & & - p\int_\Omega u^p v^{q+1} + p \int_\Omega B_1 u^{p-1} v^q \nonumber\\[5pt] & & - pq\int_\Omega u^{p-1} v^{q-1} u_x v_x + q(1-q) \int_\Omega u^p v^{q-2} v_x^2 \nonumber\\[5pt] & & + q \int_\Omega u^{p+1} v^q - q\int_\Omega u^p v^q + q\int_\Omega B_2 u^p v^{q-1} \nonumber\\[5pt] &=& p(1-p) \int_\Omega u^{p-2} v^q u_x^2 + q(p\chi+1-q) \int_\Omega u^p v^{q-2} v_x^2 \nonumber\\[5pt] & & - p(\chi-p\chi+2q) \int_\Omega u^{p-1} v^{q-1} u_x v_x \nonumber\\[5pt] & & -p\int_\Omega u^p v^{q+1} + p\int_\Omega B_1 u^{p-1} v^q \nonumber\\[5pt] & & + q\int_\Omega u^{p+1} v^q - q\int_\Omega u^p v^q + q\int_\Omega B_2 u^p v^{q-1} \qquad \mbox{for all } t\in (0,T_{max}). \end{eqnarray}
\begin{eqnarray} \frac{d}{dt} \int_\Omega u^p v^q &=& p \int_\Omega u^{p-1} v^q \cdot \Big\{ u_{xx} - \chi \Big(\frac{u}{v} v_x\Big)_x - uv + B_1 \Big\} + q\int_\Omega u^p v^{q-1} \cdot \Big\{ v_{xx} + uv - v + B_2\Big\} \nonumber\\[5pt] &=& p(1-p) \int_\Omega u^{p-2} v^q u_x^2 - pq \int_\Omega u^{p-1} v^{q-1} u_x v_x \nonumber\\[5pt] & & - p(1-p)\chi \int_\Omega u^{p-1} v^{q-1} u_x v_x + pq\chi \int_\Omega u^p v^{q-2} v_x^2 \nonumber\\[5pt] & & - p\int_\Omega u^p v^{q+1} + p \int_\Omega B_1 u^{p-1} v^q \nonumber\\[5pt] & & - pq\int_\Omega u^{p-1} v^{q-1} u_x v_x + q(1-q) \int_\Omega u^p v^{q-2} v_x^2 \nonumber\\[5pt] & & + q \int_\Omega u^{p+1} v^q - q\int_\Omega u^p v^q + q\int_\Omega B_2 u^p v^{q-1} \nonumber\\[5pt] &=& p(1-p) \int_\Omega u^{p-2} v^q u_x^2 + q(p\chi+1-q) \int_\Omega u^p v^{q-2} v_x^2 \nonumber\\[5pt] & & - p(\chi-p\chi+2q) \int_\Omega u^{p-1} v^{q-1} u_x v_x \nonumber\\[5pt] & & -p\int_\Omega u^p v^{q+1} + p\int_\Omega B_1 u^{p-1} v^q \nonumber\\[5pt] & & + q\int_\Omega u^{p+1} v^q - q\int_\Omega u^p v^q + q\int_\Omega B_2 u^p v^{q-1} \qquad \mbox{for all } t\in (0,T_{max}). \end{eqnarray}
Here in order to estimate the third summand on the right, we note that our assumption (3.9) on q warrants that
and hence
 \begin{eqnarray*} \frac{p(\chi-p\chi+2q)^2}{4(1-p)} &-& q(p\chi+1-q) \\ &=& \frac{1}{4(1-p)} \cdot \Bigg\{ \Big\{ p\chi^2 + p^3\chi^2 + 4pq^2 -2p^2 \chi^2 + 4pq\chi - 4p^2 q\chi\Big\} \\ & & - \Big\{ 4pq\chi-4p^2 q\chi + 4q - 4pq - 4q^2 + 4pq^2 \Big\} \Bigg\} \\ &=& \frac{1}{4(1-p)} \cdot \Big\{ 4q^2 - 4(1-p)q + p(1-p)^2 \chi^2 \Big\}, \\[2mm] &<& 0, \end{eqnarray*}
\begin{eqnarray*} \frac{p(\chi-p\chi+2q)^2}{4(1-p)} &-& q(p\chi+1-q) \\ &=& \frac{1}{4(1-p)} \cdot \Bigg\{ \Big\{ p\chi^2 + p^3\chi^2 + 4pq^2 -2p^2 \chi^2 + 4pq\chi - 4p^2 q\chi\Big\} \\ & & - \Big\{ 4pq\chi-4p^2 q\chi + 4q - 4pq - 4q^2 + 4pq^2 \Big\} \Bigg\} \\ &=& \frac{1}{4(1-p)} \cdot \Big\{ 4q^2 - 4(1-p)q + p(1-p)^2 \chi^2 \Big\}, \\[2mm] &<& 0, \end{eqnarray*}
so that it is possible to pick
![]() $\eta\in (0,1)$
suitably close to 1 such that still
$\eta\in (0,1)$
suitably close to 1 such that still
Therefore, by Young’s inequality, we can estimate
 \begin{eqnarray*} p(1-p) & & \!\!\!\!\! \int_\Omega u^{p-2} v^q u_x^2 + q(p\chi+1-q) \int_\Omega u^p v^{q-2} v_x^2 - p(\chi-p\chi+2q) \int_\Omega u^{p-1} v^{q-1} u_x v_x \\ &\ge& p(1-p) \int_\Omega u^{p-2} v^q u_x^2 + q(p\chi+1-q) \int_\Omega u^p v^{q-2} v_x^2 \\ & & - \eta p(1-p) \int_\Omega u^{p-2} v^q u_x^2 - \frac{p(\chi-p\chi+2q)^2}{4(1-p)\eta} \int_\Omega u^p v^{q-2} v_x^2 \\ &=& c_1 \int_\Omega u^{p-2} v^q u_x^2 + c_2 \int_\Omega u^p v^{q-2} v_x^2 \qquad \mbox{for all } t\in (0,T_{max}), \end{eqnarray*}
\begin{eqnarray*} p(1-p) & & \!\!\!\!\! \int_\Omega u^{p-2} v^q u_x^2 + q(p\chi+1-q) \int_\Omega u^p v^{q-2} v_x^2 - p(\chi-p\chi+2q) \int_\Omega u^{p-1} v^{q-1} u_x v_x \\ &\ge& p(1-p) \int_\Omega u^{p-2} v^q u_x^2 + q(p\chi+1-q) \int_\Omega u^p v^{q-2} v_x^2 \\ & & - \eta p(1-p) \int_\Omega u^{p-2} v^q u_x^2 - \frac{p(\chi-p\chi+2q)^2}{4(1-p)\eta} \int_\Omega u^p v^{q-2} v_x^2 \\ &=& c_1 \int_\Omega u^{p-2} v^q u_x^2 + c_2 \int_\Omega u^p v^{q-2} v_x^2 \qquad \mbox{for all } t\in (0,T_{max}), \end{eqnarray*}
where
![]() $c_1\;:=\;(1-\eta)p(1-p)$
is positive due to the fact that
$c_1\;:=\;(1-\eta)p(1-p)$
is positive due to the fact that
![]() $\eta<1$
, and where
$\eta<1$
, and where
thanks to (3.14).
By dropping four non-negative summands, on integrating (3.13) we thus infer that
 \begin{eqnarray} c_1 \int_t^{t+\tau} \int_\Omega u^{p-2} v^q u_x^2 &+& c_2 \int_t^{t+\tau} \int_\Omega u^p v^{q-2} v_x^2 \le \int_\Omega u^p(\cdot,t+\tau) v^q(\cdot,t+\tau) \nonumber\\ & +& p \int_t^{t+\tau} \int_\Omega u^p v^{q+1} + q \int_t^{t+\tau} \int_\Omega u^p v^q, \end{eqnarray}
\begin{eqnarray} c_1 \int_t^{t+\tau} \int_\Omega u^{p-2} v^q u_x^2 &+& c_2 \int_t^{t+\tau} \int_\Omega u^p v^{q-2} v_x^2 \le \int_\Omega u^p(\cdot,t+\tau) v^q(\cdot,t+\tau) \nonumber\\ & +& p \int_t^{t+\tau} \int_\Omega u^p v^{q+1} + q \int_t^{t+\tau} \int_\Omega u^p v^q, \end{eqnarray}
for all
![]() $t\in (0,\widehat{T}_{max}-\tau)$
. Since (3.9) particularly requires that
$t\in (0,\widehat{T}_{max}-\tau)$
. Since (3.9) particularly requires that
we may use the Hölder inequality to see that
which in view of Lemma 2.4 and Lemma 2.5 implies that there exists
![]() $c_3(T)>0$
such that
$c_3(T)>0$
such that
where
To estimate the second to last summand in (3.15), we recall that Lemma 2.4 moreover yields
![]() $c_4(T)>0$
satisfying
$c_4(T)>0$
satisfying
where
Therefore, once again by the Hölder inequality,
 \begin{eqnarray} p\int_t^{t+\tau} \int_\Omega u^p v^{q+1} &=& p \int_t^{t+\tau} \int_\Omega (uv)^p v^{q+1-p} \nonumber\\[5pt] &\le& p \bigg\{ \int_t^{t+\tau} \int_\Omega uv \bigg\}^p \bigg\{ \int_t^{t+\tau} \int_\Omega v^\frac{q+1-p}{1-p}\bigg\}^{1-p} \nonumber\\[5pt] &\le& pc_4^p(T) \bigg\{ \int_t^{t+\tau} \int_\Omega v^\frac{q+1-p}{1-p}\bigg\}^{1-p} \qquad \mbox{for all } t\in (0,\widehat{T}_{max}-\tau), \end{eqnarray}
\begin{eqnarray} p\int_t^{t+\tau} \int_\Omega u^p v^{q+1} &=& p \int_t^{t+\tau} \int_\Omega (uv)^p v^{q+1-p} \nonumber\\[5pt] &\le& p \bigg\{ \int_t^{t+\tau} \int_\Omega uv \bigg\}^p \bigg\{ \int_t^{t+\tau} \int_\Omega v^\frac{q+1-p}{1-p}\bigg\}^{1-p} \nonumber\\[5pt] &\le& pc_4^p(T) \bigg\{ \int_t^{t+\tau} \int_\Omega v^\frac{q+1-p}{1-p}\bigg\}^{1-p} \qquad \mbox{for all } t\in (0,\widehat{T}_{max}-\tau), \end{eqnarray}
and again by (3.16) we see that
![]() $\frac{q+1-p}{1-p} < 2 < 3$
and thus Lemma 3.2 becomes applicable to yield
$\frac{q+1-p}{1-p} < 2 < 3$
and thus Lemma 3.2 becomes applicable to yield
![]() $c_5(T)>0$
such that
$c_5(T)>0$
such that
with
In summary, (3.15), (3.17), (3.21) and (3.22) entail that
 \begin{eqnarray*} && c_1 \int_t^{t+\tau} \int_\Omega u^{p-2} v^q u_x^2 + c_2 \int_t^{t+\tau} \int_\Omega u^p v^{q-2} v_x^2 \le C(T)\;:=\;c_3(T) + pc_4^p(T) c_5^{1-p}(T) \\[5pt] && \quad \mbox{for all } t\in (0,\widehat{T}_{max}-\tau), \end{eqnarray*}
\begin{eqnarray*} && c_1 \int_t^{t+\tau} \int_\Omega u^{p-2} v^q u_x^2 + c_2 \int_t^{t+\tau} \int_\Omega u^p v^{q-2} v_x^2 \le C(T)\;:=\;c_3(T) + pc_4^p(T) c_5^{1-p}(T) \\[5pt] && \quad \mbox{for all } t\in (0,\widehat{T}_{max}-\tau), \end{eqnarray*}
where C(T) satisfies (3.12) due to (3.18), (3.20) and (3.23).
4 Global existence.
 $\textbf{L}^{\boldsymbol\infty}$
bounds for u and v when (H2) holds
$\textbf{L}^{\boldsymbol\infty}$
bounds for u and v when (H2) holds
As the first application of Lemma 3.3, merely relying on the first inequality (3.10) therein and the pointwise positivity properties of v from Lemma 2.3, we shall derive a bound for the first solution component in some superquadratic space-time Lebesgue norm.
Lemma 4.1 Let
![]() $p\in (0,1)$
be such that
$p\in (0,1)$
be such that
![]() $p<\frac{1}{\chi^2}$
. Then for all
$p<\frac{1}{\chi^2}$
. Then for all
![]() $T>0$
, there exists
$T>0$
, there exists
![]() $C(T)>0$
such that
$C(T)>0$
such that
where
![]() $\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
$\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
![]() $\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
. Moreover,
$\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
. Moreover,
Proof. We fix any
![]() $q\in (q^-(p),q^+(p))$
, with
$q\in (q^-(p),q^+(p))$
, with
![]() $q^\pm(p)$
taken as in (3.9), and invoke Lemma 3.3 and Lemma 2.4 to obtain
$q^\pm(p)$
taken as in (3.9), and invoke Lemma 3.3 and Lemma 2.4 to obtain
![]() $c_1(T)>0$
and
$c_1(T)>0$
and
![]() $c_2(T)>0$
such that
$c_2(T)>0$
such that
and
with
To exploit (4.3), we moreover invoke Lemma 2.3 to find
![]() $c_3(T)>0$
such that
$c_3(T)>0$
such that
with
Therefore, namely, (4.3) entails that
and since the Gagliardo–Nirenberg inequality says that with some
![]() $c_5>0$
, we have
$c_5>0$
, we have
 \begin{eqnarray*} \int_t^{t+\tau} \int_\Omega u^{p+2} &=& \int_t^{t+\tau} \|u^\frac{p}{2}(\cdot,s)\|_{L^\frac{2(p+2)}{p}(\Omega)}^\frac{2(p+2)}{p} ds \\[5pt] &\le& c_5 \int_t^{t+\tau} \bigg\{ \Big\| (u^\frac{p}{2})_x(\cdot,s)\Big\|_{L^2(\Omega)}^2 \|u^\frac{p}{2}(\cdot,s)\|_{L^\frac{2}{p}(\Omega)}^\frac{4}{p} + \|u^\frac{p}{2}(\cdot,s)\|_{L^\frac{2}{p}(\Omega)}^\frac{2(p+2)}{p} \bigg\} ds \end{eqnarray*}
\begin{eqnarray*} \int_t^{t+\tau} \int_\Omega u^{p+2} &=& \int_t^{t+\tau} \|u^\frac{p}{2}(\cdot,s)\|_{L^\frac{2(p+2)}{p}(\Omega)}^\frac{2(p+2)}{p} ds \\[5pt] &\le& c_5 \int_t^{t+\tau} \bigg\{ \Big\| (u^\frac{p}{2})_x(\cdot,s)\Big\|_{L^2(\Omega)}^2 \|u^\frac{p}{2}(\cdot,s)\|_{L^\frac{2}{p}(\Omega)}^\frac{4}{p} + \|u^\frac{p}{2}(\cdot,s)\|_{L^\frac{2}{p}(\Omega)}^\frac{2(p+2)}{p} \bigg\} ds \end{eqnarray*}
for all
![]() $t\in (0,\widehat{T}_{max}-\tau)$
, by using (4.4) we infer that
$t\in (0,\widehat{T}_{max}-\tau)$
, by using (4.4) we infer that
 \begin{eqnarray*} \int_t^{t+\tau} \int_\Omega u^{p+2} &\le& c_5 c_2^2(T) \int_t^{t+\tau} \int_\Omega (u^\frac{p}{2})_x^2 + c_5 c_2^{p+2}(T) \\[5pt] &\le& c_5 c_2^2(T) c_4(T) + c_5 c_2^{p+2}(T) \qquad \mbox{for all } t\in (0,\widehat{T}_{max}-\tau). \end{eqnarray*}
\begin{eqnarray*} \int_t^{t+\tau} \int_\Omega u^{p+2} &\le& c_5 c_2^2(T) \int_t^{t+\tau} \int_\Omega (u^\frac{p}{2})_x^2 + c_5 c_2^{p+2}(T) \\[5pt] &\le& c_5 c_2^2(T) c_4(T) + c_5 c_2^{p+2}(T) \qquad \mbox{for all } t\in (0,\widehat{T}_{max}-\tau). \end{eqnarray*}
Combined with (4.5) and (4.7) this establishes (4.1) and (4.2).
In the considered spatially one-dimensional case, the latter property turns out to be sufficient for the derivation of bounds for
![]() $v_x$
in
$v_x$
in
![]() $L^r(\Omega)$
for suitably small
$L^r(\Omega)$
for suitably small
![]() $r>1$
.
$r>1$
.
Lemma 4.2 Let
![]() $r\in (1,\frac{3}{2})$
be such that
$r\in (1,\frac{3}{2})$
be such that
![]() $r<1+\frac{1}{2\chi^2}$
. Then for all
$r<1+\frac{1}{2\chi^2}$
. Then for all
![]() $T>0$
, there exists
$T>0$
, there exists
![]() $C(T)>0$
such that with
$C(T)>0$
such that with
![]() $\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
we have
$\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
we have
where
Proof. Once more writing
![]() $\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
, from Lemma 2.1 we know that
$\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
, from Lemma 2.1 we know that
is finite, whence for estimating
it will be sufficient to derive appropriate bounds of
![]() $v_x(\cdot,t)$
in
$v_x(\cdot,t)$
in
![]() $L^r(\Omega)$
for
$L^r(\Omega)$
for
![]() $t\in (\tau,T')$
only. To this end, given any such t we represent
$t\in (\tau,T')$
only. To this end, given any such t we represent
![]() $v_x(\cdot,t)$
according to
$v_x(\cdot,t)$
according to
 \begin{eqnarray} v_x(\cdot,t) &=& \partial_x e^{\tau(\Delta-1)} v(\cdot,t-\tau) + \int_{t-\tau}^t \partial_x e^{(t-s)(\Delta-1)} u(\cdot,s)v(\cdot,s) ds \nonumber\\ && \quad + \int_{t-\tau}^t \partial_x e^{(t-s)(\Delta-1)} B_2(\cdot,s) ds, \end{eqnarray}
\begin{eqnarray} v_x(\cdot,t) &=& \partial_x e^{\tau(\Delta-1)} v(\cdot,t-\tau) + \int_{t-\tau}^t \partial_x e^{(t-s)(\Delta-1)} u(\cdot,s)v(\cdot,s) ds \nonumber\\ && \quad + \int_{t-\tau}^t \partial_x e^{(t-s)(\Delta-1)} B_2(\cdot,s) ds, \end{eqnarray}
and recall that due to known smoothing properties of the Neumann heat semigroup ([Reference Winkler50]), we can find
![]() $c_2>0$
such that for all
$c_2>0$
such that for all
![]() $\varphi\in C^0(\overline{\Omega})$
,
$\varphi\in C^0(\overline{\Omega})$
,
Therefore,
 \begin{eqnarray} \Big\|\partial_x e^{\tau(\Delta-1)} v(\cdot,t-\tau)\Big\|_{L^r(\Omega)} &\le& c_2 e^{-\tau} \cdot \tau^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})} \|v(\cdot,t-\tau)\|_{L^1(\Omega)} \nonumber\\ &\le& c_2 c_3(T) \tau^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})}, \end{eqnarray}
\begin{eqnarray} \Big\|\partial_x e^{\tau(\Delta-1)} v(\cdot,t-\tau)\Big\|_{L^r(\Omega)} &\le& c_2 e^{-\tau} \cdot \tau^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})} \|v(\cdot,t-\tau)\|_{L^1(\Omega)} \nonumber\\ &\le& c_2 c_3(T) \tau^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})}, \end{eqnarray}
where
![]() $c_3(T)>0$
has been chosen in such a way that in accordance with Lemma 2.5, we have
$c_3(T)>0$
has been chosen in such a way that in accordance with Lemma 2.5, we have
and such that
Next, again by (4.11),
 \begin{eqnarray} \bigg\| \int_{t-\tau}^t \partial_x e^{(t-s)(\Delta-1)} B_2(\cdot,s) ds \bigg\|_{L^r(\Omega)} ds &\le& c_2 \int_{t-\tau}^t (t-s)^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})} \|B_2(\cdot,s)\|_{L^1(\Omega)} ds \nonumber\\ &\le& c_2|\Omega| \|B_2\|_{L^\infty(\Omega\times (0,\infty))} \int_0^\tau \sigma^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})} d\sigma \nonumber\\[2mm] &=& c_2|\Omega| \|B_2\|_{L^\infty(\Omega\times (0,\infty))} \cdot 2r \tau^\frac{1}{2r} \end{eqnarray}
\begin{eqnarray} \bigg\| \int_{t-\tau}^t \partial_x e^{(t-s)(\Delta-1)} B_2(\cdot,s) ds \bigg\|_{L^r(\Omega)} ds &\le& c_2 \int_{t-\tau}^t (t-s)^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})} \|B_2(\cdot,s)\|_{L^1(\Omega)} ds \nonumber\\ &\le& c_2|\Omega| \|B_2\|_{L^\infty(\Omega\times (0,\infty))} \int_0^\tau \sigma^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})} d\sigma \nonumber\\[2mm] &=& c_2|\Omega| \|B_2\|_{L^\infty(\Omega\times (0,\infty))} \cdot 2r \tau^\frac{1}{2r} \end{eqnarray}
as well as
In order to further estimate the latter integral, we make use of our restrictions
![]() $r<\frac{3}{2}$
and
$r<\frac{3}{2}$
and
![]() $r<1+\frac{1}{2\chi^2}$
which enable us to pick some
$r<1+\frac{1}{2\chi^2}$
which enable us to pick some
![]() $p\in (0,1)$
satisfying
$p\in (0,1)$
satisfying
![]() $p<\frac{1}{\chi^2}$
and
$p<\frac{1}{\chi^2}$
and
![]() $p>2(r-1)$
. Then by means of the Hölder inequality, we see that
$p>2(r-1)$
. Then by means of the Hölder inequality, we see that
where the Gagliardo–Nirenberg inequality provides
![]() $c_4>0$
and
$c_4>0$
and
![]() $a\in (0,1)$
fulfilling
$a\in (0,1)$
fulfilling
In light of (4.13) and the definition of M(T ′), from (4.17) and (4.16) we thus obtain that
so that once again invoking the Hölder inequality, we infer that
 \begin{eqnarray} & & \bigg\| \int_{t-\tau}^t \partial_x e^{(t-s)(\Delta-1)} u(\cdot,s) v(\cdot,s) ds \bigg\|_{L^r(\Omega)} ds \nonumber\\ &\le& c_2 \cdot \Big\{ c_4 c_3^{1-a}(T) M^a(T') + c_4 c_3(T)\Big\} \cdot \int_{t-\tau}^t (t-s)^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,s)\|_{L^{p+2}(\Omega)} ds \nonumber\\ &\le& c_2 \cdot \Big\{ c_4 c_3^{1-a}(T) M^a(T') + c_4 c_3(T)\Big\} \cdot \bigg\{ \int_{t-\tau}^t (t-s)^{-[\frac{1}{2}+\frac{1}{2}(1-\frac{1}{r})] \cdot \frac{p+2}{p+1}} ds \bigg\}^\frac{p+1}{p+2} \nonumber\\ & & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\!\! \times \bigg\{ \int_{t-\tau}^t \|u(\cdot,s)\|_{L^{p+2}(\Omega)}^{p+2} ds \bigg\}^\frac{1}{p+2}. \end{eqnarray}
\begin{eqnarray} & & \bigg\| \int_{t-\tau}^t \partial_x e^{(t-s)(\Delta-1)} u(\cdot,s) v(\cdot,s) ds \bigg\|_{L^r(\Omega)} ds \nonumber\\ &\le& c_2 \cdot \Big\{ c_4 c_3^{1-a}(T) M^a(T') + c_4 c_3(T)\Big\} \cdot \int_{t-\tau}^t (t-s)^{-\frac{1}{2}-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,s)\|_{L^{p+2}(\Omega)} ds \nonumber\\ &\le& c_2 \cdot \Big\{ c_4 c_3^{1-a}(T) M^a(T') + c_4 c_3(T)\Big\} \cdot \bigg\{ \int_{t-\tau}^t (t-s)^{-[\frac{1}{2}+\frac{1}{2}(1-\frac{1}{r})] \cdot \frac{p+2}{p+1}} ds \bigg\}^\frac{p+1}{p+2} \nonumber\\ & & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\!\! \times \bigg\{ \int_{t-\tau}^t \|u(\cdot,s)\|_{L^{p+2}(\Omega)}^{p+2} ds \bigg\}^\frac{1}{p+2}. \end{eqnarray}
Since herein our assumption
![]() $p>2(r-1)$
warrants that
$p>2(r-1)$
warrants that
 \begin{eqnarray*} \Bigg[\frac{1}{2}+\frac{1}{2}\Big(1-\frac{1}{r}\Big)\Bigg] \cdot \frac{p+2}{p+1} = \frac{2r-1}{2r} \cdot \Big(1+\frac{1}{p+1}\Big) < \frac{2r-1}{2r} \cdot \Big(1+\frac{1}{2r-1}\Big) = 1, \end{eqnarray*}
\begin{eqnarray*} \Bigg[\frac{1}{2}+\frac{1}{2}\Big(1-\frac{1}{r}\Big)\Bigg] \cdot \frac{p+2}{p+1} = \frac{2r-1}{2r} \cdot \Big(1+\frac{1}{p+1}\Big) < \frac{2r-1}{2r} \cdot \Big(1+\frac{1}{2r-1}\Big) = 1, \end{eqnarray*}
and since from Lemma 4.1 we know that
with some
![]() $c_5(T)>0$
satisfying
$c_5(T)>0$
satisfying
it follows from (4.18) that with a certain
![]() $c_6(T)>0$
we have
$c_6(T)>0$
we have
where
Together with (4.12), (4.15) and (4.10), this shows that
with some
![]() $c_7(T)>0$
which due to (4.14) and (4.19) is such that
$c_7(T)>0$
which due to (4.14) and (4.19) is such that
In view of our definition of
![]() $c_1$
, (4.20) entails that if we let
$c_1$
, (4.20) entails that if we let
![]() $c_8(T)\;:=\;\max\{c_7(T),1\}$
then
$c_8(T)\;:=\;\max\{c_7(T),1\}$
then
and thus, since
![]() $a<1$
,
$a<1$
,
Combined with (4.21), this establishes (4.8) and (4.9).
Now, the latter provides sufficient regularity of the inhomogeneity h appearing in the identity
![]() $u_t=u_{xx}+h$
in (1.1), that is, of
$u_t=u_{xx}+h$
in (1.1), that is, of
![]() $h\;:=\;-\chi(\frac{u}{v}v_x)_x -uv+B_1$
, and especially in the crucial cross-diffusive first summand therein. This is obtained by the following statement which beyond boundedness of u, as required for extending the solution via Lemma 2.1, moreover asserts a favourable equicontinuity feature of u that will be useful in verifying the uniform decay property claimed in Theorem 1.2.
$h\;:=\;-\chi(\frac{u}{v}v_x)_x -uv+B_1$
, and especially in the crucial cross-diffusive first summand therein. This is obtained by the following statement which beyond boundedness of u, as required for extending the solution via Lemma 2.1, moreover asserts a favourable equicontinuity feature of u that will be useful in verifying the uniform decay property claimed in Theorem 1.2.
Lemma 4.3 Let
![]() $\gamma\in (0,\frac{1}{3})$
be such that
$\gamma\in (0,\frac{1}{3})$
be such that
![]() $\gamma<\frac{1}{1+2\chi^2}$
. Then for all
$\gamma<\frac{1}{1+2\chi^2}$
. Then for all
![]() $T>0$
, there exists
$T>0$
, there exists
![]() $C(T)>0$
with the properties that with
$C(T)>0$
with the properties that with
![]() $\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
$\widehat{T}_{max}\;:=\;\min\{T,T_{max}\}$
and
![]() $\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
we have
$\tau\;:=\;\min\{1,\frac{1}{3}T_{max}\}$
we have
and
Proof. Since
![]() $\gamma<\frac{1}{3}$
and
$\gamma<\frac{1}{3}$
and
![]() $\gamma<\frac{1}{1+2\chi^2}$
, it is possible to fix
$\gamma<\frac{1}{1+2\chi^2}$
, it is possible to fix
![]() $r>1$
such that
$r>1$
such that
![]() $r<\frac{3}{2}$
and
$r<\frac{3}{2}$
and
![]() $r<1+\frac{1}{2\chi^2}$
, and such that
$r<1+\frac{1}{2\chi^2}$
, and such that
![]() $1-\frac{1}{r}>\gamma$
. This enables us to choose some
$1-\frac{1}{r}>\gamma$
. This enables us to choose some
![]() $\alpha\in (0,\frac{1}{2})$
sufficiently close to
$\alpha\in (0,\frac{1}{2})$
sufficiently close to
![]() $\frac{1}{2}$
such that still
$\frac{1}{2}$
such that still
![]() $2\alpha-\frac{1}{r}>\gamma$
, which in turn ensures that the sectorial realisation of
$2\alpha-\frac{1}{r}>\gamma$
, which in turn ensures that the sectorial realisation of
![]() $A\;:=\;-(\cdot)_{xx}+1$
under homogeneous Neumann boundary conditions in
$A\;:=\;-(\cdot)_{xx}+1$
under homogeneous Neumann boundary conditions in
![]() $L^r(\Omega)$
has the domain of its fractional power
$L^r(\Omega)$
has the domain of its fractional power
![]() $A^\alpha$
satisfy
$A^\alpha$
satisfy
![]() $D(A^\alpha) \hookrightarrow C^\gamma(\overline{\Omega})$
([Reference Henry17]), meaning that
$D(A^\alpha) \hookrightarrow C^\gamma(\overline{\Omega})$
([Reference Henry17]), meaning that
with some
![]() $c_1>0$
. Moreover, combining known regularisation estimates for the associated semigroup
$c_1>0$
. Moreover, combining known regularisation estimates for the associated semigroup
![]() $(e^{-tA})_{t\ge 0}\equiv (e^{-t} e^{t\Delta})_{t\ge 0}$
([Reference Friedman15, Reference Winkler50]), we can find positive constants
$(e^{-tA})_{t\ge 0}\equiv (e^{-t} e^{t\Delta})_{t\ge 0}$
([Reference Friedman15, Reference Winkler50]), we can find positive constants
![]() $c_2$
and
$c_2$
and
![]() $c_3$
such that for all
$c_3$
such that for all
![]() $t\in (0,1)$
we have
$t\in (0,1)$
we have
and
Now to estimate
we use a variation-of-constants representation associated with the identity:
to see that thanks to (4.24),
 \begin{eqnarray} \frac{1}{c_1} \|u(\cdot,t)\|_{C^\gamma(\overline{\Omega})} &\le& \|A^\alpha u(\cdot,t)\|_{L^r(\Omega)} \nonumber\\[3pt] &\le& \Big\| A^\alpha e^{-\tau A} u(\cdot,t-\tau)\Big\|_{L^r(\Omega)} + \chi \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} \Big(\frac{u(\cdot,s)}{v(\cdot,s)} v_x(\cdot,s)\Big)_x \Big\|_{L^r(\Omega)} ds \nonumber\\[3pt] & & + \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} u(\cdot,s) v(\cdot,s) \Big\|_{L^r(\Omega)} ds + \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} B_1(\cdot,s)\Big\|_{L^r(\Omega)} ds \nonumber\\ & & + \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} u(\cdot,s)\Big\|_{L^r(\Omega)} ds \qquad \mbox{for all } t\in (2\tau,T_{max}). \end{eqnarray}
\begin{eqnarray} \frac{1}{c_1} \|u(\cdot,t)\|_{C^\gamma(\overline{\Omega})} &\le& \|A^\alpha u(\cdot,t)\|_{L^r(\Omega)} \nonumber\\[3pt] &\le& \Big\| A^\alpha e^{-\tau A} u(\cdot,t-\tau)\Big\|_{L^r(\Omega)} + \chi \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} \Big(\frac{u(\cdot,s)}{v(\cdot,s)} v_x(\cdot,s)\Big)_x \Big\|_{L^r(\Omega)} ds \nonumber\\[3pt] & & + \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} u(\cdot,s) v(\cdot,s) \Big\|_{L^r(\Omega)} ds + \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} B_1(\cdot,s)\Big\|_{L^r(\Omega)} ds \nonumber\\ & & + \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} u(\cdot,s)\Big\|_{L^r(\Omega)} ds \qquad \mbox{for all } t\in (2\tau,T_{max}). \end{eqnarray}
Here by (4.25) we see that
 \begin{eqnarray} \|A^\alpha e^{-\tau A} u(\cdot,t-\tau)\|_{L^r(\Omega)} &\le& c_2 \tau^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,t-\tau)\|_{L^1(\Omega)} \nonumber\\[3pt] &\le& c_2 c_4(T) \tau^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \qquad \mbox{for all } t\in (2\tau,\widehat{T}_{max}), \end{eqnarray}
\begin{eqnarray} \|A^\alpha e^{-\tau A} u(\cdot,t-\tau)\|_{L^r(\Omega)} &\le& c_2 \tau^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,t-\tau)\|_{L^1(\Omega)} \nonumber\\[3pt] &\le& c_2 c_4(T) \tau^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \qquad \mbox{for all } t\in (2\tau,\widehat{T}_{max}), \end{eqnarray}
where according to Lemma 2.4 we have taken
![]() $c_4(T)>0$
such that
$c_4(T)>0$
such that
and that
Moreover, in view of our restrictions on r, we see that Lemma 4.2 applies so as to yield
![]() $c_5(T)>0$
satisfying
$c_5(T)>0$
satisfying
and
which combined with the outcome of Lemma 2.5 and the continuity of the embedding
![]() $W^{1,r}(\Omega) \hookrightarrow L^\infty(\Omega)$
shows that there exists
$W^{1,r}(\Omega) \hookrightarrow L^\infty(\Omega)$
shows that there exists
![]() $c_6(T)>0$
such that
$c_6(T)>0$
such that
with
Therefore, in the third integral on the right of (4.27), we may use (4.25) and again (4.29) to estimate
 \begin{eqnarray} \int_{t-\tau}^t \Big\|A^\alpha e^{-(t-s)A} u(\cdot,s)v(\cdot,s)\Big\|_{L^r(\Omega)} ds &\le& c_2 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,s)v(\cdot,s)\|_{L^1(\Omega)} ds \nonumber\\[5pt] &\le& c_2 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,s)\|_{L^1(\Omega)} \|v(\cdot,s)\|_{L^\infty(\Omega)} ds \nonumber\\[5pt] &\le& c_2 c_4(T) c_6(T) \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} ds \nonumber\\[5pt] &=& c_2 c_4(T) c_6(T) c_7 \qquad \mbox{for all } t\in (2\tau,\widehat{T}_{max}), \end{eqnarray}
\begin{eqnarray} \int_{t-\tau}^t \Big\|A^\alpha e^{-(t-s)A} u(\cdot,s)v(\cdot,s)\Big\|_{L^r(\Omega)} ds &\le& c_2 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,s)v(\cdot,s)\|_{L^1(\Omega)} ds \nonumber\\[5pt] &\le& c_2 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,s)\|_{L^1(\Omega)} \|v(\cdot,s)\|_{L^\infty(\Omega)} ds \nonumber\\[5pt] &\le& c_2 c_4(T) c_6(T) \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} ds \nonumber\\[5pt] &=& c_2 c_4(T) c_6(T) c_7 \qquad \mbox{for all } t\in (2\tau,\widehat{T}_{max}), \end{eqnarray}
with
![]() $c_7\;:=\;\int_0^\tau \sigma^{-\alpha-\frac{1}{2}(1-\frac{1}{r})}d\sigma$
being finite since clearly
$c_7\;:=\;\int_0^\tau \sigma^{-\alpha-\frac{1}{2}(1-\frac{1}{r})}d\sigma$
being finite since clearly
![]() $\alpha+\frac{1}{2}(1-\frac{1}{r})<\alpha+\frac{1}{2}<1$
.
$\alpha+\frac{1}{2}(1-\frac{1}{r})<\alpha+\frac{1}{2}<1$
.
Likewise, upon two further applications of (4.25), we obtain from the boundedness of
![]() $B_1$
and (4.29) that
$B_1$
and (4.29) that
 \begin{eqnarray} \!\!\!\! \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} B_1(\cdot,s)\Big\|_{L^r(\Omega)} ds &\le& c_2 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|B_1(\cdot,s)\|_{L^1(\Omega)} ds \nonumber\\[5pt] &\le& c_2 |\Omega| \|B_1\|_{L^\infty(\Omega\times (0,\infty))} \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} ds \nonumber\\[5pt] &=& c_2 |\Omega| \|B_1\|_{L^\infty(\Omega\times (0,\infty))} \cdot c_7 \qquad \mbox{for all } t\in (2\tau,\widehat{T}_{max}) \end{eqnarray}
\begin{eqnarray} \!\!\!\! \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} B_1(\cdot,s)\Big\|_{L^r(\Omega)} ds &\le& c_2 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|B_1(\cdot,s)\|_{L^1(\Omega)} ds \nonumber\\[5pt] &\le& c_2 |\Omega| \|B_1\|_{L^\infty(\Omega\times (0,\infty))} \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} ds \nonumber\\[5pt] &=& c_2 |\Omega| \|B_1\|_{L^\infty(\Omega\times (0,\infty))} \cdot c_7 \qquad \mbox{for all } t\in (2\tau,\widehat{T}_{max}) \end{eqnarray}
and that
 \begin{eqnarray} \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} u(\cdot,s)\Big\|_{L^r(\Omega)} ds &\le& c_2 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,s)\|_{L^1(\Omega)} ds \nonumber\\[5pt] &\le& c_2 c_4(T) c_7 \qquad \mbox{for all } t\in (2\tau,\widehat{T}_{max}). \end{eqnarray}
\begin{eqnarray} \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} u(\cdot,s)\Big\|_{L^r(\Omega)} ds &\le& c_2 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}(1-\frac{1}{r})} \|u(\cdot,s)\|_{L^1(\Omega)} ds \nonumber\\[5pt] &\le& c_2 c_4(T) c_7 \qquad \mbox{for all } t\in (2\tau,\widehat{T}_{max}). \end{eqnarray}
Finally, in the second summand on the right-hand side in (4.27), we use that due to Lemma 2.3,
with some
![]() $c_8(T)>0$
fulfilling
$c_8(T)>0$
fulfilling
From (4.26) and (4.31), we therefore obtain that
 \begin{eqnarray} & & \chi \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} \Big(\frac{u(\cdot,s)}{v(\cdot,s)} v_x(\cdot,s)\Big)_x \Big\|_{L^r(\Omega)} ds \nonumber\\[4pt] &\le& \chi c_3 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}} \Big\|\frac{u(\cdot,s)}{v(\cdot,s)} v_x(\cdot,s) \Big\|_{L^r(\Omega)} ds \nonumber \\[4pt] &\le& \chi c_3 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}} \|u(\cdot,s)\|_{L^\infty(\Omega)} \Big\|\frac{1}{v(\cdot,s)}\Big\|_{L^\infty(\Omega)} \|v_x(\cdot,s)\|_{L^r(\Omega)} ds \nonumber\\[4pt] &\le& \frac{\chi c_3 c_5(T)}{c_8(T)} \|u\|_{L^\infty(\Omega\times (\tau,T'))} \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}} ds \nonumber\\[4pt] &=& \frac{\chi c_3 c_5(T)}{c_8(T)} \|u\|_{L^\infty(\Omega\times (\tau,T'))} \cdot \frac{\tau^{\frac{1}{2}-\alpha}}{\frac{1}{2}-\alpha} \qquad \mbox{for all } t\in (2\tau,T'). \end{eqnarray}
\begin{eqnarray} & & \chi \int_{t-\tau}^t \Big\| A^\alpha e^{-(t-s)A} \Big(\frac{u(\cdot,s)}{v(\cdot,s)} v_x(\cdot,s)\Big)_x \Big\|_{L^r(\Omega)} ds \nonumber\\[4pt] &\le& \chi c_3 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}} \Big\|\frac{u(\cdot,s)}{v(\cdot,s)} v_x(\cdot,s) \Big\|_{L^r(\Omega)} ds \nonumber \\[4pt] &\le& \chi c_3 \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}} \|u(\cdot,s)\|_{L^\infty(\Omega)} \Big\|\frac{1}{v(\cdot,s)}\Big\|_{L^\infty(\Omega)} \|v_x(\cdot,s)\|_{L^r(\Omega)} ds \nonumber\\[4pt] &\le& \frac{\chi c_3 c_5(T)}{c_8(T)} \|u\|_{L^\infty(\Omega\times (\tau,T'))} \int_{t-\tau}^t (t-s)^{-\alpha-\frac{1}{2}} ds \nonumber\\[4pt] &=& \frac{\chi c_3 c_5(T)}{c_8(T)} \|u\|_{L^\infty(\Omega\times (\tau,T'))} \cdot \frac{\tau^{\frac{1}{2}-\alpha}}{\frac{1}{2}-\alpha} \qquad \mbox{for all } t\in (2\tau,T'). \end{eqnarray}
In conclusion, (4.28), (4.35), (4.36), (4.37) and (4.39) show that (4.27) leads to the inequality:
with some
![]() $c_9(T)>0$
about which due to (4.30), (4.32), (4.34) and (4.38) we know that
$c_9(T)>0$
about which due to (4.30), (4.32), (4.34) and (4.38) we know that
Now, by compactness of the first in the embeddings
![]() $C^\gamma(\overline{\Omega})\hookrightarrow L^\infty(\Omega) \hookrightarrow L^1(\Omega)$
, according to an associated Ehrling lemma, it is possible to pick
$C^\gamma(\overline{\Omega})\hookrightarrow L^\infty(\Omega) \hookrightarrow L^1(\Omega)$
, according to an associated Ehrling lemma, it is possible to pick
![]() $c_{10}(T)>0$
such that
$c_{10}(T)>0$
such that
where thanks to (4.41) it can clearly be achieved that
Therefore, (4.40) together with (4.29) implies that
 \begin{eqnarray*} \|u(\cdot,t)\|_{C^\gamma(\overline{\Omega})} &\le& \frac{1}{2} \sup_{s\in (\tau,T')} \|u(\cdot,s)\|_{C^\gamma(\overline{\Omega})} + c_{10}(T) c_4(T) + c_9(T) \\[4pt] &\le& \frac{1}{2} M(T') + c_{10}(T) c_4(T) + c_9(T) \qquad \mbox{for all } t\in (2\tau,T') \end{eqnarray*}
\begin{eqnarray*} \|u(\cdot,t)\|_{C^\gamma(\overline{\Omega})} &\le& \frac{1}{2} \sup_{s\in (\tau,T')} \|u(\cdot,s)\|_{C^\gamma(\overline{\Omega})} + c_{10}(T) c_4(T) + c_9(T) \\[4pt] &\le& \frac{1}{2} M(T') + c_{10}(T) c_4(T) + c_9(T) \qquad \mbox{for all } t\in (2\tau,T') \end{eqnarray*}
and that hence with
![]() $c_{11}\;:=\;\sup_{t\in (\tau,2\tau]} \|u(\cdot,t)\|_{C^\gamma(\overline{\Omega})}$
, we have
$c_{11}\;:=\;\sup_{t\in (\tau,2\tau]} \|u(\cdot,t)\|_{C^\gamma(\overline{\Omega})}$
, we have
 \begin{eqnarray*} M(T') &\le& c_{11} + \sup_{t\in (2\tau,T')} \|u(\cdot,t)\|_{C^\gamma(\overline{\Omega})} \\[4pt] &\le& c_{11} + \frac{1}{2} M(T') + c_{10}(T) c_4(T) + c_9(T). \end{eqnarray*}
\begin{eqnarray*} M(T') &\le& c_{11} + \sup_{t\in (2\tau,T')} \|u(\cdot,t)\|_{C^\gamma(\overline{\Omega})} \\[4pt] &\le& c_{11} + \frac{1}{2} M(T') + c_{10}(T) c_4(T) + c_9(T). \end{eqnarray*}
Thus,
which on letting
![]() $T'\nearrow \widehat{T}_{max}$
yields (4.22) with some
$T'\nearrow \widehat{T}_{max}$
yields (4.22) with some
![]() $C(T)>0$
satisfying (4.23) because of (4.42), (4.30) and (4.41).
$C(T)>0$
satisfying (4.23) because of (4.42), (4.30) and (4.41).
4.1 Proof of Theorem 1.1
By collecting the above positivity and regularity information, we immediately obtain global extensibility of our local-in-time solution:
Proof of Theorem 1.1. Combining Lemma 4.3 with Lemma 2.3 and Lemma 4.2 shows that in (2.1), the second alternative cannot occur, so that actually
![]() $T_{max}=\infty$
and hence all statements result from Lemma 2.1.
$T_{max}=\infty$
and hence all statements result from Lemma 2.1.
4.2 Proof of Theorem 1.2
In view of the above statements on independence of all essential estimates from T when (H2) holds, for the verification of the qualitative properties in Theorem 1.2, only one further ingredient is needed which can be obtained by a refined variant of an argument from Lemma 2.4.
Lemma 4.4 If (H2) and (H1’) are satisfied, then
Proof. Since Lemma 2.3 provides
![]() $c_1>0$
such that
$c_1>0$
such that
![]() $v\ge c_1$
in
$v\ge c_1$
in
![]() $\Omega\times (0,\infty)$
, once more integrating the first equation in (1.1) we obtain that
$\Omega\times (0,\infty)$
, once more integrating the first equation in (1.1) we obtain that
In view of the hypothesis (H1’), the claim therefore results by an application of Lemma 7.2.
We can thereby prove our main result on large time behaviour in (1.1), (1.4), (1.5) in presence of the hypothesis (H2).
Proof of Theorem 1.2. Assuming that (H2) be valid, from Lemma 4.3 we obtain
![]() $\gamma>0$
and
$\gamma>0$
and
![]() $c_1>0$
such that
$c_1>0$
such that
This immediately implies (1.9), whereas the inequalities in (1.10) result from Lemma 2.3, Lemma 2.5 and Lemma 4.2, again because
![]() $W^{1,r}(\Omega) \hookrightarrow L^\infty(\Omega)$
for arbitrary
$W^{1,r}(\Omega) \hookrightarrow L^\infty(\Omega)$
for arbitrary
![]() $r>1$
. Finally, as the ArzelÀ–Ascoli theorem says that (4.44) implies precompactness of
$r>1$
. Finally, as the ArzelÀ–Ascoli theorem says that (4.44) implies precompactness of
![]() $(u(\cdot,t))_{t>1}$
in
$(u(\cdot,t))_{t>1}$
in
![]() $L^\infty(\Omega)$
, the outcome of Lemma 4.4, asserting that (H1’) entails decay of
$L^\infty(\Omega)$
, the outcome of Lemma 4.4, asserting that (H1’) entails decay of
![]() $u(\cdot,t)$
in
$u(\cdot,t)$
in
![]() $L^1(\Omega)$
as
$L^1(\Omega)$
as
![]() $t\to\infty$
, actually means that we must even have
$t\to\infty$
, actually means that we must even have
![]() $u(\cdot,t)\to 0$
in
$u(\cdot,t)\to 0$
in
![]() $L^\infty(\Omega)$
as
$L^\infty(\Omega)$
as
![]() $t\to\infty$
in this case.
$t\to\infty$
in this case.
5 Bounds for v under the assumption (H1). Proof of Theorem 1.3
In order to prove Theorem 1.3, we evidently may no longer rely on any global positivity property of v, which in view of the singular taxis term in (1.1) apparently reduces our information on regularity of u to a substantial extent. Our approach will therefore alternatively focus on the derivation of further bounds for v by merely using the second equation in (1.1) together with the class of fundamental estimates from Lemma 3.3, taking essential advantage from the freedom to choose the parameters p and q there within a suitably large range.
Our argument will at its core be quite simple in that it is built on a straightforward
![]() $L^r$
testing procedure (see Lemma 5.4); however, for adequately estimating the crucial integrals
$L^r$
testing procedure (see Lemma 5.4); however, for adequately estimating the crucial integrals
![]() $\int_\Omega uv^r$
appearing therein, we will create an iterative set-up which allows the eventual choosing of an arbitrarily large r whenever
$\int_\Omega uv^r$
appearing therein, we will create an iterative set-up which allows the eventual choosing of an arbitrarily large r whenever
![]() $\chi$
satisfies the smallness condition from Theorem 1.3.
$\chi$
satisfies the smallness condition from Theorem 1.3.
Let us first reformulate the outcome of Lemma 3.3 in a version convenient for our purpose.
Lemma 5.1 Assume that (H1) holds, and let
![]() $p\in (0,1)$
and
$p\in (0,1)$
and
![]() $q>0$
be such that
$q>0$
be such that
![]() $p<\frac{1}{\chi^2}$
and
$p<\frac{1}{\chi^2}$
and
![]() $q\in (q^-(p),q^+(p))$
with
$q\in (q^-(p),q^+(p))$
with
![]() $q^\pm(p)$
as given by (3.9). Then there exists
$q^\pm(p)$
as given by (3.9). Then there exists
![]() $C>0$
such that
$C>0$
such that
Proof. Since
 \begin{eqnarray*} \left[\Big(u^\frac{p}{2} v^\frac{q}{2}\Big)_x\right]^2 &=& \Big(\frac{p}{2} u^\frac{p-2}{2} v^\frac{q}{2} u_x + \frac{q}{2} u^\frac{p}{2} v^\frac{q-2}{2} v_x\Big)^2 \\ &\le& \frac{p^2}{2} u^{p-2} v^q u_x^2 + \frac{q^2}{2} u^p v^{q-2} v_x^2 \qquad \mbox{in } \Omega\times (0,\infty), \end{eqnarray*}
\begin{eqnarray*} \left[\Big(u^\frac{p}{2} v^\frac{q}{2}\Big)_x\right]^2 &=& \Big(\frac{p}{2} u^\frac{p-2}{2} v^\frac{q}{2} u_x + \frac{q}{2} u^\frac{p}{2} v^\frac{q-2}{2} v_x\Big)^2 \\ &\le& \frac{p^2}{2} u^{p-2} v^q u_x^2 + \frac{q^2}{2} u^p v^{q-2} v_x^2 \qquad \mbox{in } \Omega\times (0,\infty), \end{eqnarray*}
by Young’s inequality, this is an immediate consequence of Lemma 3.3.
A zero-order estimate for the coupled quantities appearing in the preceding lemma can be achieved by combining Lemma 2.4 with a supposedly known bound for v in
![]() $L^{r_\star}(\Omega)$
in a straightforward manner.
$L^{r_\star}(\Omega)$
in a straightforward manner.
Lemma 5.2 Assume that (H1) holds, and let
![]() $r_\star\ge 1, p>0$
and
$r_\star\ge 1, p>0$
and
![]() $q>0$
. Then there exists
$q>0$
. Then there exists
![]() $C>0$
with the property that if with some
$C>0$
with the property that if with some
![]() $K>0$
we have
$K>0$
we have
then
Proof. According to the hypothesis (H1), from Lemma 2.4 we know that
with some
![]() $c_1>0$
. By the Hölder inequality, we therefore obtain that
$c_1>0$
. By the Hölder inequality, we therefore obtain that
due to (5.2).
We can thereby achieve the following estimate for the crucial term
![]() $\int_\Omega uv^r$
appearing in Lemma 5.4 below, for certain r depending on the invested integrability parameter
$\int_\Omega uv^r$
appearing in Lemma 5.4 below, for certain r depending on the invested integrability parameter
![]() $r_\star$
.
$r_\star$
.
Lemma 5.3 Assume (H1) and suppose that there exists
![]() $r_\star\ge 1$
such that
$r_\star\ge 1$
such that
Moreover, let
![]() $p\in (0,1)$
be such that
$p\in (0,1)$
be such that
![]() $p<\frac{1}{\chi^2}$
, and with
$p<\frac{1}{\chi^2}$
, and with
![]() $q^\pm(p)$
as given by (3.9), let
$q^\pm(p)$
as given by (3.9), let
![]() $q\in (q^-(p),q^+(p))$
satisfy
$q\in (q^-(p),q^+(p))$
satisfy
Then there exists
![]() $C>0$
such that
$C>0$
such that
Proof. From Lemma 5.2, we know that due to (5.4) we can pick
![]() $c_1>0$
such that
$c_1>0$
such that
and since (5.5) warrants that
 \begin{eqnarray*} \frac{2q}{p[(p+1)r_\star+q]} = \frac{2}{p\cdot \Big[\frac{(p+1)r_\star}{q}+1\Big]} \le \frac{2}{p\cdot\Big[\frac{1-p}{p}+1\Big]} =2, \end{eqnarray*}
\begin{eqnarray*} \frac{2q}{p[(p+1)r_\star+q]} = \frac{2}{p\cdot \Big[\frac{(p+1)r_\star}{q}+1\Big]} \le \frac{2}{p\cdot\Big[\frac{1-p}{p}+1\Big]} =2, \end{eqnarray*}
we may combine the outcome of Lemma 5.1 with Young’s inequality to obtain
![]() $c_2>0$
fulfilling
$c_2>0$
fulfilling
As a Gagliardo–Nirenberg inequality ([Reference Winkler48, Lemma 2.2]) provides
![]() $c_3>0$
such that
$c_3>0$
such that
combining (5.8) with (5.7) we thus infer that
 \begin{eqnarray*} \int_t^{t+1} \int_\Omega uv^\frac{q}{p} &=& \int_t^{t+1} \Big\|u^\frac{p}{2}(\cdot,s) v^\frac{q}{2}(\cdot,s)\Big\|_{L^\frac{2}{p}(\Omega)}^\frac{2}{p} ds \\[5pt] &\le& c_3 \int_t^{t+1} \Big\| \Big(u^\frac{p}{2}(\cdot,s)v^\frac{q}{2}(\cdot,s)\Big)_x \Big\|_{L^2(\Omega)}^\frac{2q}{p[(p+1)r_\star+q]} \Big\| u^\frac{p}{2}(\cdot,s)v^\frac{q}{2}(\cdot,s) \Big\|_{L^\frac{2r_\star}{pr_\star+q}(\Omega)}^\frac{2(p+1)r_\star}{p[(p+1)r_\star+q]} ds \\[5pt] & & + c_3 \int_t^{t+1} \Big\|u^\frac{p}{2}(\cdot,s)v^\frac{q}{2}(\cdot,s) \Big\|_{L^\frac{2r_\star}{pr_\star+q}(\Omega)}^\frac{2}{p} ds \\[5pt] &\le& c_3 \cdot c_2 c_1^\frac{2(p+1)r_\star}{p[(p+1)r_\star+q]} + c_3 \cdot c_1^\frac{2}{p} \end{eqnarray*}
\begin{eqnarray*} \int_t^{t+1} \int_\Omega uv^\frac{q}{p} &=& \int_t^{t+1} \Big\|u^\frac{p}{2}(\cdot,s) v^\frac{q}{2}(\cdot,s)\Big\|_{L^\frac{2}{p}(\Omega)}^\frac{2}{p} ds \\[5pt] &\le& c_3 \int_t^{t+1} \Big\| \Big(u^\frac{p}{2}(\cdot,s)v^\frac{q}{2}(\cdot,s)\Big)_x \Big\|_{L^2(\Omega)}^\frac{2q}{p[(p+1)r_\star+q]} \Big\| u^\frac{p}{2}(\cdot,s)v^\frac{q}{2}(\cdot,s) \Big\|_{L^\frac{2r_\star}{pr_\star+q}(\Omega)}^\frac{2(p+1)r_\star}{p[(p+1)r_\star+q]} ds \\[5pt] & & + c_3 \int_t^{t+1} \Big\|u^\frac{p}{2}(\cdot,s)v^\frac{q}{2}(\cdot,s) \Big\|_{L^\frac{2r_\star}{pr_\star+q}(\Omega)}^\frac{2}{p} ds \\[5pt] &\le& c_3 \cdot c_2 c_1^\frac{2(p+1)r_\star}{p[(p+1)r_\star+q]} + c_3 \cdot c_1^\frac{2}{p} \end{eqnarray*}
for all
![]() $t>0$
.
$t>0$
.
We are now prepared for the announced testing procedure.
Lemma 5.4 Suppose that (H1) holds and that
for some
![]() $r_\star\ge 1$
, and let
$r_\star\ge 1$
, and let
![]() $p\in (0,1)$
be such that
$p\in (0,1)$
be such that
![]() $p<\frac{1}{\chi^2}$
. Then with
$p<\frac{1}{\chi^2}$
. Then with
![]() $q^\pm(p)$
taken from (3.9), for all
$q^\pm(p)$
taken from (3.9), for all
![]() $q\in (q^-(p),q^+(p))$
fulfilling
$q\in (q^-(p),q^+(p))$
fulfilling
one can find
![]() $C>0$
such that
$C>0$
such that
Proof. Since
![]() $\Omega$
is bounded, in view of (5.9), it is sufficient to consider the case when
$\Omega$
is bounded, in view of (5.9), it is sufficient to consider the case when
![]() $r\;:=\;\frac{q}{p}$
satisfies
$r\;:=\;\frac{q}{p}$
satisfies
![]() $r>1$
, and then testing the second equation in (1.1) against
$r>1$
, and then testing the second equation in (1.1) against
![]() $v^{r-1}$
shows that
$v^{r-1}$
shows that
Here, Young’s inequality and the boundedness of
![]() $B_2$
show that there exists
$B_2$
show that there exists
![]() $c_1>0$
such that
$c_1>0$
such that
so that
![]() $y(t)\;:=\;\int_\Omega v^r(\cdot,t)$
,
$y(t)\;:=\;\int_\Omega v^r(\cdot,t)$
,
![]() $t\ge 0$
, satisfies
$t\ge 0$
, satisfies
Now, thanks to our assumptions on p and q, we may apply Lemma 5.3 to conclude from (5.9) that there exists
![]() $c_2>0$
fulfilling
$c_2>0$
fulfilling
and therefore Lemma A.1 ensures that (5.11) is a consequence of (5.12).
5.1 Preparations for a recursive argument
As Lemma 5.4 suggests, our strategy towards improved estimates for v will consist in a bootstrap-type procedure, in the first step choosing
![]() $r_\star\;:=\;1$
in Lemma 5.4 and in each step seeking to maximise the exponent
$r_\star\;:=\;1$
in Lemma 5.4 and in each step seeking to maximise the exponent
![]() $\frac{q}{p}$
appearing in (5.11) according to our overall restrictions on p and q as well as (5.10). In order to create an appropriate framework for our iteration, let us introduce certain auxiliary functions and summarise some of their elementary properties, in the following lemma.
$\frac{q}{p}$
appearing in (5.11) according to our overall restrictions on p and q as well as (5.10). In order to create an appropriate framework for our iteration, let us introduce certain auxiliary functions and summarise some of their elementary properties, in the following lemma.
Lemma 5.5 Let
![]() $p_\star\;:=\;\min\{1,\frac{1}{\chi^2}\}$
as well as
$p_\star\;:=\;\min\{1,\frac{1}{\chi^2}\}$
as well as
for
![]() $p\in (0,p_\star)$
. Then
$p\in (0,p_\star)$
. Then
and we have
and
as well as
Proof. All statements can be verified by elementary computations.
Now the following observation explains the role of our smallness condition on
![]() $\chi$
from Theorem 1.3.
$\chi$
from Theorem 1.3.
Lemma 5.6 Suppose that
![]() $\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
. Then
$\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
. Then
is valid for the number
satisfying
Proof. We only need to observe that our assumption on
![]() $\chi$
warrants that
$\chi$
warrants that
which namely in particular yields (5.20) and moreover implies that by (5.13),
 \begin{eqnarray*} \frac{\varphi_3(p_0)}{\varphi_1(p_0)} -1 &=& \frac{(1-p_0)^2}{2p_0(p_0+1)} \cdot \Big(1-\sqrt{1-p_0\chi^2}\Big) -1 \\[5pt] &<& \frac{(1-p_0)^2}{2p_0(p_0+1)} \cdot \frac{1}{2} -1 \\[1mm] &=& 0, \end{eqnarray*}
\begin{eqnarray*} \frac{\varphi_3(p_0)}{\varphi_1(p_0)} -1 &=& \frac{(1-p_0)^2}{2p_0(p_0+1)} \cdot \Big(1-\sqrt{1-p_0\chi^2}\Big) -1 \\[5pt] &<& \frac{(1-p_0)^2}{2p_0(p_0+1)} \cdot \frac{1}{2} -1 \\[1mm] &=& 0, \end{eqnarray*}
as claimed.
Indeed, the latter property allows us to construct an increasing divergent sequence
![]() $(r_k)_{k\in\mathbb{N}}$
of exponents to be used in Lemma 5.4.
$(r_k)_{k\in\mathbb{N}}$
of exponents to be used in Lemma 5.4.
Lemma 5.7 Suppose that
![]() $\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
, and that
$\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
, and that
![]() $p_0$
is as in Lemma 5.6. Then for each
$p_0$
is as in Lemma 5.6. Then for each
![]() $r\ge 1$
, the set
$r\ge 1$
, the set
is not empty, and letting
![]() $r_0\;:=\;1$
as well as
$r_0\;:=\;1$
as well as
and
recursively defines sequences
![]() $(p_k)_{k\in\mathbb{N}} \subset (0,p_0]$
and
$(p_k)_{k\in\mathbb{N}} \subset (0,p_0]$
and
![]() $(r_k)_{k\in\mathbb{N}} \subset (1,\infty)$
satisfying
$(r_k)_{k\in\mathbb{N}} \subset (1,\infty)$
satisfying
and
as well as
Moreover, writing
we have
as well as
Proof. Observing that
![]() $\varphi_1$
and
$\varphi_1$
and
![]() $\varphi_2$
are well defined on
$\varphi_2$
are well defined on
![]() $(0,p_0)$
due to the fact that with
$(0,p_0)$
due to the fact that with
![]() $p_\star$
as in Lemma 5.5 we have
$p_\star$
as in Lemma 5.5 we have
![]() $p_0<\frac{1}{\chi^2} \le p_\star$
by (5.20), from (5.15) and (5.16) we see that
$p_0<\frac{1}{\chi^2} \le p_\star$
by (5.20), from (5.15) and (5.16) we see that
implying that indeed
![]() $S(r)\ne\emptyset$
for all
$S(r)\ne\emptyset$
for all
![]() $r\ge 1$
and that hence the definitions of
$r\ge 1$
and that hence the definitions of
![]() $(p_k)_{k\in\mathbb{N}}$
and
$(p_k)_{k\in\mathbb{N}}$
and
![]() $(r_k)_{k\in\mathbb{N}}$
are meaningful. Moreover, from (5.22) and (5.21), it is evident that
$(r_k)_{k\in\mathbb{N}}$
are meaningful. Moreover, from (5.22) and (5.21), it is evident that
![]() $p_k\in (0,p_0]$
for all
$p_k\in (0,p_0]$
for all
![]() $k\in\mathbb{N}$
, whereas (5.23) together with (5.15) guarantees (5.25) and that thus also the inclusion
$k\in\mathbb{N}$
, whereas (5.23) together with (5.15) guarantees (5.25) and that thus also the inclusion
![]() $(r_k)_{k\in\mathbb{N}} \subset (1,\infty)$
holds; as therefore
$(r_k)_{k\in\mathbb{N}} \subset (1,\infty)$
holds; as therefore
![]() $S(r_k) \subset S(r_{k-1})$
for all
$S(r_k) \subset S(r_{k-1})$
for all
![]() $k\in\mathbb{N}$
, it is also clear that (5.24) is valid.
$k\in\mathbb{N}$
, it is also clear that (5.24) is valid.
In order to verify (5.26), assuming on the contrary that
with some
![]() $r_\infty \in (1,\infty)$
, we would firstly obtain from (5.24) that
$r_\infty \in (1,\infty)$
, we would firstly obtain from (5.24) that
for otherwise there would exist
![]() $p_\infty \in (0,p_0]$
such that
$p_\infty \in (0,p_0]$
such that
![]() $p_k\ge p_\infty$
for all
$p_k\ge p_\infty$
for all
![]() $k\in\mathbb{N}$
, which by (5.13) would imply that
$k\in\mathbb{N}$
, which by (5.13) would imply that
![]() $\varphi_1(p_k)\ge c_1\;:=\;\varphi_1(p_\infty)>1$
for all
$\varphi_1(p_k)\ge c_1\;:=\;\varphi_1(p_\infty)>1$
for all
![]() $k\in\mathbb{N}$
and that hence
$k\in\mathbb{N}$
and that hence
![]() $r_k\ge c_1 r_{k-1}$
for all
$r_k\ge c_1 r_{k-1}$
for all
![]() $k\in\mathbb{N}$
due to (5.23), clearly contradicting the assumed boundedness property of
$k\in\mathbb{N}$
due to (5.23), clearly contradicting the assumed boundedness property of
![]() $(r_k)_{k\in\mathbb{N}}$
. In particular, (5.31) entails the existence of
$(r_k)_{k\in\mathbb{N}}$
. In particular, (5.31) entails the existence of
![]() $k_0\in\mathbb{N}$
such that
$k_0\in\mathbb{N}$
such that
because if this was false then for all
![]() $k\in\mathbb{N}$
we would have
$k\in\mathbb{N}$
we would have
![]() $\varphi_2(p)>\varphi_1(p)\cdot r_k$
for any
$\varphi_2(p)>\varphi_1(p)\cdot r_k$
for any
![]() $p\in (0,p_0)$
and thus
$p\in (0,p_0)$
and thus
![]() $p_k=p_0$
for all
$p_k=p_0$
for all
![]() $k\in\mathbb{N}$
by (5.22). Now combining (5.32) with (5.31), however, again using (5.16) we could infer that
$k\in\mathbb{N}$
by (5.22). Now combining (5.32) with (5.31), however, again using (5.16) we could infer that
which is incompatible with the observation that
as asserted by (5.31), (5.15) and (5.30).
To see that the numbers
![]() $q_k$
in (5.27) have the claimed properties, we firstly use their definition along with those of
$q_k$
in (5.27) have the claimed properties, we firstly use their definition along with those of
![]() $r_k$
and
$r_k$
and
![]() $\varphi_1$
to find that
$\varphi_1$
to find that
while from (5.22) and (5.21) it follows that
![]() $\varphi_1(p_k)\cdot r_{k-1} \le \varphi_2(p_k)$
and thus
$\varphi_1(p_k)\cdot r_{k-1} \le \varphi_2(p_k)$
and thus
Finally, for the derivation of the left inequality in (5.28), we make use of the property (5.18) of
![]() $p_0$
: Namely, if
$p_0$
: Namely, if
![]() $k\in\mathbb{N}$
is such that
$k\in\mathbb{N}$
is such that
![]() $\varphi_2(p)\ge \varphi_1(p) \cdot r_k$
for all
$\varphi_2(p)\ge \varphi_1(p) \cdot r_k$
for all
![]() $p\in (0,p_0)$
, then (5.22) says that
$p\in (0,p_0)$
, then (5.22) says that
![]() $p_k=p_0$
and therefore, by (5.27), (5.23), (5.25), (5.18) and (5.13),
$p_k=p_0$
and therefore, by (5.27), (5.23), (5.25), (5.18) and (5.13),
 \begin{eqnarray*} q_k &=& p_k r_k = p_k \varphi_1(p_k) r_{k-1} = p_0 \varphi_1(p_0) r_{k-1} \ge p_0 \varphi_1(p_0) \\ &>& p_0 \varphi_3(p_0) = p_k \varphi_3(p_k) = \frac{1-p_k}{2}\Big( 1-\sqrt{1-p_k\chi^2}\Big) = q^-(p_k). \end{eqnarray*}
\begin{eqnarray*} q_k &=& p_k r_k = p_k \varphi_1(p_k) r_{k-1} = p_0 \varphi_1(p_0) r_{k-1} \ge p_0 \varphi_1(p_0) \\ &>& p_0 \varphi_3(p_0) = p_k \varphi_3(p_k) = \frac{1-p_k}{2}\Big( 1-\sqrt{1-p_k\chi^2}\Big) = q^-(p_k). \end{eqnarray*}
On the other hand, in the case when
![]() $k\in\mathbb{N}$
is such that
$k\in\mathbb{N}$
is such that
![]() $\inf_{p\in (0,p_0)} \big\{ \varphi_2(p)-\varphi_1(p)\cdot r_k\big\}$
is negative, (5.22) implies that necessarily
$\inf_{p\in (0,p_0)} \big\{ \varphi_2(p)-\varphi_1(p)\cdot r_k\big\}$
is negative, (5.22) implies that necessarily
![]() $\varphi_2(p_k)=\varphi_1(p_k)\cdot r_{k-1}$
, so that
$\varphi_2(p_k)=\varphi_1(p_k)\cdot r_{k-1}$
, so that
because the restriction
![]() $p_k\le p_0$
together with (5.20) ensures that
$p_k\le p_0$
together with (5.20) ensures that
![]() $\sqrt{1-p_k \chi^2}$
must be positive.
$\sqrt{1-p_k \chi^2}$
must be positive.
5.2 Boundedness of v in
 $\textbf{L}^{\textbf{r}}\textbf{(}\boldsymbol{\Omega}\textbf{)}$
for arbitrary
$\textbf{L}^{\textbf{r}}\textbf{(}\boldsymbol{\Omega}\textbf{)}$
for arbitrary
 $\textbf{r}\textbf{<}\boldsymbol{\infty}$
$\textbf{r}\textbf{<}\boldsymbol{\infty}$
A straightforward induction on the basis of Lemma 5.4 and Lemma 5.7 leads to the following.
Lemma 5.8 Let
![]() $\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
and suppose that (H1) holds, and let
$\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
and suppose that (H1) holds, and let
![]() $(r_k)_{k\in\mathbb{N}_0} \subset [1,\infty)$
be as in Lemma 5.7. Then for all
$(r_k)_{k\in\mathbb{N}_0} \subset [1,\infty)$
be as in Lemma 5.7. Then for all
![]() $k\in\mathbb{N}_0$
and any
$k\in\mathbb{N}_0$
and any
![]() $r\in (1,r_k)\cup \{1\}$
, there exists
$r\in (1,r_k)\cup \{1\}$
, there exists
![]() $C>0$
such that
$C>0$
such that
Proof. Since for
![]() $k=0$
this has been asserted by Lemma 2.5, in view of an inductive argument, we only need to make sure that if for some
$k=0$
this has been asserted by Lemma 2.5, in view of an inductive argument, we only need to make sure that if for some
![]() $k\in\mathbb{N}$
we have
$k\in\mathbb{N}$
we have
then
In verifying this, by boundedness of
![]() $\Omega$
, we may concentrate on values of
$\Omega$
, we may concentrate on values of
![]() $r\in (1,r_k)$
which are sufficiently close to
$r\in (1,r_k)$
which are sufficiently close to
![]() $r_k$
such that with
$r_k$
such that with
![]() $p_k$
as in Lemma 5.7 and
$p_k$
as in Lemma 5.7 and
![]() $q^-(p_k)$
taken from (3.9) we have
$q^-(p_k)$
taken from (3.9) we have
which is possible since from (5.27) and (5.28) we know that
We now let
and
and observe that then
by (5.36) and
by (5.27) and (5.28), whereas (5.38) ensures that
From (5.38), it moreover follows that if
![]() $r_\star>1$
then since
$r_\star>1$
then since
![]() $r<r_k$
implies that
$r<r_k$
implies that
![]() $q<q_k$
, we have
$q<q_k$
, we have
according to (5.29). As thus (5.34) warrants that
in view of (5.39), (5.40) and (5.41) we may apply Lemma 5.4 to find
![]() $c_1>0$
such that
$c_1>0$
such that
which thanks to (5.37) yields (5.35), because r was an arbitrary number in the range described in (5.35) and (5.36).
In particular, v remains bounded in
![]() $L^r(\Omega)$
for arbitrarily large finite r:
$L^r(\Omega)$
for arbitrarily large finite r:
Corollary 5.9 Let
![]() $\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
and assume (H1). Then for all
$\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
and assume (H1). Then for all
![]() $r\ge 1$
, there exists
$r\ge 1$
, there exists
![]() $C>0$
such that
$C>0$
such that
Proof. Since Lemma 5.7 asserts that the sequence
![]() $(r_k)_{k\in\mathbb{N}}$
introduced there has the property that
$(r_k)_{k\in\mathbb{N}}$
introduced there has the property that
![]() $r_k\to\infty$
as
$r_k\to\infty$
as
![]() $k\to\infty$
, this is an immediate consequence of Lemma 5.8.
$k\to\infty$
, this is an immediate consequence of Lemma 5.8.
5.3 Hölder regularity of v
Once more relying on the first-order estimate provided by Lemma 5.1 and the basic property
![]() $\int_0^\infty \int_\Omega uv<\infty$
asserted by Lemma 2.4, from Corollary 5.9 we can now derive boundedness, and even a certain temporal decay, of the forcing term uv from the second equation in (1.1) with respect to some superquadratic space-time Lebesgue norm.
$\int_0^\infty \int_\Omega uv<\infty$
asserted by Lemma 2.4, from Corollary 5.9 we can now derive boundedness, and even a certain temporal decay, of the forcing term uv from the second equation in (1.1) with respect to some superquadratic space-time Lebesgue norm.
Lemma 5.10 Let
![]() $\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
, and assume (H1).
$\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
, and assume (H1).
Then
Proof. We first note that taking
![]() $\xi\to\infty$
in Lemma 2.4 shows that our hypothesis (H1) warrants that
$\xi\to\infty$
in Lemma 2.4 shows that our hypothesis (H1) warrants that
![]() $\int_0^\infty \int_\Omega uv<\infty$
and hence
$\int_0^\infty \int_\Omega uv<\infty$
and hence
In view of an interpolation argument, it is therefore sufficient to make sure that we can find
![]() $r>2$
and
$r>2$
and
![]() $c_1>0$
such that
$c_1>0$
such that
For this purpose, we let
![]() $p\;:=\;\frac{1}{5}$
and observe that since our assumption warrants that
$p\;:=\;\frac{1}{5}$
and observe that since our assumption warrants that
![]() $\chi^2<5$
, the numbers
$\chi^2<5$
, the numbers
![]() $q^\pm(p)$
from (3.9) are real and satisfy
$q^\pm(p)$
from (3.9) are real and satisfy
 \begin{eqnarray*} && q^+(p) -p=\frac{1-3p}{2}+\frac{1-p}{2}\sqrt{1-p\chi^2} >0 \qquad \mbox{as well as} \qquad \\[5pt] && q^-(p) -2p=\frac{1-5p}{2}-\frac{1-p}{2}\sqrt{1-p\chi^2} <0, \end{eqnarray*}
\begin{eqnarray*} && q^+(p) -p=\frac{1-3p}{2}+\frac{1-p}{2}\sqrt{1-p\chi^2} >0 \qquad \mbox{as well as} \qquad \\[5pt] && q^-(p) -2p=\frac{1-5p}{2}-\frac{1-p}{2}\sqrt{1-p\chi^2} <0, \end{eqnarray*}
so that it is possible to fix
![]() $q\in (p,2p)$
such that
$q\in (p,2p)$
such that
![]() $q\in (q^-(p),q^+(p))$
. Then the inequality
$q\in (q^-(p),q^+(p))$
. Then the inequality
![]() $q<2p$
ensures that
$q<2p$
ensures that
![]() $\frac{2(q-p)}{q}<1$
, whence we can take some
$\frac{2(q-p)}{q}<1$
, whence we can take some
![]() $r>2$
with the properties that
$r>2$
with the properties that
![]() $r<p+2$
, and that still
$r<p+2$
, and that still
![]() $\frac{(q-p)r}{q}<1$
. By means of the Hölder inequality, we can therefore estimate
$\frac{(q-p)r}{q}<1$
. By means of the Hölder inequality, we can therefore estimate
 \begin{eqnarray*} \int_\Omega (uv)^r &=& \int_\Omega \Big( u^\frac{p}{2} v^\frac{q}{2}\Big)^\frac{2r}{q} \cdot u^\frac{(q-p)r}{q} \\[5pt] &\le& \bigg\{ \int_\Omega \Big(u^\frac{p}{2} v^\frac{q}{2}\Big)^\frac{2r}{q-(q-p)r} \bigg\}^\frac{q-(q-p)r}{q} \cdot \bigg\{ \int_\Omega u \bigg\}^\frac{(q-p)r}{q} \\[5pt] &\le& c_2 \bigg\{ \int_\Omega \Big(u^\frac{p}{2} v^\frac{q}{2}\Big)^\frac{2r}{q-(q-p)r} \bigg\}^\frac{q-(q-p)r}{q} \\[5pt] &=& c_2 \Big\|u^\frac{p}{2} v^\frac{q}{2}\Big\|_{L^\frac{2r}{q-(q-p)r}(\Omega)}^\frac{2r}{q} \qquad \mbox{for all } t>0, \end{eqnarray*}
\begin{eqnarray*} \int_\Omega (uv)^r &=& \int_\Omega \Big( u^\frac{p}{2} v^\frac{q}{2}\Big)^\frac{2r}{q} \cdot u^\frac{(q-p)r}{q} \\[5pt] &\le& \bigg\{ \int_\Omega \Big(u^\frac{p}{2} v^\frac{q}{2}\Big)^\frac{2r}{q-(q-p)r} \bigg\}^\frac{q-(q-p)r}{q} \cdot \bigg\{ \int_\Omega u \bigg\}^\frac{(q-p)r}{q} \\[5pt] &\le& c_2 \bigg\{ \int_\Omega \Big(u^\frac{p}{2} v^\frac{q}{2}\Big)^\frac{2r}{q-(q-p)r} \bigg\}^\frac{q-(q-p)r}{q} \\[5pt] &=& c_2 \Big\|u^\frac{p}{2} v^\frac{q}{2}\Big\|_{L^\frac{2r}{q-(q-p)r}(\Omega)}^\frac{2r}{q} \qquad \mbox{for all } t>0, \end{eqnarray*}
with
![]() $c_2\;:=\;\sup_{t>0} \|u(\cdot,t)\|_{L^1(\Omega)}^\frac{(q-p)r}{q}$
being finite according to Lemma 2.4 and our assumption that (H1) be valid.
$c_2\;:=\;\sup_{t>0} \|u(\cdot,t)\|_{L^1(\Omega)}^\frac{(q-p)r}{q}$
being finite according to Lemma 2.4 and our assumption that (H1) be valid.
Consequently, using the Gagliardo–Nirenberg inequality, we see that with some
![]() $c_3>0$
we have
$c_3>0$
we have
 \begin{eqnarray} \int_t^{t+1} \int_\Omega (uv)^r &\le& c_3 \int_t^{t+1} \Big\| \Big(u^\frac{p}{2}(\cdot,s) v^\frac{q}{2}(\cdot,s)\Big)_x \Big\|_{L^2(\Omega)}^2 \Big\| u^\frac{p}{2}(\cdot,s) v^\frac{q}{2}(\cdot,s)\Big\|_{L^\frac{2}{p+\varepsilon q}(\Omega)}^\frac{2(r-q)}{q} ds \nonumber\\[5pt] & & + c_3 \int_t^{t+1} \Big\| u^\frac{p}{2}(\cdot,s) v^\frac{q}{2}(\cdot,s)\Big\|_{L^\frac{2}{p+\varepsilon q}(\Omega)}^\frac{2r}{q} ds \qquad \mbox{for all } t>0, \end{eqnarray}
\begin{eqnarray} \int_t^{t+1} \int_\Omega (uv)^r &\le& c_3 \int_t^{t+1} \Big\| \Big(u^\frac{p}{2}(\cdot,s) v^\frac{q}{2}(\cdot,s)\Big)_x \Big\|_{L^2(\Omega)}^2 \Big\| u^\frac{p}{2}(\cdot,s) v^\frac{q}{2}(\cdot,s)\Big\|_{L^\frac{2}{p+\varepsilon q}(\Omega)}^\frac{2(r-q)}{q} ds \nonumber\\[5pt] & & + c_3 \int_t^{t+1} \Big\| u^\frac{p}{2}(\cdot,s) v^\frac{q}{2}(\cdot,s)\Big\|_{L^\frac{2}{p+\varepsilon q}(\Omega)}^\frac{2r}{q} ds \qquad \mbox{for all } t>0, \end{eqnarray}
where we have abbreviated
Now since
![]() $\varepsilon$
is positive because
$\varepsilon$
is positive because
![]() $r<p+2$
and
$r<p+2$
and
![]() $r>2>1>q^+(p)>q$
, and since thus
$r>2>1>q^+(p)>q$
, and since thus
![]() $\frac{2}{p+\varepsilon q}<\frac{2}{p}$
, an application of Lemma 5.2 readily yields
$\frac{2}{p+\varepsilon q}<\frac{2}{p}$
, an application of Lemma 5.2 readily yields
![]() $c_4>0$
such that
$c_4>0$
such that
whereas the inequalities
![]() $p<\min \{1,\frac{1}{\chi^2}\}$
and
$p<\min \{1,\frac{1}{\chi^2}\}$
and
![]() $q^-(p)<q<q^+(p)$
ensure that due to Lemma 5.1 we can find
$q^-(p)<q<q^+(p)$
ensure that due to Lemma 5.1 we can find
![]() $c_5>0$
such that
$c_5>0$
such that
Therefore, (5.44) implies that
and hence proves (5.43) due to our definition of r.
In our first application of this, we only rely on the boundedness property implied by the decay statement in (5.42) to derive boundedness of v even in a space compactly embedded into
![]() $L^\infty(\Omega)$
.
$L^\infty(\Omega)$
.
Lemma 5.11 Let
![]() $\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
and assume (H1). Then there exist
$\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
and assume (H1). Then there exist
![]() $\gamma\in (0,1)$
and
$\gamma\in (0,1)$
and
![]() $C>0$
such that
$C>0$
such that
Proof. We fix
![]() $\beta \in (\frac{1}{4},\frac{1}{2})$
and any
$\beta \in (\frac{1}{4},\frac{1}{2})$
and any
![]() $\gamma\in (0,2\beta-\frac{1}{2})$
and then once more refer to known embedding results ([Reference Henry17]) to recall that the sectorial realisation A of
$\gamma\in (0,2\beta-\frac{1}{2})$
and then once more refer to known embedding results ([Reference Henry17]) to recall that the sectorial realisation A of
![]() $-(\cdot)_{xx}+1$
under homogeneous Neumann boundary conditions in
$-(\cdot)_{xx}+1$
under homogeneous Neumann boundary conditions in
![]() $L^2(\Omega)$
has the property that its fractional power
$L^2(\Omega)$
has the property that its fractional power
![]() $A^\beta$
satisfies
$A^\beta$
satisfies
![]() $D(A^\beta) \hookrightarrow C^\gamma(\overline{\Omega})$
. Therefore, writing
$D(A^\beta) \hookrightarrow C^\gamma(\overline{\Omega})$
. Therefore, writing
with
we can estimate
with some
![]() $c_1>0$
. As well-known regularisation features of
$c_1>0$
. As well-known regularisation features of
![]() $(e^{-tA})_{t\ge 0}$
([Reference Friedman15]) warrant the existence of
$(e^{-tA})_{t\ge 0}$
([Reference Friedman15]) warrant the existence of
![]() $c_2>0$
fulfilling
$c_2>0$
fulfilling
by using the Cauchy–Schwarz inequality we infer that
 \begin{eqnarray} \!\!\!\!\!\!\!\!\!\!\!\!\!\! \|v(\cdot,t)\|_{C^\gamma(\overline{\Omega})} &\le& c_1 c_2\|v(\cdot,t-1)\|_{L^2(\Omega)} + c_1 c_2 \int_{t-1}^t (t-s)^{-\beta} \|h(\cdot,s)\|_{L^2(\Omega)} ds \nonumber\\[5pt] &\le& c_1 c_2\|v(\cdot,t-1)\|_{L^2(\Omega)} + c_1 c_2 \bigg\{\! \int_{t-1}^t (t-s)^{-2\beta} ds \!\bigg\}^\frac{1}{2} \bigg\{ \!\int_{t-1}^t \|h(\cdot,s)\|_{L^2(\Omega)}^2 ds \!\bigg\}^\frac{1}{2}\!, \end{eqnarray}
\begin{eqnarray} \!\!\!\!\!\!\!\!\!\!\!\!\!\! \|v(\cdot,t)\|_{C^\gamma(\overline{\Omega})} &\le& c_1 c_2\|v(\cdot,t-1)\|_{L^2(\Omega)} + c_1 c_2 \int_{t-1}^t (t-s)^{-\beta} \|h(\cdot,s)\|_{L^2(\Omega)} ds \nonumber\\[5pt] &\le& c_1 c_2\|v(\cdot,t-1)\|_{L^2(\Omega)} + c_1 c_2 \bigg\{\! \int_{t-1}^t (t-s)^{-2\beta} ds \!\bigg\}^\frac{1}{2} \bigg\{ \!\int_{t-1}^t \|h(\cdot,s)\|_{L^2(\Omega)}^2 ds \!\bigg\}^\frac{1}{2}\!, \end{eqnarray}
for all
![]() $t>1$
, where we note that
$t>1$
, where we note that
thanks to our restriction
![]() $\beta<\frac{1}{2}$
. Since Corollary 5.9 provides
$\beta<\frac{1}{2}$
. Since Corollary 5.9 provides
![]() $c_3>0$
such that
$c_3>0$
such that
and since Lemma 5.10 along with the boundedness of
![]() $B_2$
in
$B_2$
in
![]() $\Omega\times (0,\infty)$
implies that
$\Omega\times (0,\infty)$
implies that
with some
![]() $c_4>0$
, the inequality in (5.45) is thus a consequence of (5.46).
$c_4>0$
, the inequality in (5.45) is thus a consequence of (5.46).
5.4 Stabilisation of v under the hypotheses (H1) and (H3). Proof of Theorem 1.3
As a final preparation for the proof of Theorem 1.3, let us now make full use of the decay property asserted by Lemma 5.10 in order to assert that under the additional assumption (H3), v indeed stabilises toward the desired limit, at least with respect to the topology in
![]() $L^2(\Omega)$
.
$L^2(\Omega)$
.
Lemma 5.12 Let
![]() $\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
and assume that (H1) and (H3) hold with some
$\chi<\frac{\sqrt{6\sqrt{3}+9}}{2}$
and assume that (H1) and (H3) hold with some
![]() $B_{2,\infty} \in L^2(\Omega)$
. Then
$B_{2,\infty} \in L^2(\Omega)$
. Then
where
![]() $v_\infty$
denotes the solution of (1.15).
$v_\infty$
denotes the solution of (1.15).

Figure 1. The evolution of the maximum concentration of criminal
![]() $\|{u(\cdot,t)}\|_{\infty}$
at a short timescale
$\|{u(\cdot,t)}\|_{\infty}$
at a short timescale
![]() $t\in [0,.05]$
with initial condition given by
$t\in [0,.05]$
with initial condition given by
![]() $(u(x,0),v(x,0))=(e^{-x},e^{-x})$
and
$(u(x,0),v(x,0))=(e^{-x},e^{-x})$
and
![]() $B_1 = B_2 =1$
.
$B_1 = B_2 =1$
.

Figure 2. The evolution of the maximum concentration of criminal
![]() $\|{u(\cdot,t)}\|_{\infty}$
at a longer timescale (
$\|{u(\cdot,t)}\|_{\infty}$
at a longer timescale (
![]() $t\in [0,5]$
) with initial condition given by
$t\in [0,5]$
) with initial condition given by
![]() $(u(x,0),v(x,0))=(e^{-x},e^{-x})$
and
$(u(x,0),v(x,0))=(e^{-x},e^{-x})$
and
![]() $B_1 = B_2 =1$
.
$B_1 = B_2 =1$
.

Figure 3. Criminal density u(x,t) at
![]() $t =20$
for various values of
$t =20$
for various values of
![]() $\chi$
.
$\chi$
.
Proof. Using (1.1) and (1.15), we compute
 \begin{align*} \frac{1}{2} \frac{d}{dt} & \int_\Omega (v-v_\infty)^2 \\[5pt] &= \int_\Omega (v-v_\infty)\cdot (v_{xx}+uv-v+B_2) \\[5pt] &= \int_\Omega (v-v_\infty)\cdot \Big\{ (v-v_\infty)_{xx} - (v-v_\infty) + uv + (B_2-B_{2,\infty}) \Big\} \\[5pt] &= - \int_\Omega (v-v_\infty)_x^2 - \int_\Omega (v-v_\infty)^2 + \int_\Omega (v-v_\infty) \cdot \Big\{ uv+ (B_2-B_{2,\infty}) \Big\} \qquad \mbox{for all } t>0, \end{align*}
\begin{align*} \frac{1}{2} \frac{d}{dt} & \int_\Omega (v-v_\infty)^2 \\[5pt] &= \int_\Omega (v-v_\infty)\cdot (v_{xx}+uv-v+B_2) \\[5pt] &= \int_\Omega (v-v_\infty)\cdot \Big\{ (v-v_\infty)_{xx} - (v-v_\infty) + uv + (B_2-B_{2,\infty}) \Big\} \\[5pt] &= - \int_\Omega (v-v_\infty)_x^2 - \int_\Omega (v-v_\infty)^2 + \int_\Omega (v-v_\infty) \cdot \Big\{ uv+ (B_2-B_{2,\infty}) \Big\} \qquad \mbox{for all } t>0, \end{align*}
where the first summand on the right is non-positive, and where the rightmost integral can be estimated by Young’s inequality according to
 \begin{eqnarray*} \int_\Omega (v-v_\infty) \cdot \Big\{ uv+ (B_2-B_{2,\infty}) \Big\} &\le& \frac{1}{2} \int_\Omega (v-v_\infty)^2 + \frac{1}{2} \int_\Omega \Big\{ uv+(B_2-B_{2,\infty}) \Big\}^2 \\[5pt] &\le& \frac{1}{2} \int_\Omega (v-v_\infty)^2 + \int_\Omega (uv)^2 + \int_\Omega (B_2-B_{2,\infty})^2 \quad \mbox{for all } t>0. \end{eqnarray*}
\begin{eqnarray*} \int_\Omega (v-v_\infty) \cdot \Big\{ uv+ (B_2-B_{2,\infty}) \Big\} &\le& \frac{1}{2} \int_\Omega (v-v_\infty)^2 + \frac{1}{2} \int_\Omega \Big\{ uv+(B_2-B_{2,\infty}) \Big\}^2 \\[5pt] &\le& \frac{1}{2} \int_\Omega (v-v_\infty)^2 + \int_\Omega (uv)^2 + \int_\Omega (B_2-B_{2,\infty})^2 \quad \mbox{for all } t>0. \end{eqnarray*}
Therefore,
![]() $y(t)\;:=\;\int_\Omega (v(\cdot,t)-v_\infty)^2$
and
$y(t)\;:=\;\int_\Omega (v(\cdot,t)-v_\infty)^2$
and
![]() $h(t)\;:=\;2\int_\Omega (u(\cdot,t)v(\cdot,t))^2 + 2\int_\Omega (B_2(\cdot,t)-B_{2,\infty})^2$
,
$h(t)\;:=\;2\int_\Omega (u(\cdot,t)v(\cdot,t))^2 + 2\int_\Omega (B_2(\cdot,t)-B_{2,\infty})^2$
,
![]() $t\ge 0$
, satisfy
$t\ge 0$
, satisfy
so that since Lemma 5.10 entails that
and that thus
thanks to (H3), the claimed property (5.47) results from Lemma A.2.
Collecting all the above, we can easily derive our main result on asymptotic behaviour under the assumptions that (H1) and possibly also (H3) hold.
Proof of Theorem 1.3. Supposing that
![]() $\chi < \frac{\sqrt{6\sqrt{3}+9}}{2}$
and that (H1) be valid, we obtain the boundedness property (1.13) of v in
$\chi < \frac{\sqrt{6\sqrt{3}+9}}{2}$
and that (H1) be valid, we obtain the boundedness property (1.13) of v in
![]() $\Omega\times (0,\infty)$
as a consequence of Lemma 5.11 and Lemma 2.1. If moreover (H3) is fulfilled with some
$\Omega\times (0,\infty)$
as a consequence of Lemma 5.11 and Lemma 2.1. If moreover (H3) is fulfilled with some
![]() $B_{2,\infty}\in L^2(\Omega)$
, then from Lemma 5.12 we know that
$B_{2,\infty}\in L^2(\Omega)$
, then from Lemma 5.12 we know that
![]() $v(\cdot,t)\to v_\infty$
in
$v(\cdot,t)\to v_\infty$
in
![]() $L^2(\Omega)$
as
$L^2(\Omega)$
as
![]() $t\to\infty$
. Since Lemma 5.11 actually even warrants precompactness of
$t\to\infty$
. Since Lemma 5.11 actually even warrants precompactness of
![]() $(v(\cdot,t))_{t>1}$
in
$(v(\cdot,t))_{t>1}$
in
![]() $L^\infty(\Omega)$
by means of the ArzelÀ–Ascoli theorem, this already implies the uniform convergence property claimed in (1.14).
$L^\infty(\Omega)$
by means of the ArzelÀ–Ascoli theorem, this already implies the uniform convergence property claimed in (1.14).
6 Numerical results
In this section, we explore the growth of solutions to (1.1) as
![]() $\chi$
increases on small timescales. The effect of large chemotaxis sensitivities on the growth of the solutions has been observed in Keller–Segel-type systems. From numerical simulations, we observe that the
$\chi$
increases on small timescales. The effect of large chemotaxis sensitivities on the growth of the solutions has been observed in Keller–Segel-type systems. From numerical simulations, we observe that the
![]() $L^\infty$
norm of the criminal density increases sharply with
$L^\infty$
norm of the criminal density increases sharply with
![]() $\chi$
in short timescales before relaxing to the steady-state solution. Indeed, the solution quickly relaxes to a steady-state solution once the dissipation is able to dominate. For all numerical experiments, we consider initial data
$\chi$
in short timescales before relaxing to the steady-state solution. Indeed, the solution quickly relaxes to a steady-state solution once the dissipation is able to dominate. For all numerical experiments, we consider initial data
![]() $u(x,0)= e^{-x}$
and
$u(x,0)= e^{-x}$
and
![]() $v(x,0)= e^{-x},$
$v(x,0)= e^{-x},$
![]() $B_1 = B_2 = 1$
and vary the parameter
$B_1 = B_2 = 1$
and vary the parameter
![]() $\chi$
. All numerical computations were made using Matlab’s pdepe function. In Figure 1, we observe the rapid growth on the short timescale (
$\chi$
. All numerical computations were made using Matlab’s pdepe function. In Figure 1, we observe the rapid growth on the short timescale (
![]() $t \in [0,.05]$
with time step
$t \in [0,.05]$
with time step
![]() $\delta t = .001$
). This figure illustrates the fact that the criminal density reaches a higher value as
$\delta t = .001$
). This figure illustrates the fact that the criminal density reaches a higher value as
![]() $\chi$
increases.
$\chi$
increases.
On the other hand, at longer timescales (although not so long
![]() $t\in [0,5]$
with
$t\in [0,5]$
with
![]() $\delta t = .05$
), the dissipation dominates and in all cases we see eventual decay. This is illustrated in Figure 2, where we can see that by time
$\delta t = .05$
), the dissipation dominates and in all cases we see eventual decay. This is illustrated in Figure 2, where we can see that by time
![]() $t=5$
the maximum density of criminals has reached a steady state.
$t=5$
the maximum density of criminals has reached a steady state.
Another interesting thing to note that is that the steady state of the maximum density of criminals increases with
![]() $\chi$
. Thus, we do not see a relaxation to the constant steady states, which in this case are
$\chi$
. Thus, we do not see a relaxation to the constant steady states, which in this case are
![]() $u\equiv \frac{1}{2}$
and
$u\equiv \frac{1}{2}$
and
![]() $v \equiv 2$
. In fact, relaxation to the homogeneous steady states occurs with
$v \equiv 2$
. In fact, relaxation to the homogeneous steady states occurs with
![]() $\chi$
small. However, as
$\chi$
small. However, as
![]() $\chi$
increases we observe to a non-constant hump solution with the maximum at the origin. Figure 3.
$\chi$
increases we observe to a non-constant hump solution with the maximum at the origin. Figure 3.
Acknowledgements
The first author was supported by the NSF Grant DMS-1516778. The second author acknowledges support of the Deutsche Forschungsgemeinschaft in the context of the project Emergence of structures and advantages in cross-diffusion systems (No. 411007140, GZ: WI 3707/5-1).
Conflict of interest
None.
A Appendix: Two ODE lemmata
Let us separately formulate two auxiliary statements on boundedness and decay in linear ODIs with inhomogeneities enjoying certain averaged boundedness and decay properties.
Lemma A.1 Let
![]() $T\in (0,\infty]$
and
$T\in (0,\infty]$
and
![]() $\tau\in (0,T)$
, and let
$\tau\in (0,T)$
, and let
![]() $y\in C^1([0,T))$
and
$y\in C^1([0,T))$
and
![]() $h\in L^1_{loc}([0,\infty))$
be non-negative and such that with some
$h\in L^1_{loc}([0,\infty))$
be non-negative and such that with some
![]() $a>0$
and
$a>0$
and
![]() $b>0$
we have
$b>0$
we have
as well as
Then
Proof. This can be found, for example, in [Reference Winkler54, Lemma 3.4].
Lemma A.2 Let
![]() $y\in C^1([0,\infty))$
and
$y\in C^1([0,\infty))$
and
![]() $h\in L^1_{loc}([0,\infty))$
be non-negative functions satisfying
$h\in L^1_{loc}([0,\infty))$
be non-negative functions satisfying
with some
![]() $a>0$
. Then if
$a>0$
. Then if
we have
Proof. An elementary derivation of this has been given in [Reference Espejo and Winkler13, Lemma 4.6], for instance.