Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-23T04:17:08.426Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-equilibrium imbibition of a porous block

Published online by Cambridge University Press:  26 September 2008

Arkady Gilman
Arkady Gilman
Affiliation:
Faculty of Civil Engineering, Technion – Israel Institute of Technology, Haifa, Israel
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a phenomenological model proposed by Barenblatt [1] for non-equilibrium two-phase flow in porous media. In the case of zero total flow it reduces to a pair of equations:

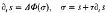
where Φ(σ) is a non-decreasing (not necessarily increasing) smooth function defined in the interval 0 ≤ σ ≤ 1. We consider initial-boundary problems for this system in which the initial data are given only for s, and the boundary data only for ς (which corresponds to the physical sense of the model). The degenerate character of the system allows us to apply simple topological methods. We show that the boundary problem is well-posed, in the sense that there exits a unique (weak) solution which satisfies the maximum principle and depends continuously on the initial data. The solution is no less smooth than the initial and boundary data.

Type
Research Article
Information
European Journal of Applied Mathematics , Volume 7 , Issue 1 , February 1996 , pp. 43 - 52
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barenblatt, G. I. 1971 The flow of two immiscible liquids in homogeneous porous medium. Izvestiya Akademii Nauk SSSR. Mekhanika Zhidkosti i Gaza 5: 144–151 (in Russian).Google Scholar
[2] Bear, J. & Bachmat, Y. 1990 Introduction to Modeling of Transport Phenomena in Porous Media. Kluwer Academic.CrossRefGoogle Scholar
[3] Barenblatt, G. I., Entov, V. M. & Ryzhik, V. M. 1991 Flow of Fluids through Natural Rocks. Kluwer Academic.Google Scholar
[4] Barenblatt, G. I. & Vinnichenko, A. P. 1980 Non-equilibrium filtration of immiscible liquids. Uspechi Mekhaniki 3: 33–50 (in Russian).Google Scholar
[5] Gilman, A. A. 1988 Analogy between two mathematical models in the theory of two-phase filtration. Inzhenerno-Fizicheskii Zhurnal 55(5): 775–778 (in Russian).Google Scholar
[6] Barenblatt, G. I. & Gilman, A. A. 1987 Mathematical model of non-equilibrium counter-current capillary imbibition. Inzhenerno-Fizicheskii Zhurnal 52(3): 456–461 (in Russian) (Also in J. Eng. Phys. in an English translation).Google Scholar
[7] Showalter, R. E. & Ting, T. W. 1970 Pseudoparabolic partial differential equations. SIAM J. Math. Anal. 1(1): 1–26.CrossRefGoogle Scholar
[8] Di Benedetto, E. & Pierre, M. 1981 On the maximum principle for pseudoparabolic equations. Indiana Univ. Math. J. 30(6): 821–854.CrossRefGoogle Scholar
[9] Lions, J. L. 1969 Quelques méthodes de resolution des problèmes aux limites non-linéaires. Dunod.Google Scholar
[10] Fučík, S. & Kufner, A. 1980 Nonlinear Differential Equations. Elsevier.Google Scholar
[11] Yosida, K. 1965 Functional Analysis. Springer-Verlag.Google Scholar