Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Tao
2012.
Optimality Conditions for a Blocking Strategy Involving Delaying Arcs.
Journal of Optimization Theory and Applications,
Vol. 152,
Issue. 2,
p.
307.
Bressan, Alberto
and
Zhang, Dongmei
2012.
Control Problems for a Class of Set Valued Evolutions.
Set-Valued and Variational Analysis,
Vol. 20,
Issue. 4,
p.
581.
Bressan, Alberto
and
Wang, Tao
2012.
On the optimal strategy for an isotropic blocking problem.
Calculus of Variations and Partial Differential Equations,
Vol. 45,
Issue. 1-2,
p.
125.
Bressan, Alberto
2013.
Advances in Applied Mathematics, Modeling, and Computational Science.
Vol. 66,
Issue. ,
p.
11.
Wang, Tao
2014.
Dynamic Sheltering Problem and An Existence Theorem for Admissible Strategies.
Set-Valued and Variational Analysis,
Vol. 22,
Issue. 2,
p.
391.
Graber, P. Jameson
2014.
Optimal Control of First-Order Hamilton–Jacobi Equations with Linearly Bounded Hamiltonian.
Applied Mathematics & Optimization,
Vol. 70,
Issue. 2,
p.
185.
Marigonda, Antonio
and
Quincampoix, Marc
2018.
Mayer control problem with probabilistic uncertainty on initial positions.
Journal of Differential Equations,
Vol. 264,
Issue. 5,
p.
3212.
Wang, Tao
2018.
An Equivalence Theorem on Minimum Sheltering Speed for Non-convex Habitats.
Set-Valued and Variational Analysis,
Vol. 26,
Issue. 3,
p.
531.
Klein, Rolf
Langetepe, Elmar
Schwarzwald, Barbara
Levcopoulos, Christos
and
Lingas, Andrzej
2019.
On a Fire Fighter’s Problem.
International Journal of Foundations of Computer Science,
Vol. 30,
Issue. 02,
p.
231.
Bressan, Alberto
and
Chiri, Maria Teresa
2022.
On the regularity of optimal dynamic blocking strategies.
Calculus of Variations and Partial Differential Equations,
Vol. 61,
Issue. 1,
 ∈F(x), starting froman initial set R 0. To block the fire, a barrier can be constructedprogressively in time. For each t> 0, the portion of the wall constructedwithin time t is described by a rectifiable setγ(t) ⊂ $\mathbb{R}^2$
∈F(x), starting froman initial set R 0. To block the fire, a barrier can be constructedprogressively in time. For each t> 0, the portion of the wall constructedwithin time t is described by a rectifiable setγ(t) ⊂ $\mathbb{R}^2$ 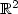 . In this paperwe show that the searchfor blocking strategies and for optimal strategies can be reduced toa problem involving one single admissible rectifiable set Γ⊂ $\mathbb{R}^2$
. In this paperwe show that the searchfor blocking strategies and for optimal strategies can be reduced toa problem involving one single admissible rectifiable set Γ⊂ $\mathbb{R}^2$ 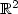 ,rather than the multifunction t $\mapsto$
,rather than the multifunction t $\mapsto$ 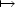 γ(t) ⊂ $\mathbb{R}^2$
γ(t) ⊂ $\mathbb{R}^2$ 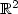 .Relying on this result, we then developa numerical algorithm for the computation ofoptimal strategies, minimizing the total area burned by the fire.
.Relying on this result, we then developa numerical algorithm for the computation ofoptimal strategies, minimizing the total area burned by the fire.