Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T17:14:15.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Control Norms for Large Control Times

Published online by Cambridge University Press:  15 August 2002

Sergei Ivanov
Sergei Ivanov*
Affiliation:
Russian Center of Laser Physics, St. Petersburg University, Ul'yanovskaya ul. 1, Petrodvorets, St. Petersburg 198904, Russia; Sergei.Ivanov@pobox.spbu.ru.
Get access

Abstract

A control system of the second order in time with control $u=u(t) \in L^2([0,T];U)$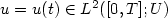 is considered. If the system is controllable in a strong sense and uT is the control steering the system to the rest at time T, then the L2–norm of uT decreases as $1/\sqrt T$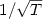 while the $L^1([0,T];U)$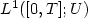–norm of uT is approximately constant. The proof is based on the moment approach and properties of the relevant exponential family. Results are applied to the wave equation with boundary or distributed controls.

Keywords

Controllabilityexponential families.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 4 , 1999 , pp. 405 - 418
Copyright
© EDP Sciences, SMAI, 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

M. Asch and G. Lebeau, Geometrical aspects of exact boundary controllability for the wave equation - a numerical study. ESAIM: Contr., Optim. Cal. Var. 3 (1998) 163-212.
S. Avdonin and S. Ivanov, Families of Exponentials. The Method of Moments in Controllability Problems for Distributed Parameter Systems, Cambridge University Press, N.Y. (1995).
Avdonin, S.A., Belishev, M.I. and Ivanov, S.A., Controllability in filled domain for the multidimensional wave equation with singular boundary control. Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 210 (1994) 7-21.
S.A. Avdonin, S.A. Ivanov and D.L. Russell, Exponential bases in Sobolev spaces in control and observation problems for the wave equation. Proc. Roy. Soc. Edinburgh (to be submitted).
Bardos, C., Lebeau, G. and Rauch, J., Sharp sufficient conditions for the observation, control and stabilization of waves from the boundary. SIAM J. Control Theor. Appl. 30 (1992) 1024-1095. CrossRef
H.O. Fattorini, Estimates for sequences biorthogonal to certain complex exponentials and boundary control of the wave equation, Springer, Lecture Notes in Control and Information Sciences 2 (1979).
Glowinski, R., Li, C.-H. and Lions, J.-L., A numerical approach to the exact controllability of the wave equation. (I) Dirichlet controls: description of the numerical methods. Japan J. Appl. Math. 7 (1990) 1-76. CrossRef
F. Gozzi and P. Loreti, Regularity of the minimum time function and minimum energy problems: the linear case. SIAM J. Control Optim. (to appear).
W. Krabs, On Moment Theory and Controllability of one-dimensional vibrating Systems and Heating Processes, Springer, Lecture Notes in Control and Information Sciences 173 (1992).
Krabs, W., Leugering, G. and Seidman, T., On boundary controllability of a vibrating plate. Appl. Math. Optim. 13 (1985) 205-229. CrossRef
Lasiecka, I., Lions, J.-L. and Triggiani, R., Nonhomogeneous boundary value problems for second order hyperbolic operators. J. Math. Pures Appl. 65 (1986) 149-192.
J.-L. Lions, Contrôlabilité exacte, stabilisation et perturbation des systèmes distribués, Masson, Paris Collection RMA 1 (1988).
N.K. Nikol'skii, A Treatise on the Shift Operator, Springer, Berlin (1986).
Russell, D.L., Controllability and stabilizability theory for linear partial differential equations: Recent progress and open questions. SIAM Rev. 20 (1978) 639-739. CrossRef
T.I. Seidman, The coefficient map for certain exponential sums. Nederl. Akad. Wetensch. Proc. Ser. A 89 (= Indag. Math. 48) (1986) 463-468.
T.I. Seidman, S.A. Avdonin and S.A. Ivanov, The ``window problem'' for complex exponentials. Fourier Analysis and Applications (to appear).
D. Tataru, Unique continuation for solutions of PDE's; between Hörmander's theorem and Holmgren's theorem. Comm. PDE 20 (1995) 855-884.