Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-14T16:12:03.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological entropy in totally disconnected locally compact groups

Published online by Cambridge University Press:  11 April 2016

ANNA GIORDANO BRUNO  and
SIMONE VIRILI
ANNA GIORDANO BRUNO
Affiliation:
Dipartimento di Matematica e Informatica, Università di Udine, Via delle Scienze 206, 33100 Udine, Italy email anna.giordanobruno@uniud.it
SIMONE VIRILI
Affiliation:
Dipartimento di Matematica Pura e Applicata, Università di Padova, Via Trieste 63, 35121 Padova, Italy email virili.simone@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

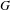Let $G$ be a topological group, let 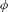$\unicode[STIX]{x1D719}$ be a continuous endomorphism of 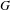$G$ and let 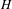$H$ be a closed 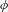$\unicode[STIX]{x1D719}$-invariant subgroup of 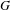$G$. We study whether the topological entropy is an additive invariant, that is,

$$\begin{eqnarray}h_{\text{top}}(\unicode[STIX]{x1D719})=h_{\text{top}}(\unicode[STIX]{x1D719}\restriction _{H})+h_{\text{top}}(\bar{\unicode[STIX]{x1D719}}),\end{eqnarray}$$
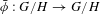where $\bar{\unicode[STIX]{x1D719}}:G/H\rightarrow G/H$ is the map induced by 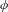$\unicode[STIX]{x1D719}$. We concentrate on the case when 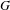$G$ is totally disconnected locally compact and $H$ is either compact or normal. Under these hypotheses, we show that the above additivity property holds true whenever 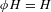$\unicode[STIX]{x1D719}H=H$ and 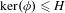$\ker (\unicode[STIX]{x1D719})\leq H$. As an application, we give a dynamical interpretation of the scale 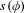$s(\unicode[STIX]{x1D719})$ by showing that 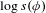$\log s(\unicode[STIX]{x1D719})$ is the topological entropy of a suitable map induced by 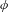$\unicode[STIX]{x1D719}$. Finally, we give necessary and sufficient conditions for the equality $\log s(\unicode[STIX]{x1D719})=h_{\text{top}}(\unicode[STIX]{x1D719})$ to hold.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 7 , October 2017 , pp. 2163 - 2186
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. L., Konheim, A. G. and McAndrew, M. H.. Topological entropy. Trans. Amer. Math. Soc. 114 (1965), 309–319.Google Scholar
Alcaraz, D., Dikranjan, D. and Sanchis, M.. Bowen’s entropy for endomorphisms of totally bounded abelian groups. Descriptive Topology and Functional Analysis (Springer Proceedings in Mathematics & Statistics, 80) . Springer International Publishing, Switzerland, 2014, pp. 143–162.Google Scholar
Berlai, F., Dikranjan, D. and Giordano Bruno, A.. Scale function vs. topological entropy. Topology Appl. 160 (2013), 2314–2334.CrossRefGoogle Scholar
Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.Google Scholar
Dikranjan, D. and Giordano Bruno, A.. Limit free computation of entropy. Rend. Istit. Mat. Univ. Trieste 44 (2012), 297–312.Google Scholar
Dikranjan, D. and Giordano Bruno, A.. Topological entropy and algebraic entropy for group endomorphisms. Proc. ICTA2011 (Islamabad, Pakistan, 4–10 July 2011). Cambridge Scientific, Cambridge, 2012, pp. 133–214.Google Scholar
Dikranjan, D., Sanchis, M. and Virili, S.. New and old facts about entropy in uniform spaces and topological groups. Topology Appl. 159 (2012), 1916–1942.Google Scholar
Giordano Bruno, A.. Entropy for automorphisms of totally disconnected locally compact groups. Topology Proc. 45 (2015), 175–187.Google Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis I. Springer, Berlin, 1963.Google Scholar
Hood, B. M.. Topological entropy and uniform spaces. J. Lond. Math. Soc. 8(2) (1974), 633–641.Google Scholar
Li, H.. Compact group automorphisms, addition formulas and Fuglede–Kadison determinants. Ann. of Math. (2) 176 (2012), 303–347.Google Scholar
Lind, D., Schmidt, K. and Ward, T.. Mahler measure and entropy for commuting automorphisms of compact groups. Invent. Math. 101(3) (1990), 593–629.Google Scholar
Miles, R.. The entropy of algebraic actions of countable torsion-free abelian groups. Fund. Math. 201(3) (2008), 261–282.Google Scholar
Nachbin, L.. The Haar Integral. Van Nostrand, Princeton, NJ, 1965, XII.Google Scholar
Ornstein, D. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48(1) (1987), 1–141.CrossRefGoogle Scholar
Reiter, H. and Stegeman, J. D.. Classical Harmonic Analysis and Locally Compact Groups, 2nd edn. Clarendon Press, Oxford, 2000.Google Scholar
Thomas, R. K.. The addition theorem for entropy of transformations of G-spaces. Trans. Amer. Math. Soc. 160 (1971), 119–130.Google Scholar
van Dantzig, D.. Studien over topologische algebra. Dissertation, Amsterdam, 1931.Google Scholar
Willis, G. A.. The structure of totally disconnected locally compact groups. Math. Ann. 300(2) (1994), 341–363.Google Scholar
Willis, G. A.. Further properties of the scale function on a totally disconnected group. J. Algebra 237(1) (2001), 142–164.Google Scholar
Willis, G. A.. The nub of an automorphism of a totally disconnected, locally compact group. Ergod. Th. & Dynam. Sys. 34(4) (2014), 1365–1394.Google Scholar
Willis, G. A.. The scale and tidy subgroups for endomorphisms of totally disconnected locally compact groups. Math. Ann. 361(1–2) (2015), 403–442.Google Scholar
Yuzvinski, S.. Metric properties of endomorphisms of compact groups. Izv. Akad. Nauk SSSR Ser. Mat. 29 (1965), 1295–1328 (in Russian); English transl. Amer. Math. Soc. Transl. 66(2) (1968), 63–98.Google Scholar