Article contents
Rigidity times for a weakly mixing dynamical system which are not rigidity times for any irrational rotation
Published online by Cambridge University Press: 03 July 2014
Abstract
We construct an increasing sequence of natural numbers 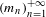 $(m_{n})_{n=1}^{+\infty }$ with the property that
$(m_{n})_{n=1}^{+\infty }$ with the property that 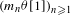 $(m_{n}{\it\theta}[1])_{n\geq 1}$ is dense in
$(m_{n}{\it\theta}[1])_{n\geq 1}$ is dense in  $\mathbb{T}$ for any
$\mathbb{T}$ for any 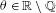 ${\it\theta}\in \mathbb{R}\setminus \mathbb{Q}$, and a continuous measure on the circle
${\it\theta}\in \mathbb{R}\setminus \mathbb{Q}$, and a continuous measure on the circle 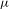 ${\it\mu}$ such that
${\it\mu}$ such that 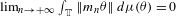 $\lim _{n\rightarrow +\infty }\int _{\mathbb{T}}\Vert m_{n}{\it\theta}\Vert \,d{\it\mu}({\it\theta})=0$. Moreover, for every fixed
$\lim _{n\rightarrow +\infty }\int _{\mathbb{T}}\Vert m_{n}{\it\theta}\Vert \,d{\it\mu}({\it\theta})=0$. Moreover, for every fixed 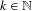 $k\in \mathbb{N}$, the set
$k\in \mathbb{N}$, the set 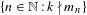 $\{n\in \mathbb{N}:k\nmid m_{n}\}$ is infinite. This is a sufficient condition for the existence of a rigid, weakly mixing dynamical system whose rigidity time is not a rigidity time for any system with a discrete part in its spectrum.
$\{n\in \mathbb{N}:k\nmid m_{n}\}$ is infinite. This is a sufficient condition for the existence of a rigid, weakly mixing dynamical system whose rigidity time is not a rigidity time for any system with a discrete part in its spectrum.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 10
- Cited by


