Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-15T04:14:46.973Z Has data issue: false hasContentIssue false
  • English
  • Français

On a generalization of the Cartwright–Littlewood fixed point theorem for planar homeomorphisms

Published online by Cambridge University Press:  11 February 2016

J. P. BOROŃSKI
J. P. BOROŃSKI*
Affiliation:
National Supercomputing Center IT4Innovations, Division of the University of Ostrava, Institute for Research and Applications of Fuzzy Modeling, 30. dubna 22, 70103 Ostrava, Czech Republic Faculty of Applied Mathematics, AGH University of Science and Technology, al. Mickiewicza 30, 30-059 Kraków, Poland email jan.boronski@osu.cz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a generalization of the fixed point theorem of Cartwright and Littlewood. Namely, suppose that $h:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$ is an orientation preserving planar homeomorphism, and let 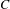$C$ be a continuum such that 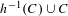$h^{-1}(C)\cup C$ is acyclic. If there is a 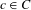$c\in C$ such that 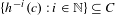$\{h^{-i}(c):i\in \mathbb{N}\}\subseteq C$, or $\{h^{i}(c):i\in \mathbb{N}\}\subseteq C$, then $C$ also contains a fixed point of 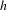$h$. Our approach is based on Brown’s short proof of the result of Cartwright and Littlewood. 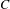In addition, making use of a linked periodic orbits theorem of Bonino, we also prove a counterpart of the aforementioned result for orientation reversing homeomorphisms, that guarantees a $2$-periodic orbit in $C$ if it contains a 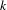$k$-periodic orbit (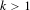$k>1$).

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 6 , September 2017 , pp. 1815 - 1824
Copyright
© Cambridge University Press, 2016 

References

Aarts, J. M. and Fokkink, R. J.. Fixed points of the bucket handle. Proc. Amer. Math. Soc. 126(3) (1998), 881–885.CrossRefGoogle Scholar
Barge, M. and Martin, J.. Chaos, periodicity, and snakelike continua. Trans. Amer. Math. Soc. 289 (1985), 355–363.Google Scholar
Barge, M. and Martin, J.. The construction of global attractors. Proc. Amer. Math. Soc. 110(2) (1990), 52–525.CrossRefGoogle Scholar
Barge, M. and Gillette, R. M.. Indecomposability and dynamics of invariant plane separating continua. Continuum Theory and Dynamical Systems (Arcata, CA, 1989) (Contemporary Mathematics, 117) . American Mathematical Society, Providence, RI, 1991, pp. 13–38.Google Scholar
Bell, H.. A fixed point theorem for plane homeomorphism. Fund. Math. 100 (1978), 119–128.Google Scholar
Bing, R. H.. A homogeneous indecomposable plane continuum. Duke Math. J. 15 (1948), 729–742.Google Scholar
Blokh, A. M., Fokkink, R. J., Mayer, J. C., Oversteegen, L. G. and Tymchatyn, E. D.. Fixed point theorems in plane continua with applications. Mem. Amer. Math. Soc. 224 (2013).Google Scholar
Bonino, M.. Nielsen theory and linked periodic orbits of homeomorphisms of S2 . Math. Proc. Cambridge Philos. Soc. 140(3) (2006), 425–430.Google Scholar
Boroński, J. P.. Fixed points and periodic points of orientation-reversing planar homeomorphisms. Proc. Amer. Math. Soc. 138 (2010), 3717–3722.CrossRefGoogle Scholar
Boroński, J. P. and Oprocha, P.. On indecomposability in chaotic attractors. Proc. Amer. Math. Soc. 143(8) (2015), 3659–3670.CrossRefGoogle Scholar
Boyles, S. M.. A counterexample to the bounded orbit conjecture. Trans. Amer. Math. Soc. 266(2) (1981), 415–422.Google Scholar
Brouwer, L. E.. Beweis des ebenen Translationssatzes. Math. Ann. 72 (1912), 36–54.Google Scholar
Brown, M.. A short short proof of the Cartwright–Littlewood theorem. Proc. Amer. Math. Soc. 65(2) (1977), 372.Google Scholar
Cartwright, M. L. and Littlewood, J. E.. Some fixed point theorems. Ann. of Math. (2) 54 (1951), 1–37, with appendix by H. D. Ursell.CrossRefGoogle Scholar
Hamilton, O. H.. A short proof of the Cartwright–Littlewood fixed point theorem. Canad. J. Math. 6 (1954), 522–524.Google Scholar
Kuperberg, K.. Fixed points of orientation reversing homeomorphisms of the plane. Proc. Amer. Math. Soc. 112(1) (1991), 223–229.Google Scholar
Kuperberg, K.. A lower bound for the number of fixed points of orientation reversing homeomorphisms. The Geometry of Hamiltonian Systems (Berkeley, CA, 1989) (Mathematical Sciences Research Institute Publications, 22) . Springer, New York, 1991, pp. 367–371.Google Scholar
Mauldin, R. D.. The Scottish Book, 2nd edn. Birkhäuser, Basel, 2015.CrossRefGoogle Scholar
Ostrovski, G.. Fixed point theorem for non-self maps of regions in the plane. Topology Appl. 160(7) (2013), 915–923.CrossRefGoogle Scholar
Pliss, V. A.. Certain questions of behavior of solutions of a periodic dissipative system of the second order. Differ. Uravn. 2 (1966), 723–735.Google Scholar
Shub, M.. What is a horseshoe? Notices Amer. Math. Soc. 52(5) (2005), 516–517.Google Scholar