Article contents
Hausdorff dimension of Dirichlet non-improvable set versus well-approximable set
Published online by Cambridge University Press: 04 August 2022
Abstract
Dirichlet’s theorem, including the uniform setting and asymptotic setting, is one of the most fundamental results in Diophantine approximation. The improvement of the asymptotic setting leads to the well-approximable set (in words of continued fractions)
 $$ \begin{align*} \mathcal{K}(\Phi):=\{x:a_{n+1}(x)\ge\Phi(q_{n}(x))\ \textrm{for infinitely many }n\in \mathbb{N}\}; \end{align*} $$
$$ \begin{align*} \mathcal{K}(\Phi):=\{x:a_{n+1}(x)\ge\Phi(q_{n}(x))\ \textrm{for infinitely many }n\in \mathbb{N}\}; \end{align*} $$
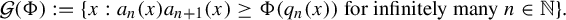 $$ \begin{align*} \mathcal{G}(\Phi):=\{x:a_{n}(x)a_{n+1}(x)\ge\Phi(q_{n}(x))\ \textrm{for infinitely many }n\in \mathbb{N}\}. \end{align*} $$
$$ \begin{align*} \mathcal{G}(\Phi):=\{x:a_{n}(x)a_{n+1}(x)\ge\Phi(q_{n}(x))\ \textrm{for infinitely many }n\in \mathbb{N}\}. \end{align*} $$
 $\Phi _{1},\Phi _{2}:[1,+\infty )\rightarrow \mathbb {R}^{+}$
be two non-decreasing positive functions. We focus on the Hausdorff dimension of the set
$\Phi _{1},\Phi _{2}:[1,+\infty )\rightarrow \mathbb {R}^{+}$
be two non-decreasing positive functions. We focus on the Hausdorff dimension of the set
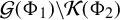 $\mathcal {G}(\Phi _{1})\!\setminus\! \mathcal {K}(\Phi _{2})$
. It is known that the dimensions of
$\mathcal {G}(\Phi _{1})\!\setminus\! \mathcal {K}(\Phi _{2})$
. It is known that the dimensions of
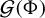 $\mathcal {G}(\Phi )$
and
$\mathcal {G}(\Phi )$
and
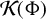 $\mathcal {K}(\Phi )$
depend only on the growth exponent of
$\mathcal {K}(\Phi )$
depend only on the growth exponent of
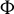 $\Phi $
. However, rather different from the current knowledge, it will be seen in some cases that the dimension of
$\Phi $
. However, rather different from the current knowledge, it will be seen in some cases that the dimension of
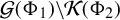 $\mathcal {G}(\Phi _{1})\!\setminus\! \mathcal {K}(\Phi _{2})$
will change greatly even slightly modifying
$\mathcal {G}(\Phi _{1})\!\setminus\! \mathcal {K}(\Phi _{2})$
will change greatly even slightly modifying
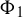 $\Phi _1$
by a constant.
$\Phi _1$
by a constant.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 5
- Cited by



