Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-19T11:51:31.931Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms of blowups of threefolds being Fano or having Picard number 1

Published online by Cambridge University Press:  12 May 2016

TUYEN TRUNG TRUONG
TUYEN TRUNG TRUONG*
Affiliation:
School of Mathematics, Korea Institute for Advanced Study, Seoul 130-722, Republic of Korea email truong@kias.re.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 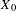$X_{0}$ be a smooth projective threefold which is Fano or which has Picard number 1. Let 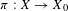$\unicode[STIX]{x1D70B}:X\rightarrow X_{0}$ be a finite composition of blowups along smooth centers. We show that for ‘almost all’ of such 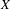$X$, if 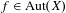$f\in \text{Aut}(X)$, then its first and second dynamical degrees are the same. We also construct many examples of blowups 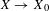$X\rightarrow X_{0}$, on which any automorphism is of zero entropy. The main idea is that, because of the log-concavity of dynamical degrees and the invariance of Chern classes under holomorphic automorphisms, there are some constraints on the nef cohomology classes. We will also discuss a possible application of these results to a threefold constructed by Kenji Ueno.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 7 , October 2017 , pp. 2255 - 2275
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramovich, D., Karu, K., Matsuki, K. and Wlodarczyk, J.. Torification and factorization of birational maps. J. Amer. Math. Soc. 15(3) (2002), 531–572.Google Scholar
Bayraktar, T. and Cantat, S.. Constraints on automorphism groups of higher dimensional manifolds. J. Math. Anal. Appl. 405 (2013), 209–213.Google Scholar
Bedford, E.. The dynamical degrees of a mapping. Proceedings of the Workshop Future Directions in Difference Equations (Colección Congresos, 69) . Servizo de Publicacións da Universidade de Vigo, Vigo, 2011, pp. 3–13.Google Scholar
Bedford, E. and Kim, K.-H.. Dynamics of rational surface automorphisms: rotation domains. Amer. J. Math. 134(2) (2012), 379–405.Google Scholar
Bedford, E. and Kim, K.-H.. Continuous families of rational surface automorphisms with positive entropy. Math. Ann. 348(3) (2010), 667–688.Google Scholar
Bedford, E. and Kim, K.-H.. Dynamics of rational surface automorphisms: linear fractional recurrences. J. Geom. Anal. 19(3) (2009), 553–583.CrossRefGoogle Scholar
Campana, F.. Remarks on an example of K. Ueno. Series of Congress Reports, Classification of Algebraic Varieties. Eds. Faber, C., van der Geer, G. and Looijenga, E.. European Mathematical Society, Zürich, 2011, pp. 115–121.Google Scholar
Cantat, S.. Dynamique des automorphismes des surfaces K3. Acta Math. 187(1) (2001), 1–57.Google Scholar
Cantat, S. and Dolgachev, I.. Rational surfaces with a large group of automorphisms. J. Amer. Math. Soc. 25(3) (2012), 863–905.Google Scholar
Colliot-Thélène, J.-L.. Rationalité d’un fibré en coniques. Manuscripta Math. 147(3–4) (2015), 305–310.Google Scholar
Catanese, F., Oguiso, K. and Truong, T. T.. Unirationality of Ueno-Campana’s threefold. Manuscripta Math. 145(3–4) (2014), 399–406.Google Scholar
Demailly, J.-P.. Complex analytic and differential geometry, Online book, version of Thursday 10 September 2009.Google Scholar
Demailly, J.-P. and Paun, M.. Numerical characterization of the Kähler cone of a compact Kähler manifold. Ann. of Math. (2) 159(3) (2004), 1247–1274.Google Scholar
Déserti, J. and Grivaux, J.. Automorphisms of rational surfaces with positive entropy. Indiana Univ. Math. J. 60(5) (2011), 1589–1622.Google Scholar
Diller, J.. Cremona transformations, surface automorphisms, and plane cubics. Michigan Math. J. 60(2) (2011), 409–440 . With an appendix by Igor Dolgachev.Google Scholar
Dinh, T.-C.. Tits alternative for automorphism groups of compact Kähler manifolds. Acta Math. Vietnam. 37(4) (2012), 513–529.Google Scholar
Dinh, T.-C. and Nguyen, V.-A.. Comparison of dynamical degrees for semi-conjugate meromorphic maps. Comment. Math. Helv. 86(4) (2011), 817–840.Google Scholar
Dinh, T.-C., Nguyen, V.-A. and Truong, T. T.. On the dynamical degrees of meromorphic maps preserving a fibration. Comm. Contemp. Math. 14(6) (2012),1250042 , 18 pp.Google Scholar
Dinh, T.-C. and Sibony, N.. Une borne supérieure pour l’entropie topologique d’une application rationnelle. Ann. of Math. (2) 161(3) (2005), 1637–1644.Google Scholar
Gromov, M.. On the entropy of holomorphic maps. Enseign. Math. 49 (2003), 217–235, Manuscript (1977).Google Scholar
Griffiths, P. and Harris, J.. Principles of Algebraic Geometry. Wiley, New York, 1978.Google Scholar
Hartshorne, R.. Algebraic Geometry (Graduate Texts in Mathematics, 52) . Springer, New York, 1977.Google Scholar
McMullen, C.. Dynamics with small entropy on projective K3 surfaces. Preprint.Google Scholar
McMullen, C.. K3 surfaces, entropy and glue. J. Reine Angew. Math. 658 (2011), 1–25.Google Scholar
McMullen, C.. Dynamics on blowups of the projective plane. Publ. Math. Inst. Hautes Études Sci. 105 (2007), 49–89.Google Scholar
McMullen, C.. Dynamics on K3 surfaces: Salem numbers and Siegel disks. J. Reine Angew. Math. 545 (2002), 201–233.Google Scholar
Oguiso, K. and Perroni, F.. Automorphisms of rational manifolds of positive entropy with Siegel disks. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 22(4) (2011), 487–504.Google Scholar
Oguiso, K.. Free automorphisms of positive entropy on smooth Kähler surfaces. Algebraic Geometry in East Asia, Taipei 2011 (Advanced Studies in Pure Mathematics, 65) . Mathematical Society of Japan, Tokyo, 2015, pp. 187–199.Google Scholar
Oguiso, K.. The third smallest Salem number in automorphisms of K3 surfaces. Algebraic Geometry in East Asia, Seoul 2008 (Advanced Studies in Pure Mathematics, 60) . Mathematical Society, Japan, Tokyo, 2010, pp. 331–360.Google Scholar
Oguiso, K.. A remark on dynamical degrees of automorphisms of hyperkähler manifolds. Manuscripta Math. 130(1) (2009), 101–111.Google Scholar
Oguiso, K.. Automorphisms of hyperkähler manifolds in the view of topological entropy. Algebraic Geometry (Contemporary Mathematics, 422) . American Mathematical Society, Providence, RI, 2007, pp. 173–185.Google Scholar
Oguiso, K. and Truong, T. T.. Explicit examples of rational and Calabi-Yau threefolds with primitive automorphisms of positive entropy. J. Math. Sci. Univ. Tokyo 22(1) (2015), 361–385 (Kodaira centennial issue).Google Scholar
Reschke, P.. Salem numbers and automorphisms of complex surfaces. Math. Res. Lett. 19(2) (2012), 475–482.Google Scholar
Truong, T. T.. On automorphisms of blowups of projective manifolds. Preprint, arXiv:1301.4957.Google Scholar
Truong, T. T.. On automorphisms of blowups of $\mathbb{P}^{3}$ . Preprint, arXiv:1202.4224.Google Scholar
Ueno, K.. Classification theory of algebraic varieties and compact complex spaces. Notes written in collaboration with P. Cherenack. (Lecture Notes in Mathematics, 439) . Springer, Berlin, 1975.Google Scholar
Yomdin, Y.. Volume growth and entropy. Israel J. Math. 57 (1987), 285–300.Google Scholar
Zhang, D.-Q.. The g-periodic subvarieties for an automorphism g of positive entropy on a compact Kähler manifold. Adv. Math. 223(2) (2010), 405–415.Google Scholar
Zhang, D.-Q.. Dynamics of automorphisms on projective complex manifolds. J. Differential Geom. 82(3) (2009), 691–722.Google Scholar
Zhang, D.-Q.. Automorphism groups and anti-pluricanonical curves. Math. Res. Lett. 15(1) (2008), 163–183.Google Scholar