Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-16T01:17:20.267Z Has data issue: false hasContentIssue false
  • English
  • Français

An ergodic transformation with trivial Kakutani centralizer

Published online by Cambridge University Press:  19 September 2008

Adam Fieldsteel  and
Daniel J. Rudolph
Adam Fieldsteel
Affiliation:
Department of Mathematics, Wesleyan University, Middletown, CT 06457, USA
Daniel J. Rudolph
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Generalizing from the centralizer of a measure-preserving dynamical system (X, ℬ, μ, T), one defines the Kakutani centralizer KC(T) of all ‘even Kakutani factor maps’ ϕ from T to itself. Such a ϕ is a composition φ2ϕ1 of an even Kakutani orbit equivalence ϕ1 and a factor map ϕ2. We construct here an ergodic T acting on a nonatomic Lebesgue space (X,ℬ,μ) with the property that any ϕ ∈ KC(T) is invertible and of the form

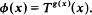
All invertible maps of this form are automatically in KC(T) and hence for this T the Kakutani centralizer is as small as possible.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 12 , Issue 3 , September 1992 , pp. 459 - 478
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[delJ, R]del Junco, A. & Rudolph, D. J.. Kakutani equivalence of ergodic Zn actions. Ergod. Th. & Dynam. Sys. 4 (1984), 89–104.CrossRefGoogle Scholar
[delJ, F, R]del Junco, A., Fieldsteel, A. & Rudolph, D. J., α-equivalence of ergodic transformations. In preparation.Google Scholar
[F, N]Feldman, J. & Nadler, D.. Reparametrization of N-flows of zero entropy. Trans. Amer. Math. Soc. 256 (1979), 289–304.Google Scholar
[F, F]Fieldsteel, A. & Friedman, N. A.. Restricted orbit changes of ergodic Zd-actions to achieve mixing and completely positive entropy. Ergod. Th. & Dynam. Sys. 6 (1986), 505–528.CrossRefGoogle Scholar
[L]Lemanczyk, M.. Weakly isomorphic transformations that are not isomorphic. Prob. Th. Rel. Fields 78 (1988), 491–507.CrossRefGoogle Scholar
[L, L]Lemanczyk, M. & Liardet, P.. Coalescence of Anzai skew products. Preprint.Google Scholar
[K]Kakutani, S.. Induced measure-preserving transformations. Proc. Imp. Acad. Tokyo 19 (1943), 635–641.Google Scholar
[N]Newton, D.. Coalescence and spectrum of automorphisms of a Lebesgue space. Z. Wahr. verw. Geb. 19 (1971), 117–122.CrossRefGoogle Scholar
[O, R, W]Ornstein, D. S., Rudolph, D. J. & Weiss, B.. Equivalence of measure-preserving transformations. Mem. Amer. Math. Soc. 37, no. 262 (1982).Google Scholar
[R1]Rudolph, D. J.. Smooth orbit equivalence of ergodic ℝd actions, d ≥ 2. Trans. Amer. Math. Soc. 253 (1979), 291–302.Google Scholar
[R2]Rudolph, D. J.. Inner and barely linear time changes of ergodic ℝk actions. Contemp. Math. 26 (1984), 351–371.CrossRefGoogle Scholar
[R3]Rudolph, D. J.. Restricted orbit equivalence. Mem. Amer. Math. Soc. 54 no. 323 (1985).Google Scholar
[R4]Rudolph, D. J.. Classifying the isometric extension of a Bernoulli shift. J. a'Analyse Math. 34 (1978), 36–59.CrossRefGoogle Scholar