Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-15T01:02:52.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity for group actions on homogeneous spaces by affine transformations

Published online by Cambridge University Press:  22 March 2016

MOHAMED BOULJIHAD
MOHAMED BOULJIHAD*
Affiliation:
ENS Lyon – UMPA, 46 allée d’Italie, 69364 Lyon, France email mohamed.bouljihad@ens-lyon.fr IRMAR, Campus de Beaulieu, bâtiments 22 et 23, 263 avenue du Général Leclerc, 35042 Rennes, France
Get access Rights & Permissions [Opens in a new window]

Abstract

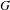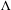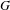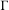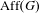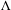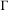We give a criterion for the rigidity of the action of a group of affine transformations of a homogeneous space of a real Lie group. Let $G$ be a real Lie group, $\unicode[STIX]{x1D6EC}$ a lattice in $G$ , and $\unicode[STIX]{x1D6E4}$ a subgroup of the affine group $\text{Aff}(G)$ stabilizing $\unicode[STIX]{x1D6EC}$ . Then the action of $\unicode[STIX]{x1D6E4}$ on 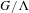$G/\unicode[STIX]{x1D6EC}$ has the rigidity property in the sense of Popa [On a class of type 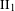$\text{II}_{1}$ factors with Betti numbers invariants. Ann. of Math. 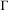(2) 163(3) (2006), 809–899] if and only if the induced action of $\unicode[STIX]{x1D6E4}$ on 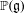$\mathbb{P}(\mathfrak{g})$ admits no 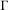$\unicode[STIX]{x1D6E4}$ -invariant probability measure, where 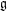$\mathfrak{g}$ is the Lie algebra of 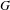$G$ . This generalizes results of Burger [Kazhdan constants for 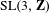$\text{SL}(3,\mathbf{Z})$ . J. Reine Angew. Math. 413 (1991), 36–67] and Ioana and Shalom [Rigidity for equivalence relations on homogeneous spaces. Groups Geom. Dyn. 7(2) (2013), 403–417]. As an application, we establish rigidity for the action of a class of groups acting by automorphisms on nilmanifolds associated to two-step nilpotent Lie groups.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 7 , October 2017 , pp. 2060 - 2076
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bekka, B., de la Harpe, P. and Valette, A.. Kazhdan’s Property (T) (New Mathematical Monographs, 11) . Cambridge University Press, Cambridge, 2008.Google Scholar
Bekka, B. and Heu, J.-R.. Random products of automorphisms of Heisenberg nilmanifolds and Weil’s representation. Ergod. Th. & Dynam. Sys. 31(5) (2011), 1277–1286.Google Scholar
Burger, M.. Kazhdan constants for SL(3, Z). J. Reine Angew. Math. 413 (1991), 36–67.Google Scholar
Conway, J. B.. A Course in Operator Theory (Graduate Studies in Mathematics, 21) . American Mathematical Society, Providence, RI, 2000.Google Scholar
Cornulier, Y. and Tessera, R.. A characterization of relative Kazhdan property (T) for semidirect products with abelian groups. Ergod. Th. & Dynam. Sys. 31(3) (2011), 793–805.Google Scholar
de Cornulier, Y.. Relative Kazhdan property. Ann. Sci. Éc. Norm. Supér. 39(2) (2006), 301–333.CrossRefGoogle Scholar
Dani, S. G. and Mainkar, M. G.. Anosov automorphisms on compact nilmanifolds associated with graphs. Trans. Amer. Math. Soc. 357(6) (2005), 2235–2251.Google Scholar
Epstein, I.. Some results on orbit inequivalent actions of non-amenable groups. PhD thesis, University of California, Los Angeles, 2008.Google Scholar
Fernós, T.. Relative property (T) and linear groups. Ann. Inst. Fourier (Grenoble) 56(6) (2006), 1767–1804.Google Scholar
Furstenberg, H.. A note on Borel’s density theorem. Proc. Amer. Math. Soc. 55(1) (1976), 209–212.Google Scholar
Gaboriau, D.. Free product actions with relative property (T) and trivial outer automorphism groups. J. Funct. Anal. 260(2) (2011), 414–427.Google Scholar
Gaboriau, D. and Popa, S.. An uncountable family of nonorbit equivalent actions of F n . J. Amer. Math. Soc. 18(3) (2005), 547–559.Google Scholar
Hjorth, G.. A converse to Dye’s theorem. Trans. Amer. Math. Soc. 357(8) (2005), 3083–3103 (electronic).Google Scholar
Ioana, A.. Relative property (T) for the subequivalence relations induced by the action of SL2(ℤ) on T2 . Adv. Math. 224(4) (2010), 1589–1617.Google Scholar
Ioana, A.. Orbit inequivalent actions for groups containing a copy of F2 . Invent. Math. 185(1) (2011), 55–73.Google Scholar
Ioana, A. and Shalom, Y.. Rigidity for equivalence relations on homogeneous spaces. Groups Geom. Dyn. 7(2) (2013), 403–417.Google Scholar
Kazhdan, D. A.. Connection of the dual space of a group with the structure of its closed subgroups. Funct. Anal. Appl. 1(1) (1967), 63–65.Google Scholar
Margulis, G. A.. Finitely-additive invariant measures on Euclidean spaces. Ergod. Th. & Dynam. Sys. 2(3–4) (1982), 383–396,1983.Google Scholar
Murray, F. J. and Von Neumann, J.. On rings of operators. Ann. of Math. (2) 37(1) (1936), 116–229.CrossRefGoogle Scholar
Ornstein, D. S. and Weiss, B.. Ergodic theory of amenable group actions I. The Rohlin lemma. Bull. Amer. Math. Soc. (N.S.) 2(1) (1980), 161–164.Google Scholar
Popa, S.. On a class of type II1 factors with Betti numbers invariants. Ann. of Math. (2) 163(3) (2006), 809–899.CrossRefGoogle Scholar
Popa, S. and Vaes, S.. Actions of F ∞ whose II1 factors and orbit equivalence relations have prescribed fundamental group. J. Amer. Math. Soc. 23(2) (2010), 383–403.Google Scholar
Shalom, Y.. Invariant measures for algebraic actions, Zariski dense subgroups and Kazhdan’s property (T). Trans. Amer. Math. Soc. 351(8) (1999), 3387–3412.Google Scholar
Valette, A.. Group pairs with property (T), from arithmetic lattices. Geom. Dedicata 112 (2005), 183–196.CrossRefGoogle Scholar