We consider partitioned graphs, by which we mean finite directed graphs with a partitioned edge set 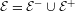${\mathcal{E}}={\mathcal{E}}^{-}\cup {\mathcal{E}}^{+}$. Additionally given a relation 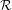${\mathcal{R}}$ between the edges in 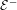${\mathcal{E}}^{-}$ and the edges in 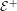${\mathcal{E}}^{+}$, and under the appropriate assumptions on 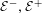${\mathcal{E}}^{-},{\mathcal{E}}^{+}$ and 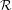${\mathcal{R}}$, denoting the vertex set of the graph by 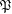$\mathfrak{P}$, we speak of an 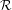${\mathcal{R}}$-graph 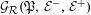${\mathcal{G}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$. From ${\mathcal{R}}$-graphs ${\mathcal{G}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$ we construct semigroups (with zero) ${\mathcal{S}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$ that we call 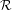${\mathcal{R}}$-graph semigroups. We write a list of conditions on a topologically transitive subshift with property 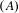$(A)$ that together are sufficient for the subshift to have an 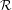${\mathcal{R}}$-graph semigroup as its associated semigroup.

Generalizing previous constructions, we describe a method of presenting subshifts by means of suitably structured finite labeled directed graphs $({\mathcal{V}},~\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706}~)$ with vertex set 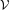${\mathcal{V}}$, edge set $\unicode[STIX]{x1D6F4}$, and a label map that assigns to the edges in $\unicode[STIX]{x1D6F4}$ labels in an ${\mathcal{R}}$-graph semigroup 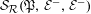${\mathcal{S}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{-})$. We denote the presented subshift by 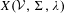$X({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ and call 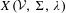$X({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ an 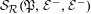${\mathcal{S}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{-})$-presentation.

We introduce a property 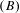$(B)$ of subshifts that describes a relationship between contexts of admissible words of a subshift, and we introduce a property 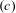$(c)$ of subshifts that in addition describes a relationship between the past and future contexts and the context of admissible words of a subshift. Property 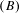$(B)$ and the simultaneous occurrence of properties 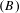$(B)$ and 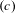$(c)$ are invariants of topological conjugacy.

We consider subshifts in which every admissible word has a future context that is compatible with its entire past context. Such subshifts we call right instantaneous. We introduce a property 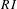$RI$ of subshifts, and we prove that this property is a necessary and sufficient condition for a subshift to have a right instantaneous presentation. We consider also subshifts in which every admissible word has a future context that is compatible with its entire past context, and also a past context that is compatible with its entire future context. Such subshifts we call bi-instantaneous. We introduce a property 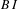$BI$ of subshifts, and we prove that this property is a necessary and sufficient condition for a subshift to have a bi-instantaneous presentation.

We define a subshift as strongly bi-instantaneous if it has for every sufficiently long admissible word $a$ an admissible word $c$, that is contained in both the future context of $a$ and the past context of $a$, and that is such that the word 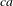$ca$ is a word in the future context of $a$ that is compatible with the entire past context of $a$, and the word 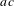$ac$ is a word in the past context of $a$, that is compatible with the entire future context of $a$. We show that a topologically transitive subshift with property $(A)$, and associated semigroup a graph inverse semigroup 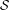${\mathcal{S}}$, has an 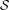${\mathcal{S}}$-presentation, if and only if it has properties 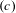$(c)$ and 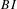$BI$, and a strongly bi-instantaneous presentation, if and only if it has properties 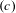$(c)$ and 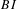$BI$, and all of its bi-instantaneous presentations are strongly bi-instantaneous.

We construct a class of subshifts with property 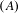$(A)$, to which certain graph inverse semigroups 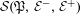${\mathcal{S}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$ are associated, that do not have 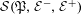${\mathcal{S}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$-presentations.

We associate to the labeled directed graphs 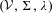$({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ topological Markov chains and Markov codes, and we derive an expression for the zeta function of 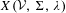$X({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ in terms of the zeta functions of the topological Markov shifts and the generating functions of the Markov codes.