Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-15T11:09:35.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Amount of failure of upper-semicontinuity of entropy in non-compact rank-one situations, and Hausdorff dimension

Published online by Cambridge University Press:  06 October 2015

S. KADYROV  and
A. POHL
S. KADYROV
Affiliation:
Department of Mathematics, Nazarbayev University, Astana, Kazakhstan email shirali.kadyrov@nu.edu.kz
A. POHL
Affiliation:
Mathematisches Institut, Georg-August-Universität Göttingen, Bunsenstrasse 3-5, 37073 Göttingen, Germany email pohl@uni-math.gwdg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Recently, Einsiedler and the authors provided a bound in terms of escape of mass for the amount by which upper-semicontinuity for metric entropy fails for diagonal flows on homogeneous spaces 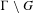$\unicode[STIX]{x1D6E4}\setminus G$, where 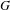$G$ is any connected semisimple Lie group of real rank one with finite center, and 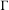$\unicode[STIX]{x1D6E4}$ is any non-uniform lattice in 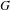$G$. We show that this bound is sharp, and apply the methods used to establish bounds for the Hausdorff dimension of the set of points that diverge on average.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 2 , April 2017 , pp. 539 - 563
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cowling, M., Dooley, A., Korányi, A. and Ricci, F.. H-type groups and Iwasawa decompositions. Adv. Math. 87(1) (1991), 1–41.CrossRefGoogle Scholar
Cowling, M., Dooley, A., Korányi, A. and Ricci, F.. An approach to symmetric spaces of rank one via groups of Heisenberg type. J. Geom. Anal. 8(2) (1998), 199–237.CrossRefGoogle Scholar
Dani, S. G.. Divergent trajectories of flows on homogeneous spaces and Diophantine approximation. J. Reine Angew. Math. 359 (1985), 55–89.Google Scholar
Einsiedler, M. and Kadyrov, S.. Entropy and escape of mass for SL3(ℤ) \backslashSL3(ℝ). Israel J. Math. 190 (2012), 253–288.CrossRefGoogle Scholar
Einsiedler, M., Kadyrov, S. and Pohl, A.. Escape of mass and entropy for diagonal flows in real rank one situations. Israel J. Math. to appear.Google Scholar
Einsiedler, M. and Lindenstrauss, E.. Diagonal actions on locally homogeneous spaces. Homogeneous Flows, Moduli Spaces and Arithmetic. Proceedings of the Clay Mathematics Institute Summer School (Centro di Recerca Mathematica Ennio De Giorgi, Pisa, Italy, June 11–July 6, 2007). American Mathematical Society, Clay Mathematics Institute, 2010, pp. 155–241.Google Scholar
Falconer, K. J.. The Geometry of Fractal Sets (Cambridge Tracts in Mathematics, 85) . Cambridge University Press, Cambridge, 1986.Google Scholar
Garland, H. and Raghunathan, M. S.. Fundamental domains for lattices in (R-)rank 1 semisimple Lie groups. Ann. of Math. (2) 92 (1970), 279–326.Google Scholar
Kadyrov, S.. Positive entropy invariant measures on the space of lattices with escape of mass. Ergod. Th. & Dynam. Sys. 32 (2012), 141–157.Google Scholar
Kleinbock, D. Y. and Margulis, G. A.. Bounded orbits of nonquasiunipotent flows on homogeneous spaces. Trans. Amer. Math. Soc. 171 (1996), 141–172.Google Scholar
McMullen, C.. Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300 (1987), 329–342.Google Scholar
Pohl, A.. Ford fundamental domains in symmetric spaces of rank one. Geom. Dedicata 147 (2010), 219–276.Google Scholar
Pesin, Ya. and Weiss, H.. On the dimension of deterministic and random Cantor-like sets. Math. Res. Lett. 1 (1994), 519–529.Google Scholar
Urbanski, M.. The Hausdorff dimension of the set of points with nondense orbit under a hyperbolic dynamical system. Nonlinearity 2 (1991), 385–397.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 2000.Google Scholar