1. Introduction
Sustainable intensification can be defined as ‘producing more output from the same area of land while reducing the negative environmental impacts and at the same time increasing contributions to natural capital and the flow of environmental services’ (Pretty et al., Reference Pretty, Toulmin and Williams2011: 7). African agriculture has a high potential for sustainable intensification (McIntyre et al., Reference McIntyre, Herren, Wakhungu and Watson2009; Pretty et al., Reference Pretty, Toulmin and Williams2011; Tilman et al., Reference Tilman, Balzer, Hill and Befort2011) and pineapple farming in Ghana is no exception (Kleemann and Abdulai, Reference Kleemann and Abdulai2013). Because the costs of extensive production and land degradation are high in Ghana (Diao and Sarpong, Reference Diao and Sarpong2007; World Bank, 2011), sustainable intensification is actively promoted by extension services, processing companies, international NGOs and development organizations (German Society for International Cooperation, 2005; USAID, 2009, 2013; Government of Ghana, 2010; Millennium Development Authority, 2011; McMillan, Reference McMillan2012). Nevertheless, the adoption rate is mixed–with mulching being used by about half of Ghana's pineapple farmers by now, but other practices are not used by even a quarter of the targeted farmers (see figure 1).
Figure 1. Diffusion of organic practices.
Mulching can mean a spectrum of techniques that all have in common that bare soils are avoided by covering them up with material to suppress weed growth and conserve soil moisture (Awodoyin et al., Reference Awodoyin, Ogbeide and Oluwole2007; Dzomeku et al., Reference Dzomeku, Mahunu, Bayorbor and Obeng-Danso2009; Snapp and Pound, Reference Snapp and Pound2011). The materials used are often plastic foil, organic materials, and sometimes textiles. It is important to note that mulching material is not living and used for the sole purpose of covering bare soils.
Other available sustainable intensification technologies in Ghana include crop rotations that include legumes and other crops that increase the nutrient content of the soil, to intercrop those plants together with the main crop, and the use of crop residues and other organic materials as natural fertilizers. Those practices are summarized in this paper under the term ‘organic fertilizer’, as their main purpose is to enrich the nutrient content of the soil. As can be seen in figure 1, these practices are far less diffused than mulching, even though both have been shown to be similarly profitable (Kleemann and Abdulai, Reference Kleemann and Abdulai2013). It has also been found that combining mulching and organic fertilizers super-linearly increases profits (Kleemann and Abdulai, Reference Kleemann and Abdulai2013), which suggests that a wider diffusion of especially organic fertilizers could pay off greatly. Two additional benefits of organic fertilizers is that their quality is under the control of the farmers, whereas it has been found that chemical fertilizer can be of varying quality (Bold et al., Reference Bold, Kaizzi, Svensson and Yanagizawa-Drott2017) and some nitrogen fertilizers lead to soil acidification, reducing nutrient availability in the future (Yeboah et al., Reference Yeboah, Kahl and Arndt2012).
The large literature on the diffusion of agricultural innovations suggests several explanations as to why seemingly profitable innovations do not quickly diffuse amongst the farmers and why the diffusion of some innovations is slower than that of others (Feder et al., Reference Feder, Just and Zilberman1985; Anderson and Feder, Reference Anderson and Feder2004; Foster and Rosenzweig, Reference Foster and Rosenzweig2010). Such explanations include heterogeneous profits, such that not all farmers actually benefit from adoption (Suri, Reference Suri2011), uninsured risk (Dercon and Christiaensen, Reference Dercon and Christiaensen2011; Karlan et al., Reference Karlan, Osei, Osei-Akoto and Udry2012), insecure tenure rights (Abdulai et al., Reference Abdulai, Owusu and Goetz2011; Fenske, Reference Fenske2011), network effects (Conley and Udry, Reference Conley and Udry2010; Wuepper et al., Reference Wuepper, Ayenew and Sauer2017) and bounded rationality (Duflo et al., Reference Duflo, Kremer and Robinson2011; Wuepper et al., Reference Wuepper, Zilberman and Sauer2016; Wuepper and Lybbert, Reference Wuepper and Lybbert2017). An especially prominent explanation is information disequilibria. Farmers need to learn about the existence, profitability, and correct application of new technologies, before they are able and willing to adopt them. Thus, if not all farmers have access to the same amount of information, it is suggested that for profitable innovations, the farmers with better information access adopt first, and the others only follow when they have received sufficient information themselves (Bandiera and Rasul, Reference Bandiera and Rasul2006; Conley and Udry, Reference Conley and Udry2010; Kabunga et al., Reference Kabunga, Dubois and Qaim2012). The main information sources in developing countries are usually other farmers and training (Moser and Barrett, Reference Moser and Barrett2006; Dercon et al., Reference Dercon, Gilligan, Hoddinott and Woldehanna2009; Rogers, Reference Rogers2010; Pan et al., Reference Pan, Smith and Sulaiman2015).
Below we investigate why mulching is so much more common than the use of organic fertilizers, as well as the effectiveness of training in fostering the adoption and diffusion of these technologies. We propose that, because mulching is less complex than the effective use of organic fertilizers, it is easier to learn through observation of its use by other farmers. In addition, the use of the right organic fertilizer depends to some extent on the individual soil characteristics and crops grown. Mulching, in contrast, has similar effects for all crops and in different locations. Hence, the transfer from one location to another is likely to yield more or less the same effects for the same. This is not, or is less, the case with organic fertilizer. This has also been reported by our sampled farmers during the survey.
If a farmer observes that a neighbor profitably uses mulching, she can imitate this neighbor and also use mulching. Even if the neighbor uses a material (say plastic foil) that is not available to the farmer, she can simply use a different material (say grass or straw). In contrast, learning that a neighbor profitably integrates legumes in her crop rotation requires the potential adopter to learn about all the requirements of that legume and how that crop interacts with the currently used farming practices, e.g., the use of agro-chemicals. Furthermore, as many organic fertilizers are living plants, they might fare differently on different plots as a function of soil moisture, micro-climate, disease pressure and soil nutrients (Snapp and Pound, Reference Snapp and Pound2011).
Investigating the implications of such differences amongst sustainable intensification technologies is a contribution to different strains of literature. First, the literature on sustainable intensification commonly emphasizes the increased knowledge intensity of the involved technologies compared to conventional farming systems, whereas we are amongst the first to focus on knowledge intensity differences amongst sustainable intensification technologies. Second, very recent literature on the diffusion of innovations finds that training is effective to start the innovation diffusion process, but not to drive it at later stages, as farmers learn better from their neighbors once there is sufficient local experience available (Krishnan and Patnam, Reference Krishnan and Patnam2014). In the following, we will show that this finding cannot be generalized, but depends on the nature of the innovation being trained. The more complex an innovation, the less effective is peer learning and the more important is training. Thus, the optimal amount of provided training is a function of how complex the technology or innovation is. Third, after Munshi (Reference Munshi2004) showed that unobserved heterogeneity can make peer learning less effective, we establish that this can make training more effective (when peer learning and training are substitutes).
We test this supposition using data on pineapple farmers from Ghana. As we do not conduct a randomized control trial, we must carefully consider the issue of unobserved heterogeneity. Empirical challenges could come from self-selection into training according to prior interest in an innovation, as well as the well-known reflection problem inherent in many analyses of social interactions (Manski, Reference Manski1993, Reference Manski2000). We use 2SLS to control for the endogeneity of estimated peer effects and selection into training by relying on an approach similar to the one suggested by Bramoullé et al. (Reference Bramoullé, Djebbari and Fortin2009), which has also been used by Krishnan and Patnam (Reference Krishnan and Patnam2014).
In section 2, we provide some background information and describe our data. We then explain our empirical framework in section 3 and present our results in section 4. In section 5, we discuss and conclude.
2. Context and data
The pineapple farmers of Ghana have received a lot of academic attention in recent years (Udry and Conley, Reference Udry and Conley2004; Udry and Anagol, Reference Udry and Anagol2006; Goldstein and Udry, Reference Goldstein and Udry2008; Conley and Udry, Reference Conley and Udry2010; Suzuki et al., Reference Suzuki, Jarvis and Sexton2011; Gatune et al., Reference Gatune, Chapman-Kodam, Korboe, Mulangu and Raktoarisoa2013; Kleemann and Abdulai, Reference Kleemann and Abdulai2013; Wuepper et al., Reference Wuepper, Zilberman and Sauer2016). One reason is the dynamism of the sector, starting with the business opportunity to grow pineapple for export to the European Union in the 1990s. Most of the pineapple farmers had previously relied on far less profitable roots, tubers, and cereals–with large shares for own consumption. With the decision to grow pineapples for export, the farmers needed to learn about how to intensify their former extensive production systems (Conley and Udry, Reference Conley and Udry2010). They also needed to learn about different contract farming arrangements (Suzuki et al., Reference Suzuki, Jarvis and Sexton2011; Gatune et al., Reference Gatune, Chapman-Kodam, Korboe, Mulangu and Raktoarisoa2013; Wuepper and Sauer, Reference Wuepper and Sauer2016). Most of these contract arrangements include the provision, or at least facilitation of access to, extension services and training, and offered prices are commonly higher and more stable than outside the contract arrangement. On the other hand, contract farming also implies a higher rejection risk, e.g., if the produced fruits do not meet the increased quality standards.
The provision of inputs and credits has been tested in the past but is currently rather uncommon. The idea is that provided information and higher prices are sufficient for the farmers to reliably produce sufficient quantities of pineapples of sufficient quality (Webber and Labaste, Reference Webber and Labaste2009).
The performance of Ghana's pineapple sector was quite strong until demand in the European Union switched around the year 2004 to a new variety, which is more expensive to grow, because it requires more inputs and is environmentally sensitive (Fold and Gough, Reference Fold and Gough2008). Many formerly successful companies went out of business, and many farmers made critical losses (Barrett et al., Reference Barrett, Bachke, Bellemare, Michelson, Narayanan and Walker2012). The pineapple industry subsequently restructured with the result being a diversification of the sector now exporting the new variety, but also processing several other varieties mainly into juice and dried fruit. The remaining pineapple farmers and processing companies still face the double challenge to intensify pineapple production, in order to be profitable, while avoiding negative side-effects from pesticide and fungicide use and land degradation (Kleemann and Abdulai, Reference Kleemann and Abdulai2013). The growing organic market worldwide (Kleemann et al., Reference Kleemann, Abdulai and Buss2014) and the growing domestic market, including the rise of supermarkets (World Bank, 2011), adds a commercial incentive for sustainable intensification of the production. A range of national and international organizations promote and support sustainable intensification. The US-American USAID, the German GIZ, the World Bank, The United Nations Millennium Development Authority, various NGOs, some of the processing companies, and Ghana's Ministry of Food and Agriculture (MOFA), all provide training to the farmers, in such diverse topics as farm management, accounting, input use, and sustainable farming practices.
Similar to Ghana's cocoa growers, Ghanaian pineapple farmers are almost all organized in farmer groups. These farmers' groups are locally organized, so that their members can meet frequently. Their sizes vary, so that sometimes, farmers from several communities are organized within one farmers' group, and sometimes, there are multiple farmers' groups in one community. Due to a lack of information about the communities, trainings can usually not be strictly targeted, e.g., towards farmers with more need, potential, or interest. The strategy of most organizations is to start training farmers in one community or group and then to move on to the next community or group. Most communities receive several training sessions a year from various organizations. These organizations usually coordinate where and what to train. Most training sessions are offered by at least two stakeholders, e.g., two development agencies or one development agency and the national extension service. As we will see below, this helps our identification strategy, as we rely on a well-coordinated diffusion of training. In addition to the training provided by development organizations, processing companies such as Blue Skies provide training specifically for the communities where they have suppliers, whereas NGOs often specifically target more remote communities. Figure A1 in the online appendix, gives an overview of the distribution of training providers. Training considered for this study focuses on mulching (to conserve soil moisture) and a range of organic fertilizers, such as incorporating certain leguminous crops into the crop rotation, to interplant such crops together with pineapple, to use crop residues, or animal manure. Increasing soil nutrient contents and moisture increases fruit quality and quantity (Norman, Reference Norman1986) and specifically for the farmers surveyed for this study, Kleemann and Abdulai (Reference Kleemann and Abdulai2013) find that sustainable intensification practices are highly profitable.
To investigate the effect of training sessions and peer-learning on the diffusion of such practices, we surveyed 398 farmers in 2013. Half of these farmers had already been surveyed in 2010 by Kleemann and Abdulai (Reference Kleemann and Abdulai2013); the other half was interviewed for the first time. The farmers from the first period are farmers who were certified for export at that time (GlobalGAP, Faitrade and/or organic certification). For our analysis, we use five-year recall data from the farmers interviewed in 2013 and we use the data from the 2010 data collection to investigate the reliability of the 2013 data. Our final dataset thus covers 398 farmers over five periods. The crucial question is how our recall data compares to panel data collected over five rounds.
In the context of African agricultural data, Beegle et al. (Reference Beegle, Carletto and Himelein2012) experimentally varied the gap between harvest and survey, to investigate whether recall bias affects data quality. They do not find a significant recall bias but they only consider short periods. De Nicola and Giné (Reference De Nicola and Giné2014) investigate the accuracy of recall data in India over longer periods and find that recall bias increases over time. In the empirical literature, a common recall period is about 10 years (e.g. Genius et al., Reference Genius, Koundouri, Nauges and Tzouvelekas2014). This period is sufficiently long to see trends and sufficiently short to avoid significant recall bias. It is, however, important that we consider the education and income of the respondents. For this study, we only use recall data for 5 years, to minimize measurement error.
As mentioned earlier, we have data available for half of our sample. The 2010 sample is not representative of the 2013 sample, because the earlier sample only includes export certified farmers while the later sample also includes non-certified farmers. However, many survey questions are exactly the same in both questionnaires and the five year recall period includes both survey periods. We compared the reported year of different kinds of trainings and the adoption of different kinds of technology (chemical fertilizer, new pineapple varieties, several organic practices) and we find no evidence for recall errors. This is not obvious, given that many of the sampled farmers have no or incomplete written records, even though this is actively promoted by development agencies, extension agencies, and processors. However, Ghana's pineapple farmers are visited frequently by researchers (from universities, the United Nations, the World Bank, and many others). It seems that the frequency of surveys increases how well the farmers can recall important economic variables, such as when they received training or when they decided to adopt a given technology.
For our sampling procedure, lists of certified farmers were readily available so a three stage stratified sampling procedure was feasible. We started with the districts where most pineapples are produced (in the Eastern Region, the Central Region, and Greater Accra), continued with the farmers' groups that are certified to export pineapples, and finished with a proportional sampling of individual farmers according to the number of pineapple producers in each group. For non-certified pineapple farmers, there are no reliable statistics available, so the sampling is based on the information provided by development agencies and extension agents. When selecting non-certified farmers without lists, special emphasis was placed on the representativeness of the farmers, so as not to disproportionally sample ‘easier to reach’ farmers. Nevertheless, very remote farmers are likely to be underrepresented because they are less likely to be on a list for the stratified random sampling, and for the other farmers, the probability to be sampled decreased with the distance to those farmers. However, such farmers are also less likely to grow pineapple (as can be seen in figure 2, they are concentrated near the coast, as pineapple growing conditions deteriorate quickly from south to north). The final sample size is 398 farmers. Figure 2 shows the south of Ghana. Circles indicate sampling locations. The stars indicate the locations of the main pineapple processors, black dots show major cities.
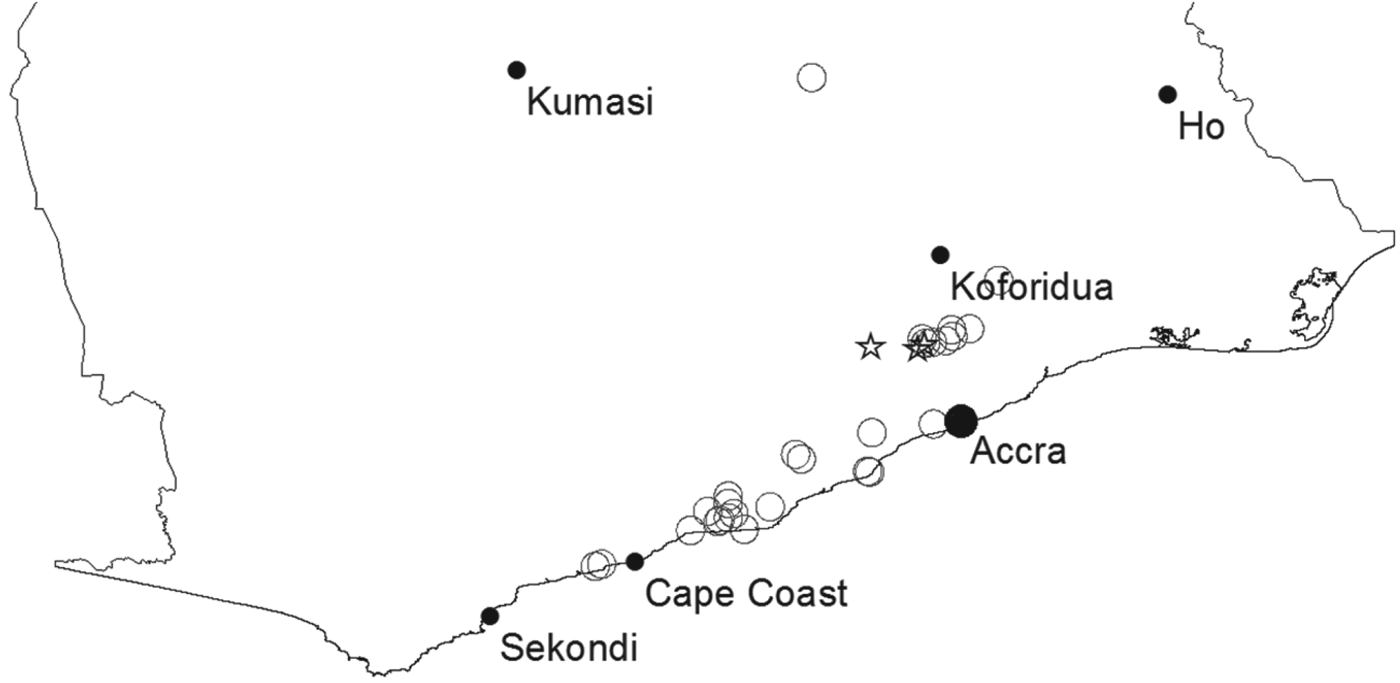
Figure 2. Sampling area.
We asked the farmers for each of their plots whether and when they adopted a sustainable intensification practice and we asked them when they received training, from whom, and about what topic. We also asked about annual values for some of our control variables, such as rainfall (on a Likert scale), prices (in GHC), credit, and contract farming (both binary). As rainfall is a very important production determinant for the farmers, we also use a gridded dataset on regional precipitation from the African Flood and Drought Monitor. The data is a combination of local weather station data and satellite remote sensing. Using both reported and measured rainfall is motivated by the fact that farmer-level conditions plausibly differ from the more aggregated, measured rainfall. In general, for the decision to adopt technology, it matters what the farmers think about the rain, not what the rainfall actually is. Furthermore, the more aggregated data likely suffers from aggregation bias (Auffhammer et al., Reference Auffhammer, Hsiang, Schlenker and Sobel2013). In our sampling region, there is a complex interaction between weather and biogeographic variables, such that one plot might be wet (surrounded by bushes and trees in a valley) whereas the neighboring plot might be dry (open on a small hill). Nevertheless, it seems important to also control for the measured rainfall, as reported rainfall is clearly no perfect substitute.
Overall, we thus use 1990 observations, for 398 farmers and 5 periods. Table 1 presents the main variables and summary statistics. It can be seen that currently, 43 per cent of the farmers use mulching but only 11 per cent use organic fertilizers (of which 72 per cent use leguminoses in their crop rotation, 51 per cent use crop residues, 35 per cent use intercropping, and 21 per cent use other organic fertilizers). In contrast to the wide difference in adoption, training in mulching and training in organic fertilizers is provided to 10 and 7 per cent of the farmers, respectively. The average farmer in our sample is 43 years old, male (women are almost entirely absent), has completed Junior Secondary School, and does not have much nonfarm income, or credit (only 21 per cent do), or a contract arrangement with a company (only 18 per cent do).
Table 1. Variables and summary statistics
Notes: Data from 398 farmers. Reported values are averages over 5 periods. N = 1990.
a Source for measured rainfall data: http://stream.princeton.edu/AWCM/WEBPAGE/interface.php?locale=en.
SD, standard deviation.
According to the farmers (table 2), they mostly discuss their farming practices with extension agents (71 per cent), followed by members of their farmers' group (30 per cent), their friends (16 per cent), and their neighbors (6 per cent).
Table 2. Information sources
3. Empirical framework
It is well known that the identification of social interactions poses a range of identification challenges (Manski, Reference Manski2000; Moffitt, Reference Moffitt2001; Blume and Durlauf, Reference Blume, Durlauf, Oakes and Kaufmann2006), such as the reflection problem described by Manski (Reference Manski1993), and the problem of exclusion bias (Guryan et al., Reference Guryan, Kroft and Notowidigdo2009; Caeyers and Fafchamps, Reference Caeyers and Fafchamps2016). In this section, we will discuss the empirical challenges first for the estimation of peer-learning and then for the effect of training. Then we discuss our analytical framework and how we address the discussed challenges.
3.1 The identification of peer-learning effects
In most economic research, social interactions are not directly observed, but only indirectly inferred from observed outcomes in the peer networks (Manski, Reference Manski2000). Identifying the right network is already the first challenge (Maertens and Barrett, Reference Maertens and Barrett2013). Foster and Rosenzweig (Reference Foster and Rosenzweig1995) and Munshi (Reference Munshi2004) assume that peer-networks are the villages of the farmers. However, networks usually differ across contexts and Conley and Udry (Reference Conley and Udry2010), for example, show that when it comes to learning about an innovation, networks are smaller than the villages. An expensive alternative is used by Van den Broeck and Dercon (Reference Van den Broeck and Dercon2011), who take a full census of each village and ask the farmers about their contacts. A less expensive alternative, used by Bandiera and Rasul (Reference Bandiera and Rasul2006), is to ask the farmers to list a small number of their peers from whom they learn. In a comparable approach, Conley and Udry (Reference Conley and Udry2010) randomly match a small number of farmers and ask them about each other's behaviors and outcomes. Finally, Krishnan and Patnam (Reference Krishnan and Patnam2014) use spatial proximity of their sampled farmers and define peer-networks to be within 1 km distance from each other. It is well known that misrepresenting the peer networks can bias the estimates of the peer effect (Maertens and Barrett, Reference Maertens and Barrett2013). In our context, the choice of the peer network is aided by the fact that the pineapple farmers are organized in 142 local farmers' groups, which are a viable approximation of their peer network (see table 2).
As it is common to use the (often lagged) outcome of one's peers as opportunity for peer-learning, we directly run into the reflection problem described by Manski, (Reference Manski1993) and the exclusion bias described by Guryan et al. (Reference Guryan, Kroft and Notowidigdo2009) and Caeyers and Fafchamps (Reference Caeyers and Fafchamps2016). The former indicates that homogeneous behavior within a peer network has more potential explanations than just peer learning. We need to distinguish between contextual effects (individuals in the same context tend to behave similarly), endogenous effects (peer learning and other externalities), and correlated effects (individuals in the same peer group share common characteristics that also produce similar behaviors). The name reflection bias comes from the example that, without additional information, it is impossible to know whether a mirror ‘reacts’ to the person in front or the other way around, as both change simultaneously. Formally, we are interested in the following model:
$$y_{izt} =\beta_1 x_{it} +\beta_2 \hat{\bar{y}}_{-izt-1} +\beta_3 \displaystyle{{\sum_{j\in \eta _i } x_{jzt} }\over{\eta _i }}+\varepsilon_{zt},$$
where y
izt
denotes the adoption of innovation z of individual i at time t, x
it
denotes her characteristics (e.g., age and education),
${\hat {\bar y}}_{ - izt - 1} = \sum\nolimits_{j \in \eta _i} {y_{jzt}/\eta _i} $
is the average innovation diffusion in her network η
i
at t − 1 (excluding farmer i's choice), and
$\sum\nolimits_{j \in \eta _i} {x_{jzt}/\eta _i} $
are the average characteristics of her network without herself (in our subsequent analysis captured with location fixed effects F). Thus, we are interested in precisely identifying β2, which is the causal effect of learning from peers on the adoption probability of the innovation. As we will further elaborate on below, we adapt the approach of Bramoullé et al. (Reference Bramoullé, Djebbari and Fortin2009) and use the lagged treatment and outcome of indirect neighbors to exogenize β2.
An issue that has not yet received much attention is the exclusion bias that is created when OLS is used to estimate β2. The exclusion bias is created when each farmer is excluded from the calculation of her peer statistics (the intuition is that an individual cannot be his/her own peer, so he/she is excluded from the calculation of peer outcomes). This creates a systematic, negative correlation between the characteristics of the peers and the characteristics of the individual, which biases the OLS estimated peer effects downwards (Guryan et al., Reference Guryan, Kroft and Notowidigdo2009) but which does not affect specifications that use the lagged outcome of the peers while controlling for the farmer's own lagged outcome and specific other setups (Caeyers and Fafchamps, Reference Caeyers and Fafchamps2016). In addition to alternatives to substantive explanations such as negative assortative matching in the endogenous peer group formation, the exclusion bias can explain why OLS estimates of peer learning are usually considerably smaller than their corresponding instrumental variables estimates (Zeitlin, Reference Zeitlin2011; Krishnan and Patnam, Reference Krishnan and Patnam2014). In our case, we use the lagged outcome of the peers while controlling for own lagged outcome.
3.2 The identification of training effects
The identification of training effects would be easiest if training were received fully randomly. This is however not the case for several reasons, such as a lack of complete lists of eligible farmers and time and resource constraints by the implementing agencies (making it attractive to use logistically efficient targeting and unattractive to stick to tedious randomization protocols). There is a likely degree of two-way selection. First, even if most training contents are decided without the farmers and offered more or less randomly, there could still be a degree of matching certain training sessions to certain farmers. Second, even though participation in a given locality is close to 100 per cent, the remaining farmers who do not participate may do so out of a reasoned lack of interest. Thus, as argued by Dercon et al. (Reference Dercon, Gilligan, Hoddinott and Woldehanna2009) and Krishnan and Patnam (Reference Krishnan and Patnam2014), unobserved heterogeneity must be considered when estimating the effect of training provision and participation. Formally, as described by Angrist and Pischke (Reference Angrist and Pischke2008), the observed difference in outcomes between the farmers who have been trained (Tr
i
= 1) and those who have not (Tr
i
= 0), is explained both by the causal effect of the training
$\kappa =y_{1i} -y_{0i}$
and a selection bias
$\lpar {E\lsqb {y_{0i} \vert Tr_{i} =1} \rsqb -E\lsqb {y_{0i} \vert Tr_{i} =0} \rsqb } \rpar $
, the latter stemming from outcome-relevant, initial differences between the farming who were trained and those who were not.
3.3 The model
To identify the causal effects of learning from training and from peers on the adoption of an innovation, we require several steps. In our case, the choice of the peer network is comparably straightforward, because the farmers are organized in local farmers' groups, which they also report as their main peer network (shown in table 2).
This is only an approximation to the actual peer network, as most farmers are part of multiple, overlapping peer groups, such as neighbors, friends, and farmers' groups. However, the farmers' group is the main and most important network of the farmers, and discussing farming practices and business decisions is a main motivation for joining or starting a local farmers' group, according to the sampled farmers. In these groups, all members are pineapple farmers. The groups' representatives take over most of the external communication for their members, e.g. with buyers, training institutions, etc.
As we are interested in a binary variable (adoption of mulching yes or no, adoption of organic fertilizers yes or no), we could use a discrete choice model, such as that proposed by Brock and Durlauf (Reference Brock and Durlauf2001). Taking into account the endogeneity of peer learning and training is not trivial this way (Angrist, Reference Angrist2001). As an example, Petrin and Train (Reference Petrin and Train2010) suggest the use of control functions, but they work better for training than for peer effects (because training is binary and peer learning is continuous). For continuous treatment variables, the Special Regressor approach of Lewbel et al. (Reference Lewbel, Dong and Yang2012) and Dong and Lewbel (Reference Dong and Lewbel2015) is feasible. However, as Angrist (Reference Angrist2001) and Angrist and Pischke (Reference Angrist and Pischke2008) argue, the analytical framework can be much simplified by using a linear model and controlling for the endogeneity of explanatory variables with instrumental variables. This approach requires comparatively mild assumptions and estimates are readily interpretable. Thus, we choose a 2SLS framework for our analysis and we instrument training treatment and peer effects following the approach developed by Bramoullé et al. (Reference Bramoullé, Djebbari and Fortin2009), which has recently been employed by Krishnan and Patnam (Reference Krishnan and Patnam2014) in a similar context to ours.
To further ease interpretability of our estimates, we use standardized variables for the right hand side throughout, meaning that variables are rescaled to have a mean of zero and a standard deviation of one.
We begin our analysis with an OLS regression, to establish that the characteristics of the trained farmers have not changed over time, which would suggest some kind of targeting or sorting:
$$\eqalign{& Tr_{izt} = \beta _1\overline {Tr} _{ - izt - 1} + \beta _2x_{it} + \beta _3F + \beta _4y_{izt - 1} + u_i + \varepsilon _{zt}\quad {\rm if }\;t \ge 2011, \cr & Tr_{izt} = \beta _5\overline {Tr} _{ - izt - 1} + \beta _6x_{it} + \beta _7F + \beta _8y_{izt - 1} + u_i + \varepsilon _{zt}\quad {\rm if }\;t \le 2011,} $$
where Tr
izt
is whether or not a farmer i is trained in a particular practice z in period t,
$\overline {Tr} _{-izt-1}$
is the share of farmers that have been trained in each district before (excluding i), x
it
is a vector of explanatory variables that could affect the likelihood of being trained, F is a vector of year and region dummies, y
izt−1 depicts whether the farmer already used the innovation in the previous period, and u
i
is a farmer random effect to pick up unobserved, time invariant heterogeneity among the farmers, and the β s are the model coefficients to be estimated. We always estimate the model with u
i
and without, as the term potentially absorbs endogeneity but also available variation in the data. Below, we only show the results of one model as the results are qualitatively similar.
To understand whether the characteristics of the trained farmers change over time, we estimate equation (3) separately for earlier and later periods, splitting our sample period in half. This reveals whether training sessions were first offered to farmers more in need (e.g., less income, more constraints) or with a higher innovation potential (e.g., more income, less constraints) or whether possible training sessions became more targeted in time, and also whether trained farmers are more or less likely to have already adopted the trained innovation before.
For this and all following models, we always estimate a few specifications, to probe the sensitivity of the estimates to the inclusion of various control variables. We usually start without any control variables, then proceed with the inclusion of strictly exogenous controls, and end with controls that are potentially endogenous. In our main specifications, standard errors are always clustered at the farmers' group level, and we include fixed effects for years and regions. We alternatively estimated random effects models at the individual farmer level and in these models we clustered the standard errors at the farmer level. The results are qualitatively similar and can be obtained upon request from the authors.
For most of our analysis, we need to consider the likely endogeneity of peer-learning and training. We use an adapted version of Bramoullé et al. (Reference Bramoullé, Djebbari and Fortin2009), that is: if peer behavior is endogenous, one can use the behavior of the peers of one's peers as an instrument. This is possible if a network is characterized by a small degree of intransitivity (farmer i is connected to farmer j, and farmer j is connected to farmer k, but farmer k is not connected to farmer i). The intuition for this instrument is that farmer k can only affect farmer i through affecting farmer j, so whatever farmer i and farmer j have in common (a common context, similar characteristics), farmer i and farmer k do not (they are not even connected). It should be noted that this approach already works if there are only a few farmers who are only indirectly connected.
The same instrument can be applied to instrument for training, but with a different rationale behind it. As we have described earlier, training sessions move from place to place, so if there was a training session organized in an adjacent community in the last period, chances are that farmers in close by communities will soon receive training themselves. The share of training that is explained by the share of trained farmers in adjacent communities in the last period is a feasible instrument, even if individual farmers participate out of specific incentives or the training content offered varies from community to community.
As a caveat, we do not have detailed GPS data on the locations of the farms but only the names of the communities. The common approach would be to construct a neighbor matrix W, e.g., defined using the K nearest neighbors of a farmer, computed by the Euclidean distance between the farms, and to interact this matrix with the outcome variable and the exogenous peer characteristics. Instead, we rely on farmers' group and community locations, so that the lagged share of trained farmers in neighboring communities is our instrument for whether or not a farmer is trained and the lagged diffusion of an innovation in close by farmers' groups is our instrument for the diffusion of that innovation in a farmer's farmers' group. As we do not have detailed GPS data on the locations of the farms but only the names of the communities, we construct the matrix by hand. We control for correlated and selection effects by taking into account the behavior of the farmer in the last period, as well as past training sessions and peer diffusion, as well as with dummies for location and period. Our 2SLS specification then looks as follows:
$$y_{izt} = \beta _1y_{izt - 1} + \beta _2x_{it} + \beta _3 \widehat{{Tr}}_{izt - 1} + \beta _4 \widehat{{\bar y}}_{ - izt - 1} + \beta _5F + u_i + \varepsilon _{zt}$$
$$\bar y_{ - izt - 1} = \alpha _1\bar y_{jzt - 1} + \alpha _2\overline {Tr} _{jzt - 1} + \beta _6y_{izt - 1} + \beta _7x_{it} + \beta _8Tr_{izt - 1} + \beta _9F + u_i + \varepsilon _{zt}$$
$$Tr_{izt - 1} = \alpha _3\bar y_{jzt - 1} + \alpha _4\overline {Tr} _{jzt - 1} + \beta _{10}y_{izt - 1} + \beta _{11}x_{it} + \beta _{12}\bar y_{ - izt - 1} + \beta _{13}F + u_i + \varepsilon _{zt},$$
where y
izt
denotes the technology choice of individual i at time t,
$\bar{y}_{-izt}$
is the adoption choice of social peers (excluding own decision), Tr
izt
is an indicator for whether the farmer received training or not, and
$\bar{y}_{jzt}$
and
$\overline {Tr} _{jzt} $
are our instrumental variables, namely the diffusion of an innovation amongst indirect neighbors (neighbors of neighbors) and the share of farmers training there. We continue to cluster the standard errors at the farmers' group level and to include location fixed effects to hold common location characteristics constant.
A variable that we have ignored so far is whether the farmer participates in contract farming. On the one hand, contract farming increases both the likelihood of being trained and also the ability and incentive to adopt innovations. On the other hand, contract farming is likely to be endogenous, so we do not want to naively enter contract farming as another control variable into the model. Instead, we estimate another 2SLS, in which we instrument whether or not the farmer has a farming contract with a company with the distance between the community of the farmer and the next company. The exclusion restriction is fulfilled because the companies are located at the center of the main pineapple production area, with sufficient distance to potential explanatory variables, such as the coast, the mountains, and especially the major cities (see figure 2).
Finally, we estimate three more models. First, we interact the model from equation (3a)–(3c) with period dummies, to estimate period specific effects of training and peer learning. Secondly, we split our sample into contract farmers and non-contract farmers, to see how much financial constraints matter for our results (assuming that contract farmers are less financially constrained than non-contract farmers). Finally, we investigate the interdependencies of our dependent variables with the adoption of chemical fertilizer, to see whether this affects our estimates in a meaningful way.
4. Results
We begin our analysis with a standard regression describing who the farmers are who receive and participate in training before and after 2011. The cut-off is set in the middle between 2009 and 2013. As table 3 shows, the best predictor for receiving training is how many other farmers have already been trained in the district. Since training sessions move from location to location and close to all farmers participate, variables such as past adoption of the innovation, age, or education do not predict trainings. Variables that explain some share of the training sessions are contract farming (because some training sessions are offered by companies and companies can also help to organize training with other organizations), and a higher share of nonfarm income (which could be a proxy for regional economic dynamism).
Table 3. Who receives training? (OLS)
Notes: The model is OLS regression with random effects at the farmer level. Standard errors are clustered at the farmers’ group level. Significance levels are 10% (*), 5% (**), and 1% (***). We control for unobservable differences between the regions with fixed effects. To see whether the training target groups have changed in time, we split the sample in the year 2011. The full sample is 1990 observations.
In general, table 3 indicates that training sessions are distributed approximately randomly and the farmers who were trained earlier are similar to the farmers who were trained later. Nevertheless, we control for a selection bias in both peer learning and training, because of the risk that selection occurs based on omitted variables.
Table 4 presents our estimates of the effectiveness of training and peer learning. The first stages are presented in the online appendix. Below the table we show the Craig Donald F-values which suggests that the share of trained neighbors and the technology diffusion amongst them are strong instruments for a farmer's training participation and opportunity for peer learning. It is suggested that training and peer learning are very similarly effective to diffuse organic fertilizers{–}at a rather low level (about 4 per cent increase in the probability that organic fertilizers are adopted). In contrast, training does not significantly increase the probability that mulching is adopted, but the main driver is peer-learning, which is very effective (with a 19 per cent increase in the probability that mulching is adopted). A few other variables are shown for comparison. It can be seen that reported rainfall (rain B) is significant for the adoption of organic fertilizers (because many organic fertilizers are living plants that require water) but not for mulching (because mulching materials are non-living). Measured rainfall (rain A) is not significant, at least as long as we include reported rainfall. This is because measured rainfall is much coarser, and does not take into account micro-climates. Nevertheless, we like to include it to test whether the farmers might misperceive their rainfall or whether there is significant recall bias, both of which seem to be absent.
Table 4. Adoption of organic practices second stage (2SLS)
Notes: The table reports estimated coefficients and standard errors in parentheses (clustered at the farmers' group). F train is the Craig Donald F value for the excluded instrument for training (the training of indirect neighbors) and F peers is the Craig Donald F value for the excluded instrument for peer-learning (the innovation diffusion amongst indirect neighbors). Significance levels are 10% (*), 5% (**), and 1% (***). We control for unobservable differences between the regions and years with fixed effects. The specifications differ by their set of control variables. Set A includes only the lagged adoption of each farmer. Set B also includes rainfall, soil quality, age, education, farm-size, risk preference, and nonfarm income. Set C additionally includes whether the farmer received a credit.
Whereas the results of table 4 are suggestive, we need to consider the effect of contract farming. Contract farming could both increase the chance of receiving training and incentivize the adoption of new technologies. However, we cannot naively control for contract farming because of a likely selection bias in who becomes a contract farmer and who does not. To exogenize contract farming, we use the distance to the closest pineapple processing company as an instrument. The exclusion restriction is fulfilled because the distance to the companies does not correlate much with any other relevant location, such as distance to the coast or the capital. We show the Craig Donald F values again at the bottom of table 5; the full first stage results can be seen in the online appendix tables A2a and A2b. The results of table 5 suggest that contract farming is only a significant adoption determinant for mulching but not for organic fertilizers. For mulching, however, the estimated effect is large and comparable to the effect of peer-learning. The basic pattern from table 4, however, does not change: training is a significant adoption determinant for organic fertilizers and mulching is mostly learned from the peers.
Table 5. Adoption of organic practices second stage (2SLS)
Notes: The table reports estimated coefficients and standard errors in parentheses (clustered at the farmers' group). F train is the Craig Donald F value for the excluded instrument for training (the training of indirect neighbors), F peers shows the same for the excluded instrument for peer-learning (the innovation diffusion amongst indirect neighbors), and F contract shows this for contract farming (the instrument is the distance to the closest company). Significance levels are 10% (*), 5% (**), and 1% (***). We control for unobservable differences between the regions and years with fixed effects. The specifications differ by their set of control variables. Set A includes only the lagged adoption of each farmer. Set B also includes rainfall, soil quality, age, education, farm-size, risk preference, and nonfarm income. Set C additionally includes whether the farmer received a credit.
To better understand the results above, we consider a few more tests. First, we estimate period specific effects for training and peer learning, to see whether there are obvious trends in our data. Secondly, we split our sample into farmers who currently have a farming contract with a company and those who do not, to investigate whether the effects of training and peer learning are distinct for these two groups (mulching, e.g., is more expensive than organic fertilizers, so we might expect contract farmers to be less constrained to adopt mulching than other farmers). Third, we investigate possible interdependencies between the adoption of sustainable intensification innovations and other inputs (e.g., chemical fertilizer). Fourth, we explore whether the training providing organizations might matter more than the type of trained innovation.
We show the results in tables A4 to A7 in the online appendix, as they only show that our results pass these additional tests. Beginning with period specific effects (table A4 in the online appendix), we do not see clear time trends in the effects of training or peer learning (between 2009 and 2013). Our basic observed pattern from above is stable over time. In table A5 in the online appendix, we investigate the role of contract farming and see that training is generally more effective for contract farmers, which could be due to the individual characteristics of these farmers or because of the complementary benefits that contract farming is providing. For the use of organic fertilizers, training increases the adoption probability by about 7 per cent for contract farmers and 3 per cent for non-contract farmers. For mulching, the adoption probability is only significantly increased for contract farmers, but the estimated effect is still very much smaller than the effect of peer learning (3 per cent versus 19 per cent). These results suggest that farmer characteristics play a role in the effectiveness of the provided training, but this role is only minor in comparison to the effect of the characteristics of the technology. Table A6 in the online appendix investigates the relationship between the adoption of organic practices and chemical fertilizer. Considering the interactions between different inputs could potentially be important if adoption decisions are interdependent. It has previously been found that Ghana's pineapple farmers super-linearly profit from combining more inputs (Kleemann and Abdulai, Reference Kleemann and Abdulai2013), which would suggest that farmers, if able and aware, might become more likely to adopt organic practices if they already farm more intensively. On the other hand, poor farmers might rather treat many inputs as substitutes, which would suggest that they either use chemical or organic fertilizer, or they choose between investing in mulching or investing in fertilizer. Table A6 shows that, on average, there is only a statistically positive significant relationship between the adoption of chemical and organic fertilizer, whereas the relationship between chemical fertilizer and mulching is also positive but not significant. In general, the decisions to adopt organic fertilizer, chemical fertilizer and mulching are close to independent in our study's context.
A final concern follows from our interpretation that the complexity of an innovation explains our finding that training is more important for the adoption of organic fertilizer whereas peer-learning is more important for the adoption of mulching. An alternative explanation could be that training providers follow distinct approaches (more top-down, more participatory, more theoretical, more practical, and so forth) and that, possibly by random chance, a more effective training approach has been chosen for organic fertilizers than for mulching. This would not explain the large peer learning effect that is observed for mulching but it could change the significance of the training. We do not have detailed information about the pursued approach of each training session, but we know which organization(s) organized which training session. Table A7 in the online appendix thus shows the results of repeating our analysis with organization specific estimates for the five largest training providers. We also continue to control for contract farming, as one of the training providers is the Blue Skies company, which targets its training to its contract farmers. Since we now have more endogenous variables than before (five training variables instead of one), we need additional instrumental variables. Recall that our training instruments are the share of farmers who have been trained close by in the last period. For the model of table A7 (online appendix), we make these instruments organization specific, meaning that we now have five instruments that reflect the share of farmers who have been trained by one of the five largest training providers in the last period in areas close by.
The results of table A7 should be interpreted with caution, as our approach is more likely to yield robust results on a more aggregate level, whereas it is not guaranteed that we avoid selection biases at the level of individual organizations. Nevertheless, the estimates shown in table A7 corroborate our main hypothesis and suggest that it is mostly the kind of innovation that determines training effectiveness. For the diffusion of organic fertilizers, especially the training of GIZ (the German development agency) and Blue Skies (a private processing company) seem effective. However, as mentioned above, this could be a selection effect, as it might be that USAID (the US development agency), Ghana's extension service, and MIDA (of the United Nations) have targeted initially poorer farmers and our instrumental variables approach does not sufficiently correct for this at such a disaggregated level. A warning sign is the estimated negative effect of the MIDA training in specification (1), which has the least control variables. It is informative, however, that the estimated effects for training in mulching are all insignificant, except for those provided by the GIZ in specifications (4) and (5). Even taking the estimate for the GIZ training at face value, it is clear that this effect is economically insignificant compared to the estimated effect of peer learning.
5. Discussion and conclusion
Using more sustainable intensification practices (such as mulching and organic fertilizers) would be beneficial for the pineapple farmers in Ghana, who are currently farming inefficiently extensive (World Bank, 2011; Kleemann and Abdulai, Reference Kleemann and Abdulai2013). Sustainable intensification practices are mostly promoted through demonstration and training sessions, financed by governments, private actors and development organizations and provided by extension agents (private and governmental), and NGOs. We find that training increases the diffusion of organic fertilizers but not of mulching. The latter is more effectively diffused through peer learning and additional training is not really necessary. The explanation we propose is that the effectiveness of training depends on the level of knowledge intensity of the technology. The profitability of organic fertilizers depends on many factors, such as rainfall, soil nutrient composition, the care in the case of live crops, whereas mulching has similar profitability levels independent of the soil composition and other characteristics. It is hence easier for farmers to learn mulching from their peers than to learn the profitable use of organic fertilizers. Thus, we conclude that it is the complexity of an innovation that determines whether it is sufficient to train relatively few farmers, and then let peer learning take over, or whether training must substitute for a lack of peer learning, so that many more farmers need to be trained. Mulching is an example of the former kind of innovation, organic fertilizers are an example of the latter.
Our finding fits well with the results of Munshi (Reference Munshi2004), who shows that unobserved heterogeneity limits the effectiveness of peer learning, and Krishnan and Patnam (Reference Krishnan and Patnam2014), who show that peer learning and learning from professional training are substitutes. Our findings can be understood as a link between these studies. When unobserved heterogeneity matters (as for organic fertilizers), the effectiveness of peer learning is reduced and training becomes critical. When unobserved heterogeneity does not matter (as for mulching), training is only important to start the diffusion process and loses its importance fast. Commonly, all sustainable intensification innovations are assumed more knowledge intensive than conventional innovations (seeds and chemical fertilizers). However, we find substantial heterogeneity amongst them and suggest that this is relevant for technology diffusion initiatives. Specifically, it can be misleading to use the findings on conventional innovation diffusion to inform policy for the diffusion of sustainable intensification practices. Sometimes their diffusion will be more expensive, as more farmers need to be trained.
A caveat of our data is that only a small share of farmers has yet been trained in sustainable intensification practices. This suggests that we have to be careful in generalizing our finding to situations where more farmers have been trained already. This seems to be promising research for the future. Other research avenues could include replicability tests in other contexts, e.g., other crops and regions within Ghana, or different countries. If panel data collection is feasible, it would be beneficial to collect direct measures of the knowledge of the farmers in the future. This would allow the researchers to better understand how it changes in response to training and peer learning and as a function of the innovation and other factors.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S1355770X1700033X
Acknowledgements
The authors thank those who supported the data collection in Ghana, including Prof. Awudu Abdulai, the GIZ staff, and the enumerators. We also thank the audience at the Bioecon Conference at the University of Cambridge who contributed feedback to an early draft. Finally, we thank the editor, Professor E. Somanathan, and two anonymous reviewers, who provided much constructive feedback.
