1. Introduction
According to the traditional view of environmental policy, regulations impose additional costs on firms and force them to devote additional inputs to abatement activities. As a result, the overall global competitiveness of regulated firms deteriorates in comparison to non-regulated firms (Palmer et al., Reference Palmer, Oates and Portney1995). This conventional paradigm was challenged by Porter (Reference Porter1991) and Porter and van der Linde (Reference Porter and van der Linde1995) who suggest that pollution is often a waste of resources, and a well-designed environmental policy can actually spur innovation at the firm level, leading the regulated firms to gain higher efficiency and competitive advantage over their unregulated rivals.
Among the growing body of work on environmental policies, two sets of studies have emerged. The focus of the first set has been on the impact of environmental policies on innovation (Jaffe and Palmer, Reference Jaffe and Palmer1997). This literature suggests that environmental regulations can provide strong incentives for firms to invest in R&D which utilizes the production process or reduces cost of inputs at the firm level. However, since these studies did not assess whether the benefits of innovation are higher than the cost of policy, they are described as the ‘weak’ version of the Porter Hypothesis.Footnote 1 In contrast, the ‘strong’ form of the environmental policies suggests that innovation induced by environmental regulations can benefit firms by more than fully offsetting the cost of the policy. In these studies, the overall impacts of environmental regulations are quantified by measuring the performance of firms in such areas as higher productivity and profit or lower production and input costs (Xepapadeas and Zeeuw, Reference Xepapadeas and de Zeeuw1999; Berman and Bui, Reference Berman and Bui2001; Alpay et al., Reference Alpay, Kerkvliet and Buccola2002; Yokoo, Reference Yokoo2009).
Although the strong form of the Porter Hypothesis is well regarded in the literature, the impact of environmental policies on market performance is not conclusive and thus the assessment of this potential ‘win-win’ situation remains an open research question. For example, a review of the existing literature on the competitiveness effect of environmental policies reveals that less attention has been given to understanding the channels through which environmental regulations lead to competitiveness. In the Porter Hypothesis, lack of innovation and technology diffusion are the main sources of inefficiency in economic activities. The total factor productivity (TFP) of an unregulated economy can be potentially higher because firms are not using the frontier abatement technologies. A well-designed environmental policy motivates innovation that increases productivity of individual firms and the whole economy thereafter. If the induced technological change is the primary source of productivity gain, then the environmental regulations lead to a Pareto improvement or a ‘win-win’ situation by not only protecting the environment, but also enhancing aggregate productivity and competitiveness.
In the assessment of the link between environmental regulations and competitiveness, the role of market competition is central. Competition is desirable since it contributes to the efficiency of economic activities and knowledge spillover (Aghion et al., Reference Aghion, Bloom, Blundell, Griffith and Howitt2005; Herrendorf and Bai, Reference Herrendorf and Bai2009). A study by Holmes and Schmitz (Reference Holmes and Schmitz2010) shows that firms that survive in an intensified competitive environment are the most likely to have larger productivity gains, and those gains often account for the majority of the overall industry benefits. The link between competition and competitiveness is also well recognized in the literature. While competition is about the nature and quality of rivalry, competitiveness refers to the outcome of competition. Therefore, competitiveness involves the ability of firms to face competition on a sustainable basis. It should be noted that, while markets work fairly well much of the time, the effective competition is not automatic, and can be harmed by policy distortions. Therefore, environmental policies lead to a higher market efficiency and competitiveness only if the regulations enhance the competitive environment too.Footnote 2
In this study, I examine the impact of environmental regulations on measures of competition and productivity. A lower average price or a larger number of competing firms are characterized as an intensified competition. To incorporate endogenous mark-ups that respond to the toughness of competition, the choice of consumer preferences is crucial. The standard Dixit–Stiglitz preferences feature a constant elasticity of substitution across varieties and are not well suited for studying the degree of competition.Footnote 3 Despite the simplicity and convenient analytical properties of the CES utility function, it implies a constant distribution of mark-ups which are unaffected by any exogenous policy change. For example, an increase in emission tax will have no effect on the average market price, or number of firms, which could potentially reflect tougher competition.Footnote 4
In this paper, I adopt the consumer preferences with a linear demand system and horizontal product differentiation following Ottaviano et al. (Reference Ottaviano, Tabuchi and Thisse2002) and Melitz and Ottaviano (Reference Melitz and Ottaviano2008). The utility function is tractable and features variable mark-ups in the way that more productive firms will charge higher mark-ups. Average productivity is endogenously determined through the selection and allocation of resources across surviving firms. To introduce the environmental concerns, I assume that pollution is a negative externality. Firms do not fully measure the economic costs of their emission produced during production. Hence, the profit inaccurately portrays firms' action as positive, leading to an inefficiency of resource allocation.
On the production side, I consider a production technology that follows closely that of Levinson and Taylor (Reference Levinson and Taylor2003). In the context of this technology, production processes yield pollution as a side-effect; however, firms can reduce pollution by abatement activities. Firms do so by allocating a fraction of their resources to production and the rest to abatement activities. To give a role for environmental policy and study its impact on abatement technology, I extend the model to allow for an endogenous investment in a clean abatement technology. Adopting a cleaner abatement technology entails higher cost than adopting a more polluting one, but a clean abatement technology increases productivity of abatement activities.
To regulate pollution, the government can choose between economic and administrative policies. In particular, the government can use an emission tax policy or impose an emission standard that directly restricts a firm's level of emission. Under an emission tax, firms pay a tax per unit of emission produced during production, whereas, under an emission standard, each firm is required to keep its emission–output ratio below an exogenous level determined by the government. A stricter environmental policy takes the form of a higher emission tax or a higher emission standard.
The findings of this study imply that a stringent environmental policy provides strong incentives for firms to adopt cleaner abatement technologies. The policy leads to increases in average productivity and environmental quality. However, the source of productivity gain is attributed to a selection effect through reallocation of resources from less productive firms to more productive firms rather than the induced abatement technology change at the firm-level. The regulations also negatively affect market competition by increasing market concentration and average prices. Marginal costs go up as a result of a stricter environmental policy and thus the expected profit prior to entry decreases. The least productive firms exit the market and inputs are reallocated to surviving firms. In contrast to the standard model of firm heterogeneity in which high productivity firms set lower prices, my model predicts that firms will set higher prices because the additional cost of abatement technology outweighs the lower marginal cost of production. Furthermore, a stringent environmental policy has a negative impact on social welfare by lowering the number of varieties produced in equilibrium.
The rest of this paper is organized as follows: section 2 describes the model with an emission tax policy. Section 3 evaluates the impact of emission tax on social welfare. Section 4 assesses the effect of an emission standard policy. Section 5 concludes.
2. Model
Consider that an economy consists of L consumers with identical preferences. Labor is the only factor of production. Each consumer is endowed with one unit of labor and x 0 c unit of numeraire good.
2.1. Consumer preferences
Consumer preferences V is given by
$$V = U + Z\comma \;$$
where U is a function of consumer utility and Z is environmental quality. The environmental quality has no effect on the consumer optimization problem. The utility function is defined over a continuum set of differentiated goods plus a homogeneous good taken to be a numeraire.
$$\matrix{U = x_0^c + \beta \vint_{\Omega} x_i^c di - {1 \over 2}\gamma \vint_{\Omega} \lpar x_i^c\rpar ^2 di - {1 \over 2} \eta \left(\vint_{\Omega}x_i^c di \right)^2 \cr \beta\comma \; \gamma\comma \; \eta \gt 0}$$
where x i indexes the quantity of variety i and x 0 is the quantity of the numeraire. β presents the intensity of preferences for the differentiated goods. β and η determine the substitution pattern between the differentiated varieties and the numeraire. An increase in β or a decrease in η shift out demand for the differentiated varieties relative to the numeraire. γ denotes the degree of product differentiation between varieties. If γ = 0, then consumers only care about their aggregate consumption level over all varieties.
The budget constraint of a representative consumer is defined over the numeraire good and other varieties as
$$I = x_0^c + \vint_{\Omega} p_i x_i^c di\comma \;$$
where I represents the indexed total of a consumer's income and p i denotes the price of variety i. Maximization of the utility function (1) subject to the budget constraint (3) gives demand for each intermediate good. With a positive demand for the numeraire good, the inverse demand function for the variety i is given by
$$p_i = \beta - \gamma x_i^c - \eta X\comma \;$$
where X = ∫Ω x i c d i is the aggregate quantity of all varieties. If only a subset of the intermediate goods is consumed in equilibrium (Ω* ∈ Ω), the inverted demand equation for variety i changes to
$$x_i^c = {\beta \over \eta N + \gamma} - {1 \over \gamma} p_i + {\eta N \over \eta N + \gamma} {1 \over \gamma} \bar{p}\comma \;$$
where
$\bar{p}$
is the average price of all the varieties N in Ω*. With L consumers in the economy, the aggregate demand for a particular variety x
i
c
is simply L x
i
c
. Hence, the aggregate demand is calculated as
$$x_i = {\beta L\over \eta N + \gamma } - {L \over \gamma} p_i + {\eta N \over \eta N + \gamma} {L \over \gamma} \bar{p}.$$
In equation (6), the demand for variety i is linear in its price p i and the average market price. x i is also determined by the size of the market and the elasticity of substitution between varieties. The maximum price that a consumer is willing to pay for a particular variety is the price that derives demand for that variety to zero. This price threshold p max is calculated as
$$p_{max} = {\gamma \beta + \eta N\bar{p} \over \eta N + \gamma}.$$
By the standard argument, a tougher competition is characterized by a lower average price or a larger number of competing firms, both of which reduce the price threshold. Then, the demand system can be written in terms of p max as
$$x_i = {L \over \gamma} \lpar p_{max} - p_i\rpar.$$
2.2. Production technology
I combined the production technology used by Levinson and Taylor (Reference Levinson and Taylor2003) with the heterogeneous firm environment of Melitz (Reference Melitz2003). There are a continuum number of firms that are heterogeneous with respect to productivity level. To enter the industry, firms must pay the irreversible fixed entry cost f e . Once a firm enters the market, it draws its productivity φ between 0 and ∞ from a known and exogenous distribution function. The productivity level of individual firms remains constant across time. Since each firm produces a single variety, I follow the literature and use φ to index operating firms in the market hereafter. Hence, the index of varieties i and firm level productivity φ are identical.
Labor is the primary factor of production and firms use a fraction of labor 1 − θ for production. Each differentiated good is produced under constant returns to scale technology by firm φ which is given by
$$x\lpar \varphi \rpar = \varphi \lpar 1 - \theta_{\varphi}\rpar l_{\varphi}.$$
The production process yields pollution as a side-effect. However, firms can reduce pollution by allocating the remaining labor input θφ to abatement activities. Firms can also invest in advanced abatement technologies that increase the productivity of pollution reduction. The pollution production function is modeled under constant returns to scale technology as
$$z\lpar \varphi \rpar = f_{\varphi}^{1 \over \alpha} \lpar b\rpar \lpar 1 - \theta_{\varphi}\rpar ^{1 \over \alpha} l_{\varphi}\comma \;$$
where
$f_{\varphi}^{1 \over \alpha} \lpar b\rpar $
denotes the abatement technology adopted by a firm with productivity φ such that f
φ (b) > 0, f
φ′ (b) < 0, and f
φ″ (b) > 0. The convexity of the abatement technology indicates that, as a firm with productivity draw φ adopts a cleaner technology, its marginal effect decreases.Footnote
5
α is exogenous and captures the effectiveness of abatement activities. A larger α indicates lower abatement efficiency.
For tractability, the abatement technology is defined as f φ (b) = 1/b φ where b φ∈ (0,1) and is summarized by the cost function c φ (b), where 1/b φ denotes the level of abatement technology and x(φ) refers to the firm's output.Footnote 6
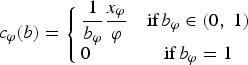$$c_{\varphi}\lpar b\rpar = \left\{\matrix{ \displaystyle{1 \over b_{\varphi}} \displaystyle{x_{\varphi} \over \varphi} &\hbox{if}\, b_{\varphi}\in \lpar 0\comma \; 1\rpar \hfill \cr 0 \hfill & \hbox{if}\, b_{\varphi} = 1}\right.$$
The optimal investment in the abatement technology is described as follows. After firms observe their productivity level, they have access to a standard abatement technology which is not environmentally friendly but is free. This standard technology is captured by b φ = 1. With the standard abatement technology, the emission production function converts to the one in Levinson and Taylor (Reference Levinson and Taylor2003). Firms can also invest in an advanced level of abatement technology at a cost that depends on output size and productivity draw. Not all firms would be willing to use the more advanced abatement technology since it would require them to cope with the higher costs and complexity of a technology which needs highly specialized employees and inputs. Thus, only more productive firms would be able to afford the investment in a cleaner abatement technology. If the productivity draw demonstrates a low level of productivity relative to the technology advancement, firms may select a simple abatement technology.Footnote 7
2.3. Environmental policy
Governments can use many forms of emission reduction policies including voluntary actions, regulatory mechanisms and price incentives. However, there is a growing agreement among economists that putting a price on emissions is essential to reducing pollution. An emission tax imposes a direct fee on the pollution that a firm emits. The government can also use a regulatory mechanism to enforce an emission reduction policy by setting a limit on level of emissions. In this study, I examine the impact of both an emission tax and an emission standard on the performance of firms.
First, let us assume that the government introduces an emission-reduction regulation in the form of an ad valorem tax τ on emission. Under a relatively low emission tax rate, no abatement occurs and θ remains zero. Therefore, I assume that the emission tax is high enough to motivate firms to engage in abatement activities. The joint production function of intermediate goods and pollution is derived by combining equations (9) and (10).
$$x\lpar \varphi\rpar = {1 \over b_{\varphi}} \varphi z_{\varphi}^{\alpha} l_{\varphi}^{1 - \alpha}$$
The joint production function takes the form of a Cobb–Douglas production function. The pollution is incorporated as an additional factor of production implying that production needs pollution as an undesirable input.Footnote 8 The joint production technology features two productivity parameters: the firm's productivity level (φ) and its abatement technology (1/b φ).
Within a competitive labor market, firms hire labor at wage w and emit at cost τ to produce intermediate goods. The standard cost minimization problem determines demands for labor and pollution.
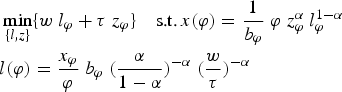$$\eqalign{&\min_{\lcub l\comma z\rcub } \lcub w \; l_{\varphi} + \tau \; z_{\varphi} \rcub \quad \hbox{s.t.}\, x\lpar \varphi\rpar = {1 \over b_{\varphi}} \; \varphi \; z_{\varphi}^{\alpha} \; l_{\varphi}^{1 - \alpha} \cr & l\lpar \varphi\rpar = {x_{\varphi} \over \varphi} \; b_{\varphi} \; \lpar {\alpha \over 1 - \alpha}\rpar ^{-\alpha} \; \lpar {w \over \tau}\rpar ^{-\alpha}}$$
$$z\lpar \varphi\rpar = {x_{\varphi} \over \varphi} \; b_{\varphi} \; \lpar {\alpha \over 1-\alpha}\rpar ^{1 - \alpha} \; \lpar {w \over \tau}\rpar ^{1 - \alpha}$$
The relative factor price for a firm with productivity φ is independent of the firm's productivity level, and the abatement technology and is given by
$${w \over \tau} = {1 - \alpha \over \alpha} {z \over l}.$$
The substitution of equation (9) into (15) gives the optimal resource allocation as
$$1 - \theta_{\varphi } = {1 \over b_{\varphi}} \left[{\alpha \over 1 - \alpha} {w \over \tau} \right]^{\alpha}.$$
The efficient fraction of labor devoted to production 1 − θ depends on the level of clean technology as well as the emission tax rate. With a cleaner technology, firms can allocate less labor to abatement and maintain the same level of emissions. In addition, at a given abatement technology, a stricter environmental policy reduces the allocation of primary input (labor) to production.
2.4. Profit maximization problem
Consider a monopolist firm with productivity level φ that faces market demand x(φ), pollution tax τ, and wage rate w. The maximum one period profit function subject to (8), (9), (10), and (11) must satisfy
$$\pi \lpar \varphi\rpar = \max_{ \lcub p\comma b\rcub } \lcub p_{\varphi} x_{\varphi } - w l_{\varphi } - \tau z_{\varphi } - c_{\varphi} - f_{e}\rcub .$$
Conditional upon remaining in operation, firm φ chooses the optimal abatement technology and price of intermediate good such that
$$p\lpar \varphi\rpar = \left({1 \over 2} \right)p_{max} + {1 \over \varphi}\alpha^{-{\alpha \over 2}} \lpar 1 - \alpha\rpar ^{-{1 - \alpha \over 2}} w^{{1- \alpha \over 2}} \tau^{{\alpha \over 2}}$$
$$1/b^{\ast} = \alpha^{-{\alpha \over 2}} \lpar 1 - \alpha\rpar ^{-{1 - \alpha \over 2}} w^{1 - \alpha \over 2} \tau^{\alpha \over 2}$$
The optimal level of abatement technology is independent of the firm's productivity level φ. Hence, all firms choose the same level of abatement technology (1/b*) in equilibrium. Prices in the market are directly associated with productivity levels of competing firms. Hence, the firm that sets the highest price in the market is the one with the lowest level of productivity or so called cut-off productivity φ*. Firms with a productivity draw below this cut-off cannot stay in the market' and exit. From (17), the price bound is calculated as
$$p_{max} = {2 \over \varphi^{\ast }} \lpar 1/b^{\ast}\rpar ^{{1 \over 2}}.$$
Substitution of p max in (17) gives a new expression for the price in terms of the cut-off productivity level and abatement technology.
$$p\lpar \varphi\rpar = \lpar 1/b^{\ast}\rpar ^{{1 \over 2}} \left[{1 \over\varphi^{\ast}} + {1 \over \varphi} \right]$$
Output, income and profit of each producer are given by
$$x\lpar \varphi\rpar = {L \over \gamma}\lpar 1/b^{\ast}\rpar ^{1 \over 2} \left[{1 \over \varphi^{\ast}} - {1 \over \varphi} \right]$$
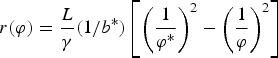$$r\lpar \varphi\rpar = {L \over \gamma} \lpar 1/b^{\ast}\rpar \left[\left({1 \over \varphi^{\ast}} \right)^2 - \left({1 \over \varphi} \right)^2 \right]$$
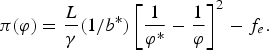$$\pi \lpar \varphi\rpar = {L \over \gamma} \lpar 1/b^{\ast}\rpar \left[{1 \over \varphi^{\ast}} - {1 \over \varphi} \right]^2 - f_e.$$
2.5. Equilibrium
There are a large number of entrants. Firms do not know their productivity ex ante before entering the market. In this context, firms ex ante are identical. Each firm must pay a fixed cost to enter the market. The fixed cost will be dropped once a firm enters. After entry, a firm draws its productivity level from a common distribution function. The ex post distribution will be determined by the initial probability function conditioned on successful entry.
Following Melitz (Reference Melitz2003) and Melitz and Ottaviano (Reference Melitz and Ottaviano2008), I assume that productivity distribution follows the Pareto distribution given byFootnote 9
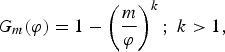$$G_{m} \lpar \varphi\rpar = 1 - \left({m \over \varphi} \right)^{k}\semicolon \; k \gt 1\comma \;$$
where m is the minimum possible value of productivity and k is the shift parameter. A firm will only learn about its levels of productivity after paying the fixed cost. Hence, the distribution of productivity conditional on entry becomes
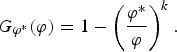$$G_{\varphi^{\ast}} \lpar \varphi\rpar = 1 - \left({\varphi^{\ast} \over \varphi} \right)^k.$$
2.6. Free entry condition
The free entry condition implies that any firm can pay the fixed cost and enter the market. Prior to their entry, each monopolistic producer observes their expected profit of production and compares it to the fixed entry cost. Only if the expected profit is greater than the entry cost does the firm enter. As long as some firms produce, the expected profit is driven to zero. Firms continue to enter until
$$\lpar 1 - G_{m} \lpar \varphi^{\ast}\rpar \rpar \vint_{\varphi^{\ast}}^{\infty} \pi_{\varphi}\, \hbox{d}G_{\varphi^{\ast}} \lpar \varphi\rpar = f_{e}\comma \;$$
where (1 − G m (φ*)) is the ex post distribution of the productivity level after a successful entry into the industry. Solving for φ gives the cut-off productivity equation
$$\varphi^{\ast} = \varphi_{f}^{\ast} \lpar 1/b^{\ast}\rpar ^{{1 \over k + 2}}\comma \;$$
where
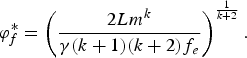$$\varphi_{f}^{\ast} = \left({2Lm^{k} \over \gamma \lpar k + 1\rpar \lpar k + 2\rpar f_e} \right)^{{1 \over k + 2}}.$$
The cut-off productivity crucially determines the distribution of resources across firms and the reallocation of producers across activities. The cut-off productivity threshold increases if the market becomes larger, the emission tax goes up, the entry cost decreases, or products become less substitutable (an increase in γ ). The labor market clearing condition features the distribution of income among consumers as
$$wL = N\vint_{\varphi^{\ast}}^{\infty} r_{\varphi}\, \hbox{d}G_{\varphi^{\ast}} \lpar \varphi\rpar.$$
It is straightforward to calculate the number of competing firms in equilibrium as
$$N = {L \over \lpar k + 1\rpar f_e} \left({m \over \varphi^{\ast}} \right).$$
In this equation, L/(k + 1)f e is the total number of entrants and m/φ* is the probability of successful entry. The number of firms in an industry goes up with the size of the market. An increase in the emission tax also reduces the number of competing firms through a lower probability of successful entry. The average productivity is calculated from the weighted averages of the firms' productivity levels and is given by
$$\bar{\varphi} = {k \over k - 1} \varphi_f^{\ast} \lpar 1/b^{\ast}\rpar ^{{1 \over k + 2}}.$$
An increase in the market size induces a deeper division of labor among surviving firms which leads to an increase in the firm's productivity. A higher emission tax also increases the average productivity indirectly through the adoption of cleaner technology. Using the equation for the density function, it can be shown that the weighted average of a firm's performance is determined by the cut-off productivity level, abatement technology, and the distribution of productivity across firms. In particular, the average price, average output and average pollution are given by
$$\bar{p} = {2k + 1 \over k + 1} \varphi_f^{\ast} \lpar 1/b^{\ast}\rpar ^{{K \over k + 2}}$$
$$\bar{x} = {L \over \gamma\lpar k + 1\rpar } \varphi_f^{\ast} \lpar 1/b^{\ast}\rpar ^{{k \over k + 2}}$$
$$\bar{\pi} = {f_e \over m^k} \varphi_{f}^{\ast} \lpar 1/b^{\ast}\rpar ^{{-k \over k + 2}}.$$
In equations (28) to (30), the cut-off productivity completely summarizes the performance of firms in the economy. Several results can be obtained from these equations. The effect of market size on productivity and other performance measures is similar to the Krugman (Reference Krugman1980) argument. The number of firms in the industry goes up with an increase in the market size. The larger market pushes the cut-off productivity up, which leads to the exit of less productive producers. However, because the number of new entrants outweighs the exit rate, the average productivity and average output (or size of each producer) is higher. In a larger market, firms set lower prices, produce more output and make a smaller profit, all of which demonstrate intensified competition in the economy.
Similar to the effect of market size, a lower entry fee enhances competition too. With a lower entry fee, more firms are able to operate in the market. The average prices and profits are lower but, on average, firms produce less output. When products are more substitute (smaller γ), consumers only care about the overall consumption rather than the consumption of each variety. Firms will expect lower profits and only highly productive producers could remain in operation (selection effect). Hence, there are fewer firms operating in equilibrium, and the average output and average productivity are higher.
The effect of environmental regulation on the market is different. A higher emission tax encourages firms to invest in a cleaner abatement technology, which imposes an additional cost on firms. The policy decreases the expected profit of each producer upon entry. With a lower probability of successful entry, the cut-off productivity goes up in favor of higher productivity firms. Since the total number of entrants remains unchanged, L/(k + 1)f e , fewer firms successfully enter the market. The reallocation of resources from less productive firms to more productive firms forces the least productive producers to exit. The average productivity increases because less productive producers exit the market and the surviving firms are those with highest levels of productivity. Therefore, tougher environmental regulations make the market more concentrated. The output share of each producer goes up; firms set higher mark-ups and make larger profits.
3. Welfare analysis
Environmental policy is expected to impact social welfare though change in market performance. The welfare of consumers in this study depends on the consumer's preferences which feature a continuum set of differentiated goods. To get the impact of the policy on the utility function, let's denote variance of the market price by var(p) and variance of the output by var(x). By standard arguments, they are defined as
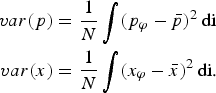$$\eqalign{var\lpar p\rpar &= {1 \over N} \vint \lpar p_{\varphi} - \bar{p}\rpar ^2 \, \hbox{di} \cr var\lpar x\rpar &= {1 \over N} \vint \lpar x_{\varphi} - \bar{x}\rpar ^{2} \, \hbox{di.}}$$
From equation (4), the variance of market price can be written in terms of the variance of output as
$$var\lpar p\rpar = \gamma^2 var\lpar x\rpar .$$
The average demand for variety i produced by a firm φ is also given by
$\bar{x} = {\beta -\bar{p} \over \gamma + N\eta}$
. Now, the indirect utility function is evaluated as
$$U = x_0^c + \beta N\bar{x} - {N \over 2} \left({1 \over \gamma} var\lpar p\rpar - \bar{x} \lpar \beta -\bar{p}\rpar \right).$$
The total of a consumer's income is denoted by I
c
and it is easy to show that
$I^{c} = x_{0}^{c} + N\bar{p}\bar{x} - {N \over \gamma} var\lpar p\rpar $
. Then, the indirect utility function can be written as
$$U=I^{c} + {N \over 2} \left({1 \over \gamma} var\lpar p\rpar + \lpar \gamma + N\eta\rpar \bar{x}^2 \right)\comma \;$$
where the variance of market price is defined:
$var \lpar p\rpar = x_0^c + N\bar{p}\bar{x} - {N \over \gamma} var\lpar p\rpar $
.
Equation (31) implies that the indirect utility function rises with a decrease in the average prices and its variance, as the consumers re-optimize their consumption by shifting expenditures towards lower priced varieties as well as the numeraire good. In addition, the indirect utility function exhibits love of variety, indicating that welfare is enhanced by an increase in the number of varieties produced in the economy.Footnote 10
To examine the impact of an emission tax on the indirect utility function, let us substitute the average price from (28), the average output from (29), and the variance of market price in (31). With some calculation, it can be shown that
$$U = I^c + {N \over 2\gamma} \left({\beta \over k + 1} \lpar \varphi_f^{\ast}\rpar ^{-1} \lpar 1/b^{\ast}\rpar ^{{k \over k + 2}} - {2 \over k + 2} \lpar \varphi_f^{\ast}\rpar ^{-2} \lpar 1/b^{\ast}\rpar ^{{2k \over k + 2}} \right).$$
Social welfare remains increasing with a lower entry cost and higher degree of product substitution. However, an environmental policy impacts welfare through two channels: (1) welfare is enhanced by a stricter environmental policy since regulation gives incentive to firms to adopt a cleaner abatement technology (lower 1/b*) which improves productivity of abatement activities, (2) the policy reduces welfare because a higher emission tax harms the competitive environment. A tough environmental policy leads to the exit of less productive producers (higher φ f *). The number of varieties decreases in equilibrium and surviving firms have more market power and set higher prices accordingly. This dominates the positive effect of abatement technology adoption and welfare drops in the economy.
4. Emission standard policy
As was discussed, the government can use an emission standard instead of an emission tax policy to regulate pollution. For simplicity, let us consider that there is only a standard abatement technology available, represented by b = 1. To meet the regulations, firms are required to keep their emission–output ratios below an exogenous level s determined by the government. The emission standard requirement is defined as
$${z_{\varphi} \over x_{\varphi}} \leq s.$$
Combining this with equations (9) and (10) gives a new expression for the pollution–output ratio as
$${z_{\varphi} \over x_{\varphi}} = {1 \over \varphi}\lpar 1 - \theta_{\varphi}\rpar ^{{1 \over \alpha} - 1} \leq s.$$
Firms with a higher level of productivity naturally benefit from a lower emission–output ratio. Let us define φ s as the level of productivity that just meets the emission standard requirement. Firms with productivity below φ s are not permitted by law to operate in the market. φ s also represents the new cut-off productivity level.
$${1 \over \varphi_s} \lpar 1 - \theta_{\varphi}\rpar ^{{1 \over \alpha} - 1} = s$$
A monopolist producer maximizes profit p φ x φ − wl φ subject to the joint production technology (12), demand for variety (8), and emission ratio constraint. The first-order condition determines the allocation of resources to production and abatement according to the pricing rule given by
$$p\lpar \varphi\rpar = {1 \over 2} \left(p_{max} + \varphi^{{1 \over \alpha -1}} s^{{\alpha \over \alpha -1}} w \right).$$
A firm with the lowest level of productivity (φ s ) charges the maximum price that consumers are willing to pay (p max ).
$$p_{max} = \varphi_s^{{1 \over \alpha} - 1} s^{{\alpha \over \alpha - 1}} w$$
The substitution of (35) back in the pricing rule gives the market price in terms of cut-off productivity as
$$p\lpar \varphi \rpar = {1 \over 2} s^{{\alpha \over \alpha - 1}} w \left(\varphi_{s}^{{1 \over \alpha - 1}} + \varphi^{{1 \over \alpha - 1}} \right).$$
Output and profit become
$$x\lpar \varphi\rpar = {L \over 2\gamma} s^{{\alpha \over \alpha - 1}} w \left(\varphi_s^{{1 \over \alpha - 1}} - {\varphi}^{{1 \over \alpha - 1}} \right)$$
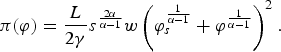$$\pi \lpar \varphi\rpar = {L \over 2\gamma} s^{{2\alpha \over \alpha -1}} w \left(\varphi_{s}^{{1 \over \alpha - 1}} + \varphi^{{1 \over \alpha -1}} \right)^2.$$
With a tougher emission standard, firms set higher prices, produce more and make larger profits. Given the Pareto distribution of productivity, the free entry condition implies that
$$\varphi_{s} = \left({Lm^{k} s^{{-2\alpha \over 1 - \alpha}} \over 4\gamma \lpar k + {1 \over 1 - \alpha}\rpar \lpar k + {2 \over 1 - \alpha}\rpar f_e} \right)^{{1 - \alpha \over k\lpar 1 - \alpha \rpar + 2}}$$
where φ s is the new expression for cut-off productivity. The labor market clearing condition determines the equilibrium number of firms as
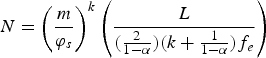$$N = \left({m \over \varphi_s} \right)^k \left({L \over \lpar {2 \over 1 - \alpha}\rpar \lpar k + {1 \over 1 - \alpha}\rpar f_e} \right)$$
where
$\lpar {m \over \varphi_s}\rpar ^k$
is the probability of successful entry and the other expression is the total number of entrants to the industry. A higher emission standard has no effect on the number of new incumbent firms but reduces the probability of successful entry and expected profit. This increases the cut-off productivity level in favor of high productivity firms and forces less productive producers to exit the market. The average productivity and average market price are given by
$$\bar{\varphi_s} = {k + 1 \over k} \varphi_s$$
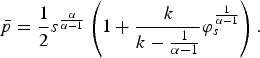$$\bar{p} = {1 \over 2}s^{{\alpha \over \alpha -1}} \left(1 + {k \over k - {1 \over \alpha -1}} \varphi_{s}^{{1 \over \alpha - 1}} \right).$$
Surviving firms respond to the emission regulation by setting higher prices to maintain mark-ups. Hence, the average prices are higher with a higher emission standard. In contrast to some studies that show that emission standards and emission taxes have different impacts on a firm's performance, this study finds that both policies enhance average productivity in the market but also harm the competitive environment.Footnote 11
5. Conclusion
This study proposed to understand the link between environmental regulations, average productivity, and market competition. In the literature surrounding the Porter hypothesis, the lack of innovation is the main source of inefficiency and a well-designed environmental policy triggers innovation that increases productivity of individual firms and competitiveness of the economy. My study suggests that, if an environmental policy leads to a higher level of productivity through induced innovation, then the policy should sustain environmental quality and economic competitiveness too. However, if the productivity gain is attributed to reallocation of resources across firms through selection effect, then it is important to assess the subsequent changes in the competitive environment and social welfare.
I developed a tractable model with firm heterogeneity that incorporates endogenous mark-ups that respond to the toughness of competition. In the model, average productivity is determined by the distribution of firm-level productivity and allocation of resources across firms as well as the abatement technology. I assessed the impact of two different environmental policies: an emission tax and an emission standard. My overall findings imply that environmental regulations incentivize firms to adopt a cleaner abatement technology which improves environmental quality, and average productivity. However, the regulations harm the competitive environment by increasing market concentration and the average prices in the market.
Without environmental legislation being enforced, abatement will not occur in the economy and firms will have no incentive to invest in a cleaner abatement technology. When the market is regulated, firms choose a level of clean technology so that they can devote fewer resources to abatement activities. The cost of abatement technology raises the overall marginal cost of production and reduces the expected profit of firms prior to the entry. The policy reallocates inputs from less productive firms to more productive firms and then forces less productive producers to exit the market. The surviving firms in the concentrated market will have stronger market power which enables them to set higher prices. Hence, the market becomes more productive on average but less competitive. Welfare is increasing with the adoption of a cleaner abatement technology. However, because environmental regulation harms market competition by reducing the number of operating firms in equilibrium, the welfare goes down.
This paper contributes to the existing literature by studying the links between environmental policies, measures of productivity and market competition. The results of this study also include important insights into the debates surrounding the Porter hypothesis.
Appendix: Indirect utility function
To find the indirect utility function, note that by definition,
$$\bar{x} = {1 \over N} \vint x_{i}^{c} di\, \hbox{and}\, var\lpar x\rpar = {1 \over N} \vint \lpar x_i - \bar{x}\rpar ^2\, \hbox{di}.$$
Substitution into consumer preferences yields
$$U = x_0^c + \beta N \bar{x} - {N \over 2\gamma} var\lpar p\rpar - {N \over 2} \bar{x}^2 \lpar \gamma + \eta N\rpar$$
where var(p) = γ2
var(x). From demand function p
i
= β− γx
i
c
− ηX, we can show that
$\bar{x} = {\beta -\bar{p} \over \gamma + \eta N}$
.
Then, the consumer's preferences become
$$U = x_0^c + \beta N \bar{x} - {N \over 2\gamma} var\lpar p\rpar - {N \over 2} \bar{x} \lpar \beta - \bar{p}\rpar .$$
The consumer's budget constraint is denoted by I c and is defined by
$$I^{c} = x_0^c + \vint p_i x_i^c \, di.$$
From p
i
= β− γx
i
c
− ηX, and
$X = N\bar{x}$
, we can show that
$$\vint p_{i}\, x_{i}\, di = N\bar{x}\bar{p} - {N \over \gamma} var\lpar p\rpar .$$
Then, the total consumer's budget constraint becomes
$$I^{c} = x_{0}^{c} + N\bar{x}\bar{p} - {N \over \gamma} var\lpar p\rpar .$$
Substituting I c in U yields the indirect utility function as
$$U = I^c + {N \over 2\gamma} var\lpar p\rpar + {1 \over 2} N\bar{x} \lpar \beta - \bar{p}\rpar .$$
In order to evaluate the indirect utility function, by definition we have
$\bar{\varphi} = {k + 1 \over k} \varphi^{\ast}$
, and we can calculate
$$var \left({1 \over \varphi} \right)= {k \over \lpar k + 1\rpar ^{2}\lpar k + 2\rpar } \lpar \varphi^{\ast}\rpar ^{-2}.$$
Then, from (19)
$$var\lpar p\rpar = \lpar 1/b^{\ast}\rpar ^{2} {k \over \lpar k + 1\rpar ^{2}\lpar k + 2\rpar } \lpar \varphi^{\ast}\rpar ^{-2}.$$
This equation along with (18), (28), and (29) gives equation (32) in the text.
$$U = I^c + {N \over 2\gamma} \left({\beta \over k + 1} \lpar \varphi_f^{\ast}\rpar ^{-1} \lpar 1/b^{\ast}\rpar ^{{k \over k + 2}} - {2 \over k + 2} \lpar \varphi_f^{\ast}\rpar ^{-2} \lpar 1/b^{\ast}\rpar ^{{2k \over k + 2}} \right).$$
