Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T11:03:35.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Environmental and population externalities

Published online by Cambridge University Press:  21 May 2009

FRANK JÖST  and
MARTIN F. QUAAS
FRANK JÖST
Affiliation:
Department of Economics, University of Heidelberg, Bergheimerstrasse 20, 69115 Heidelberg, Germany. Email: frank.joest@uni-hd.de
MARTIN F. QUAAS
Affiliation:
Department of Economics, University of Kiel, Wilhelm-Seelig-Platz 1, 24118 Kiel, Germany. Email: quaas@economics.uni-kiel.de.
Rights & Permissions [Opens in a new window]

Abstract

We analyze the external effects that arise in the decisions of firms on polluting emissions and in the decisions of parents on the number of births in an optimal control model with three stock variables representing population, economic capital, and pollution. We distinguish two different types of households, which represent opposite ends of a spectrum of potential familial structures: ‘dynastic households’, in which the family sticks together forever and ‘micro-households’, in which children leave their parent's household immediately after birth. We show that the decision of parents on the number of births involves an externality that is qualitatively different for both types of familial structure. Hence, population policy should be different, according to the type of household. A first best result may be obtained in the case of dynastic households if an appropriate tax on the household size is applied, or, in the case of micro-households, if an appropriate tax on children is applied.

Type
Research Article
Information
Environment and Development Economics , Volume 15 , Issue 1 , February 2010 , pp. 1 - 19
Copyright
Copyright © Cambridge University Press 2009

1. Introduction

During the past five decades world population has more than doubled to 6.7 billion in 2007 (United Nations, 2007), while global gross domestic product has increased by a factor 4.4 between 1960 and 2001 (World Bank, 2003). At the same time the use of resources and the emissions from producing goods have also increased substantially. For example, total anthropogenic CO2-emissions have increased by more than 330 per cent. For many people these observations show that population growth and the necessary expansion of the production of goods in order to fulfill the needs of a larger population are the main sources of the ongoing environmental degradation (e.g., Ehrlich and Ehrlich, Reference Ehrlich and Ehrlich2002). However, even if there is a consensus that population and the environment are closely related, the links between them are complex and ambiguous (e.g., Robinson and Srinivasan, Reference Robinson, Srinivasan, Rosenzweig and Stark1997). In many circumstances the use of the environment as a sink for wastes is determined by population rather indirectly. The amount and type of emissions are not only determined by the number of people living on earth, but depend also on production technologies and consumption patterns. Furthermore, if we accept that people decide on the number of births, one would also expect that per-capita consumption and environmental quality play a role in this decision.

Because of these complex interdependencies between demographic change, economic development, and the use of the environment, it is not surprising that one cannot definitively answer the question whether or not present population growth is too high in order to protect the environment. There exists a broad range of results from studies which try to calculate the carrying capacity of our planet in terms of total population size (Heilig, Reference Heilig and Lutz1996: 196).

It is the aim of our paper to contribute to a better understanding of the interactions between demographic change, economic development, and environmental deterioration within the framework of the economic theory of externalities. Even if this economic point of view is rather a narrow and particular perspective on the complex interactions between population and the environment it helps to clarify how far the individual decisions concerning the number of births, consumption, and production lead to an undesirable outcome for the society. And it gives insights into the direction of interventions in the individual decisions and appropriate policy instruments. In particular we want to answer the following two questions:

  1. 1. Do individual decisions concerning consumption, the amount of emissions, and the number of children lead to overpopulation and environmental deterioration?

  2. 2. If this is the case, which policy instruments are suitable to solve these problems?

There are only a few contributions in population and environmental economics dealing with environmental externalities and external effects of the decisions concerning fertility simultaneously. The endogenous fertility literature mainly analyzes the decision of individuals concerning their number of children in a setting without environmental problems (Becker, Reference Becker1960; Raut and Srinivasan, Reference Raut and Srinivasan1994; Yip and Zhang, Reference Yip and Zhang1997; Becker et al., Reference Becker, Glaeser and Murphy1999; Galor and Weil, Reference Galor and Weil1999). The bulk of environmental economics papers assumes that population is given and constant over time. One of the few contributions dealing with endogenous fertility and environmental problems at the same time is the monograph of Shah (Reference Shah1998). He shows in a static framework that the individual decisions can lead to an inferior outcome for the society, because individuals do not take into account that additional children contribute to negative effects due to a higher population density or due to an overall decrease in the marginal product of labor. Hence there is a difference between the outcome of individual decisions and the social optimum. A similar result is derived by Dasgupta (Reference Dasgupta2000). Nerlove (Reference Nerlove1991) and Nerlove and Meyer (Reference Nerlove, Meyer, Dasgupta and Mäler1997) derive a similar conclusion in a dynamic framework. These models describe regional environmental problems of rural areas in developing countries. In contrast, the approach by Cronshaw and Requate (Reference Cronshaw and Requate1997) is adequate to investigate the interlinkages between population size and environmental damage due to emissions that occur in industrial production. They discuss the effects of variations in population size on environmental quality and consumption possibilities in a comparative static analysis. However, the static framework restricts the possibilities to analyze the dynamic effects of population growth.

Two contributions of Harford (Reference Harford1997, Reference Harford1998) are close in their intention to our paper. Harford addresses the issue of environmental and population externalities in a dynamic model of nonoverlapping generations. A stock of environmental pollution emerges as a joint product of output. The production system, however, is not explicitly modeled. The only possibility to abate pollution is to sacrifice some output of the consumption commodity. Parents are assumed to be altruistic toward their descendants. As a consequence, the utility of the present generation is also affected by the childrens' (and their childrens' and so on . . .) disutility from future pollution. To derive the optimal dynamic allocation, he considers a social planner for each generation separately, who optimizes the utility of a representative individual of the current generation, but takes as given all decisions of individuals living in the future. By comparing this optimum to the individual decisions, Harford concludes that both the pollution emissions per capita as well as the number of children are too high in comparison to the social optimum. Harford (Reference Harford1997) derives taxes on output and children under which individual decisions lead to the optimal allocation.

We aim to extend this literature on the interrelation between environmental and population externalities in two respects: (i) We explicitly consider industrial production to be the source of environmental pollution. Emissions can be abated by substituting labor or capital for polluting inputs, or by technical progress (which we consider to be exogenous in our model). (ii) We analyze how the externalities depend on the institutional setting of individual decision making. For this sake, we distinguish different types of households, that is, different types of institutional units in which the decision on the number of children takes place. The two types of households under consideration may be regarded as two extremes: On the one hand, we consider ‘dynastic households’, in which the family sticks together as a decision-making unit forever. On the other hand, we consider ‘micro households’, in which children leave their parent's household immediately after birth and form a new decision-making unit. In the case of dynastic households, the number of households is constant over time, but the size of the household changes. In contrast to this, in the case of micro-households the size of the household is constant, but the number of households changes over time. The main difference between both types is to which degree households take into account the future population growth (or decline) in their decision on the birth rate: in the case of dynastic households, the future population growth is taken into account over the whole future; in the case of micro-households, future population growth is not taken into account at all.Footnote 1 Although these cases are not realistic in the extreme form, there may be some relations to different ways of living together found in different cultures. While the life in rural areas in developing countries might be similar to the case of dynastic households; the situation in urban areas of modern industrialized countries is more similar to the case of micro-households. Hence, considering ‘dynastic households’ on the one hand and ‘micro-households’ on the other hand provides insight, because they are – in some sense – at two opposite ends of a spectrum of realistic family structures.

We develop an optimal control model which comprises three stock variables representing population, the economic capital stock, and the pollutant stock in the natural environment. We conclude that for both institutional settings of decision making the decentralized outcome is inefficient due to two externalities: one occurs in the individual decision on polluting emissions, the other one in the individual decision on the number of births. It turns out that the externality from individual decisions on polluting emissions is of the same kind for both types of households. This externality may be internalized by a Pigouvian tax on emissions.

By contrast, the kind of external effect from the household's decision on fertility is qualitatively different for both types of households. Accordingly, different policy instruments are required to internalize the externalities. We show that in the case of micro-households, the first best development of the model economy is obtained, if an appropriate tax on the number of newly born children is applied. In the case of dynastic households, the household size has to be taxed, while the optimal tax on the number of newly born children is zero.

The paper is organized as follows: in section 2 we develop an optimal growth model of an economy with endogenous fertility and environmental deterioration and derive conditions for the socially optimal development. In section 3 we analyze two different models for decentralized economies, where households decide about the number of births and consumption and where firms choose the amount of environmentally harmful emissions. The two models differ with respect to the two types of households, in which the decisions take place. We compare the results of these two different decision settings with the results of the central planned economy in order to show how the decentralized decisions lead to a suboptimal outcome. Furthermore, we derive policy instruments that allow to achieve the social optimum in a decentralized economy. Finally, we summarize our results in section 4 and discuss the policy implications of our model in a broader perspective.

2. Endogenous fertility, optimal population, and the environment

2.1 The model

Here, we consider a model economy with an endogenous population of V identical individuals.Footnote 2 A representative individual j's utility function is

(1)
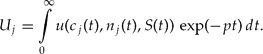
\begin{equation} U_j = \int\limits_0^\infty u (c_j (t),n_j (t),S(t))\,\exp ( - pt)\,dt.\end{equation}

Here, cj (t) denotes individual j's consumption, nj (t) the birth rate, and S(t) the pollutant stock in the environment at time t.Footnote 3 Instantaneous utility of each individual u(cj , nj , S), increases in consumption uc j > 0, and the birth rate u n j > 0. To model the influence of environmental quality on welfare, we assume that production generates emissions ej (t) which accumulate to a pollutant stock S(t) in the environment. This stock generates disutility, i.e., us < 0. Utility is discounted at a constant rate ρ > 0.

As Barro and Sala-I-Martin (Reference Barro and Sala-I-Martin1995) show in a model without environmental pollution, the utility function (1) can be derived from a dynastic utility function as employed by Barro and Becker (Reference Barro and Becker1989), where parents are altruistic toward their descendants. The degree of altruism is captured by the discount rate of utility ρ: the lower the ρ, the higher the parents' altruism. In contrast to Barro and Becker (Reference Barro and Becker1989), we assume that the parents' utility does not increase with the number of adult children. While the quantitative results of the model (e.g., the optimal population size) depend on this assumption, the qualitative results would largely remain unchanged, if we would alternatively assume that utility increases the number of adult descendants of the representative household.

The dynamics of the three subsystems population, environment, and economy are described by three stock variables and corresponding control variables. As outlined above, N denotes the absolute population size with the per-capita birth rate (n) being the corresponding control variable. The stock of pollutant in the environment (S) is controlled by per-capita emissions (e). Per-capita physical capital (k) is controlled by per-capita consumption (c). Here, we formulate the three differential equations describing the dynamics of these subsystems.

Equation (2) expresses the dynamics of population growth, where we neglect the age structure and define an exogenous and constant death rate d.Footnote 4

(2)
\begin{equation} \dot N = (n - d)N. \end{equation}

Per-capita capital accumulation $\dot k$ is governed by

(3)
\begin{equation} \dot k = f(k,e,t) - c - (n - d)k - b\,n\,k. \end{equation}

The per-capita output f(·) in equation (3) is divided into consumption c, investment $\dot k$, and costs of raising children. Interpreting (n − d) as net per-capita birth rate, the term −(n − d)k expresses the fact that each new population member has to be endowed with the per-capita amount of capital. Hence, this amount has to be subtracted from production output.

The term −bnk, with the constant b > 0, denotes the cost of raising children. Here, average per-capita capital is used as a proxy for the relative size of the opportunity costs of raising children. This is an easy way to model the fact that opportunity costs for raising children are higher in developed countries, especially for women. The higher per-capita capital stock in developed countries in comparison to developing regions corresponds to better working opportunities for women. These better opportunities increase their opportunity costs of raising children (Barro and Sala-I-Martin, Reference Barro and Sala-I-Martin1995: 313). Here, we assume that the costs of raising children are covered by a single, large outlay at the time of their birth. Therefore, only the birth rate n occurs in equation (3).

With regard to production we assume constant returns to scale, i.e., there exists a linear homogeneous production function F(N, N k, Ne, t). The production inputs are labor, capital, and emissions.Footnote 5 We assume that every person supplies one unit of labor inelastically. Hence, the total labor input is equal to the population size N. We further assume that there exists an abatement technology which allows emissions arising in the production process to be cleaned up. This is integrated into the production function by assuming that emissions are inputs into the production process and can be substituted by other input factors. Furthermore we assume that the production function is time dependent, i.e., that technical progress may occur.

Finally, equation (4) describes the dynamics of the stock of pollutant in the natural environment in a much simplified way.

(4)
\begin{equation} \dot S = N\,e - \delta \,S. \end{equation}

Here, we assume that the pollutant is equally distributed throughout the environment. Pollution degradation is proportional to the concentration S of the pollutant in the environmental system with δ being the natural degradation rate of the pollutant.Footnote 6

2.2 The social optimum

In order to determine the optimal development of the economy, we assume that a planner maximizes the utility of a representative individual, given by equation (1), subject to the dynamics of the three subsystems population, economy, and environment (equations (2)– (4)), by choosing the time paths of the three control variables birth rate (n), consumption (c), and emissions (e).

We thus consider a setting different from that in Harford (Reference Harford1997): while in his model each generation has a social planner who takes as given the choices of all other generations, in our model the social planner considers the entire time horizon. The informational requirements for both models are the same: in both approaches, the planner needs complete information about future preferences and the future development of population, economy, and the environment. In our approach the planner has more flexible opportunities, however, as she decides about present and future control variables.

In order to solve the optimization problem we define the current-value Hamiltonian

(5)
\begin{eqnarray} H &=& u(c,n,N,S) + \lambda ^k [f(k,e,t) - c - (n - d)k - b\,n\,k]\nonumber\\ && +\, \lambda ^n (n - d)N + \lambda ^{s\,} [N\,e - \delta \,S]. \end{eqnarray}

Denoting a derivative with respect to one of the control or state variables by the corresponding subscript, the first-order conditions for an optimum read

(6)
\begin{equation} H_c = 0\quad u_c - \lambda ^k = 0 \end{equation}
(7)
\begin{equation} H_n = 0\quad u_n - \lambda ^k [k + b\,k] + \lambda ^N N = 0 \end{equation}
(8)
\begin{equation} H_e = 0\quad \lambda ^k f_e + \lambda ^S N = 0 \end{equation}
(9)
\begin{equation} H_k = \rho \lambda ^k - \dot \lambda ^k \quad \lambda ^k [f_k - (n - d) - bn] = p\lambda ^k - \dot \lambda ^k \end{equation}
(10)
\begin{equation} H_N = \rho \lambda ^N - \dot \lambda ^N \quad \lambda ^N (n - d) + \lambda ^S e = p\lambda ^N - \dot \lambda ^N \end{equation}
(11)
\begin{equation} H_S = \rho \lambda ^S - \dot \lambda ^S \quad u_s - \lambda ^S \delta = p\lambda ^S - \dot \lambda ^S \end{equation}

The transversality condition (Michel, Reference Michel1982)

(12)
\begin{equation} \mathop {\lim }\limits_{t \to \infty } \,H^0 \,\exp ( - pt) = 0 \end{equation}

Footnote 7 allows us to derive values for the control variable for t → ∞. The solution of the set of equations (2)–(11) together with the transversality condition (12) yields the optimal time path for every set of initial conditions N(t = 0), k(t = 0), and S(t = 0).Footnote 8

From condition (6), we obtain the shadow price for the capital stock. As capital can be freely converted into consumption, the shadow price of capital simply equals marginal utility of consumption, λ k = uc .

In order to provide some intuition about the optimal dynamics of the system, we consider the steady state. To derive results about the steady-state growth rates of the endogenous variables, we specify the following log-linear instantaneous utility functionFootnote 9 :

(13)
\begin{equation} u(c,n,S) = \ln c + \nu \,n^{1 - \in } + \sigma \,\ln (\bar S - S), % \end{equation}

where ν, ∈, σ, and $\bar S$ are strictly positive constants, and ∈ < 1. Thus, utility is increasing in consumption and the number of births, and decreasing in environmental pollution. $\bar S$ represents the carrying capacity of the environment, i.e., an upper bound for the stock of pollutants. We further specify the production function

(14)
\begin{equation} f(k,e,t) = k^\alpha e^\beta \exp (x\,t), \end{equation}

with α, β > 0 and α + β < 1. Exogenous technical progress occurs at a rate x > 0.

In a steady state, the birth rate has to be constant. Thus, from (9) we obtain

(15)
\begin{equation} - (1 - \alpha )\frac{{\dot k}}{k} + \beta \frac{{\dot e}}{e} + x = 0. \end{equation}

Using this in (3), we obtain $\dot c/c = \dot k/k$. From (11), we obtain that the stock of the pollutant has to be constant in a steady state. Using this, (4) implies that $\dot N/N + \dot e/e = 0$, and (11) that $\dot \lambda ^S = 0$. Differentiating (8) with respect to time and using these results we obtain

(16)
\begin{equation} - \frac{{\dot k}}{k} - (2 - \beta )\frac{{\dot e}}{e} + x = 0. \end{equation}

From equations (15) and (16), we derive the steady-state growth rates of capital and emissions. Summing up, the growth rates are

(17)
\begin{eqnarray} \frac{{\dot S}}{S} = \frac{{\dot n}}{n} = 0;\quad \frac{{\dot k}}{k} = \frac{{\dot c}}{c} = \frac{{2x}}{{2 - \alpha (2 - \beta )}};\quad {\rm and}\,\frac{{\dot N}}{N} = - \frac{{\dot e}}{e} = \frac{{\alpha x}}{{2 - \alpha (2 - \beta )}}.\qquad \end{eqnarray}

Consumption and the capital stock per capita increase at a rate which is larger than the rate of technical progress. The growth rate is however less than it would be in a setting where emissions are no essential input (i.e., where β = 0; in that case we would obtain the standard result that the growth rate is x/(1 − α)). Population grows and per-capita emissions decline at a rate which is less than the rate of technical progress. The more important the polluting inputs are in production (i.e., the higher β is), the slower is the steady-state population growth.

We now determine the shadow prices for population (λN) and pollution (λ S ) in a steady state.Footnote 10 The steady-state shadow price of pollution is derived from condition (11),

(18)
\begin{equation} \hat \lambda ^S = \frac{{\hat u_S }}{{p + \delta }}. \end{equation}

Hence, the steady-state shadow price of pollution is the present value of marginal damage from pollution over an infinite time interval. The discount factor consists of the rate ρ of time preference and the depreciation rate δ of the pollutant stock. Since pollution is constant, the shadow price of pollution is constant, too. Using $\dot e/e = - \dot N/N = \hat n - d$ in equation (10) we find that N λ N is constant, i.e., $\lambda ^N (n - d) = \dot \lambda ^{N}$. Hence, we obtain from (10)

(19)
\begin{equation} \hat \lambda ^N = \frac{{\hat \lambda ^{S{\hat e} } }}{\rho } = \hat e\frac{{\hat u_S }}{{\rho (\rho + \delta )}}. \end{equation}

The steady-state shadow price of population is the present value of the social environmental damage of an additional individual, i.e., of the (shadow) value of the additional emissions caused by this individual. Since emissions per capita decrease in a steady state, the shadow price of population also decreases over time.

3. Household decisions, endogenous fertility, and externalities

Here we analyze the above given economy by assuming that households decide on the number of children and consumption, and that firms decide on production plans. By comparing the results of the individual decisions of households and firms with the optimal solution of the social planner we can identify externalities of individual decisions. In particular, we expect that individual decisions fail to reach the social optimum due to the public-good problem of environmental pollution. From a welfare-theoretic point of view such an inefficiency requires regulating the markets. Therefore we investigate how the identified externalities could be internalized by Pigouvian taxes.

We look at two different institutional settings of decision making: in section 3.2 we assume ‘dynastic households’, where the founder of a dynasty decides about the birth rates and consumption for all succeeding generations. In particular, she takes into account that the size of the household grows or decreases according to her choice of birth rates. In section 3.3 we assume ‘micro-households’. Their characteristic feature is that they consist only of the parents. In this setting, decision makers care about birth rates only insofar as their utility or budget constraint are directly affected. For both types of households we derive policy measures which guarantee that the individual decisions are efficient. We restrict our analysis on taxes imposed by a central regulator. Tax revenues are redistributed lump sum to the households such that the regulator's budget is balanced.

Every individual inelastically supplies one unit of labor on a competitive labor market and earns a wage w, receives the rent r on capital and the profit π of shares of firms it owns. For simplicity, we assume that each individual owns one firm, such that there are N firms. This assumption is without loss of generality, as there are constant returns to scale in production. The firms produce a homogenous output using labor, capital, and emissions with identical production technologies given by the production function f(k, e, t). The entrepreneurs decide on labor and capital inputs and on the amount of emissions.

Within this framework we analyze the intertemporal allocation which results from the profit-maximizing behavior of firms and the utility-maximizing behavior of households. We identify externalities according to individual decisions and we make policy recommendations how to implement a social optimal development of the economy. In the first step we consider the production side, which we model identically for both types of households.

3.1 Firms' decisions

All N firms produce the homogenous output using the same technology described by the production function f(ki , ei ,t). The index i indicates that the capital and emission inputs may differ between firms. We assume perfect competition on labor and capital markets and on the market for the consumption good. The owners of the firm decide on per-capita capital ki and per-capita emissions ei . The regulator imposes a tax τ on emissions, which will be discussed later.

Each firm i maximizes its profit π i , which is given as the difference between revenues f(ki , e i, t) and costs rki + w + τei .

(20)
\begin{equation} \mathop {\max }\limits_{k_i ,e_i } \,\pi _i = \mathop {\max }\limits_{k_i ,e_i } f(k_i ,e_i ,t) - rk_i - w - \tau e_{i.} \end{equation}

The first-order conditions of this problem are given by

(21)
\begin{equation} f_{k_i } = r \end{equation}
(22)
\begin{equation} f_{e_i } = \tau , \end{equation}

Hence, the firms choose per-capita inputs such that the value of the marginal product of the inputs equals the price of the inputs.Footnote 11

Since the production functions of the firms fulfill the usual neoclassical assumptions, the necessary conditions for a profit maximum are sufficient as well. As all firms are identical, their factor inputs and profits are the same in equilibrium

\[ k_i = k,\,e_i = e,\,{\rm and}\,\pi _i = \pi , \]

i.e., we may drop the index i which decides between firms.

We now turn to the decision problem of a representative household. In section 3.2 we consider the case of dynastic households; in section 3.3 we consider micro-households.

3.2 Dynastic households

In this section, we consider dynastic households, in which the decision on consumption and the number of children takes place. Since in the setting of dynastic households all children stay in the household as the relevant decision-making unit, the number of households I is constant. Thus, the number Mj of members of the household j equals the Ith part of the number of descendants of the representative individual at t = 0,

(23)
\begin{equation} M_j = N_j /I. \end{equation}

The budget constraint of household j in per-capita terms reads

(24)
\begin{equation} rk_j + w + \pi + T = \dot k_j + c_j + (n_j - d)k_j + bn_j k_j + \theta \,n_j + \Theta \,M_j . \end{equation}

The left-hand side of the budget constraint describes the income of the household. It is the sum of wage (w) and capital (r kj ) earnings, profits π j , and a lump-sum transfer T from the regulator. The right-hand side of (24) contains the expenditures of the household. They consist of investment $\dot k_j$, consumption cj , the costs of children, which are the result from an endowment of a growing household with capital (nj − d)kj , and the costs of raising children bnj kj . Furthermore, the household has to pay a tax θ nj on the number of newly born children and a tax Θ Mj , which depends on its size, and which has to be paid for each member of the household. The regulator chooses the lump-sum transfer T such that tax revenues are fully redistributed.

The second constraint taken into account by the dynasty's founder is the change of the household size Mj resulting from the birth rate nj . This constraint reads (similar to the development of total population, equation (2))

(25)
\begin{equation} \dot M_j = (n_j - d)M_j . \end{equation}

Using (23), this constraint can also be expressed in terms of the descendants of the representative individual at time t = 0,

(26)
\begin{equation} \dot N = (n_j - d)N_j . \end{equation}

The dynasty's founder decides on two variables: per-capita consumption cj and birth rate nj . We assume that she has no influence on the firm's decision on the amount of polluting emissions in production. Hence, she does not take into account a constraint concerning the environment, as the environment is not affected by her decisions.Footnote 12 Thus, the dynasty's founder maximizes the stream of utility of her dynasty subject to the budget constraint (24) and the change in household size (26).

The optimization problem of the founder of a dynasty has the following form:

(27)
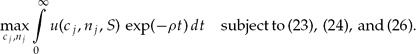
\begin{equation} \mathop {\max }\limits_{c_j ,n_j } \int\limits_0^\infty {u(c_j } ,n_j ,S)\,\exp ( - \rho t)\,dt\quad{\rm subject}\,{\rm to}\,(23),\,(24),\,{\rm and}\,(26). \end{equation}

The current-value Hamiltonian is

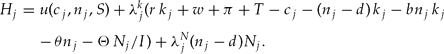
\begin{eqnarray*} H_j & =& u(c_j ,n_j ,S) + \lambda _j^k (r\,k_j + w + \pi + T - c_j - (n_j - d)\,k_j - bn_j\, k_j \\ && -\, \theta n_j - \Theta \,N_j /I) + \lambda _j^N (n_j - d)N_j . \end{eqnarray*}

And we obtain the following necessary conditions for an optimum:Footnote 13

(28)
\begin{equation} \frac{\partial H_j}{\partial c_j}=0\quad u_{c_j}-\lambda^k_j=0 \end{equation}
(29)
\begin{equation} \frac{\partial H_j}{\partial n_j}= 0 \quad u_{n_j}-\lambda^k_j\left[ k_j+b\,k_j+\theta\right] +\lambda^N_jN_j=0 \end{equation}
(30)
\begin{equation} \frac{\partial H_j}{\partial k_j}=\rho\,\lambda^k_j-{\dot\lambda^k}_j\quad \lambda^k_j\left[r-(n_j-d)-b\,n_j\right] =\rho\,\lambda^k_j-{\dot\lambda^k }_j \end{equation}
(31)
\begin{equation} \frac{\partial H_j}{\partial N_j}=\rho\,\lambda^N_j-\dot\lambda^{N}_j\quad \lambda ^{N}_j\,(n_j-d)-\lambda^k_j\,\Theta/I= \rho\,\lambda^k_j-\dot\lambda^{N}_j. \end{equation}

Comparing these conditions as well as conditions (21) and (22) for the firm's profit maximum with the corresponding equations (6)–(11) determining the social optimum leads to the following result.

Proposition 1. The market equilibrium in the case of dynastic symmetric households is a social optimum if the following taxes are imposed: (i) a tax on emissions with rate

(32)
\begin{equation} \tau = - \frac{{\lambda ^S N}}{{\lambda ^k }}, \end{equation}

(ii) a tax on the household size with rate

(33)
\begin{equation} \Theta = - Ie\frac{{\lambda ^S }}{{\lambda ^k }},\quad {\rm and} \end{equation}

(iii) no tax on the number of births

(34)
\begin{equation} \theta = 0, \end{equation}

where λS and λk are the shadow prices of the pollutant and capital stock in the social optimum (determined by conditions (6)– (12)).

Proof. The optimal emission tax is derived by comparing condition (22) for the amount of emissions in the firm's profit maximum and the corresponding condition (8) for the socially optimal amount of emissions. As, by symmetry, ei = e and ki = k, we may substitute equation (22) in (8) and find the optimal tax rate by rearranging,

\[ \tau = - N\frac{{\lambda ^S }}{{\lambda ^k }}.\]

Next we derive the optimal tax rate Θ on the household size. The tax rate Θ has to be chosen such that condition (31) is equal to the corresponding condition (10) for the social optimum. This is the case, if −Iλ k j Θ = λ S e, i.e., if

\begin{equation*} \Theta = - I\,e\frac{{\lambda ^S }}{{\lambda _j^k }} = - I\,e\frac{{\lambda ^S }}{{\lambda ^k }}, \end{equation*}

where the last requirement λ k j = λ k holds by symmetry.

Finally, comparing conditions (29) and (7), we obtain θ = 0.

The intuition for the result that two policy instruments are necessary in order to achieve the social optimum is as follows. In the market equilibrium two decisions generate external effects: the decision concerning emissions and the decision concerning fertility. On the one hand the emissions are too high for a given size of the population. This externality can be internalized by the Pigouvian tax r on emissions. In addition, there is a further externality due to the decision on the birth rate: the dynasty's founder does not take into account the social costs of an increased population that arise, because each additional individual increases total emissions given the level of per-capita emissions. It will do so for its whole lifetime. Therefore, the regulative tax has to address the stock variable and correct the shadow price λ N of the population size (cf. equation (31)). A tax on the birth rate would not solve the problem, because the household's valuation of the population stock is incorrect from a social point of view, not the valuation of the number of births. Thus, the environmental problem in our model economy leads to two different externalities.

If there was no environmental deterioration, the individual decisions concerning consumption and the number of children were optimal: the shadow price λ S of the pollutant stock would be zero. Thus, according to proposition 1, both taxes τ and Θ were equal to zero. From this we obtain as a special case without environmental problems a result from Razin and Sadka (Reference Razin and Sadka1995), who show in a model without emissions that children should not be taxed, because the individual decisions concerning the number of children lead to a social optimum.

The tax on the size of the household is a linear argument of the per-capita budget constraint. This means the tax-burden per household i is equal to ΘN 2 i , and hence, increasing quadratic in Ni . A linearly increasing tax would be equivalent to a constant deduction from wage income. Because of the perfect labor market, such a tax would not influence the household decision. If the tax is quadratic in Ni each member of the household does not only pay taxes for itself, but for all other members too. By this, the effect of the population growth is taken into account by the individual decisions in an appropriate way.

If we know the solution for the social planner's optimization problem, i.e., the optimal paths for the control variables and shadow prices, we can express the tax rates τ and Θ in real terms.Footnote 14 They read

(35)
\begin{equation} \tau = f_e (k,e) \end{equation}
(36)
\begin{equation} \Theta = \frac{I}{N}e\,\tau, \end{equation}

where the values of the optimal paths have to be inserted for k, e, and N, respectively. The tax payments on the household size equal the pollution taxes each member of the household has to pay.

From condition (36) it is obvious that the tax on the population is positive. This means that the private costs of having a large household in the case without taxation are less than social costs. In this sense, there exists a problem of ‘overpopulation’, unless the household size is taxed in the appropriate way which is given by proposition 1.

To get a more intuitive interpretation for the tax rates, we consider the value of the tax rates in a steady state. Using conditions (6), (18) and (19), we can express the tax rates τ and Θ in real terms,

(37)
\begin{equation} \hat \tau = - \frac{{\hat N\,\hat u_S }}{{\hat u_c }}\frac{1}{{p + \delta }} \end{equation}
(38)
\begin{equation} \hat \Theta = - \frac{{I\hat e\,\hat u_S }}{{\hat u_c }}\hat \tau = - \frac{1}{{p + \delta }}. \end{equation}

The tax rate on emissions is the present value of the sum of marginal rates of substitution between environmental damage and consumption over all $\hat N$ individuals; the discount rate is given by the sum of the rate of time preference and the depreciation rate of the pollutant stock in the environment.

The tax rate on the household size is the present value of the sum of marginal rates of substitution between the additional environmental damage caused by a larger household size (which would lead to additional emissions ê and consumption over all I households. Again, the discount rate is given by the sum of the rate of time preference and the depreciation rate of the pollutant stock in the environment.

3.3 Micro-households

Here we discuss a different setting of households which decide on consumption and fertility. Instead of dynasties, where all children stay in the household as the decision-making unit, we consider the opposite theoretical extreme case that children leave their parent's household immediately after birth. The size of such ‘micro-households’ is fixed, as they consist only of the parents, but the number N of households varies, as children found their own households. This is in contrast to the case of dynastic households, where the size of households varies whereas the number of households in the economy is fixed.

The budget constraint of micro-household j in per-capita terms isFootnote 15

(39)
\begin{equation} rk_j + w + \pi + T = \dot k_j + c_j + bn_j k_j + \vartheta \,k_j + \theta \,n_j . \end{equation}

The income is described by the left-hand side of the constraint and is equal to the sum of capital and wage incomes, profits, and the lump-sum transfer. The right-hand side captures the expenditures. They consist of investments $\dot k_i$, consumption ci , and costs of raising children bniki . Instead of a tax Θ on the household size we have introduced a tax ϑ on the number of children in equation (24). Since the household size is constant, a tax on the size of a micro-household would not alter the micro-household's decisions. Furthermore we introduced a tax ϑ on per-capita capital that is necessary because otherwise the micro-household would not take into account that a rising population has to be endowed with capital.

The micro-household j decides on two variables: per capita consumption Cj (t) and the birth rate nj (t). Similar to the case of dynastic households, we assume that the micro-household has no influence on the firm's decision on the amount of polluting emissions generated in production. As each micro-household's offspring contributes to population only to a negligible extent, decision makers take population development as exogenously given, i.e., they do not take into account any change in population size resulting from their decision on the birth rate. Thus, the only side condition for the optimization of the micro-household j is the budget constraint. The representative micro-household's decision problem is

(40)
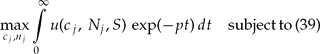
\begin{equation} \mathop {\max }\limits_{c_j ,n_j } \int\limits_0^\infty {u(c_j ,\,N_j ,S)} \, \exp ( - pt)\,dt\quad {\rm subject}\,{\rm to}\,(39) \end{equation}

The current-value Hamiltonian for this problem is given by

\begin{align*} H_j=\;&u\left(c_j,n_j,S\right) \\ &+ \lambda^k_j\, \left(r\, k_j + w + \pi + T-c_j-b\,n_j\,k-\vartheta\,k_j-\theta\,n_j\right). \end{align*}

The individual optimum is determined by the following first-order conditions:

(41)
\begin{equation} \frac{\partial H_j}{\partial c_j}=0 \quad u_{c_j} -\lambda ^{k}_j=0 \end{equation}
(42)
\begin{equation} \frac{\partial H_j}{\partial n_j}=0\quad u_{n_j}-\lambda^k_j\left[b\,k+ \theta\right] =0 \end{equation}
(43)
\begin{equation} \frac{\partial H_j}{\partial k_j}=\rho \lambda^k_j-{\dot\lambda^k}_j \quad \lambda^k_j[ r-b\,n_j-\vartheta] = \rho\,\lambda^k_j-{ \dot\lambda^k}_j. \end{equation}

Equation (41) is the same as the corresponding optimality condition (6). The remaining equations are identical to the corresponding optimality conditions, if the tax rates τ, θ, and ϑ are set in the appropriate way.

Proposition 2. A market equilibrium with micro-households is a social optimum in the symmetric case if the following taxes are imposed: (i) a tax on emission with rate

(44)
\begin{equation} \tau = - \frac{{\lambda ^S N}}{{\lambda ^k }}, \end{equation}

(ii) a tax on per-capita capital with rate

(45)
\begin{equation} \vartheta = n - d,\,\hbox{\it and} \end{equation}

(iii) a tax on the number of newly born children with rate

(46)
\begin{equation} \theta = k - \frac{{\lambda ^N N}}{{\lambda ^k }}. \end{equation}

Proof. The optimal rate of the emission tax results from the comparison of equation (22) with the optimality condition (8). Completely analogous to the proof of proposition 1, we obtain

\begin{equation*} \tau = - \frac{{\lambda ^S N}}{{\lambda ^k }}. \end{equation*}

To obtain the optimal tax rate on per-capita capital, we compare condition (43) (using (21)) with the corresponding condition for the socially optimal capital portfolio balance (9). This yields

\begin{equation*} \vartheta = n - d. \end{equation*}

Finally, the optimal tax rate θ on the birth rate results from comparing condition (42) for the household's optimal birth rate – using the symmetry conditions kj = k, ei = e, and λ k j = λ k − with condition (7) for the socially optimal birth rate. Both equations are equal, if

\[\theta = k - N\frac{\lambda ^N}{\lambda ^k}. \]

This result shows that in the case of micro-households the same kind of pollution tax is necessary to implement the social optimum in a decentralized economy as in the case of dynastic households. We discussed this tax rate in the previous section.

Secondly, a tax on the per-capita capital stock is required, because micro-households do not take into account that capital has to be accumulated in order to endow additional workers with capital. Accordingly, for an increasing population, n − d > 0, the tax rate θ = n − d is positive and equal to the population growth rate.

In contrast to the case of dynastic households, a tax on the number of newly born children has to be set rather than a tax on the household size. To provide an intuition for this tax, we express the tax rate on the birth rate in real terms. Using equations (6) and (7) in (46), we obtain

(47)
\begin{equation} \theta = \frac{{u_n }}{{u_c }} - b\,k. \end{equation}

The tax rate on the birth rate equals the difference between the marginal rate of substitution between newly born children and consumption and the costs of raising an additional child in the socially optimal development. That is, the tax rate equals the net benefit of an additional child in the social optimum (in units of marginal utility from consumption). Plugging this expression into condition (42), we find that the individually chosen birth rate is socially optimal if the tax on the birth rate is such that the micro-household's net benefit of an additional child equals the social net benefit.

The social net benefit may be positive or negative in the first place. In a steady state, however, θ is unambiguously positive. To show this, we plug conditions (6) and (19) into (46). This leads to

(48)
\begin{equation} \hat\theta = \hat k-\frac{\hat N\,\hat e\,\hat u_S}{\hat u_c} \,\frac1{\rho\,(\rho+\delta)}=\hat k+\frac{\hat\tau\,\hat e}{\rho} . \end{equation}

The tax on each newly born child consists of two terms. The first term is the capital that has to be spent to endow the additional worker. The second term is the present value of the emission taxes it will have to pay during its whole lifetime. The second term is similar to the expression found by Harford (Reference Harford1998: 103), who found that the ‘child-bearing tax has a size equal to the discounted present value of the pollution taxes paid by each child and all of that child's descendants’. There is a difference between our and Harford's result however, as according to Harford the child has to pay for all of its descendants while in our model only for its own future emissions. This difference is due to a dissimilarity in the models: Harford does not explicitly consider the production side of the economy. Because he assumes that the rate of return to capital is exogenously given, per-capita consumption decreases with the population size in his model. Hence, marginal utility of consumption increases with an increasing population size and also the tax on child-bearing increases, which is expressed in units of marginal utility from consumption.

4. Conclusions and discussion

We have analyzed externalities which occur when parents decide on the number of births and consumption in an economy, in which the production of consumption goods causes environmentally harmful emissions. Our analysis shows that the individual decisions of households concerning consumption and fertility and the decisions of firms concerning production lead to an inefficient development of the economy.

Previous studies have already shown that an endogenous population size could lead to an inefficient outcome. Our contribution to this literature is to focus on the household as the decision-making unit. We have shown that the type of externality associated with parents' decisions about the number of births is different, depending on the household type considered.

In the case of dynastic households the resulting size of the population is higher than that in the social optimum. Total emissions are higher than socially optimal, because the decision makers do not take into account the additional pollutant emissions which are caused by additional members of the household. The decision of the dynastic household would be socially optimal, if there was no environmental problem. Therefore one can say that the environmental problem causes an additional population problem, as it generates two distinct external effects. In the setting of micro-households, the decision maker does not take into account future population development at all. In particular, she does not take into account the pollution, each additional child would generate during its whole lifetime. In the steady state, the resulting birth rate is higher than socially optimal.

From a welfare-theoretic point of view these results give reason for a regulating intervention into the individual decisions. We have shown that with an appropriate choice of regulative taxes, a regulator is able to achieve the social optimum. It is important to note that such a regulation is substantially different from existing command-and-control policies which fix the number of children parents are allowed to have (as e.g., China's ‘one-child policy’), because it preserves the parents' freedom to choose the number of children.

The difference between the tax rate on the birth rate in the case of micro-households and the tax rate on the household size in the case of dynastic households is significant: In the case of dynastic households, the tax payments equal the emission taxes that have to be paid currently by each member of the household. In the case of micro-households, the tax payments equal the pollution taxes each newly born child will have to pay over its whole lifetime. The intuitive reason for this result is that in the case of dynastic households the future number of descendants of each individual is adequately taken into account while in the case of micro-households this is not the case and therefore the taxation has to correct for this failure, too.

At a first glance it seems to be surprising that different types of taxes are needed to regulate the population development in the two institutional settings. However, the reason can easily be understood. Compared to the socially optimal allocation, the excessively high number of adults causes the environmental problem in both settings. Accordingly, the number of adults has to be regulated. In the case of micro-households, it is not feasible to directly impose a tax on the number of adults, as children leave the household immediately after birth. Hence, the regulator has to tax the birth rate. By contrast, in the case of dynastic households the founder of the dynasty takes into account all of her descendants. Hence the socially optimal allocation can be reached by a direct tax on the future household size.

Footnotes

1 The case of micro-households is similar to the model of Weil (Reference Weil1989). Similar to his results we also find that even in the absence of environmental pollution, the equilibrium outcome can be inefficient. In our paper, we focus on the inefficiency caused by environmental pollution, however.

2 Therefore, we extend approaches of Barro and Sala-I-Martin (Reference Barro and Sala-I-Martin1995) and Yip and Zhang (Reference Yip and Zhang1997) by introducing environmental quality as an argument in the welfare function and by taking into account that production causes polluting emissions.

3 Here, we omit the time dependency of the variables for reasons of more convenient notation. Variables as subscripts to functions denote the partial derivatives with respect to the corresponding variables.

4 In the model, we treat N and n as continuous variables. This approximation is valid because we exclusively regard large numbers for population size N. Hence, n denotes an average birth rate. With the same rationale, instead of regarding an individual's probability of death, we employ an average death rate d for the whole population.

5 In physical terms, emissions are unwanted outputs of production. However, for purposes of analysis they are formally treated as production inputs (Pethig, Reference Pethig2006).

6 For CO2 this assumption is reasonable if one exclusively considers the anthropogenic CO2 excess above the natural level. Furthermore, this excess has to be comparatively small and timescales regarded must not be too long. For a critical comment on the use of a single differential equation for the description of the accumulation of greenhouse gases in the environment see Joos et al. (Reference Joos, Müller-Fürstenberger and Stephan1999) and Moslener and Requate (Reference Moslener and Requate2007).

7 The maximized Hamiltonian H 0 is the function H after we have substituted the control variables by (6)– (8).

8 The first-order conditions are also sufficient for a welfare maximum, if the maximized Hamiltonian H 0 is concave in the state variables (Arrow and Kurz, Reference Arrow and Kurz1970). For the sake of this analysis, we assume that this is the case.

9 This specification extends the one used by Yip and Zhang (1997: 100), who do not take environmental pollution into account.

10 Here, we denote the steady state by a hat ‘^’ on top of the variables.

11 Because of the constant returns to scale technology the marginal product of the per-capita inputs is equal to the marginal product in absolute terms, i.e., FK i = fk i and FE i = fe i . The optimal labor input is given by $w = \frac{{d(N_i \,f(k_i ,e_i ,t))}}{{dN_i }} = f(k_i ,e_i ,t) - k_i f_{k_i } - e_i f_{e_i }$.

12 A similar problem with constant population size is analyzed in Aronsson et al. (Reference Aronsson, Johansson and Lögren1997).

13 Under the appropriate taxation system, these conditions are identical to the conditions (6)– (11) for the optimal solution. Thus, they are also sufficient, provided the first-order conditions for the social optimum are also sufficient.

14 This is done by rearranging the necessary conditions for an optimum with respect to the shadow prices and using these conditions in equations (32) and (33) for the taxes.

15 In total rather than aggregate terms, the budget constraint is (without taxes and transfers) $\dot K_j = \pi \,K_j + r\,Kj + w\,N_j - cN_j - b\,n_j \,K_j$. Since the size Nj of the micro-household is fixed, we have $\dot k_j = \dot K_j /N_j$. Hence the term (nj − d)kj which appears in (3) and (24) is missing in (39). We thank a referee of this journal for pointing this out.

References

Aronsson, T., Johansson, P., and Lögren, K. (1997), Welfare Measurement, Sustainability and Green National Accounting – A Growth Theoretical Approach, New Horizons in Environmental Economics, Cheltenham: Edward Elgar.Google Scholar
Arrow, K.J. and Kurz, M. (1970), Public Investment, The Rate of Return, and Optimal Fiscal Policy, Baltimore, MD: Resources for the Future, John Hopkins Press.Google Scholar
Barro, R.J. and Becker, G.S. (1989), ‘Fertility choice in a model of economic growth’, Econometrica 57 (2): 481–501.CrossRefGoogle Scholar
Barro, R.J. and Sala-I-Martin, X. (1995), Economic Growth, New York: Mc Graw-Hill.Google Scholar
Becker, G.S. (1960), ‘An Economic Analysis of Fertility’, in Demographic and Economic Change in Developed Countries, Princeton: National Bureau of Economic Research, pp. 209–231.Google Scholar
Becker, G.S., Glaeser, E.L., and Murphy, K.M. (1999), ‘Population and economic growth’, AEA Papers and Proceedings 89 (2): 145–149.Google Scholar
Cronshaw, M.B. and Requate, T. (1997), ‘Population size and environmental quality’, Journal of Population Economics 10: 229–316.CrossRefGoogle ScholarPubMed
Dasgupta, P. (2000), ‘Population and resources: an exploration of reproductive and environmental externalities’, Population and Development Review 26 (4): 643–689.CrossRefGoogle Scholar
Ehrlich, P.R. and Ehrlich, A.H. (2002), ‘Population, development, and human resources’, Envrionment and Development Economics 7: 158–170.CrossRefGoogle Scholar
Galor, O. and Weil, D.N. (1999), ‘From malthusian stagnation to modern growth’, AEA Papers and Proceedings 89 (2): 150–154.Google Scholar
Harford, J.D. (1997), ‘Stock pollution, child-bearing externalities, and the social discount rate’, Journal of Environmental Economics and Management 33: 94–105.CrossRefGoogle Scholar
Harford, J.D. (1998), ‘The ultimate externality’, American Economic Review 88 (1): 260–265.Google Scholar
Heilig, G.K. (1996), ‘How many people can be fed on Earth?’, in Lutz, W. (ed), The Future Population of the World. What Can We Assume Today, London: Earthscan (revised and updated edition).Google Scholar
Joos, F., Müller-Fürstenberger, G., and Stephan, G. (1999), ‘Correcting the carbon cycle representation: how important is it for the economics of climate change’, Environmental Modeling Assessment 4: 133–140.CrossRefGoogle Scholar
Michel, P. (1982), ‘On the transversality condition in infinite horizon optimal problems’, Econometrica 50 (4): 975–985.CrossRefGoogle Scholar
Moslener, U. and Requate, T. (2007), ‘Optimal abatement in dynamic multi-pollutant problems when pollutants can be complements or substitutes’, Journal of Economic Dynamics and Control 31: 2293–2316.CrossRefGoogle Scholar
Nerlove, M. (1991), ‘Population and the environment: a parable of firewood and other tales’, American Journal of Agricultural Economics 73 (5): 1334–1347.CrossRefGoogle ScholarPubMed
Nerlove, M. and Meyer, A. (1997), ‘Endogenous fertility and the environment: a parable of firewood’, in Dasgupta, P. and Mäler, K.-G. (eds), The Environment and Emerging Development Issues, Oxford: Clarendon Press, chapter 10, pp. 259–282.Google Scholar
Pethig, R. (2006), ‘Non-linear production, abatement, pollution and materials balance reconsidered’, Journal of Environmental Economics and Management 51 (2): 185–204.CrossRefGoogle Scholar
Raut, L.K. and Srinivasan, T. (1994), ‘Dynamics of endogenous growth’, Economic Theory 4: 791–797.CrossRefGoogle Scholar
Razin, A. and Sadka, E. (1995), Population Economics, Cambridge, MA: The MIT Press.Google Scholar
Robinson, J.A. and Srinivasan, T. (1997), ‘Long-term consequences of population growth: technological change, natural resources, and the environment’, in Rosenzweig, M.R. and Stark, O. (eds), Handbook of Population and Family Economics, Amsterdam: Elsevier, chapter 21, pp. 1175–1297.CrossRefGoogle Scholar
Shah, A. (ed) (1998), Ecology and the Crisis of Overpopulation – Future Prospects for Global Sustainablility, Cheltenham: Edward Elgar.Google Scholar
United Nations (2007), ‘World Population Prospects: The 2006 Revision’, Population Division of the Department of Economic and Social Affairs of the United Nations Secretariat, New York.Google Scholar
Weil, P. (1989), ‘Overlapping families of infinitely-lived agents’, Journal of Public Economics 38: 183–198.CrossRefGoogle Scholar
World Bank (2003), ‘World Development Indicators on CD-ROM’.Google Scholar
Yip, C.K. and Zhang, J. (1997), ‘A simple endogenous growth model with endogenous fertility: indeterminacy and uniqueness’, Journal of Population Economics 10: 97–110.CrossRefGoogle ScholarPubMed