‘Institutions matter!’ This is the battle cry of a continuing intellectual revolution that began in the late 20th century. So-called new institutionalist movements have emerged in economics, political science, history and philosophy, and even in disciplines like sociology that have always recognized the importance of institutions. But exactly what are institutions? Much of the path-breaking research on institutions over the past several decades has proceeded without a clear answer to this question. Indeed, many of the great figures of the current institutionalist wave base their work on what would best be regarded as various proto-analyses of institutions. In Understanding Institutions, Francesco Guala presents a rules-in-equilibrium theory of institutions that builds upon joint work with Frank Hindriks (Hindriks and Guala Reference Hindriks and Guala2015) and that unifies the most important of these different threads. As the name suggests, the rules-in-equilibrium theory is game-theoretic, and is designed to summarize what institutions are, how they can be created and how they might be changed. Guala applies this theory to some important issues in social ontology and the philosophy of science. In particular, Guala argues that the rules-in-equilibrium theory can be developed in an individualistic mode, without the need for incorporating irreducible collectivist entities such as the plural subjects or joint intentions that underpin the approaches to explaining social phenomena advanced by scholars such as Margaret Gilbert (Reference Gilbert1989, Reference Gilbert2014) and Raimo Tuomela (Reference Tuomela2013). And Guala argues against the thesis defended by David-Hillel Ruben (Reference Ruben, Lawson and Appignanesi1989) and Amie Thomasson (Reference Thomasson2003) that social kinds depend ontologically on our representations. Guala concludes that on his analysis, the nature of an institution is determined by its function rather than what the individuals the institution regulates happen to think about it, so one need not embrace the ontological dependence thesis, which in turn implies that one need not embrace antirealism and infallibilism regarding social kinds.
Below I focus my remarks on the specifics of the rules-in-equilibrium theory of institutions itself rather than Guala's applications of this theory, important as they are. The applications turn on the rules-in-equilibrium theory, which is designed to integrate three main approaches to understanding the nature of institutions, namely, the rules-based, equilibrium-based and constitution-based approaches. I review how Guala executes this part of his project in Section 1. In Section 2, I take some issue with the scope of Guala's theory. Guala adopts a ‘big tent’ view of institutions. The rules-in-equilibrium theory reflects this view and includes social phenomena too simple to be genuine institutions. The rules-in-equilibrium theory, I argue, should be augmented so as to require that an institution have mechanisms for restoring the equilibrium of general compliance when its default rules are violated. Including such a requirement into an analysis of institutions would shrink Guala's tent somewhat, but would also, I argue, get to the heart of much that is central in the study of institutions.
1. A UNIFIED THEORY OF INSTITUTIONS
Three main ways of understanding institutions are well illustrated in three contemporary classic works. In A Theory of Justice, John Rawls stresses the different roles of an institution and their accompanying rights and obligations.
By an institution I shall understand a public system of rules which defines offices and positions with their rights and duties, powers and immunities, and the like. These rules specify certain forms of action as permissible, others as forbidden; and they provide for certain penalties and defenses, and so on, when violations occur. (Rawls Reference Rawls1971: 55)
In The Economic Theory of Social Institutions, Andrew Schotter characterizes an institution as a stable pattern of social conduct, where the stability can be maintained by the members of the regulated society themselves or from the outside.
A social institution is a regularity in social behavior that is agreed to by all members of society, specifies behavior in specific recurrent situations, and is either self-policed or policed by some external authority. (Schotter Reference Schotter1981: 11, italics in the original)
And in Institutions, Institutional Change and Economic Performance, Douglass North describes an institution as a system of rules that both enable and constrain social interactions.
Institutions are the rules of the game in society or, more formally, are the humanly devised constraints that shape human interaction. . . . Institutions reduce uncertainty by providing a structure to everyday life. They are a guide to human interaction, so that when we wish to greet friends on the street, drive an automobile, buy oranges, borrow money, form a business, bury our dead, or whatever, we know (or can learn easily) how to perform these tasks. (North Reference North1990: 3–4)
North's and Schotter's informal definitions respectively represent the rules-based and the equilibrium-based approaches. Not surprisingly, game theory provides an analytical framework for developing these approaches. According to the rule-based approach, an institution is a subset of a game form that is the set of strategies available to the agents involved. According to the equilibrium-based approach, an institution is a certain type of equilibrium of this game.
Social scientists have for some time recognized that the game form and equilibrium analyses of institutions are complementary. Guala goes further, and argues that neither the rule-based nor the equilibrium-based approaches can stand alone (Chapter 1). A simple body-of-rules analysis will not do, since agents must be motivated to actually follow the rules, which they cannot be expected to do if the rules require out-of-equilibrium behaviour. But a purely equilibrium-based approach will not do either, since some equilibria are essentially institution-independent. To illustrate the point, consider the Trust Game summarized in Figure 1. The Client either trusts (T) by providing the Investor a monetary stake of value 1 or mistrusts (M) by withholding her stake. If the Client trusts, the Investor uses the stake to generate a net value 2α > 2 and then either cooperates (C) by sharing the proceeds equally with the Client or defects (D) by keeping all the proceeds. One can expect the Client and Investor to follow the inefficient equilibrium (M, D-if −T), since D is the Investor's strictly dominant choice if the Client follows T and the Client can only forestall this worst outcome for her by following M. To reach the efficient outcome (T, C-if −T), the Client and the Investor need an institution, as I will illustrate in Section 2.
Figure 1. Trust Game
The rules-in-equilibrium theory unites the rules-based and equilibrium-based approaches in terms of Aumann's (Reference Aumann1974, Reference Aumann1987) correlated equilibrium concept. The following variation of one of Guala's examples illustrates the theory: Two itinerant farmers each would like to take sole possession of an abandoned farm that is too small to remain productive if divided or shared. The Hawk-Dove game of Figure 2 summarizes their interaction, where each can either try to take possession of the farm and use it to produce and maintain crops or livestock (P) or leave the farm for others to use (L). Hawk-Dove is a conflictual coordination game with strict Nash equilibria (P, L) and (L, P) where exactly one tries to take possession and consequently becomes sole possessor, and where if each follows her end of her most preferred outcome they end up at (P, P) where they fight. These farmers settle the question of who takes possession peaceably by following a rule their community has adopted for resolving such problems:
-
(R1) P if I am the first to enter the empty farm cottage, and L otherwise.
In this case there are two relevant possible worlds, ω1 where Farmer 1 enters the empty cottage first and ω2 where Farmer 2 enters the empty cottage first. The regulative rule (R1) characterizes the strategy system
$$\begin{equation*}
\bm{h}\left( \omega \right) = \left\{ {\begin{array}{@{}*{1}{c}@{}} {\left( {P,L} \right){\rm{ if }}\;\omega = {\omega _1}}\\ {\left( {L,P} \right){\rm{ if }}\;\omega = {\omega _2}} \end{array}} \right.
\end{equation*}$$
summarized in Figure 3, where the shaded matrix cells indicate which outcomes the farmers follow according to the possible worlds.
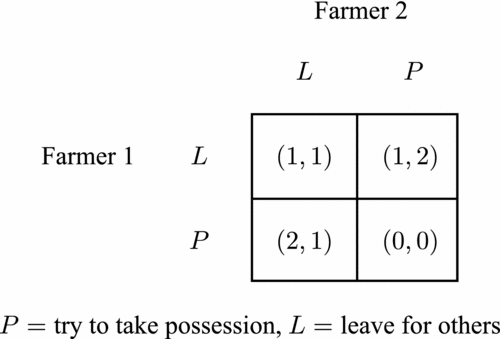
Figure 2. Hawk-Dove
Figure 3. h Equilibrium of Hawk-Dove
h is a correlated equilibrium since each farmer prefers to conform to her end of h given that the other farmer conforms to h . But there are other ways the farmers can resolve their problem peaceably involving different sets of regulative rules. For example, given some λ ∈ [0, 1] if both follow the regulative rule
-
(Rλ ) P if I win a called coin toss using a coin that lands ‘heads-up’ with probability λ, and L if the other wins this coin toss.
then they follow a correlated equilibrium where they alternate between (P, L) and (L, P) according to who wins this called coin toss. According to the rules-in equilibrium theory, (R1) is an institution as this regulative rule system characterizes an equilibrium of the game summarizing the agents’ interaction possibilities where the agents are capable of following many different regulative rules systems that characterize distinct correlated equilibria of the game (Chapter 4).
What about the constitution-based approach represented by Rawls’ informal definition? John Searle (Reference Searle1995, Reference Searle2010, Reference Searle2015) argues that institutions are actually characterized by constitutive rules of the form
$$\begin{equation*}
X\,{\rm is}\, Y\,{\rm if}\, C
\end{equation*}$$
where X is some pre-institutional entity, Y indicates a certain status and C specifies conditions where the status applies. Searle maintains that constitutive rules are the real foundation of institutions since these are the rules that create the roles, duties and rights that characterize actual institutions. Searle believes the constitution-based approach is orthogonal to the rules-based and equilibrium-based approaches. Guala (Chapter 5) argues that constitutive rules can in fact be integrated into the rules-in-equilibrium theory because constitutive rules are analysable in terms of regulative rules. Guala illustrates this reduction using a term ‘property*’ indicating a status possibly simpler than the ordinary status of owning property. Using the above example, one can give a pair of constitutive rules
This farm is the property* of Farmer 1 if she is the first to enter its empty cottage.
This farm is the property* of Farmer 2 if he is the first to enter its empty cottage.
defining the relevant statuses of the two farmers. But what does it mean for the farm to be property* of Farmer 1? The status indicated by the Y 1 term
$$\begin{equation*}
{Y_1} = {\rm the\,property}^{*}\,{\rm of\,Farmer}\,1
\end{equation*}$$
can be defined using regulative rules such as
$$\begin{equation*}
\begin{array}{@{}*{1}{l}@{}} {{{{Z}}_{{\rm{11}}}}{\rm{ = Farmer}}\,{\rm{1}}\,{\rm{takes}}\,{\rm{possession}}\,{\rm{of}}\,{\rm{this}}\,{\rm{farm}}}\\ {{{{Z}}_{{\rm{21}}}}{\rm{ = Farmer}}\,{\rm{1}}\,{\rm{uses}}\,{\rm{this}}\,{\rm{farm}}\,{\rm{to}}\,{\rm{produce}}\,{\rm{and}}\,{\rm{maintain}}\,{\rm{crops}}\,{\rm{or}}\,{\rm{livestock}}} \end{array}
\end{equation*}$$
so that if C 1 describes ω1 and X refers to the farm, the constitutive rule defining Farmer 1’s status can be written in the form
$$\begin{equation*}
{\rm{If}}\,{C_{\rm{1}}}\;{\rm{then\ }}\,X\,{\rm{is}}\,{Y_1}{\rm{, and}}\,{\rm{if}}\,{Y_1}\,{\rm{then}}\,{Z_{11}}\,{\rm{and}}\,{Z_{21}}
\end{equation*}$$
As Guala points out this XYZ-formula makes explicit a set of actions associated with the status term Y (64–5). The status is definable in terms of the associated acts. Guala goes on to show how one can analyse the deontic powers of an institution in terms of the rules-in-equilibrium theory (Chapter 6). This completes what I regard a successful integration of the rules-based, the equilibrium-based and the constitution-based approaches. But has Guala given us a fully adequate theory of institutions? I turn to this question next.
2. SELF-CORRECTION MECHANISMS
The rules-in-equilibrium theory sets no restrictions on what can count as an institution beyond the equilibrium condition that ensures that the regulated agents have incentives to comply with the rules. A single rule that defines a convention such as motorists driving on the right side of the road qualifies as an institution according to the rules-in-equilibrium theory, as Guala clearly acknowledges (66–7). Some philosophers who study institutions would say the rules-in-equilibrium theory is too inclusive. Seumas Miller (Reference Miller and Zalta2014) and Searle (Reference Searle2015) regard conventions like the drive-on-the-right convention as social phenomena plainly too primitive to be institutions. Interestingly, while many, including Guala, regard David Lewis’ (Reference Lewis1969) Convention: A Philosophical Study a foundational work in equilibrium analyses of institutions, Lewis himself may have agreed with Miller and Searle. In a rare passage in Convention where Lewis explicitly discusses institutions, he expresses doubts that a convention that assigns exclusive use of a good suffices to characterize the institution of property, since our ordinary understanding of property incorporates related laws and offices (1969: 48). On this point I am inclined to side with Miller and Searle. I find much to admire in the rules-in-equilibrium theory, and in fact I have proposed a correlated equilibrium analysis of conventions (Vanderschraaf Reference Vanderschraaf1998) that Guala uses to help motivate this theory (47–8). But I also think not all conventions are institutions. Institutions specify rights, obligations and especially roles that vary across the individuals they regulate. Indeed, I think the constitution-based approach has some intuitive appeal precisely because constitutive rules are convenient for describing such variable rights, obligations and roles. Guala can of course counter that ours is a purely verbal disagreement, and maintain that simple conventions like drive-on-the-right are simply the lowest level institutions in terms of their complexity. But I think one can give conditions that come closer to capturing the more complex conceptions of institutions of scholars like Miller and Searle that would refine the rules-in-equilibrium theory without compromising its best features.
In particular, I propose that an institution necessarily has self-correction mechanisms that can restore the system to the equilibrium state defined by its default rules in case some have disrupted this equilibrium by disobeying the default rules. A convention as simple as drive-on-the-right has no such self-correction mechanism for dealing with instances where a motorist violates the default rule requiring one to drive on the right. This convention might self-correct following some miscoordination if not too many have disobeyed the default rule, but the motorists have no rules for restoring the original equilibrium if this equilibrium is dislodged by sufficient disobedience. To illustrate a self-correction mechanism, I return to the commitment problem of the Client and the Investor. If this interaction is one of a series where at each trading period an individual in the Client role is matched with an individual in the Investor role, the agents involved can follow an efficient equilibrium with the aid of an institution as follows: Each trading period, the Investor first either registers (R) with a Guarantor for a fee ε ∈ (0, 1) or does not register (N). If the Investor registers, he places a security deposit worth d > 2α in the Guarantor's custody and the Guarantor then monitors the transaction between this Investor and his current Client. If this Client trusts and the Investor then defects, the Guarantor keeps the deposit. Otherwise the Guarantor returns the deposit to the Investor. Figure 4 summarizes this Extended Trust Game. In this game, which is based on an example due to Robert Tadelis (Reference Tadelis2013: 205–7), since α − ε > 0 and 2α − ε − d < 0, according to the backwards induction solution the Investor registers, the Client trusts and the Investor then cooperates. The respective default regulative rules for Investor and Client are
-
RI : R, then C if Client follows T.
-
RC : T if Investor follows R, M if Investor follows N.
These default rules characterize an efficient correlated equilibrium where the relevant possible worlds are ω R where the Investor is registered and ω N where the Investor is not registered. The Guarantor serves as a self-correction mechanism, since even if registered Investor individuals occasionally defect, the Client and Investor individuals in subsequent periods are willing to resume the system of default rules RI and RC because of the activity of the Guarantor. This system characterizes a simple institution, albeit an incomplete or open institution since this system assumes the Client individuals and the Guarantor follow their parts automatically. To achieve a fully closed institution where the agents in all three roles – Client, Investor and Guarantor – are in correlated equilibrium when they all follow the regulative rules, this system would need to be extended with mechanisms for dealing with cases such as the current Client mistrusting her registered Investor or the Guarantor keeping the security deposit of a registered Investor who cooperates. Closure of this system is in fact achievable, but this simple open institution conveys the main idea. Guala can, and I think should, refine the rules-in-equilibrium theory by requiring institutions to have self-correction mechanisms.
Figure 4. Extended Trust Game with Guarantor
CONCLUSION
Understanding Institutions is an admirably ecumenical work. Guala fully appreciates how the rule-based, equilibrium-based and constitution-based approaches each advance our understanding of institutions. He lays the foundation for an integrated analysis of institutions, even if his specific version of the rules-in-equilibrium theory is too inclusive. Guala's engaging, accessible presentation will appeal to a wide philosophical audience. Indeed, Understanding Institutions could serve as a substantive introduction to both game-theoretic analyses of social processes such as conventions and elements of social ontology. For years to come, Guala's work deserves to be a starting point for those interested in the main philosophical questions that our renewed interest in institutions has raised.
