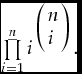‘If a tree falls in a forest and no one is around to hear it, does it make a sound?’
1. INTRODUCTION
Subjective probability quantifies a decision maker’s degree of belief in the likelihoods of events about which reasonable decision makers might disagree. Borel (Reference Borel, Kyburg and Smokler1924) and Ramsey (Reference Ramsey, Braithwaite and Plumpton1926) proposed the key idea that subjective probabilities may be inferred from the odds a decision maker is willing to offer (or accept) when betting on events or the truth of certain propositions. Both authors require that the event on which a bet is placed be observable, so that the uncertainty is resolved and the payments can be affected. In the words of Borel, ‘I can in the same way offer to someone who enunciates a judgment capable of verification a bet on his judgment’ (Borel Reference Borel, Kyburg and Smokler1924 [1964]: 57)Footnote 1 .
To formalize the idea of resolution of uncertainty, Savage (Reference Savage1954) introduced the idea of state of nature, ‘a description of the world so complete that, if true and known, the consequences of every action would be known’ (Arrow Reference Arrow1971: 45). Implicit in this definition is the notion that there is a unique true state that is fully depicted by the consequences associated with every possible action. In practice, however, decision theorists and economists routinely specify a state space as a primitive constituent of the decision problem. Savage himself applied this ‘state-first’ approach when he wrote, ‘If two different acts had the same consequences in every state of the world, there would from the present point of view be no point in considering them different acts at all. An act may therefore be identified with its possible consequences. Or, more formally, an act is a function attaching a consequence to each state of the world’ (Savage Reference Savage1954: 14). However, treating the state space as a primitive ingredient of the model tends to conceal critical aspects of the notion of states and imposes tacit and unnecessary restrictions on its usefulness.
The purpose of this note is twofold. First, it discusses and elaborates an approach to modelling the resolution of uncertainty described in Fishburn (Reference Fishburn1970), Schmeidler and Wakker (Reference Schmeidler, Wakker, Eatwell, Milgate and Newman1987), and Karni and Schmeidler (Reference Karni, Schmeidler, Hildenbrand and Sonnenschein1991). Footnote 2 Second, it examines the implications of this approach for the modelling of the choice set in the theory of decision making under uncertainty.
2. STATES OF NATURE
2.1. Reality and perception
Albert Einstein is reported to have asked Niels Bohr whether he believed that the moon does not exist if nobody is looking at it. Bohr replied that however hard he (Einstein) might try, he would not be able to prove that it does. In other words, following Quine (Reference Quine1948/1949), an object is a theoretical interpretation of perceived sensory information in order to represent and understand the environment. In this sense, an object that cannot be perceived cannot be known to exist and, indeed, need not exist. This concept of knowledge is pertinent to understanding Savage’s idea of state of nature. To paraphrase the epigram ‘if a state of nature obtains but leaves no perceived manifestations, does it obtain?’ In what follows I argue that a state of nature is a perception and that the specific interpretation of sensory information lends a state of nature its meaning. Moreover, to serve as a meaningful ingredient of a decision model, states of nature must be observable, in the sense that independent observers must agree on and communicate what has been observed.Footnote 3
2.2. The approach
According to the approach advanced here, the set of states of nature, or the state space, is constructed using two basic ingredients: a set, A, of basic actions, and a set, C, of feasible consequences.Footnote 4 Basic actions depict alternative, implementable, courses of action; feasible consequences are outcomes that may result from these actions. A state of nature, s, is a mapping from the set of basic actions to the set of feasible consequences. The state space is the set of all such mappings. Formally, the state space is CA .
The particular sets of basic actions and consequences that are used in their construction lend the states their meanings. The basic actions may be taken by a decision maker or by someone else, provided that the outcomes are observable and can be agreed upon. For example, running a horse race is a basic action taken by a racing organization. Taking protective measures to reduce (the verifiable damage) from an approaching hurricane is a basic action taken by the decision maker. In both cases one may place a bet on the observed outcome. In the case of hurricane damage, the bet is an insurance policy.
However, if there is a unanimous agreement that some basic actions cannot possibly result in some consequences, then there is agreement that certain states are null (e.g. if, given an act, a, the attainment of the consequence c defies the laws of physics). Formally, for each a ∈ A, denote by C(a) the set of consequences that are feasible under a.Footnote 5 Then the states s ∈ CA such that, for some a ∈ A, s(a)∉C(a) are null. Imposing these ‘feasibility constraints’ allows a parsimonious depiction of the state space as consisting of the event of all non-null states. Formally, the parsimonious state space is S = {s: A → C∣s(a) ∈ C(a), ∀a ∈ A}. If the sets of consequences that are deemed feasible under different basic actions are a matter of subjective belief, then the null states subjective. Put differently, a state that assigns an action a a consequence c∉C(a) is, by definition, null insofar as a decision maker who believes that C(a) is the set of feasible consequences under a is concerned.
This definition of the state space does not preclude the existence of salient background states. It does not contradict the idea that a tree might make a noise when it falls even if there no one is there to hear it. It does presume, however, that, insofar as decision theory is concerned with modelling and characterizing choice behaviour, such salient states are immaterial. To paraphrase Savage, if two different states have the same consequences for every basic action, then from the present point of view, there would be no point in considering them different states at all. In other words, two salient states are regarded as equivalent if and only if every basic action has equal consequences in both of them. Hence, the definition of the state space proposed here can be regarded as a quotient state space embedded in some larger salient state space.
Because each state assigns a unique consequence to each basic action, it constitutes, by definition, a complete resolution of uncertainty, and the states are mutually disjoint. However, basic actions are mutually exclusive and states are lists of counterfactuals.Footnote 6 For example, a patient who decides to undergo surgery at Johns Hopkins University Hospital cannot find out what would have been the outcome if he had chosen instead to undergo the same surgery at the Mayo Clinic. Thus, a complete resolution of uncertainty is inherently impossible. More generally, the implementation of a basic action, a, excludes other basic actions. Hence, if an outcome, c, is observed, then the uncertainty is only partially resolved. Only the event (that is, a subset of S) consisting of all the states that assign the consequence c to the basic action a, can be known to have been obtained.Footnote 7
2.3. Examples
The most obvious example of a state of nature is a depiction of a natural phenomenon – tomorrow’s temperature in Baltimore, the force of the next earthquake to hit San Francisco. These natural phenomena are perceived through measurements. Thus, the set of basic actions consists of measurements; the set of feasible consequences are the sets of measurable values corresponding to each measurement. If only one measurement is taken, then the state space consists of all the possible values taken by the measurement. If several measurements of the same phenomenon are taken, the measurements might not agree (e.g. because of inaccuracy of the instrument or the conditions under which the measurements are taken). In this case, the state space consists of all the configurations of values taken by the different measurements. If measurements are taken of different phenomena, then the state space consists of the Cartesian product of the set of the possible values of the measurements.Footnote 8
An important class of states of nature are an organism’s states of health. These phenomena are perceived by direct sensations, diagnostic tests and/or response to treatments. Presumably, some underlying causes determine the organism’s state of health and the corresponding symptoms. According to the approach described here, the only meaningful definition of a state of health is its perceived symptoms (that is, the results of diagnostic tests and/or response to treatments). In other words, recommended treatments and insurance coverage for such treatments are based on the perceived symptoms rather than the underlying causes. The latter are salient states.
Other prevalent class constitutes of states induced by competitive sporting events, such as horse races.Footnote 9 In the case of a horse race the basic actions correspond to the sets of horses that enter the race and the set of consequences are the possible orders according to which the horses cross the finish line. Running the race is a way of measuring the relative and/or absolute speed of the horses, which determine the states. In this particular example, the set of states is identical to the set of consequences. Other contests, such as presidential elections, beauty contests, and jury trials, should also be thought of as forms of measurement. In the case of presidential elections, for instance, the outcome of the vote is a measurement of the support for the competing candidates and the platforms on which they run. In the case of a beauty contest the outcome is a measurement of the opinions of the panel of judges. In the case of a jury trial, the outcome measures the weight of the evidence in the minds of the jurors.
2.4. Savage’s omelette
To grasp the difference between the traditional approach to modelling decision making under uncertainty and the approach advocated here, it is instructive to compare Savage’s analysis to the analysis according to the approach of this paper of the following scenario:
Your wife has just broken five good eggs into a bowl when you come and volunteer to finish making the omelette. A sixth egg, which for some reason must either be used for the omelette or wasted altogether, lies unbroken beside the bowl. You must decide what to do with this unbroken egg. Perhaps it is not too great an oversimplification to say that you must decide among three actions only, namely, to break it into the bowl containing the other five, to break an egg into a saucer for inspection, or to throw it away without inspection. (Savage Reference Savage1954: 13)
Savage takes the state space and the set of consequences as primitives and defines the actions to be the functions from the set of states to the set of consequences as follows:
The approach advanced here takes the sets of basic actions and feasible consequences as primitives and constructs the state space. The basic actions are: a 1: Inspect the egg in the bowl, a 2: Inspect the egg in the saucer, a 3: Do not inspect. The corresponding feasible consequences are C(a 1) = {c 1, c 2}, C(a 2) = {c 3, c 4}, and, because under a 3 the only observable consequence is a five-egg omelette, or c 6, the distinction between c 5 and c 6 not perceivable. Consequently, C(a 3) = {c 6}, and the state space is depicted in the following matrix.
The inclusion of the states s 2 = (c 1, c 4, c 6) and s 3 = (c 2, c 3, c 6) suggests that the two forms of inspection might yield opposite conclusions, which is possible if the inspections are subject to error. If inspections are perfect, as is implicitly assumed in Savage’s analysis, then the states s 2 and s 3 are inherently inconsistent, and the only remaining states are s 1 and s 4, in which the two inspection methods agree. These states are, respectively, the good and rotten states in Savage’s analysis. Notice, however, that according to Savage’s analysis it is the observer who decides whether or not the inspections are perfect, and the observer’s perception determines the state space. By contrast, according to the approach advocated here the decision maker determines whether or not the inspections are infallible (that is, whether or not the event E = {s 2, s 3} is null). Consequently, the state space is conceptualized by the decision maker and reflects his understanding of the environment.
2.5. Expansion and contraction of the state space
An important advantage of the approach taken here is the flexibility it affords in allowing the state space to be redefined and expanded when new basic actions and/or consequences are discovered or the understanding of the links connecting actions and consequences is modified.Footnote
10
Karni and Vierø (Reference Karni and Vierø2013, Reference Karni and Vierø2015a, Reference Karni and Vierø2015b) exploited this advantage to model reverse Bayesianism and decision makers’ anticipation of discovery of consequences that, in their current state of ignorance, they cannot imagine and may even lack the language to describe.Footnote
11
More specifically, the discovery that a basic action, say a ∈ A, resulted in an unfamiliar consequence
$ \hat{c}\notin C$
requires a redefinition of the state space. Formally, let
$ \hat{C}=C\cup \lbrace \hat{c}\rbrace ,$
then the new, expanded state space is
$\hat{C} ^{A}.$
Similarly, the introduction and/or discovery of a new basic action
$ \hat{a}\notin A,$
for instance, taking an additional measurement of a natural phenomenon or the invention of a new financial asset (e.g. options) requires the redefinition of the state space. Formally, let
$\skew8\hat{A}=A\cup \lbrace \hat{a}\rbrace ,$
then the new state space is
$C^{\skew8\hat{A}}.$
It is worth emphasizing that while
$\hat{C}^{A}$
constitutes a genuine expansion of the state space, CA
,
$C^{\skew8\hat{A}}$
is a refinement of CA
. Put differently, the event
$\hat{C}^{A}\backslash C^{A}$
is constituted of states
$s\left( a\right) =\hat{c},$
for some a ∈ A, that were not part of the description of the original state space. By contrast, if
$\hat{a}$
may be associated with all the consequences in C, corresponding to each state, s, in the original state space, CA
, there is an event E(s) ≔ {Π
a ∈ A
s(a) × c∣c ∈ C} in the state space
$C^{\skew8\hat{A}}.$
Thus, the state space
$C^{\skew8\hat{A}}$
is a uniform refinement (filtration) of the original state space CA
. The sets E(s), s ∈ S, described above constitute a partition of the state space
$C^{\skew8\hat{A}}.$
Our approach to modelling the state space avoids pitfalls in the analysis of decision making under uncertainty. For instance, Ahn and Ergin (Reference Ahn and Ergin2010) present a model in which the choice set consists of acts that are measurable with respect to partitions, interpreted as alternative descriptions of a fixed underlying state space. According to them, preference relations over measurable acts are partition dependent. They invoke the notion of filtration (that is, a uniform refinements of the partition of the state space) and gradual filtration (that is, a refinement of a partition that does not split all the non-null cells of the original partition).Footnote 12 In terms of the approach presented here, every basic action, a, induces a partition of the state space CA defined by {a −1(c)∣c ∈ C}. Viewed in this way, the descriptions of the state space have concrete meanings – namely, they are the consequences of the basic actions. Moreover, filtration corresponds to refinements of the space in the wake of discovery of new basic actions. However, gradual filtration is inconsistent with either the discovery of a new basic action or that of new consequences. This raises the following question: How, and in what language, is the gradual filtration described?
2.6. Subjective states and coarse contingencies
Kreps (Reference Kreps1979, Reference Kreps, Dasgupta, Gale, Hart and Maskin1992) introduced the notion of subjective state space derived from preferences over menus displaying ‘preference for flexibility’. According to Kreps, subjective states are resolutions of the uncertainty regarding choices from menus (that is non-empty sets of alternatives) having the interpretation of preference relations on alternatives in the menus.
The approach of this paper can be applied to the definition of subjective state space as follows: Analogous to the set of consequences is a finite set, F, of alternatives. Corresponding to basic actions are non-empty subsets of F, dubbed menus.Footnote
13
Menus are analogous to basic actions. Let
${\cal M}_{F}$
denote the set of all menus consisting of elements of F. By definition, the set of alternatives in each menu is the set of feasible consequences given the basic action represented by that menu. The subjective state space induced by
${\cal M}_{F}$
is the set of mappings
$\Omega _{F}:=\lbrace \omega :{\cal M}_{F}\rightarrow F\mid \omega \left( M\right) \in M,\forall M\in {\cal M}_{F}\rbrace$
.Footnote
14
If alternatives are observable (that is, agreed upon by distinct observers), then the derived state space is objective and determined independently of the preferences of the decision maker.
In general, the states in Ω
F
do not correspond to complete and transitive preference relations and are therefore of little interest. However, suppose that there is a choice function
$c:{\cal M}_{F}\rightarrow {\cal M}_{F}$
(that is, c(M)⊆M, for all
$M\in {\cal M }_{F})$
that satisfies the weak axiom of revealed preference (that is, for any pair f, f′ ∈ F and
$M,M^{\prime }\in {\cal M}_{F},$
if f, f′ ∈ M∩M′, f ∈ c(M) and f′∉c(M), then f′∉c(M′)). It is easy to show that if ω(M) ∈ c(M) then each state correspond to a complete and transitive preference relation, ≽ω on F, and that c(M) = {f ∈ M∣f≽ω
f′ for all f′ ∈ M}.Footnote
15
Moreover, if f, f′ ∈ c(M)∩c(M′) for some
$M,M^{\prime }\in {\cal M }_{F}$
then the preference relation corresponding to the states ω, ω′ ∈ Ω
F
such that ω(M) = f, ω(M′) = f′, ω′(M) = f′, ω′(M′) = f and ω(M′′) = ω′(M′′), for all
$M^{\prime \prime }\in {\cal M}_{F}\backslash \lbrace M,M^{\prime }\rbrace ,$
satisfy ≽ω = ≽ω′. Hence, multiple states may be equivalent in the sense of corresponding to the same preference relation. By definition, equivalent states assign to different menus indifferent alternatives.
This approach to defining subjective state spaces may be useful for interpreting some results in the literature. In particular, Epstein et al. (Reference Epstein, Marinacci and Seo2007) present axiomatic models based on menu choice with coarse contingencies. In their models, contingencies are subjective states and coarse contingencies are events in this space. According to them a decision maker might be aware of her inability to describe in detail all the contingencies that may affect her ex post behaviour (that is, choice from a menu). In terms of our definition of the state space, coarse contingencies arise when the decision maker neglects to consider certain menus in
${\cal M} _{F}$
when constructing the subjective state space. Put differently, the decision maker considers only menus in a subset
${\cal M}\subset {\cal M} _{F}$
and defines the state space
$\Omega =\lbrace \omega :{\cal M}\rightarrow F\mid \omega \left( M\right) \in c\left( M\right) ,\forall M\in {\cal M}\rbrace $
on the restricted domain. If the decision maker knows F and hence possesses all the information necessary to construct the entire state space, then the coarseness may be attributed to implicit cost associated with the complexity of detailed depiction of the entire state space. The decision maker is aware of, voluntarily, acting on the basis of incomplete articulation of the relevant alternatives to form the full set of contingencies.
An alternative interpretation of coarseness is that the decision maker is aware of only a proper subset of the alternatives known to the modeller. This interpretation can be related to the effect of discovery of new alternatives. If a decision maker becomes aware of a new alternative,
$\skew3\bar{f },$
then the set of menus becomes
${\cal M}_{F^{\prime }},$
where
$F^{\prime }=F\cup \lbrace \skew3\bar{f}\rbrace .$
The subjective state space induced by
${\cal M} _{F^{\prime }}$
is
$\Omega _{F^{\prime }}=\lbrace \omega :{\cal M}_{F^{\prime }}\rightarrow F^{\prime }\mid \omega \left( M\right) \in c\left( M\right) ,\forall M\in {\cal M}_{F^{\prime }}\rbrace .$
Note that Ω
F
⊂Ω
F′. Thus, Ω
F′ represents a refinement of the original subjective state space, as the new alternative expands the domain of the definition of states. Each state or preference relation in Ω
F
, constitutes an event in the new state space consisting of states that agree on
${\cal M}_{F}$
and differ in the set of subset menus
$\lbrace \skew4\bar{M}\in {\cal M}_{F^{\prime }}\mid \skew4\bar{M}=M\cup \lbrace \skew3\bar{f} \rbrace ,M\in \Omega _{F}\rbrace .$
Interpreting states as preference relations that satisfy the weak axiom of revealed preference, the refinement of the state space due to discovery of new alternatives does not affect the preference relations derived from the menus in
${\cal M}_{F}$
. Consequently, it has no implication for models of menu choice.
3. THE CHOICE SET
3.1. Grand world, small worlds
Two different approaches can be used to model decision making under uncertainty. The first approach envisions a framework that includes the set of all basic actions and the corresponding feasible consequences to construct a grand state space along the lines described above. According to this approach, decision makers entertain beliefs about the likely realizations of the events (subsets) of this grand state space and act on these beliefs when facing specific decisions. This approach imposes consistency of beliefs across decision problems.
According to the second approach, when facing specific decision problems, decision makers construct the relevant ‘small world’ state space by listing the relevant basic actions and consequences and defining the relevant states to be the mapping from the set of relevant basic actions to the set of relevant feasible consequences. This approach does not require that a decision maker’s beliefs across decision problems be consistent.Footnote 16
The two approaches to formulating the decision problem are essentially the same. The difference is the definition of the relevant primitive sets of basic actions and consequences.
3.2. Feasible and conceivable acts
Once the state space is fixed, the choice set may be defined. In Schmeidler and Wakker (Reference Schmeidler, Wakker, Eatwell, Milgate and Newman1987); Karni and Schmeidler (Reference Karni, Schmeidler, Hildenbrand and Sonnenschein1991); and Karni and Vierø (Reference Karni and Vierø2013, Reference Karni and Vierø2015a, Reference Karni and Vierø2015b), the choice space consists of the original basic actions and the set of conceivable acts (that is, all the mappings from the set of states to the set of feasible consequences). As Gilboa and Schmeidler (Reference Gilboa and Schmeidler1995) note, the cardinality of the set of conceivable acts is twice that of the basic actions.Footnote 17 Since subjective expected utility theory requires that decision makers be characterized with complete preference relations on the set of conceivable acts (whereas, in practice they may choose only among the basic actions) the preference relations in subjective expected utility theory are inherently hypothetical. This is ‘a far cry from the behavioral foundations of Savage’s original model’ (Gilboa and Schmeidler Reference Gilboa and Schmeidler1995: 626). According to Gilboa (Reference Gilboa, Pestlewaite and Schmeidler2009) this is a problem. ‘But the problem we encounter here is that the choice between elements of F (the set of conceivable acts) cannot be observable in principle.’ (Gilboa Reference Gilboa, Pestlewaite and Schmeidler2009: 116).Footnote 18 The view expressed here is different, allowing the determination of subjective probabilities without requiring the elicitation of preferences among hypothetical conceivable acts. Perhaps the best way to illustrate this is to consider betting on the outcome of a horse race.
Taking the small world approach, suppose, for the sake of simplicity of exposition, that two horses enter the race, Incumbent and Challenger and that there are three possible outcomes: o 1 (Incumbent wins), o 2 (Challenger wins), and o 3 (dead heat). The relevant set of basic action is a singleton {a}, ‘running the race between Incumbent and Challenger’. Let the set of relevant consequences consist of the outcomes of the race, O = {o 1, o 2, o 3} and a subset I of the reals representing monetary payoffs (that is, C = O∪I). Because elements of I are not associated with a, the set of feasible consequences associated with a is C(a) = O. Hence, according to our approach, the parsimonious state space consists of three states, S = {o 1, o 2, o 3}.
Conceivable acts include all the mappings from S to O∪I. Some conceivable acts are hypothetical. For instance, the conceivable constant act whose image is o 1 has the interpretation of running a race under the condition that Challenger cannot possibly win. By contrast, conceivable acts whose payoffs are sums of money (that is, elements of I) are feasible. They correspond to betting on the outcome of the horse race. For example, the conceivable act that pays off x ∈ I if o 1 obtains, y ∈ I if o 2 obtains, and 0 otherwise, where x > 0 > y, has a concrete meaning – namely, a bet on Incumbent winning the race. More generally, the set of bets B ≔ {b: S → O∪I∣b(s) ∈ I, ∀s ∈ S} is a subset of the set of conceivable acts that is feasible .Footnote 19 The proposals of Borel (Reference Borel, Kyburg and Smokler1924) and Ramsey (Reference Ramsey, Braithwaite and Plumpton1926) are naturally applicable in this setting.
In some situations, decision makers can contemplate choosing simultaneously a basic action and a bet. Hence, the conceivable choice set,
${\mathbb {C}} :=\lbrace \left( a,b\right) :S\rightarrow O\times I\mid \left( a,b\right) \in A\times B\rbrace$
, where A denotes the set of relevant basic actions and B is the corresponding set of bets, is the set of conceivable act-bet pairs that map the state space S to the product set O × I. For example, facing the prospect of an approaching hurricane, a decision maker may choose among basic actions, such as boarding up his house, or moving to a shelter, to minimize the potential damage and, simultaneously, take out insurance. The potential damages represent the observable outcomes of the basic actions and the insurance policies are bets.Footnote
20
3.3. The separation of states and consequences
A crucial aspect of Savage’s (Reference Savage1954) model is the separation of tastes and beliefs. The valuation of the consequences (that is, tastes) is independent of the events in which they are affected, and the assessment of the likelihoods of events (that is, beliefs) is independent of valuation of the consequences assigned to them. This separation is not always natural, however, and in some important situations states and consequences are confounded and the preference relation is not state independence.
Consider, for example, the following situation, described by Aumann in a letter to Savage dated January 1971.Footnote 21 A man’s love for his wife makes his life without her ‘less ‘worth living’’. The wife falls ill. To survive, she must undergo a routine but dangerous operation. The husband is offered a choice between betting $100 on his wife’s survival or on the outcome of a coin flip. Even supposing that the husband believes that his wife has an even chance of surviving the operation, he may still rather bet on her survival, because winning $100 if she does not survive is ‘somehow worthless’. Betting on the outcome of a coin flip, the husband might win but not be able to enjoy his winnings because his wife dies. In this situation, argues Aumann, Savage’s notion of states (that is, whether the wife is dead or alive) and consequences are confounded to the point that there is nothing that one may call a consequence (that is, something whose value is state independent).
In his response, Savage admits that the difficulty Aumann identifies is indeed serious. In defence of his model, Savage writes, ‘The theory of personal probability and utility is, as I see it, a sort of framework into which I hope to fit a large class of decision problems. In this process, a certain amount of pushing, pulling, and departure from common sense may be acceptable and even advisable. . . . To some – perhaps to you – it will seem grotesque if I say that I should not mind being hung so long as it be done without damage to my health or reputation, but I think it desirable to adopt such language so that the danger of being hung can be contemplated in this framework’ (Drèze Reference Drèze1987: 78). To the specific example of Aumann, Savage responds, ‘In particular, I can contemplate the possibility that the lady dies medically and yet is restored in good health to her husband’ (Drèze Reference Drèze1987: 80). The presumption that decision makers engage in such mental exercises when making decisions seems farfetched.
The source of the problem is the formulation of the state space. Both Aumann and Savage take for granted that there are two states, the wife lives and the wife dies. However, because the wife’s death affects the husband’s well-being, it is also a consequence. It is the double role of the wife’s health that confounds states and consequences. This problem can be avoided if the states space is defined using the approach outlined above.
In the scenario described by Aumann, there are two basic actions (undergo surgery, a 1, and avoid surgery, a 2) and two feasible consequences (the wife lives, c 1, and the wife dies, c 2). (Note that C(a 1) = C(a 2) = {c 1, c 2}.) They generate four states:
If the husband believes that if his wife is to survive she must undergo the operation (that is, the husband believes that a 2 must necessarily result in c 2) then for him the event {s 1, s 3} is null.
In this context, the constant act that yields the outcome ‘the wife lives’, c 1, in every state amounts to conceiving a medical procedure, not currently available, that is guaranteed to save the wife’s life. Denote this conceivable treatment by a 3 and suppose that C(a 3) = {c 1}. Augmenting the depiction of the states by adding the consequence of this conceivable constant act yields s 2 = (c 1, c 2, c 1) and s 4 = (c 2, c 2, c 1). The state s 4 is a description of a situation in which the wife would die under all currently available treatments but not under treatment a 3. Savage’s statement ‘I can contemplate the possibility that the lady dies medically and yet is restored in good health to her husband’ is problematic, because if the outcome ‘the wife dies during the operation’ is a state of nature, then the constant act that delivers the consequence c 1 (the wife lives) must be possible in the state in which she is dead, which is absurd. However, according to the approach advanced here, the same statement translates into ‘I can contemplate the possibility of a treatment that would restore the wife in good health to her husband in circumstance in which she would have died under the currently available treatments’. This statement, far from being absurd, is quite conceivable.
Consider next the husband’s betting decision. The availability of a coin flip, f, introduces another basic action and two new feasible consequences, ‘heads up’ (denoted H) and ‘tails up’ (denoted T). Betting also requires monetary payoffs. For simplicity assume that the set of monetary payoffs is a doubleton M = {$0, $100}. This modification requires the expansion of the state space. Since C(f) = {H, T} , the relevant set of consequences is C = C(a 1)∪C(a 2)∪C(f)∪M. Since M and C(a 1)∪C(a 2)∪C(f) are disjoint, the parsimonious state space consists of four states: s 2H = (c 1, c 2, H), s 2T = (c 1, c 2, T), s 4H = (c 2, c 2, H) and s 4T = (c 2, c 2, T).
Bets are conceivable acts: ‘bet on heads’ (denoted b 1) and ‘bet on tails’ (denoted b 2). The bet b 1 pays off $100 in the event H ≔ {s 2H , s 4H } and $0 in the event T ≔ {s 2T , s 4T }. A bet on the survival of the wife, b 3, pays off $100 in the event E 2 ≔ {s 2H , s 2T } and $0 in the event E 4 ≔ {s 4H , s 4T }. In other words, betting on the wife’s survival is betting that the operation succeeds. Since the husband’s evaluation of the monetary payoff is not independent of whether the wife is dead or alive, according to the traditional approach, the preference relation does not satisfy state independence. By contrast, under the approach advanced here the husband can contemplate such a bet even if he does not choose a 1. For example, the husband can conceive of choosing simultaneously the imaginary treatment a 3 and the aforementioned bet. If the husband imagines choosing (a 3, b 1) ∈ A′ × B, then the consequences that would have followed are the payoff (c 1, $100) in the event H and the payoff (c 1, $0) in the event T.Footnote 22 Similarly, imagining choosing (a 3, b 3) would pay off (c 1, $100) in the event E 2 and (c 1, $0) in the event E 4. Thus, the consequences of both bets are identical. Therefore, if the husband is an expected utility maximizer and believes that an operation has an equal chance of succeeding or failing, he is indifferent between betting on the outcome of the coin flip and betting on the success of the operation. Thus, the approach to the construction of the state space advanced here disentangles states and consequences and lends credence to the supposition that the preferences display state independence.
However, the elicitation of the husband’s beliefs is a thought experiment whose outcome hinges on a bet the payoff of which depends on the outcome of the act a 1 when a 3 is supposed to be implemented. If the implementation of the imaginary medical treatment a 3 precludes the implementation of a 1, then the scenario described above is inherently hypothetical, hence such a bet cannot possibly be settled in practice. The conclusion requires the admission of preferences over hypothetical choices expressed verbally admitting preferences over counterfactuals. This departure from the revealed preference methodology raises methodological issues that cannot be addressed here. I conclude, therefore, by restating Savage’s position on this issue: ‘There is a mode of interrogation between what I called the behavioral and the direct. One can, namely, ask the person, not how he feels but what he would do in such and such situation. In so far as the theory of decision under development is regarded as an empirical one, the intermediate mode is a compromise between economy and rigor. But in the theory’s more normative interpretation as a set of criteria of consistency for us to apply to our decisions, the intermediate mode is just the right one’ (Savage Reference Savage1954: 28).
4. CONCLUDING REMARKS
This paper presents an approach to modelling states of nature as functions from a set of basic actions to feasible consequences and examines its implications for the specification of the choice set in the theory of decision making under uncertainty. The key idea is that the events (subsets of the state space) must be verifiable so that bets placed on the realization of events can be settled. The advantage of this approach is illustrated by examples of pitfalls its adoption helps sidestep and the flexibility it affords in expanding and refining the state space in the wake of discovery of new consequences and/or basic actions.
According to this approach, insofar as choice-based decision theory is concerned, events such as ‘it will rain tomorrow in Baltimore’ or ‘Incumbent wins the horse race’ are defined by their manifested effects. These effects include, in the former instance, the measured quantity of rainfall in Baltimore tomorrow and, in the latter instance, Incumbent being the first horse to cross the finish line. The subjective probabilities of these events can be readily inferred from the odds a decision maker is willing to offer when betting on these events, depicted by the aforementioned measurements and/or observations, or by applying one of the procedures for probability elicitation (e.g. Karni Reference Karni2009) to these measurement.
One-time events are extreme examples of a dynamic outlook expressed in the dictum of Heraclitus of Ephesus ‘No man ever steps in the same river twice’. The idea of measuring the degree of belief in the likely realization of such events by subjective probabilities might seem to defy the scientific exigencies of revisiting the same event repeatedly under similar, if not identical, conditions. This observation raises concerns regarding the appropriateness of invoking the notion of a state space in a theory dealing with choice behaviour in the face of one-time events.
At one extreme, defining the state-space as sequences of repeated measurements of natural phenomenon, such as the temperature at a given place during the same day every year, corresponds to the scientific notion of repeated observations under the similar conditions. Assessing probabilities on such states comes close to calculating relative frequencies, which has the flavour of objectivity. At the other extreme, the issue becomes problematic when the states space corresponds to the possible outcomes of the next presidential election in the United States, as measured by the vote of the electoral college. This is a one-time event that, by definition, does not allow for repeated observations under similar conditions. Nevertheless, when facing investment decisions whose consequences are contingent on who is the next president of the United States, decision makers must evaluate the alternative courses of action based on their degree of belief in outcome of the presidential election.
Arguably, the analytical framework described here is more readily applicable to the case of repeated measurements than to the modelling of the uncertainty associated with one-time events.Footnote 23 Yet it is not only conceivable but actually possible to bet on the outcome of the next US presidential elections in the same way one bets on the outcome of the roll of a die. The odds offered allows an assessment of the subjective probabilities of the underlying events. These personal assessments need not converge. Nevertheless, the procedure is not scientifically vacuous. First, if the behavioural underpinnings, depicted by the axioms, are common in many decisions, one may still use the theory to make predictions. Second, the elicited personal beliefs, using well-established procedures, can be confronted with the odds a decision maker is ready to offer when betting on a particular one-time event, thus providing a test of the consistency of choice behaviour governed by beliefs. Third, combining the elicited probabilities with updating rules (e.g. Bayes, rule), the theory may be tested by the validity of its predictions of choice behaviour contingent on the acquisition of new information.
ACKNOWLEDGEMENTS
Part of this work was conducted during my visits to EIEF, Rome and the Berglas School of Economics at Tel Aviv University. I am grateful to both institutions for their support and hospitality. I am also grateful to Jean Baccelli, Richard Bradley, Itzhak Gilboa, Marco Mariotti, Peter Hammond, Zvi Safra, Marie-Louise Vierø and an anonymous referee for their useful comments and suggestions.
