3.1. Explanation

Individuals choosing terms in the social contract have preferences over a set of moral or political rules, each representing a lottery over particular policy decisions or operational outcomes. The term ‘rule’ here is used very loosely, as a stand-in for whatever it is – institutions, moral principles, distributional shares, etc. – that the contractarian theorist posits as the object of choice. A ‘rule’ may even be a whole system of rules.^{Footnote 17} In order to determine which moral-political rules to support at the contractual stage, individuals must make predictions that map these rules to actual outcomes. Social science, especially its models of how individuals behave under varying rules or institutions, bridges this gap between abstract rules and concrete outcomes. Given that social science provides imperfect guidance, these models and their predictions will also be imperfect. Individuals will face social-scientific uncertainty. They will not choose outcomes, but lotteries over outcomes.^{Footnote 18} This is not to assert that moral-political rules operate in a probabilistic or indeterminate way. The reason that agents view moral-political rules as lotteries is purely subjective: agents, even utilizing the best social-scientific theory available, are unsure how a given moral-political rule will operate or exactly which outcome(s) it will produce. This is true even if the outcomes arise in a purely deterministic manner once the rule has been chosen and implemented.

Figure 1 depicts the nature of choice in the social contract. Individuals evaluate some rule, ${r_i}$ , by considering the value of the outcomes, ${o_1}, \ldots ,{o_j}$ that it might produce and the probability that it will produce these outcomes.^{Footnote 19} Social-scientific uncertainty appears in the gap between each rule, ${r_i}$ , and the various outcomes, ${o_1}, \ldots ,{o_j}$ that it may give rise to – hence the dotted lines in Figure 1. Under the condition of perfect certainty, $j = 1$ and the probability of ${o_j}$ , is equal to 1. Under the condition of social-scientific uncertainty, the value of ${r_1}$ , for example, would be its expected utility: ${p_1}u({o_1}) + {p_2}u({o_2}) + ... + {p_k}u({o_k})$ , where ${p_i}$ is the probability that outcome ${o_i}$ comes about, and $u({o_i})$ is the evaluation of that outcome.

Figure 1. Subjective Uncertainty in the Social Contract.

One barrier to consensus that I wish to set aside is disagreement as to which final outcomes are most desirable. The Agreement Model aims to show that unanimous agreement leads to unsatisfactory results. Granting that parties agree as to which results they want is both charitable and simplifying – charitable in that it allows us to eliminate a serious barrier to achieving satisfactory results; simplifying in that it allows us to isolate a different, epistemic source of poor outcomes. Moreover, certain contractarians have explicitly sought to ‘normalize’ preferences in just this way.^{Footnote 20} So, if the analysis provided here did not grant this assumption, it might fail to apply to these variations of contractarianism.^{Footnote 21} One plausible way, though certainly not the only way, of understanding this concurrence on the value of final outcomes, is to suppose that such outcomes receive a utility score corresponding to their impact on the well-being of the average individual. This would be the case if, for example, social-scientific uncertainty were so great that individuals could not predict with any accuracy the effect of a policy on any particular person, themselves included. In this case, all individuals would have identical preferences over the final outcomes because they evaluate these outcomes according to how they impact the average individual. Crucially, even in this extreme case, identical preferences over final outcomes do not imply identical preferences over rules or institutions. Although decision-makers may identically rank the final outcomes, or perhaps even lower-level political choices, they may still differ as to the probabilities they assign to each outcome. Disagreement may result from different predictions as to (i) the impact of a lower-level collective choice or (ii) the probability of various lower-level collective decisions following the selection of a moral-political rule at the contractual stage.

This predictive disparity can persist even if all decision-makers have the same exact information – so long as that information is not fully adequate to make accurate predictions. As James Buchanan and Roger Faith have argued, if the given information is insufficient to establish a uniquely reasonable probability distribution over specific outcomes, then subjective differences between individuals will lead to divergent predictions, even if all individuals possess the same (incomplete) information:

Importantly, this implies that no amount of deliberation and discussion, insofar as this merely involves the exchange of information, will lead to a convergence of preferences over rules.^{Footnote 22} This result, theoretically grounded in the mathematics of Bayesian belief formation, is also corroborated empirically: our best social scientists exhibit vehement disagreement when it comes to future predictions.^{Footnote 23} If the information possessed, even once aggregated and disseminated, is insufficient to make definite predictions or to determine a uniquely reasonable probability assignment, then subjective differences will generate diverse preferences – not over final outcomes, but over moral-political rules, chosen at the contractual level. Thus, despite having identical preferences over final outcomes, individuals will assign different expected utility to the rules under consideration. In other words, the same moral-political rule will represent a different lottery to each individual. The lottery differs, not in virtue of the desirability of the final outcomes that might occur if it is chosen, but rather in virtue of assigning different probability to the occurrence of those outcomes.

In virtue of individuals’ homogeneous preferences over final outcomes, the model is free to treat the goodness or badness of each moral-political rule – considered in terms of its outcome and not as an object of choice – as an objective fact. There are two important facts to bear in mind here. First, individuals assign different subjective probability to the final outcomes possible under different rules, but it remains the fact that different rules will lead to one final outcome (or, perhaps, generate an objective probability distribution over final outcomes) independent of the subjective beliefs of agents. Thus, the model treats moral-political rules as lotteries when they are objects of choice, but this does not imply anything about the internal structure or the functioning of such rules in an objective sense. Such rules may produce outcomes that are objectively good or bad, even though subjective beliefs lead to differing expectations and conflicting choice behaviour on the part of agents. Second, for contractarians, the goodness or badness of such rules will depend only on the preferences of decision-makers over the final outcomes, i.e. the actual impact on individuals that will result from the selection of that rule. The ‘objective’ goodness or badness of a contractually chosen rule depends on the homogeneous preferences of individuals over the final outcomes and not on some objective standard of correctness. This is crucial, since positing some independent standard of good and bad would violate the contractarian’s commitment to deriving normative standards solely from instrumental rationality.^{Footnote 24} Also important is the fact that the Agreement Model does not specify exactly how utilities defined over outcomes (not expected utilities) map onto goodness or badness. There are multiple ways to define this relationship – e.g. a good rule is the one that maximizes outcome utility within the budget set – but the Agreement Model leaves the details of this relationship undefined so as to achieve maximal applicability to various contractarian models. These models may posit different relationships between individual preferences and social optimality. The Agreement Model need not choose one specification of this relationship, but should remain consistent with as many such specifications as possible.

With this framework in place, the details of the Agreement Model can now be considered. In determining the terms of their social contract, individuals evaluate one rule at a time, deciding whether to accept or reject it. They each have some prediction, a private signal, as to whether the rule is good or bad – i.e. whether its final outcome produces a high or a low average payoff.^{Footnote 25} Since individuals choose under conditions of social-scientific uncertainty, their predictions as to whether a rule is good or bad will differ, even while their preferences over final outcomes remain identical – allowing for the ‘objective’ goodness or badness of the rule. Charitably, the model assumes that predictions are reasonably accurate. That is, every individual’s prediction of the objective goodness or badness of a constitutional rule – its impact on the utility of the average individual – is more likely to be correct than incorrect. After determining whether the rule is more likely to be good or bad, each individual makes a decision: accept or reject. Since unanimity is the condition for group acceptance at the contractual level (section 1), each individual has the ability to veto any rule by choosing to reject it.

Models of naïve choice within groups assume that an individual will observe his or her private signal (i.e. prediction) as to whether the rule is good or bad and then choose in accordance with that signal.^{Footnote 26} Call this informative choice. This behavioural assumption fails to capture the additional information that an individual gleans from the choice behaviour of others. It also fails to capture considerations of how an individual’s choice will actually affect that individual’s payoff. We thus require a more sophisticated version of rational choice within groups. Consider, as an alternative, what we may call Bayesian choice. Bayesian choice differs from informative choice in two related ways. First, the decision-maker updates her beliefs or predictions based on the assumption that she is pivotal. This aspect of Bayesian choice incorporates the core contribution of this paper, i.e. the inclusion of rational belief formation in the contractarian model. Second, the decision-maker restricts her focus to pivotal choices, that is, to situations where her choice actually impacts the group choice. This follows simply from expected utility maximization, since a non-pivotal choice for player i, by definition, makes no difference to the group choice or to player i’s payoff. Under a unanimity rule, player i’s choice is not pivotal whenever some player $j \ne i$ has chosen to reject the rule. By contrast, player i’s choice is pivotal when, and only when, all other players have chosen to accept the rule change. In that scenario an individual finds herself in a position characterized by power and information: power, since her choice determines whether the rule passes or whether it is rejected, and information, since she may now assume that all others have chosen to accept the rule as good. Outside of such a scenario, on the other hand, her choice makes no difference whatsoever to her payoff, since it will not affect the group’s choice.^{Footnote 27}

The key feature of the pivotal choice situation, the feature which affects the choice calculus of the individual by providing additional information for belief formation, is the fact that every single other individual has chosen to accept the rule. An individual who finds himself in the position of a pivotal chooser must therefore ask himself: ‘What information can I glean from the fact that every single other individual has chosen to accept this moral-political rule?’

To better understand this situation, consider the famous Asch Conformity Experiment, in which Solomon Asch studied the tendency to conform one’s beliefs to those of the group. In this experiment, eight individuals were lined up in order to conduct a ‘vision test’ in which each would announce which of three displayed lines – A, B or C – matched the length of a fourth line, the ‘target line’ (see Figure 2).

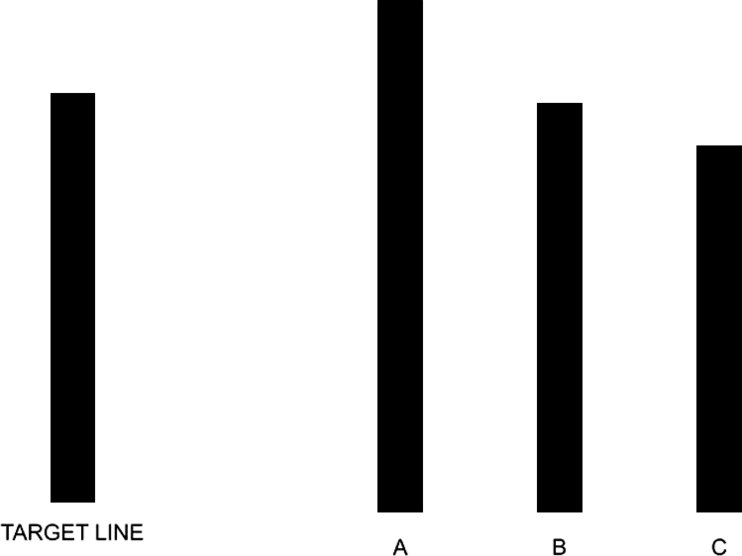
Figure 2. Asch’s Lines.

Unbeknownst to the eighth individual, the other seven were confederates of the experimenter, who told them to give an incorrect, though uniform answer. A shocking 37% of subjects ended up mirroring the obviously incorrect judgement of the seven confederates, even though fewer than 1% of subjects gave incorrect responses when choosing alone (Asch Reference Asch and Guetzkow1951).

Many interpret this experiment as a cautionary tale against the distorting influence of peer pressure and the tendency towards group conformity. This may very well be the correct interpretation of the results. For the purpose of understanding the model presented in this paper, however, consider another, less pessimistic interpretation: the judgements of other individuals provide additional evidence to the experimental subject. Under the assumption that the other individuals in the room are fellow test subjects, honestly attempting to report the evidence of their senses, their answers provide additional information to the eighth person. Because one’s senses are imperfect and sometimes misleading, it seems wise to grant evidential weight to the perceptual judgements of others. In fact, as a general principle, when determining the correct answer to a question, it is usually rational to consider both one’s personal belief and the expressed beliefs of others. When these judgements diverge, it becomes necessary to compare the likelihood that one’s belief is erroneous to the likelihood that the expressed beliefs of the others are erroneous. For a significant number of Asch’s subjects, the first likelihood seemed greater.^{Footnote 28}

In precisely the same way, individuals in the Agreement Model must decide (when pivotal) whether their signal is more likely to be in error, or whether the choices of every single other member of the group are likely to be in error. Only if the latter is more likely, only if the choices of every single other member of the group are more likely to be erroneous, will the pivotal individual choose according to her private signal. That is, choosing informatively, according to one’s private signal, will be the optimal strategy only when one’s private signal is less likely to be erroneous than the choices of every other member of the group.^{Footnote 29}

A misunderstanding often arises here concerning the information the pivotal player receives from his or her pivotal position. It is not as if some special player gets to choose last, while all the other players must choose beforehand, revealing their choices; nor is it that the other players credibly divulge to some unique pivotal player how they plan to choose. Instead, each player, in determining his or her strategy, considers only the scenario where he or she occupies a pivotal position. No other possible scenario, regardless of how likely it may be, is relevant for deciding how to choose, since no possible scenario except for that in which the player is pivotal affords the player an opportunity to affect the outcome. Choice in the agreement model may therefore be instantaneous, and prior communication as to how each agent plans to vote is unnecessary (though permitted). Each agent simply restricts her attention to the pivotal position and, accordingly, updates her beliefs conditional upon occupying that position.

The complexity of group choice, and the consequent need to rely on a mathematical model rather than intuition, becomes clear when we note that all individuals in the group will reason similarly. In consequence, no individual, even when pivotal, can take for granted that the choices of other individuals reveal their private signals – for other individuals are also Bayesian choosers, considering only the situation in which they are pivotal and basing their choice on the information implicit in that situation. Nevertheless, their choice does provide some information about their private signal. The extent to which it does so and how this information should affect the updated beliefs and choice behaviour of a given decision-maker must be investigated in the formal version of this model (sections 3.2–3.4). Intuition has led us to see that individuals may not vote informatively when they seek to maximize expected utility and when they take the choices of others as providing new information. But beyond this insight, intuition leaves us grasping, and further progress requires formal deductions.

In the following subsections, these deductions will demonstrate that informative choice does not (generally) emerge as a Nash equilibrium in the model.^{Footnote 30} In fact, there is only one responsive, symmetric Nash equilibrium. This equilibrium is derived by assuming that individuals apply Bayesian belief updating to their prior beliefs (their initial signals), conditional on being pivotal. This equilibrium, unfortunately, has a very undesirable property: a high prevalence of accepting bad rules. In statistical terms, type-1 error, consisting of ‘false positives’, is rampant. The group frequently chooses rules that no member of the group wants.

If this model accurately represents contractarian choice, then the hypothetical contracts of contractarian theorists would not, in fact, yield justified decisions. If we find, as our model shows, that the unanimity rule under conditions of uncertainty does not benefit each member of the social group – and in fact benefits no member of the social group – then the justificatory power of the contractarian approach is highly suspect. Aside from the addition of Bayesian belief formation, the model relies only on assumptions, discussed in section 1, that are standard in contractarian models: expected utility maximization, uncertainty and unanimity. Thus, its results appear readily applicable to many, if not all, variants of contractarianism, though this question must be examined further (section 4).

In what follows, the exact specifications of the model are laid out (section 3.2), some of its important features are highlighted (section 3.3), and four propositions are presented with a description of their importance (section 3.4). Proofs of the four propositions, being tedious and unenlightening, are quarantined to the Appendix.

3.2. Set-up

Moving beyond the limits of philosophical intuition requires a formal model. Timothy Feddersen and Wolfgang Pesendorfer have developed a model, originally intended to examine jury decisions, that perfectly captures the epistemic interdependence and strategic behaviour of agents under the unanimity rule.^{Footnote 31} By reinterpreting this model as a contractarian procedure among rational Bayesian agents, the results of Bayesian choice, i.e. of epistemic interdependence and strategic behaviour, can be examined. Rather than jurors, we have parties to the contract; rather than desiring to convict the guilty and acquit the innocent, agents wish to accept good rules and reject bad ones; rather than private signals about the guilt or innocence of a defendant, agents have private (prior) appraisals of the goodness or badness of the rule under consideration. More precisely …

• There are n ‘choosers’: $N = \{ 1,...,n\} $

• There are two possible states of the world, one where the rule being considered is Good, ‘G’ and one where the rule being considered is Bad, ‘B’: $\Omega = \{ B,G\} $

• There are two types of decision-maker, defined by the ‘signal’ they receive about the state of the world (i.e. their best guess about whether the rule is good or bad): ${t_i} \in \{ g,b\} $

  • – g stands for ‘good’, and b stands for ‘bad’

• The signals are more likely to be correct than incorrect, that is:^{Footnote 32} $p = Pr(G|g) = Pr(B|b) \in (0.5,1)$

  • – $Pr(B|g) = Pr(G|b) = 1 - Pr(G|g) = 1 - Pr(B|b) \lt 0.5$

• Decision-makers may either choose to Accept, A, or Reject, R, the rule, or they may randomize:

  • – Pure strategy set: ${S_i} = \{ A,R\} $

  • – Mixed strategy set: $Pr(A,{t_i}) \in {\Sigma _i} = [0,1]$

• The preferences of decision-makers can be represented by utility functions with the following payoffs:

  • – ${U_i}(A,G) = {U_i}(R,B) = 0$

  • – ${U_i}(A,B) = - q;{\kern 1pt} {U_i}(R,G) = - (1 - q)$

  • – Where bold A, R signify that the group has come to that decision (rather than just the individual i) and where $q \in (0,1)$

• The unanimity rule stipulates that bold A is collectively chosen if and only if ${s_i} = A,\forall i \in N$ , and bold R is chosen otherwise (i.e. $\exists j \in N:{s_j} \ne A$ )

3.3. Some important features

A first important feature of the Agreement Model is the individual’s updated belief, call it ‘ $\beta $ ’, that a rule is good upon observing k g-signals. That is, if we imagine that each decision-maker i’s private information were public and that each i could view the signals of every other $j \in N$ what would this generic i believe about the probability of a rule being good or bad? $\beta $ is a function of k, the number of good signals, and n, the number of decision-makers. More specifically, applying Bayes’s rule, we get:

(T) $$\beta (k,n) = \displaystyle{ {[{p^k}{{(1 - p)}^{n - k}}]}\over{[{p^k}{{(1 - p)}^{n - k}}] + [{p^{(n - k)}}{{(1 - p)}^k}]}}$$

with p as defined above (Feddersen and Pesendorfer Reference Feddersen and Pesendorfer1998: 24).

Secondly, Federsen and Pesendorfer note an important threshold (without deriving it):

Lemma. If $q \lt \beta (k,n)$ , then a pivotal chooser will prefer to Accept, rather than to Reject the rule upon viewing k g-signals out of n total signals.

Proof. See Appendix, section 0.□

As defined above (section 3.2), q is a measure of how much decision-makers resent accepting a bad rule. In other words, q is the cost of type-1 error. $\beta $ , on the other hand, measures a decision-maker’s belief that a rule is good. A higher $\beta $ , resulting from the ‘observation’ of more g-signals, means a greater confidence in the goodness of a rule. What our Lemma states is that, for any degree of confidence $\beta $ that a rule is good, there exists some q that makes the decision-maker indifferent between accepting and rejecting the rule. Moreover, if q is higher than this indifference threshold, the decision-maker will reject the rule, while if q is lower than this threshold, the decision-maker will accept it. In other words, for any level of confidence (less than 100%) in the goodness of a rule, type-1 error can be so odious that the decision-maker will choose reject. Or, viewing things from the other axis, q determines a threshold such that, if $\beta $ is greater than q, choosing to Accept is a best-response, while if $\beta $ is less than q, choosing to Reject is a best-response.

In Figure 3, what I call the ‘Threshold of Acceptance’ is given by the line separating a region of acceptance from a region of rejection. This line gives the value of q required to make a decision-maker exactly indifferent between Accepting and Rejecting a rule, given that decision-maker’s posterior belief, $\beta $ .

Figure 3. Threshold of Acceptance.

A final important observation is that it is mathematically possible – for certain parameters n, q, p – for a decision-maker to observe $\left(n - 1\right)$ g-signals (i.e. every other decision-maker thinks it is a good rule), but to still prefer Reject to Accept. In mathematical terms, it is possible that $q \gt \beta (n - 1,n)$ . This will be an important fact for Propositions 1 and 4, laid out in the next subsection.

3.4. Four propositions

The significance of this proposition is that it clears away many of the assumptions that weigh in favour of the unanimity rule. For example, the assumption that a unanimity rule will minimize type-1 errors: the error of accepting a bad rule (a false positive).^{Footnote 33} The unanimity rule does indeed minimize type-1 error in the case of informative choice, where the probability that an accepted rule would be: $Pr(G|A) = {p^n}/[{p^n} + {(1 - p)^n}]$ . In the case of informative choice, we can apply a logic similar to that operating in the Condorcet jury theorem: if $\left(n - 1\right)$ others choose to Accept, then that means that $\left(n - 1\right)$ others received signal g. Since the probability of receiving an accurate signal is greater than the probability of receiving an inaccurate signal, this means that the probability that the rule is genuinely good quickly goes to 1 as n increases. In this case, the best-response of player i is to choose Accept.

Yet, if there is not a direct link between the choices of other players and the signals that they have received, then the connection between player i’s best-response and the choices of other players is not so straightforward. In particular, if those other decision-makers are not choosing informatively, but as Bayesians, then the information that player i may glean from their choice behaviour depends on how much influence their signals actually have on their actions. It remains to be seen how players will respond to one another in the case of non-informative, i.e. Bayesian, choice. Feddersen and Pesendorfer identify a unique (slightly refined) Nash equilibrium, the formulation of which is stated in their original paper.

Proposition 2. There is a unique, responsive symmetric Nash equilibrium, given by:

(*) $$\sigma _i^*(p,q,n) = {{{{\left( {(1 - q)(1 - p)qp} \right)}^{1/(n - 1)}}p - (1 - p)} \over {{{\left( {p - (1 - q)(1 - p)qp} \right)}^{1/(n - 1)}}(1 - p).}}$$

A responsive equilibrium is one where each decision-maker’s strategy is responsive in the sense that her action changes as a function of the signal she receives. More technically, the probability of choosing Accept, given that one’s signal is g, is not equal to the probability of choosing Accept, given that the signal is b. Restricting our attention to responsive equilibria allows us to rule out equilibria that are unrealistic, definitional oddities. That is, equilibria that satisfy the technical definition of Nash equilibrium without presenting a convincing or interesting representation of human behaviour. For example, it is technically a Nash equilibrium for all individuals to Reject no matter what signal they receive. In such a situation, an individual will never be pivotal, so all actions yield the same payoff. By definition, then, choosing Reject is a best-response (so is choosing Accept).

A symmetric equilibrium is one in which all decision-makers play the same strategy. That is, if two individuals have the same information, then they will choose Accept with the same probability as one another. More technically, $\left({\sigma _i}\left(b\right),{\sigma _i}\left(g\right)\right) = \left({\sigma _j}\left(b\right),{\sigma _j}\left(g\right)\right),\forall i,j \in N$ . The intuition behind symmetry is that identical decision-makers facing identical incentives should choose identical strategies. With identical preferences (assumed throughout), identical priors and identical signals (and hence posterior beliefs), the basis on which we could justify ascribing different actions to such players is unclear. Nevertheless, there are cases where this assumption could break down, and asymmetric equilibria are a real possibility.^{Footnote 34} For the present purpose, however, the existence of a Nash equilibrium that predictably results in high rates of error suffices to establish the main claim: rational belief formation raises issues for contractarian justification. The fact that this Nash equilibrium uniquely satisfies certain intuitive conditions – viz. responsiveness and symmetry – serves to compound this worry.

With responsiveness and symmetry in place, the assumption that $q \lt \beta (n - 1,n)$ implies that we are seeking a mixed strategy profile in which ${\sigma _i}(b) \in (0,1)$ and ${\sigma _i}(g) = 1$ . As shown in the formal Appendix, this is the only Nash equilibrium strategy that emerges under these constraints. For my argument, the importance of this Nash equilibrium lies in its various properties, identified by Feddersen and Pesendorfer. These are laid out in Proposition 3.

For our purposes, this is the central proposition of the model. Surprisingly, unanimous agreement leads to the selection of bad rules, rules that no individual actually wants. Figure 4 illustrates this tendency towards high degrees of type-1 error with some specific parameters. If the models employed by contractarians aim to identify justified rules and if these rules are justified in virtue of their ability to ‘benefit each member of the social group’ (Buchanan and Tullock Reference Buchanan and Tullock2004: 15),^{Footnote 35} then this result poses a problem for contractarian justification. It would seem that unanimous agreement (among uncertain Bayesian decision-makers) does not reliably produce beneficial rule changes. This undermines the contractarian’s claim to have provided a tool for evaluation and legitimation.

Figure 4. Type-1 Error as a Function of n (for parameter $p = 0.75$ ).

Proposition 4 is significant due to the solution it suggests: smaller groups of decision-makers may avoid altogether the appeal of Bayesian choice. Intuitively, this results from the fact that there are not enough other decision-makers to override each individual’s confidence in his or her private information. Even if I suppose that $\left(n - 1\right)$ others Accept, my best response if I think the rule is bad, is to Reject. Due to this fact – i.e. that decision-makers with a b-signal will Reject even when pivotal – informative choice is prescribed by the Nash equilibrium strategy, and type-1 error, though still present, will not rapidly approach high levels, as occurs when Bayesian choice diverges from informative choice.

3.5. Simplifications and limitations of the model

Like all models, the Agreement Model makes a host of simplifying assumptions. It is worthwhile to make these explicit for at least two reasons. First, simplifications can range from clarifying, to innocuous, to misleading. To determine whether a given simplification falls under one of these descriptions requires explicitly identifying it and considering which aspect of the world the scientist aims to model and how the model is meant to illuminate that aspect.^{Footnote 36} To assess the importance of a model’s results, we must determine whether its assumptions, given the model’s purposes, clarify or distort the phenomena it represents. This requires identifying and scrutinizing these assumptions. Second, explicit identification of assumptions facilitates scientific progress by signalling where new models might advance upon old ones. Models rarely, if ever, have the last word on their subjects. New models emerge by modifying, relaxing or abandoning the assumptions of older ones.

Several assumptions of Agreement Model – e.g. expected utility maximization and Bayesian belief updating – have already been discussed (section 1). However, some of these assumptions bear further comment, while others have thus far remained implicit. Before continuing, this section identifies and discusses some of the most conspicuous assumptions of the Agreement Model.

A first assumption worth discussing is that of homogeneous preferences (over final outcomes) among agents in the Agreement Model. This assumption is substantive, and given the recent attention to diversity in social contract theory it may appear controversial.^{Footnote 37} Nevertheless, there are several convincing reasons for accepting the assumption of preference homogeneity in this instance.

The primary justification for this assumption is that preference homogeneity has typically been criticized for trivializing the task of the social contract theorist.^{Footnote 38} In other words, homogeneity makes the contractarian’s job too easy. Since this paper aims to present a problem for contractarianism, it is actually desirable to present a version of contractarianism that is as easy to defend as possible. Homogeneity can thus be viewed as a charitable concession to the contractarian position.

Furthermore, since there are multiple ways in which a contractarian argument might founder, adopting the assumption of preference homogeneity allows us to isolate the particular issue identified in this paper. Disagreement about values in the contractual scenario generates its own issues (Muldoon et al. Reference Muldoon, Lisciandra, Colyvan, Martini, Sillari and Sprenger2014). The present paper, however, wishes to explore a distinct set of problems, arising, not from disagreement about values, but from rational belief formation and strategic choice behaviour.

A third reason for assuming preference homogeneity is the fact that, in many contractarian projects at least, the modelled agents do not know how the chosen rules will affect them as particular individuals. Thus, as Buchanan and Tullock explain, ‘The self-interest of the individual participant … leads him to take a position as a ‘representative’ or ‘randomly distributed’ participant in the succession of collective choices anticipated. Therefore, he may tend to act, from self-interest, as if he were choosing the best set of rules for the social group’ (Buchanan and Tullock Reference Buchanan and Tullock2004: 91). Or as Buchanan put it elsewhere, ‘A person who remains uncertain as to how a particular rule will impact on her own circumstances will be led, through rational choice precepts, to prefer that rule (or principles or set of rules) that will best further the interest of the anonymous member of the group’ (Buchanan Reference Buchanan2002: 489). In light of this, it is plausible to model agents as if they all aim to select rules that will maximize the same set of preferences over final outcomes, i.e. rules that further the interests of the average individual. Disagreements will arise, not over the value of final outcomes, but over which rules will best achieve the desired outcome.

A final point on preference homogeneity: in no way do I wish to argue that preference homogeneity is the only, or even the best, assumption to make for all models or projects. For the reasons enumerated above, however, I do claim that it is defensible and worthwhile to examine the contractarian model under this assumption. It might be valuable to explore the implications of a modified Agreement Model in which agents differ in their evaluations of final outcomes. For example, a model that incorporates ‘noise’ into the signals that agents receive would be an illuminating way of exploring preference diversity. If we consider the main mechanism by which the Agreement Model obtains its result – viz. the informational content of other agents’ choices and the strategic responses to this information – then there is good reason to believe that the result will hold under some amount of preference heterogeneity. As long as preferences are not totally independent, the choice behaviour of other agents will provide information, prompt Bayesian updating, and elicit strategic responses. But this issue should be examined more rigorously. By incorporating rational belief formation into the contractarian model, this paper is novel and exploratory. It thus serves as an invitation for further work, not as a definitive statement on the topic.

A second assumption of the model worth discussing concerns the procedure by which rules are selected. In the Agreement Model, parties consider rules one at a time, making a binary choice between accept and reject. The main reason for adopting this assumption is that most social contract theorists, when explicit on the matter, endorse this choice procedure. For Hobbes there is a single, stark choice between accepting or rejecting an absolute sovereign (Hobbes Reference Hobbes1991: 120). Many contractarians, moreover, have employed bargaining theory to derive conclusions about the choice of rules in the social contract. The most notable projects of this type are Gauthier’s early theory (henceforth ‘Gauthier 1.0’) as presented in Morals by Agreement and Kenneth Binmore’s intricate, naturalistic contractarianism as presented in multiple volumes and papers (Gauthier Reference Gauthier1986; Binmore Reference Binmore1994b, Reference Binmore2004, Reference Binmore2005). Although bargaining theorists in both game theory and in philosophy often apply an axiomatic approach, it is not difficult to conceive of bargaining as a game in which players consider proposals and face a binary choice between ‘accept’ and ‘reject.’ Indeed, Ariel Rubinstein famously employed this exact set-up to prove that a dynamic bargaining game will yield the same result as Nash’s axiomatic approach, which Binmore explicitly endorses.^{Footnote 39} Gauthier 1.0 describes his bargaining process quite similarly, as involving proposals and a binary choice among bargainers between accept and reject (Gauthier Reference Gauthier1986: 133). The fact that this binary structure, a choice between accept and reject, is so ubiquitous in contractarianism supports its use in the Agreement Model.

Despite its wide use, this choice procedure exhibits two apparent defects. First, this procedure will often fail to select a unique rule from a list of options. Suppose, for example, that there are three property rules under consideration – ${r_1},{r_2},{r_3}$ – and agents go through each rule, determining by the unanimity criterion which rules are good and which are bad. Will they select at most one rule from the set? Well, no: they might decide to accept both ${r_1}$ and ${r_3}$ – even if they all strictly prefer ${r_3}$ to ${r_1}$ . More generally, the decision rule employed here may simply partition the set of rules into two categories, the accepted and the rejected, with no guarantee that a given rule in the accepted category will be optimal. The issue, of course, is that contractarian procedures select a unique rule (or set of rules) to govern each domain; they do not merely partition the set of possible rules into two rough categories. Although this issue would not arise in a Hobbes-like case, where only one rule needs to be chosen, most contractarians posit unanimous agreement as the basis for selecting a large, unique set of moral-political rules. If the Agreement Model differs in this significant way from other contractarian models, then it fails to accurately represent them. If it fails to accurately represent them, then it also fails to offer a cogent critique of these models.

As already pointed out, however, the Agreement Model is quite malleable; its results hold under a wide variety of specifications. This malleability allows it to apply to a diverse set of contractarian models. In this case, we might look at the bargaining process to see if the Agreement Model can be specified so as to avoid the issue of non-uniqueness. Bargaining models typically apply the bargain to one specific case at a time, e.g. how to distribute the gains from a cooperative interaction, and stop the choice procedure once unanimity is attained. So, returning to our simple example, if agents consider rules ${r_1},{r_2},{r_3}$ (each of which presents a mutually exclusive rule for governing a single issue/realm of interaction), and if they reach unanimous agreement on ${r_1}$ before they even consider ${r_2}$ or ${r_3}$ , then ${r_1}$ is the chosen rule. It is unique, even though, as noted above, parties would also have agreed unanimously to ${r_3}$ if they had considered it. Hence, in the non-Hobbesian case where parties must select from a large set of rules, we can construe the Agreement Model as follows: for each realm or issue, agents will consider rules one at a time, voting to accept or reject them. The process for one realm or issue stops and agents move on to the next realm or issue as soon as unanimity obtains. In this way, agents choose a unique rule for each realm or issue, and the Agreement Model avoids the issue of non-uniqueness.

This procedure, however, brings to light the second defect of the binary choice procedure: path-dependence.^{Footnote 40} Since the procedure stops at the first unanimously acceptable rule, there is no reason to believe that the best rule has been selected. This is because the order in which the rules are considered will crucially affect which ones are chosen. In the above example, if agents consider rules in the order ${r_1},{r_2},{r_3}$ , then they will choose ${r_1}$ , while if they consider them in the order ${r_2},{r_3},{r_1}$ , they will choose ${r_3}$ . Not just the quality of the rules, but also the order of consideration thus determines the final choice.

Such path dependence clearly poses a problem for a choice procedure meant to justify its output, but this does not necessarily mean that the Agreement Model fails to represent contractarian choice procedures. First of all, path dependence is a problem with social contract theories, generally. John Thrasher has recently argued that path dependence is endemic in multi-stage social contract choice procedures (Thrasher Reference Thrasher2019: 440). Gerald Gaus has considered the path dependence that inevitably arises due to the functional interdependence of different rules, concluding that the costs of avoiding it are prohibitive and that the social contract theorist is better off embracing it, at least in a mitigated form.^{Footnote 41} Path dependence, therefore, seems to be a normal feature of social contract theory. Its appearance in the Agreement Model, which attempts to model such theories, should not surprise us.

One might object, however, that the path dependence exhibited by the Agreement Model is of a different sort than the inevitable types identified by Thrasher and Gaus. Here, path dependence occurs not because of doxastic diversity, as in Thrasher, nor the interdependence of moral-political rules, as in Gaus, but due to the ability of unanimous agreement to occur when superior options are available. But this points us towards a deeper reply to the issue of path dependence, namely that such path dependence closely relates to the core critique that the Agreement Model presents. Returning to the simple property rule example, suppose n agents with fairly accurate beliefs (as the Agreement Model assumes) are choosing from $\{ {r_1},{r_2},{r_3}\} $ . Suppose, in addition, that ${r_3}$ is the best rule from the set. We should expect more than half of the population to prefer ${r_3}$ to ${r_1}$ , but only before the epistemic effects of group choice are present. In other words, most individuals would reject ${r_1}$ if considering it in isolation. They consider ${r_3}$ to be a preferable alternative, hence ${r_1}$ fails to make it into the choice set. Once they start to think strategically, however, and consider the epistemic importance of being a pivotal chooser, they will vote to accept ${r_1}$ . Thus, it is only the role of unanimity and the Bayesian choice that players face in a group context that allows path dependence to emerge so forcefully. Path dependence, seen in this way, is not a defect of the Agreement Model, but an aspect of its critique of unanimous choice within contractarian theory. The claim, therefore, is that if existing contractarian models were to incorporate rational belief formation into their choice procedure, they, too, would exhibit this sort of path dependence. The challenge for the contractarian is to contrive some way of avoiding these consequences, perhaps by rejecting Bayesian belief formation, the unanimity rule, social-scientific uncertainty or expected utility maximization.

A final assumption worth discussing is that, following Feddersen and Pesendorfer, the Agreement Model employs (Bayesian) Nash Equilibrium as its solution concept. Although this is a standard approach, it faces challenges from a significant minority of game theorists. Michael Bacharach has argued that, although all solutions must be Nash equilibria, even a unique Nash Equilibrium need not be a bona fide solution to the game (Bacharach Reference Bacharach1987: 44).^{Footnote 42} Bacharach demonstrates this rather pessimistic conclusion (pessimistic for the prospects of developing an explanatory game theory) using an example involving limited knowledge about the actions of other players. The key idea is that we can define beliefs that render action profiles rationalizable, even if such profiles are not comprised solely of best responses (Bacharach Reference Bacharach1987: 45). In other words, a strategy that is not a best response (given the strategies of others) need not be a strictly dominated strategy.

It would go far beyond the present topic to contribute to this important methodological discussion. However, there is reason to believe that the Agreement Model does not exhibit the features that may undermine the solution status of a unique Nash equilibrium. Agents in the Agreement Model do not choose based on their best guess as to what other players will choose, as in Bacharach’s example. Rather, agents choose based on the hypothetical scenario in which they are pivotal, since this is the only situation in which their strategy will affect their payoffs one way or the other. Hence, unlike Bacharach’s example, agents in the Agreement Model can assume that they know the actions of all other players (i.e. that they all choose Agree) with 100% probability. Agents then select their strategy on this basis. This undermines the logic of Bacharach’s argument that unique Nash equilibrium and a game’s solution can come apart, an argument that relies upon agents not knowing which ‘world’ they are in, and consequently, not knowing what action the other player(s) will take (i.e. not knowing whether the second player will, in fact, play a best response to the first player’s Nash equilibrium strategy). There may be other conditions that render Nash equilibria untenable as solutions, but the Agreement Model escapes, at least, those conditions identified by Bacharach.^{Footnote 43}

In addition, as Bacharach notes elsewhere, game theory can fail as a predictive or explanatory endeavour without failing as a prescriptive one (Bacharach Reference Bacharach1976: 2–3). In the context of contractarianism, this point is especially important. Real individuals could hardly be moved by the result of a hypothetical contract if this result were not a Nash equilibrium, since in that case one or more of them would be expected to play a strategy that is not a best response. Employing Nash equilibrium thus seems especially justifiable in the normative, contractarian context – indeed more justifiable than in its use by Feddersen and Pesendofer to explain and predict jury decisions.

3.6. Final comment

The conclusions of the Agreement Model are significant. If the contractarian model is essentially a normative-epistemic tool for revealing rational constraint, then it is essential that the agents in the model choose as rationally as possible and that the constraints they choose command rational adherence. Yet, the Agreement Model shows that once we idealize agents to the point of forming rational beliefs, their choices – however individually rational – yield undesirable outcomes. In taking account of the process of rational belief formation, the agreement model has demonstrated that unjustified results can emerge from unanimous agreement among hyper-rational agents. The challenge for contractarianism is thus set: if the unanimous agreement among Bayesian decision-makers under conditions of uncertainty often yields universally undesired results, how can contractarian choice purport to identify justified rules? Or, alternatively, which assumption will the contractarian model reject and why: Unanimity? Uncertainty? Expected utility maximization? Rational, Bayesian belief formation? None of these assumptions are arbitrary. None can be rejected without some explanation.

The purpose of this paper is to explore the implications of accepting a Bayesian framework in the contractarian model. So one of its important conclusions may be that contractarians must reject Bayesian updating in their models of the social contract. Recognizing that one must reject an otherwise plausible assumption in order to make the model work does not, however, justify the rejection of that assumption. Instead, it demands that one either provide a good reason to reject that assumption or construct an alternative model. Before this burden may be attributed to any particular contractarian project, however, one must assess how well the Agreement Model represents the model employed in that particular project. The following section provides two examples of this kind of assessment.