1. INTRODUCTION
Contrary to the ‘new welfare economics’ of the 1930s and 1940s, which grew out of scepticism about interpersonal comparisons of welfare and which still underlies much economic policy evaluation, several contemporary areas of welfare economics seek to evaluate states of affairs as a function of interpersonally comparable individual utilities. Here the aim is to map each state of affairs onto a list (or vector) of individual utilities, and then to produce an ordering of these vectors that can be represented by a mathematical function assigning a real number to each – ‘the better the state of affairs, the higher the number awarded to it’ (Dasgupta Reference Dasgupta2001: 20; see also Adler Reference Adler2012: ch. 2). When this approach (the only approach I'll consider in this paper) is used to evaluate policies having intertemporal effects, a central theoretical question concerns the evaluative weight to be applied to utility coming at different times. This question concerns the so-called rate of pure time preference, which is one key determinant of the social discount rates that can profoundly influence intertemporal evaluation. Often, the rate of pure time preference is characterized as the rate at which future utility declines in value ‘simply because it is in the future’. One aim of this article is to explain why that descriptor mischaracterizes pure time preference as it features in many intertemporal economic analyses.
A second and related aim is to criticize the standard philosophical account of what economists are doing when they adopt a positive rate of pure time preference. I will argue that the standard account, which traces at least to Rawls's A Theory of Justice, improperly ascribes to economists a methodological commitment they need not, and often do not, accept. At the center of my argument is a distinction between two kinds of ranking exercise, which correspond to two conceptions of what it means to say that a vector of utilities is better than another. I will argue that whereas economists frequently apply pure time preference within one sort of ranking exercise, philosophers tend to assume it is applied within a different sort. (I will use ‘pure time preference’ as shorthand for ‘a positive rate of pure time preference’.) I then evaluate three further objections to pure time preference, and I suggest that at least one form of it can, under certain circumstances, evade these objections. I shall close by articulating, but not defending, a final argument against pure time preference that is suggested by the ‘Social, Economic and Ethical Concepts and Methods’ chapter of the most recent Intergovernmental Panel on Climate Change (IPCC) report. If this further argument is sound, it would constitute a decisive objection to pure time preference as it currently figures in much intertemporal welfare economics.
A final prefatory remark: It has become customary in this literature to distinguish between ‘prescriptivist’ and ‘descriptivist’ approaches to discounting (Arrow et al. Reference Arrow, Cline, Maler, Munasinghe, Squitieri, Stiglitz and Bruce1996). While prescriptivists maintain that discount rates should be chosen on the basis of philosophical argument concerning intergenerational ethics, descriptivists tell us to look instead to market interest rates and to the preferences and values that individuals reveal in their consumer decisions. This debate between prescriptivism and descriptivism is important to resolve, but I will not address it here. My aim in this paper is to address the debate over pure time preference among those willing to advance ‘prescriptivist’ ethical arguments.Footnote 1
2. CONSUMPTION DISCOUNTING, UTILITY DISCOUNTING AND THE RAMSEY FORMULA
When economists employ social discount rates in their intertemporal evaluations of public policy, these rates typically discount the value of future consumption. Economists measure a person's or a group's consumption by totalling the monetary value of all commodities consumed.Footnote 2 Discount rates are then used to express the relative value of consumption tomorrow as compared to consumption today. Nowadays, economists and philosophers generally agree that there can be reasons to discount the value of future consumption that would not apply when the focus is instead on future well-being. Suppose, for instance, that future people will be richer than we are today. In that case, an increase in present consumption will produce more well-being than would flow from the same (inflation-adjusted) increase in future consumption. This simply reflects the diminishing marginal utility of consumption, and it does seem to be a good reason to treat units of future consumption as less valuable than equivalent units of present consumption. But this is not yet any reason to discount the value of the well-being that results from consumption. That, after all, is why classical utilitarians – utilitarians in the tradition of Bentham and Mill – can remain impartial between the value of any two units of well-being while still acknowledging the diminishing marginal utility of consumption (Broome Reference Broome1994).
Economists incorporate the diminishing marginal utility of consumption into their models via the parameter η, which figures in their formula for determining the rate at which the value of future consumption should be discounted. Yet while economists routinely refer to η as the ‘elasticity of the marginal utility of consumption’, it can and often does reflect more than just the declining rate at which individuals convert consumption into personal well-being. For example, in the standard ‘workhorse model’ in climate change economics, η ‘is effectively a coefficient of social inequality aversion, in particular to the distribution of consumption across individuals’ (Dietz et al. Reference Dietz, Hepburn, Stern, Basu and Kanbur2009: 377–8). As such, η is often used to reflect moral considerations that are at odds with the straightforwardly aggregative framework of classical utilitarianism. To illustrate: Partha Dasgupta considers the suggestion that η be set so that the following two outcomes are valued equally in economic analyses of climate change: (1) decreasing Adam's $360 of annual consumption by 1%; (2) decreasing Beth's $36,000 of annual consumption by 50% (Dasgupta Reference Dasgupta2008: 151–2). For Dasgupta, the question is not whether Adam loses just as much well-being from his $3.60 decrease as Beth does from her $18,000 decrease; rather, Dasgupta's focus is on the respective declines among which economists should be indifferent if they are to be properly averse to consumption inequality (Dasgupta Reference Dasgupta2008: 151–2). When that is the goal, one uses η to reflect both the rate at which individuals convert personal consumption into personal well-being and the further moral conviction that there is something undesirable about interpersonal consumption inequality.Footnote 3
Economists use the following formula to work out the discount rate on future consumption, δ:
This is the so-called Ramsey formula, named after Frank Ramsey who first proposed it in a 1928 paper on optimal national savings rates (Ramsey Reference Ramsey1928). In the Ramsey formula, g is the estimated annual growth rate in consumption. If g is positive, it means that people in the future are expected to be richer than present people and thus expected to enjoy higher consumption. When this is the case, a positive value of η will discount future consumption for reasons to do with inequality aversion and diminishing marginal utility.Footnote 4 That leaves ρ, the annual rate of pure time preference. Sometimes the rate of pure time preference is called the ‘utility discount rate’. This is because of the role that ρ plays in the following mathematical expression, from which the Ramsey formula is derivedFootnote 5 :
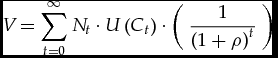 $$\begin{equation*}
{V_{}} = \mathop \sum \limits_{t = 0}^\infty {N_t} \cdot U\left( {{C_t}} \right) \cdot \left( {{\rm{\ }}\frac{1}{{{{\left( {1 + {\rm{\rho }}} \right)}^t}}}{\rm{\ }}} \right)
\end{equation*}$$
$$\begin{equation*}
{V_{}} = \mathop \sum \limits_{t = 0}^\infty {N_t} \cdot U\left( {{C_t}} \right) \cdot \left( {{\rm{\ }}\frac{1}{{{{\left( {1 + {\rm{\rho }}} \right)}^t}}}{\rm{\ }}} \right)
\end{equation*}$$
Here Nt represents the number of people alive at t. The function U, which is a function of consumption at a given time, is routinely called the ‘utility function’, and it customarily takes the following ‘isoelastic’ form:
 $$\begin{equation*}
U\left( {{C_t}} \right) = \left( {\frac{{{C_t}^{1 - {\rm{\eta }}}}}{{1 - {\rm{\eta }}}}} \right)
\end{equation*}$$
$$\begin{equation*}
U\left( {{C_t}} \right) = \left( {\frac{{{C_t}^{1 - {\rm{\eta }}}}}{{1 - {\rm{\eta }}}}} \right)
\end{equation*}$$
As I have already indicated, when the parameter η is used to reflect both the diminishing marginal well-being of individual consumption and social inequality aversion, the U-function must be given a different philosophical interpretation from that which it is given under classical utilitarianism. For classical utilitarianism has no theoretical room for the sort of interpersonal inequality-aversion that economists frequently also use η to express. This is why one must take with a grain of salt economists’ use of the term ‘utility function’ for the U-function.Footnote 6 Nevertheless, given that economists do call U the ‘utility function’, I can now explain why ρ, the rate of pure time preference, is sometimes called the ‘utility discount rate’. This will also help to explain how the Ramsey formula is related to V.
Like U, V is a mathematical function whose role is take arguments (i.e. the inputs to the function) and assign a real number to each (this is said to be the value of the V-function for that argument). In intertemporal welfare economics, V’s arguments are usually intertemporal consumption streams (sometimes called consumption sequences). As an example of a consumption stream, consider the vector (C 0, C 1, . . ., C t, . . .), where C t is a population's per capita consumption at time t. Obviously, a stream of this sort leaves out information that one might well want to know; for example, do the per capita numbers mask intra-population inequalities? The real-world answer will almost always be Yes. But to keep already complex matters tractable, I will adopt the simplifying assumption, which is standard in many theoretical discussions, that intra-temporal consumption is equal. I will also assume that population size is constant across time, so that Nt is no longer needed as a term in V; this is again merely to keep things simple.
So V takes intertemporal streams of consumption as its arguments, and assigns a real number to each stream. To do this, V takes the per capita consumption associated with the first time period in a given stream – i.e. C
0 – and runs it through the U-function. (I will sometimes refer to both time periods and the people who occupy them as ‘generations’, but nothing of substance turns on that choice of terminology.) V then multiplies the resulting U-number by the first period's discount factor, the formula for which is given by:
![]() $( {\ \frac{1}{{{{( {1 + {\rm{\rho }}} )}^t}}}\ } )$
. This is why ρ is also called the ‘utility discount rate’: it is the rate used to generate the discount factor that gets applied to U-numbers. The discount factor for the first item in the stream, C
0, will be equal to 1, since
$( {\ \frac{1}{{{{( {1 + {\rm{\rho }}} )}^t}}}\ } )$
. This is why ρ is also called the ‘utility discount rate’: it is the rate used to generate the discount factor that gets applied to U-numbers. The discount factor for the first item in the stream, C
0, will be equal to 1, since
![]() $( {\ \frac{1}{{{{( {1 + {\rm{\rho }}} )}^0}}}\ } )$
is equal to 1 for any value of ρ. By contrast, the discount factor to be applied to the next generation's U-number will be less than 1 whenever the rate of pure time preference, ρ, is positive; in that case, the U-number associated with any future generation will be given less weight by V than V would give to that very same number if it were associated with the first generation. That is what it means to adopt (a positive rate of) pure time preference. V’s task is then to move through the entire consumption stream, first running each generation's consumption-number, C
t, through the U-function, then multiplying each generation's resulting U-number by the generation's respective discount factor, and then finally adding up all of these discount-factor-adjusted numbers. When ρ is positive, the upshot is often called the stream's ‘discounted sum’; when ρ = 0, it is sometimes called the stream's ‘undiscounted sum’. I shall use ‘discounted sum’ as a general term covering both of these possibilities; thus a discounted sum is the sum of generational U-numbers after they have all been multiplied by each generation's respective discount factor, whatever those discount factors happen to be. The task is then to run all relevant consumption streams through this same procedure, and to rank the streams in order from largest discounted sum to smallest.Footnote
7
Ramsey in effect showed that it is not necessary to first run generational consumption numbers through U and then apply the generation's utility discount factor to each U number. One can instead generate a generation's consumption discount factor,
$( {\ \frac{1}{{{{( {1 + {\rm{\rho }}} )}^0}}}\ } )$
is equal to 1 for any value of ρ. By contrast, the discount factor to be applied to the next generation's U-number will be less than 1 whenever the rate of pure time preference, ρ, is positive; in that case, the U-number associated with any future generation will be given less weight by V than V would give to that very same number if it were associated with the first generation. That is what it means to adopt (a positive rate of) pure time preference. V’s task is then to move through the entire consumption stream, first running each generation's consumption-number, C
t, through the U-function, then multiplying each generation's resulting U-number by the generation's respective discount factor, and then finally adding up all of these discount-factor-adjusted numbers. When ρ is positive, the upshot is often called the stream's ‘discounted sum’; when ρ = 0, it is sometimes called the stream's ‘undiscounted sum’. I shall use ‘discounted sum’ as a general term covering both of these possibilities; thus a discounted sum is the sum of generational U-numbers after they have all been multiplied by each generation's respective discount factor, whatever those discount factors happen to be. The task is then to run all relevant consumption streams through this same procedure, and to rank the streams in order from largest discounted sum to smallest.Footnote
7
Ramsey in effect showed that it is not necessary to first run generational consumption numbers through U and then apply the generation's utility discount factor to each U number. One can instead generate a generation's consumption discount factor,
![]() $( {\ \frac{1}{{{{( {1 + {\rm{\delta }}} )}^t}}}\ } )$
, where δ, the consumption discount rate, = η · g + ρ. One arrives at the same discounted sum regardless of whether one runs a stream through V or whether one takes Ramsey's shortcut by applying consumption discount factors to each item in a consumption stream and adding up the discounted consumption numbers to yield the stream's discounted sum.
$( {\ \frac{1}{{{{( {1 + {\rm{\delta }}} )}^t}}}\ } )$
, where δ, the consumption discount rate, = η · g + ρ. One arrives at the same discounted sum regardless of whether one runs a stream through V or whether one takes Ramsey's shortcut by applying consumption discount factors to each item in a consumption stream and adding up the discounted consumption numbers to yield the stream's discounted sum.
As I noted in the Introduction, a further common claim made about ρ is that it serves to discount a future benefit ‘simply because it is in the future’ (Stern Reference Stern2007: 161; Quiggin Reference Quiggin2009: 199). Yet in at least some cases this is highly misleading. Consider, for instance, that in his now-famous report on climate change, Nicholas Stern set ρ to 0.001 to reflect a 10 per cent chance that humanity would be extinct in 100 years (Stern Reference Stern2007: 53). Whatever one thinks of this prediction, Stern does not discount future consumption using a positive ρ ‘simply’ because it is in the future. Rather, he does this because the future happens to contain specific risks that could bring humanity's consumption to a halt. Now, I plan to set aside issues of risk and uncertainty by assuming that the current generation can accurately predict what would happen in the future under different policies; this enables me to examine the issues related to pure time preference that remain when risk and uncertainty are removed from the picture.Footnote 8 But it is nevertheless crucial to my project that we not start from the mistaken assumption that when economists use a positive rate of ‘pure time’ preference they are discounting future benefits ‘simply because they are in the future’. If that turns out to be true in any particular case, Stern's reason for a positive ρ shows that it will not be true by definition. We will soon encounter further reasons to reject that characterization of ρ.
So, if one wishes to rank intertemporal streams of consumption by using the mathematical construct V, or by using the consumption discount rate shortcut that Ramsey derived from V, should one use a positive rate of pure time preference, ρ? Philosophers routinely answer No; economists are more divided. In Section 4, I will answer Maybe. But any answer to that question presupposes an answer to a prior and absolutely fundamental question about V that is frequently answered in quite different ways by different theorists. I turn now to that issue.
3. TWO APPROACHES TO EVALUATIVE SCOPE
In this section I aim to show that different parties to the debate over pure time preference have quite different ideas about which evaluative considerations properly bear on V-ranking exercises. If I am right about this, then at least one common way of characterizing the consumption discount rate is formally correct while nevertheless lacking in crucial philosophical content. Consider, for example, Nicholas Stern's definition of the consumption discount rate as ‘simply the proportionate rate of fall of the value of the numeraire [i.e. consumption] used in the policy evaluation’ (Stern Reference Stern, Gardiner, Caney, Jamieson and Shue2010: 50). This means that if the consumption discount rate, δ, is 5%, then while conferring an extra marginal unit of consumption to the current generation increases the overall value of the V-function by 1, an extra marginal unit of consumption accruing to the next generation will increase the value of V by only 0.95; thus as Stern says, δ expresses the rate at which the value of consumption – as measured by the effect its presence in the stream has on the overall numerical value of the V-function – declines as time progresses. It is this way of characterizing δ that is purely formal. For without an answer to the prior question of what sorts of considerations are relevant to the V-rankings that welfare economics is concerned with, all that can be said is that the value of a unit of consumption at a given point in time is that unit's contribution to the overall ‘score’ assigned by V to the consumption stream in which that unit figures. Since the proper approach to ‘scoring’ consumption streams depends essentially upon the evaluative considerations that are relevant to the ranking exercise, the notion of value at work in Stern's formulation is purely mathematical until we settle what I shall call the issue of evaluative scope, i.e. the issue of which evaluative/normative/moral considerations do or should bear on the V-ranking exercise. The same warning applies to Dasgupta's definition of the consumption discount rate as the ‘the marginal social rate of indifference between consumption in adjacent [time] periods’ (Dasgupta Reference Dasgupta, Hahn and Ulph2012: 109). This is again a standard and accurate definition of δ, but it too raises the prior question, Social indifference with respect to which considerations? The issue of evaluative scope is therefore crucial for interpreting any real-world V-ranking exercise.
As it happens, there is stark disagreement on V’s evaluative scope within intertemporal welfare economics. This has profound consequences for the debate over pure time preference, as quite different rates of pure time preference can be defensible depending on which evaluative scope is adopted. That in turn means that theorists who disagree on the discount rate can talk past one another simply because they implicitly adopt different stances on the issue of V’s evaluative scope. Indeed, I think that is frequently the case, especially (but not only) when it comes to disagreements between economists and philosophers. One aim of this paper is to substantiate this diagnosis.
Generally speaking, two broad approaches have been taken on the issue of V’s evaluative scope, and while each has adherents in the literature, the important differences between them are rarely acknowledged and hardly ever discussed at length.Footnote 9 As a way into the issue, consider a distinction drawn by the working group – Working Group III (WG3) – that was responsible for the ‘Social, Economic, and Ethical Concepts and Methods’ chapter of the most recent IPCC report (Kolstad et al. Reference Kolstad, Urama, Broome, Edenhofer, Pichs-Madruga and Sokona2014: 215).Footnote 10 WG3 draws a substantive philosophical distinction between justice and value. (I call this distinction ‘substantive’ to indicate that value is here given more determinate philosophical content than the exclusively formal/mathematical content it had in Stern's definition of consumption discount rates, as discussed above.) Justice, WG3 claims, refers to that domain of ethics concerned with ‘justice, fairness and rights’ (Kolstad et al. Reference Kolstad, Urama, Broome, Edenhofer, Pichs-Madruga and Sokona2014: 215). By contrast, value (again in WG3’s substantive sense) is concerned with ‘improving the world: making it a better place’ (Kolstad et al. Reference Kolstad, Urama, Broome, Edenhofer, Pichs-Madruga and Sokona2014: 215). WG3 adopts this distinction from John Broome, one of WG3’s lead authors. In his book Climate Matters, Broome uses the famous ‘Transplant’ thought-experiment to illustrate the distinction between justice and value. Broome explains that while it is unjust for a doctor to kill a healthy patient to use his organs to save five others (as this would violate his rights), doing this might well promote value – that is, it might well make the world a ‘better’ place in the sense that a world with one death and five continued lives is better than a world with just one continued life and five deaths (Broome Reference Broome2012: 51). Elsewhere, Broome observes that the UK's National Health Service will give hospitalized patients an analgesic for a headache, even though the money spent on headache treatments will over time be enough to save a life with an expensive operation. Broome writes, ‘Evidently, the Health Service thinks that curing all those headaches is as valuable as saving a life. I agree’ (Broome Reference Broome, Murray, Salomon, Mathers and Lopez2002: 728). The notion of value employed here is the same as WG3’s: it allows for the possibility that even if no one has a claim to an analgesic, and even if the Health Service's policy is unfair to the person who will die, still the policy is justified because of the degree to which the world is improved by preventing all those headaches. In this case (but not in the Transplant case), value considerations trump any justice considerations, one might say.
Hewing closely to Broome's discussion in Climate Matters, WG3 claims that within climate economics, the V-function is used to evaluate consumption streams (and the policies that generate them) solely with respect to Broomean value considerations – that is, solely with respect to the degree to which the stream ‘improves the world’. After setting out Broome's distinction, WG3 writes, ‘Since the methods of economics are concerned with value, they do not take account of justice and rights in general’ (Kolstad et al. Reference Kolstad, Urama, Broome, Edenhofer, Pichs-Madruga and Sokona2014: 224; see also p. 220 and sec. 3.4.6).Footnote 11 Thus, because the consumption discount rate is the marginal social rate of indifference between consumption in adjacent periods, WG3’s approach to V’s evaluative scope holds that discount rates reflect marginal social indifference with respect to Broomean value considerations only.
This understanding of V fits nicely with Ramsey's own seminal treatment. For Ramsey presupposed classical utilitarianism, which maintains, first, that the right action or policy is always that which maximally improves the world in WG3’s sense, and, second, that individual rights and claims – those things that WG3 calls considerations of justice – are not genuine fundamental components of ethics. So Ramsey's V-function certainly was focused exclusively on what Broome and WG3 refer to as value considerations. The same goes for at least some prioritarians, with the key difference being that prioritarians say well-being's capacity to improve the world diminishes as the beneficiaries of additional well-being have more and more of it. For instance, in a recent paper on climate change economics, prioritarians Matthew Adler and Nicolas Treich, who refer to V as a social welfare function (SWF), write:
[T]he SWF is a framework for welfarist ethical deliberation. Welfarists see individual well-being as the foundation for ethical thought: if two outcomes are identical with respect to everyone's well-being, they are equally ethically good. (Adler and Treich Reference Adler and Treich2015: 282)
A key difference between Ramsey, on the one hand, and WG3 and Adler and Treich, on the other, is that only Ramsey would claim that V-rankings in terms of Broomean value are ipso facto rankings of streams’ overall, all-things-considered choiceworthiness. By contrast, WG3 claims that, ‘values constitute only one part of ethics’, so that ‘if an action will increase value overall it by no means follows that it should be done’ (Kolstad et al. Reference Kolstad, Urama, Broome, Edenhofer, Pichs-Madruga and Sokona2014: 220). This is because WG3 holds that there are genuine justice-based considerations that V does not aim to capture. And while the welfarism of Adler and Treich is generally hostile to claims about rights, Adler and Treich do allow that prioritarian value considerations might be counterbalanced by ‘quite rational’ considerations of ‘prudence’, such that ‘The recommendations that follow from the SWF construct are, in our view, one input into the climate decisionmaker's rational calculus’ (Adler and Treich Reference Adler and Treich2015: 285; emphasis in original). These differences notwithstanding, WG3, Adler and Treich, and Ramsey all seem to agree that considerations of rights and justice are simply not relevant to V’s ranking exercise; those considerations fall outside of V’s evaluative scope, they would say. This makes it likely that these three sets of theorists will all be more or less on the same page when they turn to the question of whether V should include a positive rate of pure time preference.
To be more precise about what these theorists will be ‘on the same page’ about, let us call any ranking of consumption streams solely in terms of the streams’ Broomean value a goodness ordering. And when an ordering is put forward as a ranking that determines what ought to be done all things considered, let us signify this by calling it an ordering*. Thus, sometimes goodness orderings are also put forward by theorists as goodness orderings*, and sometimes not. For example, while WG3 and Adler and Treich hold that the V-function within climate economics is used to generate goodness orderings, we have seen that each gives reasons against treating these as orderings*. By contrast, and by virtue of his classical utilitarianism, Ramsey used V to generate goodness orderings*. Yet despite this disagreement about whether a goodness ordering should in addition be classified as an ordering*, all of these theorists agree that the question of whether to adopt pure time preference is the question of whether to do so within the context of ranking consumption streams in terms of the goodness they contain.Footnote 12
Consider now a very different conception of V-rankings that leading environmental economists Dasgupta and Geoffrey Heal once claimed is ‘[q]uite possibly the most common position that welfare economists have held’ (Dasgupta and Heal Reference Dasgupta and Heal1979: 275). It is an interpretation that Dasgupta and Heal associate with the economist Tjalling Koopmans. The first feature of the Koopmans-inspired conception – a feature that (contra WG3) Dasgupta and Heal imply all V-rankings share – is that V-rankings are essentially rankings that determine what ought, all things considered, to be done. To use the signifier I introduced just above, the Koopmans-inspired approach conceives of V-rankings as orderings that are also orderings*:
Let Ɔ denote the set of all feasible consumption sequences. The problem that we are concerned with is the question of ordering the elements of this set in a manner that is ethically defensible. The aim ultimately will be to choose that programme which is judged best in terms of this ordering. (Dasgupta and Heal Reference Dasgupta and Heal1979: 258; emphasis added)
It is not surprising that Dasgupta and Heal would tie the Koopmans-inspired approach to the task of producing orderings*. For Koopmans helped pioneer ‘optimal growth theory’, in which ‘[t]he most basic notion is that of a preference ordering of growth paths’ (where consumption streams are examples of growth paths) (Koopmans Reference Koopmans1965: 226; emphasis added). The issue for Koopmans, as it was for Ramsey, was to provide a framework to be used in practice for determining government investment and spending policy. The term ‘preference ordering’ connotes this practical aim, as preferences have clear and tight connections to choice. Indeed, as I have defined ‘ordering*’, it is more or less synonymous with ‘an ordering that is put forward as a social preference ordering’.
A second distinguishing feature of the Koopmans-inspired view, according to Dasgupta and Heal, is that V is to rank consumption streams on the basis of an ‘intuitionist conception’ of ethics (Dasgupta and Heal Reference Dasgupta and Heal1979: sec. 6). As Dasgupta elaborates later in a solo-authored work:
Rawls (p. 34 [of Rawls Reference Rawls1971]) introduced Intuitionism as ‘. . . the doctrine that there is an irreducible family of first principles which have to be weighed against one another by asking ourselves which balance, in our considered judgment, is the most just . . . Intuitionist theories . . . have two features: first, they consist of a plurality of first principles which may conflict to give contrary directives in particular types of cases; and second, they include no explicit method, or priority rules, for weighing these principles against one another: we are simply to strike a balance by intuition, by what seems to us most nearly right.’ . . . [T]he version of Intuitionism I rely on here is the one that refers to the plurality of moral principles, whether or not they are basic. (Dasgupta Reference Dasgupta2011: 478)
Dasgupta maintains that the Koopmans-inspired conception of V is ‘particularly attractive’ because ‘it leaves open the door for further ethical deliberations’ that are foreclosed when the task is to construct goodness orderings (Dasgupa Reference Dasgupta, Lillehammer and Mellor2005: 161). I shall use the term Dasgupta-Koopmans ordering* to refer to a ranking of consumption streams that (1) is intended to be an ordering* (i.e. an ordering that determines what ought to be done) but that (2) is not a goodness ordering. (I will refine this definition further in a moment.)
Let me give some examples of economists using V to yield what seem to be Dasgupta-Koopmans orderings*. Take first William Cline, who argues that the decision about the rate of pure time preference must be responsive to the moral asymmetry that exists in commonsense morality between harming and not-aiding. Cline criticizes Thomas Schelling for likening climate change mitigation projects to foreign aid projects. Schelling notes that since rich countries seem to discount the distant suffering they could prevent with increased foreign aid, it is not surprising that rich countries would also discount the future suffering they could prevent with stricter climate change mitigation policies (Schelling Reference Schelling1995: 397). Cline responds by claiming that even if rich countries are right to discount the foreign suffering they could prevent with aid now, there is a key ethical difference in the case of climate change. He writes that Schelling makes
the mistake of equating greenhouse gas mitigation decisions to the bestowal of a benefit, whether to Bangladesh today or our own unknown descendants in the future. Instead, the issue is the imposition of a damage. Surely there is an ethical difference between refraining from conveying a gift, on the one hand, and imposing a damage, on the other. Americans might feel no compelling obligation to increase aid to Bangladesh today, but surely they would be loath to despoil Bangladesh today (for example, by holding nuclear tests close by offshore). (Cline Reference Cline and Nordhaus1998: 100)
In part for this reason, Cline's economic analysis of climate change was among the first to argue for a rate of pure time preference of zero (Cline Reference Cline1992). As he puts it, ‘morally there is greater responsibility to avoid imposing harm on others than there is to make sure they can enjoy an extra benefit at a cheap cost. Call it an intergenerational Hippocratic Oath’ (Cline Reference Cline2012: 7).Footnote 13
Now, the distinction between harming and not-aiding does seem to be a consideration that WG3 would associate with the ethical category of justice and contrast with the category of value. We typically think people have rights against being harmed, and it is this consideration that is so starkly illustrated by Broome's Transplant example. Cline therefore does not seem to be interested in what I have called goodness orderings. But does he seek an ordering*? That is not as clear. True, a good explanation of Cline's insistence that harm-based considerations be reflected in V is that he aims to construct an all-things-considered ranking – an ordering* – in which consumption streams are penalized – moved down the list – if they violate Cline's ‘intergenerational Hippocratic Oath’. Yet for all Cline says, there may be still further moral considerations that he wishes to exclude from V’s evaluative scope.Footnote 14 This interpretive question need not detain us, however. The key point right now is that V has been used in intertemporal welfare economics to yield something other than goodness orderings. Eventually I will make the case that a great many economists do in fact use V to generate what I have called Dasgupta-Koopmans orderings*. And once we see this as a possibility, it opens the door for the claims I shall defend in section 4 concerning the plausibility of pure time preference.
Here is another example of harm-based considerations entering into a V-ranking exercise within climate economics. It involves Dasgupta's arguments concerning η, rather than ρ. Despite questioning the egalitarian and prioritarian rationales that would justify setting η as high as 2 or 3 in intra-generational economic analyses, Dasgupta argues that intra-generational analyses should nevertheless use a value of η in that range. Why? His answer is that while pure differences in wealth are not as morally important as egalitarians and prioritarians claim, it does matter how those differences arose. And according to him, today's rich world is not primarily responsible for the poverty found in today's poor world (Dasgupta Reference Dasgupta2008: 159). By contrast, he writes: ‘We should be anxious over the plight of future generations caused by climate change because we are collectively responsible for amplifying that change; the rich world especially so. If future generations inherit a hugely damaged Earth, it is we who would be in part responsible’ (Dasgupta Reference Dasgupta2008: 159). For this reason, Dasgupta maintains that today's rich countries have stronger obligations to those who will be richer than them in the future than they do to those who are poorer than them now, and this is because today's rich countries have been actively harming future people, but not today's poor. Dasgupta concludes that while today's rich don't owe much to today's poor, helping today's poor may be the best way to help the future people that today's rich have been harming. For example, Dasgupta might recommend helping to improve the current economy in today's poor nations, so that over time the benefits of economic growth can be enjoyed by those future people to whom we have strong harm-based obligations. As he puts it, a good way to improve ‘tomorrow's people in today's poor world’ is simply to improve today's poor world; this is not because we have obligations to ‘others today’, but rather because we have obligations to ‘tomorrow's they’ (Dasgupta Reference Dasgupta, Hahn and Ulph2012: 121). So despite reluctance about intra-generational egalitarianism and prioritarianism, Dasgupta supports intra-generational redistribution on harm-based grounds. This is to be achieved, he says, by using an η between 2 and 3 in economic analyses of intra-generational policies.
Dasgupta's, Cline's and others’ (e.g. Clarkson and Deyes Reference Clarkson and Deyes2002: 15, 52; Davidson Reference Davidson2014: sec. 6) harm-based arguments for choosing certain values for the Ramsey formula's parameters are not what one would expect to see if WG3 were right that the V-function in intertemporal welfare economics is used exclusively to yield goodness orderings. Yet one might at this point ask whether Cline and Dasgupta are simply treating harms, injustices and rights-violations as events whose occurrence makes the world worse than it might otherwise be. That is, perhaps they are employing a technique that some philosophers refer to as ‘consequentializing’ traditionally non-consequentialist moral notions. To consequentialize a non-consequentialist notion such as rights-violations or injustice is to treat each as yet another ‘bad thing’ that can impede world-improvement (Brown Reference Brown2011). In other words, consequentializers seek to assimilate all normatively relevant considerations into the category of value, and this perhaps provides a way to say that Dasgupta and Cline are focused on goodness orderings after all.
A full discussion of consequentializing is well beyond the scope of this paper. Fortunately we need not wade into those waters. Instead, I can refine the distinction between goodness orderings and Dasgupta-Koopmans orderings* to ensure that, even if Cline and Dasgupta are consequentializers, their understanding of the role of the V-function is still philosophically distinct from the role that WG3 says it always has in climate economics. Thus, I propose to add the following additional features to the distinction between goodness orderings and Dasgupta-Koopmans orderings*: (1) a Dasgupta-Koopmans ordering*’s evaluative scope essentially includes at least some ‘agent-relative’ considerations; (2) the evaluative scope of a goodness ordering essentially excludes all agent-relative considerations. I shall adopt the fairly standard account of an ‘agent-relative’ consideration given by Larry Alexander and Michael Moore:
An agent-relative reason is so-called because it is a reason relative to the agent whose reason it is; it need not (although it may) constitute a reason for anyone else. Thus, an agent-relative obligation is an obligation for a particular agent to take or refrain from taking some action; and because it is agent-relative, the obligation does not necessarily give anyone else a reason to support that action. (Alexander and Moore Reference Alexander, Moore and Zalta2012: sec. 2.1)
Regardless of whether Cline and Dasgupta view harm-infliction, injustice and rights-violations as just additional ‘bad things’ in the world – that is, regardless of whether they are consequentializers – it seems clear that each appeals to agent-relative reasons when they stress the reasons we have to avoid inflicting harm on others. For Cline and Dasgupta each grants that we may not have strong obligations to poor people whose situation we did not materially contribute to; but in addition, each claims that we are not so innocent when it comes to the harm that future people will experience from climate change.
By introducing the notion of an agent-relative consideration, we can bypass the issue of consequentializing, for it seems clear that the evaluative scope of both Ramsey's V-function and WG3’s V-function excludes agent-relative considerations. Certainly that was true of Ramsey's classical utilitarianism, which is thoroughly impartial. WG3, for its part, suggests that whenever one agent has an agent-relative reason to help another, this will be because the latter has a claim on the former to be given what is owed to him, or what he has a right to. And according to WG3, what one has a claim to is a matter of justice or fairness, not value. WG3 gives the example of a transfer from a rich country to a poor country. When this transfer is made as ‘an act of restitution’, WG3 treats it as a matter of justice; when it is made simply because it will be ‘beneficial to people in the poor country’, WG3 treats it as a matter of world-improvement, a matter of value (Kolstad et al. Reference Kolstad, Urama, Broome, Edenhofer, Pichs-Madruga and Sokona2014: 215). This strongly suggests that WG3 would treat agent-relative reasons as irrelevant to the value-based V-rankings it says climate economics is concerned with. So the distinction between impartial considerations and agent-relative considerations seems to track WG3’s broad distinction between value and justice. Similarly, Dasgupta claims that a central difference between the Ramsey-inspired conception of V and the Koopmans-inspired conception is that the former ‘evaluates social states of affairs by studying the point of view of an Ideal Observer . . . [who] has no particular point of view’, whereas in the Koopmans framework, ‘The evaluator is the concerned citizen herself’ (Dasgupta Reference Dasgupta, Hahn and Ulph2012: 105–6; emphasis in original). So regardless of whether it is possible to ‘consequentialize’ agent-relative considerations, my refined distinction between goodness orderings and Dasgupta-Koopmans orderings* seems sufficient to capture the very different portrait of V-ranking exercises that one gets from WG3, on the one hand, and Cline and Dasgupta on the other. Moreover, this distinction is all I need to make the points I wish to make in this paper about the rate of pure time preference.Footnote 15
Earlier I said that ‘V takes intertemporal streams of consumption as its arguments, and assigns a real number to each stream’, and that might suggest that V is essentially welfarist in Amartya Sen's sense of ‘making no use of any information about the social states [to be ranked] other than that of the personal welfares generated in them’ (Sen Reference Sen1977: 1559). Yet if we are now to allow rankings of the Dasgupta-Koopmans variety, V-ranking exercises cannot be exclusively welfarist, since agent-relativity can enter only if we allow evaluations that are responsive to non-welfarist information such as the fact that B has rights that have been or will be violated by A.Footnote 16 How, then, should such information enter into the ranking exercise? There has been little discussion of this in the literature, beyond some brief and elliptical remarks by Sen and Dasgupta. In one discussion of discounting, Sen claims that if V-rankings are to reflect such values as the right of future generations to be free of oppression imposed by the present generation, then ‘evaluative weights’ such as η and ρ ‘cannot be made functions only of personal welfare information, and the analysis requires supplementation by nonwelfaristic considerations of liberty’ (Sen Reference Sen and Lind1982: 347; emphasis in original); ‘[T]he choice of social rates of discount for investments in the development of natural resources (including energy) is certainly not independent of these issues [i.e. issues of liberty, rights, claims, entitlement, desert, and oppression]’ (Sen Reference Sen and Lind1982: 346; see also p. 345). Sen then gives an example that is very similar to Dasgupta's analysis of η:
Suppose the investment project in question will eliminate some pollution that the present generation will otherwise impose on the future. Even if the future generation may be richer and may enjoy a higher welfare level, and even if its marginal utility from the consumption gain is accepted to be less than the marginal welfare loss of the present generation, this may still not be accepted to be decisive for rejecting the investment when the alternative implies long-term effects of environmental pollution. The avoidance of oppression of the future generations has to be given a value of its own . . . The evaluation of investments and the choice of relevant social rates of discount cannot, therefore, be reduced simply to considerations involving personal welfare data relating to the present and the future. (Sen Reference Sen and Lind1982: 347; emphasis in the original)
As far as I know neither Sen nor anyone else has attempted to construct the ‘evaluative weight functions’ that would take as arguments non-welfarist facts about social states and (perhaps together with the welfarist information contained in traditional consumption streams) yield values for η and ρ. The tack that seems more likely to be used is Dasgupta's, in which one performs ‘sensitivity analyses’ by varying the discounting parameters to yield an intuitively plausible Dasgupta-Koopmans ordering*. As Dasgupta comments, ‘Such analyses are thought experiments, resembling laboratory tests. They give us a sense of how the interplay of facts and values in complicated worlds tells us what we should do. Rawls called the termination of iterative processes involving such thought experiments, ‘reflective equilibria’’ (Dasgupta Reference Dasgupta2008: 157). I shall not pursue the question of whether this approach is fully adequate to the task confronting proponents of the Dasgupta-Koopmans framework; I simply want to flag that it is a task they must at some point take on.
Consider now a further argument for pure time preference that invokes non-welfarist agent-relative considerations. This argument is much more common among economists than are the harm-based arguments advanced by Cline and Dasgupta, and it is also the argument that has received the most attention by philosophers. Moreover, there is strong reason to believe that any economist who makes this argument conceives of V as generating orderings*. Here is Kenneth Arrow's version of the argument (although he attributes the main idea to Koopmans):
[I]magine that an investment opportunity occurs, available only to the first generation. For each unit sacrificed by them, a perpetual stream of α per unit time is generated. If there were no time preference [i.e. no pure time preference], what would the optimal solution be? Each unit sacrificed would yield a finite utility loss to the first generation, but to compensate, there would be a gain, however small, to each of an infinity of generations. Thus, any sacrifice by the first generation is good. Strictly speaking, we cannot say that the first generation should sacrifice everything, if marginal utility approaches infinity as consumption approaches zero. But, we can say that given any investment, short of the entire income, a still greater investment would be preferred. (Arrow Reference Arrow, Portney and Weyant1999: 14, emphasis in the original)
In response, Arrow says:
I find this to be an incredible and unacceptable strain on the present generation . . . I therefore conclude that the strong ethical requirement that all generations be treated alike, itself reasonable, contradicts a very strong intuition that it is not morally acceptable to demand excessively high savings rates of any one generation, or even of every generation. (Arrow Reference Arrow, Portney and Weyant1999: 16)Footnote 17
Arrow concludes that we must acknowledge ‘a principle of self-regard, of the individual as an end and not merely a means to the welfare of others’, which in turn grants each generation the moral right to ‘maximize a weighted sum of its own utility and the sum of utility of all future generations, with less weight on the latter’ (Arrow Reference Arrow, Portney and Weyant1999: 16; see also Beckerman and Hepburn Reference Beckerman and Hepburn2007). The ‘weighted sum’ here is a clear reference to a V-function that involves a positive rate of pure time preference. Elsewhere, after setting out the same argument, Arrow says, ‘Very tentatively, it would seem that the rate of pure time preference should be about 1% [i.e. ρ = .01]’ (Arrow Reference Arrow1995: 17).
It seems plain that Arrow is concerned to construct a Dasgupta-Koopmans ordering*; not only is his principle of self-regard quintessentially agent-relative, but he also appears to conceive of V-rankings as rankings of consumption streams in terms of their overall choiceworthiness. If he did not, he would have no pressing need to use pure time preference to ensure that consumption streams involving very low current consumption are ranked lower than streams with higher current consumption. And given the popularity that this particular ‘argument from excessive sacrifice’ has in the literature, it would seem that Dasgupta and Heal were correct to say that it is not uncommon for intergenerational welfare economists to conceive of V-rankings in this way. In a more recent example, William Nordhaus invokes Koopmans and agent-relativity to illustrate the ‘heavy burden of very low discounting’. Nordhaus writes:
How might we think about our obligations to our children, grandchildren, and so on further down the generational line? I will use the example of parental concerns to illustrate the point. As parents, we naturally feel intense concern for our children . . . We also care deeply for our grandchildren, but our anxieties are mediated by the knowledge that their parents – our children – are also caring for them. Similarly, our great-grandchildren and great-great-grandchildren are more remote from our anxieties. In a sense, they have an ‘anxiety discount’ because we cannot judge the circumstances in which they will live, and because our children and grandchildren will be there to care for them after we are gone . . . Now take the example of zero discounting, which is sometimes advocated by philosophers . . . [S]uppose that we have no anxiety discounting for future generations, so that we are just as anxious about our grandchildren as about our children . . . In this situation, most of us would dissolve into a sea of anxiety . . . We would simply be unable to decide what to do. Zero discounting is like an infinitely heavy load on our shoulders. This argument sounds like a bit of flaky pseudo-mathematics, but it is exactly the nub of the deep mathematical analysis of zero discounting made by Nobel Prize-winning economist Tjalling Koopmans. (Nordhaus Reference Nordhaus2013: 192–3)
Here too, Nordhaus appears to view V-rankings as orderings*; why else would ‘zero discounting’ entail a heavy load on our shoulders? He also agrees with Arrow that it is reasonable to tailor discount rates to protect oneself and one's generation from drowning in a sea of concern for the well-being of those to whom one is not closely related. Nordhaus's analogy with parental concern thus strongly implicates agent-relative considerations, and suggests that he, like Arrow, is interested in producing Dasgupta-Koopmans orderings*, rather than mere goodness orderings.
And yet ever since Rawls, many philosophers simply assume without argument that the economist's V-function is essentially a tool for generating goodness orderings. Consider, for instance, Rawls's own response to the ‘excessive sacrifice argument’ for pure time preference that Arrow, Nordhaus and many others find so compelling. Rawls claims that by adopting a positive rate of pure time preference within a V-function, economists are applying an ‘ad hoc’ adjustment to ‘the utilitarian principle’ (Rawls Reference Rawls1999: 262). As I interpret this line of criticism, Rawls assumes that economists set out to construct a classical utilitarian goodness ordering*, and then, upon not liking utilitarianism's practical implications, they seek to diminish the degree to which future well-being improves the world by adopting pure time preference. Rawls criticizes this as a theoretical move that has ‘no intrinsic ethical appeal’ and that ‘simply mitigates the consequences of mistaken principles’ (Rawls Reference Rawls1999: 262).
But in light of the Koopmans-inspired conception of V-ranking exercises, Rawls's line of criticism against pure time preference attributes to economists a methodological commitment they need not, and often do not, endorse. For Dasgupta-Koopmans orderings* have no essential connection to classical utilitarianism. Dasgupta, recall, claims that the main virtue of the Koopmans-inspired approach is its ability to reflect a plurality of ethical considerations. He adds:
Ramsey's ethics was overtly Utilitarian. Nearly five decades of work by economists working on the ethics of the long run has shown that ethics will not do. It has shown that, agreeably, there is a compelling theory that has the same mathematical structure as the one invented by Ramsey. So, although Ramsey's ethics cannot be accepted, the techniques he devised for evaluating the just rate of saving can be adapted for use in worlds that are ethically far richer than the one he considered. (Dasgupta Reference Dasgupta, Lillehammer and Mellor2005: 169)
It seems not to have occurred to Rawls to conceive of the V-function in this way (or if it did, he mistakenly decided it was not a conception worth engaging with).
The broad objection that Rawls pressed against pure time preference is by far the most common objection in the philosophical literature. For example, Simon Caney notes that Arrow explicitly invokes Samuel Scheffler's idea of an ‘agent-centered prerogative’, which is an example of what I have termed an agent-relative consideration that confers upon individuals the moral right to a certain degree of freedom to pursue their own goals and interests (Scheffler Reference Scheffler1994). While Caney thinks Scheffler's idea is ‘very plausible’ (Caney Reference Caney2008: 550), he also thinks Arrow misunderstands it:
The whole point of [Scheffler's] argument is that persons do not have a duty to maximize well-being. That is why his book is called The Rejection of Consequentialism. To invoke agent-centered prerogatives whilst also affirming a maximizing consequentialism thus misunderstands Scheffler's argument and the conclusions that he plausibly derives from it. (Caney Reference Caney2008: 550)
Like Rawls, Caney seems to think that Arrow starts from, and dearly wishes to stick to, a mistaken conception of ethics that is committed to maximizing goodness. Yet now that we possess the concept of a Dasgupta-Koopmans ordering*, we must ask why one should think that the conception of ethics underlying Arrow's argument is appreciably different from the non-consequentialist Schefflerian one that Caney himself finds attractive.Footnote 18 On my reading of Arrow, his suggestion that each generation ‘maximize a weighted sum of its own utility and the sum of utility of all future generations, with less weight on the latter’ is simply the claim that the current generation is morally entitled to prefer consumption streams that are gentler on it than a goodness ordering* would be. I find no basis to infer, for example, that Arrow takes future well-being to improve the world at a slower rate than present well-being.Footnote 19 Indeed, Arrow explicitly endorses an obligation to ‘treat everyone else equally’ (Arrow Reference Arrow, Portney and Weyant1999: 16). His seems to be the pluralist view that equal-treatment and self-concern is each a genuine component of intergenerational ethics. Again as he puts it, ‘One can only say that both the universal other and the self impose obligations on an agent’ (Arrow Reference Arrow, Portney and Weyant1999: 16; emphasis in the original). This strongly suggests that Arrow is doing exactly what Caney wants him to do, viz. adopting something very much like Scheffler's view. I believe that is exactly what Arrow seeks to do when he seeks to build both ‘impersonally moral obligation’ and agent-relative moral convictions into his V-function (Arrow Reference Arrow, Portney and Weyant1999).
Many other philosophers appear to offer the same analysis of pure time preference as Rawls and Caney. Responding to the economist's claim that a pure discount rate of zero would be too onerous on the current generation, Dominic Roser replies that, ‘the whole underlying theory of utilitarianism is to be rejected and not simply the discount rate of zero within utilitarianism’ (Roser Reference Roser2009: 15; emphasis added). Darrel Moellendorf says that adopting a positive pure discount rate within a framework having ‘utilitarian origins’ amounts to ‘a bad fix to a rotten theory’ (Moellendorf Reference Moellendorf2014: 105, 116). And Tyler Cowen and Derek Parfit write:
If we aim for the greatest net sum of benefits over time, this may require a very unequal distribution between different generations. We may wish to deny that there ought to be such inequality. And we can avoid this conclusion, in some cases, if we discount later benefits. But, as Rawls points out, this is the wrong way to avoid this conclusion. If we believe that such inequality would be unjust, we should not simply aim for the greatest net sum of benefits. We should have a second moral aim: that these benefits be fairly shared between different generations. To our principle of utility we should add a principle about fair distribution. This more accurately states our real view. And it removes our reason for discounting later benefits. (Cowen and Parfit Reference Cowen, Parfit, Laslett and Fishkin1992: 149)
Each of these remarks suggests that pure time preference is the economist's way of holding onto the goodness-maximizing ‘principle of utility’ while still accommodating ostensibly non-utilitarian ideas. They characterize discounting as an operation that dilutes a policy's capacity to produce goodness, so that the policy becomes less attractive from a classical utilitarian point of view. And they suggest that the proper way to respect non-utilitarian ideals is not to embrace pure time preference, but rather to admit that the principle of utility is not the only fundamental moral principle.
I have argued that this standard philosophical account of what pure time preference within a V-function essentially consists in is mistaken. As I have shown, Cline and Dasgupta use consumption discount rates in part to reflect a traditionally non-consequentialist distinction between harming and not-aiding, while Arrow uses a positive rate of pure time preference to reflect Scheffler's non-consequentialist commitment to agent-centred prerogatives. I see no reason for characterizing the theoretical choices Cline, Dasgupta and Arrow make concerning the parameters η and ρ as ‘adjustments to the utilitarian principle’, rather than simply attempts to construct a mathematical function that can represent a plausible non-utilitarian ordering*. Dasgupta summarizes the situation nicely: ‘[B]ecause [the V-function] has the appearance of discounted utilitarianism, it's easy to be misled into thinking that Koopmans’ theory is only a vulgar form of Classical Utilitarianism’ (Dasgupta Reference Dasgupta, Hahn and Ulph2012: 106). I believe this is exactly the trap that philosophers frequently fall into.Footnote 20
My goal in this section has been to articulate what economists are not committed to simply by virtue of using a V-function to rank consumption streams. They are not committed to classical utilitarianism or any cousin thereof; nor are they committed to focusing only on what I have called goodness orderings. But precisely because this fact is missed by many, it is possible that at least some of the real-world debate over pure time preference amounts to talking at cross-purposes. Consider, for example, that in Nicholas Stern's report on the economics of climate change, Stern claims that he will employ ‘the ethical framework of standard welfare economics’, which ‘looks first only at the consequences of actions . . . [and] has no room, for example, for ethical dimensions concerning the process by which outcomes are reached’. He adds: ‘Some different notions of ethics, including those based on concepts of rights, justice and freedoms, do consider process’ (Stern Reference Stern2007: 32). This account of the ‘standard’ ethical framework underlying intertemporal welfare economics contrasts sharply with the frameworks that Cline, Dasgupta, Sen and Arrow appear to operate within. I am not in a position to speculate how this came to be. But given that it is so, there is some reason to think that Stern's stance on the evaluative scope of the V-function is partly responsible for the heated controversy his report caused by employing a very low rate of pure time preference. If Stern thinks that intertemporal welfare economics is exclusively concerned with goodness orderings, then it is possible that he and his critics are not really disagreeing.Footnote 21 For as I will stress in the next section, it is not inconsistent to reject pure time preference within a V-function designed to yield a goodness ordering while simultaneously embracing pure time preference within a distinct V-function designed to provide a Dasgupta-Koopmans ordering*.
4. EVALUATING PURE TIME PREFERENCE
I have drawn a distinction between economic analyses that use V-functions to generate goodness orderings and analyses that use them to generate Dasgupta-Koopmans orderings*. Let us distinguish further between a consumption stream's DK value, which reflects its ranking in a Dasgupta-Koopmans ordering*, and its Goodness value, which reflects its place in a goodness ordering. Derivatively, conceive of the DK value and Goodness value of a given time-stamped increment of consumption as the degree to which its presence in a consumption stream increases, relative to the status quo, the score assigned by a given Dasgupta-Koopmans V-function and a given goodness-focused V-function, respectively.
A crucial point emerges once these two notions of value are distinguished. For it is now conceptually possible to defend pure time preference when evaluating consumption's DK value while rejecting it when evaluating consumption's Goodness value. To illustrate: in the Transplant case, the policy of killing the one healthy person to save the five sick people carries the most Goodness value, since there is no compelling reason to discount the Goodness value of any of the six lives at issue. But if it is all-things-considered wrong to kill one to save the five, then the doctor should treat the policy of killing one patient as having less DK value than the policy that involves letting five die. Thus a Dasgupta-Koopmans V-function that seeks to represent a plausible Dasgupta-Koopmans ordering* will, in this case, discount the DK value of the well-being that would be produced by killing. While this is not an instance of ‘discounting for time’, it does illustrate the crucial point, which is that there can be good reasons to discount a benefit's DK value even if there are no good reasons to discount its Goodness value. And now that it is possible for these to come apart, we can see that philosophical objections to discounting the one do not immediately constitute objections to discounting the other.
From this point on, I will assume that it is indeed improper to adopt pure time preference when evaluating consumption streams’ Goodness value. For it is in the context of goodness orderings that pure time preference wrongly degrades the moral status of future people by implying that their consumption is, merely by virtue of their placement in time, less able to improve the world. It is here that the common complaint about ‘discrimination by date of birth’ has its grip.Footnote 22 But if we now agree that it is wrong to apply pure time preference to future consumption's Goodness value, what should we say about pure time preference in the context of future consumption's DK value? Or as I shall put the question, how should we think of pure DK discounting?
Before I can answer that question, I must introduce a further distinction of John Broome's. Pure time preference, Broome says, can be adopted in either a temporally neutral or a temporally relative way. Temporal neutrality is the view that value ‘does not depend on a temporal perspective’, whereas temporal relativity holds that value ‘depends on the perspective of the particular time when it is evaluated’ (Broome Reference Broome2012: 149). Each of these positions allows for pure time preference. Temporal relativity, for example, allows for pure time preference to be applied both forwards and backwards from whatever time the evaluation is being done. Such a view tilts in favour of the generation doing the evaluation, for it tends to engineer orderings whose top-ranked consumption streams are friendly to the consumption of the evaluating generation. To see that temporal neutrality also allows for pure time preference, note that one can convert a temporally relative V-function into a temporally neutral V-function simply by fixing the privileged year in time.Footnote 23 For example, if we fix 2016 as the privileged year, then although consumption in 2015 and 2017 will each have a rate of pure time preference applied to it, this will be so regardless of whether the evaluation is done in 2016 or 3500 or 1500 BCE. And that is enough to make the V-function temporally neutral. (It is, of course, not a very plausible way to adopt temporal neutrality.)
With this distinction between temporal neutrality and temporal relativity in hand, let us consider the plausibility of (1) temporally neutral pure DK discounting and (2) temporally relative pure DK discounting. (Since I have granted it is a moral mistake to apply pure time preference in the context of consumption's Goodness value, I shall have nothing more to say about it.)
It might at first seem incoherent to speak of temporally neutral pure DK discounting, given that I have built agent-relativity into the very concept of a Dasgupta-Koopmans ordering*. But we might be able to make sense of it. Consider a V-function that applies ‘exponential’ pure time preference throughout all history. (‘Exponential’ means that the rate of pure time preference is constant.) Thus, regardless of the evaluator's location in time (and setting aside inequality aversion), a unit of consumption in 1504 will be worth more than a unit of consumption in 1505, and a unit of consumption in 2049 will be worth more than a unit of consumption in 2050. Because it privileges no temporal vantage point, this V-function is temporally neutral. Still, it is possible for it to reflect agent-relative considerations, as well. To see this, consider Broome's response to Rawls's claim that the parties in his Original Position ‘will not consent to a [pure discounting] principle that weighs nearer periods more or less heavily’ (Rawls Reference Rawls1999: 260). Broome replies that ‘exponential discounting treats each generation less favourably relative to its predecessors. But in compensation, it treats each more favourably relative to its successors. And it has the advantage, compared with an impartial principle, of putting less strain on each generation's self control’ (Broome Reference Broome1992: 97–8). He concludes that the parties to Rawls's Original Position might well agree that exponential discounting adequately promotes their self-interest. Since concern for self is clearly an agent-relative concern, Broome's response to Rawls illustrates one way to adopt a temporally neutral V-function that still reflects agent-relative considerations.
But is this combination of temporal neutrality and pure DK discounting plausible? In his writings on discounting, Broome, like the other philosophers I've cited, interprets economists as focused on Goodness value. For example, after Broome himself carefully distinguishes between considerations of goodness and considerations of justice and rights, he says without argument that when economists express views on discounting, they are expressing ‘judgments about goodness’ (Broome Reference Broome2012: 150; see also Broome Reference Broome2008). Yet Broome at one point offers an objection to pure time preference that differs from the moral status-related objection that I have agreed is a problem when pure time preference is applied to consumption's Goodness value. And Broome's different objection can also be lodged against temporally neutral pure DK discounting:
[This view] requires later wellbeing to count for less than earlier wellbeing, whatever date it is regarded from. Wellbeing in 2010 counts for a fraction of wellbeing in 1910, say, and that is so from the perspective of 1920, 2010 or any other date. So major sacrifices would be worthwhile in 2010 if they could bring small benefits in 1910. This seems implausible. It is hard to test its plausibility, because it is hard to see how sacrifices made in 2010 could possibly bring benefits in 1910. But we can invent a thought experiment. Some people think it is good for a person to be famous after her death . . . Whatever you think of this idea, imagine for a moment it is correct. Then it would be possible to benefit Thomas Hardy by propagating his fame in 2010. And if wellbeing in 1910 is worth so much more than wellbeing in 2010, it would be worth great sacrifices on our part in 2010 to propagate Hardy's fame. It would be much more valuable than propagating the fame of a contemporary author. This is hard to believe. (Broome Reference Broome2004: 71)
Because Broome speaks of what could justify making great sacrifices in practice, his objection can be pressed against a Dasgupta-Koopmans V-function that gives consumption in the distant past much greater DK value than equivalent amounts of present consumption. And when pressed in that context, the objection does seem rather compelling – at least if we are willing to play along with Broome's fanciful example. Should we be willing? I'll return to this in a moment. Suppose for now that Broome's thought-experiment does reveal the implausibility of temporally neutral pure DK discounting. What about temporally relative pure DK discounting? Broome formulates a worry having to do with ‘reversals of value’ (Broome Reference Broome2004: 75; Reference Broome2012: 150–2) that can again be lodged against this kind of discounting, as it is a worry that is especially relevant when the task is that of placing one's options into an ordering*:
Suppose you now have a choice between two options A and B. If A is better than B relative to the present time, then [temporal-relativity] says you ought to choose A. Suppose you do as you ought and choose A. But suppose that relative to some later time, B is better than A. Then at the later time you ought not to have chosen A. You choose rightly, but it later turns out you chose wrongly. Indeed, it may turn out that you ought later to undo what you rightly did. Moreover, you might be able to foresee even as you choose A that just this would happen. This is a most implausible sort of incoherence in your activity. (Broome Reference Broome2004: 75)
Now, while I do not agree with Broome that Arrow is focused on goodness, Broome is on firmer ground when he says that Arrow discounts in a temporally relative way. As Broome puts it, ‘Being a practical man, [Arrow] does not consider past well-being, but we can assume that he would not assign enormous value to past events in the way that [temporally-] neutral discounting implies’ (Broome Reference Broome2012: 150). This, at any rate, is the interpretation supported by Arrow's appeal to an agent-relative principle of self-regard. So let us ask: is the prospect of value-reversals a fatal problem for the sort of pure DK discounting that Arrow seems to endorse? Arrow actually suggests not. His view appears to be that even if the morality of Schefflerian prerogatives initially recommends temporally relative pure DK discounting to each generation, a game-theoretic analysis of decision-making by successive generations will commend to each generation policies that mimic temporally neutral DK discounting (Arrow Reference Arrow, Portney and Weyant1999: 17). I do not have the space to evaluate Arrow's argument here. I will simply note that, so far, the only objection to it that we've encountered is Broome's ‘Thomas Hardy’ objection. Is that enough to sink Arrow's view? I am not prepared to say it is. After all, the Hardy objection applies only if it is possible to benefit dead people to a significant degree.Footnote 24 Yet if it is reasonable to ignore the possibility of posthumous benefits, and if Arrow's game-theoretic account of the practical upshot of agent-relative considerations is sound, then Arrow's view may offer a tolerable way to respect Schefflerian prerogatives while avoiding value reversals in practice.
Broome, though, has a third and final objection. He argues that even if agent-relative considerations do support the discounting of DK value, that is still no reason to embrace pure DK discounting. Instead, Broome suggests, prioritarianism can capture whatever is reasonable about prerogatives, and prioritarianism is expressed by adjusting η, not ρ. He writes:
What attraction does [pure time preference] have, anyway? Most of the arguments that have been presented in its favor are versions of this one: [classical] utilitarianism, which does not allow discounting, has implications that seem too demanding. It implies that we should be saving and investing much more for the future than seems plausible . . . Pure discounting at a fast enough rate is another way to evaporate the problem. But it does not attack the problem's intuitive source, which is that we should not be asked to make a big sacrifice for better-off people. Pure discounting is an ad hoc fix. (Broome Reference Broome2012: 152–3)
Broome thinks the source of the problem of intergenerational demandingness is the conviction that we should not be asked ‘to make such a big sacrifice for future generations even if those generations will be better off than us’ (Broome Reference Broome2012: 152). If he were right about that, then the problem could indeed be addressed by increasing η in the V-function, because that's how one dilutes the DK value of consumption that would accrue to better-off people. But is Broome correct that prioritarianism fully addresses the problem of intergenerational demandingness? Consider a world without human-caused climate change in which an avoidable natural disaster (e.g. a preventable volcanic eruption) is expected in 2200.Footnote 25 Suppose everyone in the current generation enjoys the same level of consumption enjoyed by the average American today. Now suppose the current generation must choose between the following two options:
Business As Usual, in which everyone living until 2200 enjoys the current generation's level of consumption and all people living after 2200 enjoy the consumption-level of the average American in 1980.
Prevention, in which the current generation sacrifices to prevent the volcanic eruption, thereby reducing their consumption to that of the Average American in 1985; as a result, all future people enjoy the consumption-level of the average American in 1985.
I suspect many will take the view that members of the current generation may exercise Schefflerian prerogatives to protect their own consumption levels, especially since they (ex hypothesi) do not cause the volcanic eruption. But now note that the prerogative-friendly option, Business as Usual, cannot be defended by increasing η within a Dasgupta-Koopmans V-function. For in both Business as Usual and Prevention, future generations’ consumption is lower than the current generation's. This means the growth rate in consumption, g, is negative in both cases, and thus the consumption discount rate is also negative (assuming we're forswearing pure time preference for the sake of argument). Just as a high positive η combined with a positive g enables us to sharply discount the consumption that accrues to better off future people, a high positive η combined with a negative g leads to sharply discounting our own consumption for the sake of consumption that will accrue to future people who are worse off than we are. So increasing η for prioritarian reasons would support choosing Prevention. The only plausible way to rank Business as Usual above Prevention – at least within a V-function – is to embrace pure DK discounting within the Dasgupta-Koopmans V-function.
I wish to stress that I am not defending business as usual in the actual world, where the consumption of future generations is gravely threatened not by a natural disaster but by potentially catastrophic human-induced climate change. Nor am I even defending Business as Usual in the example above (though I do have the intuition that Business as Usual is morally permissible). The point is only that there are conceivable cases in which pure DK discounting is not necessarily ad hoc. Whether it is defensible in the real world depends crucially on what one wants to say about the larger question of climate change and intergenerational ethics. If it turns out that the current generation is morally entitled to assert even a weak Schefflerian prerogative when evaluating its climate change-related obligations, then at least some pure DK discounting may be justified. Pace Broome and others (Asheim and Buchholz Reference Asheim and Buchholz2003; Dasgupta Reference Dasgupta2008: 157), the independent prospect of increasing η for prioritarian reasons does not change this.
5. CONCLUSION
My goal in this article has been to clarify the conceptual landscape against which the debate over pure time preference unfolds, and to begin to evaluate the arguments for and against pure time preference within the Dasgupta-Koopmans framework that many economists appear to adopt. My conclusion to this point is that we need further substantive discussions of intergenerational ethics to decide whether pure DK discounting should be a part of the current generation's response to the situation it faces. At the very least, pure time preference is not the obvious ethical non-starter that most philosophers and many economists insist it is.
I want to close by noting that even if the current generation is justified in invoking Schefflerian prerogatives in its policy responses to future threats like climate change, there may still be strong reasons to jettison pure time preference from intertemporal welfare economics. Consider, for example, the following claims made by WG3:
Justice is concerned with ensuring that people get what is due to them . . . Justice and rights are correlative concepts. On the other hand, criteria of value are concerned with improving the world: making it a better place. (Kolstad et al. Reference Kolstad, Urama, Broome, Edenhofer, Pichs-Madruga and Sokona2014: 215)
What ethical considerations can economics cover satisfactorily? Since the methods of economics are concerned with value, they do not take account of justice and rights in general . . . Economics is not well suited to taking into account many other aspects of justice, including compensatory justice. (Kolstad et al. Reference Kolstad, Urama, Broome, Edenhofer, Pichs-Madruga and Sokona2014: 215)
There are two claims here. The first concerns what the ‘methods of economics are concerned with’; the second concerns what the methods of economics are ‘well suited’ for. In its first claim, WG3 falsely implies that welfare economists never attempt to take account of justice and rights when they discuss η and ρ. As I have argued, that is precisely what Dasgupta, Cline and Arrow are doing when they set values to η and ρ. However, I am more interested now in WG3’s second claim. Even if WG3 means only that the methods of welfare economics, in their current state of development, are ‘not well suited to taking into account many other aspects of justice’, that could still have profound implications for the issue of pure time preference. For if V-functions should not be used to generate Dasgupta-Koopmans orderings*, then Dasgupta, Cline, Arrow and Sen would be wrong to tailor η and ρ to reflect agent-relative considerations concerning intergenerational harming and Schefflerian prerogatives. Welfare economics would then be forced to retreat into the role of providing goodness orderings only, which would leave economists only the options of pure time preference as applied to Goodness value (which I have granted is a morally problematic form of discrimination) and the more plausible form of discounting Goodness value that can be supported by egalitarian and/or prioritarian reasons and that is captured by η. Thus, depending on the ultimate limitations of intertemporal welfare economics, Broome might actually be right that η can capture all the reasons there are to discount future consumption in economic evaluations of climate change policy. But that will be so only if economists should radically restrict the use to which V-functions are put. If V-functions should be used to rank consumption streams solely in terms of their Goodness value, and not (as is often the case) in terms of their DK value, then it would be true after all that the rate of pure time preference, ρ, should always be set to zero.Footnote 26
ACKNOWLEDGEMENTS
I presented material from this paper at conferences on ethical issues in climate economics at the University of Salamanca (an ECPR workshop), the Martin School at Oxford University (an ESRC workshop), Duke University and Cornell University. I am grateful to participants for valuable feedback. For very helpful written comments and/or conversation, I thank Simon Beard, John Broome, Mark Budolfson, Simon Caney, Partha Dasgupta, Marc Davidson, Steven Durlauf, David Grober-Morrow, Lauren Hartzell Nichols, Daniel Hausman, Avram Hiller, Douglas MacLean, Christopher McKelvey, Antony Millner, Kian Mintz-Woo, John Mullahy, Matthew Rendall, Dominic Roser and two anonymous referees for Economics and Philosophy, one of whom provided extensive detailed comments that led to many improvements and helped me avoid several mistakes.



