1. INTRODUCTION
Belief revision plays a fundamental role in human decision making, and determines to a large extent the choices we make. Indeed, the beliefs we hold today may be contradicted by new evidence tomorrow, and at that point in time we must be prepared to change our beliefs as to accommodate the new piece of information. The choices we make tomorrow will therefore crucially depend upon how we revise these beliefs.
So, in order to understand how people make decisions in a dynamic environment we must first investigate how they may revise their beliefs upon observing new facts. Of course there are many different ways of changing beliefs, and in order to develop a meaningful theory of belief revision we must present a list of desirable properties that a belief revision process should satisfy. In the 1980s, Alchourrón et al. (1985) presented one such list of properties – known today as the AGM-axioms – that would have a fundamental impact on the development of belief revision theory. The class of belief revision policies satisfying the AGM-axioms still serves as a central model of belief change in many works in various different areas.Footnote 1
Some years later, Grove (1988) proved a beautiful characterization result which states that the belief revision policies satisfying the AGM-axioms are precisely those that can be derived from some plausibility ordering over states of the world. By the latter we mean that the decision-maker ranks all possible states of the world in terms of their (subjective) plausibility, and upon receiving a new piece of information restricts his new belief to the most plausible states that are compatible with the new information. This plausibility ordering not only determines the decision-maker’s initial belief – namely the set of states he deems most plausible overall – but also how the decision-maker changes his belief in case the new information completely – or partially – contradicts his initial belief. In this case, the decision-maker restricts his attention to a smaller set of states – namely those that are not ruled out by the new information – and among these states he selects those that he finds most plausible. This will then serve as his new, revised belief. In my view, plausibility orderings provide a very natural way of inducing a belief revision policy, and Grove’s representation theorem confirms that the AGM-axioms indeed establish an intuitive list of postulates, leading to a natural class of belief revision rules.
Belief revision is of special importance in dynamic games, where players may learn new facts about the past behaviour of their opponents during the game. In such cases, players may need to revise their beliefs about the opponents’ strategy choices, and the eventual choices made by the players will crucially depend on how they revise these beliefs. As an illustration, consider the dynamic game in Figure 1.
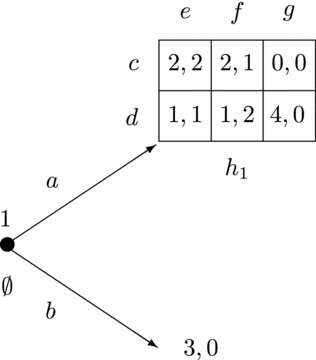
Figure 1. Belief revision matters for choices
For player 2 it seems reasonable to initially believe – before anything has happened – that player 1 will choose b and end the game immediately. To see this, note that for player 2 it is irrational to choose g. Hence, if player 1 believes that player 2 would choose rationally upon choosing a, then player 1 expects not to get more than 2 by choosing a, and therefore would rather choose b.
But what would player 2 do in this game? If it is player 2’s turn to make a move, he knows that player 1 has chosen a, and not b, so player 2 has to revise his initial belief about player 1. But how? We will describe two plausible belief revision scenarios for player 2 in this game, leading to two different choices.
In the first scenario, player 2 believes that choosing a was a conscious, optimal choice for player 1. In that case, however, player 2 must believe that player 1 will subsequently choose d, as this is the only way for player 1 to obtain more than 3 – the utility he could have guaranteed by choosing b at the beginning. So, player 2 will respond by choosing f. Note that in this scenario, player 2, upon observing a, can no longer believe that player 1 believes that player 2 will choose rationally after a. Namely, in order to rationalize player 1’s move a, player 2 must believe that player 1 ascribes a high probability to player 2 making the irrational choice g, as only then can player 1 achieve more than 3 by choosing a. This belief revision scenario corresponds to the forward induction concept of ‘common strong belief in rationality’ as developed by Battigalli and Siniscalchi (2002), and which is based upon the ‘extensive-form rationalizability procedure’ by Pearce (1984). The main idea in this concept is that a player, when he observes an unexpected move by his opponent, tries to interpret this move as being part of an optimal strategy, whenever this is possible. This is precisely what player 2 does in the game of Figure 1 under the belief revision scenario described above, when he observes the unexpected move a by player 1. He interprets a as being part of an optimal strategy by player 1, but then he must believe that player 1 will choose the follow-up action d, and hence player 2 will choose f himself.
This is not the only plausible way for player 2 to revise his belief, however. If he observes that player 1 has – surprisingly – chosen a, he could also believe that this was a mistake by player 1, but that player 1 will still choose rationally in the game that lies ahead, and that player 1 still believes that player 2 will choose rationally in the remainder of the game. In that case, player 2 will believe that player 1 believes that player 2 will not choose g. Hence, player 2 will believe that player 1 chooses c after a – and not d as in the belief revision scenario above. As a consequence, player 2 will respond by choosing e – and not f as in the scenario above. This second belief revision scenario is implicit in the backward induction concept of ‘common belief in future rationality’ as proposed by Perea (2014) and Baltag et al. (2009). The key condition in this concept is that a player, upon observing an unexpected move by his opponent, always believes that the opponent will choose rationally from now on, and that the opponent believes that the other players will also choose rationally from now on, and so forth. However – and that is the main difference with ‘common strong belief in rationality’ – the player need not believe that the opponent’s past choice was an optimal choice, even when believing so is possible. In fact, the player is free to believe that the unexpected move he observed was actually a mistake by the opponent. What is important is that the player believes that from now on everything is back to normal – that is, that the opponent will choose rationally from now on, and that the opponent believes that everybody else will choose rationally from now on, and so forth. In this sense the concept is entirely forward looking, as it only imposes conditions on how players reason about current and future moves, and not about past moves. That is why we call it a backward induction concept, as opposed to forward induction reasoning which requires players to also reason critically about opponents’ past moves.
We thus see that the forward induction concept of ‘common strong belief in rationality’ and the backward induction concept of ‘common belief in future rationality’ do not only describe different belief revision scenarios for player 2 in the game above, but also lead to different choices for player 2. This shows that belief revision crucially matters for how players choose in a dynamic game.
Since belief revision is so important for the study of dynamic games, it seems only natural to embed the analysis of dynamic games within the framework of belief revision theory. But somewhat surprisingly, this approach has hardly been adopted so far in the game theory literature – some exceptions being the works by Bonanno (2009, 2011, 2013) and Baltag et al. (2009).
The purpose of this paper is to enhance this connection by building a bridge between the study of dynamic games on the one hand, and the idea of plausibility orderings in belief revision theory on the other hand. For this investigation we restrict our attention to the concepts of ‘common strong belief in rationality’ and ‘common belief in future rationality’ mentioned above. In general, these two concepts do not prescribe a unique belief revision policy for a player, but typically select for every dynamic game a whole collection of belief revision policies for this player. Of course, these belief revision policies must share some common feature, since they all correspond to the same game-theoretic concept. The question we want to address for each of the two concepts is whether the entire collection of belief revision policies selected for a given player can be summarized by a common plausibility ordering. That is, can we find, for every player i, a unique plausibility ordering such that the belief revision policies selected for player i by the concept at hand are precisely those belief revision policies that respect this plausibility ordering. If that is true, then the common feature that these belief revision policies share is precisely this common plausibility ordering. In fact, the whole game-theoretic concept could then be summarized by one plausibility ordering for each of the players, which would constitute a very simple and natural representation of the concept. It would also reveal a clear intuition for the concept at hand, as the concept would require every player to revise his beliefs according to this common plausibility ordering – nothing more and nothing less.
We find that the collection of belief revision policies selected by ‘common strong belief in rationality’ can indeed by summarized by a single plausibility ordering for each of the players, whereas this is not always possible for ‘common belief in future rationality’ in some games. Moreover, we show in Theorem 6.4 what this plausibility ordering looks like for ‘common strong belief in rationality’. In contrast, for the concept of ‘common belief in future rationality’ a unique plausibility ordering is often not enough to characterize all belief revision policies for a given player in the game. We provide an example for this in Section 7.2.
At the end of this paper we focus on the special class of games with perfect information, in which players move one at a time, and always observe precisely what their opponents have done so far. We show by means of a counterexample that even in such games, the collection of belief revision policies selected for a given player by ‘common belief in future rationality’ cannot be characterized by a unique plausibility ordering. However, we show that the concept can be refined to a stronger concept, ‘common belief in rationality at future and parallel information sets’, where these collections of belief revision policies can be characterized by a common plausibility ordering for this special class of games, provided there are no relevant ties in the game. Moreover, the latter concept, like ‘common belief in future rationality’, always induces the backward induction strategies in such games.
For the class of games with perfect information, Baltag et al. (2009) have defined the concept of ‘common knowledge of stable belief in dynamic rationality’, which has exactly the same spirit as ‘common belief in future rationality’, and show that it also uniquely yields the backward induction strategies in case there are no relevant ties. One difference with ‘common belief in future rationality’ is that their concept assumes, from the beginning, that the belief revision policies are given by a unique plausibility ordering for every player. So, in that sense the concept is similar to ‘common belief in rationality at future and parallel information sets’ which is also characterized by a unique plausibility ordering for every player in perfect information games without relevant ties, and also uniquely leads to the backward induction strategies there. These insights show that for perfect information games, backward induction can be characterized by suitably chosen plausibility orderings.
The paper is organized as follows. In Section 2 we give a formal definition of a dynamic game and its associated strategies. In Section 3 we introduce hierarchies of conditional beliefs in dynamic games, and show how these can be encoded by means of an epistemic model with types. We also show how belief revision can be captured within this model. In Section 4 we give a definition of a ‘reasoning context’ for dynamic games, describing the possible belief hierarchies that a player can hold for any such game. The concepts of ‘common strong belief in rationality’ and ‘common belief in future rationality’ are thus special cases of a ‘reasoning context’. In Section 5 we introduce plausibility orderings in dynamic games, and define what it means for a reasoning context to be characterized by a unique plausibility ordering for every player. This means that for every player, the whole collection of selected belief hierarchies can be summarized by a unique plausibility ordering for this player – precisely the idea we have discussed above. In Section 6 we formally introduce the concept of ‘common strong belief in rationality’ and show that it can always be characterized by a unique plausibility ordering for every player. In Section 7 we formally define the concept of ‘common belief in future rationality’ and demonstrate that it cannot always be characterized by a unique plausibility ordering for every player. In Section 8 we investigate the class of games with perfect information, as discussed above. In Section 9 we end with a discussion. All proofs are collected in the appendix.
2. DYNAMIC GAMES
2.1 A Model of Dynamic Games
In a dynamic game, players may have to choose more than once during the course of the game, and may partially or completely observe what other players have done in the past when it is their time to make a choice. Throughout this paper we assume that the dynamic game is finite – that is, the game ends after finitely many moves, and every player has finitely many choices available at every moment in time where it is his turn to move. Formally, a finite dynamic game G consists of the following ingredients.
There is a finite set of players I. The instances where one or more players must make a choice are given by a finite set X of non-terminal histories. The possible instances where the game ends are described by a finite set Z of terminal histories. By ∅ we denote the beginning of the game.
Consider a non-terminal history x where it is player i’s turn to move. As player i may not fully observe what his opponents have done in the past, player i may not be able to distinguish x from other non-terminal histories. Formally, we model player i’s information at x by an information set h that contains all non-terminal histories that, from player i’s point of view, are indistinguishable from x. We denote by Hi the collection of all information sets for player i in the game. We assume that there is perfect recall, meaning that a player never forgets what he previously did, and what he previously knew about the opponents’ past choices.
Consider a non-terminal history x at which player i must make a choice. By Ci(x) we denote the finite set of choices that are available to player i at x. Let h ∈ Hi be the information set for player i to which x belongs. As on the one hand, player i cannot distinguish x from other non-terminal histories in h, but on the other hand is assumed to know the set of choices available to him, we must require that Ci(y) = Ci(x) for all non-terminal histories y ∈ h. But then, we may as well use the notation Ci(h), specifying the (unique) set of choices available to player i at information set h ∈ Hi.
We explicitly allow for simultaneous moves in the dynamic game. That is, we allow for non-terminal histories at which several players make a choice. Formally, this means that for some non-terminal histories x there may be different players i and j, and information sets h ∈ Hi and h′ ∈ Hj, such that x ∈ h and x ∈ h′. In this case, we say that the information sets h and h′ are simultaneous. So, two information sets h ∈ Hi and h′ ∈ Hj are simultaneous if they have a non-empty intersection. For instance, in the game of Figure 1 we see that players 1 and 2 simultaneously move at information set h 1. In that game, the information set for player 1 at that stage is identical to the information set for player 2 at that stage – both are equal to h 1. But in general there may also be different information sets h ∈ Hi and h′ ∈ Hj that are simultaneous. Consider, for instance, two non-terminal histories x and y where both i and j make a choice. Suppose that player i knows at x that x has been reached. So, h = {x} is an information set for player i. Suppose that player j does not know at x whether x or y has been reached. So, h′ = {x, y} is an information set for player j. Then, h and h′ are simultaneous – yet different – information sets.
Consider a non-terminal history x where I(x) is the set of active players. That is, I(x) contains those players who must make a choice at x. Then, every combination of choices (ci)i ∈ I(x) is assumed to move the game from the non-terminal history x to some other (terminal or non-terminal) history y. These transitions can formally be described by a move-function m, which assigns to every non-terminal history x, and every combination of choices (ci)i ∈ I(x), the (terminal or non-terminal) history m(x) that follows.
We say that history y follows some other history x if y can be reached from x by a suitable sequence of choice combinations, given the move-function m. Similarly, we say that an information set h follows some other information set h′ if there are histories x ∈ h and y ∈ h′ such that x follows y. We say that information set h weakly follows h′ if either h follows h′, or h and h′ are simultaneous. We assume, throughout this paper, that there is an unambiguous ordering of the information sets in the game. That is, if information set h follows information set h′, then h′ does not follow h. Or, equivalently, there cannot be histories x, y ∈ h, and histories x′, y′ ∈ h′ such that x follows x′, and y′ follows y.
Players are assumed to have preferences over the possible outcomes in the game, representable by utility functions over the set of terminal histories Z. Formally, for every terminal history z ∈ Z and player i, we denote by ui(z) the utility for player i at z, representing how desirable he deems the outcome z.
2.2 Strategies
Intuitively, a strategy for a player is a complete plan which describes what he will, or would, do in every situation that could possibly arise in the game. By definition, the possible situations in the game where player i must make a choice are exactly the information sets in Hi. So, a possible definition of a strategy for player i – and this is in fact the traditional definition of a strategy in game theory – would be a function that assigns an available choice to each of player i’s information sets. The problem with this definition, however, is that it may contain some redundant information, as certain future information sets of player i can be excluded by choices at earlier information sets of player i. In that case, it is no longer relevant to specify what this player would do at those excluded future information sets, as those information sets will certainly not be reached if the player implements the strategy correctly – as we suppose him to do. Consider, for instance, the game in Figure 1. If player 1 decides to go for b at the beginning of the game, he is certain that his future information set h 1 will not be reached. So in that case it is redundant to specify what player 1 would do were h 1 to be reached, as h 1 is clearly avoided by the choice b. We may therefore view b as a complete plan, although b is not a strategy in the traditional sense. In fact, we will accept b as a full description of a strategy for player 1.
An argument that is often used in defence of the traditional definition of a strategy is that the choices specified at precluded information sets reflect the opponents’ counterfactual beliefs about his future behaviour if the player decides to deviate from his plan. See Rubinstein (1991) for a discussion of this issue. But this would mean that the strategy represents both choices and beliefs – something I consider highly undesirable. In my opinion, we should always clearly separate objects of choice from beliefs, and to put them in the same object is likely to cause confusion. After all, the term strategy suggests that it reflects only the plan of choices of a player. The beliefs of the players will anyhow be modelled separately in the next section, so there is no need to mix them with the players’ choices.
Having said this, we opt for a definition of a strategy that only prescribes choices at those information sets not precluded by earlier choices. To define this formally, consider two information sets h and h′ for player i, and an available choice c ∈ Ci(h) at h. We say that choice c avoids information set h′ if h precedes h′, and if for every non-terminal history x ∈ h, choosing c at x can never lead to a non-terminal history in h′.
Definition 2.1 (Strategy)A strategy for player i is a function 
$s_{i}:\hat{H} _{i}\rightarrow \cup _{h\in \hat{H}_{i}}C_{i}(h)$where (1) 
$\hat{H }_{i}\subseteq H_{i},$(2) si(h) ∈ Ci(h) for all 
$h\in \hat{H}_{i},$(3) for every 
$h\in \hat{H}_{i}$there is no 
$h^{\prime }\in \hat{H}_{i}$such that the prescribed choice si(h′) avoids h, and (4) for every h ∈ Hi, if h is not avoided by any prescribed choice si(h′) with 
$h^{\prime }\in \hat{H }_{i},$then h must be in 
$\hat{H}_{i}.$
Conditions (3) and (4) thus guarantee that 
$\hat{H}_{i}$ contains exactly those information sets not precluded by earlier choices – not more and not less. The definition of a strategy we use corresponds to what Rubinstein (1991) calls a plan of action.
Let us denote by Si the set of all strategies for player i. Since the dynamic game G is finite, the set Si will be finite as well. By S ≔ ×i ∈ ISi we denote the set of all strategy combinations, and for every player i we denote by S − i ≔ ×j ∈ I\{i}Sj the set of strategy combinations for i’s opponents. For a given information set h ∈ Hi, let S(h) be the set of strategy combinations that reach h – that is, the set of strategy combinations (sj)j ∈ I that reach some history in h if every player j carries out his strategy sj. By Si(h) we denote the set of strategies si for player i for which there is some opponents’ strategy combination s − i ∈ S − i such that (si, s − i) ∈ S(h). We say that strategies in Si(h) possibly reach h. Similarly, S − i(h) denotes the set of strategy combinations s − i ∈ S − i for which there is some strategy si ∈ Si such that (si, s − i) ∈ S(h). We say that strategy combinations in S − i(h) possibly reach h.
Consider some information set h ∈ Hi for player i. As we assume that the game G has perfect recall, player i remembers at h each of his past choices, and hence h is preceded by a unique sequence of past choices for player i. So, Si(h) contains precisely those strategies that prescribe this unique sequence of player i choices preceding h. But then, it is not difficult to see that S(h) = Si(h) × S − i(h) for every h ∈ Hi.
3. MODELLING BELIEF HIERARCHIES
We now wish to model the players’ beliefs in a dynamic game. There are at least two complications that we face here.
First, when players reason about their opponents in a dynamic game, they do not only hold beliefs about what other players do (first-order beliefs), but also hold second-order beliefs about the opponents’ first-order beliefs about what others do, and third-order beliefs about the opponents’ second-order beliefs, and so on. So, players hold a full infinite belief hierarchy.
Secondly, a player in a dynamic game may have to revise his belief if the game moves from one of his information sets to another. That is, a player will hold at each of his information sets a new conditional belief about the opponents which is compatible with the event that this particular information set has been reached. Consider, namely, some player i who observes that his information set h ∈ Hi has been reached. Then he knows that his opponents’ must be implementing some combination of strategies in S − i(h) – the set of opponents’ strategy combinations that make reaching h possible – and hence player i must at h restrict his belief to opponents’ strategy combinations in S − i(h). And this conditional belief may be – partially or completely – contradicted at some later information set, in which case he must change his belief there.
Consider, for instance, the game in Figure 1, and suppose that player 2 initially believes that player 1 chooses b. Then, if player 2 is required to make a choice at h 1, he knows that player 1 has chosen a, and hence his previous belief was wrong. Player 2 must therefore substitute it by a new conditional belief at h 1 that only considers strategies for player 1 that are still possible – namely (a, c) and (a, d).
Summarizing, we see that we need to model conditional belief hierarchies for a player, which specify at each of his information sets what he believes about the opponents’ strategy choices, the opponents’ first-order beliefs, the opponents’ second-order beliefs, and so on. But how can we model such complicated objects? One way to do so is by using a Harsanyi-style model with types (Harsanyi 1967–1968) and adapt it to dynamic games. To see how this works, consider a player i who at information set h ∈ Hi holds a belief about the opponents’ strategies, the opponents’ first-order beliefs, the opponents’ second-order beliefs, and so on. In other words, this player holds at h a belief about the opponents’ strategies and the opponents’ conditional belief hierarchies. So, a conditional belief hierarchy for player i specifies at each of i’s information sets a conditional belief about the opponents’ strategy choices and the opponents’ conditional belief hierarchies. If we substitute the word ‘belief hierarchy’ by the word ‘type’ – as Harsanyi did – then we obtain the following definition.
Definition 3.1 (Epistemic model)Consider a dynamic game G. An epistemic model for G is a tuple M = (Ti, bi)i ∈ Iwhere
(a) Ti is a set of types for player i,
(b) bi is a function that assigns to every type ti ∈ Ti, and every information set h ∈ Hi∪{∅}, a probability distribution bi(ti, h) ∈ Δ(S − i(h) × T − i).
Recall that S − i(h) represents the set of opponents’ strategy combinations that possibly reach h. By T − i ≔ ×j ∈ I{j}Tj we denote the set of opponents’ type combinations. For every set X, we denote by Δ(X) the set of probability distributions on X. Clearly, player i must at h only assign positive probability to opponents’ strategy combinations in S − i(h), as these are the only strategy combinations compatible with the event that h is reached. This explains the condition in (b) that bi(ti, h) ∈ Δ(S − i(h) × T − i). Note that in part (b) we require player i to hold a conditional belief also at ∅ – the beginning of the game – even when player i is not active there. Hence, we assume that every player holds an initial belief before the start of the game.
From now on, we will use the notation H*i ≔ Hi∪{∅}. So, at every information set h ∈ H*i type ti holds a conditional probabilistic belief bi(ti, h) about the opponents’ strategies and types. In particular, type ti holds conditional beliefs about the opponents’ strategies. As every opponent’s type holds conditional beliefs about the other players’ strategies, every type ti holds at every h ∈ Hi also a conditional belief about the opponents’ conditional beliefs about the other players’ strategy choices. And so on. Since a type may hold different beliefs at different histories, a type may, during the game, revise his belief about the opponents’ strategies, but also about the opponents’ conditional beliefs. In fact, for a given type ti within an epistemic model, we can derive the complete belief hierarchy it induces.
4. REASONING CONTEXTS
A reasoning context imposes restrictions on the way a player reasons about his opponents in a dynamic game. Remember from the previous section that we have summarized the reasoning of a player by a conditional belief hierarchy, which describes at each of his information sets what he believes about the opponents’ strategy choices, the opponents’ first-order beliefs, the opponents’ second-order beliefs, and so on. In turn, such belief hierarchies have been modelled by epistemic models with types, which may be seen as an easy way to encode such infinite belief hierarchies.
But if this is true, then we could attempt to formalize a reasoning context as follows: Take an arbitrary dynamic game G and an epistemic model M. Then, a reasoning context selects for a given player a subset of types within M, representing those belief hierarchies that are ‘allowed for’ by the reasoning context. Although this may seem reasonable there is one major problem with this attempt, namely that the epistemic model at hand may not contain all belief hierarchies that we are interested in – some belief hierarchies that we would wish to select are simply not present in the epistemic model. In order to avoid this problem we assume the epistemic model to be belief completeFootnote 2(cf. Brandenburger 2003).
Definition 4.1 (Belief complete epistemic model)Consider a dynamic game G and an epistemic model M = (Ti, bi)i ∈ Ifor G. The epistemic model M is belief complete if for every player i, and every possible conditional belief vector βi = (βi(h))h ∈ H*ifor player i, where βi(h) ∈ Δ(S − i(h) × T − i) for every h ∈ H*i, there is some type ti ∈ Ti for which bi(ti, h) = βi(h) for every h ∈ H*i.
That is, for every possible conditional belief vector that we can construct within our model there is a type that has precisely this belief vector. It is not at all obvious that such models will always exist. Battigalli and Siniscalchi (1999), however, have shown that for every finite dynamic game, we can always construct a belief complete epistemic model which assumes (common belief in) Bayesian updating. A similar construction can be employed to build a belief complete epistemic model without Bayesian updating, as we use here. Formally speaking, there may be various different belief complete epistemic models for a given dynamic game. However, all such belief complete epistemic models may be viewed as ‘equivalent’, since each of these encodes all possible conditional belief hierarchies we can think of.
So, if we work with a belief complete epistemic model, then we are sure not to miss out on any conditional belief vector we could possibly have constructed within our model. With this definition at hand, we can now define a reasoning context as a mapping that selects a subset of belief hierarchies within a belief complete epistemic model.
Definition 4.2 (Reasoning context)A reasoning context is a mapping ρ that assigns to every finite dynamic game G, every belief complete epistemic model M = (Ti, bi)i ∈ Ifor G, and every player i ∈ I, some subset ρi(G, M)⊆Ti of types.
So, effectively, a reasoning context selects for every dynamic game a set of belief hierarchies for every player – those belief hierarchies that are deemed ‘most plausible’ by this reasoning context.
5. PLAUSIBILITY ORDERINGS
5.1 Plausibility Orderings in Dynamic Games
Plausibility orderings are a very natural way to generate, or characterize, belief revision policies by agents. Consider an agent whose space of uncertainty is given by a set X of possible states of the world. Now suppose that, before receiving any new information, this agent ranks the possible states in X according to a plausibility ordering. That is, for every pair of states x and y, the agent specifies which of these two states he deems more plausible, if any. If the agent subsequently receives new information revealing that the true state must be in E⊆X, then it makes intuitive sense for the agent to concentrate his conditional belief only on states in E that he deems ‘most plausible’.
This approach plays an important role both in belief revision theory and counterfactual logic. Grove (1988) has shown that the belief revision policies that follow the AGM axioms are exactly those that can be characterized by plausibility orderings over states. So, in a sense, the AGM axioms for belief revision are logically equivalent to the use of plausibility orderings. In his paper, Grove uses systems of spheres instead of plausibility orderings, but we will see below that both approaches are equivalent. Lewis (1973) and Stalnaker (1968), on the other hand, use plausibility orderings to evaluate counterfactual statements. More precisely, they assume for every state x a plausibility ordering over states that deems x, and only x, as most plausible. According to the Lewis-Stalnaker theory, a conditional statement ‘if p then q’ is true at that state x if q is true at all ‘most plausible p-states’. By the latter, we mean states at which p is true, and which are most plausible amongst the states at which p is true. Unlike Lewis, Stalnaker assumes that there is always a unique most plausible p-state, but apart from this the two approaches are basically equivalent. An important difference between the Grove model and the Lewis–Stalnaker model is that Grove assumes just one global plausibility ordering, whereas Lewis and Stalnaker consider a local plausibility ordering for every state x.
In a dynamic game, a player holds at each of his information sets some conditional belief about the opponents’ strategies and belief hierarchies. In the previous section we have seen that the players’ belief hierarchies can be encoded by means of types within a epistemic model M = (Ti, bi)i ∈ I. Moreover, M is guaranteed to capture, for every player i, all possible conditional belief vectors on S − i × T − i if we require M to be belief complete. So, if we take a belief complete epistemic model M = (Ti, bi)i ∈ I, then the space of uncertainty for player i is given by S − i × T − i – the set of all opponents’ strategy-type combinations. Consequently, a plausibility ordering for player i is an ordering over the set S − i × T − i.
Definition 5.1 (Plausibility ordering)Consider a dynamic game G and a belief complete epistemic model M = (Ti, bi) for G. Then, a plausibility ordering for player i is a binary relation ≽ion S − i × T − ithat is
(a) total, i.e. for every two strategy-type combinations x and y in S − i × T − ieither x ≽iy or y≽ix,
(b) reflexive, i.e. x ≽ix for every x ∈ S − i × T − i, and
(c) transitive, i.e. x≽iz whenever there is some y with x ≽iy and y≽iz.
The meaning of x ≽iy is that player i deems the opponents’ strategy-type combination x at least as plausible as y. Consider now a player i who holds a plausibility ordering ≽i on S − i × T − i, and who observes that his information set h has been reached. Then, player i knows that the opponents’ strategy-type combination must be somewhere in S − i(h) × T − i, as S − i(h) contains precisely those opponents’ strategy combinations that make reaching h possible. If player i’s belief revision policy is governed by his plausibility ordering ≽i, then player i should concentrate his conditional belief at h on those strategy-type combinations in S − i(h) × T − i that he deems most plausible. That is, player i must concentrate his conditional belief on the set
\begin{equation*}
\text{max}_{\succcurlyeq _{i}}(S_{-i}(h)\times T_{-i}):=\lbrace x\in S_{-i}(h)\times T_{-i}\text{ }|\text{ }x \succcurlyeq _{i}y\text{ for all }y\in S_{-i}(h)\times T_{-i}\rbrace .
\end{equation*}
But for this conditional belief to be well-defined, we must require that the set max≽i(S − i(h) × T − i) is non-empty. So, we must require that at each of player i’s information sets, there is at least one most plausible strategy-type combination in S − i(h) × T − i. This condition is not automatically satisfied as the set T − i is infinite – in fact uncountably infinite – whenever the epistemic model is belief complete and the game is non-trivial. A plausibility ordering that satisfies this additional requirement is called well-ordered.
Definition 5.2 (Well-ordered)A plausibility ordering ≽ion S − i × T − iis well-ordered if the set max ≽i(S − i(h) × T − i) is non-empty for every information set h ∈ Hi.
It turns out that there is a close connection between well-ordered plausibility orderings and systems of spheres as used in Grove (1988). Namely, for a given well-ordered plausibility ordering ≽i, consider for every x ∈ S − i × T − i the set
\begin{equation*}
sphere_{x}:=\lbrace y\in S_{-i}\times T_{-i}\text{ }|\text{ }y\succcurlyeq _{i}x\rbrace .
\end{equation*}
Then, the collection of sets {spherex | x ∈ S − i × T − i} is nested, that is, either spherex⊆spherey or spherey⊆spherex for all x, y. Moreover, the well-ordering condition guarantees that for every information set h ∈ Hi there is a smallest sphere in the collection that intersects S − i(h) × T − i. Hence, the collection {spherex | x ∈ S − i × T − i} corresponds to a system of spheres as in Grove (1988). The other direction is also true: If we start from a Grovean system of spheres on S − i × T − i, then this naturally induces a well-ordered plausibility ordering on S − i × T − i. We may therefore interchangeably speak about well-ordered plausibility orderings and systems of spheres – both ways of modelling are equivalent.
5.2 Unique Plausibility Orderings for Reasoning Contexts
Consider a dynamic G and a belief complete epistemic model M = (Ti, bi)i ∈ I. Then, every type ti ∈ Ti holds at every information set h ∈ H*i a conditional belief bi(ti, h) ∈ Δ(S − i(h) × T − i) on the space of uncertainty S − i × T − i. In particular, the support of bi(ti, h) – which we denote by supp bi(ti, h) – represents the set of opponents’ strategy-type pairs that ti deems possible at h.
Now, fix a well-ordered plausibility ordering ≽i on S − i × T − i. Then, we say that the type respects the plausibility ordering ≽i if at every information set h ∈ H*i, the type ti only deems possible strategy-type pairs that are deemed most plausible at h by ≽i. We can formally state this as follows.
Definition 5.3 (Type respecting a plausibity ordering)Consider a dynamic game G and a belief complete epistemic model M = (Ti, bi)i ∈ I. For a given player i, consider a type ti ∈ Ti and a well-ordered plausibility ordering ≽ion S − i × T − i. Then, type ti respects the plausibility ordering ≽iif
\begin{equation*}
\text{ \textsl {supp} }b_{i}(t_{i},h)\subseteq \text{\textsl {max}} _{\succcurlyeq _{i}}(S_{-i}(h)\times T_{-i})
\end{equation*}
at every information set h ∈ H*i.
In a sense, the plausibility ordering ≽i imposes at every information set h ∈ H*i an upper bound – max≽i(S − i(h) × T − i) – on the (support of the) conditional beliefs that can be held there. In terms of sphere systems, the above definition states that at every information set h the type ti looks for the smallest sphere A that intersects S − i(h) × T − i, and concentrates at h on the intersection of S − i(h) × T − i with A. This is diagrammatically represented in Figure 2, where A is the sphere with the thick border.
Figure 2. Type respecting a plausibility ordering
Consider next a reasoning context ρ, which selects for the dynamic game G and the epistemic model M some subset of types ρi(G, M)⊆Ti for player i. That is, the reasoning context ρ puts some restrictions on player i’s belief hierarchies in G. The question we are interested in is whether these restrictions can be characterized by a unique plausibility ordering ≽i on S − i × T − i. So, can we find a single plausibility ordering ≽i on S − i × T − i such that the reasoning context ρ selects for player i precisely those types ti that respect ≽i?
Definition 5.4 (Reasoning context characterized by plausibility ordering)Consider a dynamic G, a belief complete epistemic model M = (Ti, bi)i ∈ Iand a reasoning context ρ, selecting for every player i some subset of types ρi(G, M)⊆Ti. For every player i, consider a well-ordered plausibility ordering ≽ion S − i × T − i. Then, the reasoning context is characterized at (G, M) by the profile (≽i)i ∈ Iof plausibility orderings if for every player i,
\begin{equation*}
\rho _{i}(G,M)=\lbrace t_{i}\in T_{i}\text{ }|\text{ }t_{i}\text{ respects } \succcurlyeq _{i}\rbrace .
\end{equation*}
Hence, if we know the single plausibility ordering ≽i for player i, then we also know precisely which belief hierarchies are selected for player i by the reasoning context.
5.3 Discussion
The definition above can be decomposed into two separate parts. The first part states that all player i belief hierarchies selected by the reasoning context ρ should respect the same plausibility ordering ≽i. That is, at every information set h ∈ H*i there is a common upper bound – max≽i(S − i(h) × T − i) – for the (supports of) all conditional beliefs selected by ρ. This condition alone is not very restrictive, however. What one can always do is to take the trivial plausibility ordering ≽triviali, which deems all opponents’ strategy-type combinations as equally plausible, and which has the property that max≽i(S − i(h) × T − i) = S − i(h) × T − i for every information set h ∈ H*i. Then, it is trivially true that every type ti ∈ Ti respects ≽triviali.
The second part requires, in turn, that every type ti ∈ Ti which respects the plausibility ordering ≽imust necessarily be selected by the reasoning context ρ. So, not only does ≽i impose, at every information set h ∈ H*i, a common upper bound – max≽i(S − i(h) × T − i) – on the (supports of) all conditional beliefs selected by ρ, but these upper bounds are also sharp. By the latter we mean that the reasoning context ρ will select at least one type ti for which
\begin{equation*}
\text{supp }b_{i}(t_{i},h)=\text{max}_{\succcurlyeq _{i}}(S_{-i}(h)\times T_{-i})
\end{equation*}
at all information sets h ∈ H*i. That is, the bounds imposed by the plausibility ordering ≽i will actually be covered by some of the belief hierarchies selected by the reasoning context ρ.
By combining these two parts we make sure that the full set of belief hierarchies for player i selected by ρ can actually be characterized by one and the same plausibility ordering ≽i on S − i × T − i. Not only do all belief hierarchies selected by ρ respect the same, common plausibility ordering ≽i, but also all belief hierarchies that do respect this plausibility ordering ≽i are actually selected by ρ. It is thus justified to say that the reasoning context ρ is characterized by ≽i.
A similar condition could be stated for individual types or belief hierarchies. For a single type ti ∈ Ti and plausibility ordering ≽i on S − i × T − i, we could say that ti is qualitatively characterized by ≽i if
\begin{equation*}
\text{supp }b_{i}(t_{i},h)=\text{max}_{\succcurlyeq _{i}}(S_{-i}(h)\times T_{-i})
\end{equation*}
for all information sets h ∈ H*i. But by Grove’s (1988) theorem this would be equivalent to stating that for type ti, the induced qualitative (non-probabilistic) conditional beliefs, supp bi(ti, h), must satisfy the AGM-axioms. In particular, every type ti that satisfies Bayesian updating whenever possible, can always be qualitatively characterized by some plausibility ordering ≽i on S − i × T − i.
But what we require in Definition 5.4 goes much beyond the AGM-axioms, or Bayesian updating. Instead of requiring that every individual type can be characterized by an individual plausibility ordering, we impose that the full set of selected types can be characterized by a common plausibility ordering that applies to all types simultaneously.
6. COMMON STRONG BELIEF IN RATIONALITY
6.1 Definition
The reasoning context of ‘common strong belief in rationality’ has been developed by Battigalli and Siniscalchi (2002). They have shown that the strategies that can rationally be chosen by players who reason in accordance with this concept correspond precisely to the extensive form rationalizable strategies as defined by Pearce (1984) and Battigalli (1997). The main idea behind ‘common strong belief in rationality’ is that a player must believe in the opponents’ rationality whenever this is possible. More precisely, if player i finds himself at information set h, and concludes that h could be reached if his opponents choose rationally, then player i must believe at h that his opponents choose rationally. We say that player i strongly believes in the opponents’ rationality. Moreover, if h could be reached if his opponents choose rationally, then player i asks a second question, namely whether h could still be reached if his opponents do not only choose rationally but also strongly believe in their opponents’ rationality. If the answer is yes, then player i must believe at h that his opponents choose rationally and strongly believe in their opponents’ rationality. By iterating this argument, we arrive at ‘common strong belief in rationality’. To formalize this notion, let us first define what we mean by rationality and strong belief.
Consider a type ti for player i, an information set h ∈ Hi and a strategy si that possibly reaches h. By ui(si, bi(ti, h)) we denote the expected utility that player i gets if the game is at h, player i chooses si there, and holds the conditional belief bi(ti, h) about the opponents’ strategy-type combinations. Note that this expected utility does not depend on the full conditional belief that ti holds at h, but only on the conditional belief about the opponents’ strategy choices.
Definition 6.1 (Rational choice)Consider a type ti for player i, an information set h ∈ Hi and a strategy si that possibly reaches h. Strategy si is rational for type ti at information set h if ui(si, bi(ti, h)) ⩾ ui(s′i, bi(ti, h)) for all alternative strategies s′ithat possibly reach h. Strategy si is rational for type ti if it is so at every information set h ∈ Hi that si possibly reaches.
In words, a strategy is rational for a type if at every relevant information set it yields the highest expected utility, given the conditional belief held by the type at that information set. We next define the notion of strong belief.
Definition 6.2 (Strong belief)Consider a type ti within a belief complete epistemic model M = (Ti, bi)i ∈ I, and an event E⊆S − i × T − i. Type ti strongly believes the event E if bi(ti, h)(E) = 1 at every information set h ∈ H*iwhere (S − i(h)∩T − i)∩E is non-empty.
That is, at every information set h where the event E is consistent with the event of h being reached, player i must concentrate his belief fully on E. The reasoning context of ‘common strong belief in rationality’ can now be defined as follows.
Definition 6.3 (Common strong belief in rationality)Consider a dynamic game G and a belief complete epistemic model M = (Ti, bi)i ∈ I. For every player i we recursively define sets Tki and Rki as follows.
Induction start.Define T 0i ≔ Ti and R 0i ≔ {(si, ti) ∈ Si × T 0i | si rational for ti}.
Induction step.Let k ⩾ 1, and suppose T k − 1iand R k − 1ihave been defined for all players i. Then,
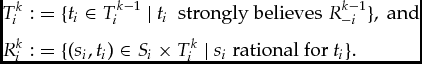\begin{eqnarray*}
T_{i}^{k} &:&=\lbrace t_{i}\in T_{i}^{k-1}\text{ }|\text{ }t_{i}\text{ \textsl { strongly believes} }R_{-i}^{k-1}\rbrace,\text{ \textsl {and}} \\
R_{i}^{k} &:&=\lbrace (s_{i},t_{i})\in S_{i}\times T_{i}^{k}\text{ }|\text{ }s_{i} \text{ \textsl {rational for} }t_{i}\rbrace .
\end{eqnarray*}
Common strong belief in rationality selects for every player i the set of types 
$T_{i}^{\infty }:=\cap _{k\in \mathbb {N} }T_{i}^{k}.$
Here, R k − 1− i denotes the set × j ∈ I\{i}R k − 1j. We say that a type ti expresses ‘common strong belief in rationality’ if ti ∈ T ∞i. Battigalli and Siniscalchi (2002) show that the sets of types T ∞i are always non-empty for every finite dynamic game, and that the strategies which are optimal for a type in T ∞i are precisely the extensive form rationalizable strategies as defined in Pearce (1984) and Battigalli (1997). By construction, the sets of types Tki are monotonically shrinking in k, that is, T k + 1i⊆Ti k for every k. It turns out, actually, that typically these sets will be strictly shrinking for every k. That is, typically T k + 1i⊂Ti k for every k, where ⊂ means strict set inclusion.Footnote 3 However, the intersection of all these sets – which is T ∞i – will always be non-empty.
6.2 Characterization Result
We will now prove that the reasoning context of ‘common strong belief in rationality’ can be characterized by a unique plausibility ordering for every player, and show how such plausibility orderings can be defined.
Theorem 6.4 (Characterization by plausibility orderings)Consider a dynamic game G and belief complete epistemic model M = (Ti, bi)i ∈ I. For every player i consider the binary relation ≽ion S − i × T − igiven by
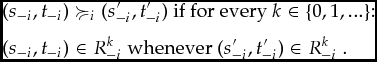\begin{eqnarray*}
&&(s_{-i},t_{-i})\succcurlyeq _{i}(s_{-i}^{\prime },t_{-i}^{\prime })\text{ \textsl {if for every} }k\in \lbrace 0,1,...\rbrace {:}\text{ } \\
&&(s_{-i},t_{-i})\in R_{-i}^{k}\text{ \textsl {whenever} }(s_{-i}^{\prime },t_{-i}^{\prime })\in R_{-i}^{k}\text{ .}
\end{eqnarray*}
Then, ≽iis a well-ordered plausibility ordering for every player i, and ‘common strong belief in rationality’ is characterized at (G, M) by the profile (≽i)i ∈ Iof plausibility orderings.
The proof can be found in the appendix. As the proof of the theorem above shows, the concept of ‘common strong belief in rationality’ can alternatively be characterized by the Grovean system of spheres
\begin{equation*}
R_{-i}^{-1}\supseteq R_{-i}^{0}\supseteq R_{-i}^{1}\supseteq ...\supseteq R_{-i}^{\infty }
\end{equation*}
for every player i, where we set R −1− i ≔ S − i × T − i. That is, player i will look at every information set h ∈ Hi for the smallest sphere Rk − i that intersects S − i(h) × T − i, and will concentrate his conditional belief at h on the intersection between S − i(h) × T − i and this smallest sphere Rk − i. This is diagrammatically represented in Figure 3.
Figure 3. Characterization of ‘common strong belief in rationality’ by Grovean system of spheres
In this picture, we have taken R 1− i to be the smallest sphere that intersects S − i(h) × T − i.
7. COMMON BELIEF IN FUTURE RATIONALITY
7.1 Definition
The concept of ‘common belief in future rationality’ has been defined in Perea (2014), and is very similar to the notion of ‘common knowledge of stable belief in dynamic rationality’ by Baltag et al. (2009). The main difference between the two is that the latter notion restricts to dynamic games with perfect information whereas the first is applicable to all finite dynamic games. The key idea is that a player must always believe, at every stage of the game, that his opponents will choose rationally in the game that lies ahead. We say that this player believes in his opponents’ future rationality. Baltag et al. (2009) refer to this condition as ‘stable belief in dynamic rationality’. Not only this, a player must also always believe that his opponents always believe in their opponents’ future rationality, and so on. This eventually leads to the concept of ‘common belief in future rationality’.
This concept is completely forward looking, as a player need not necessarily believe that his opponents have chosen rationally in the past even when believing so is possible. At the same time, a player must always hold on to the belief that his opponents will choose rationally in the future even when it is evident that these same opponents have chosen irrationally in the past. So, in a sense, it requires a degree of ‘stubbornness’ by the players that is not present in ‘common strong belief in rationality’. To formally define the concept, we first state precisely what we mean by ‘belief in future rationality’.
For a given strategy si for player i, let Hi(si) denote the collection of information sets for player i that are possibly reached by si. Consider a belief complete epistemic model M = (Ti, bi)i ∈ I for the dynamic game G at hand. For every information set h in the game, let
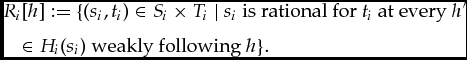\begin{eqnarray*}
&&R_{i}[h]:=\lbrace (s_{i},t_{i})\in S_{i}\times T_{i}\text{ }|\text{ }s_{i}\text{ is rational for }t_{i}\text{ at every }h^{\prime }\nonumber\\
&&\quad \in H_{i}(s_{i})\text{ weakly following }h\rbrace .
\end{eqnarray*}
Remember that h′ weakly follows h if either h′ follows h, or h′ and h are simultaneous. Hence, Ri[h] contains those strategy-type pairs where the strategy is optimal for the type ‘from h onwards’.
Definition 7.1 (Belief in future rationality)A type ti believes in his opponents’ future rationality if at every information set h ∈ H*i, the conditional belief bi(ti, h) assigns probability 1 to the event R − i[h].
Here, R − i[h] ≔ ×j ∈ I\{i}Rj[h]. So, no matter what has happened in the game so far, type ti will always at every information set h assign probability 1 to the event that his opponents will choose rationally from h onwards. With this definition at hand, we can now formally introduce ‘common belief in future rationality’.
Definition 7.2 (Common belief in future rationality)Consider a dynamic game G and a belief complete epistemic model M = (Ti, bi)i ∈ I. For every player i we recursively define sets Tki as follows.
Induction start.Define T 1i ≔ {ti ∈ Ti | ti believes in his opponents’ future rationality }.
Induction step.Let k ⩾ 1, and suppose T k − 1ihas been defined for all players i. Then,
\begin{equation*}
T_{i}^{k}:=\lbrace t_{i}\in T_{i}^{k-1}\text{ }|\text{ }b_{i}(t_{i},h)(S_{-i} \times T_{-i}^{k-1})=1\text{ \textsl {for all }}h\in H_{i}^{\ast }\rbrace .
\end{equation*}
Common belief in future rationality selects for every player i the set of types 
$T_{i}^{\infty }:=\cap _{k\in \mathbb {N} }T_{i}^{k}.$
Hence, a type in Tki always believes that every opponent j holds a type in T k − 1j. In Perea (2014) it is shown that the set T ∞i is always non-empty for every finite dynamic game. Moreover, both Perea (2014) and Baltag et al. (2009) show that in every dynamic game with perfect information without relevant ties, the strategies selected by the concept are precisely the backward induction strategies.
7.2 Impossibility Result
We show that the reasoning context of ‘common belief in future rationality’ can not always be characterized by a unique plausibility ordering for every player. Consider the game G in Figure 4, which is known as ‘Battle-of-the-sexes-with-outside-option’ and constitutes one of the classical forward induction examples in the literature.
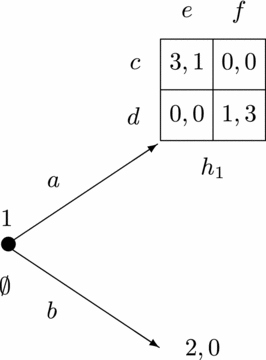
Figure 4. A game in which ‘common belief in future rationality’ cannot be characterized by plausibility orderings
Take an arbitrary belief complete epistemic model M = (Ti, bi)i ∈ I. We show that the reasoning context of ‘common belief in future rationality’ cannot be characterized at (G, M) by any profile of plausibility orderings.
We first show that there must be a type t*2 ∈ T 2 for player 2 that expresses ‘common belief in future rationality’, and which initially believes that player 1 chooses (a, c). Namely, as the model M is belief complete, there must be types t*1 ∈ T 1 and t*2 ∈ T 2 with the following conditional beliefs:
\begin{equation*}
\begin{array}{ll}b_{1}(t_{1}^{\ast },\emptyset )=(e,t_{2}^{\ast }), & b_{1}(t_{1}^{\ast },h_{1})=(e,t_{2}^{\ast }) \\
b_{2}(t_{2}^{\ast },\emptyset )=((a,c),t_{1}^{\ast }), & b_{2}(t_{2}^{\ast },h_{1})=((a,c),t_{1}^{\ast }). \end{array}
\end{equation*}
Here, b 1(t*1, ∅) = (e, t*2) means that type t*1 ascribes at ∅ probability 1 to the event that player 2 chooses strategy e while being of type t*2. Similarly for the other three beliefs.
It can easily be verified that both types t*1 and t*2 believe in the opponent’s future rationality. Consider, for instance, the type t*2. That type believes at ∅ that player 1 chooses (a, c) and that player 1 is of type t*1. As type t*1 believes, at ∅ and h 1, that player 2 chooses e, strategy (a, c) is optimal for t*1 at ∅ and h 1. Hence, type t*2 believes at ∅ that player 1 chooses optimally at ∅ and h 1, so t*2 believes at ∅ in 1’s future rationality. Similarly, it can be checked that the same type t*2 believes at h 1 that player 1 chooses optimally at h 1. Therefore, t*2 believes in 1’s future rationality overall. In the same way it can be checked that type t*1 also believes in his opponent’s future rationality. As t*1 believes throughout the game that player 2’s type is t*2, and t*2 believes throughout the game that player 1’s type is t*1, it immediately follows that both t*1 and t*2 express ‘common belief in future rationality’. In particular, t*2 ∈ T 2 is a type that expresses ‘common belief in future rationality’, and which initially believes that player 1 chooses (a, c).
On the other hand, (a, d) can never be an optimal strategy for player 1 at the beginning, as choosing b always yields him a strictly better outcome. So, under ‘common belief in future rationality’, player 2 cannot initially ascribe positive probability to player 1 choosing (a, d). Consequently, there is no type t 2 ∈ T 2 that expresses ‘common belief in future rationality’ and that initially assigns positive probability to player 1 choosing (a, d).
Now suppose, contrary to what we want to show, that the concept of ‘common belief in future rationality’ is characterized at (G, M) by a profile (≽i)i ∈ I of well-ordered plausibility orderings. Then, in particular,
\begin{equation}
T_{2}^{\infty }=\lbrace t_{2}\in T_{2}\text{ }|\text{ }t_{2}\text{ respects } \succcurlyeq _{2}\rbrace,
\end{equation}
\begin{equation*}
\text{supp }b_{2}(t_{2},\emptyset )\subseteq \text{max}_{\succcurlyeq _{2}}(S_{1}(\emptyset )\times T_{1})
\end{equation*}
for all t 2 ∈ T ∞2. Obviously, S 1(∅) = S 1, so we have that
\begin{equation*}
\text{supp }b_{2}(t_{2},\emptyset )\subseteq \text{max}_{\succcurlyeq _{2}}(S_{1}\times T_{1})
\end{equation*}
for all t 2 ∈ T ∞2. As the type t*2 above is in T ∞2, and b 2(t*2, ∅) = ((a, c), t*1), it follows that
\begin{equation}
((a,c),t_{1}^{\ast })\in \text{max}_{\succcurlyeq _{2}}(S_{1}\times T_{1}).
\end{equation}
\begin{equation}
((a,d),t_{1})\notin \text{max}_{\succcurlyeq _{2}}(S_{1}\times T_{1})\text{ for all }t_{1}\in T_{1}.
\end{equation}
\begin{equation}
((a,d),t_{1})\notin \text{max}_{\succcurlyeq _{2}}(S_{1}(h_{1})\times T_{1}) \text{ for all }t_{1}\in T_{1}.
\end{equation}
$\hat{t}_{2}\in T_{2}^{\infty }$ which at h 1 assigns probability 1 to player 1 choosing (a, d). As the model M is belief complete, there must be types 
$\hat{t}_{1}\in T_{1}$ and 
$\hat{t}_{2}\in T_{2}$ with the following conditional beliefs:
\begin{equation*}
\begin{array}{ll}b_{1}(\hat{t}_{1},\emptyset )=(f,\hat{t}_{2}), & b_{1}(\hat{t}_{1},h_{1})=(f, \hat{t}_{2}) \\
b_{2}(\hat{t}_{2},\emptyset )=(b,\hat{t}_{1}), & b_{2}(\hat{t} _{2},h_{1})=((a,d),\hat{t}_{1}). \end{array}
\end{equation*}
Note that type 
$\hat{t}_{2}$ revises his belief about player 1’s strategy choice during the game: at the beginning, $\hat{t}_{2}$ believes that player 1 chooses b, whereas at h 1 type $\hat{t}_{2}$ believes that player 1 chooses (a, d).
It may be verified that both types 
$\hat{t}_{1}$ and $\hat{t}_{2}$ believe in the opponent’s future rationality. Consider, for instance, the type 
$\hat{ t}_{2},$ which believes at ∅ that player 1 chooses b while being of type 
$\hat{t}_{1}.$ As type $\hat{t}_{1}$ believes at ∅ that player 2 chooses f, strategy b is optimal for type $\hat{t}_{1}$ at ∅. Hence, $\hat{t}_{2}$ believes at ∅ that player 1 chooses rationally at ∅. Strategy b for player 1 makes reaching h 1 impossible, so we conclude that type $\hat{t}_{2}$ believes at ∅ in 1’s future rationality. At h 1, the same type $\hat{t}_{2}$ believes that player 1 chooses (a, d) while being of type 
$\hat{t} _{1}.$ As type $\hat{t}_{1}$ believes at h 1 that player 2 chooses f, strategy (a, d) is optimal for type $\hat{t}_{1}$ at h 1. Indeed, among the two strategies for player 1 that reach h 1 – which are (a, c) and (a, d) – strategy (a, d) is optimal under the belief that player 2 chooses f. So, type $\hat{t}_{2}$ believes at h 1 that player 1 chooses rationally at h 1. Overall, we may conclude that type $\hat{t}_{2}$ believes at ∅ and h 1 in 1’s future rationality. That is, $\hat{t}_{2}$ believes in 1’s future rationality. Note, however, that $\hat{t}_{2}$ believes at h 1 that player 1 has chosen irrationally in the past, as b is better than (a, d) for $\hat{t}_{1}$at the beginning. This is not a problem, as ‘common belief in future rationality’ only requires players to believe in the opponents’ future rationality, not necessarily in the opponents’ past rationality.
In a similar fashion, it may be verified that also type $\hat{t}_{1}$ believes in his opponent’s future rationality. As $\hat{t}_{1}$ believes throughout that player 2 is of type 
$\hat{t}_{2},$ and $\hat{t}_{2}$ believes throughout that player 1 is of type 
$\hat{t}_{1},$ it follows that both $\hat{t}_{1}$ and $\hat{t}_{2}$ express ‘common belief in future rationality’. In particular, we have found a type 
$\hat{t}_{2}\in T_{2}^{\infty }$ which at h 1 assigns probability 1 to player 1 choosing (a, d).
But then, by (4), it follows that
\begin{equation*}
\text{supp }b_{2}(\hat{t}_{2},h_{1})\nsubseteq \text{max}_{\succcurlyeq _{2}}(S_{1}(h_{1})\times T_{1}).
\end{equation*}
Hence, $\hat{t}_{2}$ does not respect the plausibility ordering ≽2, which contradicts the assumption (1). We are therefore led to conclude that the concept of ‘common belief in future rationality’ cannot be characterized at (G, M) by a unique plausibility ordering for every player.
So, in a nutshell, the reason why ‘common belief in future rationality’ cannot be characterized by plausibility orderings in the game of Figure 4 is as follows. Under ‘common belief in future rationality’, player 1 can rationally choose (a, c) but not (a, d). Therefore, player 2 types which express ‘common belief in future rationality’ may initially deem (a, c) possible, but certainly not (a, d). Hence, if ‘common belief in future rationality’ were to be characterized by a unique plausibility ordering on player 1’s strategy-type pairs, then this plausibility ordering must necessarily deem (a, c) more plausible than (a, d). But then, upon reaching h 1, player 2 must necessarily conclude that player 1 did not choose (a, d), which is not true since under ‘common belief in future rationality’ player 2 can believe at h 1 that player 1 chooses (a, d).
8. GAMES WITH PERFECT INFORMATION
A dynamic game is said to be with perfect information if different players never choose simultaneously, and every player, when making a choice, always knows exactly what the other players have done so far. Formally this means that at every non-terminal history exactly one player is active, and every information set consists of precisely one non-terminal history. We say that the game is without relevant ties (see Battigalli 1997) if for every player i, every information set h ∈ Hi, and every two different terminal histories z, z′ following h, it holds that ui(z) ≠ ui(z′). Hence, two different choices for player i always lead to different utilities for that player.
It is well-known that in every perfect information game without relevant ties, the backward induction procedure yields a unique choice cbi(h) at every information set h. We will refer to these choices as the backward induction choices in the game. The backward induction strategy for player i is the unique strategy sbii that selects the backward induction choice cbi(h) at every h ∈ Hi possibly reached by sbii.
In Perea (2014) it is shown that in every perfect information game without relevant ties, the concept of ‘common belief in future rationality’ uniquely selects the backward induction strategy for every player. Indeed, in such games there is only one strategy that a player can rationally choose if his belief hierarchy expresses ‘common belief in future rationality’, namely his backward induction strategy.
However, even for such games the concept of ‘common belief in future rationality’ may not be characterizable by plausibility orderings, as the game in Figure 5 shows.
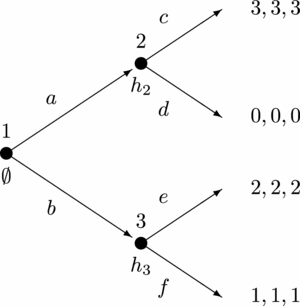
Figure 5. A perfect information game in which ‘common belief in future rationality’ cannot be characterized by plausibility orderings
Clearly, under ‘common belief in future rationality’, player 2 must believe at ∅ that player 1 believes at ∅ that (a) player 2 will choose c and (b) player 3 will choose e. Also, player 2 must believe at ∅ that player 1 chooses rationally at ∅ and that player 3 chooses rationally at h 3. As such, under ‘common belief in future rationality’ player 2 must believe at ∅ that player 1 will choose a and that player 3 would choose e at h 3. If ‘common belief in future rationality’ were to be characterized by a unique plausibility ordering ≽2 for player 2, then ≽2 must deem the strategy combination (a, e) most plausible overall. But then, player 2 should still believe at h 2 that player 1 has chosen a and that player 3 would have chosen e at h 3. However, under ‘common belief in future rationality’, player 2 is free to believe at h 2 that player 3 would have chosen f, as player 3’s information set h 3 does not follow h 2. Hence, in this game with perfect information, ‘common belief in future rationality’ cannot be characterized by a unique plausibility ordering for player 2.
At the same time, the example in Figure 5 shows that ‘common belief in future rationality’ is perhaps a bit too permissive. Indeed, there is no good reason why player 2 at h 2 should suddenly drop his belief that player 3 would choose rationally at h 3. This leads to the question whether we can strengthen the concept of ‘common belief in future rationality’ such that the new, more restrictive concept can be characterized by plausibility orderings in perfect information games without relevant ties. We will see that this is indeed possible.
Instead of only requiring a player to believe that his opponents will choose rationally at future information sets, let us look at a stronger condition which states that at any point in time, a player also believes that his opponents would have chosen rationally at information sets that have been avoided by past choices. We call such information sets parallel information sets. For instance, in Figure 5 the information set h 3 is parallel to information set h 2 as it is avoided by the past choice a that leads to h 2. A more formal way of stating it is to say that an information set h′ is parallel to another information set h if h′ does not weakly precede, nor weakly follow, h.
The condition above, that a player always believes that his opponents will choose rationally in the future, and would have chosen rationally at parallel information sets, can formally be stated as follows. Consider a dynamic G – not necessarily with perfect information – and a belief complete epistemic model M = (Ti, bi)i ∈ I for G. For every player i, and every information set h in G, define the event
\begin{eqnarray*}
\hat{R}_{i}[h]&:=&\lbrace (s_{i},t_{i})\in S_{i}\times T_{i}\text{ }|\text{ }s_{i} \text{ is rational for }t_{i}\text{ at every }h^{\prime }\in H_{i}(s_{i}) \\
&& \text{ weakly following }h,
\text{and every }h^{\prime }\in H_{i}(s_{i})\text{ that is parallel to }h\rbrace .
\end{eqnarray*}
Definition 8.1(Belief in rationality at future and parallel information sets) A type ti believes in his opponents’ rationality at future and parallel information sets if at every information set h ∈ H*i, the conditional belief bi(ti, h) assigns probability 1 to the event 
$\hat{R}_{-i}[h].$
Here, 
$\hat{R}_{-i}[h]:=\times _{j\in I\backslash \lbrace i\rbrace }\hat{R}_{j}[h].$ With this basic condition at hand, the reasoning context of ‘common belief in rationality at future and parallel information sets’ can then be defined in the obvious way.
Definition 8.2(Common belief in rationality at future and parallel information sets) Consider a dynamic game G and a belief complete epistemic model M = (Ti, bi)i ∈ I. For every player i we recursively define sets Tki as follows.
Induction start.Define T 1i ≔ {ti ∈ Ti | ti believes in his opponents’ rationality at future and parallel information sets }.
Induction step.Let k ⩾ 1, and suppose T k − 1ihas been defined for all players i. Then,
\begin{equation*}
T_{i}^{k}:=\left\lbrace t_{i}\in T_{i}^{k-1}\text{ }|\text{ }b_{i}(t_{i},h\right) \left(S_{-i} \times T_{-i}^{k-1})=1\text{ \textsl {for all }}h\in H_{i}^{\ast }\right\rbrace .
\end{equation*}
Common belief in rationality at future and parallel information sets selects for every player i the set of types 
$T_{i}^{\infty }:=\cap _{k\in \mathbb {N}}T_{i}^{k}.$
It can be shown that the sets of types T ∞i that express ‘common belief in rationality at future and parallel information sets’ will always be non-empty, and will always be included in the sets of types that express ‘common belief in future rationality’. However, the two concepts are ‘behaviourally equivalent’ as they always select the same sets of strategies for every player. The reason is that for player i’s choice at information set h it is only relevant what player i believes about the opponents’ past and future choices, not what he believes about the opponents’ possible behaviour at parallel information sets. Clearly, the two concepts above impose no conditions on player i’s belief about his opponents’ past choices, and impose exactly the same conditions on his belief about the opponents’ future choices. As such, it does not matter for player i’s choice at information set h whether his beliefs are restricted by ‘common belief in rationality at future and parallel information sets’ or only by ‘common belief in future rationality’. Therefore, the two concepts only differ in the restrictions they impose on the players’ conditional beliefs, but not in the strategy choices they select for the players. The formal proofs for the insights above are not difficult, and we leave these to the reader for the sake of brevity.
As discussed above, the concept of ‘common belief in future rationality’ uniquely filters the backward induction strategies for every perfect information game without relevant ties. It then immediately follows also that ‘common belief in rationality at future and parallel information sets’ uniquely selects the backward induction strategies in such games, as it is behaviourally equivalent to ‘common belief in future rationality’. We can actually say a little more: Under ‘common belief in rationality at future and parallel information sets’, there will be a unique belief for every player i at each of his information sets h ∈ H*i about the opponents’ strategy choices, namely that his opponents will choose the backward induction choices at all future and parallel information sets. This is not true for ‘common belief in future rationality’. In the game of Figure 5, for instance, player 2 may believe at h 2 under ‘common belief in future rationality’ that player 3 would choose f at h 3, although f is not the backward induction choice at h 3.
Formally speaking, for a given player i and information set h in the game, let sbii[h] be the unique strategy that (a) at every h′ ∈ Hi preceding h selects the unique choice leading to h, and (b) at every h′ ∈ Hi not preceding h selects the backward induction choice cbi(h′) whenever h′ is possibly reached by sbii[h]. So, sbii[h] possibly reaches h, and selects the backward induction choices at all future and parallel information sets to h. We call sbii[h] the backward induction strategy conditional on h. For a player i and information set h ∈ H*i, let sbi − i[h] ≔ (sj bi[h])j ∈ I\{i} be the combination of opponents’ backward induction strategies conditional on h.
It can be shown that under ‘common belief in rationality at future and parallel information sets’, a type for player i must at every h ∈ H*i assign probability 1 to the strategy profile sbi − i[h] by the opponents. This proof is not difficult, and is left to the reader. Hence, every player i holds a unique vector βbii of conditional beliefs about the opponents’ strategy choices. But then, every player i must believe throughout the game that every opponent j holds the belief vector βbij, and must believe throughout that every opponent j believes throughout that every other player k holds the conditional belief vector βbik, and so on. Clearly, this leads to the conclusion that under ‘common belief in rationality at future and parallel information sets’, the full belief hierarchy of every player is uniquely determined. That is, the set T ∞i of types expressing ‘common belief in rationality at future and parallel information sets’ is a singleton. Let us denote by tbii the unique type for player i that expresses ‘common belief in rationality at future and parallel information sets’. Then, at every information set h ∈ H*i the conditional belief of type tbii about the opponents’ strategy-type combinations is given by
\begin{equation*}
b_{i}\left(t_{i}^{bi},h\right)=\left(s_{-i}^{bi}[h],t_{-i}^{bi}\right).
\end{equation*}
That is, at h ∈ H*i type tbii assigns probability 1 to the event that every opponent j chooses the backward induction strategy sbij[h] conditional on h while being of type tbjj. This insight will be important for proving the following result, which states that for perfect information games without relevant ties, the reasoning context of ‘common belief in rationality at future and parallel information sets’ can be characterized by a unique plausibility ordering for every player.
Theorem 8.3 (Characterization by plausibility orderings)Consider a perfect information game G without relevant ties and a belief complete epistemic model M = (Ti, bi)i ∈ I. For every player i consider the binary relation ≽ion S − i × T − igiven by: (s − i, t − i)≻i(s′− i, t′− i) if either
(a) t − i = tbi − iand t′− i ≠ tbi − i, or
(b) s − i = sbi − i[h] for some h ∈ H*iand s′− i ≠ s − ibi[h] for any h ∈ H*i, or
(c) s − i ≠ s′− i, and there are some h, h′ ∈ H*i, where h′ follows h, such that s − i = sbi − i[h] and s′− i = s − ibi[h′].
Then, ≽iis a well-ordered plausibility ordering for every player i, and ‘common belief in rationality at future and parallel information sets’ is characterized at (G, M) by the profile (≽i)i ∈ Iof plausibility orderings.
The proof can be found in the appendix. The theorem above cannot be extended to general dynamic games, however. Consider for instance the game in Figure 4. For that game, the concept of ‘common belief in rationality at future and parallel information sets’ is fully equivalent – also in terms of beliefs – to ‘common belief in future rationality’ as there are no parallel information sets in that game. Hence, even the concept of ‘common belief in rationality at future and parallel information sets’ cannot be characterized by plausibility orderings in that game.
The theorem above shows, in particular, that for perfect information games without relevant ties we can always find a reasoning context that (a) uniquely selects the backward induction strategy for every player, and (b) can be characterized by plausibility orderings. In that respect, the result is very similar to Baltag et al. (2009). These authors, namely, assume from the beginning that the conditional beliefs of the players are characterized by a unique plausibility ordering for every player. Based on this assumption they then derive the notion of ‘common knowledge of stable belief in dynamic rationality’, which is very similar to ‘common belief in future rationality’, but now with the additional assumption that conditional beliefs are derived from plausibility orderings. In Corollary 4.5 they then prove that the concept of ‘common knowledge of stable belief in dynamic rationality’ uniquely yields the backward induction strategies in every perfect information game without relevant ties. So Baltag et al. (2009) also present a reasoning context that is characterized by plausibility orderings and that uniquely returns the backward induction strategies in perfect information games without relevant ties.
9. DISCUSSION
We have seen that for the concept of ‘common strong belief in rationality’, the whole collection of selected belief hierarchies for a given player can be summarized by a single plausibility ordering, whereas this is not always possible for ‘common belief in future rationality’. Can this be viewed as an argument in favour of the first concept, and against the second? Not necessarily. A player in a dynamic game is in general not interested in finding all possible belief hierarchies that he could reasonably hold, relative to a given reasoning context, but rather aims at producing one such reasonable belief hierarchy. The property above, that all selected belief hierarchies for a given player can be summarized by a unique plausibility ordering, is therefore of interest mainly to the game-theorist or analyst – who looks at the game from a meta-perspective – rather than to the players themselves. In fact, there is nothing wrong with the concept of ‘common belief in future rationality’ – the concept is logically sound and is based on rather intuitive assumptions. Moreover, from a player’s perspective the concept is not more complex than ‘common strong belief in rationality’. From a meta-perspective, however, ‘common strong belief in rationality’ can be viewed as somewhat simpler since the entire set of belief hierarchies selected for a given player is characterized by a single plausibility ordering.
But even from a meta-perspective, it is not necessarily true that ‘common strong belief in rationality’ is more natural than ‘common belief in future rationality’. Indeed, why should we necessarily require that all selected belief hierarchies for a given player share the same plausibility ordering? Within the bounds of ‘common belief in future rationality’, it is often the case that different belief hierarchies for the same player are based on different plausibility orderings. At the same time, these belief hierarchies still share an important common feature, namely that they believe in the opponents’ future rationality, believe that the other players believe in their opponents’ future rationality, and so on. The difference with ‘common strong belief in rationality’ is that this common feature cannot be reduced to a common plausibility ordering. But why should this be the case?
The investigation we have carried out in this paper is therefore primarily of a descriptive – and not of a normative – character. We do not make any normative judgements about the concepts of ‘common strong belief in rationality’ and ‘common belief in future rationality’ – in fact we believe that both concepts are quite natural, and have their own intuitive appeal.
APPENDIX
Proof of Theorem 6.4. Fix a player i. We first show that the binary relation ≽i defined in the statement of the theorem is total, reflexive, transitive and well-ordered. To prove so, it will be helpful to introduce some additional objects.
Let R −1− i ≔ S − i × T − i, and 
$R_{-i}^{\infty }:=\cap _{k\in \mathbb {N}}R_{-i}^{k}.$ Then we have that
\begin{equation*}
S_{-i}\times T_{-i}=R_{-i}^{-1}\supseteq R_{-i}^{0}\supseteq R_{-i}^{1}\supseteq ...\supseteq R_{-i}^{\infty }.
\end{equation*}
Define K ≔ { − 1, 0, 1, . . .}∪{∞}. So, the collection {Rk − i | k ∈ K} of subsets is nested, with R 1− i being the full space S − i × T − i. Moreover, R ∞− i is non-empty as shown in Battigalli and Siniscalchi (2002).
For every element x ∈ S − i × T − i, define the number k(x) ≔ max {k ∈ K | x ∈ Rk − i}. It is easily seen that k(x) is well-defined. Namely, if x ∈ R ∞− i, then k(x) = ∞ by definition. Suppose, on the other hand, that x∉R ∞− i. Since R ∞− i
$=\cap _{k\in \mathbb {N}}R_{-i}^{k},$ there must be some k ∈ K\{∞} such that x ∈ Rk − i but x∉R k + 1− i. But then, k(x) = k. So, indeed, k(x) is well-defined for every x ∈ S − i × T − i.
By definition of ≽i we have that
\begin{equation*}
x\succcurlyeq _{i}y\text{ if and only if }k(x)\ge k(y)
\end{equation*}
for all x, y ∈ S − i × T − i. But then, it is immediately clear that ≽i is total, reflexive and transitive.
It remains to show that ≽i is well-ordered. Consider some information set h ∈ H*i. Define the number
\begin{equation*}
k(h):=\max \lbrace k\in K\text{ }|\text{ }R_{-i}^{k}\cap (S_{-i}(h)\times T_{-i}) \text{ is non-empty}\rbrace .
\end{equation*}
We first show that the number k(h) is well-defined. For every opponent j ≠ i and every k ∈ K\{ − 1}, let
\begin{equation*}
S_{j}^{k}:=\lbrace s_{j}\in S_{j}\text{ }|\text{ }s_{j}\text{ rational for some } t_{j}\in T_{j}^{k}\rbrace .
\end{equation*}
Let Sk − i ≔ ×j ∈ I\{i}Skj. So, Sk − i is the set of opponents’ strategy combinations present in Rk − i. As the dynamic game G is finite, the set S − i of opponents’ strategy-combinations is finite as well. But then, there must be some 
$k^{\ast }\in K\backslash \mathbb {\lbrace }-1,\mathbb {\infty \rbrace }$ such that S ∞− i = S − ik*. Now, to show that the number k(h) is well-defined we distinguish two cases. Suppose first that R ∞− i∩(S − i(h) × T − i) is non-empty. Then, k(h) = ∞ by definition. Suppose, on the other hand, that R ∞− i∩(S − i(h) × T − i) is empty. Then, S ∞− i∩S − i(h) is empty. Since S ∞− i = S − ik* we have that S k*− i∩S − i(h) is empty, so R k*− i∩(S − i(h) × T − i) is empty as well. But then, there must be some k < k* such that Rk − i∩(S − i(h) × T − i) is non-empty but R k + 1− i∩(S − i(h) × T − i) is empty. In that case, k(h) = k. So, indeed, k(h) is well-defined.
By definition of ≽i we have at information set h ∈ H*i that
\begin{equation}
\text{max}_{\succcurlyeq _{i}}(S_{-i}(h)\cap T_{-i})=R_{-i}^{k(h)}\cap (S_{-i}(h)\cap T_{-i}),
\end{equation}
We now show that
\begin{equation}
T_{i}^{\infty }=\lbrace t_{i}\in T_{i}\text{ }|\text{ }t_{i}\text{ respects } \succcurlyeq _{i}\rbrace,
\end{equation}
For every information set h ∈ H*i, remember that k(h) is the highest number k ∈ K for which Rk − i∩(S − i(h)∩T − i) is non-empty. By definition of ‘common strong belief in rationality’, T ∞i contains precisely those types ti ∈ Ti that strongly believe each of the events Rk − i, k ∈ {0, 1, . . .}. But then, it follows that
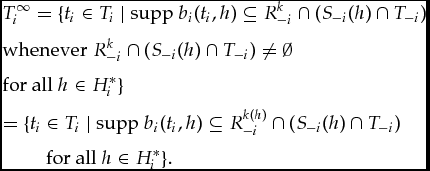\begin{eqnarray*}
&&T_{i}^{\infty }=\lbrace t_{i}\in T_{i}\text{ }|\text{ supp }b_{i}(t_{i},h) \subseteq R_{-i}^{k}\cap (S_{-i}(h)\cap T_{-i}) \\
&& \text{whenever }R_{-i}^{k}\cap (S_{-i}(h)\cap T_{-i})\ne \emptyset \\
&& \text{for all }h\in H_{i}^{\ast }\rbrace \\
&& =\lbrace t_{i}\in T_{i}\text{ }|\text{ supp }b_{i}(t_{i},h)\subseteq R_{-i}^{k(h)}\cap (S_{-i}(h)\cap T_{-i}) \\
&& \text{ \qquad for all }h\in H_{i}^{\ast }\rbrace .
\end{eqnarray*}
By (5), we obtain that
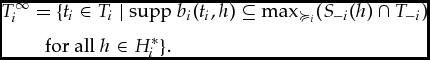\begin{eqnarray*}
&&T_{i}^{\infty }=\lbrace t_{i}\in T_{i}\text{ }|\text{ supp }b_{i}(t_{i},h) \subseteq \text{max}_{\succcurlyeq _{i}}(S_{-i}(h)\cap T_{-i}) \\
&& \text{ \qquad for all }h\in H_{i}^{\ast }\rbrace .
\end{eqnarray*}
Hence, (6) must hold. So, we conclude that ‘common strong belief in rationality’ is characterized at (G, M) by ≽i for player i. This holds for every player i, and hence the proof is complete. 
$\hfill\blacksquare$
Proof of Theorem 8.3. Let M = (Ti, bi)i ∈ I be a belief complete epistemic model for G. First of all, it can easily be verified that the binary relation ≽i defined above is a well-ordered plausibility ordering. We leave this to the reader. Now, let ρ be the reasoning context of ‘common belief in rationality at future and parallel information sets’. As we have seen above, there is for every player i a unique type tbii in ρi(G, M), and at every information set h ∈ H*i this type holds the conditional belief bi(tbii, h) = (sbi − i[h], t − ibi). So, in order to prove that ρ is characterized by the plausibility orderings above, we must show that
\begin{equation}
\text{max}_{\succcurlyeq _{i}}(S_{-i}(h)\times T_{-i})=\left\lbrace (s_{-i}^{bi}[h],t_{-i}^{bi})\right\rbrace
\end{equation}
Fix a player i and some information set h ∈ H*i. As, by construction, sbi − i[h] ∈ S − i(h), it follows that (sbi − i[h], t − ibi) ∈ S − i(h) × T − i. Hence, it remains to show that
\begin{equation}
(s_{-i}^{bi}[h],t_{-i}^{bi})\succ _{i}(s_{-i},t_{-i})\text{ for all } (s_{-i},t_{-i})\!\in\! S_{-i}(h)\times T_{-i}\text{ with } (s_{-i},t_{-i})\ne \left(s_{-i}^{bi}[h],t_{-i}^{bi}\right).\hspace*{-16pt}
\end{equation}
Take some arbitrary (s − i, t − i) ∈ S − i(h) × T − i with (s − i, t − i) ≠ (sbi − i[h], tbi − i). We distinguish the following cases.
Case 1. If t − i ≠ tbi − i then, by (a) in the statement of the theorem, (sbi − i[h], t − ibi)≻i(s − i, t − i).
Case 2. If s − i ≠ sbi − i[h′] for any h′ ∈ H*i then, by (b) in the statement of the theorem, (sbi − i[h], t − ibi)≻i(s − i, t − i).
So, from now on we assume that t − i = tbi − i and s − i = sbi − i[h′] for some h′ ∈ H*i. That is, (s − i, t − i) = (sbi − i[h′], tbi − i). We continue by distinguishing the following cases.
Case 3. If h′ follows h then, by (c) in the statement of the theorem, (sbi − i[h], t − ibi)≻i(sbi − i[h′], tbi − i).
Case 4. Suppose now that h′ precedes h. By definition, sbi − i[h′] selects the backward induction choices at all information sets weakly following h′. Moreover, by construction of the argument, sbi − i[h′] is in S − i(h), so all selected choices weakly following h′ lie on the path to h. Hence, we conclude that all opponents’ choices between h′ and h are backward induction choices. This, however, would imply that sbi − i[h] = s − ibi[h′], which is a contradiction to our assumption that (s − i, t − i) ≠ (sbi − i[h], tbi − i).
Case 5. Suppose finally that h′ does not precede nor follow h. That is, h′ is parallel to h. Let h* be the last information set in H*i that precedes both h and h′. By definition, sbi − i[h′] selects the backward induction choices at all information sets parallel to h′. In particular, sbi − i[h′] selects the backward induction choices at all information sets strictly between h* and h. Moreover, by construction of the argument, sbi − i[h′] is in S − i(h), so all selected choices at information sets strictly between h* and h lie on the path to h. Hence, we conclude that all opponents’ choices between h* and h are backward induction choices. This implies that sbi − i[h] = s − ibi[h*]. As h′ follows h* we have, by (c) in the statement of the theorem, that (sbi − i[h*], t − ibi)≻i(sbi − i[h′], tbi − i), and hence (sbi − i[h], t − ibi)≻i(sbi − i[h′], tbi − i).
This covers all possible cases. Hence, we see that, indeed, (sbi − i[h], t − ibi)≻i(s − i, t − i) for all (s − i, t − i) ∈ S − i(h) × T − i with (s − i, t − i) ≠ (sbi − i[h], tbi − i), proving (8). This, in turn, implies (7). Hence, we conclude that the reasoning context of ‘common belief in rationality at future and parallel information sets’ is characterized by the profile (≽i)i ∈ I of plausibility orderings. This completes the proof. 
$\hfill\blacksquare$
