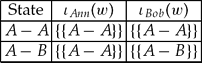1. INTRODUCTION
Interpersonal coordination is a recurrent theme in both game theory and philosophical theories of intentions. Various ‘solutions’ to coordination problems have been proposed in game theory, viz., various accounts of how a number of agents acting simultaneously can coordinate their choices in order to avoid undesired outcomes (Harsanyi and Selten Reference Harsanyi and Selten1988; Sugden Reference Sugden2003; Bacharach Reference Bacharach, Gold and Sugden2006; Brandenburger Reference Brandenburger2007). One also finds accounts of coordination in the philosophy of action, cast there in terms of intentions. Intentions carry a relatively stable commitment to action which, it is claimed, helps to solve coordination problems (Harman Reference Harman1976; Bratman Reference Bratman1987; Wallace Reference Wallace2006; Velleman Reference Velleman, Leist and Baumann2008).
Epistemic conditions occupy a central place in these bodies of literature on coordination, but hitherto they have had little contact with each other. Results in epistemic game theory and epistemic logic have pointed out that successful coordination often rests on mutual and higher-order expectations, i.e., expectations about expectations, but little attention has been paid to intentions. In the philosophical literature, on the other hand, a great deal of attention has been paid to intentions with a ‘we-content’ (Velleman Reference Velleman1997; Bratman Reference Bratman1999) and how they ground mutual expectations in interaction. Little is known, however, about how intention-based accounts of coordination relate to those in epistemic game theory and epistemic logic.
In this paper I draw these areas together, showing that this brings new insights, both for the philosophical theories of intentions and for game-theoretical and logical analyses of interpersonal coordination. The focus is on intentions with a we-content, and on the conditions under which it is legitimate to form such intentions. In the philosophical literature, these conditions have been formulated in terms of higher-order information about intentions, what I call here ‘epistemic support’. In section 4, I show that this support is not in general sufficient for coordination in games, and use this result to cast doubt on whether the notion of epistemic support really provides enough control for intentions with a we-content to count as genuine intentions. I show that this control requirement can be fulfilled by strengthening the notion of epistemic support, but then argue that such strong support rests on implausible informational conditions. In view of this, in section 5 I provide an alternative, belief-based set of conditions that are jointly sufficient for coordination in games. I argue that these conditions constitute a plausible alternative to the notion of epistemic support, and then compare them with existing accounts of coordination in the game-theoretical literature. Sections 2 and 3 lay down the philosophical and mathematical background. Taken as a whole, the present work can be seen as an attempt to join together a number of contributions in the theory of coordination and collective intentionality, showing that important insights arise from this encounter.
2. BACKGROUND CONCEPTS
In this section I introduce the general problem of coordination in games and the philosophical theory of intention upon which I draw.
2.1 Coordination in games
Game theory is the study of ‘interdependent decisions’ Schelling (Reference Schelling1980), of rational decision making in situations where many agents interact with each other. The most widely used game-theoretic representations of such situations are the strategic and the extensive forms. In this paper I concentrate on the former.
A game in strategic form (von Neumann and Morgenstern Reference von Neumann and Morgenstern1944; Myerson Reference Myerson1991; Osborne and Rubinstein Reference Osborne and Rubinstein1994) is a representation of a situation in which a number of agents have to choose simultaneously an action or a strategy in order to reach some outcome. Formally, such a game ![]() is a tuple 〈I, S i, ⪰i〉 where I is the set of agents or players and S i is the set of available choices or pure strategies of each agent i. In this paper I assume that these sets are finite, and I do not consider mixed strategies, i.e. probability distributions over each Si. A strategy profile is a combination of choices, one for each player. In a game
is a tuple 〈I, S i, ⪰i〉 where I is the set of agents or players and S i is the set of available choices or pure strategies of each agent i. In this paper I assume that these sets are finite, and I do not consider mixed strategies, i.e. probability distributions over each Si. A strategy profile is a combination of choices, one for each player. In a game ![]() these are vectors of strategies σ∈Πi∈ISi. The strategy si which i plays in the profile σ is denoted σi.
these are vectors of strategies σ∈Πi∈ISi. The strategy si which i plays in the profile σ is denoted σi.
The simultaneous decision of all agents in a strategic game uniquely determines the outcome of the game, which I identify with strategy profiles. I do not consider games with exogenous uncertainty (Myerson Reference Myerson1991: ch. 2), where the outcome can also depend on non-deterministic processes.
The relation ⪰i is i's binary preference relation over the possible outcomes of the games, i.e. over the set Πi∈ISi of strategy profiles. This relation is reflexive (σ ⪰i σ for all σ in Πi∈ISi), transitive (if σ ⪰i σ′ and σ′ ⪰i σ″ then σ ⪰i σ″) and total (σ ⪰i σ′ or σ′ ⪰i σ for all σ and σ′ in Πi∈ISi). Expressions of the form σ ⪰i σ′ should thus be read as ‘agent i considers outcome σ at least as good as outcome σ′’. I define the strict version of this relation, denoted ≻i, as follows: σ ≻i σ′ if and only if σ ⪰i σ′ but not σ′ ⪰i σ. A standard argument shows that this relation is transitive and irreflexive (for no σ in Πi∈ISi we have σ ≻i σ). When σ ≻i σ′ we say that agent i strictly prefers σ to σ′.
In this paper I am interested in a particular type of game in strategic form, namely coordination games. These are games with a specific structure, where the agents are better off when they coordinate their action. Here I represent them as games in strategic form where all agents have identical options, that is Si = Sj for all i and j in I, and where the coordination profiles, those where all agents choose the same strategy, are always strictly better than the non-coordination ones. Formally, this means that σ ≻i σ′ for all σ and σ′ such that σi = σj for all i, j in I, and σ′i≠σ′j for some i and j.
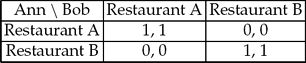
Table 1 is a typical coordination game. Two agents, Ann and Bob, have agreed to meet for dinner but they have forgotten whether it was at restaurant A or B. Each agent can go to only one of the restaurants, and they have no way of communicating their decision to the other. Ann's options are represented as the rows in Table 1, and Bob's as the columns. Their preferences are represented by pairs of utility values in each cell, the left one being Ann's and the right one Bob's. Both thus have the same preferences in the game: it doesn't matter where they meet, as long as they succeed in coordinating their actions; that is, as long as they end up in the same restaurant.
Table 1. A coordination game.
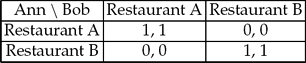
This simple example encapsulates the challenge of interpersonal coordination in games: to account for ‘convergent expectations’ (Schelling Reference Schelling1980: 92, my emphasis) among the players, on the basis of which they can base their decision. In the next section I turn to one proposal as to how agents could form such expectations, drawn from contemporary philosophy of action: on the basis of intentions.
2.2 The planning theory of intentions
The planning theory of intentions (Bratman Reference Bratman1987, Reference Bratman1999, Reference Bratman2006) provides a philosophical account of how decisions made in advance influence further actions and deliberations through future-directed intentions. Here I survey a small part of this theory. More details can be found in the references above, as well as in Harman (Reference Harman1976), Velleman (Reference Velleman, Leist and Baumann2008) and Wallace (Reference Wallace2006).
Future-directed intentions are taken to be relatively stable mental states which ensue from practical reasoning; states which carry both a volitive and a reasoning-centred commitment with respect to future actions or to the realization of some states of affairs. The volitive commitment concerns the motivational power of intentions. Like desires, intentions are taken to be conative states, that is states which move to action. Intentions are, however, intrinsically ‘conduct-controlling’ (Bratman Reference Bratman1987: 16, emphasis in the original): unless unexpected circumstances arise, an agent with a genuine intention to act in a certain way should carry out this action in due time. Desires do not carry such a strong commitment to action. The reasoning-centred commitment concerns the way previously adopted intentions constrain and trigger deliberations. They put pressure on planning agents to deliberate about means to achieve what they intend, and they impose a ‘filter of admissibility’ (Bratman Reference Bratman1987: 33) on the options that are to be considered in practical reasoning.
The volitive and the reasoning-centred commitment of intentions are usually taken to stem from various norms of consistency and coherence which apply to these attitudes (Wallace Reference Wallace2003; Velleman Reference Velleman, Leist and Baumann2008; Bratman Reference Bratman, Timmerman, Skorupski and Robertson2009). Rational intentions should be internally consistent (Bratman Reference Bratman1987: 31), i.e. agents should not intend impossible things or plain contradiction. Intentions should also be strongly consistent with the agent's beliefs, in the sense that ‘it should be possible for my entire plan to be successfully executed given that my beliefs are true’ (Bratman Reference Bratman1987: 31). The norm of agglomerativity is also recurrent in the literature – see the references just given – although how exactly we are to understand it is less clear. Here I adopt Yaffe's (Reference Yaffe2004: 511) reading of this norm, namely that it should be possible for an agent to close her intentions under conjunction without violating internal or strong-belief consistency. In this sense agglomerativity ‘makes conflicts evident to [agents], when there is doubt as to the rationality of the conjunctive intentions’, (Yaffe Reference Yaffe2004), but it does not require the agent systematically to agglomerate her intentions. Another important norm on intentions, albeit one that is less significant for the present analysis, is the ‘means-end coherence’ requirement, requiring that the agents form auxiliary intentions about means to achieve the ends they already intend.
The planning theory has it that intentions satisfying these normative constraints provide a firm base for interpersonal coordination, precisely because their relative stability and the commitments they carry can anchor mutual expectations. Agents who form intentions, it is argued, are more capable of coordinating their actions because they can rely on each other to do what they intend. In many cases, however, this seems to require that the agents have intentions of a particular form, namely intentions with a ‘we-content’, to which I now turn.
2.3 Intentions with a we-content
It is philosophically contentious whether individuals can form genuine intentions to achieve interpersonal coordination, and not merely to play their part in it, because coordination is something they cannot achieve alone. To fix terminology, let me state that intentions that agents can only achieve by means of the others playing their part are intentions with a we-content. By intending to meet Bob at restaurant A, for instance, Ann intends that they, Ann and Bob, meet at Restaurant A. Her intention is of the form ‘I (Ann) intend that we (Ann and Bob) meet at Restaurant A’. Observe that despite its plural content, such an intention remains individualistic in the sense that an individual can in certain circumstances form and hold it alone. Intentions with a we-content are different from ‘shared intentions’ (Searle Reference Searle1995; Tuomela Reference Tuomela1995), although one can view the latter as emerging from an interlocking web of the former (Bratman Reference Bratman1999).
It has been argued in several papers that individual intentions with a we-content are not genuine intentions, because agents can only intend what they have the power to achieve, control or settle. Either intentions with a we-content require that the agents have control of aspects of the situation that are beyond their reach (Baier Reference Baier1970; Stoutland Reference Stoutland, Alanen and Wallgreen1997), or forming and acting on such intentions is not sufficient for the agent to settle the matters (Velleman Reference Velleman1997). On this account, Ann can hope or wish to meet at restaurant A but, it is argued, she cannot really intend it.
This view has been questioned on the ground that, in specific conditions, it is legitimate for agents to form intentions that they cannot achieve by themselves (Velleman Reference Velleman1997: ftn. 11; Bratman Reference Bratman1999). These circumstances are phrased in terms of a background of information about interdependent intentions:
Suppose now that the issue of whether we paint together is one that is obviously salient to both of us. [. . .] I know you would settle on this course of action if only you were confident about my appropriate attitude. I infer that if you knew that I intend that we paint, then you would intend that we paint, and we would then go on to paint together. Given this prediction, I form the intention that we paint and make it known to you [. . .]. (Bratman Reference Bratman1999: 155, my emphasis)
On this account, my intention ‘that we paint’ should be based on background knowledge that you would form the corresponding intention if you knew that I have this intention. More generally, an intention with a we-content of an agent i is epistemically supported whenever i knows that those involved in the achievement of this intention would also form the corresponding intention if they were to know that i has this intention.
Such informational background, it is argued (Bratman Reference Bratman1999: 150–152), ensures that the agent has a sufficiently, but not excessively, high level of control over the matters at hand to consider her intention a genuine one. This is so because it provides her with reliable knowledge that the others will form the required intention and take action, if they get to know that she intends to do so as well. Given this informational background, the agents can take on the relevant actions and ‘settle the matter’, once they ‘make [their intentions] known’ to the others (Bratman Reference Bratman1999: 155). This agentive control, however, does not seem to bear on the autonomous decisions of the other agents involved. An agent with epistemically supported intentions does not force the others into forming the corresponding intentions. She is well-informed about how her intentions are entangled with those of others, but it remains up to them whether they will form the required intentions or not.
Even though this notion of control is arguably the cornerstone of arguments as to why intentions with a we-content can count as genuine intentions, it is not clear how much of it is required. On the one hand, having an epistemically supported intention does not seem always to result in the achievement of the intended goal, and indeed none of the authors cited above make this claim, since this would look like plain control over the others' decision. On the other hand, it is important that, somehow, by forming such intentions and ‘making it known’ to others, the agent is able to settle the matter. It has been proposed that this informational background should give effective control in the ‘normal background absence of human sabotage of our effort’ (Baier Reference Baier, Hein″amaa and Wallgren1997: 25), or that the agent should be ‘in a position reliably to make the appropriate predictions’ (Bratman Reference Bratman1999: 156) about the actions of others, and secure ‘other-agent conditional mediation’ (Bratman Reference Bratman1999: 152).
In what follows I use game-theoretical and logical tools to explore this control condition in the benchmark case of coordination games. To do so I must first introduce some more mathematical machinery, in order to model the agents' mutual expectations and the various rationality constraints on intentions mentioned above.
Before moving further, however, it is important to stress that the object of the investigation below is epistemic support for intentions with a we-content, and not for the formation of full-blown shared intentions. Shared intentions seem to require a substantially stronger web of interlocking intentions, together with a symmetric informational background, ‘meshing sub-plans’, and common knowledge of these two conditions (Bratman Reference Bratman1999). Although the formal apparatus I use could also shed light on the formation of shared intentions, it is not the focus of the present paper. Rather, I am interested in the more basic notion of intention with a we-content, and its role in interpersonal coordination.
3. MODELS OF INTENTIONS AND INFORMATION IN STRATEGIC FORM GAMES
In this section I move from the generic description of games to models of game-playing situations (de Bruin Reference de Bruin2010), which include not only the agents' strategies and preferences but also their information, mutual expectations and, in the present case, their intentions. I first consider intentions, and then standard models from epistemic game theory (Brandenburger Reference Brandenburger2007; Aumann and Dreze Reference Aumann and Dreze2008) and epistemic logic (Fagin et al. Reference Fagin, Halpern, Moses and Vardi1995; van Ditmarsch et al. Reference van Ditmarsch, Hoek and Kooi2007).
3.1 Intention sets
I model previously adopted intentions by directly endowing the agents with an intention set. I do not consider the processes of intention formation or revision, which have been investigated formally elsewhere (Bratman et al. Reference Bratman, Israel, Pollack, Pollock and Cummins1991; Georgeff et al. Reference Georgeff, Pell, Pollack, Tambe, Wooldridge, Muller, Singh and Rao1998; van der Hoek et al. Reference van der Hoek, Jamroga and Wooldrige2007). My goal is rather to study cases in which agents make their decisions against a background of previously adopted intentions, and how such intentions formed at a postulated ex ante stage, and information about them, can anchor mutual expectations.
Given a strategic game ![]() , an intention set ιi for agent i ∈ I is thus a collection of sets of outcomes, that is, a collection of sets of strategy profiles. I call a vector ι of intention sets, one for each agent, an intention profile. A set A in an intention set ιi should be seen as the intention to reach an outcome in this set. Borrowing from propositional modal logic parlance, one can think of A ∈ ιi as the fact that i has the intention to achieve the state of affairs denoted by the proposition A, to achieve what is true in exactly all profiles σ ∈ A. If, for example, {(Restaurant A, Restaurant A), (Restaurant B, Restaurant B)} is in ιAnn for the game in Table 1, I say that Ann has the intention to coordinate with Bob. I say that an outcome σ is consistent with i's intentions whenever σ ∈ A for all A ∈ ιi. I use ↓ιi to denote the set of outcomes that are consistent with i's intentions.
, an intention set ιi for agent i ∈ I is thus a collection of sets of outcomes, that is, a collection of sets of strategy profiles. I call a vector ι of intention sets, one for each agent, an intention profile. A set A in an intention set ιi should be seen as the intention to reach an outcome in this set. Borrowing from propositional modal logic parlance, one can think of A ∈ ιi as the fact that i has the intention to achieve the state of affairs denoted by the proposition A, to achieve what is true in exactly all profiles σ ∈ A. If, for example, {(Restaurant A, Restaurant A), (Restaurant B, Restaurant B)} is in ιAnn for the game in Table 1, I say that Ann has the intention to coordinate with Bob. I say that an outcome σ is consistent with i's intentions whenever σ ∈ A for all A ∈ ιi. I use ↓ιi to denote the set of outcomes that are consistent with i's intentions.
By defining intention sets in this way I automatically allow for intentions with a we-content, a notion which can be spelled out precisely in terms of alpha-effectivity. Say that i is alpha-effective for the set of outcomes A in the game ![]() whenever there is a strategy s i ∈ Si such that {σ:σi=si}⊆A. The intention A ∈ ιi has then a we-content whenever i is not alpha-effective for A.
whenever there is a strategy s i ∈ Si such that {σ:σi=si}⊆A. The intention A ∈ ιi has then a we-content whenever i is not alpha-effective for A.
Two of the normative constraints mentioned in section 2.2 can readily be translated in terms of the structural properties of intention sets. Once again following the analogy from propositional modal logic, an intention set of agent i is said to be internally consistent whenever neither ιi=∅ nor ∅∈ιi. It is agglomerative whenever for any set A and B in ιi, A∩B≠∅. Agglomerativity in this sense does not require full closure, i.e. that A∩B∈ιi for all A, B ∈ ιi. However, for any non-trivial intention set, i.e. ιi≠∅, agglomerativity implies that ∅ ∉ ιi, the second part of the internal consistency constraint.
I now proceed to integrate this simple representation of previously adopted intentions into the broader picture of game-playing situations.
3.2 Doxastic-epistemic models
I use epistemic-doxastic models (Board Reference Board2004; Baltag and Smets Reference Baltag, Smets, Bonanno, Hoek and Wooldridge2008) to represent the information and beliefs of the agents in a particular game playing situation. An epistemic-doxastic model ![]() of a given game
of a given game ![]() is thus a tuple 〈W, {~i, ≤i}i, f〉 with W a set of states, for each agent i ∈ I an epistemic accessibility relation ~i and a binary plausibility ordering ≤i over W, and a function f which assigns to all states in W a strategy and an intention profile in
is thus a tuple 〈W, {~i, ≤i}i, f〉 with W a set of states, for each agent i ∈ I an epistemic accessibility relation ~i and a binary plausibility ordering ≤i over W, and a function f which assigns to all states in W a strategy and an intention profile in ![]() . The strict plausibility ordering <i is defined as for the strict preferences: w <i w′ iff w ≤i w′ but not w′ ≤i w.
. The strict plausibility ordering <i is defined as for the strict preferences: w <i w′ iff w ≤i w′ but not w′ ≤i w.
A state in such a model describes two kinds of facts of a given ex interim situation (Brandenburger Reference Brandenburger2007; Aumann and Dreze Reference Aumann and Dreze2008): the basic facts, concerning what the agents choose and intend at each state, and the informational facts, concerning their information and beliefs in those states. The basic facts are specified by the function f, which assigns a strategy and an intention profile to each state. For convenience I write σi(w) for i's component of the strategy profile assigned to w by f, ιi(w) for i's intention set, and f i(w) for i's component in the two coordinates of f(w). Similarly, I write σ(w) and ι(w) for the strategy and intention profiles assigned to w by f. Observe that the set of states W in a model of a given game ![]() does not need to be in one-to-one correspondence with the set of strategy profiles of
does not need to be in one-to-one correspondence with the set of strategy profiles of ![]() , nor with the set of all possible vectors of intention sets for that game.
, nor with the set of all possible vectors of intention sets for that game.
The relation ~i describes the agents' hard information (van Benthem Reference van Benthem2007a): what they are fully and truthfully informed about. For each state w, it gives all the states w′ that are not ruled out by agent i's information (Lewis Reference Lewis1996). I call any set of states E⊆W an event in a model ![]() , and say that an agent i knows that E at state w whenever E occurs in all states that she considers possible at w; that is, whenever w′ ∈ E for all w′ such that w ~i w′. I use K i(E) to denote the set of states where i knows that E occurs, and say that i knows that E occurs at w whenever w ∈ K i(E). An agent knows that E does not occur at w, denoted w ∈ K i(¬E), when there is no w′ that she considers possible where E occurs. An agent i is uncertain whether E occurs, or does not know whether E, when both w ∉ K i(E) and w ∉ K i(¬E).
, and say that an agent i knows that E at state w whenever E occurs in all states that she considers possible at w; that is, whenever w′ ∈ E for all w′ such that w ~i w′. I use K i(E) to denote the set of states where i knows that E occurs, and say that i knows that E occurs at w whenever w ∈ K i(E). An agent knows that E does not occur at w, denoted w ∈ K i(¬E), when there is no w′ that she considers possible where E occurs. An agent i is uncertain whether E occurs, or does not know whether E, when both w ∉ K i(E) and w ∉ K i(¬E).
I follow general practice in epistemic game theory and epistemic logic, assuming that this information is truthful and strongly introspective. Truthfulness boils down to requiring that E occurs in all states where i knows that E. Introspectiveness, in turn, states that whenever an agent knows something she knows that she knows it; and whenever she does not know something she knows that, too. It is well known that introspectiveness and truthfulness together correspond to ~i being an equivalence relation. See Blackburn et al. (Reference Blackburn, de Rijke and Venema2001) for details.
The agents' uncertainty in epistemic-doxastic models concerns the choices and information of others; they know very little, in this very strong sense of ‘know’, except the structure of the model itself and their own strategy choice. I follow this idea here, with the additional constraint that agents know their own intentions as well. Formally, this boils down to requiring that w ~i w′ implies f i(w) = f i(w′). In contrapositive: an agent's hard information at a given state w excludes at least all states where she chooses another strategy and has different intentions than at w′. This captures the idea that game playing situations model the ex interim stage of a particular play of the game, where the agents have made their decisions on the basis of a given set of intentions, but are uncertain about the choices and intentions of others.
Two notions of group knowledge will be important below: mutual and common knowledge. Mutual knowledge of E at state w is defined as the fact that all agents know that E at that state, i.e. E is mutually known in all states w ∈ M(E)=⋂iKi(E). I say that E is mutually known to degree n at w, written w ∈ Mn(E) whenever it is mutually known that it is mutually known that . . . E, for n iteration of ‘it is mutually known that’. E is common knowledge at w, written w ∈ CI(E) when it is mutually known to all degree n<ω. Alternatively, E is common knowledge at w when it is mutually known that E and that E is common knowledge: CI(E) iff M(E∩CI(E)).
The agents' beliefs are given by the relation ≤i, in conjunction with the agents' hard information at each state. I say that, at a state w, i believes that E occurs whenever E occurs in all the most plausible states that are not ruled out by i's information that w. Formally, whenever w′ ∈ E for all w′ in the set max ≤i[w]i = {v: v ~iw and for all v′ such that v′ ~i w, v′ ≤i v}.
Beliefs are not necessarily veridical, but the present modelling makes them fully introspective. A standard argument shows that this happens if and only if the relation ≤i is transitive and Euclidean (if w≤iw′ and w≤iw″ then w′ ≤iw″). This assumption simplifies the formal exposition, but here it is innocuous: it is nowhere used in the results below. The relation ≤i is often assumed to be total on W, but here I use a slightly weaker condition, namely that it is locally connected (Baltag and Smets Reference Baltag, Smets, Bonanno, Hoek and Wooldridge2008), i.e. that a given agent i is always able to compare the relative plausibility of two states v, v′ if these are not ruled out by i's hard information at a given state w. Observe that with this definition, i's knowing that E at a state implies i's believing that E at that very state, but not the other way around. Agents will usually believe more than they know.
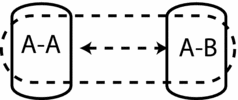
Figure 1 exhibits an epistemic-doxastic model for the coordination game of Table 1, with the intention sets omitted. In this particular case we represent the states by the strategy profile which they are assigned by the function f, ‘A-A’ meaning, for instance, that Ann chooses Restaurant A, and Bob does too. The dashed and solid arrows respectively represent Ann and Bob's plausibility orderings, with an arrow going from one state to the other meaning that the second is strictly more plausible than the first, and a double arrow, as in figure 2, meaning that w≤iw′ and w′≤iw. The dashed solid rectangles represent Ann's and Bob's epistemic accessibility relation. At all states in this example both agents know their own strategy choices, but are uncertain about the choice of their opponent. In all states, however, they both believe that the other is coordinating his choice. This belief turns out to be correct at both states where they do coordinate, but mistaken at the two other states.

Figure 1. An epistemic-doxastic model for the coordination game of Table 1, with the intention sets omitted.
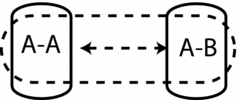
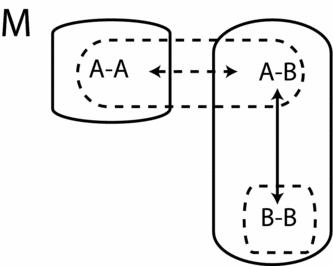
Figure 2. An epistemic-doxastic model where coordination occurs at A−A even though Ann's intention in not epistemically supported.
With this in hand we can spell out strong belief consistency of intentions. Recall that strong belief consistency requires that ‘it should be possible for my entire plan to be successfully executed given that my beliefs are true’ (Bratman Reference Bratman1987: 31). Here I take the notion of the ‘entire plan’ to refer to all the agent's intentions in her set ιi(w) at a state w. I thus say that ιi(w) is strongly consistent, relative to i's beliefs whenever for all intention A in ιi(w), there is a state w′, among those i considers the most plausible at w, in which A has realized, i.e. for which σ(w′) ∈ A. Negatively, ιi(w) is strongly belief inconsistent when one of her intentions would be impossible to realize, if her beliefs were true. Note that strong belief consistency does not require i to believe that all her intentions will be realized together, much less to know it. An agent can have belief consistent intentions and yet consider it possible, and even highly plausible, that he will not realize them. See Bratman (Reference Bratman1987, forthcoming) for arguments in favour of this possibility.
Together with the fact that agents know their own strategy choice at each state, strong belief consistency implies that the intentions are conduct controlling, in the sense that the agent acts on them. In general this constraint can be translated in term of consistency between one's intentions and one's strategy choice at a given state. We say that the intention to achieve A of agent i is conduct controlling at a state w in a model ![]() whenever there is a σ′ ∈ A such σ′i=σi(w). In words: i's intention to realize A is conduct controlling at a state whenever i's choice at w does not rule out the realization of A. Strongly belief consistent intentions are always conduct controlling, by knowledge of one's own strategy choice, but not the other way around.
whenever there is a σ′ ∈ A such σ′i=σi(w). In words: i's intention to realize A is conduct controlling at a state whenever i's choice at w does not rule out the realization of A. Strongly belief consistent intentions are always conduct controlling, by knowledge of one's own strategy choice, but not the other way around.
Epistemic-doxastic models also allow to strengthen the idea of agglomerativity to exclude potential violation of strong belief consistency. We say that i's intentions are strongly agglomerative at state w whenever they are agglomerative and, if ιi(w)≠∅, then there is w′ ∈ max ≤i[w] such that σ(w′)∈↓ιi. In words, an intention set of agent i at a state w is strongly agglomerative whenever there is a state which i considers most plausible where all his intentions are realized. Clearly, strong agglomerativity implies strong belief consistency and agglomerativity, but not the other way around.
The stage is now set to look at the import of intentions in the theory of coordination in games. In the next section we investigate the epistemic support of intentions with a we-content, after which we provide a general intention-based characterization of coordination with intentions, using the known epistemic characterization of equilibrium play.
4. EPISTEMIC SUPPORT FOR INTENTIONS WITH A WE-CONTENT
The notion of epistemic support for intentions with a we-content can readily be expressed in epistemic-doxastic models. Recall from the quote earlier that an agent's intention that A is epistemically supported whenever i knows that the others would also adopt this intention if they knew of his. Let I i A be the set {w:A∈ιi(w)} where agent i intends A. The set of states where i knows that j intends that A is thus Ki(IjA)={w:w′∈IjA for all w′~iw}, and I write Ki(IjA)→IiA for the set of states w where either w ∉ K i(I jA) or w∈IiA. If i intends A at state w, then we say that this intention is epistemically supported if:
Epistemically supported intentions to coordinate are neither necessary nor sufficient for the agents to achieve coordination, even when it is common knowledge that all the normative constraints mentioned above are satisfied. For failure of necessity, consider the model of Figure 2, with states directly labelled by the strategy profile assigned to them by f and the intention sets specified in Table 2. The reader can check that in both states Ann and Bob's intentions are internally consistent and strongly agglomerative, and thus that this is common knowledge. In both states Bob knows that Ann intends to meet at restaurant A, an intention for which she is not alpha-effective, and so Ann knows that Bob knows this. She, however, is uncertain about Bob's intention and strategy choice. Despite Bob's knowledge of her intentions, she considers it possible that he might just as well go to restaurant B, with the corresponding intentions, and thus the failure of epistemic support for her intention at state A−A. Nevertheless, at that stage they manage to coordinate. This reflects the simple fact that agents can simply be lucky and coordinate, even though their information does not support their intentions.
Table 2. The intentions for the model in Figure 2.
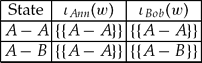
To see that epistemic support is not sufficient either, return to the model in Figure 1, completed with ιi(w)={{A−A, B−B}} for i either Ann or Bob and all states w ∈ W. Ann and Bob intend to coordinate, this intention is strongly agglomerative, and thus strongly belief consistent, and all this is common knowledge. At A−B and B−A, however, coordination fails even though Ann's and Bob's intentions are epistemically supported. Observe, moreover, that ‘making [each other's] intentions known’ (Bratman Reference Bratman1999) is not sufficient at these states either, as Ann and Bob know about each other's intentions in the strongest sense possible: their intentions are common knowledge.
This failure of epistemic support to ensure coordination is not a consequence of the fact that very few constraints bear on the relation between intentions and hard information, as indeed two weaker forms of ‘doxastic’ support are also insufficient for coordination. An inspection of the model of Figure 1, together with the intentions as specified in Table 3, reveals that Ann knows at A−B that Bob's believing that she intends to meet at restaurant B implies that he also intends to meet at that same restaurant. This holds trivially at A−B itself, since there Bob mistakenly believes that Ann intends to meet at Restaurant A, but at B−B he correctly believes that Ann intends to meet at Restaurant B, and he has the corresponding intention. This epistemic-doxastic support is thus not sufficient for coordination either, and the same holds for an even weaker fully doxastic support, since if Ann knows at A−B that ‘Bob's believing that she intends to meet at restaurant B implies that he also intends to meet at that same restaurant’, then she believes this too.
Table 3. Another assignment of intentions for the model in Figure 1.

These results cast doubts on whether epistemic support provides the required ‘other-agent conditional mediation’ (Bratman Reference Bratman1999: 152). In the counter-example above, epistemic support does provide reliable information about the fact that the agents will form, and indeed have the required intentions. These intentions, however, fail to provide the required conditional mediation of the other agents. More is needed for epistemic support to establish this mediation, which seems to be crucial in considering their attitudes as genuine intentions.
Under additional constraints, epistemic support can enforce conditional mediation. It does so, for instance, under internal and strong belief-consistency, if we constrain the intended set A to a singleton, and by maintaining the conditions that intentions are mutually known. To see this, consider a singleton set of outcome A = {σ} for which agent i is not alpha-effective in a game ![]() . Take a state w in a model
. Take a state w in a model ![]() for
for ![]() such that the intentions of all agents are internally and strongly belief-consistent at w. Assume that this intention is epistemically supported and that all other agents j≠i know that i intends that A. Since hard information is truthful, we know by the epistemic support condition that w∈(Kj(IiA)→IjA) for all j≠i. By assumption and, again, truthfulness of hard information, we then know that w ∈ IjA for all j ∈ I. But by strong belief consistency this means that there must be a w′ ∈ max ≤i[w such that σ(w′) ∈ A, which boils down to σ(w′)=σ because A is a singleton. But since w′≥iw implies w′~iw we know that σj(w′)=σj(w)=σj for all j ∈ I. This means that σ(w) = σ, and thus that all agents realize their intentions at w.
such that the intentions of all agents are internally and strongly belief-consistent at w. Assume that this intention is epistemically supported and that all other agents j≠i know that i intends that A. Since hard information is truthful, we know by the epistemic support condition that w∈(Kj(IiA)→IjA) for all j≠i. By assumption and, again, truthfulness of hard information, we then know that w ∈ IjA for all j ∈ I. But by strong belief consistency this means that there must be a w′ ∈ max ≤i[w such that σ(w′) ∈ A, which boils down to σ(w′)=σ because A is a singleton. But since w′≥iw implies w′~iw we know that σj(w′)=σj(w)=σj for all j ∈ I. This means that σ(w) = σ, and thus that all agents realize their intentions at w.
Mutual knowledge of intentions turns out to be crucial here, as without it epistemically supported intentions fail to be conducive of their achievement. The model in Figure 1 completed with the intentions in Table 3 provides a counter-example. In this model all intentions are singleton sets, and it is common knowledge that these intentions are internally consistent and strongly agglomerative. At state A−B, however, the reader can check that Ann's intention is epistemically supported, but that coordination nevertheless fails because Bob is uncertain about what she intends.
This stronger epistemic support, however, seems too strong. It requires the agents to have hard knowledge about the intentions of others, and about how these intentions are responsive to what the others know. This knowledge condition boils down to the agent having truthful, fully reliable and irrefutable information about the fact that the other will form the required intentions, if she forms it herself. In other words, the agent is absolutely certain, and she is right about it, that by making her intention known to the others she will make him adopt this intention. As noted above, and argued notably in Lewis (Reference Lewis1996), very few facts can sustain the claim of such hard knowledge after examination. The intentions of others appear to be a typical kind of fact about which it is extremely difficult to acquire hard knowledge, at least as long as it remains up to the others to adopt them or not. The knowledge condition in this strengthened version of epistemic support excludes this possibility, though. With hard knowledge, the agents are bound to form the required intentions, something which goes beyond the acceptable level of control that epistemic support is intended to provide.
It is important to note that this does not call into question the collective character of epistemically supported intentions with a we-content. Epistemic support makes the agents' intentions entangled in a way that intentions with a purely ‘I-content’ would not be. The strong plural character of the content of such intentions thus remains.
These results rather take issue with the idea that epistemic support gives the agents enough control of the situation in a way that does not bear excessively on the other agents' attitudes. They show that, in general, epistemic support does not provide reliable control of the situation, but if one considers a natural strengthening of this notion, which does allow the agents to ‘take action and settle the matters’, it seems they have illegitimate control of the intentions of others.
In view of this, in the next section I propose an alternative notion of support for intention with a we-content in coordination games, based on known characterizations of equilibrium play from epistemic game theory. This notion, I argue, fares better than epistemic support in terms of plausibility, and reflects the fact that coordination is also a state which ‘rational’ players will try to achieve.
5. INTENTIONS AND EQUILIBRIUM PLAY
5.1 Self-fulfilling expectations about intentions
The first step towards providing alternative conditions for support of intentions with a we-content in coordination games is to observe that, in such games, all and only the coordination profiles are pure strategy Nash equilibria. A Nash equilibrium is a strategy profile where no player would strictly profit from unilaterally changing her strategy. Formally, σ is a pure Nash equilibrium whenever for all i in I and all si≠σi, we have that σ ⪰i (s i, σj≠i).
Sufficient conditions for Nash equilibrium are usually formulated in terms of information about mutual expectations and Bayesian rationality (Aumann Reference Aumann1987; Aumann and Brandenburger Reference Aumann and Brandenburger1995; Aumann and Dreze Reference Aumann and Dreze2008). In probabilistic models of beliefs, Bayesian rationality boils down to choosing ‘strategies that maximize [the players'] utilities given their subjective distributions over the other players' strategy choices’ (Aumann Reference Aumann1987: 2).
Bayesian rationality, taken as expected utility maximization, implies choosing a strategy which is not strictly dominated given the agent's information – see Brandenburger and Dekel (Reference Brandenburger and Dekel1987) and the references therein – and this latter notion has a straightforward correspondent in epistemic-plausibility models. I say that an agent i plays a strongly dominated strategy given her beliefs at a state w whenever there is a strategy si different from the one she chooses at w, si≠σi(w), such that in all states w′ that i considers the most plausible, she strictly prefers the outcome of playing si against the strategy that the other chooses at w′ to the outcome she is actually reaching at w′, i.e. (s i, σj≠i(w′)) ≻i σ(w′) for all w′ ∈ max ≤i[w]i. I then say that an agent is irrational at a state w whenever she plays a strongly dominated strategy, given her beliefs. Observe that the negation of irrationality is a form of ‘weak rationality’ (van Benthem Reference van Benthem2007b), strictly weaker than classical maximization of expected utility. The latter implies the former, but not the other way around.
With this in hand one can formulate sufficient conditions for coordination in terms of self-fulfilling mutual expectations about intentions. Let ![]() be a coordination game, σ* a coordination profile in it,
be a coordination game, σ* a coordination profile in it, ![]() an epistemic-doxastic model for
an epistemic-doxastic model for ![]() , and w a state in W. Then σ(w)=σ*, i.e. the agents do coordinate on σ* at w, and this outcome is consistent with their intentions, whenever the following two conditions hold, for all players i ∈ I:
, and w a state in W. Then σ(w)=σ*, i.e. the agents do coordinate on σ* at w, and this outcome is consistent with their intentions, whenever the following two conditions hold, for all players i ∈ I:
1. No agent is irrational, and all of them have strongly belief consistent intentions.
2. They believe that the others have strongly belief consistent intentions and intend to coordinate on σ*, i.e. each agent i believes that {σ*}∈ιj for all j≠i.
The argument for this runs as follows. Observe first that whenever an agent j has strongly belief consistent intentions and intends to coordinate on σ* at a state w, then this intention is conduct-controlling: σj(w)=σ*j. Agent i believing that this is the case for all her co-players boils down to saying that for all w′ ∈ max ≤i[w]i, the profile σj≠i(w′) played by the other players at w′ is just the others' component in the coordination profile, i.e. σj≠i(w′)=σ*j≠i. But then it is irrational for i not to coordinate, viz. not to play σ*i. If σi(w)≠σ*i then, by definition of a coordination game, σ*i, σj≠i(w′)) ≻i σ(w′), for all w′ ∈ max ≤i[w]i, simply because σj≠i(w′)=σ*j≠i and so that (σ*i, σj≠i(w′)) is just σ*, while σ(w′) itself is not a coordination profile. In other words, if σi(w)≠σ*i then i plays a strongly dominated strategy given her beliefs at a state w, and so if i is not irrational it must be that σi(w)=σ*i. Since this holds for an arbitrary i we thus know that σ(w)=σ*, i.e. that the agents do coordinate on σ* at that w. Moreover, since each agent i knows her own strategy choice at each state, this argument shows that σ(w′)=σ* for all w′ ∈ max ≤i[w]i. But then by strong belief consistency this means that σ*∈A for all A∈ιi(w), and thus that this profile is strongly consistent with i's intentions at w. Again, this holds for all i since we took an arbitrary agent in I.
The set of sufficient conditions just provided features self-fulfilling expectations in the sense that the mutual belief that all other agents intend to coordinate on a particular outcome entails that they are, in fact, playing their parts in reaching that outcome. In other words, the result above shows that, given strong belief consistency, if all agents believe that all others intend to coordinate on a particular outcome, then they also believe that the others play their part in reaching that outcome. This belief, in turn, implies that they play their part themselves, if they are not irrational, thus fulfilling the others' expectations. Another way to see this is that besides weak rationality and strong belief consistency, there is no constraint on the agents' intentions in the antecedents of this result. The agents have beliefs about the intentions of others, but these beliefs need not be correct. That the agents do in fact choose to play their part in the coordinated action is a consequence of these beliefs, thus the idea of self-fulfilling expectations.
These conditions are tight, in the sense that the implication stated fails if any of them is weakened. For instance, it might not be irrational to play something other than one's part in a coordination profile if one does not believe that all the others intend to reach this outcome, but only that reaching this outcome is compatible with the intentions of all the others. The interested reader can find detailed arguments for this claim in the appendix.
The conditions provided above are substantially weaker, and more plausible than those for epistemic support. Observe, first, that agglomerativity is not needed in this result, nor is common or even a lower-order level of knowledge that the others are not irrational. Non-irrationality and a first-order belief about a basic fact of the game-playing situation, namely the intentions of the other players, are sufficient. This belief system, in turn, is essentially first-order, in comparison with epistemic support, which is essentially second-order. That no hard knowledge about intentions is required leaves it open for each agent to adopt the required intentions or not. The agents, in other words, do not have illegitimate control of the intentions of others. It is through their entangled web of preferences, beliefs and intentions that the agents influence each others' decision, and this web in turns allows each agent to take action and settle matters. This entanglement in the agents' attitudes also gives a strong collective character to intentions with a we-content.
This is thus an account of how intentions with we-content can be supported in coordination games, in a way that gives enough control to the agents, while avoiding excessively strong influence on each others' decision, and doing justice to the plural character of such intentions. It could of course be argued that the fulfilment of all the rationality constraints on intention mentioned above, including agglomerativity, is something that should be common knowledge in an ideal game-playing situation. The above result would of course still hold in such a case.
That self-fulfilling expectations about each-other's intentions are sufficient for coordination does not, however, explain why the agents should form such expectations in the first place. The characterization only states that if these expectations are in place, then the agents will coordinate if they are not irrational. In this sense the argument provided here has the same structure as standard characterizations of solution concepts in epistemic game theory (Brandenburger Reference Brandenburger2007), providing sufficient epistemic conditions for certain behaviour in situations of interaction, but leaving aside the justification for these conditions.
In some specific forms of coordination games the claim that the required set of mutual expectations about intentions will arise does seem to be supported, though. It might be argued, first, that mutual and even higher-order belief in strongly belief-consistent intentions is natural for agents who know that they are interacting with other rational ‘planning agents’ (Bratman Reference Bratman1987), in the same fashion as common belief in rationality is often taken to be a natural assumption for ideal game-playing situations. Concerning the more contentious part of the above characterization result, namely the mutual expectation in playing a specific coordination profile, it seems natural in games that contain a specific ‘cue’ (Schelling Reference Schelling1980) or ‘focal point’ (Harsanyi and Selten Reference Harsanyi and Selten1988). Coordination games with a unique Pareto-optimal Nash equilibrium, such as ‘Hi-Lo’ games (Bacharach Reference Bacharach, Gold and Sugden2006), are an obvious case in point. The empirical evidence cited by Bacharach (Reference Bacharach, Gold and Sugden2006) suggests that agents do in fact expect each other to coordinate on the Pareto-optimal profile, and it is natural to interpret these expectations as bearing on each others' intentions. Of course, this argument is only available for coordination games with a specific structure but, together with the characterization just provided, it is nevertheless sufficient to support the claim that, in some situations, intentions with a we-content can provide the required amount of control.
5.2 Comparing self-fulfilling expectations and epistemic support
Epistemic support and the sufficient conditions for coordination formulated in the previous section are independent of each other. That the first does not imply the second is a direct consequence of the fact that only one of them is sufficient for coordination. The implication is indeed falsified by the same model I used to show that epistemic support is not sufficient for coordination, viz. the model of Figure 1 with the intentions as in Table 3. For the other direction, consider again the model in Figure 2, but with A−A AnnA−B instead of the double arrow, and take the intentions specified in Table 2. At A−A Ann now believes that Bob intends to meet her at restaurant A, and that this intention is strongly consistent with his beliefs, and the same holds for Bob, mutatis mutandis. These beliefs turn out to be correct at this state, where, furthermore, Ann and Bob are rational. Ann's intentions remain epistemically unsupported, however, because she does not know that Bob intends to meet her at restaurant A, even though she correctly believes this.
The conditions provided in the previous section can of course be strengthened to imply epistemic support, simply by substituting knowledge for belief. Indeed, take a state w of an epistemic-doxastic model ![]() for a game
for a game ![]() , and suppose that agent i intends to achieve A at w, an intention for which she is not alpha-effective. If i knows at w that for all agents j, j also have the strongly belief consistent intention to achieve A then, by simple propositional reasoning and closure of knowledge under logical consequence, i's intention is epistemically supported. Observe that to get this one only uses i's knowledge about j's intentions. Non-irrationality and strong belief consistency play no role here.
, and suppose that agent i intends to achieve A at w, an intention for which she is not alpha-effective. If i knows at w that for all agents j, j also have the strongly belief consistent intention to achieve A then, by simple propositional reasoning and closure of knowledge under logical consequence, i's intention is epistemically supported. Observe that to get this one only uses i's knowledge about j's intentions. Non-irrationality and strong belief consistency play no role here.
This strengthening of the sufficient conditions for coordination, however, has the same shortcoming as epistemic support itself, namely that it requires agents to have hard information about the intentions of others. As I noted earlier, this would seem to be a rather implausible requirement.
5.3 Self-fulfilling expectations and characterization of equilibrium play
The two-agent case of the above result is closely related to Aumann and Brandenburger's (Reference Aumann and Brandenburger1995) general characterization of Nash equilibrium play for two players. They show that rationality, understood as maximization of expected utility, and mutual knowledge of strategy choice are sufficient for Nash equilibrium play in the two-player case. The characterization just given uses two weaker conditions, namely non-irrationality instead of expected utility maximization and mutual beliefs in having the intention to coordinate instead of straightforward knowledge of each others' choices. However, the argument for the result reveals that the above belief condition implies mutual beliefs about each other's choices. The result for two agents can thus be read along the line of Aumman and Brandenburger's two-player characterization: non-irrationality and mutual beliefs in each other's choices, here induced by mutual beliefs about each other's intentions, implies Nash equilibrium in coordination games. That these two weaker notions are still sufficient here is due to the simple structure of such games. For each player there is a unique best response to what she believes the other is playing. A quick check of the argument reveals, in fact, that the above characterization not only holds for coordination profiles, but for any ‘strict’ Nash equilibrium.
The result differs, however, from Aumann and Brandenburger's (Reference Aumann and Brandenburger1995) general characterization when we move to more than two players. This requires mutual knowledge of rationality and common knowledge of ‘conjectures’, which in the case of pure strategies boils down to common knowledge of strategy choice. They show, furthermore, that the common knowledge requirement is tight, in the same sense as above. In comparison, the present result uses much weaker conditions. Not only does it use beliefs instead of knowledge, but here the move to an arbitrary number of agents does not require us to go higher up the mutual knowledge/belief hierarchy. Intentions, together with the simple structure of coordination games, play a key role here. As Bratman (Reference Bratman1987) puts it, they directly ‘anchor’ mutual expectations, and coordination indirectly, and by doing so they allow the agents to bypass the reasoning about higher-order expectations that is crucial in characterizations of equilibrium play for arbitrary games.
6. CONCLUSION
In this paper I have cast doubts as to whether epistemic support for intentions with a we-content guarantees the other agents' conditional mediation, and I have provided an alternative set of conditions that do ensure coordinated play. These conditions call for many extensions, though. The analysis of epistemic support for intentions with a we-content has not used the logical techniques for counterfactual conditionals, and it will be important to examine whether the result still holds in such an extended framework. From the game-theoretic perspective it will also be important to explore the connection between the intention-based approaches and current teams-oriented proposals (Sugden Reference Sugden2003; Bacharach Reference Bacharach, Gold and Sugden2006). Intentions with a we-content, even though they are in essence individual states, have a clearly interactive character, which they might share with group- or team-related approaches. It would also be illuminating to explore the connection with existing formal work on intention in multi-agent systems and artificial intelligence (Wooldridge Reference Wooldridge2000; van der Hoek et al. Reference van der Hoek, Jamroga and Wooldrige2007; Shoham Reference Shoham2009).
The results in this paper draw both from the contemporary philosophical literature on intentions and from game-theoretical and logical models of knowledge and beliefs in interaction. This shows the importance of philosophical theories of intention in the game-theoretical and logical study of coordination and, in turn, that the game-theoretic and logical perspective sheds light on various claims in the philosophical literature. This interplay between these disciplines is, I believe, a fruitful one, which should be explored further.
APPENDIX – TIGHTNESS OF THE RESULT STATED IN SECTION 5
I show in this appendix that if any of the conditions in the result are relaxed, then the implication fails.
• Irrationality. Take the model in Figure 2, except that A−A AnnA−B. Let the intentions be assigned as follows: ιAnn(A−A)=ιAnn(A−B)=ιBob(A−A)={{A−A}} and ιBob(A−B)={{A−B}}. At A−B Bob has strongly belief consistent intentions and he believes that Ann has strongly consistent intentions and intends to coordinate on A−A. Bob, however, is not rational at this state, and Ann and he do indeed fail to coordinate.
• Failure of strong belief consistency. Take the model in Figure 3 and let the intentions be assigned as follows: ιAnn(A−A)=ιAnn(A−B)={{A−A}, {A−A, A−B}}, ιAnn(B−B)={{B−B}, {A−A, A−B}}, and for all states w in
 , ιBob(w)={{A−A}, {A−A, B−B}}. The reader can check that at all states both Ann and Bob are not irrational, that they all correctly believe that the other intends to achieve A−A, and that their intentions are internally consistent and agglomerative. At A−B, however, Bob has no strongly belief consistent intentions, since he believes, and in fact he knows that his intention to achieve A−A is impossible to realize at that state, where coordination fails.
, ιBob(w)={{A−A}, {A−A, B−B}}. The reader can check that at all states both Ann and Bob are not irrational, that they all correctly believe that the other intends to achieve A−A, and that their intentions are internally consistent and agglomerative. At A−B, however, Bob has no strongly belief consistent intentions, since he believes, and in fact he knows that his intention to achieve A−A is impossible to realize at that state, where coordination fails.• Belief that one of the others does not have strongly belief consistent intentions. As in the previous case the model provides a sufficient counterexample, because at A−B Ann is correct in not believing that Bob has strongly belief consistent intentions. It is illustrative, however, to consider a case in which all agents do have strongly belief consistent intentions but where coordination fails because one of them is mistaken about this. So take the same set of states as before, but set plausibility relations and the intentions as follows: A−B<AnnA−A and A−B<BobB−B; ιAnn(A−A)=ιAnn(A−B)=ιAnn(B−B)ιBob(A−A)={{A−A}} and ιBob(A−B)=ιBob(B−B)={{B−B}}. In this case, at A−B Bob believes that Ann intends to coordinate on A−A but that this intention is not consistent with what she believes is possible, because Bob thinks the most plausible state here is B−B.
• Belief that one of the others does not intend to achieve the coordination profile. Again, take the model in Figure 3, and let the intentions be as before, except ιBob(w)={{A−A, B−B}}. Here both Ann and Bob are rational, and their intentions are strongly belief-consistent, agglomerative and internally consistent. This means in particular that at A−B Ann believes that Bob has strongly belief-consistent intentions. She knows, however, that Bob does not intend A−A, even though this outcome is compatible with his intentions.
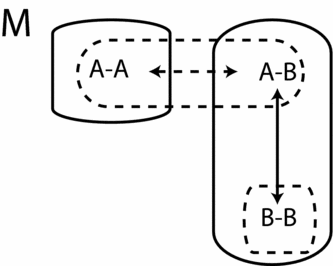
Figure 3. Failure of the implication with intentions that are not strongly belief consistent.