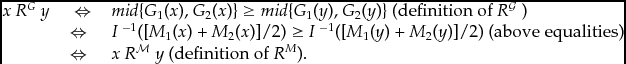1. INTRODUCTION
The Arts and Humanities Research Council in Britain evaluates research proposals by convening a panel. It assigns to each proposal two ‘introducers’, who award one of six numerical grades. Later the panel agrees on a grade for each proposal, and ranks them all from better to worse. This is an example of grading in groups. There are many others. Experts on a systematic review panel rate the quality of medical evidence as High, Moderate or Low. The Michelin company awards restaurants from no stars to three after visits by its inspectors. Editors accept or reject submitted articles after taking advice from reviewers. In Tromsø, two teachers separately assign each student's work a letter grade and then get together to decide the final result. The students in turn go online to evaluate their teachers and courses, and potential employers will rank them as job candidates on the basis of the grades awarded their coursework. Michel Balinski and Rida Laraki (Reference Balinski and Laraki2010) discuss many examples of grading in groups, from the evaluation of wine, sports, music and more.
Often there is no saying precisely how good or bad things are. Relevant information is missing, or expertise is lacking, or criteria of evaluation are unclear – and always time is short. We can award grades even so. This is because they are coarse grained, each grade covering a range of degrees of merit. Again, often we don't even want precise knowledge, and grades ease communication by smoothing over unimportant differences. It helps that they are contextual, their interpretation varying somewhat from person to person, and from case to case. Grades are supposed to cover small differences, not amplify them, and with some scope to set the thresholds between grades to the case at hand we can hope to ensure that any items that are about equally good will receive the same grade. In these ways the coarse grain and contextuality of grades promote timely appraisal and effective dissemination of results.
Grades can be misleading, though, and the same features that make them useful are responsible also for this. Say Jack and Jill are up for a job. You are to recommend one or the other, on the basis of their results in two tests. It's late, and you're still at the office. So, who will it be? Jack has a B on both tests; Jill one B and a C. It must seem to you that Jack is to be considered the better of the two. There's a good chance that those who graded the tests wouldn't agree, though. Grades are coarse grained. If on the one test Jill got a ‘high’ C and Jack a ‘low’ B then the difference between them there might be very small. If her B was also high, and his other B also low, then the graders might well think that she is the better of the two. Or they might come to think so, anyway, if ever they got together to compare notes.
High Cs and low Bs are much of a muchness. What if grades are further apart? It is natural to call Jack an overall B, since that is what he got on both tests. Suppose that, instead of the one C, Jill had a D. It is tempting then to ‘split the difference’ between her B and D, calling it on balance a C, and so to conclude once again that Jack must be considered better than her. But this too would be wrong. Grades are contextual. Thresholds vary from case to case, and one test might well have been graded more leniently than the other. Say the tests were scored first on a scale from 0 to 100%, and letter grades awarded later on the basis of that. Mr Easy rewarded scores as low as 60% with a B. Ms Measly required for a B at least 85%, and up to 65% could result in a D from her – low B territory, for him. Such large differences in the interpretation of grades are not unusual.Footnote 1 It might have been so, for all you could know. And, if it was so, then it is quite possible that, in the minds of the graders, Jill is the better of the two. It is compatible with the awarded grades that she has a 64% (that was the D, from Measly) and an 89% (B, from Easy), to Jack's 63% (B, from Easy) and 88% (B, from Measly). Jill's underlying scores in this case are higher although her grades are worse. Easy and Measly might count her better, after comparing notes. And you, with only the grades to go by, would never know.
The point of course is that while such possibilities as these have not been excluded, any impression that Jack must be considered better than Jill is an illusion. It is an artifact of the coarse grain and contextual shiftiness of grades. Certainly he might be considered better. But he also might not and the grades by themselves cannot settle the matter.Footnote 2 Meanwhile, it is only getting later. Now you really must choose! Jack is the only one you can justify recommending, given their grades. So, Jack it will be. Such dubious judgements must have helped many careers, and held others back. They are in several ways wrong.Footnote 3
Sometimes it is possible to remove all uncertainty about the thresholds between grades by stipulating them. The National Rifle Association in the United States assigns politicians grades from A to a menacing F according to their support for its positions. In principle it could specify exactly which proportions of votes will earn which grades.Footnote 4 But evaluation is not always this single-minded, and the possibilities for pinning down thresholds accordingly are limited. When evaluating research proposals, relevant criteria are the significance of the proposed research, the reputations of the investigators, and the quality of the proposals themselves. With restaurants we care about ingredients, technique, ambience and value-for-money. People differ in the importance they attach to these factors, though, and without settling weights or priorities in advance it cannot be completely clear just what it is that grades are supposed to measure. There can be no saying precisely how good or bad things must be to get one grade or the other.
Grades get their meanings in part from other evaluative language. The Research Council defines a Grade 4 research proposal as:
A very good proposal demonstrating high international standards of scholarship, originality, quality and significance.
Three Michelin stars stands for:
Exceptional cuisine where diners eat extremely well, often superbly. Distinctive dishes are precisely executed, using superlative ingredients.
Defining grades in natural language surely promotes a common understanding, the more so when people share not only a language but also their culture. But it cannot be expected to remove all uncertainty about thresholds. Expressions such as ‘very good’, ‘high standards’, ‘superb’ and ‘extremely well’ are themselves highly contextual. Depending whom you ask, and where and when you ask, ‘distinctive dishes’ and ‘precisely executed’ – perhaps even ‘diners eat extremely well’ – could cover anything from dinner with Paul Bocuse all the way down to driving through a McDonald's. Interpretations of grades must float somewhat freely, together with our understanding of other evaluative language to which they are bound.
This is a study of the consequences of uncertainty about grading thresholds. There is a range of cases to consider. At one end there is no such uncertainty. It is known exactly where each grader draws the lines between grades, and for each grader it is the same. At the other end, nothing is known about this. Each grader might have any thresholds at all, independently of the others.
In the first case, we will see, grading in groups makes good sense. A rule for aggregating grades can be, in a technical sense, sound. Intuitively, what this means is that any judgement that one item is better than another, reached on the basis of the grades awarded to them, is bound to reflect the graders’ underlying estimations of the items’ merit. At the other extreme, we will see, collective grading cannot be relied on in the same way. When nothing at all is known about the graders’ thresholds, collective grading under certain plausible assumptions is always unsound. No matter which rule we use for forming judgements on the basis of awarded grades, and no matter how we reckon the graders’ collective sense of the merit of the items, we cannot rule out the sort of illusion that we saw earlier on, when Jack was judged to be better than Jill even though, for all anyone knows, the graders themselves think her better.
The first step will be to set up a technical framework within which to study collective grading. Section 2 adapts to this purpose the standard Arrow–Sen framework from social choice theory, introducing grading rules as procedures for ranking things on the basis of grades awarded by several people. Section 3 translates the conditions of Arrow's ‘impossibility’ theorem to the case in which people grade things instead of ranking them. Section 4 introduces soundness as a further constraint on grading. An example shows that it is possible to satisfy this new condition as well as the Arrow conditions, if everybody's grading thresholds are known to be the same. Section 5 states the unsoundness theorem. It says that with too much uncertainty about thresholds no grading rule can satisfy all the Arrow conditions and still be sound. Section 6 discusses in light of these findings a proposal of Balinski and Laraki to use grading in political elections.
2. THE QUESTION
In every collective grading problem there are some graders, and there are some things for them to grade. Just who and what they are depends on the case. They might be members of a committee and project proposals. They might be teachers and course papers, or members of a review panel and bodies of medical evidence. We will fix some representative grading problem and study that. Let N be a finite set of graders, and let X be a set of things. They could be just about anyone and anything but they do have to be some particular ones. Fix also a finite set ![]() $\mathcal{G}$, the vocabulary of available grades, with a linear ordering > from better to worse.Footnote 5
$\mathcal{G}$, the vocabulary of available grades, with a linear ordering > from better to worse.Footnote 5
Example 1. Let ![]() $\mathcal{G}$ be {A, B, C, D, F}, and let A > B > C > D > F. This is the language of grades that is used, with minor modifications, in colleges and universities throughout the world.
$\mathcal{G}$ be {A, B, C, D, F}, and let A > B > C > D > F. This is the language of grades that is used, with minor modifications, in colleges and universities throughout the world.
There is also an aggregator, whose job it is to rank all of the items from better to worse on the basis of the grades awarded to them. For ease of exposition let the aggregator be – you. Taking on this role doesn't mean that you cannot at the same time be one of the graders. It doesn't even mean that you are a person. In online course evaluation, the aggregator is an algorithm running on a computer.
One question straight away is this: Just how will you proceed, once the graders have told you which grades they have awarded? That is, how will you assimilate their input into a single evaluation of all the items? To study this question it will help first to make it precise, using ideas from the theory of social choice (List Reference List and Zalta2013). For any individual grader i, let an individual appraisal Gi be a function assigning to each item in the set X some grade in ![]() $\mathcal{G}$. That is, Gi(x) ∈
$\mathcal{G}$. That is, Gi(x) ∈ ![]() $\mathcal{G}$. Think of Gi as a report that this one grader i might hand you, saying which grades he has awarded to which items. A grade profile
$\mathcal{G}$. Think of Gi as a report that this one grader i might hand you, saying which grades he has awarded to which items. A grade profile ![]() $\mathcal{G}$ is a list <G1, . . ., Gn> of individual appraisals, one for each grader i. It is a possible report from all the graders. For instance:
$\mathcal{G}$ is a list <G1, . . ., Gn> of individual appraisals, one for each grader i. It is a possible report from all the graders. For instance:
Example 1 (continuation). Let X be {a, b, c}, let N be {1, 2}, and let G1(a) = A, G1(b) = C, G1(c) = C, G2(a) = C, G2(b) = A, G2(c) = F. <G1, G2> is a grade profile.
A grade domain ![]() $\mathcal{D}$ is a set of grade profiles. Intuitively, these are all the reports that, as far as you know, the graders might produce. They needn't be all conceivable ones. Perhaps only some of the grades are made available to the graders at first, the others being held in reserve to smooth over differences during aggregation if the graders disagree. A grade domain that does not include all ‘logically possible’ reports is said to be restricted.
$\mathcal{D}$ is a set of grade profiles. Intuitively, these are all the reports that, as far as you know, the graders might produce. They needn't be all conceivable ones. Perhaps only some of the grades are made available to the graders at first, the others being held in reserve to smooth over differences during aggregation if the graders disagree. A grade domain that does not include all ‘logically possible’ reports is said to be restricted.
Example 2. Let X, N and ![]() $\mathcal{G}$ be as in Example 1. Let
$\mathcal{G}$ be as in Example 1. Let ![]() $\mathcal{D}$ be the set of all grade profiles G such that for any i ∈ N and x ∈ X: Gi(x) ∈ {A, C, F}.
$\mathcal{D}$ be the set of all grade profiles G such that for any i ∈ N and x ∈ X: Gi(x) ∈ {A, C, F}.
This domain is suitable for analysing a grading problem in which the two graders are allowed to award only an A, a C or an F, with the intermediate grades B and D held in reserve.Footnote 6
You will use a fixed procedure or rule for aggregating the grades into a ranking of the items. This will keep you consistent. Also, you will choose this rule in advance, before you find out just what grades everybody happens to turn in. This will keep you straight. You cannot go back and change your mind, if some favourite of yours happens not to come out on top. Let a grading rule be a function F that maps any given report G, taken from some domain of possibilities, to a binary relation F(G) on X. For any given x and y, the intended interpretation of x F(G) y is: were the graders to hand in report G then your judgement on that basis, using rule F, would be that x is as good as y, perhaps better. The question is now: Which grading rule will you use?
Here is a rule that will illustrate several points later on.
Example 3. Let N and ![]() $\mathcal{G}$ be as in the previous examples. For any g ∈
$\mathcal{G}$ be as in the previous examples. For any g ∈ ![]() $\mathcal{G}$, let mid{g, g} be g. For any g1 and g3 ∈
$\mathcal{G}$, let mid{g, g} be g. For any g1 and g3 ∈ ![]() $\mathcal{G}$ such that some further grade g2 lies, in the sense of >, in the middle between g1 and g3, let mid{g1, g3} be this g2. If on the other hand there is no such g2 then let mid{g1, g3} go undefined. For instance, mid{D, D} = D, mid{A, C} = B and mid{F, A} = C; but mid{B, C} and mid{B, F} are undefined. Now, for any suitable domain, we define a grading rule F as follows: for a given profile G we let F(G) be that relation R ⊆ X 2 such that xRy if mid{G1(x), G2(x)} and mid{G1(y), G2(y)} are both defined, and mid{G1(x), G2(x)} >mid{G1(y), G2(y)}.The following point is important for what is to come. Let G be any profile in the domain
$\mathcal{G}$ such that some further grade g2 lies, in the sense of >, in the middle between g1 and g3, let mid{g1, g3} be this g2. If on the other hand there is no such g2 then let mid{g1, g3} go undefined. For instance, mid{D, D} = D, mid{A, C} = B and mid{F, A} = C; but mid{B, C} and mid{B, F} are undefined. Now, for any suitable domain, we define a grading rule F as follows: for a given profile G we let F(G) be that relation R ⊆ X 2 such that xRy if mid{G1(x), G2(x)} and mid{G1(y), G2(y)} are both defined, and mid{G1(x), G2(x)} >mid{G1(y), G2(y)}.The following point is important for what is to come. Let G be any profile in the domain ![]() $\mathcal{D}$ of Example 2. Then R is a weak ordering of X, both transitive and complete.Footnote 7R inherits its transitivity from the linear ordering > of the grades. Completeness follows from the domain restriction. Because the grades that 1 and 2 assign to any given x are either identical or sufficiently far apart, mid{G1(x), G2(x)} is always defined.Footnote 8
$\mathcal{D}$ of Example 2. Then R is a weak ordering of X, both transitive and complete.Footnote 7R inherits its transitivity from the linear ordering > of the grades. Completeness follows from the domain restriction. Because the grades that 1 and 2 assign to any given x are either identical or sufficiently far apart, mid{G1(x), G2(x)} is always defined.Footnote 8
So far this setup is only a slight extension of the framework that Kenneth Arrow introduced in order to study problems of social choice (Arrow Reference Arrow1951). Notice the one important difference. In Arrow's framework there is no grading of social alternatives. Instead people rank these from better to worse. This matters because we can say more by grading things than by ranking them. When for instance the Michelin company awards one restaurant three stars and the other just two, it says that the first restaurant is better than the second. It says more than just this, though, because different grades correspond to the same ranking: had the second restaurant instead received just a single star, or no star, the implicit comparison would have been the same. There is more information in the grades than in the corresponding ranking.
Notice also that, even so, there is a way in which people typically can say less when asked to grade things than when they are allowed to rank them as they see fit. Grading vocabularies tend to be small. There are just four Michelin categories, for instance, from no stars to three. The Michelin company evaluates tens of thousands of restaurants around the world, though, and so there have to be many, many ties; it is out of the question to express using Michelin stars, say, a linear ordering of all the restaurants, which would mean assigning to each one a unique grade. When grades can capture some given ranking they might do so in more ways than one. Typically, though, there are rankings they cannot capture at all.
3. CHOOSING A GRADING RULE: SOME CONSIDERATIONS
So now you are on the lookout for a good grading rule. Here are some features to consider. All are desirable in a range of grading problems. They are closely related to requirements that Arrow (Reference Arrow1951) imposed on social welfare functions.
A first feature that a grading rule F might be expected to have is:
Completeness (C). For each grade report G in the domain of F, F(G) is a complete relation.
Completeness is good when our purpose in evaluating things is to choose from among them. Say we are to rank some candidates for a job. If we can be sure to end up with a complete ordering of the different ones then, if somehow we lose the very best candidate, perhaps to another employer, there will always be a second-best candidate to fall back on.
In order to express the next feature it will help to have some notation for the ranking implicit in the grades awarded by an individual i. Given an individual appraisal Gi, let Ği, or flat Gi, be the binary relation on X such that x Ği y if Gi(x) >Gi(y).Footnote 9 We can also flatten whole profiles: Ğ = <Ği> is the list of everybody's implicit rankings. Now, let S be some subset of X, and let <Ği>|S be <Ği|S>, the result of restricting each ranking in the list to S. The relevant feature is now:
Ordinally Unrestricted Domain with respect to S (OU-S). For each list <Ri> of |N| weak orderings of S, the domain of F includes some report G such that Ğ|S = <Ri>.
OU-S requires the grading rule to handle a certain variety among inputs. The graders N might put the items S in any order, and they might do so independently of one another; the rule has to be able to cope no matter what rankings the graders produce. This is a plausible requirement in some grading problems. When evaluating research proposals, for instance, little might be known in advance about the merit of the different ones. Then, perhaps, the graders’ appraisals could turn out to be anything, and the grading rule had better be ready for everything. Notice that it is possible for a grading rule to satisfy OU-S only if there are as many grades in the vocabulary ![]() $\mathcal{G}$ as there are items in S. With ‘pass-fail’ grading for instance there are just two grades. All implicit rankings Ği are dichotomous and imposing OU-S makes sense only for pairs S.Footnote 10
$\mathcal{G}$ as there are items in S. With ‘pass-fail’ grading for instance there are just two grades. All implicit rankings Ği are dichotomous and imposing OU-S makes sense only for pairs S.Footnote 10
Writing R instead of F(G), when the context makes clear which grading rule F and profile G are meant, let P be the strict component of R: xPy means that, on the basis of the grades reported in G, x is counted really better than y – not merely as good.Footnote 11 A further condition is then:
Weak Pareto (WP). For any x, y ∈ X and any G in the domain of F, if, for each i ∈ N, Gi(x) > Gi(y), then xPy.
This says that when everybody awards one thing a higher grade than another, it must be counted strictly better.
Another feature that might be desirable, for any given set S of items, is:
Non-Dictatorship with respect to S (D-S). There is no δ ∈ N such that for any x, y ∈ S and any G in the domain of F, if Gδ(x) > Gδ(y) then xPy.
D-S rules out choosing some particular grader in advance and, when the grade report comes in, whichever it may be, just reading off the resultant ranking from the grades that this one ‘dictator’ has awarded. Indeed, that would seem to defeat a main purpose of grading in a group, which is to pool information. Depending on the domain, though, D-S also excludes some perfectly democratic ways of proceeding. A ‘dictator’ here is just someone whose grades invariably agree with the judgements of the group. That doesn't entail any power or influence over these.Footnote 12
Finally, writing R for F(G) and R* for F(G*), we have:
Independence of Irrelevant Alternatives (I). For any x, y ∈ X, and any G and G* in the domain of F, if G|{x, y} = G*|{x, y}, then R|{x, y} = R*|{x, y}.
I says that the final ranking of any two given items is fixed by the grades awarded just them. It does not depend on any other features of these items that are not reflected in their grades, or on which grades are awarded to items outside the pair.
Condition I is always satisfied when, as in Example 3, each item is first awarded a resultant grade on the basis of the grades awarded to it by the different graders, and then the ranking R of all the items is read off from their resultant grades. Determining resultant grades ‘on a curve’, on the other hand, with some fixed quota set in advance for each grade, may be expected to lead to violations of I. Be this as it may, appraising things separately, each according to the grades awarded just to it, seems quite natural. Arguably, it is only proper when merit is something that things have all by themselves, not in virtue of how they compare with other things. To this extent I is a reasonable constraint on grading rules.
Now it is not difficult to see that:
Example 3 (continuation). As defined on the domain ![]() $\mathcal{D}$ of Example 2, the grading rule F of Example 3 satisfies conditions C, OU-X, WP, D-X and I.
$\mathcal{D}$ of Example 2, the grading rule F of Example 3 satisfies conditions C, OU-X, WP, D-X and I.
Arrow's (Reference Arrow1951) social welfare functions are rules for assimilating individual preference rankings into a single ‘social’ ordering. His ‘impossibility’ theorem says that no social welfare function satisfies a short list of conditions (for discussion of these, see Morreau Reference Morreau and Zalta2014). Now C, OU-X, WP, D-X and I are versions of Arrow's conditions, adapted to the case in which people grade things instead of ranking them; since the grading rule of Example 3 satisfies them all, it seems that grading opens up possibilities that are not there in Arrow's framework.Footnote 13 Balinski and Laraki see this as one advantage of their preferred method of majority judgement which, they say, ‘overcomes’ Arrow's impossibility (Balinski and Laraki Reference Balinski and Laraki2010: xiii). Critical to the solution, in their view, is that a common language of grades enables ‘absolute’ judgements of each item separately (Balinski and Laraki Reference Balinski and Laraki2010: 185).
One main point in the following is that Arrow's impossibility is still there in the background – common language, absolute judgements and satisfaction of the adapted Arrow conditions notwithstanding. It is hiding behind an implicit assumption. Uncertainty about thresholds can destroy much of the information in grades. Suppose for instance that you as aggregator have no idea where one of the graders draws the line between a B and a C. Then, when you hear that he has awarded Jack a B and Jill a C, all you've really learned is that he thinks Jack is better than Jill: you have a ranking but that is all. The hidden assumption is that enough is known about everybody's thresholds so that grades carry more information than just rankings. When too little is known we might as well be back in Arrow's framework, where individual inputs are limited to rankings right from the start; and then, as section 5 shows, it is not possible to satisfy the adapted Arrow conditions together with a further condition of ‘soundness’. That is how Arrow's impossibility reappears.
4. SOUND GRADING
We have been developing the following model of grading in groups. First, each grader estimates the merit of each item, privately and in more or less precise terms. Second, each grader awards a grade to each item, on the basis of his estimation of it. Third, all the grades go to you, the aggregator. Finally, using a grading rule, you assimilate the grades into resultant ranking of all the items. It is inherent in this model that information about merit takes an indirect path from the graders to you, passing through the linguistic medium of grades. Intuitively, your grading rule is sound if, to the best of your knowledge, the resultant ranking must always agree with the result that a direct aggregation of the underlying estimations would have produced – if only, somehow, you could have access to these.
The qualification ‘to the best of your knowledge’ is crucial. This is where uncertainty about thresholds comes in. Section 4.2 shows how to capture this qualification by quantifying over all combinations of individual estimations of merit that, for all you can tell, are compatible with the reported grades. These combinations make up what I shall call the ‘import’ of the grade report. Section 4.3 defines soundness and gives an example of a sound grading rule. Meanwhile, section 4.1 lays a foundation for all this by introducing the dimensions of merit that grades measure.
4.1. Degrees of merit
Grades measure the goodness of things, or their quality, or value. Here, the term ‘merit’ will cover these. Merit has a finer grain than grades: two things might both deserve the same grade even though one of them is better than the other. A merit structure is a pair (![]() $\mathcal{M}$, >), of which
$\mathcal{M}$, >), of which ![]() $\mathcal{M}$ is a non-empty set, the degrees of merit. It is ordered by > from better to worse. For example, in education we sometimes assign students letter grades on the basis of their percentage scores in a separate test. Then
$\mathcal{M}$ is a non-empty set, the degrees of merit. It is ordered by > from better to worse. For example, in education we sometimes assign students letter grades on the basis of their percentage scores in a separate test. Then ![]() $\mathcal{M}$ includes the numbers between 0 and 100%. There can be more numerical structure than this minimal requirement of a better–worse relation. Sometimes, we can add up degrees of merit, and average them.
$\mathcal{M}$ includes the numbers between 0 and 100%. There can be more numerical structure than this minimal requirement of a better–worse relation. Sometimes, we can add up degrees of merit, and average them.
I shall assume that comparative merit is a complete ordering: for any distinct degrees of merit m and n, either m > n or n > m. With many evaluation problems this is quite unrealistic. Think of two restaurants. If one has a better menu than the other, but not such a nice view, there might be no saying which of them is, overall, best. Nor do we seem to think they are equally good, though. A further slight improvement in the menu at the first restaurant – there's an additional special today! – won't tip the balance and make it quite simply the better of the two, overall. The restaurants do not seem to be comparable in terms of the standard value relations ‘strictly better’ and ‘equally good’.
So, which will it be for lunch? When alternatives are incomparable there might be no uniquely best one, nor even a tie for best, and therefore no scope either for maximizing choice. But there is a way in which two alternatives, though not comparable by the standard value relations, might still be roughly equal. Say we count both restaurants as excellent. They are to this extent comparable with one another. If in addition they are better than all the other alternatives then it would seem quite appropriate just to flip a mental coin and get on with lunch, as we might with options that really are tied for best. This idea recalls Ruth Chang's (Reference Chang2002) notion of ‘parity’ and the role she sees for it in supporting rational choice. Indeed, Chrisoula Andreou's (Reference Andreou2015) account of parity relies on categorical judgements that are very much like my grade assignments. Thus the theory of grading, when comparative overall merit is an incomplete relation, might underwrite maximizing choice in some cases where it has seemed there can be none.
Balinski and Laraki distinguish grades, messages about merit, from what they call the graders’ ‘deep preferences or utilities’. These utilities, they explain, in the context of voting, are ‘relative measures of satisfaction’. They illustrate this point with the example of the 2002 French presidential elections:
The voters of the left would have hated to see Jacques Chirac defeat Lionel Jospin: their utilities for a Chirac victory would have been the lowest possible. The same voters were delighted to see Chirac roundly defeat Le Pen in the second round: their utilities for a Chirac victory were the highest possible. On the other hand, these same voters would probably have given Chirac a grade of Acceptable or Poor . . . were he standing against Jospin, Le Pen, or anybody else. (Balinski and Laraki Reference Balinski and Laraki2010: 185)
Now, in my account, a voter's estimation of Chirac's merit is what underlies the appraisal of him as an Acceptable candidate, or a Poor one, as the case may be. This estimation is likely to have been the same, more or less, irrespective of who the other candidates were. My degrees of merit, then, are not relative measures.
I shall now again borrow the Arrow–Sen framework by introducing merit profiles. A first notion is that of an individual merit assignment Mi. This is a function mapping each x to some degree Mi(x) of merit. Intuitively, Mi is a possible fact about i’s private estimation of each item, on the basis of which i will award grades to the different ones. A merit profile M is a list <M1, . . ., Mn> of individual merit assignments, one for each grader. Notice that merit profiles are not reports. They are not linguistic items, or any other sort of thing that can in any direct way be made public. Rather, a merit profile is a possible fact about how good or bad all the individual graders might privately take everything to be. Merit profiles will figure, here, in an account of the content of grade reports – of the information that these convey from the graders to you, the aggregator.
A merit domain is a set of merit profiles. We will assume that merit domains are unrestricted. That is, they include all ‘logically possible’ lists of individual merit assignments. This does not have any obvious empirical consequences. It does not constrain the set of items to be evaluated, or how the graders will determine which grades to assign to them, or any other special features of the grading problem being studied.
The unsoundness theorem in section 5 relies on two assumptions about merit. First, the merit ordering is dense. That is, whenever m1 > m3 there is a further degree of merit m2 in between: m1 > m2 > m3. Second, it is unbounded above and below: there is no m such that, for each other n, m > n; and there is no n such that, for each other m, m > n. These assumptions are used in the proof of the crucial Lemma 11. They are strong. Either entails that ![]() $\mathcal{M}$ is infinite, which limits the applicability of this framework. Sometimes, presumably, grades are awarded on the basis of estimations of merit that are themselves coarse grained, only less so, and finite in number. Also, these assumptions are psychologically unrealistic. I expect that the first can be done away with by requiring instead that, in between any two degrees of merit that an individual function Mi actually assigns, there are in
$\mathcal{M}$ is infinite, which limits the applicability of this framework. Sometimes, presumably, grades are awarded on the basis of estimations of merit that are themselves coarse grained, only less so, and finite in number. Also, these assumptions are psychologically unrealistic. I expect that the first can be done away with by requiring instead that, in between any two degrees of merit that an individual function Mi actually assigns, there are in ![]() $\mathcal{M}$ as many other degrees of merit as there are grades in the (finite) vocabulary
$\mathcal{M}$ as many other degrees of merit as there are grades in the (finite) vocabulary ![]() $\mathcal{G}$. The second assumption could be replaced by a requirement that no Mi shall assign an extreme value. No grader will ever find any of the items under consideration to be so utterly good or so excruciatingly bad that it is not even imaginable that something could be better, or worse.
$\mathcal{G}$. The second assumption could be replaced by a requirement that no Mi shall assign an extreme value. No grader will ever find any of the items under consideration to be so utterly good or so excruciatingly bad that it is not even imaginable that something could be better, or worse.
A merit function F ![]() $^\mathcal{M}$ maps each merit profile M in its domain onto a weak ordering of X. Intuitively, it is a procedure for aggregating several estimations of merit into a single collective comparison. One equitable way to do so is to average them:
$^\mathcal{M}$ maps each merit profile M in its domain onto a weak ordering of X. Intuitively, it is a procedure for aggregating several estimations of merit into a single collective comparison. One equitable way to do so is to average them:
Example 4. Let X and N be as in the previous examples. Let ![]() $\mathcal{M}$ be the real interval (0, 1) with the obvious ordering. This fixes the merit domain: {<M1, M2>: Mi: X → (0, 1)}. Now for any such M = <M1, M2> in this domain, and for any x, y ∈ X, let F
$\mathcal{M}$ be the real interval (0, 1) with the obvious ordering. This fixes the merit domain: {<M1, M2>: Mi: X → (0, 1)}. Now for any such M = <M1, M2> in this domain, and for any x, y ∈ X, let F ![]() $^\mathcal{M}$(M) be that binary relation R on X such that:
$^\mathcal{M}$(M) be that binary relation R on X such that:
The earlier grading rules have the same co-domain as merit functions, all rankings of the set X, but they take grade profiles as input, not merit profiles. For clarity, let us from now on use a superscript when referring to grading rules as well: F ![]() $^\mathcal{G}$ will be a grading rule, and F
$^\mathcal{G}$ will be a grading rule, and F ![]() $^\mathcal{M}$ a merit function.
$^\mathcal{M}$ a merit function.
4.2. Import
We will now need an account of the information carried by grade reports. The basic notion is that of an interpretation. It fixes grading thresholds. That is, it tells us precisely how good or bad things have to be in order to get one grade or another. This idea is familiar from the grading keys or scales used to turn numerical scores into letter grades. Let us refer to the vocabulary ![]() $\mathcal{G}$ of grades more formally now, along with the linear ordering > from better to worse, as a grading language (
$\mathcal{G}$ of grades more formally now, along with the linear ordering > from better to worse, as a grading language (![]() $\mathcal{G}$, >). Technically, an interpretation maps each grade from
$\mathcal{G}$, >). Technically, an interpretation maps each grade from ![]() $\mathcal{G}$ onto an interval of (
$\mathcal{G}$ onto an interval of (![]() $\mathcal{M}$, >), the better the grade the higher the interval:
$\mathcal{M}$, >), the better the grade the higher the interval:
Definition 5. An interpretation of (![]() $\mathcal{G}$, >) in (
$\mathcal{G}$, >) in (![]() $\mathcal{M}$, >) is a function I mapping each grade g from
$\mathcal{M}$, >) is a function I mapping each grade g from ![]() $\mathcal{G}$ onto a subset I(g) of
$\mathcal{G}$ onto a subset I(g) of ![]() $\mathcal{M}$, such that:
$\mathcal{M}$, such that:
For each g ∈ ![]() $\mathcal{G}$, I(g) is convex: if m1, m3 ∈ I(g) and m1 > m2 > m3, then m2 ∈ I(g); and
$\mathcal{G}$, I(g) is convex: if m1, m3 ∈ I(g) and m1 > m2 > m3, then m2 ∈ I(g); and
I is orderly: for any g1, g2 ∈ ![]() $\mathcal{G}$, m1 ∈ I(g1), and m2 ∈ I(g2), if g1 > g2 then m1 > m2.
$\mathcal{G}$, m1 ∈ I(g1), and m2 ∈ I(g2), if g1 > g2 then m1 > m2.
These are the basic requirements. We can stipulate as well that for each degree of merit there is some corresponding grade, and that for each grade there is some degree of merit:
∪g∈![]() $\mathcal{G}$I(g) =
$\mathcal{G}$I(g) = ![]() $\mathcal{M}$; and
$\mathcal{M}$; and
For each g ∈ ![]() $\mathcal{G}$, I(g) ≠ ∅.
$\mathcal{G}$, I(g) ≠ ∅.
These further requirements are not as basic but we will impose them as well.Footnote 14 Here is an example of an interpretation:
Example 6. Let ![]() $\mathcal{G}$ and
$\mathcal{G}$ and ![]() $\mathcal{M}$ be as in the previous examples. Let I(A) = [0.8, 1.0), I(B) = [0.6, 0.8), I(C) = [0.4, 0.6), I(D) = [0.2, 0.4) and I(F) = (0.0, 0.2). Then I is an interpretation of
$\mathcal{M}$ be as in the previous examples. Let I(A) = [0.8, 1.0), I(B) = [0.6, 0.8), I(C) = [0.4, 0.6), I(D) = [0.2, 0.4) and I(F) = (0.0, 0.2). Then I is an interpretation of ![]() $\mathcal{G}$ within
$\mathcal{G}$ within ![]() $\mathcal{M}$.Footnote 15
$\mathcal{M}$.Footnote 15
Say all the graders have finished their work. They produce a report G saying who has awarded which grade to what. Their report tells you, the aggregator, something about how good they take everything to be. Just what it tells you, though, depends on how much you know about their thresholds. The information about merit carried by G will now be captured in the notion of the import of G, written ⟦G⟧. This is a set of merit profiles. Intuitively, M ∈ ⟦G⟧ means that the information in M is, as far as you can tell, compatible with that in G. The less you know about everybody's thresholds, the more compatible merit assignments there are, and the more inclusive is ⟦G⟧.
First, here is a notion of import for individual graders.
Definition 7. The import ⟦Gi⟧I of Gi, relative to I, is {Mi: for each x ∈ X, Mi(x) ∈ I(Gi(x))}.
⟦Gi⟧I includes Mi if i’s estimation of any given x, according to Mi, is compatible with the grade that i has awarded to x, according to Gi, on the assumption that i’s thresholds are I.
Now an import function ⟦⟧ maps each profile G in its domain to some set ⟦G⟧ of suitable merit profiles.
Example 8. Let X, N, ![]() $\mathcal{G}$ and
$\mathcal{G}$ and ![]() $\mathcal{M}$ be as in the previous examples, and let I be any interpretation. Consider any suitable grade domain
$\mathcal{M}$ be as in the previous examples, and let I be any interpretation. Consider any suitable grade domain ![]() $\mathcal{D}$. For any given G ∈
$\mathcal{D}$. For any given G ∈ ![]() $\mathcal{D}$, let ⟦G⟧, the import of G, be:
$\mathcal{D}$, let ⟦G⟧, the import of G, be:
Intuitively, the import function of Example 8 says which assessments of merit by both graders are compatible with any given report G on which grades they have awarded, assuming they have in common the grading thresholds I. In some tightly constrained cases this assumption is reasonable. The case described before, where grades are awarded on the basis of percentage scores, could be one of these – if the graders have settled on a common grading key, and if you as aggregator happen to know just which one it is. Let us have a name for import functions of this sort.
Definition 9. ⟦⟧ is grounded and rafted if there is some I such that for each G in the domain, ⟦G⟧ = ⨉i ∈N ⟦Gi⟧I.
Grades are less misleading when the aggregator knows this much. Consider again the case of Jack and Jill. According to the report G you received, one grader gave Jack a B and the other gave Jill a D: G1(Jack) = B and G2(Jill) = D. If ⟦⟧ is grounded and rafted then, irrespective of I, the graders cannot, like Mr Easy and Ms Measly, have had different thresholds. ⟦G⟧ doesn't include any M such that MEasy(Jack) = 63% and MMeasly(Jill) = 64%. There is no common interpretation I such that:
This is because interpretations are orderly (see Definition 5). Since B is a higher grade than D, each degree of merit in I(B) must be greater than each degree of merit in I(D), but 63% is not greater than 64%. When import is grounded and rafted, then, the false impression that Jack is better than Jill cannot arise, at least not in the same way. Your judgement, based on the grades, might accurately reflect the collective judgement of the graders. Example 8 (continuation) describes a case in which it reliably does.
At the other extreme we know nothing about the graders’ thresholds. Letting ![]() $\mathscr{I}$ be the set of all interpretations,
$\mathscr{I}$ be the set of all interpretations,
Definition 9 (continuation). ⟦⟧ is floating and unrafted if for each G in the domain,
When ⟦⟧ is floating and unrafted, M ∈ ⟦G⟧ if there are any I1, . . ., In such that, for each i, Mi ∈ ⟦Gi⟧Ii. Intuitively, this is so if there is any way at all, by choosing thresholds for the different graders, to square the fine-grained estimations (of M) with the awarded grades (according to G).
Grade reports do not tell us very much when import is afloat and unrafted because they do not rule out very much. For instance, to continue with the example of Jack and Jill, we can square the offending M with G by allowing the graders to have their own interpretations IEasy and IMeasly such that:
This is precisely how, in section 1, grades created the false impression that Jack must be better than Jill. Section 5 argues that, when import is floating and unrafted, grading in groups is in a sense radically unreliable. Under the conditions set out in Section 3, it cannot be counted on to track the collective judgement of the graders, no matter how that is reckoned.
The coming discussion will consider grading in groups at these extremes: the case in which import is grounded and rafted, and that in which it is floating and unrafted. There are many other possibilities, some of them quite realistic. We might know which interpretation each grader has, but that these are not the same for everyone. Then, for each i there is some perhaps distinct interpretation Ii such that ⟦G⟧ = ⨉i∈N ⟦Gi⟧Ii. Again, perhaps we know that the graders have settled on a grading key, but not which one it is. Then any grader might interpret the grades in any way at all, but we needn't reckon with the further possibility of different graders having different thresholds: ⟦G⟧ = ∪I ∈![]() $\mathscr{I}$⨉i∈N⟦Gi⟧I. Many other kinds of import functions can be imagined.
$\mathscr{I}$⨉i∈N⟦Gi⟧I. Many other kinds of import functions can be imagined.
4.3. Soundness
Finally, here is what it is for a grading rule to be sound. I shall write R ![]() $^\mathcal{G}$ for F
$^\mathcal{G}$ for F ![]() $^\mathcal{G}$(G), and P
$^\mathcal{G}$(G), and P ![]() $^\mathcal{G}$ for the strict part of R
$^\mathcal{G}$ for the strict part of R ![]() $^\mathcal{G}$. Similarly, R
$^\mathcal{G}$. Similarly, R ![]() $^\mathcal{M}$ is F
$^\mathcal{M}$ is F ![]() $^\mathcal{M}$(M), and P
$^\mathcal{M}$(M), and P ![]() $^\mathcal{M}$is the strict part of R
$^\mathcal{M}$is the strict part of R ![]() $^\mathcal{M}$. Now we have:
$^\mathcal{M}$. Now we have:
Definition 10.F ![]() $^\mathcal{G}$ is sound with respect to F
$^\mathcal{G}$ is sound with respect to F ![]() $^\mathcal{M}$, given ⟦⟧, if for any G ∈
$^\mathcal{M}$, given ⟦⟧, if for any G ∈ ![]() $\mathcal{D}$ and any x, y ∈ X:
$\mathcal{D}$ and any x, y ∈ X:
(a) if x R
 $^\mathcal{G}$y then for every M ∈ ⟦G⟧, x R
$^\mathcal{G}$y then for every M ∈ ⟦G⟧, x R  $^\mathcal{M}$y; and
$^\mathcal{M}$y; and(b) if x P
 $^\mathcal{G}$y then for every M ∈ ⟦G⟧, x P
$^\mathcal{G}$y then for every M ∈ ⟦G⟧, x P  $^\mathcal{M}$y.
$^\mathcal{M}$y.
Soundness means that your judgement that one thing is (strictly) better than another, based just on the grades, is sure to reflect the graders’ underlying views of the merit of these things – whatever, as far as you can tell from the grades, and given what you know about everybody's thresholds, these views might have been. Remember that when more is known about thresholds, there are fewer possibilities in ⟦G⟧. The requirements of Definition 10 are in this case correspondingly mild. Knowing more about how everybody interprets the grades therefore makes it easier to find a sound grading rule.
Say we are going to choose a grading rule for ranking some research proposals, on the basis of grades awarded by two experts. We have discussed the criteria and their relative importance. We have considered the judgements of previous panels, and have held a calibration session. As a result we know a certain amount about the graders’ thresholds. This knowledge is embodied in an import function ⟦⟧. Since it is for use under the given circumstances that we need a grading rule, we hold ⟦⟧ fixed. Now we can enquire simply whether any given candidate procedure F ![]() $^\mathcal{G}$ is sound with respect to any given merit function F
$^\mathcal{G}$ is sound with respect to any given merit function F ![]() $^\mathcal{M}$. Let us say we also have a preferred F
$^\mathcal{M}$. Let us say we also have a preferred F ![]() $^\mathcal{M}$. We are going to average individual estimates, say, as in Example 4. With both ⟦⟧ and F
$^\mathcal{M}$. We are going to average individual estimates, say, as in Example 4. With both ⟦⟧ and F ![]() $^\mathcal{M}$ held fixed, we can ask simply whether F
$^\mathcal{M}$ held fixed, we can ask simply whether F ![]() $^\mathcal{G}$ is sound.
$^\mathcal{G}$ is sound.
Why should we care whether it is or not? Soundness guarantees that there are no false impressions like those created by Mr Easy and Ms Measly, in section 1. No matter which grades the experts end up reporting, the resultant ranking of the proposals is sure to agree with what they really think of the proposals – collectively, and as reckoned by our preferred method. Clause (b) of Definition 10 concerns the case in which proposal x is ranked strictly higher than proposal y on the basis of their grades, while (a) covers the case in which the two proposals are judged to be on a par. Soundness is desirable because decisions made using sound procedures can be rationalized. If someone wants to know why their proposal was not funded there will be an answer. We can say that these (G) are the grades awarded by the experts; that these (⟦G⟧) are the only estimations the experts could possibly have of the merit of the proposals, given what we know from the training sessions about their understanding of the grades; that the comparison (R ![]() $^\mathcal{M}$) based on any of these possibilities (M), will confirm the resultant ranking (R
$^\mathcal{M}$) based on any of these possibilities (M), will confirm the resultant ranking (R ![]() $^\mathcal{G}$) we reckoned by the grades (G) – and that, in this very strong field of competitors, the proposal in question sadly could not be counted among the very best.
$^\mathcal{G}$) we reckoned by the grades (G) – and that, in this very strong field of competitors, the proposal in question sadly could not be counted among the very best.
To rationalize the decision is not to justify it, because different parts of the rationalization are themselves subject to criticism. The disappointed author can still argue that our assumptions about grading standards, embodied in ⟦⟧, are incorrect (‘the training of the panel members was inadequate!’); or that agreement with R ![]() $^\mathcal{M}$ is beside the point because we haven't used an acceptable method F
$^\mathcal{M}$ is beside the point because we haven't used an acceptable method F ![]() $^\mathcal{M}$ for reckoning collective comparisons (‘one of your so-called ‘experts’ knows almost nothing about the specific area of this proposal, and his views should carry less weight!’). Still, the rationalization is a beginning. It provides the main structure for a justification and indicates points at which it could be shored up or brought down.
$^\mathcal{M}$ for reckoning collective comparisons (‘one of your so-called ‘experts’ knows almost nothing about the specific area of this proposal, and his views should carry less weight!’). Still, the rationalization is a beginning. It provides the main structure for a justification and indicates points at which it could be shored up or brought down.
Here is an example of a sound rule:
Example 8 (continuation). More specifically, let ![]() $\mathcal{D}$ be as in Example 2, and let I be as in Example 6. Consider again F
$\mathcal{D}$ be as in Example 2, and let I be as in Example 6. Consider again F ![]() $^\mathcal{G}$ from Example 3. Let the merit function F
$^\mathcal{G}$ from Example 3. Let the merit function F ![]() $^\mathcal{M}$ be defined as follows. For any suitable M and any x, y ∈ X, we put
$^\mathcal{M}$ be defined as follows. For any suitable M and any x, y ∈ X, we put
This notion of the inverse I −1 of I is natural but not standard: for example, since I(C) = [0.4, 0.6) we have I −1(0.5) = C. Intuitively, x R ![]() $^\mathcal{M}$y means that the graders would collectively award x as high a grade as they would y, perhaps a higher one, were they to proceed in the following way: First, the individual graders estimate the merit of every item; second, for each one they calculate a collective estimate, by averaging their individual estimations of it; finally, using the common grading key – it is implicit in I – for each item they look up the grade that it deserves, given their collective estimation of it.
$^\mathcal{M}$y means that the graders would collectively award x as high a grade as they would y, perhaps a higher one, were they to proceed in the following way: First, the individual graders estimate the merit of every item; second, for each one they calculate a collective estimate, by averaging their individual estimations of it; finally, using the common grading key – it is implicit in I – for each item they look up the grade that it deserves, given their collective estimation of it.
Now we will see that F ![]() $^\mathcal{G}$ is sound with respect to F
$^\mathcal{G}$ is sound with respect to F ![]() $^\mathcal{M}$ assuming ⟦⟧ (the import function of Example 8). This follows directly from:
$^\mathcal{M}$ assuming ⟦⟧ (the import function of Example 8). This follows directly from:
Fact.For any G ∈ ![]() $\mathcal{D}$, x, y ∈ X, and M ∈ ⟦G⟧: x R
$\mathcal{D}$, x, y ∈ X, and M ∈ ⟦G⟧: x R ![]() $^\mathcal{G}$y if and only if x R
$^\mathcal{G}$y if and only if x R ![]() $^\mathcal{M}$y.
$^\mathcal{M}$y.
To verify this fact, note first that for any g1, g2 ∈ {A, C, F}, and for any m1 ∈ I(g1) and m2 ∈ I(g2)
To see this, check all the possibilities; really, there are only three. Now consider any G ∈ ![]() $\mathcal{D}$ and any M ∈ ⟦G⟧. By choice of the import function ⟦⟧, for any x, y ∈ X and i ∈ N we have Mi(x) ∈ I(Gi(x)) and Mi(y) ∈ I(Gi(y)), so in particular:
$\mathcal{D}$ and any M ∈ ⟦G⟧. By choice of the import function ⟦⟧, for any x, y ∈ X and i ∈ N we have Mi(x) ∈ I(Gi(x)) and Mi(y) ∈ I(Gi(y)), so in particular:
Therefore:
This completes the demonstration of the fact and with it the soundness of F ![]() $^\mathcal{G}$ with respect to F
$^\mathcal{G}$ with respect to F ![]() $^\mathcal{M}$, assuming ⟦⟧.
$^\mathcal{M}$, assuming ⟦⟧.
In the discussion surrounding Theorem 14, in the next section, it will be relevant that F ![]() $^\mathcal{M}$ of Example 8 (continuation) satisfies Condition I. That is, for any x, y ∈ X, and any M, M* in the domain of F
$^\mathcal{M}$ of Example 8 (continuation) satisfies Condition I. That is, for any x, y ∈ X, and any M, M* in the domain of F ![]() $^\mathcal{M}$, if M|{x, y} = M*|{x, y}, then R
$^\mathcal{M}$, if M|{x, y} = M*|{x, y}, then R ![]() $^\mathcal{M}$|{x, y} = R
$^\mathcal{M}$|{x, y} = R ![]() $^\mathcal{M}$*|{x, y}. That it does is obvious because, for any merit profile M, whether x R
$^\mathcal{M}$*|{x, y}. That it does is obvious because, for any merit profile M, whether x R ![]() $^\mathcal{M}$y just depends on M1(x), M1(y), M2(x) and M2(y), the degrees of merit that the different people attribute to x and y.
$^\mathcal{M}$y just depends on M1(x), M1(y), M2(x) and M2(y), the degrees of merit that the different people attribute to x and y.
Example 8 (continuation) illustrates soundness in a case where a lot is known about grading thresholds. The next section shows how the possibilities for sound grading can turn on how much is known.
5. WHEN THERE CAN ONLY BE FALSE IMPRESSIONS
Uncertainty about thresholds seriously undermines grading in groups. It does this by destroying some of the information in grades. In extreme cases, we will see, there is only comparative information left. People then might as well forget the finer distinctions that can be made by awarding grades and just rank things from better to worse; to you, the aggregator, it will be the same. And then, as we will see, under certain conditions, no grading rule is sound.Footnote 16
Recall that Ği is the ordering of X implicit in an individual appraisal Gi. Ği|S is the ordering of S ⊆ X. The following lemma plays a crucial part in the coming discussion of the destruction of information:
Lemma 11.Let S ⊆ X be finite, let Gi and Hi be individual appraisals such that Ği|S = Ȟi|S, let J be an interpretation of the grading language, and let Ni ∈ ⟦Hi⟧J. There are I and Mi ∈ ⟦Gi⟧I such that Mi|S = Ni|S.
There is a proof of Lemma 11 in the Appendix.Footnote 17 It relies on two earlier assumptions about the merit structure (![]() $\mathcal{M}$, >): that > is dense, and that there is in
$\mathcal{M}$, >): that > is dense, and that there is in ![]() $\mathcal{M}$ no greatest degree of merit, and no least degree.
$\mathcal{M}$ no greatest degree of merit, and no least degree.
In intuitive terms, suppose an underlying estimation of the merit of things is compatible with the grades that someone has awarded. Then, the lemma tells us, by assuming (in general) different thresholds, this same underlying estimation can be made compatible with any other grades that this grader might have awarded instead, if only everything is in the same order. More slowly: say for simplicity's sake that S is the whole set of items, X. Then the restrictions ‘|S’ can be ignored, and Mi|S = Ni|S means that Mi = Ni. Now, suppose the same ranking is implicit in appraisals Gi and Hi. That is, suppose Ği = Ȟi. And suppose furthermore that some estimation Ni can be squared with either one of them, let it be Hi, by choosing thresholds for the different grades (there is an interpretation J of all the grades such that Ni ∈ ⟦Hi⟧J). Then this same Ni can also be squared with the other one, Gi, by choosing suitable grading thresholds, in general different ones (Ni = Mi ∈ ⟦Gi⟧I, for some I).
Again putting S = X, Lemma 11 has the direct consequence:
Corollary 12.Suppose X is finite and Ği = Ȟi. Then ∪I ∈![]() $_{\mathscr{I}}$⟦Gi⟧I = ∪I ∈
$_{\mathscr{I}}$⟦Gi⟧I = ∪I ∈![]() $_{\mathscr{I}}$⟦Hi⟧I.
$_{\mathscr{I}}$⟦Hi⟧I.
Intuitively, if i’s thresholds could be anything then any two grade reports from him can be squared with the same underlying fine grained assessments, if these reports determine the same ranking.
Now we will see the havoc that uncertainty about thresholds can wreak on collective grading. From Definition 9 and Corollary 12 we have:
Corollary 13.Suppose X is finite and ⟦⟧ is floating and unrafted. If Ğ = Ȟ, then ⟦G⟧ = ⟦H⟧.
This says that if nothing special is known about the graders’ thresholds, then their grade reports carry no more than ordinal information about merit. We are in effect back in Arrow's framework. The graders can be as fastidious as they want about what gets which grade; it will come to nothing because all their report will tell us, in the end, is how they rank everything. All information over and above the implicit orderings has been dissipated by our uncertainty about what grades mean, in the mouths and common language of the graders. Now, this can rob collective grading of all content:
Theorem 14.Let X be finite, and let S ⊆ X include at least 3 items. Let ⟦⟧ be floating and unrafted. Let grading rule F ![]() $^\mathcal{G}$ satisfy Ordinally Unrestricted Domain with respect to S, Completeness, Weak Pareto, and Non-Dictatorship with respect to S; and let a merit function F
$^\mathcal{G}$ satisfy Ordinally Unrestricted Domain with respect to S, Completeness, Weak Pareto, and Non-Dictatorship with respect to S; and let a merit function F ![]() $^\mathcal{M}$satisfy Independence of Irrelevant Alternatives. Then F
$^\mathcal{M}$satisfy Independence of Irrelevant Alternatives. Then F ![]() $^\mathcal{G}$is not sound with respect to F
$^\mathcal{G}$is not sound with respect to F ![]() $^\mathcal{M}$, assuming ⟦⟧.
$^\mathcal{M}$, assuming ⟦⟧.
Theorem 14 is a consequence of Arrow's ‘impossibility’ theorem (Arrow Reference Arrow1951). The proof in the Appendix is a reductio. Given an import function, grading rule and merit function satisfying the conditions of Theorem 14, it is possible to construct an Arrow-style domain and a social welfare function. In outline, the domain is the set of all lists of weak orderings obtained by ‘flattening’ grade profiles from the domain of F ![]() $^\mathcal{G}$ (flattening is discussed in the beginning of section 3). The social welfare function is then ‘read off’ from the import of these grade profiles, using the merit function. This is where the soundness assumption comes in. It makes sure that all merit assignments compatible with any given grade report ‘speak with the same voice’ about which items are ‘socially better’ than which. That import is floating and rafted ensures, through Corollary 13, that a function is obtained in this way. It ensures that whenever flattening makes some grade profiles indistinguishable, their import – and hence, by this construction, also the derived social ordering – are the same. The social welfare function in question is shown to satisfy all assumptions of Arrow's ‘impossibility’ theorem, on the basis of the corresponding conditions in Theorem 14. Meanwhile, of course, Arrow's theorem tells us precisely that no such function exists.
$^\mathcal{G}$ (flattening is discussed in the beginning of section 3). The social welfare function is then ‘read off’ from the import of these grade profiles, using the merit function. This is where the soundness assumption comes in. It makes sure that all merit assignments compatible with any given grade report ‘speak with the same voice’ about which items are ‘socially better’ than which. That import is floating and rafted ensures, through Corollary 13, that a function is obtained in this way. It ensures that whenever flattening makes some grade profiles indistinguishable, their import – and hence, by this construction, also the derived social ordering – are the same. The social welfare function in question is shown to satisfy all assumptions of Arrow's ‘impossibility’ theorem, on the basis of the corresponding conditions in Theorem 14. Meanwhile, of course, Arrow's theorem tells us precisely that no such function exists.
Theorem 14 concerns the case of extreme uncertainty: the graders might have any thresholds at all, independently of one another. Under its conditions, grading in groups is radically unsound. Earlier, Examples 3 and 8 illustrated the possibilities at the other extreme, where all the graders’ thresholds are known to be the same. There was an example of a sound rule satisfying all assumptions of Theorem 14 – except of course the one about the import of grades. Evidently, then, the possibilities for sound grading really do turn on what is known about grading thresholds. They turn somewhere in between these extremes, where a certain amount known but not enough to pin things down completely. There remains a lot to be learned about the possibilities for collective grading in these cases.Footnote 18 Apart from any theoretical interest there might be practical consequences. Knowing more about the consequences of mismatched grading thresholds we might be able to develop training that will improve the judgement of juries, committees and expert panels.
Notice a family resemblance between Theorem 14 and Sen's (Reference Sen1970: theorem 8*2) demonstration that measuring individual utilities on a cardinal scale is not by itself enough to escape Arrow's theorem. In each case there is something that destroys information beyond mere comparisons from better to worse: with Sen, it is interpersonal incomparability of utilities; here, it is uncertainty about how people use words. Beneath this similarity there are differences of substance. I don't know that we can make utilities interpersonally comparable, but it is quite common to constrain how people use words. Committees and expert panels provide descriptions of grades in natural language, paradigm examples, grading protocols and checklists, calibration exercises and so on.
6. GRADING AND VOTING
the great Augustus himself, in possession of that power which ruled the world, acknowledged he could not . . . appoint what idea any sound should be a sign of, in the mouths and common language of his subjects. (John Locke Reference Locke1961 [1690] Vol. 2: 14–15)
Say voters rank the candidates in some election from better to worse on a ballot. Their rankings will be compiled by some method into a collective ranking, and whoever ends up on top has won. Arrow's theorem describes a theoretical limitation: no method for arriving at collective rankings can satisfy a short list of desiderata (Arrow Reference Arrow1951). Some have taken this to mean that there cannot be any such thing as democracy, conceived as government by a common will of the people, as revealed by voting. Supposedly the very idea of that, captured by the desiderata, is incoherent. Others draw the less dramatic conclusion that more information is needed in elections than just voters’ rankings of the candidates. Now, by grading you can convey more than just a ranking. Also, the extra information seems to be enough to solve some of the problems with traditional voting methods, such as Arrow's impossibility. That emerged here in section 3. Balinski and Laraki (Reference Balinski and Laraki2010) argue, for this reason among others, that we should stop using these traditional methods in elections. Voters should grade candidates instead of ranking them. This study raises a question about their proposal.
Grading in groups is familiar from expert panels, committees and so on, where trained people work in close contact with one another. Balinski and Laraki provide other examples and in each case, except for voting, it is the same. The graders are judges of sports competitions, or dancing, or music, or wine. Now, with a lot of shared training and culture we may expect there to be a good common understanding of how grades are to be interpreted. Professional meetings will provide opportunities for further coordination, if need be. In section 4.3 we found reason to expect that, under favourable circumstances such as these, grading in groups can be a meaningful exercise.
Voting in political elections typically involves much larger and above all much looser collections of people. The example of Jack and Jill showed how easily we can gain false impressions when graders might have different thresholds. More extremely, the unsoundness theorem of section 5 tells us that when nothing is known about the graders’ thresholds, results cannot be counted on to reflect any collective sense at all of better and worse. In large, culturally and linguistically diverse democracies, such as those of India or the United States, people surely don't have the same understanding of expressions such as Excellent, Good and Fair, and there can be few opportunities for bringing about further coordination. The question is simply this: How under such conditions can grading be a good way to pick winners?
The problem of unsoundness is in one way more pernicious than the familiar problems with traditional voting methods. That pairwise majority voting sometimes delivers up cycles of collective preference can be found out by studying it. So can the susceptibility of Borda counting to strategic manipulation. These problems are visible, so to speak, ‘from within’. They emerge from the details of the voting methods themselves. A grading rule, though, is sound with respect to some assumptions about what people mean by grades and unsound with respect to others. We'd like to know that the rule we use is sound with respect to reasonable assumptions of this sort, ideally with respect to the truth of the matter, and whether it is obviously depends on more than the internal workings of the procedure itself. It depends on which assumptions are reasonable and which are true, and that might be quite hard to find out. There are substantive disagreements about what is good and what fair. There are conceptual disagreements about what it is to be good or fair. How to tell the one kind of disagreement from the other?
Balinski and Laraki discuss at some length the idea that there will have to be a common grading language, if grading is to be used in political elections. Also, they seem to think that the people will need a common understanding of the applicable grades. They list media coverage, campaign materials and debates among the factors that, they say, will give the public a ‘good sense of what the language of grades means’, the first time it is used (Balinski and Laraki Reference Balinski and Laraki2010: 174, 251). But it is unlikely that media coverage and the rest will have this effect, if what is needed is that everyone will converge on the same grading thresholds. Public communications rely on natural languages, with all their vagueness and contextual shiftiness.
Natural language definitions do contribute to a common understanding on juries and professional panels but there they are supplemented by other methods. There is training with paradigm examples; there is discussion of difficult cases; there are calibration meetings, checklists and more. In the grade approach to evaluating medical evidence, for example, there is a protocol for assigning grades (see Balshem et al. Reference Balshem, Helfand, Schünemann, Oxman, Kunz, Brozek, Vist, Falck-Ytter, Meerpohl, Norris and Guyatt2011: tables 2 and 3). Presumably all these efforts contribute to the capacity of groups to estimate merit, but it is unthinkable that there could be any similar training of voters before elections. Turnout is often considered too low as things stand, even with no rigorous educational requirements attached! Anyway, the whole idea smacks of interference. Who is to tell me that instead of ticking the Excellent box next to my favourite candidate, I should mind my words and tick the Good box instead? Very much the same problem of linguistic differences arises in public surveys, and the possibilities for training respondents are similarly limited there. Political scientists have developed methods correcting people's responses for linguistic variation after these have been recorded, for example using anchoring vignettes (King et al. Reference King, Murray, Salomon and Tandon2004). But there can be no correcting ballots after elections. That would be tampering. Now I've in fact ticked the Excellent box, who is to count this as only a Good?
This is not to say that grading cannot be a better way to run elections. The point is rather that if it turns out to be a reliable way to identify the candidates that are best, in some independently understood sense, then this fact is interesting and deserves further study. Juries, committees and expert panels are very small compared with electorates. Perhaps when there are more graders it is enough for their grading thresholds to be distributed around a central norm, so that differences cancel out. Diversity in their thresholds might even turn out to be an advantage if for every hard grader there is another who is correspondingly easy. This would be an interesting finding in itself. We might in this case expect that, other things being equal, grading will track merit less reliably when practiced in smaller, more homogeneous groups. Contrary to what has seemed intuitive, it might sometimes not be good for panel members to coordinate their understanding of grades.
7. CONCLUSION
When too little is known about thresholds, grading in groups cannot be counted on to tell us how good or bad people take things to be. What can make it more reliable? Several academic disciplines may be expected to help answer this question. Philosophers of language and linguists might tell us what it is for different people's understandings of words to agree. Linguistic and psychological studies into language learning, categorization and elicitation methods might give us a better idea of how such coordination can be brought about in practice, whether in small groups of experts or in large, culturally diverse electorates. Realistically, depending on the case, we may expect to succeed only to some extent in bringing about a common understanding. Analytical work using techniques from social choice theory and political science might tell us how much coordination will be needed. It is this last kind of work that has been started here.
ACKNOWLEDGEMENTS
I thank for comments and suggestions Constanze Binder, Mark Burgman, Ruth Chang, Christian List, Samir Okasha, Sarah Stroud, Peter Vallentyne, John Weymark and two anonymous referees.
APPENDIX
Proof of Lemma 11. If S is the empty set then the requirement that Mi|S = Ni|S is vacuous and the lemma asserts no more than the existence of I and Mi such that Mi ∈ ⟦Gi⟧I. So let S be finite and non-empty. Assuming Ği|S = Ȟi|S and Ni ∈ ⟦Hi⟧J, we will construct a function I: ![]() $\mathcal{G}$ →
$\mathcal{G}$ → ![]() $\mathcal{P}$ow(
$\mathcal{P}$ow(![]() $\mathcal{M}$) and a function Mi: X →
$\mathcal{M}$) and a function Mi: X → ![]() $\mathcal{M}$ such that:
$\mathcal{M}$ such that:
(a) Mi|S = Ni|S
(b) For each x in the domain of Mi, Mi(x) ∈ I(Gi(x))
(c) For each grade g in the domain of I, I(g) is convex: if m1, m3 ∈ I(g) and m1 > m2 >m3, then m2 ∈ I(g)
(d) I is orderly: for any g1 and g2 in the domain of I, and any m1 ∈ I(g1) and m2 ∈ I(g2), if g1 > g2 then m1 > m2, and
(e) For each g in the domain of I, I(g) ≠ ∅.
Comparing conditions (c)–(e) with Definition 5, such a function I differs from an interpretation of (![]() $\mathcal{G}$, >) in (
$\mathcal{G}$, >) in (![]() $\mathcal{M}$, >) only in that (perhaps) not ∪g∈
$\mathcal{M}$, >) only in that (perhaps) not ∪g∈![]() $_\mathcal{G}$I(g) =
$_\mathcal{G}$I(g) = ![]() $\mathcal{M}$. That is, the intervals that I assigns to grades might not together exhaust
$\mathcal{M}$. That is, the intervals that I assigns to grades might not together exhaust ![]() $\mathcal{M}$. It is not difficult to see that such a function I can be turned into an interpretation, though, by expanding the intervals it assigns so that they do come to exhaust
$\mathcal{M}$. It is not difficult to see that such a function I can be turned into an interpretation, though, by expanding the intervals it assigns so that they do come to exhaust ![]() $\mathcal{M}$, while maintaining satisfaction of (a)–(e). Then in light of (a), and of (b) (which by Definition 7 for any interpretation I and individual merit assignment Mi means that Mi ∈ ⟦Gi⟧I), the proof of Lemma 11 will be complete.
$\mathcal{M}$, while maintaining satisfaction of (a)–(e). Then in light of (a), and of (b) (which by Definition 7 for any interpretation I and individual merit assignment Mi means that Mi ∈ ⟦Gi⟧I), the proof of Lemma 11 will be complete.
The construction is inductive. The sought functions appear at the end of a sequence of pairs I and Mi with ever more-inclusive domains. All pairs in this sequence satisfy (a)–(e), and in addition (to get the induction going) also:
(f) The domain of Mi includes each x ∈ X such that, for some g in the domain of I, Gi(x) = g; and
(g) For each g in the domain of I, I(g) includes both an upper bound and a lower bound.
The domains ![]() $\mathcal{G}$S and XS of the functions at the beginning of this sequence are, respectively, {g ∈
$\mathcal{G}$S and XS of the functions at the beginning of this sequence are, respectively, {g ∈ ![]() $\mathcal{G}$: for some s ∈ S, Gi(s) = g} and {x ∈ X: for some g ∈
$\mathcal{G}$: for some s ∈ S, Gi(s) = g} and {x ∈ X: for some g ∈ ![]() $\mathcal{G}$S, Gi(x) = g}. That is,
$\mathcal{G}$S, Gi(x) = g}. That is, ![]() $\mathcal{G}$S includes just those grades that Gi assigns to an element of S, and XS includes all of S as well as anything else to which Gi assigns one of those grades. The base step of the construction provides I:
$\mathcal{G}$S includes just those grades that Gi assigns to an element of S, and XS includes all of S as well as anything else to which Gi assigns one of those grades. The base step of the construction provides I: ![]() $\mathcal{G}$S →
$\mathcal{G}$S → ![]() $\mathcal{P}$ow(
$\mathcal{P}$ow(![]() $\mathcal{M}$) and Mi: XS →
$\mathcal{M}$) and Mi: XS →![]() $\mathcal{M}$ that satisfy (a)–(g). The induction step extends these functions one grade at a time while preserving satisfaction of (a)–(g) until, finally, we arrive at an I whose domain includes all of the (finite) set
$\mathcal{M}$ that satisfy (a)–(g). The induction step extends these functions one grade at a time while preserving satisfaction of (a)–(g) until, finally, we arrive at an I whose domain includes all of the (finite) set ![]() $\mathcal{G}$ of grades. Since the corresponding Mi satisfies (f), its domain is X (because Gi is a total function). Then the construction is complete.
$\mathcal{G}$ of grades. Since the corresponding Mi satisfies (f), its domain is X (because Gi is a total function). Then the construction is complete.
Base Step: We construct I: ![]() $\mathcal{G}$S →
$\mathcal{G}$S → ![]() $\mathcal{P}$ow(
$\mathcal{P}$ow(![]() $\mathcal{M}$) and Mi: XS →
$\mathcal{M}$) and Mi: XS →![]() $\mathcal{M}$ satisfying (a)–(g). First, note that, since S is finite and non-empty, for any g ∈
$\mathcal{M}$ satisfying (a)–(g). First, note that, since S is finite and non-empty, for any g ∈ ![]() $\mathcal{G}$S the set {Ni(s): s ∈ S and Gi(s) = g} includes a minimal element and a maximal element (which might be the same). We now let I interpret g as the closed interval of
$\mathcal{G}$S the set {Ni(s): s ∈ S and Gi(s) = g} includes a minimal element and a maximal element (which might be the same). We now let I interpret g as the closed interval of ![]() $\mathcal{M}$ that spans these:
$\mathcal{M}$ that spans these:
Second, for any s ∈ S, let Mi(s) = Ni(s), and for any x ∈ XS\S let Mi(x) be some element of I(Gi(x)). It is obvious that conditions (a), (c), (e), (f) and (g) are satisfied. We will verify (b) and (d).
Condition (b): Consider any x ∈ XS. If x ∈ XS\S, it is immediately obvious from the construction that Mi(x) ∈ I(Gi(x)). If on the other hand x ∈ S then we have:
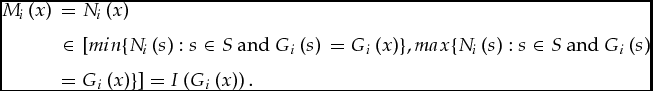 $$\begin{eqnarray*}
{M_i}\left( x \right){\rm{ }} &=& {\rm{ }}{N_i}\left( x \right)\\
& \in & [min\{ {N_i}\left( s \right):{\rm{ }}s \in S{\rm{ }}\ {\rm and} \ {\rm{ }}{G_i}\left( s \right){\rm{ }} = {\rm{ }}{G_i}\left( x \right)\} ,{\rm{ }}max\{ {N_i}\left( s \right):{\rm{ }}s \in S{\rm{ }}\ {\rm and}\ {\rm{ }}{G_i}\left( s \right){\rm{ }}\\
& = & {\rm{ }}{G_i}\left( x \right)\} ]{\rm{ }} = I\left( {{G_i}\left( x \right)} \right).
\end{eqnarray*}$$
$$\begin{eqnarray*}
{M_i}\left( x \right){\rm{ }} &=& {\rm{ }}{N_i}\left( x \right)\\
& \in & [min\{ {N_i}\left( s \right):{\rm{ }}s \in S{\rm{ }}\ {\rm and} \ {\rm{ }}{G_i}\left( s \right){\rm{ }} = {\rm{ }}{G_i}\left( x \right)\} ,{\rm{ }}max\{ {N_i}\left( s \right):{\rm{ }}s \in S{\rm{ }}\ {\rm and}\ {\rm{ }}{G_i}\left( s \right){\rm{ }}\\
& = & {\rm{ }}{G_i}\left( x \right)\} ]{\rm{ }} = I\left( {{G_i}\left( x \right)} \right).
\end{eqnarray*}$$Condition (d): Consider any g1, g2 ∈ ![]() $\mathcal{G}$S such that g1 > g2, and consider any m1 ∈ I(g1) and m2 ∈ I(g2). By assumption of the lemma Ği|S = Ȟi|S, so there are h1, h2 ∈
$\mathcal{G}$S such that g1 > g2, and consider any m1 ∈ I(g1) and m2 ∈ I(g2). By assumption of the lemma Ği|S = Ȟi|S, so there are h1, h2 ∈ ![]() $\mathcal{G}$such that h1 > h2, while for any s ∈ S, Gi(s) = g1 iff Hi(s) = h1, and Gi(s) = g2 iff Hi(s) = h2.
$\mathcal{G}$such that h1 > h2, while for any s ∈ S, Gi(s) = g1 iff Hi(s) = h1, and Gi(s) = g2 iff Hi(s) = h2.
Now, by choice of I:
It is an assumption of the lemma that Ni ∈ ⟦Hi⟧J, from which we can infer that:
Because J is an interpretation, J(h1) is convex. So the three claims above entail m1 ∈ J(h1). By identical reasoning (put ‘2’ instead of ‘1’ throughout), m2 ∈ J(h2). Now, since h1 > h2, and since J is orderly, we have, as required, m1 > m2. This completes the demonstration that I satisfies condition (d), and the base step of the construction.
Induction Step: Let I*: ![]() $\mathcal{G}$* →
$\mathcal{G}$* → ![]() $\mathcal{P}$ow(
$\mathcal{P}$ow(![]() $\mathcal{M}$) and Mi*: X* →
$\mathcal{M}$) and Mi*: X* → ![]() $\mathcal{M}$ satisfy (a)–(g), with
$\mathcal{M}$ satisfy (a)–(g), with ![]() $\mathcal{G}$* ⊆
$\mathcal{G}$* ⊆ ![]() $\mathcal{G}$ and X* ⊆ X. Pick any g ∈
$\mathcal{G}$ and X* ⊆ X. Pick any g ∈ ![]() $\mathcal{G}$/
$\mathcal{G}$/![]() $\mathcal{G}$*. We will construct I:
$\mathcal{G}$*. We will construct I: ![]() $\mathcal{G}$*∪{g} →
$\mathcal{G}$*∪{g} → ![]() $\mathcal{P}$ow(
$\mathcal{P}$ow(![]() $\mathcal{M}$) and Mi: X*∪{x ∈ X : Gi(x) = g} →
$\mathcal{M}$) and Mi: X*∪{x ∈ X : Gi(x) = g} → ![]() $\mathcal{M}$ that also satisfy (a)–(g). There are three cases to consider:
$\mathcal{M}$ that also satisfy (a)–(g). There are three cases to consider:
i. g is a higher grade than any in
 $\mathcal{G}$*: for each h ∈
$\mathcal{G}$*: for each h ∈  $\mathcal{G}$*, g > h
$\mathcal{G}$*, g > hii. there are in
 $\mathcal{G}$* two grades immediately greater and lesser than g: there are h1, h3 ∈
$\mathcal{G}$* two grades immediately greater and lesser than g: there are h1, h3 ∈  $\mathcal{G}$* such that h1 > g > h3 while for no h2 ∈
$\mathcal{G}$* such that h1 > g > h3 while for no h2 ∈  $\mathcal{G}$*, h1 > h2 > g or g > h2 >h3; and
$\mathcal{G}$*, h1 > h2 > g or g > h2 >h3; andiii. g is a lower grade than any in
 $\mathcal{G}$*: for each h ∈
$\mathcal{G}$*: for each h ∈  $\mathcal{G}$*, h > g.
$\mathcal{G}$*, h > g.
We proceed as follows in each case:
Case (i): let h be the highest grade in ![]() $\mathcal{G}$*. I* by induction hypothesis satisfies condition (g). Let n ∈ I*(h) be the upper bound of I*(h) (by the ordering of the degrees of merit).
$\mathcal{G}$*. I* by induction hypothesis satisfies condition (g). Let n ∈ I*(h) be the upper bound of I*(h) (by the ordering of the degrees of merit). ![]() $\mathcal{M}$ we have assumed does not have an upper bound, so in particular this n is not one. So it is possible to choose from
$\mathcal{M}$ we have assumed does not have an upper bound, so in particular this n is not one. So it is possible to choose from ![]() $\mathcal{M}$ some m > n, and to extend I* and M*i to I and Mi by putting:
$\mathcal{M}$ some m > n, and to extend I* and M*i to I and Mi by putting:
 $$\begin{equation*}
\begin{array}{*{20}{l}} {I\left( g \right) = {\rm{ }}\left[ {m,m} \right],{\rm while}\,{\rm for}\,{\rm all}\;h \in {\mathcal {G}}^{*},I\left( g \right) = I^{*}\left( h \right)}\\ {M_i}\left( x \right) = m,{\rm for}\,{\rm each}\,x \in X\,{\rm such}\,{\rm that}\,{G_i}(x) = g,{\rm and}\,M_{i}(x) = M^*{_i}\\
\quad \left( x \right),{\rm for}\, {\rm each}\,x \in X^{*}.\end{array}
\end{equation*}$$
$$\begin{equation*}
\begin{array}{*{20}{l}} {I\left( g \right) = {\rm{ }}\left[ {m,m} \right],{\rm while}\,{\rm for}\,{\rm all}\;h \in {\mathcal {G}}^{*},I\left( g \right) = I^{*}\left( h \right)}\\ {M_i}\left( x \right) = m,{\rm for}\,{\rm each}\,x \in X\,{\rm such}\,{\rm that}\,{G_i}(x) = g,{\rm and}\,M_{i}(x) = M^*{_i}\\
\quad \left( x \right),{\rm for}\, {\rm each}\,x \in X^{*}.\end{array}
\end{equation*}$$Case (ii): let h1 and h3 be the immediately greater and lesser grades, let m1 be the lower bound of I*(h1) and let m3 be the upper bound of I*(h3). Since I* satisfies (d), m1 > m3. This ordering > of the degrees of merit is assumed to be dense, so it is possible to choose some degree m that lies between these two: m1 > m > m3. Now define I and Mi as in Case (i).
Case (iii): this is a mirror image of Case (i).
It remains to be verified that I and Mi satisfy (a)–(g). We will consider only (d), because satisfaction of the other conditions is obvious. Let g1, g2 ∈ ![]() $\mathcal{G}$*∪{g} be such that g1 > g2, and consider any m1 ∈ I(g1) and m2 ∈ I(g2). To be shown is that m1 > m2. If neither g1 nor g2 is the ‘new’ grade g then, since by Induction Hypothesis I* satisfies (d), we are already done. Suppose on the other hand that one of g1 and g2 is g. We will consider only the case where it is g1; the other is analogous. In parallel with the construction of I, there are three cases to consider; we will consider only Case (i) since the others can be handled using similar reasoning.
$\mathcal{G}$*∪{g} be such that g1 > g2, and consider any m1 ∈ I(g1) and m2 ∈ I(g2). To be shown is that m1 > m2. If neither g1 nor g2 is the ‘new’ grade g then, since by Induction Hypothesis I* satisfies (d), we are already done. Suppose on the other hand that one of g1 and g2 is g. We will consider only the case where it is g1; the other is analogous. In parallel with the construction of I, there are three cases to consider; we will consider only Case (i) since the others can be handled using similar reasoning.
Condition (d), Case (i): Let g > g2 ∈ ![]() $\mathcal{G}$*, m1 ∈ I(g) = [m, m], and m2 ∈ I(g 2) = I*(g2). It is sufficient to show that m > m2. In the construction, h is the highest grade in
$\mathcal{G}$*, m1 ∈ I(g) = [m, m], and m2 ∈ I(g 2) = I*(g2). It is sufficient to show that m > m2. In the construction, h is the highest grade in ![]() $\mathcal{G}$*, so either h = g2, or h > g2. n from the construction is the upper bound of I*(h), so either n = m2 or n > m2 (by induction hypothesis I* satisfies (d) and by choice of n also n ∈ I*(h)). By the construction m > n, so either way m > m2.
$\mathcal{G}$*, so either h = g2, or h > g2. n from the construction is the upper bound of I*(h), so either n = m2 or n > m2 (by induction hypothesis I* satisfies (d) and by choice of n also n ∈ I*(h)). By the construction m > n, so either way m > m2.
This completes the induction step and the proof of Lemma 11.
Proof of Theorem 14. We assume for a contradiction that a grading rule is sound with respect to a merit function. Together with the assumptions of the theorem, it is then possible to construct a social welfare function in the sense of Arrow (Reference Arrow1951) that meets all conditions of his ‘impossibility’ theorem. This refutes the initial soundness assumption.
Let X be finite, and let S ⊆ X be such that |S| ≥ 3. Let ⟦⟧ be floating and unrafted. Let F ![]() $^\mathcal{G}$ satisfy the conditions Ordinally Unrestricted Domain with respect to S, Completeness, Weak Pareto and Non-Dictatorship with respect to S; and let F
$^\mathcal{G}$ satisfy the conditions Ordinally Unrestricted Domain with respect to S, Completeness, Weak Pareto and Non-Dictatorship with respect to S; and let F ![]() $^\mathcal{M}$ satisfy Independence of Irrelevant Alternatives. Finally, for the contradiction, assume that F
$^\mathcal{M}$ satisfy Independence of Irrelevant Alternatives. Finally, for the contradiction, assume that F ![]() $^\mathcal{G}$ is sound with respect to F
$^\mathcal{G}$ is sound with respect to F ![]() $^\mathcal{M}$, assuming ⟦⟧.
$^\mathcal{M}$, assuming ⟦⟧.
Letting ![]() $\mathcal{D}$ be the common domain of ⟦⟧ and of F
$\mathcal{D}$ be the common domain of ⟦⟧ and of F ![]() $^\mathcal{G}$, first we have:
$^\mathcal{G}$, first we have:
Fact 15. For any G ∈ ![]() $\mathcal{D}$ and M, N ∈ ⟦G⟧, F
$\mathcal{D}$ and M, N ∈ ⟦G⟧, F ![]() $^\mathcal{M}$(M) = F
$^\mathcal{M}$(M) = F ![]() $^\mathcal{M}$(N).
$^\mathcal{M}$(N).
Proof of Fact 15. Letting M, N ∈ ⟦G⟧, suppose x F ![]() $^\mathcal{M}$(M) y. To be shown is that x F
$^\mathcal{M}$(M) y. To be shown is that x F ![]() $^\mathcal{M}$(N) y. We have x R
$^\mathcal{M}$(N) y. We have x R ![]() $^\mathcal{G}$y, since otherwise by Completeness of F
$^\mathcal{G}$y, since otherwise by Completeness of F ![]() $^\mathcal{G}$, and therefore of R
$^\mathcal{G}$, and therefore of R ![]() $^\mathcal{G}$, we would have y P
$^\mathcal{G}$, we would have y P ![]() $^\mathcal{G}$x, and so, by part (b) of Definition 10, we would not have x F
$^\mathcal{G}$x, and so, by part (b) of Definition 10, we would not have x F ![]() $^\mathcal{M}$(M) y. (Recall that, following the convention, y P
$^\mathcal{M}$(M) y. (Recall that, following the convention, y P ![]() $^\mathcal{M}$x by definition means that y F
$^\mathcal{M}$x by definition means that y F ![]() $^\mathcal{M}$(M) x but not x F
$^\mathcal{M}$(M) x but not x F ![]() $^\mathcal{M}$(M) y.) Now N ∈ ⟦G⟧ so by part (a) of Definition 10, since x R
$^\mathcal{M}$(M) y.) Now N ∈ ⟦G⟧ so by part (a) of Definition 10, since x R ![]() $^\mathcal{G}$y, also x F
$^\mathcal{G}$y, also x F ![]() $^\mathcal{M}$(N) y. By symmetrical reasoning, if x F
$^\mathcal{M}$(N) y. By symmetrical reasoning, if x F ![]() $^\mathcal{M}$(N) y then x F
$^\mathcal{M}$(N) y then x F ![]() $^\mathcal{M}$(M) y.
$^\mathcal{M}$(M) y.
Notice that this fact only requires the soundness and completeness properties. The flattening Ğ of a grade profile G is a list of weak orderings of X. It is a profile, in the sense of Arrow (Reference Arrow1951). Now we will construct an Arrow-style social welfare function f, whose domain ![]() $\mathcal{A}$ is {Ğ: G ∈
$\mathcal{A}$ is {Ğ: G ∈ ![]() $\mathcal{D}$}. For each profile Ğ ∈
$\mathcal{D}$}. For each profile Ğ ∈ ![]() $\mathcal{A}$, we choose some M ∈ ⟦G⟧ and put f(Ğ) = F
$\mathcal{A}$, we choose some M ∈ ⟦G⟧ and put f(Ğ) = F ![]() $^\mathcal{M}$(M). By Fact 15, it doesn't matter which such M we choose. For this definition of f to succeed it had better be that f(Ğ) = f(Ȟ) whenever Ğ = Ȟ. This is ensured by Corollary 13. It tells us that, because ⟦⟧ is floating and unrafted, in this case ⟦G⟧ = ⟦H⟧.
$^\mathcal{M}$(M). By Fact 15, it doesn't matter which such M we choose. For this definition of f to succeed it had better be that f(Ğ) = f(Ȟ) whenever Ğ = Ȟ. This is ensured by Corollary 13. It tells us that, because ⟦⟧ is floating and unrafted, in this case ⟦G⟧ = ⟦H⟧.
We now verify that f satisfies the following conditions: Universal Domain with respect to S (U-S), Ordering (O), Weak Pareto (WP), Non-Dictatorship with respect to S (D-S) and Independence of Irrelevant Alternatives (I). Subsequent restriction of both f and ![]() $\mathcal{A}$ to S will yield an Arrovian domain and social welfare function satisfying the familiar conditions of Arrow's theorem (see for example List Reference List and Zalta2013). Of the above conditions, only U-S and D-S might need definitions, for the rest are already standard. Their definitions are by this stage unsurprising: we say that f satisfies U-S if for every list <Ri> of |N| weak orderings of S, there is some profile Q in the domain of f such that Q|S = <Ri>. We say that f satisfies D-S if f has no S-dictator; that is, there is no δ ∈ N such that for any x, y ∈ S and profile Q in the domain of f, if xPδy then xPy. A dictator with respect to S is someone whose strict preferences among elements of S invariably are strict social preferences, as well. That these conditions are satisfied by f, as defined above for the domain
$\mathcal{A}$ to S will yield an Arrovian domain and social welfare function satisfying the familiar conditions of Arrow's theorem (see for example List Reference List and Zalta2013). Of the above conditions, only U-S and D-S might need definitions, for the rest are already standard. Their definitions are by this stage unsurprising: we say that f satisfies U-S if for every list <Ri> of |N| weak orderings of S, there is some profile Q in the domain of f such that Q|S = <Ri>. We say that f satisfies D-S if f has no S-dictator; that is, there is no δ ∈ N such that for any x, y ∈ S and profile Q in the domain of f, if xPδy then xPy. A dictator with respect to S is someone whose strict preferences among elements of S invariably are strict social preferences, as well. That these conditions are satisfied by f, as defined above for the domain ![]() $\mathcal{A}$, is now readily verified:
$\mathcal{A}$, is now readily verified:
U-S: Consider any list <Ri> of |N| weak orderings of S. Since by assumption F
 $^\mathcal{G}$ satisfies Ordinally Unrestricted Domain with respect to S, there is some G ∈
$^\mathcal{G}$ satisfies Ordinally Unrestricted Domain with respect to S, there is some G ∈  $\mathcal{D}$ such that Ğ|S = <Ri>. Now, Ğ ∈
$\mathcal{D}$ such that Ğ|S = <Ri>. Now, Ğ ∈ $\mathcal{A}$.
$\mathcal{A}$.O: f(Ğ) is a weak ordering of X because, by definition of a merit function, F
 $^\mathcal{M}$(M) always is.
$^\mathcal{M}$(M) always is.WP: Suppose for each i, xĞiy but not yĞix. Then, for each i, Gi(x) > Gi(y), and since the grading rule F
 $^\mathcal{G}$ satisfies Weak Pareto we have xP
$^\mathcal{G}$ satisfies Weak Pareto we have xP  $^\mathcal{G}$y. Now consider any M ∈ ⟦G⟧. By soundness of F
$^\mathcal{G}$y. Now consider any M ∈ ⟦G⟧. By soundness of F  $^\mathcal{G}$ with respect to F
$^\mathcal{G}$ with respect to F  $^\mathcal{M}$, we have x P
$^\mathcal{M}$, we have x P  $^\mathcal{M}$y. So by choice of f and Fact 15, xPy.
$^\mathcal{M}$y. So by choice of f and Fact 15, xPy.D-S: Suppose for contradiction that δ is an S-dictator of f. We will see that, contrary to the assumption of the theorem, δ is an S-dictator of F
 $^\mathcal{G}$. To this end, take any G ∈
$^\mathcal{G}$. To this end, take any G ∈  $\mathcal{D}$ and x,y ∈ S, and suppose that Gδ(x) > Gδ(y). It is sufficient to show that x P
$\mathcal{D}$ and x,y ∈ S, and suppose that Gδ(x) > Gδ(y). It is sufficient to show that x P  $^\mathcal{G}$y. We have in this case x Ğδ y but not y Ğδ x, and so, since δ is an S-dictator of f, x P y. Choose any M ∈ ⟦G⟧. By Fact 15 and choice of f we have x P
$^\mathcal{G}$y. We have in this case x Ğδ y but not y Ğδ x, and so, since δ is an S-dictator of f, x P y. Choose any M ∈ ⟦G⟧. By Fact 15 and choice of f we have x P  $^\mathcal{M}$y. By soundness therefore x P
$^\mathcal{M}$y. By soundness therefore x P  $^\mathcal{G}$y (otherwise, because R
$^\mathcal{G}$y (otherwise, because R  $^\mathcal{G}$ is complete we have y R
$^\mathcal{G}$ is complete we have y R  $^\mathcal{G}$x and, by part (a) Definition 10, y R
$^\mathcal{G}$x and, by part (a) Definition 10, y R  $^\mathcal{M}$x, contradicting x P
$^\mathcal{M}$x, contradicting x P  $^\mathcal{M}$y).
$^\mathcal{M}$y).
I: Show: for any x, y ∈ X and Ğ, Ȟ ∈ ![]() $\mathcal{A}$: if Ğ |{x, y} = Ȟ |{x, y}, then f(Ğ) |{x, y} = f(Ȟ) |{x, y}.
$\mathcal{A}$: if Ğ |{x, y} = Ȟ |{x, y}, then f(Ğ) |{x, y} = f(Ȟ) |{x, y}.
Suppose Ğ|{x, y} = Ȟ|{x, y}. Choose any N ∈ ⟦H⟧. It is sufficient that there is some M ∈ ⟦G⟧ such that M|{x, y} = N|{x, y}, for then, since by assumption F ![]() $^\mathcal{M}$ satisfies Independence of Irrelevant Alternatives, we have, by definition of f and Fact 15:
$^\mathcal{M}$ satisfies Independence of Irrelevant Alternatives, we have, by definition of f and Fact 15:
So let N ∈ ⟦H⟧. Consider any i, 1 ≤ i ≤ |N|. Since ⟦⟧ is floating and unrafted, there is some interpretation Ji such that Ni ∈ ⟦Hi⟧Ji. By our initial supposition that Ğ|{x, y} = Ȟ|{x, y}, also Ği|{x, y} = Ȟi|{x, y}. Using Lemma 11, choose some I i and some Mi ∈ ⟦Gi⟧Ii such that Mi|{x, y} = Ni|{x, y}. Repeating for each i, construct M = <M1,. . . Mn>. Plainly, M|{x, y} = N|{x, y}. Since ⟦⟧ is floating and unrafted, by Definition 9 we have M ∈ ⟦G⟧. We have now verified that f satisfies I.
We have seen that f of the construction almost satisfies the conditions of Arrow's theorem, as standardly stated, but not quite: two of the above conditions concern the subset S, not all the alternatives X. It remains only to read off, by restricting ![]() $\mathcal{A}$ and f to the set of alternatives S, a social welfare function g satisfying the conditions in their standard form. To this end, let the domain be {Ğ|S: Ğ ∈
$\mathcal{A}$ and f to the set of alternatives S, a social welfare function g satisfying the conditions in their standard form. To this end, let the domain be {Ğ|S: Ğ ∈ ![]() $\mathcal{A}$} and put g(Ğ|S) = (fĞ)|S. It is not difficult to show that g satisfies the relevant conditions.
$\mathcal{A}$} and put g(Ğ|S) = (fĞ)|S. It is not difficult to show that g satisfies the relevant conditions.
This completes the proof of Theorem 14.