1. INTRODUCTION
In the second half of the 17th century, Blaise Pascal introduced the rudiments of decision theory by making one of the most provocative and intriguing arguments in the history of philosophy as well as theology: that the infinite reward of heaven implies that a person who assigns any positive probability, no matter how small, to God existing, should rationally choose to ‘wager’ that God exists and live one’s life accordingly (Pascal Reference Pascal and Krailsheimer1995 [1670]). There is now an immense philosophy literature that criticizes, defends and further develops Pascal’s Wager.Footnote 1
Following Pascal’s approach, virtually all of this literature is decision-theoretic.Footnote 2 There is a single decision-maker, a human, who (i) has actions (wager or don’t wager), (ii) has preferences over outcomes, and (iii) assigns probabilities to possible states of the world that could be true, in this case whether or not a supreme being or deity exists.Footnote 3 The human then chooses the action that provides the highest expected utility.
But from a game-theoretic perspective, such analyses are incomplete. In particular, if the deity exists, then he presumably has the option of revealing his existence to the human, in which case the human would not have to wager at all, and could instead act on certainty. Alternatively, he might choose to not reveal his existence to the human, in which case the human would choose whether or not to wager on the basis of the prior probability that she assigns to the deity existing.Footnote 4 If the deity’s strategy is to reveal his existence, then if the human does not observe the deity revealing his existence, the human’s Bayes’ rule inference in a Bayesian equilibrium is to assign probability 0 to the deity existing, and therefore she chooses to not wager even though she begins the interaction assigning positive probability to the deity existing, and assigns an infinite utility for heaven (the outcome where she wagers and the deity exists).
This suggests that a game-theoretic analysis of Pascal’s Wager is warranted, which I conduct here. For the human, I use the preferences that are standard in decision-theoretic analyses of Pascal’s Wager (e.g. Hájek Reference Hájek2003: 28), and for the deity, I use the reasonable preference ordering stipulated in Brams (Reference Brams1982, Reference Brams2007, Reference Brams2011).Footnote 5 It turns out that there is an equilibrium in which the human chooses to wager that the deity exists and Pascal’s Wager thus operates. However, unlike in the decision-theoretic setting, there is also an equilibrium in which the human chooses to not wager. Because both equilibria exist, we can say that in a game-theoretic setting in which both the human and the deity are decision-makers, Pascal’s Wager is indeterminate: wagering and not wagering are both consistent with equilibrium behaviour.
The rest of the paper is organized as follows. Section 2 presents the model. Section 3 presents the main results. To examine the robustness of the main results, I then consider a variety of alternative specifications. Section 4 considers Pascal’s first wager payoffs rather than the more standard second wager payoffs (for the human). Section 5 considers an alternative specification of the deity’s payoffs. Section 6 considers when all of the human’s payoffs are finite. Section 7 concludes.
2. MODEL
The model is shown in Figure 1. It begins with ‘chance’ or ‘nature’ probabilistically choosing the state of the world, in this case whether or not the deity exists. The state of the world where the deity exists occurs with probability 0 < p < 1, and the state where the deity does not exist occurs with probability 1 − p. The human does not observe this move by chance, but knows the probabilities. Therefore, these probabilities essentially represent the human’s prior belief that the deity exists.Footnote 6
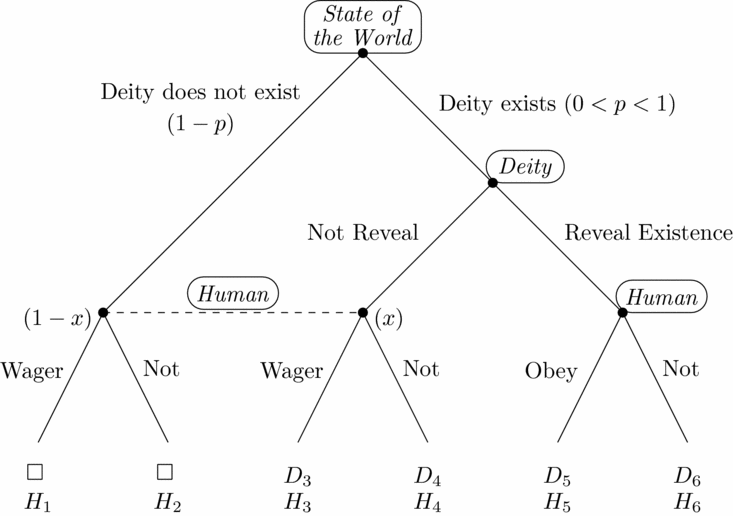
Figure 1. The Model
If the deity exists, then he decides whether or not to reveal his existence to the human.Footnote 7 If he reveals his existence, then the human has to decide whether or not to obey the deity’s wishes. If the deity does not reveal his existence, then the human has to decide whether or not to wager that the deity exists (i.e. live her life as though the deity exists).Footnote 8 This decision node for the human is part of an information set containing another decision node for the human in which the history that has occurred is that chance chose the state of the world where the deity does not exist. That is, if the human does not observe the deity revealing his existence, the human does not know whether this is because the deity does not exist, or because the deity exists but chose to not clearly reveal his existence.
Decision-theoretic models of Pascal’s Wager essentially conduct the entire analysis at the information set, and take the probabilities labelled x (the deity exists) and 1 − x (the deity does not exist) as exogenous. The argument is that if the human’s utility for heaven (H 3) is infinite and the human’s other three payoffs at the information set are finite (e.g. Hájek Reference Hájek2003: 28), then for any x > 0 the expected-utility-maximizing choice is to wager. But in a Bayesian equilibrium of a game-theoretic analysis, x is endogenously derived from the deity’s strategy using Bayes’ rule, and the key result will be that there exists an equilibrium in which x = 0 even though p > 0, and hence the human chooses to not wager.
Turning to payoffs, there are six possible outcomes of the interaction. Going from left to right, the human’s payoffs for these six outcomes are labelled H 1—H 6. Similarly for the deity’s payoffs, although these are only defined for outcomes 3—6. For the deity’s payoffs, following Brams (Reference Brams1982, Reference Brams2007: 17—19; Reference Brams2011: 82), I assume that D 3 > D 5 > max{D 4, D 6}. That is, the deity’s most-preferred outcome is where he does not reveal his existence and the human chooses to wager, and his second-most-preferred outcome is where he reveals his existence and the human obeys his wishes. Both of these are preferred to the outcomes where the human chooses to not wager, or chooses to not obey. The deity wants the human to follow his wishes, but ideally without revealing his existence (i.e. on the basis of ‘faith’ or wagering). (Later, I consider an alternative preference ordering for the deity.)Footnote 9
For the human’s payoffs, it is natural to assume that H 5 > H 6: if the human knows that the deity exists, then presumably the human prefers obeying the deity to not obeying. For the human’s payoffs at the information set, I adopt the standard assumption in the decision-theoretic literature on Pascal’s Wager that H 3 = ∞ (presumably H 5 = ∞ as well, although all that is needed for the results below is that H 5 > H 6), and that H 1, H 2 and H 4 are finite (e.g. Hájek Reference Hájek2003: 28). Following Pascal’s second wager (the major focus of the literature) rather than the first wager, I will also assume that H 2 > H 1. That is, if the deity does not exist then the human would rather not wager, and hence the human’s choice at the information set is a dilemma (Melkonyan and Pingle Reference Melkonyan and Pingle2009). (Later, I consider the first wager, under which H 2 = H 1: ‘if you lose you lose nothing’ by wagering (Pascal Reference Pascal and Krailsheimer1995 [1670]: 123). I also later consider when all utilities are finite.)Footnote 10
3. RESULTS
For sequential-move games of imperfect information, the standard solution concept is perfect Bayesian equilibrium (henceforth PBE). The proofs of all results are in the Appendix.
Proposition 1 This game has two PBE:
-
(a) (‘Wager Equilibrium’) The deity’s strategy is {not reveal}. The human’s strategy is {wager; obey}. By Bayes’ rule, x = p.
-
(b) (‘Don’t-Wager Equilibrium’) The deity’s strategy is {reveal}. The human’s strategy is {not wager; obey}. By Bayes’ rule, x = 0.
In any equilibrium, the human’s strategy is to obey if the deity reveals his existence. In the Wager Equilibrium, the human’s strategy is to wager. Because of this, if the deity exists, he chooses to not reveal his existence, as this leads to his most-preferred outcome. Given this strategy of the deity, by Bayes’ rule x = p (>0) (no updating from the prior occurs when the human does not observe the deity revealing his existence), and hence the human’s optimal strategy is indeed to wager (given that H 3 = ∞). When p > 0, i.e. the human begins the interaction assigning positive probability to the deity existing, there exists an equilibrium in which the human chooses to wager, and hence in which Pascal’s Wager operates.
However, there also exists an equilibrium in which the human’s strategy is to not wager. Given this strategy choice of the human, if the deity exists, he chooses to reveal his existence, as this leads to his second-most-preferred outcome. And given this strategy choice of the deity, by Bayes’ rule x = 0 (updating occurs if the human does not observe the deity revealing his existence), and hence the human’s utility-maximizing choice is indeed to not wager (given that H 2 > H 1).
Thus, in a game-theoretic setting, there exists an equilibrium in which the human does not wager, even though the two foundational premises of Pascal’s Wager are being maintained: (i) the human begins the interaction assigning positive probability (p > 0) to the deity existing, and (ii) the human assigns infinite utility (H 3 = ∞) to heaven.
Because both equilibria exist,Footnote 11 we can say that in a game-theoretic setting Pascal’s Wager is indeterminate: wagering and not wagering are both consistent with equilibrium behaviour.Footnote 12
4. FIRST WAGER PAYOFFS
Although the second wager is the major focus of the literature because the human’s choice is actually a dilemma, it turns out that the Don’t-Wager Equilibrium exists even when the human has more of an incentive to wager, namely the first wager payoffs H 2 = H 1: there is nothing to lose in wagering.
Proposition 2 When H2 = H1, the game has three PBE:
-
(a) (‘Wager Equilibrium’) The deity’s strategy is {not reveal}. The human’s strategy is {wager; obey}. By Bayes’ rule, x = p.
-
(b) (‘Don’t-Wager Equilibrium’) The deity’s strategy is {reveal}. The human’s strategy is {not wager; obey}. By Bayes’ rule, x = 0.
-
(c) (Mixed Strategy Equilibria) The deity’s strategy is {reveal}. The human’s strategy is {wager with any probability 0 < y ⩽ (D5 − D4)/(D3 − D4) ∈ (0, 1) and not wager with probability 1 − y; obey}. By Bayes’ rule, x = 0.
The Don’t-Wager Equilibrium still exists, because when x = 0 the human can be choosing to not wager, as she is indifferent between wagering and not wagering. Even if there is nothing to be lost by wagering, not wagering is still consistent with equilibrium behaviour. (Because she is indifferent, there also exists a third class of equilibria (c) in which the human mixes. In them, she chooses to wager with low enough probability that the deity chooses to reveal, thus ensuring that x = 0 and hence the human is indifferent. In these equilibria the human is choosing to not wager with positive probability, reinforcing the point about not wagering being consistent with equilibrium behaviour.)Footnote 13
5. AN ALTERNATIVE PREFERENCE ORDERING FOR THE DEITY
It turns out that there is a way of resolving this game-theoretic ‘problem’ for Pascal’s Wager. Suppose that the deity’s preference ordering is instead min{D 3, D 4} > max{D 5, D 6}. That is, the deity’s optimal strategy is to not reveal his existence, regardless of what the human’s strategy is: not revealing is a strictly dominant strategy.Footnote 14
Proposition 3 Regardless of whether H2 > H1 (second wager payoffs) or H2 = H1 (first wager payoffs), this game has a unique PBE, a ‘Wager Equilibrium’: the deity’s strategy is {not reveal}. The human’s strategy is {wager; obey}. By Bayes’ rule, x = p.
With this alternative preference ordering, in any PBE, the deity’s strategy is to not reveal, and hence by Bayes’ rule x = p (>0). The human therefore chooses to wager (given that H 3 = ∞). If the deity’s strictly dominant strategy is to not reveal his existence, then a game-theoretic setting poses no problem for Pascal’s Wager; there is a unique equilibrium, and in it the human chooses to wager.
6. ALL UTILITIES ARE FINITE
Given that the assumptions that justify expected utility maximization as being the appropriate decision-making principle under risk (von Neumann and Morgenstern Reference von Neumann and Morgenstern1944; Savage Reference Savage1954) do not allow for infinite utilities (e.g. McClennen Reference McClennen and Jordan1994; Østerdal Reference Østerdal2004; Melkonyan and Pingle Reference Melkonyan and Pingle2009), it is worth considering how this game-theoretic ‘problem’ for Pascal’s Wager fares under the alternative assumption that H 3 and H 5 (the heaven payoffs) are finite. We continue to assume that H 5 > H 6 and H 3 > H 4.
Then at the information set, the human strictly prefers to wager if and only if (x)(H 3) + (1 − x)(H 1) > (x)(H 4) + (1 − x)(H 2), which can be rewritten as x > (H 2 − H 1)/[(H 2 − H 1) + (H 3 − H 4)]. That is, the human chooses to wager if and only if the probability that the human assigns to the deity existing when choosing whether or not to wager exceeds a certain threshold (McClennen Reference McClennen and Jordan1994: 126; Mougin and Sober Reference Mougin and Sober1994: 383). Let us call this threshold x critical . If the human has the first wager payoffs, i.e. H 2 = H 1, then x critical = 0. If the human has the second wager payoffs, i.e. H 2 > H 1, then x critical ∈ (0, 1).
6.1. First Wager Payoffs (H 2 = H 1)
With the first wager payoffs, the finite-utility results are exactly the same as the infinite-utility results, for both preference orderings for the deity.
Proposition 4 If the deity has the original contingent-revealer preference ordering D3 > D5 > max{D4, D6}, then the game has the same three PBE as in Proposition 2:
-
(a) (‘Wager Equilibrium’) The deity’s strategy is {not reveal}. The human’s strategy is {wager; obey}. By Bayes’ rule, x = p.
-
(b) (‘Don’t-Wager Equilibrium’) The deity’s strategy is {reveal}. The human’s strategy is {not wager; obey}. By Bayes’ rule, x = 0.
-
(c) (Mixed Strategy Equilibria) The deity’s strategy is {reveal}. The human’s strategy is {wager with any probability 0 < y ⩽ (D5 − D4)/(D3 − D4) ∈ (0, 1) and not wager with probability 1 − y; obey}. By Bayes’ rule, x = 0.
Proposition 5 If the deity has the strictly-dominant-non-revealer preference ordering min{D3, D4} >max{D5, D6}, then the game has the same unique PBE of Proposition 3, a ‘Wager Equilibrium’: the deity’s strategy is {not reveal}. The human’s strategy is {wager; obey}. By Bayes’ rule, x = p.
To the point, if the deity has the original contingent-revealer preference ordering, then there exists a Don’t-Wager Equilibrium. But if the deity’s strictly dominant strategy is to not reveal his existence, then the Wager Equilibrium is the unique equilibrium.
6.2. Second Wager Payoffs (H 2 > H 1)
With the second wager payoffs, however, the results change.
Proposition 6 Suppose that the deity has the original contingent-revealer preference ordering D3 > D5 > max{D4, D6}.
-
(i) If p < xcritical then the game has a unique PBE, a ‘Don’t-Wager Equilibrium’: the deity’s strategy is {reveal}. The human’s strategy is {not wager; obey}. By Bayes’ rule, x = 0.
-
(ii) If p ⩾ xcritical then the game has two PBE in pure strategies:
-
(a) (‘Wager Equilibrium’) The deity’s strategy is {not reveal}. The human’s strategy is {wager; obey}. By Bayes’ rule, x = p.
-
(b) (‘Don’t-Wager Equilibrium’) The deity’s strategy is {reveal}. The human’s strategy is {not wager; obey}. By Bayes’ rule, x = 0.
-
-
(iii) If p = xcritical (a knife-edge condition) then the game also has the following PBE in mixed strategies: the deity’s strategy is {not reveal}. The human’s strategy is {wager with any probability ycritical ⩽ y < 1 and not wager with probability 1 − y, where ycritical = (D5 − D4)/(D3 − D4) ∈ (0, 1); obey}. By Bayes’ rule, x = p ( = xcritical).
-
(iv) If p > xcritical then the game also has the following PBE in mixed strategies: the deity’s strategy is {not reveal with probability z = [(1 − p)xcritical]/[p(1 − xcritical)] ∈ (0, 1) and reveal with probability 1 − z}. The human’s strategy is {wager with probability y = (D5 − D4)/(D3 − D4) ∈ (0, 1) and not wager with probability 1 − y; obey}. By Bayes’ rule, x = [pz]/[pz + (1 − p)] = xcritical.
With a finite utility for heaven and the deity having the original contingent-revealer preference ordering, the game-theoretic ‘problem’ for Pascal’s Wager is even stronger than in the infinite-utility case. As in the infinite-utility case, a Don’t-Wager Equilibrium always exists. But in the infinite-utility case, a Wager Equilibrium also always exists, whereas in the finite-utility case a Wager Equilibrium only exists when p ⩾ x critical , i.e. the human’s prior belief that the deity exists is at least as large as her belief-threshold for wagering. If the human begins the interaction assigning a sufficiently low probability to the deity existing (i.e. p < x critical ), then the Don’t Wager Equilibrium is the unique one.Footnote 15 (When p ⩾ x critical , then mixed-strategy equilibria also exist. In them, the human chooses to not wager with positive probability, reinforcing the ‘problem.’)
Proposition 7 Suppose that the deity has the strictly-dominant-non-revealer preference ordering min{D3, D4} > max{D5, D6}.
-
(i) If p < xcritical then the game has a unique PBE, a ‘Don’t-Wager Equilibrium’: the deity’s strategy is {not reveal}. The human’s strategy is {not wager; obey}. By Bayes’ rule, x = p.
-
(ii) If p > xcritical then the game has a unique PBE, a ‘Wager Equilibrium’: the deity’s strategy is {not reveal}. The human’s strategy is {wager; obey}. By Bayes’ rule, x = p.
-
(iii) If p = xcritical (a knife-edge condition) then the above two pure-strategy PBE exist, as well as the following PBE in mixed strategies: the deity’s strategy is {not reveal}. The human’s strategy is {wager with any probability y ∈ (0, 1) and not wager with probability 1 − y; obey}. By Bayes’ rule, x = p ( = xcritical).
With a finite utility for heaven and the deity having the strictly-dominant-non-revealer preference ordering, the ‘problem’ is again stronger than in the infinite-utility case. In the infinite-utility case, this preference ordering for the deity ensures that the Wager Equilibrium is the unique one, and hence completely resolves the ‘problem’. But in the finite-utility case, this requires p > x critical ; if p < x critical , then the Don’t-Wager Equilibrium not only exists, it is in fact the unique one. With a finite utility for heaven, even the deity having a strictly dominant strategy of not revealing his existence does not ensure that the human chooses to wager; instead, the human’s strategy choice depends on the value of the prior p relative to her belief-threshold x critical . (When the knife-edge condition p = x critical holds, then mixed-strategy equilibria also exist.)
7. CONCLUSION
Almost all existing formal analyses of Pascal’s Wager are decision-theoretic, with a human as the sole decision-maker. However, if the deity whose existence the human is considering wagering on exists, then presumably the deity has the option of choosing whether or not to clearly reveal his existence to the human. This suggests that a game-theoretic analysis of Pascal’s Wager is warranted, which is what I conduct here.
Using the standard infinite-utility-for-heaven Pascal’s Wager preferences for the human, and Brams’ (Reference Brams1982, Reference Brams2007, Reference Brams2011) plausible contingent-revealer preference ordering for the deity, it turns out that a Wager Equilibrium exists in which the human chooses to wager and Pascal’s Wager thus operates, but a Don’t-Wager Equilibrium also exists (even if the human has the first wager preferences in which there is nothing to lose by wagering). Thus, in a game-theoretic setting Pascal’s Wager is indeterminate: wagering and not wagering are both consistent with equilibrium behaviour.
If the deity instead has a strictly dominant strategy of not revealing his existence, then wagering is the unique equilibrium outcome and hence Pascal’s Wager is ‘restored’. But with a finite utility for heaven, the problem is more severe, and assuming that the deity’s strictly dominant strategy is to not reveal his existence does not necessarily resolve it. In summary, Pascal’s Wager faces some novel problems in a game-theoretic setting that do not arise in the decision-theoretic setting.
ACKNOWLEDGEMENTS
My thanks to the participants in a Program in Ethics and Political Science workshop at Texas A&M University in May 2016, as well as to two anonymous reviewers.
APPENDIX
This appendix presents the proofs of all of the propositions. Since we assume that H 5 > H 6 throughout, in every PBE the human chooses to obey.
PROPOSITION 1: Suppose there is a PBE in which x > 0. Then the human’s strictly optimal choice is to wager. Given this, the deity’s strictly optimal choice is to not reveal. Then x = p (>0) by Bayes’ rule. This gives PBE (a).
Suppose there is a PBE in which x = 0. Then the human’s strictly optimal choice is to not wager. Given this, the deity’s strictly optimal choice is to reveal. Then x = 0 by Bayes’ rule. This gives PBE (b).
We have analysed every possible value of x, and hence there are no other PBE. Q.E.D.
PROPOSITION 2: For PBE (a), the existence argument is exactly the same as in Proposition 1.
Suppose there is a PBE in which x = 0. Then the human is indifferent between wagering and not wagering. CASE (I): Suppose the human is choosing to not wager. Given this, the deity’s strictly optimal choice is to reveal. Then x = 0 by Bayes’ rule. This gives PBE (b). CASE (II): Suppose the human is choosing to wager. Given this, the deity’s strictly optimal choice is to not reveal. But then x = p (>0) by Bayes’ rule, inconsistent with our supposition that x = 0, and hence there is no PBE here. CASE (III): Suppose the human is choosing to wager with probability y ∈ (0, 1) and not wager with probability 1 − y. Maintaining our supposition that x = 0 requires that the deity be choosing to reveal. The deity at least weakly prefers to reveal if and only if (y)(D 3) + (1 − y)(D 4) ⩽ D 5, which can be rewritten as y ⩽ (D 5 − D 4)/(D 3 − D 4) ∈ (0, 1). This gives PBE (c).
We have analysed every possible value of x, and hence there are no other PBE. Q.E.D.
PROPOSITION 3: Because not revealing is the deity’s strictly dominant strategy, in any PBE the deity chooses to not reveal. Therefore x = p (>0) by Bayes’ rule. Therefore the human’s strictly optimal choice is to wager. This gives the PBE, and also establishes its uniqueness. Q.E.D.
PROPOSITIONS 4 AND 5: The key thing here is to notice that when H 2 = H 1, then x critical = 0: the human strictly prefers to wager if and only if x > 0, and is indifferent if x = 0. Therefore, the exact same proofs as for Propositions 2 and 3 carry through. Q.E.D.
PROPOSITION 6: When H 2 > H 1, then x critical ∈ (0, 1). Suppose there is a PBE in which the human’s strategy is to not wager. Given this, the deity’s strictly optimal choice is to reveal. Then x = 0 ( < x critical ) by Bayes’ rule, and hence the human’s strategy of not wagering is indeed optimal (in fact, strictly). This gives the existence of PBE (i) and (ii)(b), and establishes that the Don’t-Wager Equilibrium exists regardless of the value of p relative to x critical .
Suppose there is a PBE in which the human’s strategy is to wager. Given this, the deity’s strictly optimal choice is to not reveal. Then x = p by Bayes’ rule, and hence the human’s strategy of wagering is (at least weakly) optimal if and only if p ⩾ x critical . This gives PBE (ii)(a), and establishes that the Wager Equilibrium exists if and only if p ⩾ x critical .
Finally, suppose there is a PBE in which the human’s strategy is: wager with probability y ∈ (0, 1) and not wager with probability 1 − y. This requires x = x critical , so that the human is indifferent. The deity strictly prefers to reveal if and only if (y)(D 3) + (1 − y)(D 4) < D 5, which can be rewritten as y < (D 5 − D 4)/(D 3 − D 4) ≡ y critical ∈ (0, 1). CASE (I): First suppose that 0 < y ⩽ y critical and the deity is choosing to reveal. Then x = 0 by Bayes’ rule, which is inconsistent with our requirement that x = x critical (>0), and hence there is no PBE here. CASE (II): Now suppose that y critical ⩽ y < 1 and the deity is choosing to not reveal. Then x = p by Bayes’ rule, and hence this is a PBE if and only if the knife-edge condition p = x critical holds. This gives PBE (iii). CASE (III): Finally, suppose that y = y critical , and the deity is choosing to not reveal with probability z ∈ (0, 1), and reveal with probability 1 − z. This is a PBE as long as z is such that x = x critical . By Bayes’ rule, x = [pz]/[pz + (1 − p)], and setting this equal to x critical and solving for z gives z = [(1 − p)x critical ]/[p(1 − x critical )]. Note that z > 0. Also, z < 1 can be simplified to p > x critical , and hence this PBE exists if and only if p > x critical . This gives PBE (iv), and also establishes the uniqueness claim in the statement of PBE (i). Q.E.D.
PROPOSITION 7: Because not revealing is the deity’s strictly dominant strategy, in any PBE the deity chooses to not reveal. Therefore x = p by Bayes’ rule. CASE (I): If p < x critical , then x = p < x critical , and hence the human’s strictly optimal choice is to not wager. This gives PBE (i), and also establishes its uniqueness. CASE (II): If p > x critical , then x = p > x critical , and hence the human’s strictly optimal choice is to wager. This gives PBE (ii), and also establishes its uniqueness. CASE (III): If the knife-edge condition p = x critical holds, then x = p = x critical , and hence the human is indifferent between wagering and not wagering. Hence PBE (i) and (ii) both exist, as do mixed-strategy PBE in which the human chooses to wager with any probability y ∈ (0, 1), and to not wager with probability 1 − y. This gives PBE (iii). Q.E.D.




