Of the major disciplines concerned with social behaviour, game theory alone, it seems, has eschewed, and got along to date without, group notions.
Michael Bacharach (Reference Bacharach, Gold and Sugden2006: 72)
1. INTRODUCTION
If group members aim to fulfil a collective obligation, they must act in such a way that the composition of their individual actions amounts to a group action that fulfils the collective obligation. We use a game-theoretical formalism to study a strong sense of joint action in which the members of a group, using team reasoning, design and then publicly adopt a group plan. By highlighting particular group actions, a group plan specifies the individual actions that are the components of these highlighted group actions and thus specifies for every group member what she ought to do to contribute to the group’s fulfilling its collective obligation. The public adoption of a group plan changes the context in which group members and other agents make a decision about what to do.Footnote 1 We give necessary and sufficient conditions under which a group plan that is designed to fulfil a collective obligation is a good plan, that is, it successfully coordinates the individual actions of the group members. Our central theorem concerns what happens if such a good plan is publicly adopted. We show that if the group members publicly adopt a good group plan, then the decision context is changed in such a way that for every group member it holds that she acts according to the group plan if and only if she performs an action that is one of the best things she can do in the changed decision context, regardless of the actions taken by all the others.
We illustrate our game-theoretical formalism with concepts and ideas from the philosophical and economics literature on deontic logic, team reasoning, collective intentionality and joint action. This serves two purposes. On the one hand, the concepts and ideas from philosophy and economics help to clarify what our formalism is meant to model and thereby provide a partial conceptual justification for our formal analysis of the relation between collective obligations, group plans and individual actions. On the other hand, we submit that our formalization captures important aspects of concepts and ideas that have been developed in the philosophical and economics literature and that therefore our formal results are of central relevance to the debate on team reasoning, collective intentionality and joint action. To illustrate this, we briefly discuss the relation between collective and individual rationality and the relation between collective and individual blameworthiness from the perspective of our formalism. We do not, however, engage in a prolonged philosophical discussion with the main protagonists in the debate, since our current purpose is to present our game-theoretical formalism and our results on the relation between collective obligations, group plans and individual actions.
The paper is set out as follows. In Section 2, we define individual and collective obligations in terms of deontically optimal actions in a (single-shot) coordination game involving a single deontic ideality function. An individual agent is said to fulfil her individual obligation if and only if she performs one of her deontically optimal individual actions. Likewise, a group fulfils its collective obligation if and only if it performs one of its deontically optimal group actions. (For readability, we drop the adverb ‘deontically’ in ‘deontically optimal’.) We show that the fulfilment of a collective obligation is neither necessary nor sufficient for the fulfilment of individual obligations. In Section 3, we define a group plan as a set of group actions that are available to the group as a whole. Given such a group plan, a group member fulfils her member obligation specified by the plan if and only if she performs an action that is her component action of one of the group actions in the plan. We model the public adoption of a group plan as an update of the deontic ideality of the action profiles in a coordination game. In Section 4, we give necessary and sufficient conditions under which a group plan is a good plan, that is, conditions under which a group plan guarantees that if every group member fulfils her member obligation specified by the plan, then the group itself fulfils its collective obligation. Our central theorem is proved in Section 4.3: if a coordination game is updated with a good plan, then for every individual group member it holds that she fulfils her member obligation specified by the plan if and only if she fulfils her individual obligation in the coordination game that results from updating the original coordination game with the plan. Consequently, if a group publicly adopts a good plan, then a collective failure to fulfil a collective obligation is always due to an individual failure to fulfil a member obligation specified by the plan, or equivalently, an individual failure to fulfil an individual obligation in the coordination game that results from updating the original coordination game with that plan. A brief discussion of the relation between collective and individual rationality follows. In Section 5, we show that almost all our findings on coordination games transfer to what we call ‘zero-preserving cooperation games’ involving group-relative utility functions. On the basis of our discussion of cooperation games we then compare our approach to cooperation with the team-reasoning account of cooperation. In the concluding section, we use our formal analysis of collective obligations, group plans and individual actions to study some logical aspects of backward-looking collective moral responsibility.
2. INDIVIDUAL AND COLLECTIVE OBLIGATIONS IN COORDINATION GAMES
We use coordination games to study relations between collective obligations, group plans and obligations of individual agents.Footnote 2 (In Section 5, we investigate these relations using ‘cooperation games’.) A coordination game involves a finite set N = {i 1, …, i n } of individual agents. Each individual agent i in N has a non-empty and finite set A i of available individual actions. We use a i and a′ i as variables for individual actions in the set A i . The Cartesian product × i ∈ N A i of all the individual agents’ sets of actions gives the full set A of action profiles. We use a and a′ as variables for action profiles in the set A.Footnote 3 A deontic ideality function d assigns to each action profile a in A a value d(a) that is either 1 (if a is deontically ideal) or 0 (if a is not deontically ideal):Footnote 4
Definition 1 (Coordination Game)
A coordination game S is a triple ⟨N, (Ai ), d⟩, where N is a finite set of individual agents, for each agent i in N it holds that A i is a non-empty and finite set of actions available to agent i, and d is a deontic ideality function that assigns to each action profile a in A ( = × i ∈ N A i ) a value d(a) ∈ {0, 1}.
To prove some of our claims about collective obligations, group plans and obligations of individual agents, we must rule out coordination games in which no action profile is deontically ideal. Such coordination games are flat:
Definition 2
Let S = ⟨N, (Ai ), d⟩ be a coordination game. Then S is flat if and only if for all action profiles a ∈ A it holds that d(a) = 0.
For each group
$\mathcal {G}\subseteq N$
we define the set
$A^{}_\mathcal {G}$
of group actions that are available to group
$\mathcal {G}$
as the Cartesian product
$\times ^{}_{i\in \mathcal {G}}A^{}_i$
of all the individual group members’ sets of actions. We use
$a^{}_\mathcal {G}$
and
$a^{\prime }_\mathcal {G}$
as variables for group actions in the set
$A^{}_\mathcal {G}$
(
$=\times ^{}_{i\in \mathcal {G}}A^{}_i$
). Moreover, if
$a^{}_\mathcal {G}$
is a group action of group
$\mathcal {G}$
and if
$\mathcal {F}\subseteq \mathcal {G}$
, we use
$a^{}_\mathcal {F}$
to denote the subgroup action that is
$\mathcal {F}$
’s component subgroup action of the group action
$a^{}_\mathcal {G}$
. Finally, we use
$-\mathcal {G}$
to denote the relative complement
$N-\mathcal {G}$
.
We follow John Horty’s (Reference Horty1996, Reference Horty2001) deontic logic of agency and analyse a group’s collective obligations in terms of its optimal group actions that are in turn defined using a dominance ordering of the group actions that are available to the group. Intuitively, group action
$a^{}_\mathcal {G}$
weakly dominates group action
$a^{\prime }_\mathcal {G}$
in coordination game S (notation:
$a^{}_\mathcal {G}\succeq ^{}_S a^{\prime }_\mathcal {G}$
) if and only if
$a^{}_\mathcal {G}$
promotes deontic ideality in S at least as well as
$a^{\prime }_\mathcal {G}$
, regardless of what the group’s non-members do:
Definition 3 (Dominance)
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
be a group of agents. Let
$a^{}_\mathcal {G},a^{\prime }_\mathcal {G}\in A^{}_\mathcal {G}$
be actions available to group
$\mathcal {G}$
. Then
$$\begin{equation*}
a^{}_\mathcal {G}\succeq ^{}_S a^{\prime }_\mathcal {G}\quad \hbox{iff} \quad \hbox{for all} \ a^{\prime \prime }_{-\mathcal {G}}\in A_{-\mathcal {G}} \ \hbox{it holds that} \ d(a^{}_\mathcal {G},a^{\prime \prime }_{-\mathcal {G}})\ge d(a^{\prime }_\mathcal {G},a^{\prime \prime }_{-\mathcal {G}}).
\end{equation*}$$
Strong dominance is defined in terms of weak dominance:
$a^{}_\mathcal {G}\succ ^{}_S a^{\prime }_\mathcal {G}$
if and only if
$a^{}_\mathcal {G}\succeq ^{}_S a^{\prime }_\mathcal {G}$
and
$a^{\prime }_\mathcal {G}\not\succeq ^{}_S a^{}_\mathcal {G}$
.
We define the set of optimal group actions that are available to a group
$\mathcal {G}$
of agents in a coordination game S in terms of the dominance ordering of
$A^{}_\mathcal {G}$
. A group action
$a^{}_\mathcal {G}$
in
$A^{}_\mathcal {G}$
is optimal if and only if it is not strongly dominated by any group action in
$A^{}_\mathcal {G}$
:
Definition 4 (Optimal Actions)
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
be a group of agents. Then the set of
$\mathcal {G}$
’s optimal actions in
S, denoted by
$\textit{Optimal}_S(\mathcal {G})$
, is given by
$$\begin{equation*}
\textit{Optimal}_S(\mathcal {G}) = \lbrace a^{}_\mathcal {G}\in A^{}_\mathcal {G}:\mbox{ there is no }a^{\prime }_\mathcal {G}\in A^{}_\mathcal {G}\mbox{ such that }a^{\prime }_\mathcal {G}\succ ^{}_S a^{}_\mathcal {G}\rbrace.
\end{equation*}$$
Note that this definition implies that for every non-empty group of agents there is at least one optimal action (see Lemma 1 in the Appendix). Because there are optimal actions for any non-empty group and any of its non-empty subgroups, it makes sense to enquire about the relation between optimal group actions and optimal subgroup actions. First, note that an optimal group action is not necessarily composed of optimal subgroup actions. In the coordination game S 1 of Figure 1 it holds that (a′ i , a′ j ) is optimal for the group {i, j}, although a′ i is not optimal for agent i and a′ j is not optimal for agent j.
Figure 1. Coordination game S 1
Secondly, the composition of optimal subgroup actions is not necessarily an optimal group action. In the coordination game S 2 of Figure 2 it holds that a i is optimal for agent i and a′ j is optimal for agent j, although (a i , a′ j ) is not optimal for the group {i, j}.
Figure 2. Coordination game S 2
Finally, we say that a group
$\mathcal {G}$
fulfils its collective obligation in coordination game S if and only if it performs one of its optimal group actions. (Likewise, an agent i fulfils her individual obligation in coordination game S if and only if she performs one of her optimal individual actions.) Our discussion of Figures 1 and 2 shows that collective obligations and individual obligations do not match: the fulfilment of a collective obligation is neither necessary nor sufficient for the fulfilment of individual obligations. To fulfil its collective obligation the group members must ensure that the group action composed of the individual actions performed by them is an optimal group action. The gap between collective obligations and individual agency is filled by member obligations. Intuitively, a member obligation is what a group member ought to do in order to help ensure that the group fulfils its collective obligation, that is, in order to help ensure that the group performs an optimal group action. In this paper we consider member obligations as following from a collective obligation via a group plan.
3. GROUP PLANS AND MEMBER OBLIGATIONS
A group that aims to fulfil a collective obligation has a coordination problem: the group members must cooperate to ensure that the composition of their individual actions amounts to an optimal group action. In contrast to most coordination theorists, we assume that group members are able to communicate and to agree on a group plan to solve their coordination problem.Footnote 5 By agreeing on a group plan, it becomes common knowledge among the members of the group that the plan has been adopted. A group plan, once agreed upon, coordinates the individual actions of the members of the group: it allows them to act simultaneously and unconditionally, in the full belief that every group member acts according to plan. Group actions that are regulated by a group plan constitute a strong sense of joint action.Footnote 6 Raimo Tuomela calls this sense of acting together proper joint action:
Acting together involves sociality in the relatively strong sense that such action must be based on joint intention or shared collective goal. This makes any case of acting together cooperative at least to the extent that the persons are collectively committed to making true a certain state of affairs.…In the strongest sense of acting together we require acting on a joint, agreed-upon plan. This I will call proper joint action. (Tuomela Reference Tuomela2000: 7)
To design a group plan the group members must discover which are the best courses of action they can take as a group. To do so, group members must abandon their individual perspective and reason from the standpoint of a group and the group actions that are available to it. This kind of reasoning is known as team reasoning (Sugden Reference Sugden1993, Reference Sugden2000, Reference Sugden2003; Bacharach Reference Bacharach1999, Reference Bacharach, Gold and Sugden2006) or we-reasoning (Tuomela Reference Tuomela2013).Footnote 7 We take it that team reasoning permits the group members to come up with and agree on a group plan.Footnote 8 Once adopted, a group plan provides ‘a filter on options that are potential solutions’ (Bratman Reference Bratman1987: 35) to a group’s coordination problem. By filtering out group actions, a group plan specifies the remaining group actions and in consequence it highlights the individual actions that are the components of these highlighted group actions. Accordingly, a group plan specifies for each group member what she ought to do.
We intend to understand how a group plan gives rise to member obligations by way of Margaret Gilbert’s account of joint commitments. We submit that by adopting a group plan, a group of agents enters a joint commitment to execute the plan.Footnote 9 After entering such a joint commitment, the group members ‘owe each other conformity to the commitment. Thus, they have obligations towards each other’ (Gilbert Reference Gilbert2006a: 156). Such obligations of joint commitment are genuine obligations, Gilbert argues: they meet the condition that ‘one who has an obligation to perform some action will have sufficient reason for performing it, sufficient reason that is independent of his own inclinations or self-interest and that cannot be eradicated by his own fiat’ (Gilbert Reference Gilbert2006a: 157). Nonetheless, obligations of joint commitment are social rather than moral obligations.
The relation between a joint commitment and its concomitant social obligations is, Gilbert claims, a priori: the mere fact of entering a joint commitment implies social obligations on the members of the group.Footnote 10 They ‘owe each other actions by virtue of their participation in the joint commitment and that alone. Consideration of what bad consequences might flow from violation of the commitment, for instance, is not relevant to the issue’ (Gilbert Reference Gilbert1999: 151). A publicly adopted plan thus generates member obligations, regardless of whether or not the group members correctly assume that it is a good plan.Footnote 11 Robert Sugden concurs:
To act as a member of the team is to act as a component of the team. It is to act on a concerted plan, doing one’s allotted part in that plan without asking whether, taking other members’ actions as given, one’s own action is contributing towards the team’s objective.…It must be sufficient for each member of the team that the plan itself is designed to achieve the team’s objective: the objective will be achieved if everyone follows the plan. (Sugden Reference Sugden1993: 86)Footnote 12
We suggest that a group plan
$P^{}_\mathcal {G}$
of a group
$\mathcal {G}$
in coordination game S be thought of as any subset of the set
$A^{}_\mathcal {G}$
of group actions that are available to
$\mathcal {G}$
in S. By adopting a group plan, the group members enter a joint commitment to perform one of the group actions in the plan. Given an adopted group plan
$P^{}_\mathcal {G}$
and an individual group member i of
$\mathcal {G}$
, agent i fulfils her member obligation specified by the plan
$P^{}_\mathcal {G}$
if and only if she performs an action that is her component action of one of the group actions in the plan, that is, if and only if she performs an action from the set
$\lbrace a^{}_i:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace$
.
3.1. Updating coordination games by group plans
We have argued that the adoption of a group plan generates member obligations and that these member obligations are specified by the group plan. There is, however, a second way in which the adoption of a group plan generates obligations. The adoption of a group plan can also be understood as inducing a change of the deontic ideality of the action profiles in a coordination game.Footnote 13 Because a change in deontic ideality might affect the dominance ordering of an agent’s set of actions, such a change might lead to a different set of actions with which an agent, whether individual or group, might fulfil her individual or its collective obligation.
Technically, we model the adoption of a group plan in coordination game S as an update of the deontic ideality function of the game’s action profiles. We use
$S\uparrow P^{}_\mathcal {G}$
to denote the coordination game that results from updating coordination game S with a group plan
$P^{}_\mathcal {G}$
. To keep the update of the deontic ideality function technically manageable, we require that the group plan be adopted publicly. We may hence assume that after the public adoption of a group plan it is common knowledge among the agents in the game, whether or not they are members of the group that adopts the plan, that the plan has been adopted. The public adoption of a group plan hence changes the decision context not only for group members, but also for agents who are not in the group. After the public adoption of a group plan each agent in the outgroup decides what to do, on the supposition that the group members act according to plan. To implement this in a simple way, we consider the update of the deontic ideality function to be uniform for all agents in the game.Footnote
14
Accordingly, updating a game with a group plan amounts to this: if an action profile is forbidden by the plan, its deontic ideality becomes 0; and if an action profile is permitted by the plan, its deontic ideality remains unchanged. Or equivalently, an action profile a is deontically ideal in
$S\uparrow P^{}_\mathcal {G}$
if and only if (1) the action profile a is deontically ideal in S; and (2) the group’s component action
$a^{}_\mathcal {G}$
of the action profile a is a group action in
$P^{}_\mathcal {G}$
:
Definition 5 (Plan Updates)
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Then the update of S with
$P^{}_\mathcal {G}$
, notation:
$S\uparrow P^{}_\mathcal {G}$
, is the coordination game
$S\uparrow P^{}_\mathcal {G}=\langle N,(A_i),d^\uparrow \rangle$
, where
$$\begin{equation*}
d^\uparrow (a) = \left\lbrace \begin{array}{ll}d(a), & \mbox{if }a^{}_\mathcal {G}\in P^{}_\mathcal {G}\\
0, & \mbox{if }a^{}_\mathcal {G}\not\in P^{}_\mathcal {G}. \end{array} \right.
\end{equation*}$$
Because an update of a coordination game with a group plan might change the deontic ideality of the game’s action profiles, it might also change the dominance ordering of any group’s group actions. There is one exception. Updating a coordination game with a group plan leaves the dominance ordering of the group actions in the plan unaffected (all claims are proved in the Appendix):
Observation 1
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Let
$a^{}_\mathcal {G},a^*_\mathcal {G}\in P^{}_\mathcal {G}$
. Then
$$\begin{equation*}
a^{}_\mathcal {G}\succeq _S a^*_\mathcal {G}\quad \hbox{iff} \quad a^{}_\mathcal {G}\succeq _{S\uparrow P_\mathcal {G}}a^*_\mathcal {G}.
\end{equation*}$$
Although an update with a group plan does not change the dominance ordering of the group actions in the plan, it might change the dominance ordering of the individual actions that are component actions of the group actions in the plan. Ideally, an update with a group plan should change the dominance ordering of these individual actions in such a way that an individual action is a component of one of the group actions in the plan if and only if that individual action is an optimal individual action in the coordination game that results from updating the original coordination game with the plan. Not all group plans have this updating property. We show that if a group plan is a good plan (in the sense defined below), then it has this updating property.
4. GOOD PLANS AND BAD PLANS
There are good plans and bad plans. A good plan guarantees that if every group member fulfils her member obligation specified by the plan, then the group itself fulfils its collective obligation.Footnote 15 Or equivalently, a good plan guarantees that if the group itself does not fulfil its collective obligation, then at least one group member does not fulfil her member obligation specified by the plan.Footnote 16 A bad plan fails to do so. By agreeing on a bad plan, even though it thereby becomes common knowledge that the plan has been adopted, the group members do not rule out the possibility that every group member fulfils her member obligation specified by the plan, while the composition of the group members’ actions does not amount to a group action that fulfils their collective obligation. Accordingly, there are two conditions on fulfilling a collective obligation by way of a group plan: first, the group members must act according to plan, and secondly, the plan itself must be good. But what makes a group plan a good plan? We submit that a plan is a good plan if and only if it is optimal and interchangeable.
4.1. Optimal plans
The aim of a group plan is to fulfil a collective obligation. A group fulfils its collective obligation if and only if it performs an optimal group action. A good plan should hence be designed such that if all group members act according to plan, then the composition of their actions amounts to an optimal group action. The first design requirement of a good plan therefore is that the plan only consists of optimal group actions (as we shall see below, this is a necessary but not a sufficient condition). We say that a group plan is optimal if and only if it is a non-empty subset of the group’s optimal group actions:
Definition 6 (Optimal Plans)
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Then
$P^{}_\mathcal {G}$
is optimal if and only if
$P^{}_\mathcal {G}\ne \emptyset$
and
$P^{}_\mathcal {G}\subseteq \textit{Optimal}_S(\mathcal {G})$
.
What happens if we update a coordination game with such an optimal plan? Ruling out flat coordination games (in which there is no deontically ideal action profile), an update of a coordination game with an optimal plan does not introduce optimal group actions that were not in the plan and does not eliminate optimal group actions that were in the plan. The set of optimal group actions in the coordination game that results from updating a coordination game with an optimal plan equals the set of group actions in the plan:
Observation 2
Let S = ⟨N, (Ai
), d⟩ be a non-flat coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
be optimal. Then
$$\begin{equation*}
\textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})=P^{}_\mathcal {G}.
\end{equation*}$$
This observation implies that every group action that is optimal in the coordination game
$S\uparrow P{}_\mathcal {G}$
that results from updating a non-flat coordination game S with an optimal plan
$P^{}_\mathcal {G}$
is an optimal group action in the original coordination game S, that is,
$\textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})\subseteq \textit{Optimal}_S(\mathcal {G})$
. Accordingly, an update with an optimal plan highlights particular optimal group actions in the original coordination game.
However, it is not sufficient to require of a good plan that it be optimal. Indeed, if a plan consists of several optimal group actions and if each group member does her share of an optimal group action in the plan, then the composition of the group members’ actions need not be an optimal group action. Writing on action profiles in games with individual utility functions rather than on group actions in games with a deontic ideality function, David Gauthier (Reference Gauthier1975: 201) observes: ‘If each person performs an action which has a best equilibrium as a possible outcome, and if there are several best equilibria, then the outcome need not be a best equilibrium.’ Because of this, coordination theorists standardly assume that a solution to a coordination problem consists in singling out a unique action profile:
Several best equilibria are too many of a good thing. … What we need is a way to restructure our conception of the situation so that we are left with but one. We must restrict the possible actions which we consider, in such a way that we convert our representation of the situation into one with but one best equilibrium. (Gauthier Reference Gauthier1975: 210)Footnote 17
In the present setting, we do not need this methodological assumption. To tackle our current problem of specifying the conditions under which a group plan successfully coordinates the actions of group members, we do not have to assume that the agents must somehow agree on a unique group action. We show that it suffices to require of good plans not only that they be optimal, but also interchangeable.
4.2. Interchangeable plans
An optimal plan does not guarantee that if all group members act according to plan, then the group itself performs an optimal group action. We therefore need an additional requirement. This second design requirement of a good plan is that the plan be closed under component individual actions. We say that a group plan is interchangeable if and only if for any two group actions in the plan it holds that the composition of a group member’s contribution to the first group action and the joint contribution of all other group members to the second group action amounts to a group action that is also in the plan:Footnote 18
Definition 7 (Interchangeable Plans)
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Then
$P^{}_\mathcal {G}$
is interchangeable if and only if for all
$a^{}_\mathcal {G},a^{\prime }_\mathcal {G}\in P^{}_\mathcal {G}$
and all
$i\in \mathcal {G}$
it holds that
$(a^{}_i,a^{\prime }_{\mathcal {G}-i})\in P^{}_\mathcal {G}$
.
A few examples: in coordination game S 3 of Figure 3 the plan {(a i , a j )} is interchangeable (as is every plan consisting of a single group action). Likewise, {(a i , a j ), (a i , a′ j ), (a i , a′′ j )} is interchangeable. The plan {(a i , a j ), (a i , a′ j ), (a′ i , a j )} is not, because (a′ i , a′ j ) is not in it. Finally, {(a i , a j ), (a i , a′′ j ), (a′ i , a j ), (a′ i , a′′ j )} is interchangeable.
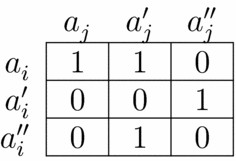
Figure 3. Coordination game S 3
Our definition implies that a plan is interchangeable if and only if for any two group actions in the plan it holds that the composition of a subgroup’s contribution to the first group action and the joint contribution of all other group members to the second group action amounts to a group action that is also in the plan:
Observation 3
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Then
$P^{}_\mathcal {G}$
is interchangeable if and only if for all
$a^{}_\mathcal {G},a^{\prime }_\mathcal {G}\in P^{}_\mathcal {G}$
and all
$\mathcal {F}\subseteq \mathcal {G}$
it holds that
$(a^{}_\mathcal {F},a^{\prime }_{\mathcal {G}-\mathcal {F}})\in P^{}_\mathcal {G}$
.
We have argued above that a group plan does not need to single out a unique group action to successfully coordinate the individual actions of the group members. To make this clear, consider again the coordination game S 3 of Figure 3. To solve their coordination problem, group members i and j must agree on a plan that successfully coordinates their actions. Even though it consists of several group actions, the optimal and interchangeable plan {(a i , a j ), (a i , a′ j )} does the job. The plan specifies the following member obligations on agents i and j: agent i ought to perform action a i and agent j ought to perform one of the actions a j and a′ j . The plan hence gives some leeway to agent j. Nonetheless, the plan ensures that if both group members act according to plan, they perform an optimal group action and hence the group itself fulfils its collective obligation.
This point can be made fully general: an optimal and interchangeable plan guarantees that if every group member fulfils her member obligation specified by the plan, then the group itself fulfils its collective obligation. Let us see why this is so. If every group member fulfils her member obligation specified by an optimal and interchangeable plan, then every group member performs an action that is a component action of one of the group actions in the plan. Because the plan is interchangeable, the combination of the actions performed by the group members must also be in the plan. Because the plan is optimal, it only contains optimal group actions, and hence this combination of group member actions is an optimal group action. The group members hence perform an optimal group action and thus fulfil the group’s collective obligation. Therefore, if every group member acts according to an optimal and interchangeable plan, then the group itself fulfils its collective obligation.
4.3. Updates with optimal and interchangeable plans
Our central theorem concerns what happens if we update a coordination game with an optimal and interchangeable group plan. We show that if we update a non-flat coordination game with such a plan, then for any subgroup of this group it holds that an action of that subgroup is an optimal subgroup action in the coordination game that results from updating the original coordination game with the plan if and only if that subgroup action is a component subgroup action of one of the group actions in the plan:
Theorem 1
Let S = ⟨N, (Ai
), d⟩ be a non-flat coordination game. Let
$\mathcal {F}\subseteq \mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A{}_\mathcal {G}$
be optimal and interchangeable. Then
$$\begin{equation*}
\textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {F})=\lbrace a^{}_\mathcal {F}:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace.
\end{equation*}$$
Our theorem shows that updates of coordination games with optimal and interchangeable plans relate collective obligations to individual obligations. Indeed, by setting
$\mathcal {F}=\lbrace i\rbrace$
for any individual member i of
$\mathcal {G}$
we obtain
$\textit{Optimal}_{S\uparrow P_\mathcal {G}}(i)=\lbrace a^{}_i:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace$
. Accordingly, if we update a non-flat coordination game with an optimal and interchangeable group plan, then for every group member it holds that she fulfils her member obligation specified by the plan if and only if she fulfils her individual obligation in the coordination game that results from updating the original coordination game with the plan. Consequently, under the given assumptions, a group member acts according to plan if and only if she performs an optimal individual action in the changed decision context. It follows that, under the given assumptions, if every group member performs an optimal individual action in the changed decision context, then the group itself performs an optimal group action.
If we think of acting rationally as performing those actions that best promote deontic ideality, then we could say that an individual action is individually rational if and only if it is an optimal individual action, and that a group action is collectively rational if and only if it is an optimal group action. Within the narrow confines of our idealizing assumptions, Theorem 1 would then relate collective rationality to individual rationality and thereby give a tentative answer to Bratman’s questions:
Are there norms that are in some way fundamental to shared agency? If so, how precisely are they related to shared agency, and how are they related to norms of individual rationality? (Bratman Reference Bratman2014: 4)
The answer runs as follows. A group action is collectively rational if and only if it is an optimal group action. To perform an optimal group action, the group members must adopt a good plan to ensure that the combination of their actions is an optimal group action. After the public adoption of such a plan, a group member’s action is rational with respect to the group’s objective of performing an optimal group action if and only if this action is permitted by the plan.Footnote 19 Moreover, when the plan has been publicly adopted and thereby changed the context in which agents make a decision about what to do, an individual action is individually rational if and only if it is an optimal individual action in the changed decision context. Our theorem shows that, under the given assumptions, a group member’s action is rational with respect to the group’s objective of performing an optimal group action if and only if that action is individually rational in the decision context that results from the public adoption of the plan. It follows that, under the given assumptions, if every group member performs an individually rational action in the changed decision context, then the group itself performs a collectively rational group action. Therefore, if we think of acting rationally as performing those actions that best promote deontic ideality, our theorem would establish a connection between collective rationality and individual rationality.
5. ZERO-PRESERVING COOPERATION GAMES
Thus far, we have used coordination games involving a single deontic ideality function to study the relation between collective obligations, group plans, and individual actions. In this section we show that almost all our findings on coordination games transfer to ‘cooperation games’ involving group-relative utility functions, provided these utility functions are ‘zero-preserving’. The only exception is the right-to-left inclusion of Theorem 1. In the context of zero-preserving cooperation games this property is undesirable. To show all of this let us first introduce cooperation games.
A cooperation game involves a finite set of individual agents. Each individual agent has a non-empty, finite set of available individual actions. Each group of agents assigns to each action profile a non-negative group utility:
Definition 8 (Cooperation Game)
A cooperation game
S is a triple
$\langle N,(A_i),(u_\mathcal {H})\rangle$
, where N is a finite set of individual agents, for each agent i in N it holds that A
i
is a non-empty and finite set of actions available to agent i, and for each group of agents
$\mathcal {H}$
from N it holds that
$u^{}_\mathcal {H}$
is a utility function that assigns to each action profile a in A ( = ×
i ∈ N
A
i
) a utility
$u^{}_\mathcal {H}(a)\in \mathbb {R}_{\ge 0}$
.
To prove our claims about cooperation games we rule out cooperation games in which a group assigns to every action profile a utility of 0. Such games are flat with respect to that group:
Definition 9
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Let
$\mathcal {G}\subseteq N$
. Then S is
$\mathcal {G}$
-flat if and only if for every action profile a ∈ A it holds that
$u^{}_\mathcal {G}(a)=0$
.
To define the
$\mathcal {G}$
-optimal group actions that are available to a group
$\mathcal {G}$
, we first define a dominance ordering: group action
$a^{}_\mathcal {G}$
weakly
$\mathcal {G}$
-dominates group action
$a^{\prime }_\mathcal {G}$
in cooperation game S (notation:
$a^{}_\mathcal {G}\succeq ^{}_S a^{\prime }_\mathcal {G}$
) if and only if
$a^{}_\mathcal {G}$
promotes the utility of group
$\mathcal {G}$
in S at least as well as
$a^{\prime }_\mathcal {G}$
, regardless of what
$\mathcal {G}$
’s non-members do:
Definition 10 (
$\mathcal {G}$
-Dominance)
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Let
$\mathcal {G}\subseteq N$
. Let
$a^{}_\mathcal {G},a^{\prime }_\mathcal {G}\in A^{}_\mathcal {G}$
. Then
$$\begin{equation*}
a^{}_\mathcal {G}\succeq ^{}_S a^{\prime }_\mathcal {G}\quad {\it iff} \quad \hbox{for all} \ a^{\prime \prime }_{-\mathcal {G}}\in A_{-\mathcal {G}}\ {\it it\ holds\ that}\ u^{}_\mathcal {G}(a^{}_\mathcal {G},a^{\prime \prime }_{-\mathcal {G}})\ge u^{}_\mathcal {G}(a^{\prime }_\mathcal {G},a^{\prime \prime }_{-\mathcal {G}}).
\end{equation*}$$
Strong
$\mathcal {G}$
-dominance is defined in terms of weak
$\mathcal {G}$
-dominance:
$a^{}_\mathcal {G}\succ ^{}_S a^{\prime }_\mathcal {G}$
if and only if
$a^{}_\mathcal {G}\succeq ^{}_S a^{\prime }_\mathcal {G}$
and
$a^{\prime }_\mathcal {G}\not\succeq ^{}_S a^{}_\mathcal {G}$
.
A group action is
$\mathcal {G}$
-optimal in cooperation game S if and only if it is not strongly
$\mathcal {G}$
-dominated by any group action that is available to the group in S:
Definition 11 (
$\mathcal {G}$
-Optimal Actions)
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Let
$\mathcal {G}\subseteq N$
. Then
$$\begin{equation*}
\textit{Optimal}_S(\mathcal {G}) = \lbrace a^{}_\mathcal {G}\in A^{}_\mathcal {G}:\mbox{ there is no }a^{\prime }_\mathcal {G}\in A^{}_\mathcal {G}\mbox{ such that }a^{\prime }_\mathcal {G}\succ ^{}_S a^{}_\mathcal {G}\rbrace.
\end{equation*}$$
Just as in coordination games, a group
$\mathcal {G}$
fulfils its collective obligation in cooperation game S if and only if it performs one of its
$\mathcal {G}$
-optimal actions. Likewise, an agent i fulfils her individual obligation in cooperation game S if and only if she performs one of her i-optimal actions.
As before, a group plan
$P^{}_\mathcal {G}$
of group
$\mathcal {G}$
in a cooperation game S can be any subset of the set
$A^{}_\mathcal {G}$
of group actions that are available to group
$\mathcal {G}$
in S. Again, given an adopted group plan
$P^{}_\mathcal {G}$
and a group member i of
$\mathcal {G}$
, agent i fulfils her member obligation specified by the plan if and only if she performs an action that is her component action of one of the group actions in the plan.
In analogy to the plan updates of Section 3.1, we now model the public adoption of a group plan in a cooperation game as an update of the game’s utility functions. Updating a cooperation game with a group plan amounts to the following: if an action profile is forbidden by the plan, then for every group the group utility of that action profile becomes 0; and if an action profile is permitted by the plan, then for every group the group utility of that action profile remains unchanged:
Definition 12 (Plan Updates)
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Then the update of S with
$P^{}_\mathcal {G}$
, notation:
$S\uparrow P^{}_\mathcal {G}$
, is the cooperation game
$S\uparrow P^{}_\mathcal {G}=\langle N,(A_i),(u^\uparrow _\mathcal {H})\rangle$
, where
$$\begin{equation*}
u^\uparrow _\mathcal {H}(a) = \left\lbrace \begin{array}{ll}u^{}_\mathcal {H}(a), & \mbox{if }a^{}_\mathcal {G}\in P^{}_\mathcal {G}\\
0, & \mbox{if }a^{}_\mathcal {G}\not\in P^{}_\mathcal {G}. \end{array} \right.
\end{equation*}$$
As in coordination games, an update of a cooperation game with a group plan leaves the dominance ordering of the group actions in the plan unaffected:
Observation 4
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Let
$a^{}_\mathcal {G},a^*_\mathcal {G}\in P^{}_\mathcal {G}$
. Then
$$\begin{equation*}
a^{}_\mathcal {G}\succeq _S a^*_\mathcal {G}\quad \hbox{iff} \quad a^{}_\mathcal {G}\succeq _{S\uparrow P_\mathcal {G}}a^*_\mathcal {G}.
\end{equation*}$$
$\mathcal {G}$
-optimal plans and interchangeable plans are formally defined as in Definitions 6 and 7 above. A group plan is
$\mathcal {G}$
-optimal if and only if it is a non-empty subset of the group’s
$\mathcal {G}$
-optimal actions. A group plan is interchangeable if and only if for any two group actions in the plan it holds that the composition of a group member’s contribution to the first group action and the joint contribution of all other group members to the second group action amounts to a group action that is also in the plan. Again, a
$\mathcal {G}$
-optimal and interchangeable plan guarantees that if every group member fulfils her member obligation specified by the plan, then the group itself fulfils its collective obligation. For an informal proof of this conditional, see the end of Section 4.2.
After updating a non-
$\mathcal {G}$
-flat cooperation game with a
$\mathcal {G}$
-optimal group plan
$P^{}_\mathcal {G}$
it holds that a group action is a
$\mathcal {G}$
-optimal group action in the cooperation game that results from the update if and only if it is one of the group actions in the plan:
Observation 5
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a non-
$\mathcal {G}$
-flat cooperation game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
be
$\mathcal {G}$
-optimal. Then
$$\begin{equation*}
\textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})=P^{}_\mathcal {G}.
\end{equation*}$$
To transfer our findings on coordination games to cooperation games, we must relate group utilities to subgroup utilities. To do this, we require the relation between subgroup utilities and group utilities to be zero-preserving. A cooperation game is zero-preserving if and only if there is no action profile in the game which has a non-zero utility for some group, while it does have zero utility for some subgroup of that group:
Definition 13 (Zero-Preservation)
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Then S is zero-preserving if and only if for all non-empty groups
$\mathcal {F}^{}_1\subseteq \mathcal {F}^{}_2\subseteq N$
and for all action profiles a ∈ A it holds that if
$u^{}_{\mathcal {F}^{}_1}(a)=0$
, then
$u^{}_{\mathcal {F}^{}_2}(a)=0$
.
Although this might seem a rather strong condition, any cooperation game can be transformed into a zero-preserving one by linearly transforming the game’s utility functions: adding 1 to each utility in the game makes it zero-preserving. Apart from using linear transformations to ensure that a cooperation game is zero-preserving, some social welfare functions always ensure zero-preservation. The Rawlsian social welfare function
$u{}_{\mathcal {H}}(a)=\min _{i\in \mathcal {H}}(u^{}_i(a))$
is but one example. Other social welfare functions, such as summing or averaging, only meet this condition in some cooperation games – the Hi-Lo game that we discuss in Section 5.1 is a case in point.Footnote
20
Plan updates sustain zero-preservation:
Observation 6
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Let
$\mathcal {G}\subseteq N$
and let
$P{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Then
If S is zero-preserving, then
$S\uparrow P^{}_\mathcal {G}$
is zero-preserving.
Finally, the left-to-right inclusion of Theorem 1 also holds for cooperation games. We show that if we update a zero-preserving non-
$\mathcal {G}$
-flat cooperation game with a
$\mathcal {G}$
-optimal group plan
$P^{}_\mathcal {G}$
, then for any subgroup
$\mathcal {F}$
of
$\mathcal {G}$
it holds that if an action of that subgroup is an
$\mathcal {F}$
-optimal subgroup action in the cooperation game that results from updating the original cooperation game with the plan, then that subgroup action is a component subgroup action of one of the group actions in the plan:
Observation 7
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a zero-preserving non-
$\mathcal {G}$
-flat cooperation game. Let
$\mathcal {F}\subseteq \mathcal {G}\subseteq N$
be non-empty and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
be
$\mathcal {G}$
-optimal. Then
$$\begin{equation*}
\textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {F})\subseteq \lbrace a^{}_\mathcal {F}:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace.
\end{equation*}$$
Analogous to Theorem 1, our observation shows also that updates of cooperation games with
$\mathcal {G}$
-optimal plans relate collective obligations to individual obligations. Indeed, by setting
$\mathcal {F}=\lbrace i\rbrace$
for any individual member i of
$\mathcal {G}$
we obtain
$\textit{Optimal}_{S\uparrow P_\mathcal {G}}(i)\subseteq \lbrace a^{}_i:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace$
. Accordingly, if we update a zero-preserving non-
$\mathcal {G}$
-flat cooperation game with a
$\mathcal {G}$
-optimal plan, then for every group member it holds that she fulfils her member obligation specified by the plan if she fulfils her individual obligation in the cooperation game that results from updating the original cooperation game with the plan. Consequently, under the given assumptions, a group member i acts according to plan if she performs an i-optimal individual action in the changed decision context. (Notice that, until now, we have not required the plan to be interchangeable.) It follows that, under the given assumptions, a
$\mathcal {G}$
-optimal and interchangeable plan guarantees that if each group member i performs an i-optimal individual action in the changed decision context, then the group itself performs a
$\mathcal {G}$
-optimal group action.
The right-to-left inclusion does not hold, because plan updates do not affect utilities of action profiles that are permitted by the plan. This means that if we update a zero-preserving non-
$\mathcal {G}$
-flat cooperation game with a
$\mathcal {G}$
-optimal and interchangeable group plan, then it might be that a group member acts according to plan without performing an i-optimal individual action in the changed decision context. To see this, consider the zero-preserving non-
$\mathcal {G}$
-flat cooperation game S
4 of Figure 4, where each action profile a is assigned a triple of utilities ⟨u
i
(a), u
j
(a), u
i, j
(a)⟩. (The utility function of the empty group is suppressed.)
Figure 4. Cooperation game S 4
Updating S
4 with the
$\mathcal {G}$
-optimal and interchangeable plan P
i, j
= {(a′
i
, a′
j
), (a′′
i
, a′
j
)} results in the cooperation game S
4↑P
i, j
of Figure 5, where it holds that a′
i
∈ {a
i
: a
i, j
∈ P
i, j
} and
$a^{\prime }_i\not\in \textit{Optimal}_{S_4\uparrow P_{i,j}}(i)$
.
Figure 5. Cooperation game S 4↑P i, j
5.1. The team-reasoning account of cooperation
Our discussion of cooperation games permits us to compare our account of the relation between collective obligations, group plans and individual actions and the team-reasoning account of cooperation. Disregarding the differences in their accounts of cooperation, Bacharach and Sugden both argue that if we wish to give a game-theoretical explanation of cooperation in single-shot games, then an individualist perspective will not do.Footnote 21 Therefore, they propose to extend traditional game theory with group notions. Given a group of agents, team reasoning describes the reasoning process by which a group member first identifies the best combination of actions that the group members can perform and then decides to perform the individual action that is her part in that combination. To see how this works, consider the Hi-Lo cooperation game S 5 of Figure 6, where each action profile a is assigned a triple of utilities ⟨u i (a), u j (a), u i, j (a)⟩ such that u i, j (a) is the sum of u i (a) and u j (a).
Figure 6. Cooperation game S 5
Agent i is engaged in team reasoning only if she reaches her decision about what to do by reasoning from the standpoint of the team consisting of i and j. First, it will then be clear to her that, of the four courses of action that are available to the group, the combination (a′ i , a′ j ) is the best. She therefore decides to do her part in that combination and perform action a′ i . Reasoning in an analogous fashion, agent j decides to perform action a′ j . Accordingly, if both agents engage in team reasoning, they will perform the best group action. In contrast to traditional game theory, the team-reasoning account explains cooperation in Hi-Lo games even if communication is impossible.
Contrary to the team-reasoning account of cooperation, we assume that communication is possible and that agreement is unproblematic. Our research agenda therefore differs from that set by Bacharach and Sugden. Our account of cooperation starts from the assumption that the agents i and j are able to communicate and make agreements about what to do. If they decide to act as a group, they should abandon their individual perspective and evaluate the actions available to them from the standpoint of the group.Footnote 22 Because it will be clear to them that (a′ i , a′ j ) is the only {i, j}-optimal group action, they should agree on the group plan {(a′ i , a′ j )}. At the moment they have publicly adopted this group plan, agent i has the member obligation to perform action a′ i and agent j has the member obligation to perform a′ j . Moreover, by publicly adopting this group plan, the decision context is changed into cooperation game S 5↑{(a′ i , a′ j )} of Figure 7. In this changed decision context, agent i has the individual obligation to perform action a′ i and agent j has the individual obligation to perform action a′ j .
Figure 7. Cooperation game S 5↑{(a' i , a' j )}
Our analysis hence suggests that, given a decision context in which the agents are able to communicate and make agreements, it holds that if they decide to act as a group
$\mathcal {G}$
of agents, and if there is a unique
$\mathcal {G}$
-optimal group action, then the group members should agree on the group plan that only consists of this unique
$\mathcal {G}$
-optimal group action. The member obligations specified by the plan and the individual obligations in the decision context that results from publicly adopting the plan coincide with the recommendations that issue from the team-reasoning account. Therefore, if there is a unique
$\mathcal {G}$
-optimal group action, our account and the team-reasoning account of cooperation give similar recommendations to group members. Things are different, however, if there are several
$\mathcal {G}$
-optimal group actions: whereas the team-reasoning account has nothing much to offer, our analysis still applies.
We have argued that if the group members design and adopt a group plan to solve their coordination problem, and if we allow a group plan to consist of several group actions (thereby giving some leeway to at least some group members), the plan might fail to guarantee that if every group member acts according to plan, then the combination of their actions is a
$\mathcal {G}$
-optimal group action. Some such plans do guarantee this, however. The focus of our study has therefore been on the structural conditions that a group plan must meet in order to successfully coordinate the individual actions of the group members, and on what happens to a decision context when such a group plan is publicly adopted.
6. CONCLUSION
What, if anything, does our account of collective obligations, group plans and individual actions tell us about the concept of collective blameworthiness, that is, backward-looking collective moral responsibility? The complexity of this concept has led some to argue that formal methods are hardly any use in the study of collective moral responsibility. Margaret Gilbert, for example, writes:
What does the blameworthiness of the collective’s act imply about the personal blameworthiness of any one member of that collective? From a logical point of view, the short answer is: nothing. Everything depends on the details of a given member’s particular situation. (Gilbert Reference Gilbert2006b: 109)Footnote 23
Gilbert notes that some members of a blameworthy collective might have authorized others to decide and that this may make a difference to the attribution of blame to those members. At present, our formal analysis is too coarse to capture these structural aspects of collective moral responsibility. Nonetheless, even our relatively simple formalization of the relation between collective obligations, group plans and individual actions brings to the fore some central aspects of the logic of backward-looking collective responsibility.
We take it that the concept of backward-looking individual responsibility supports the claim that not fulfilling an obligation is a necessary condition for being individually blameworthy: if an individual agent is individually blameworthy, then she has failed to fulfil an obligation. The converse does not hold, because she might have a plausible excuse for not doing what she ought to do. Analogously, we submit that not fulfilling a collective obligation is a necessary, but not a sufficient condition for being collectively blameworthy. We thus obtain the following implication: if a group is collectively blameworthy, then it does not fulfil a collective obligation.
Our account of the relation between collective obligations, group plans and individual actions brought to light that a good plan has two key characteristics. First, a good plan guarantees that if every group member fulfils her member obligation specified by the plan, then the group itself fulfils its collective obligation. Secondly, if the group members, aiming to fulfil a collective obligation, publicly adopt a good plan to coordinate their individual actions, then for any group member it holds that if she fulfils her individual obligation in the decision context that results from publicly adopting the plan, then she fulfils her member obligation specified by the plan. We thus obtain a second implication (which holds for both coordination games and cooperation games): given that the group members, aiming to fulfil a collective obligation, publicly adopt a good plan to coordinate their individual actions, it holds that their failure to fulfil the collective obligation logically implies that at least one of them failed to fulfil her member obligation specified by the plan, which in turn entails that at least one group member failed to fulfil her individual obligation in the changed decision context.
Combining the two implications, we conclude: given that the group members, aiming to fulfil a collective obligation, publicly adopt a good plan to coordinate their actions, it holds that the collective blameworthiness of the group logically implies that at least one of the group members failed to act according to plan, which in turn entails that at least one group member failed to fulfil her individual obligation in changed decision context.Footnote 24 If, however, for some reason or other, the group members fail to agree on a group plan or if they agree on a bad plan, then it is not so clear how being collectively blameworthy relates to the failure of individuals to fulfil their obligations. The study of these cases must be left to another occasion.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge financial support from the ERC-2013-CoG project REINS, no. 616512. A first version of this paper was written during a research stay at the Higher School of Economics in Moscow. Support from the Basic Research Program of the National Research University Higher School of Economics is gratefully acknowledged. We thank Michael Bratman, Jan Broersen, Sjur Dyrkolbotn, Paul Harrenstein, Frank Hindriks, Stefan Heßbrüggen-Walter, Jesse Mulder, Teddy Seidenfeld, Peter Timmerman, the two reviewers of this journal, and the audiences who attended our presentations in Bayreuth, Dublin, Groningen, Helsinki, Moscow, Tilburg, Utrecht and Venice for their questions, comments and suggestions.
APPENDIX
Coordination Games: Proofs
Lemma 1 (Horty Reference Horty2001: 74)
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
be a non-empty group of agents. Then
$$\begin{equation*}
\textit{Optimal}_S(\mathcal {G})\ne \emptyset.
\end{equation*}$$
Proof. Assume that
$\textit{Optimal}_S(\mathcal {G})=\emptyset$
. By definition of S, it holds that
$A^{}_\mathcal {G}$
is finite and non-empty. Then for all
$a^{\prime }_\mathcal {G}\in A^{}_\mathcal {G}$
there is an
$a^{}_\mathcal {G}\in A^{}_\mathcal {G}$
such that
$a^{}_\mathcal {G}\succ _S a^{\prime }_\mathcal {G}$
. Because
$A^{}_\mathcal {G}$
is finite, there must be a cycle
$a^n_\mathcal {G}\succ ^{}_S a^{n-1}_\mathcal {G}\succ ^{}_S\ldots \succ ^{}_S a^2_\mathcal {G}\succ ^{}_S a^1_\mathcal {G}=a^n_\mathcal {G}$
with all members
$a^k_\mathcal {G}$
in
$A^{}_\mathcal {G}$
. Because ≻
S
is transitive, it holds that
$a^n_\mathcal {G}\succ ^{}_S a^n_\mathcal {G}$
, that is,
$a^n_\mathcal {G}\succeq ^{}_S a^n_\mathcal {G}$
and
$a^n_\mathcal {G}\not\succeq ^{}_S a^n_\mathcal {G}$
. Contradiction. Therefore,
$\textit{Optimal}_S(\mathcal {G})\ne \emptyset$
. □
Lemma 2 (Kooi and Tamminga Reference Kooi and Tamminga2008: 9)
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {F}\subseteq \mathcal {G}\subseteq N$
. Let
$a^{}_\mathcal {F},a^{\prime }_\mathcal {F}\in A^{}_\mathcal {F}$
and let
$a^{\prime \prime }_{\mathcal {G}-\mathcal {F}}\in A^{}_{\mathcal {G}-\mathcal {F}}$
. Then
$$\begin{equation*}
{\it If}\ a^{}_\mathcal {F}\succeq _S a^{\prime }_\mathcal {F},\ \hbox{then}\ (a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\succeq _S (a^{\prime }_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}}).
\end{equation*}$$
Proof. Assume
$a^{}_\mathcal {F}\succeq _S a^{\prime }_\mathcal {F}$
. Let
$a^{\prime \prime }_{\mathcal {G}-\mathcal {F}}\in A^{}_{\mathcal {G}-\mathcal {F}}$
. Suppose
$a^{\prime \prime \prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
. Then
$(a^{\prime \prime }_{\mathcal {G}-\mathcal {F}},a^{\prime \prime \prime }_{-\mathcal {G}})\in A_{-\mathcal {F}}$
. Hence, by our assumption it must be that
$d(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}},a^{\prime \prime \prime }_{-\mathcal {G}})\ge d(a^{\prime }_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}},a^{\prime \prime \prime }_{-\mathcal {G}})$
. Therefore, for all
$a^{\prime \prime \prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$d(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}},a^{\prime \prime \prime }_{-\mathcal {G}})\ge d(a^{\prime }_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}},a^{\prime \prime \prime }_{-\mathcal {G}})$
. Hence,
$(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\succeq _S (a^{\prime }_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})$
. □
Lemma 3
Let S = ⟨N, (Ai
), d⟩ be a non-flat coordination game. Let
$\mathcal {G}\subseteq N$
. Then
If
$a^{}_\mathcal {G}\in \textit{Optimal}_S(\mathcal {G})$
, then there is an
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
such that
$d(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=1$
.
Proof. Suppose that
$a^{}_\mathcal {G}\in \textit{Optimal}_S(\mathcal {G})$
. Suppose that for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$d(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=0$
. Because S is non-flat, there is an a* ∈ A such that d(a*) = 1. Consider
$a^*_\mathcal {G}$
. It holds that
$a^*_\mathcal {G}\succ _S a^{}_\mathcal {G}$
, that is (1)
$a^*_\mathcal {G}\succeq _S a^{}_\mathcal {G}$
and (2)
$a^{}_\mathcal {G}\not\succeq _S a^*_\mathcal {G}$
. We have (1), because for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$d(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=0$
. We have (2), because
$d(a^{}_\mathcal {G},a^*_{-\mathcal {G}})=0$
and
$d(a^*_\mathcal {G},a^*_{-\mathcal {G}})=d(a^*)=1$
. Hence,
$a^{}_\mathcal {G}\not\in \textit{Optimal}_S(\mathcal {G})$
. Contradiction. □
Observation 1
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Let
$a^{}_\mathcal {G},a^*_\mathcal {G}\in P^{}_\mathcal {G}$
. Then
$$\begin{equation*}
a^{}_\mathcal {G}\succeq _S a^*_\mathcal {G}\quad \hbox{iff} \quad a^{}_\mathcal {G}\succeq _{S\uparrow P_\mathcal {G}}a^*_\mathcal {G}.
\end{equation*}$$
Proof. It is given that
$a^{}_\mathcal {G},a^*_\mathcal {G}\in P^{}_\mathcal {G}$
. By construction of
$S\uparrow P^{}_\mathcal {G}$
, for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$d(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=d^\uparrow (a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})$
and
$d(a^*_\mathcal {G},a^{\prime }_{-\mathcal {G}})=d^\uparrow (a^*_\mathcal {G},a^{\prime }_{-\mathcal {G}})$
. Then the following four statements are equivalent: (1)
$a^{}_\mathcal {G}\succeq _S a^*_\mathcal {G}$
; (2) for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$d(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})\ge d(a^*_\mathcal {G},a^{\prime }_{-\mathcal {G}})$
; (3) for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$d^\uparrow (a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})\ge d^\uparrow (a^*_\mathcal {G},a^{\prime }_{-\mathcal {G}})$
; and (4)
$a^{}_\mathcal {G}\succeq _{S\uparrow P_\mathcal {G}} a^*_\mathcal {G}$
. □
Lemma 4
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}$
be optimal. Then
If S is non-flat, then
$S\uparrow {P^{}_\mathcal {G}}$
is non-flat.
Proof. Suppose that S is non-flat. Because
$P^{}_\mathcal {G}$
is optimal, there is an
$a^{}_\mathcal {G}\in P^{}_\mathcal {G}$
such that
$a^{}_\mathcal {G}\in \textit{Optimal}_S(\mathcal {G})$
. By Lemma 3 there is an
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
such that
$d(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=1$
. By the construction of
$S\uparrow P^{}_\mathcal {G}$
, it must be that
$d^\uparrow (a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=1$
. Therefore,
$S\uparrow P^{}_\mathcal {G}$
is non-flat. □
Observation 2
Let S = ⟨N, (Ai
), d⟩ be a non-flat coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
be optimal. Then
$$\begin{equation*}
\textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})=P^{}_\mathcal {G}.
\end{equation*}$$
Proof. (⊆) Suppose that
$a^{}_\mathcal {G}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})$
. By Lemma 4,
$S\uparrow P^{}_\mathcal {G}$
is non-flat. By Lemma 3, it must be that there is an
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
such that
$d^\uparrow (a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=1$
. By construction of
$S\uparrow P^{}_\mathcal {G}$
, it must be that
$a^{}_\mathcal {G}\in P^{}_\mathcal {G}$
.
(⊇) Suppose that
$a^{}_\mathcal {G}\in P^{}_\mathcal {G}$
. It is given that
$a^{}_\mathcal {G}\in \textit{Optimal}_S(\mathcal {G})$
and that S is non-flat. Suppose that
$a^{}_\mathcal {G}\not\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})$
. Then there is an
$a^*_\mathcal {G}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})$
such that
$a^*_\mathcal {G}\succ _{S\uparrow P_\mathcal {G}}a^{}_\mathcal {G}$
. By the first part of this proof,
$a^*_\mathcal {G}\in P^{}_\mathcal {G}$
. By Observation 1, it must be that
$a^*_\mathcal {G}\succ _S a^{}_\mathcal {G}$
. Hence,
$a^{}_\mathcal {G}\not\in \textit{Optimal}_S(\mathcal {G})$
. Contradiction. Therefore,
$a^{}_\mathcal {G}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})$
. □
Observation 3
Let S = ⟨N, (Ai
), d⟩ be a coordination game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Then
$P^{}_\mathcal {G}$
is interchangeable if and only if for all
$a^{}_\mathcal {G},a^{\prime }_\mathcal {G}\in P^{}_\mathcal {G}$
and all
$\mathcal {F}\subseteq \mathcal {G}$
it holds that
$(a^{}_\mathcal {F},a^{\prime }_{\mathcal {G}-\mathcal {F}})\in P^{}_\mathcal {G}$
.
Proof. By straightforward induction on the number of members of
$\mathcal {F}$
. □
Theorem 1
Let S = ⟨N, (Ai
), d⟩ be a non-flat coordination game. Let
$\mathcal {F}\subseteq \mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
be optimal and interchangeable. Then
$$\begin{equation*}
\textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {F})=\lbrace a^{}_\mathcal {F}:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace.
\end{equation*}$$
Proof. (⊆) Suppose that
$a{}_\mathcal {F}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {F})$
. By Lemma 3, there is an
$a^{\prime }_{-\mathcal {F}}\in A^{}_{-\mathcal {F}}$
such that
$d^\uparrow (a^{}_\mathcal {F},a^{\prime }_{-\mathcal {F}})=1$
. By the construction of
$S\uparrow P^{}_\mathcal {G}$
, it must be that
$(a^{}_\mathcal {F},a^{\prime }_{\mathcal {G}-\mathcal {F}})\in P^{}_\mathcal {G}$
. Therefore,
$a{}_\mathcal {F}\in \lbrace a^{}_\mathcal {F}:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace$
.
(⊇) Suppose that
$a{}_\mathcal {F}\in \lbrace a^{}_\mathcal {F}:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace$
. Then there is an
$a^{\prime }_{\mathcal {G}-\mathcal {F}}\in A^{}_{\mathcal {G}-\mathcal {F}}$
such that
$(a^{}_\mathcal {F},a^{\prime }_{\mathcal {G}-\mathcal {F}})\in P^{}_\mathcal {G}$
. Suppose that
$a^{}_\mathcal {F}\not\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {F})$
. Then there is an
$a^*_\mathcal {F}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {F})$
such that
$a^*_\mathcal {F}\succ _{S\uparrow P_\mathcal {G}}a^{}_\mathcal {F}$
. Then there must be an
$a^{**}_{-\mathcal {F}}\in A^{}_{-\mathcal {F}}$
such that
$d^\uparrow (a^*_\mathcal {F},a^{**}_{-\mathcal {F}})>d^\uparrow (a^{}_\mathcal {F},a^{**}_{-\mathcal {F}})$
. Let
$a^{\prime \prime }=(a^*_\mathcal {F},a^{**}_{-\mathcal {F}})$
. Then d
↑(a′′) = 1. By construction of
$S\uparrow P^{}_\mathcal {G}$
, it must be that
$a^{\prime \prime }_\mathcal {G}=(a^{\prime \prime }_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})=(a^*_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\in P^{}_\mathcal {G}$
. By Observation 3, it must be that
$(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\in P^{}_\mathcal {G}$
. Because
$a^*_\mathcal {F}\succeq _{S\uparrow P_\mathcal {G}}a^{}_\mathcal {F}$
and Lemma 2, it must be that
$(a^*_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\succeq _{S\uparrow P_\mathcal {G}}(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})$
. Because it holds that
$d^\uparrow (a^*_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}},a^{\prime \prime }_{-\mathcal {G}})=d^\uparrow (a^*_\mathcal {F},a^{**}_{-\mathcal {F}})=1$
and
$d^\uparrow (a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}},a^{\prime \prime }_{-\mathcal {G}})=d^\uparrow (a^{}_\mathcal {F},a^{**}_{-\mathcal {F}})=0$
, we have
$(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\not\succeq _{S\uparrow P_\mathcal {G}}(a^*_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})$
. Then it must be that
$(a^*_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\succ _{S\uparrow P_\mathcal {G}}(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})$
. By Observation 1, it must be that
$(a^*_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\succ _S(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})$
. Then
$(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\not\in \textit{Optimal}_S(\mathcal {G})$
which contradicts the fact that
$(a^{}_\mathcal {F},a^{\prime \prime }_{\mathcal {G}-\mathcal {F}})\in P^{}_\mathcal {G}$
. Therefore,
$a^{}_\mathcal {F}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {F})$
. □
Cooperation Games: Proofs
Lemma 5
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a non-
$\mathcal {G}$
-flat cooperation game. Let
$\mathcal {G}\subseteq N$
. Then
If
$a^{}_\mathcal {G}\in \textit{Optimal}_S(\mathcal {G})$
, then there is an
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
such that
$u^{}_\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})>0$
.
Proof. Suppose that
$a^{}_\mathcal {G}\in \textit{Optimal}_S(\mathcal {G})$
. Suppose that for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$u^{}_\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=0$
. Because S is non-
$\mathcal {G}$
-flat, there is an a* ∈ A such that
$u^{}_\mathcal {G}(a^*)>0$
. Consider
$a^*_\mathcal {G}$
. It holds that
$a^*_\mathcal {G}\succ _S a^{}_\mathcal {G}$
, that is (1)
$a^*_\mathcal {G}\succeq _S a^{}_\mathcal {G}$
and (2)
$a^{}_\mathcal {G}\not\succeq _S a^*_\mathcal {G}$
. We have (1), because for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$u^{}_\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=0$
. We have (2), because
$u^{}_\mathcal {G}(a^{}_\mathcal {G},a^*_{-\mathcal {G}})=0$
and
$u^{}_\mathcal {G}(a^*_\mathcal {G},a^*_{-\mathcal {G}})=u^{}_\mathcal {G}(a^*)>0$
. Hence,
$a^{}_\mathcal {G}\not\in \textit{Optimal}_S(\mathcal {G})$
. Contradiction. □
Observation 4
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Let
$a^{}_\mathcal {G},a^*_\mathcal {G}\in P^{}_\mathcal {G}$
. Then
$$\begin{equation*}
a^{}_\mathcal {G}\succeq _S a^*_\mathcal {G}\quad \hbox{iff} \quad a^{}_\mathcal {G}\succeq _{S\uparrow P_\mathcal {G}}a^*_\mathcal {G}.
\end{equation*}$$
Proof. It is given that
$a^{}_\mathcal {G},a^*_\mathcal {G}\in P^{}_\mathcal {G}$
. By construction of
$S\uparrow P^{}_\mathcal {G}$
, for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$u^{}_\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})=u^\uparrow _\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})$
and
$u^{}_\mathcal {G}(a^*_\mathcal {G},a^{\prime }_{-\mathcal {G}})=u^\uparrow _\mathcal {G}(a^*_\mathcal {G},a^{\prime }_{-\mathcal {G}})$
. Then the following four statements are equivalent: (1)
$a^{}_\mathcal {G}\succeq _S a^*_\mathcal {G}$
; (2) for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$u^{}_\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})\ge u^{}_\mathcal {G}(a^*_\mathcal {G},a^{\prime }_{-\mathcal {G}})$
; (3) for every
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
it holds that
$u^\uparrow _\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})\ge u^\uparrow _\mathcal {G}(a^*_\mathcal {G},a^{\prime }_{-\mathcal {G}})$
; and (4)
$a^{}_\mathcal {G}\succeq _{S\uparrow P_\mathcal {G}} a^*_\mathcal {G}$
. □
Lemma 6
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A{}_\mathcal {G}$
be
$\mathcal {G}$
-optimal. Then
If S is non-
$\mathcal {G}$
-flat, then
$S\uparrow {P^{}_\mathcal {G}}$
is non-
$\mathcal {G}$
-flat.
Proof. Suppose that S is non-
$\mathcal {G}$
-flat. Because
$P^{}_\mathcal {G}$
is
$\mathcal {G}$
-optimal, there is an
$a^{}_\mathcal {G}\in P^{}_\mathcal {G}$
such that
$a^{}_\mathcal {G}\in \textit{Optimal}_S(\mathcal {G})$
. By Lemma 5, there is an
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
such that
$u^{}_\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})>0$
. By the construction of
$S\uparrow P^{}_\mathcal {G}$
, it must be that
$u^\uparrow _\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})>0$
. Therefore,
$S\uparrow P^{}_\mathcal {G}$
is non-
$\mathcal {G}$
-flat. □
Observation 5
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a non-
$\mathcal {G}$
-flat cooperation game. Let
$\mathcal {G}\subseteq N$
and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
be
$\mathcal {G}$
-optimal. Then
$$\begin{equation*}
\textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})=P^{}_\mathcal {G}.
\end{equation*}$$
Proof. (⊆) Suppose that
$a^{}_\mathcal {G}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})$
. By Lemma 6,
$S\uparrow P^{}_\mathcal {G}$
is non-
$\mathcal {G}$
-flat. By Lemma 5, there is an
$a^{\prime }_{-\mathcal {G}}\in A^{}_{-\mathcal {G}}$
such that
$u^\uparrow _\mathcal {G}(a^{}_\mathcal {G},a^{\prime }_{-\mathcal {G}})>0$
. By construction of
$S\uparrow P^{}_\mathcal {G}$
, it must be that
$a^{}_\mathcal {G}\in P^{}_\mathcal {G}$
.
(⊇) Suppose that
$a^{}_\mathcal {G}\in P^{}_\mathcal {G}$
. It is given that
$a^{}_\mathcal {G}\in \textit{Optimal}_S(\mathcal {G})$
and that S is non-
$\mathcal {G}$
-flat. Suppose that
$a^{}_\mathcal {G}\not\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})$
. Then there is an
$a^*_\mathcal {G}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})$
such that
$a^*_\mathcal {G}\succ _{S\uparrow P_\mathcal {G}}a^{}_\mathcal {G}$
. By the first part of this proof,
$a^*_\mathcal {G}\in P^{}_\mathcal {G}$
. By Observation 4, it must be that
$a^*_\mathcal {G}\succ _S a^{}_\mathcal {G}$
. Hence,
$a^{}_\mathcal {G}\not\in \textit{Optimal}_S(\mathcal {G})$
. Contradiction. Therefore,
$a^{}_\mathcal {G}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {G})$
. □
Observation 6
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a cooperation game. Let
$\mathcal {G}\subseteq N$
and let
$P{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
. Then
If S is zero-preserving, then
$S\uparrow P^{}_\mathcal {G}$
is zero-preserving.
Proof. Suppose that S is zero-preserving. Suppose that
$\mathcal {F}^{}_1\subseteq \mathcal {F}^{}_2\subseteq N$
are non-empty and suppose that a ∈ A. There are two cases: (1)
$a^{}_\mathcal {G}\in P^{}_\mathcal {G}$
and (2)
$a^{}_\mathcal {G}\not\in P^{}_\mathcal {G}$
. If we have (1), then by construction of
$S\uparrow P^{}_\mathcal {G}$
it holds that
$u^\uparrow _{\mathcal {F}^{}_1}(a)=u^{}_{\mathcal {F}^{}_1}(a)$
and
$u^\uparrow _{\mathcal {F}^{}_2}(a)=u^{}_{\mathcal {F}^{}_2}(a)$
. It is given that if
$u^{}_{\mathcal {F}^{}_1}(a)=0$
, then
$u^{}_{\mathcal {F}^{}_2}(a)=0$
. Hence, if
$u^\uparrow _{\mathcal {F}^{}_1}(a)=0$
, then
$u^\uparrow _{\mathcal {F}^{}_2}(a)=0$
. If we have (2), then by construction of
$S\uparrow P^{}_\mathcal {G}$
it holds that
$u^\uparrow _{\mathcal {F}^{}_1}(a)=0$
and
$u^\uparrow _{\mathcal {F}^{}_2}(a)=0$
. Hence, if
$u^\uparrow _{\mathcal {F}^{}_1}(a)=0$
, then
$u^\uparrow _{\mathcal {F}^{}_2}(a)=0$
. Therefore,
$S\uparrow P^{}_\mathcal {G}$
is zero-preserving. □
Lemma 7
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a zero-preserving cooperation game. Let
$\mathcal {F}^{}_1\subseteq \mathcal {F}^{}_2\subseteq N$
be non-empty. Then
If S is
$\mathcal {F}^{}_1$
-flat, then S is
$\mathcal {F}^{}_2$
-flat.
Proof. Suppose that S is
$\mathcal {F}^{}_1$
-flat. Then for every a ∈ A it holds that
$u^{}_{\mathcal {F}^{}_1}(a)=0$
. Because S is zero-preserving, for every a ∈ A it holds that
$u^{}_{\mathcal {F}^{}_2}(a)=0$
. Therefore, S is
$\mathcal {F}^{}_2$
-flat. □
Observation 7
Let
$S=\langle N,(A_i),(u_\mathcal {H})\rangle$
be a zero-preserving non-
$\mathcal {G}$
-flat cooperation game. Let
$\mathcal {F}\subseteq \mathcal {G}\subseteq N$
be non-empty and let
$P^{}_\mathcal {G}\subseteq A^{}_\mathcal {G}$
be
$\mathcal {G}$
-optimal. Then
$$\begin{equation*}
\textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {F})\subseteq \lbrace a^{}_\mathcal {F}:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace.
\end{equation*}$$
Proof. Suppose that
$a{}_\mathcal {F}\in \textit{Optimal}_{S\uparrow P_\mathcal {G}}(\mathcal {F})$
. By Lemma 7, S is non-
$\mathcal {F}$
-flat. By Lemma 5, there is an
$a^{\prime }_{-\mathcal {F}}\in A^{}_{-\mathcal {F}}$
such that
$u^\uparrow _\mathcal {F}(a^{}_\mathcal {F},a^{\prime }_{-\mathcal {F}})>0$
. By the construction of
$S\uparrow P^{}_\mathcal {G}$
, it must be that
$(a^{}_\mathcal {F},a^{\prime }_{\mathcal {G}-\mathcal {F}})\in P^{}_\mathcal {G}$
. Therefore,
$a{}_\mathcal {F}\in \lbrace a^{}_\mathcal {F}:a^{}_\mathcal {G}\in P^{}_\mathcal {G}\rbrace$
. □
