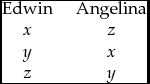In the Autumn semester of 1968–69, Kenneth Arrow, John Rawls and Amartya Sen conducted a legendary seminar at Harvard University. One of the six registered students was Allan Gibbard, who was enrolled in Harvard’s Ph.D. programme in Philosophy. Gibbard wrote a phenomenal paper for this seminar that was awarded the Goldsmith Prize for the best term paper submitted to the Economics Department that year.Footnote 1 In spite of never having been published, this paper has had a significant impact on social choice theory for the oligarchy theorem that first appeared in it. In addition, this paper includes Gibbard’s first discussion of rights in social choice, a topic he returned to in Gibbard (Reference Gibbard1974). Gibbard’s seminar paper is being published in this issue of Economics and Philosophy (see Gibbard, Reference Gibbard2014b) so as to make it more widely available to the scholarly community.
In this paper, Gibbard introduces the oligarchy theorem that he obtained by relaxing the requirement in Arrow’s (Reference Arrow1963, Reference Arrow, Laslett and Runciman1967) Impossibility Theorem that social preferences be transitive to quasitransitivity (i.e. only the strict part of the social preference must be transitive).Footnote 2 Futhermore, Gibbard provides an insightful analysis of the lessons to be learned from Arrow’s Theorem and a discussion of how Arrow’s Unrestricted Domain, Collective Rationality and Independence conditions interact. In doing this, he was one of the first to consider what came to be known as non-binary social choice.
Gibbard frames his discussion of Arrow’s Theorem in terms of rights. Moreover, his paper includes an example in which he argues that unacceptable conclusions follow from the combination of quasitransitivity, the Pareto principle, and a generally accepted right, even without Arrow’s Independence condition. Below I consider this example in some detail and explain how it differs from the kind of conflict between Pareto and rights assignments identified by Sen (Reference Sen1970b). Although the idea of there being a private domain in which an individual is decisive can be attributed to Mill (Reference Mill1859), Gibbard and Sen were the first to use this idea in social choice theory.Footnote 3
Gibbard recalls being intrigued by Arrow’s Social Choice and Individual Values when he came across it in the Harvard Philosophy Department’s Robbins Library. When Gibbard heard that Arrow was moving to Harvard and would be organizing a joint seminar with Rawls and a visiting economist from the Delhi School of Economics whom he had not heard of before, he asked Rawls about the seminar and was told that it was only for Economics graduate students. Rawls relented and let Gibbard enrol when he became insistent. Gibbard had majored in Mathematics at Swarthmore College and was already familar with the set theory and symbolic logic employed by Arrow and Sen.
As Arrow (Reference Arrow1963, ch. VIII) has documented, much of the early response to the first edition of Social Choice and Individual Values in 1951 was that he had not formulated the problem of social choice in an appropriate way. In large part due to Arrow’s powerful arguments defending his approach, attention instead turned in the late 1960s to investigating whether Arrow’s impossibility result could be averted by weakening or dropping some of his conditions. Sen played a major role in initiating this line of research. Moreover, it was Sen’s presentation to the Harvard seminar of his then unpublished result that Arrow’s conditions are compatible if the requirement that social preferences be transitive is weakened to quasitransitivity while still requiring these preferences to be connected (i.e. complete) that motivated Gibbard to work on this issue as he did not believe that this relaxation could allow for any appealing way of making collective decisions. Sen’s own example (see Sen Reference Sen1969), the Pareto extension rule, regards Pareto non-comparable alternatives as being indifferent; a strict preference requires unanimity.
In the choice-theoretic formulation of Arrow’s problem used in Arrow (Reference Arrow, Laslett and Runciman1967) and adopted by Gibbard and Sen, the objective is to choose a non-empty subset f(S, R 1, . . ., Rn) of the set of available alternatives S for each n-tuple of individual preference orderings R 1, . . ., Rn of the set of all alternatives V. Arrow’s Collective Rationality condition requires that for each n-tuple of individual preferences R 1, . . ., Rn, there is an associated connected and transitive social preference R = h(R 1, . . ., Rn) of V that is used to determine the social choice from each set S of available alternatives by maximizing R on S.
The formal theorem presented in Gibbard’s paper characterizes the social choice functions that satisfy Arrow’s conditions with social transitivity weakened to quasitransitivity. Specifically, Gibbard shows that there must exist a set of individuals A such that for any alternatives x and y, (i) if everybody in A agrees that x is strictly preferred to y, then this is the social preference and (ii) if anybody in A weakly prefers x to y, then society cannot strictly prefer y to x. The second condition gives each member of A a veto, so there is social indifference if two of them strictly disagree on how to rank two alternatives. Gibbard calls this group of individuals a liberum veto oligarchy, although it is now simply known as an oligarchy. Gibbard regards an oligarchy as being a terrible way of making collective decisions – decision-making is very undemocratic when it is small, whereas extreme consensus is required to reach agreement when it is large. As a consequence, relaxing social transitivity to quasitransitivity does not provide a satisfactory escape from Arrow’s Theorem.
While it is the oligarchy theorem that Gibbard’s paper is known for, he recollects that his main objective was to investigate the lessons one can and cannot draw from Arrow’s Theorem. In this endeavour, Gibbard interprets Arrow’s problem as choosing just alternatives based on the non-ethical preferences of the individual members of society. It is this interpretation that led him to couch his discussion in terms of rights. The focus on rights is evident in the opening dialogue between Meletus and Socrates, whose purpose is to provide an intuitive account in the two-person case of a key step in the proof of Arrow’s Theorem. Gibbard, like Sen, formulates rights in terms of decisiveness relations of the social choice procedure. In Arrow (Reference Arrow1963) and in the chapter on Arrow’s Theorem in Sen (Reference Sen1970a), no interpretations of the decisiveness concepts are offered. Rather, there are both formal and informal definitions. Decisiveness has also been interpreted in terms of the power of groups of individuals to determine the social choice. See, for example, Austen-Smith and Banks (1999).
To show that dropping Independence from the conditions used in his oligarchy theorem does not result in satisfactory social choice procedures, Gibbard constructs a remarkable example showing how rights assignments can be problematic. In this example, there are three alternatives:
x: Edwin marries Angelina;
y: Edwin marries Beatrice;
z: Edwin and Angelina remain single.
The preferences of Edwin and Angelina are given by:
Beatrice wants whatever makes Edwin happy. Gibbard is not particularly clear if Beatrice’s preferences are to be explicitly taken into account in his argument, but if the Pareto condition is to be invoked, they need to be. So it seems that Gibbard’s statement about Beatrice wanting whatever will make Edwin happy should be taken literally to mean that Beatrice’s preferences are the same as those of Edwin. Angelina has the right to choose whether to remain single instead of marrying Edwin. That is, she is decisive for z against x. She prefers to remain single, so zPx. By Pareto, xPy. Hence, by quasitransitivity, zPy.
Gibbard regards this conclusion as implying that Edwin has no right to marry Beatrice. But this is true without any argument. Whereas a single individual has the right not to marry someone, nobody has the right to marry anyone. The right to marry is a group right. Beatrice and Edwin would have the right to marry each other if the two of them are decisive for y against z. They both prefer to marry each other than remain single, so what Gibbard’s argument shows is that Beatrice and Edwin do not have the right to marry each other, not that Edwin does not have the right to marry Beatrice. So, for Gibbard to regard his example as resulting in an unacceptable conclusion, he must appeal to group rights. In contrast, in his impossibility of a Paretian liberal theorem, Sen (Reference Sen1970b) only appeals to the rights of single individuals.Footnote 4 Interestingly, Gibbard raises the question of whether his formulation of a right is correct, and briefly considers the implications of waiving a right, which is an issue that he considers at some length in Gibbard (Reference Gibbard1974).
In his paper, Gibbard also analyses other relaxations of the Arrow conditions. For example, Gibbard considers weakening Collective Rationality to what he calls Fixity, the requirement that the choices out of different sets of available alternatives be generated by maximizing a fixed connected social preference (which is equivalent to requiring social preferences to be connected and acyclic). Gibbard shows that the implications of Independence and Fixity are unacceptable even if the individual preferences are restricted to those that might arise in practice. He goes on to argue that Arrow’s information argument for Independence is plausible.Footnote 5 But if Independence is maintained, then Fixity must be abandoned.
Gibbard also provides a direct argument against Fixity. Suppose, for example, that the set of available alternatives expands from S to T for fixed individual preferences. The individual preferences for the alternatives in T may tell us something about whether the preferences for the alternatives in S are malicious or about their preference intensities. But if that is the case, then the social ranking of the alternatives in S may be revised so as to take account of the new information provided by the preferences for the alternatives in T, thereby violating Fixity. Without Fixity, we enter the world of non-binary social choice theory in which it is no longer required that social choices be generated by a social preference.Footnote 6
While Gibbard’s term paper was not intended to be published, he did want to prepare a paper based on his oligarchy theorem for publication. A few months after the term paper was completed, Frederic Schick published a paper in Philosophy of Science (see Schick Reference Schick1969) in which he argues that Arrow’s Impossibility Theorem is not troubling because, except in special circumstances, the transitivity of social indifference is ‘untenable’. That gave Gibbard a new way to motivate his theorem. Sometime in 1969–70 as an Assistant Professor of Philosophy at the University of Chicago, he rewrote his theorem as a response to Schick, recasting his presentation using the formalism of symbolic logic (see Gibbard Reference Gibbard2014a). However, Guha (Reference Guha1972) and Mas-Colell and Sonnenschein (1972) had independently established essentially the same result, and so when Gibbard received their papers from them, he abandoned his intention of publishing the oligarchy theorem himself.Footnote 7 Nevertheless, Gibbard’s version of this result became well-known and it provided a foundation for subsequent research that relaxed Arrow’s Collective Rationality condition (see Austen-Smith and Banks Reference Austen-Smith and Banks1999). However, except for the re-emergence of the marriage example in Gibbard (Reference Gibbard1974), the rest of Gibbard’s paper has largely disappeared from sight until now. Hopefully, its publication in Economics and Philosophy will make it more widely known how prescient that student term paper turned out to be.