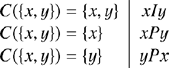The range of possible preference relations in the traditional framework for dyadic preference relations, according to which preferences are analysed in terms of pairwise choices, is exhausted by preference (in either direction) and indifference. Hence, there is no conceptual room in the framework for preference relations that hold when neither preference nor indifference do. In order to account for non-traditional preference relations, such as incommensurateness and instability, this paper develops a new, richer framework for preference relations. This new framework models traditional preference relations as well as non-traditional ones in terms of swaps, which are conceived of as transfers from one alternative state to another.
1. THE TRADITIONAL FRAMEWORK
A standard way of bringing out the relation between preferences and behaviour is through dispositions for choice.Footnote 1
Choice dispositions
C(A) ⇔def the set of options in A that the agent is disposed to choose from A.
The traditional framework defines preference and indifference between two objects x and y in terms what choices an agent is disposed to choose from the choice set {x, y}. Table 1 shows a taxonomy of the traditional trichotomy of preference relations.Footnote 2
Table 1. Taxonomy of preference relations in terms of pairwise choice.
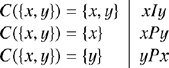
Although common, the dispositional account of preferences is not without critics. For example, James M. Joyce argues that the dispositional account makes it hard to make sense of rationalizing explanations of an agent's choice behaviour.Footnote 3 If a preference for x over y just means that one is disposed to choose x over y, then a preference for x over y would be circular as a rationale for a disposition to choose x over y. According to Joyce the behavioural interpretation needs to be abandoned for an analysis based on desires.
Desires
C(A) ⇔def the set of options in A that are at least as desired as every option in A.
This alternative definition of the choice function C, however, yields a structurally very similar account since in terms of C we still define preference relations as in Table 1. But, as seen in Table 1, there is no additional possible preference relation in the pairwise choice framework other than preference and indifference.
2. THE SWAP FRAMEWORK
To make room for more preference relations than preference and indifference we shall now develop a new richer framework. Rather than just dispositions or desires for pairwise choice between the alternatives, this framework is based on dispositions or desires for swaps between the alternatives. A swap is not merely a choice of an alternative, it is a transfer from an alternative state to an alternative state.
Swap
![]() swap alternative x for alternative y.
swap alternative x for alternative y.
Keep
![]() .
.
Rather than just C({x, y}), this approach will use dispositions or desires over two separate sets of swaps: ![]() and
and ![]() . Note that C now takes a set of swaps and keeps of alternatives as argument rather than a set of the compared alternatives.
. Note that C now takes a set of swaps and keeps of alternatives as argument rather than a set of the compared alternatives.
Consider two hypothetical choice situations, one in which you can keep a or swap a for b, and one in which you can keep b or swap b for a. Given that you prefer b to a, how would you swap? Clearly you would not swap b for a when you can keep b, which you prefer to a, and you would not keep a if you could swap to the preferred alternative b. What if you instead were indifferent between a and b? Since you are indifferent between a and b it seems obvious that you might both keep a or b or swap a or b for the other alternative.
We can now define preference and indifference in terms of swaps:
Even though the swap approach should be compatible with both readings of the C function, it fits better with the desire-based reading. One reason for this is the existence of pairs between which swaps are impossible or only possible in one direction. Although one could desire a hypothetical albeit impossible swap – for example, a desire at age 30 to be 25 once more – it seems less plausible that one could be disposed to make an impossible swap.
The possible combinations of swaps between two alternatives are illustrated in Table 2. The rows denote the swaps in the case in which you start with x and are confronted with a choice of whether to keep x or to swap to y. The columns denote the swaps in the case in which you start with y and are confronted with a choice of whether to keep y or to swap to x.
Table 2. Possible combinations of swaps.

As can be seen in Table 2, the cases where one of xPy, xIy, and yPx holds do not exhaust the logical space of swaps between the alternatives x and y. We are therefore able to express more relations between alternatives than those expressible in terms of preference and indifference, which is an advantage of the swap framework. This makes the framework based on swaps richer than the traditional one based on pairwise choice.
One of the relations between two alternatives x and y that is not expressible in terms of preference and indifference is the relation that holds when there is a desire to keep any alternative over a swap to the other. We will call this symmetric relation incommensurateness:
The idea is that if x and y are incommensurate you would not swap one for the other but you might keep either. For an example of incommensurateness, consider the following alternatives:Footnote 4
a = $1000.
b = friendship.
If any one of the relations aPb, bPa, or aIb holds, you might swap a for b or b for a. But this does not seem to be the case. It seems that you would keep both $1000 and friendship, but that you would neither swap friendship for $1000 nor swap $1000 for friendship. The intuition is that you do not buy or sell friendship. A more fitting interpretation than preference and indifference of the relation between a and b is incommensurateness. With a#b you might keep either a or b but you would not swap a and b.
Furthermore, this new preference relation makes possible a new interpretation of the endowment effect.Footnote 5 Examples of this effect are subjects who have been shown to be willing to pay up to $2 for a coffee cup while willing to accept no less than $5 for the cup.Footnote 6 Given the traditional framework it seems that a subject's preference between the cup and $4 depends on whether the subject has the cup, which seems strange. However, with the swap framework the subject may consistently hold that the cup and $4 are incommensurate. Thus, under this interpretation the acquisition of the cup need not affect the subject's preferences.
Here one might object that it seems odd to say that the cup is incommensurable with money since some amounts of money are preferred over the cup and further the cup is preferred over some other amounts. However, the claim is not the general one that cups are incommensurable with money; it is just that one cup is incommensurate with $4.
Note that incommensurateness is not merely defined negatively as the absence of some other preference relations.Footnote 7 Incommensurateness is here positively characterized in terms of either dispositional behaviour or desires. It is therefore separate from incomparability, that is, the absence of any positive preference relation.
Another relation can be called semi-incommensurateness. It is defined as:
In other words if x is semi-incommensurate to y then the agent might keep x and keep y but would only swap from y to x. For an illustration of this relation consider the following alternative states:Footnote 8
c = life as single.
d = married life.
In this case it seems that some reasonable agents would, if they had d, keep d and not swap d for c. If one of the relations cPd, dPc, or cId had to hold in this case it would imply that these agents prefer d to c. This implies that they would not keep c if they had the option to swap to d, that is, they would not stay unmarried if they could get married. This rules out that they might keep c if they had c while they still might swap c for d and avoid swapping d for c. But intuitively this behaviour does not seem to be irrational.
On the new framework these agents can hold d to be semi-incommensurate to c. Given that dOc they might stay unmarried or they might get married but they would not swap from married life back to unmarried life. This could not be the case if one of cPd, dPc, or cId held.
One of the more exotic combinations of swaps in Table 2 is the following:
In other words, two alternatives are unstable if the agent would not keep either of them but would swap any one of them for the other. This symmetric relation is an attempt to capture the unstable relation between alternatives such as those in Allan Gibbard and William L. Harper's Death in Damascus example. In this example there is a man who expects to meet death in the city he will decide to stay in tomorrow:
Now suppose the man knows the following. Death works from an appointment book which states time and place; a person dies if and only if the book correctly states in what city he will be at the stated time. The book is made up weeks in advance on the basis of highly reliable predictions. An appointment on the next day has been inscribed for him. Suppose, on this basis, the man would take his being in Damascus the next day as strong evidence that his appointment with death is in Damascus, and would take his being in Aleppo the next day as strong evidence that his appointment is in Aleppo. [. . .] If [. . .] he decides to go to Aleppo, he then has strong grounds for expecting that Aleppo is where death already expects him to be, and hence it is rational for him to prefer staying in Damascus. Similarly, deciding to stay in Damascus would give him strong grounds for thinking that he ought to go to Aleppo: once he knows he will stay in Damascus, he can be almost sure that death already expects him in Damascus, and hence that if he had gone to Aleppo, death would have sought him in vain.Footnote 9
Let e denote the alternative ‘reside in Damascus’, and let f denote the alternative ‘reside in Aleppo’. What is problematic in this case if we define preference in the traditional way in terms of pairwise choice, is that if you choose e, f is preferable to e but if you choose f, e is preferable to f. This breaks a natural condition of invariance: how an alternative is judged to another does not depend on which alternative is chosen.
My proposal is that f is unstable to e. A nice feature of this relation is that f*e would hold regardless of which alternative is chosen. Alas, this will not make the agent's decision in this situation any easier, but in the present framework at least his comparison of the alternatives can be invariant of his decision.
A similar relation to instability is the following:
If x is semi-unstable to y then the agent might swap either of x and y for the other and he might keep y but he would not keep x.
For an illustration of semi-instability we change the Death in Damascus case so that the agent for some reason, never mind why, cannot die in Damascus. If the appointment with Death is in Damascus he will not die. But he still takes his being in Damascus as strong evidence that his appointment with Death is in Damascus. And if he decides to go to Aleppo, he then has strong evidence that his appointment with Death is in Aleppo.
This version differs in that the agent might stay in Damascus since an appointment with Death is harmless there. He might also go to Aleppo since the agent has strong evidence that his meeting with Death is in Damascus. But if he goes to Aleppo he still would not stay there as he then has strong evidence that his appointment with Death will be there. He might therefore go to Damascus. In this case f is semi-unstable to e. The difference from f being unstable to e is that there is one alternative which the agent might always keep or swap to. In this case the agent always might stay in Damascus or go to Damascus.
Thus, we have an interpretation of all possible combinations of swaps in Table 2. These preference relations are mapped out in the taxonomy of preference relations in terms of swaps in Table 3.
Table 3. Taxonomy of preference relations in terms of swaps.