1. INTRODUCTION
The joint investigation of nonstationarity and nonlinearity in
economics has recently assumed great significance. There has also been
increasing concern that the information revealed by the analysis of a
linear time series model may be insufficient to give definitive inference
on important economic hypotheses. In this regard attention has fallen
almost exclusively on regime-switching-type models, though there is no
established theory suggesting a unique approach for specifying econometric
models that embed various types of change in regimes.
Estimation of cointegrated models subject to (regime-switching)
nonlinear dynamics has been quite prominent. Balke and Fomby (1997) have popularized an estimation method where the
dynamics are subject to three-regime threshold cointegration, the case
where a process may follow a unit root in a middle regime while at the
same time being globally geometrically ergodic. Another popular nonlinear
scheme being applied in conjunction with cointegration is based on the
smooth transition regression (STR), following Granger and Teräsvirta
(1993). Michael, Nobay, and Peel (1997) analyze nonlinearity in the long-run purchasing
power parity (PPP) relationship by adopting a null of a unit root for real
exchange rates while taking an alternative hypothesis of nonlinear smooth
transition autoregressive (STAR) stationarity. Finally, Psaradakis, Sola,
and Spagnolo (2004) consider Markov-switching
error correction models (ECMs) in which deviations from the long-run
equilibrium follow a process that is nonstationary in one state of nature
and mean-reverting in the other. These papers argue forcefully that the
assumption of linear adjustment is likely to be too limited in various
economic situations, particularly where transaction costs and policy
interventions are present. For similar modeling approaches see Granger and
Swanson (1996), Corradi, Swanson, and White
(2000), Choi and Saikkonen (2004), and Saikkonen and Choi (2004).
With regard to statistical inference, there is a large literature
proposing tests for unit roots against threshold autoregressive (TAR)
alternatives, e.g., Enders and Granger (1998),
Caner and Hansen (2001), Bec, Guay, and Guerre
(2004), and Kapetanios and Shin (2006). In particular, Kapetanios, Shin, and Snell
(2003) develop the testing framework for a
linear unit root null against an exponential STAR alternative and show
that their proposed test is more powerful than the Dickey–Fuller
(1979) test. See also Kiliç (2003) for its bootstrap-based extension. There is also
a growing literature analyzing cointegration subject to nonlinear dynamic
adjustment, e.g., Escribano and Pfann (1998),
Escribano and Mira (2002), Bec and Rahbek (2004), Escribano (2004), and
Saikkonen (2005).
However, studies that directly specify and derive the asymptotic
properties of cointegration tests against nonlinear alternatives are still
relatively few. For example, although Gallagher and Taylor (2001) and Hansen and Seo (2002) conduct cointegration analysis with nonlinear
alternatives in mind, they all adopt linear cointegration tests to
establish the existence of cointegration and only allow nonlinearity to
enter the analysis at the estimation stage once cointegration has been
established. Although such linear tests will have power against nonlinear
alternatives, it seems far more sensible to use a test in the first stage
that is designed to have power against the alternative of interest,
namely, nonlinear dynamic adjustment.
In this paper we address this issue by deriving a cointegration test
designed to have power against alternatives where the cointegrating error
is stationary and follows STR dynamics. We model an equilibrium process
where its error correction adjustment is slower when the cointegrating
residual is close to zero and where the change in speed of this adjustment
process is assumed smooth rather than sharp (as with TAR models).
Therefore, we focus on the case in which the EC term follows a globally
stationary process under the STR alternative. In particular, our approach
is motivated by the implication of economic theory applied to asset
arbitrage under noise trading and transaction costs arising from the
bid-ask spread. Campbell and Kyle (1993) develop
a model of finite-lived traders some of whom misperceive true fundamental
asset values and show that the larger are the pricing errors in these
models, the larger is the expected degree of arbitrage and hence the
speedier is the price response to disequilibrium. Snell and Tonks (2003) show that in an adapted version of the
sequential auction model of Kyle (1985) where
informed agents who suffer liquidity costs trade with a risk neutral
market maker, the prices offered by the market maker follow an ECM with a
speed of adjustment parameter that moves smoothly in response to the
conditional variance of the disequilibrium price error. To put it more
concisely, higher disequilibrium pricing errors are associated with larger
ECM adjustment parameters and faster rates of error correction toward
equilibrium.
Using a general nonlinear exponential STR (ESTR) ECM framework and
following a pragmatic residual-based two-step procedure in the style of
Engle and Granger (1987), we propose that a null
hypothesis of no cointegration against an alternative of a globally
stationary ESTR cointegration be tested directly by examining the
significance of the parameter controlling the degree of nonlinearity in
the speed of adjustment. We develop two operational test statistics,
denoted FNEC
(tNEC) and tNEG,
respectively, and derive their asymptotic distributions. The
FNEC (tNEC) test
refers to the F-type (t-type) statistic obtained
directly from the nonlinear ESTR error correction regression, whereas the
tNEG test is the nonlinear analogue to the
Engle and Granger (EG) statistic for linear cointegration.
The small-sample performance of the suggested tests is compared to
that of the linear EG and Johansen (1995) tests
via Monte Carlo experiments. We find that our proposed nonlinear tests
have good size and superior power properties compared to the linear tests.
In particular, both the FNEC and
tNEC tests are superior to both linear or
nonlinear EG tests when the regressors are weakly exogenous in a
cointegrating regression. This supports similar findings made in linear
models by Kremers, Ericsson, and Dolado (1992),
Hansen (1995), Banerjee, Dolado, and Mestre
(1998), Arranz and Escribano (2000), and Pesaran, Shin, and Smith (2001) that the EG test loses power relative to
ECM-based cointegration tests because of the loss of potentially valuable
information from the correlation between the regressors and the underlying
disturbances.
We provide an application to investigating the presence of
cointegration of asset prices and dividends for eleven stock portfolios
(Germany, Belgium, Canada, Denmark, France, Ireland, Italy, Japan,
Netherlands, United Kingdom, and United States) allowing for nonlinear STR
adjustment to equilibrium. Interestingly, our new tests are able to reject
the null of no cointegration in majority cases, whereas the linear EG test
rejects only twice. Given the strength of evidence in favor of ESTR
cointegration we also estimate adjustment parameters under the
alternative, and we find that these estimates are well defined in all
cases. We further evaluate the impulse response functions (IRFs) of the
error correction term with respect to initial impulses of one to four
standard deviation shocks. The striking finding is that the time taken to
recover one-half of a one standard deviation shock varies between 5 and 20
years, whereas the time taken to recover one-half of larger shocks varies
between just 4 to 18 months. This implies that data periods dominated by
extreme volatility may display substantial reversion of prices toward
their NPV (net present value) relationship, although in
“calmer” times where the error in the NPV relationship takes
on smaller values, the process driving it may well look like a unit
root.
The plan of the paper is as follows. Section 2 discusses general
modeling issues and derives the nonlinear STR error correction models.
Section 3 develops the proposed test statistics and derives their
asymptotic distributions. Section 4 evaluates the small-sample performance
of the proposed tests that take account of the STR nonlinear nature of the
alternative. Section 5 presents an empirical application to price-dividend
relationships. Section 6 contains some concluding remarks. Mathematical
proofs are collected in the Appendix.
2. NONLINEAR STR ERROR CORRECTION
MODELS
We begin with the following general nonlinear vector error correction
(VEC) model for the n × 1 vector of I(1) stochastic
processes, zt:
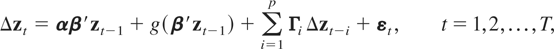
where α(n × r), β
(n × r), and Γi
(n × n) are parameter matrices with α
and β of full column rank and
is a nonlinear function. A conventional linear VEC model is obtained by
choosing
g(β′zt−1) =
0 or
g(β′zt−1) =
−αμ′ where μ is an
n × 1 vector of level parameters.
Recently, analogues of Granger's representation theorem have been
studied in the context of the nonlinear VEC model, (2.1), e.g., Escribano
and Mira (2002) and Bec and Rahbek (2004). Here we follow Saikkonen (2005) and make the following assumption.
Assumption 1. (i) The errors εt in (2.1) are
iid(0, Σ), with Σ being an
n × n positive definite matrix and
E|εt|[ell ]
< ∞ for some [ell ] > 6. (ii) The distribution of
εt in (2.1) is absolutely continuous with
respect to the Lebesgue measure and has a density that is bounded away
from zero on compact subsets of
.
(iii) The initial observations Z0 ≡
(z−p,…,z0)
are given. (iv) Let A(z) be given by
.
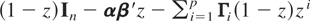
If det A(z) = 0, then |z| > 1
or z = 1, where the number of unit roots is equal to n
− r. (v) g([bull ]) is asymptotically no greater
than a linear function of xt.
Assumptions 1(i)–(iv) are standard in the cointegration
literature, whereas Assumption 1(v) is imposed to deal with nonlinearity
of the underlying model (2.1). Under Assumption 1, Saikkonen (2005, Thm. 2) proves that there exists a choice of
initial values
z−p,…,z0
such that Δzt and
β′zt−1 are strictly
stationary.
In this paper we aim to analyze at most one conditional long-run
cointegrating relationship between yt and
xt, and we focus on the conditional modeling
of the scalar variable yt given the
k-vector xt (k = n
− 1) and the past values of zt and
Z0, where we decompose zt
=
(yt,xt′)′.
For this we rewrite (2.1) as
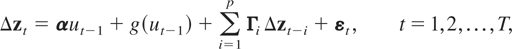
where α is an n × 1 vector of adjustment
parameters and
with βx being a k × 1
vector of cointegrating parameters.
We now make the following assumption.
Assumption 2. (i) The nonlinear function g(·) in (2.2)
follows the exponential smooth transition functional form
where we assume θ ≥ 0 for identification purposes and
c is a transition parameter. (ii) Partition α =
(ζ, αx′)′ and
φ = (γ,
φx′)′ conformably with
zt =
(yt,xt′)′.
Then, αx =
φx = 0. (iii) There is no
cointegration among the k-vector of I(1) variables,
xt. (iv) ζ < 0.
Assumptions 2(ii) and (iii) imply that the process
xt is weakly exogenous and therefore the
parameters of interest in (2.6) are variation-free from the parameters in
(2.7), e.g., Pesaran et al. (2001). Assumptions
2(i) and (iv) imply that Assumption 1(v) is satisfied but also ensure that
the underlying (nonlinear) error correction mechanism in (2.2) is globally
stationary. In practice various functional forms of g([bull ]) can
also be considered to allow for the presence of nonlinear adjustment to
the error correction mechanism, but we focus on ESTR here.
Next, partitioning εt conformably with
zt as εt =
(εyt,
εxt′)′ and its variance
matrix as
,
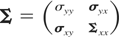
we may express εyt conditionally in terms of
εxt as
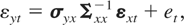
where et ∼
iid(0,σe2),
σe2 ≡ σyy
− σyx
Σxx−1σxy,
and et is uncorrelated with
εxt by construction. Substituting (2.5) and
(2.4) into (2.2), partitioning Γi =
(γyi′,
Γxi′)′, i =
1,…,p, defining φ = ζ − γ, and under
Assumption 2, we obtain the following conditional exponential smooth
transition regression error correction model (STR ECM) for
Δyt and the marginal vector
autoregression (VAR) model for Δxt:1
The exponential transition function in (2.6) is
bounded between zero and 1, i.e.,
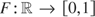
has the properties F(0) = 0;
limx→±∞ F(x) = 1,
and is symmetrically U-shaped around zero.
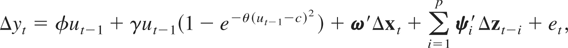
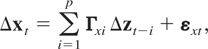
where ω ≡
Σxx−1σxy
and ψi′ ≡
γyi −
ω′Γxi, i =
1,…,p. We notice that (2.6) is a reparameterization of
(2.2) under Assumption 2, which will become more convenient for the
construction of the cointegration tests we propose in the next section,
and Assumption 2(iv) implies that φ + γ < 0. See also
Kapetanios et al. (2003).
We call (2.6) the (conditional) nonlinear STR ECM. The representation
(2.6) makes economic sense in that many economic models predict that the
underlying system tends to display a dampened behavior toward an attractor
when it is (sufficiently far) away from it but shows some instability
within the locality of that attractor. We note in passing that Assumption
1 is trivially satisfied for our final model specifications (2.6) and
(2.7). Therefore, applying Saikkonen's Theorem 2 directly to our
model, we may conclude that there exists a choice of initial values
z−p,…,z0
such that ut−1 and
Δzt are strictly stationary.2
Kapetanios et al. (2003) show that the ut(=
yt −
βx′xt)
are geometrically ergodic so long as φ + γ < 0 in the
univariate context where the cointegrating parameters
βx are assumed given.
For a growing literature on the joint analysis of cointegration and
STR models see also Gallagher and Taylor (2001),
van Dijk, Teräsvirta, and Franses (2002),
Choi and Saikkonen (2004), and Saikkonen and
Choi (2004). In practice different lag orders
for Δyt and
Δxt in (2.6) can be selected using
standard model selection criteria or significance testing procedures
without loss of generality or change in the asymptotic analysis, e.g., Ng
and Perron (1995).
3. TESTING FOR NONLINEAR COINTEGRATION UNDER
STR ECM
To fix ideas for the motivation of the tests, we follow Kapetanios et
al. (2003) and impose φ = 0 in (2.6),
implying that ut follows a unit root process
in the middle regime; see also Balke and Fomby (1997) in the context of threshold ECMs. Note that for
the operational versions of the tests we suggest later we consider both
the case φ = 0 and φ ≠ 0. It is then straightforward to show
that the test of the null of no cointegration against the alternative of
globally stationary cointegration can be based on the single parameter
θ. Hence, we set the null hypothesis of no cointegration as3
The null and alternative are expressed
alternatively as H0 : θγ = 0 and
H1 : θγ < 0. This formulation clearly
shows the lack of identification of either θ or γ when the other
is zero. It also makes it clearer why we will develop t- or
F-type tests that do not depend on the value of the unidentified
parameter.
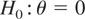
against the alternative of nonlinear ESTR cointegration of
H1 : θ > 0, where the positive value of θ
determines the stationarity properties of ut.
We note in passing that the null hypothesis implies in terms of the
preceding model that φ = 0 and θ = 0. Under the alternative
hypothesis ut follows a nonlinear but
globally stationary process as described in Section 2.
We propose a number of operational versions of the cointegration test
under the nonlinear STR ECM framework given by (2.6). To this end we
follow Engle and Granger (1987) and take a
pragmatic residual-based two-step approach. In the first stage, we obtain
the residuals,
,
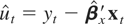
with
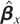
being the ordinary least squares (OLS) estimate of
βx. In the second stage and to overcome
the Davies (1987) problem that γ in (2.6) is
not identified under the null, we follow Luukkonen, Saikkonen, and
Teräsvirta (1988) and Kapetanios et al.
(2003), approximate (2.6) by a first-order
Taylor series approximation to (1 −
e−θ(ut−1−c)2),
while allowing φ ≠ 0 under the alternative hypothesis, and obtain
the following auxiliary testing regression:
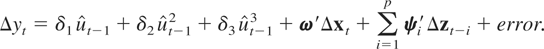
For this model, we consider an F-type test for
δ1 = δ2 = δ3 = 0 given by
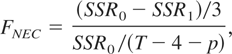
where SSR0 and SSR1 are the
sum of squared residuals obtained from the specification with and without
imposing the restrictions δ1 = δ2 =
δ3 = 0 in (3.2), respectively. It is interesting to note
that (3.2), which is called the cubic polynomial nonlinear error
correction (NEC) model, has been analyzed by Escribano (1986, 2004) and his
coauthors for the estimation of the UK money demand function although it
is important to add that these authors did not provide the formal testing
framework that we give in this paper.
There are prior theoretical justifications for restricting the switch
point, c, to be zero in many economic and financial applications
in the ESTR function, in which case we obtain the following (restricted)
auxiliary testing regression:
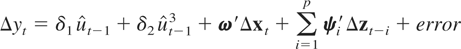
and obtain the following F-type statistic:
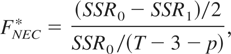
where SSR0 and SSR1 are the
sum of squared residuals obtained from the specification with and without
imposing δ1 = δ2 = 0 in (3.4),
respectively.
Finally, under the further assumption that φ = 0 (which is the
maintained assumption made in Kapetanios et al.,
2003) (3.4) is simplified to
For this model, we propose a t-type statistic for δ = 0
(no cointegration) against δ < 0 (ESTR cointegration), which is
given by
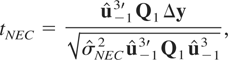
where
,
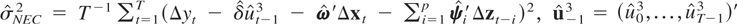
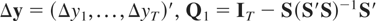
is the T × T idempotent matrix, S =
(ΔX,ΔZ−1,…,ΔZ−p)
is the T × (k + p(k + 1)) data
matrix with ΔX =
(Δx1,…,ΔxT)′
and ΔZ−i =
(Δz1−i,…,ΔzT−i)′,
i = 1,…,p, and
,
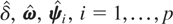
are the OLS estimates of δ, ω,
ψi in (3.6).
Alternatively and in keeping with the tradition in linear
cointegration, we propose a companion test statistic, one that is the
analogue to the EG statistic for linear cointegration, which is obtained
by estimating the following approximate regression:
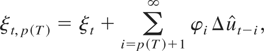
where
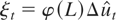
is the error term associated with an infinite autoregressive (AR)
representation of
,
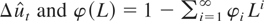
e.g., Phillips and Ouliaris (1990, (A.14)).
This is so even if the underlying process zt
follows a finite-order VAR(p) model with p ≥ 2. Hence
we now need to allow p(T) to tend to grow with
T for consistent estimation of (3.8). We follow Phillips and
Ouliaris (1990) and impose the condition
p(T) = o(T1/3),
4 This upper bound follows from Berk (1974), who shows that this bound is sufficient for the
second sample moment matrix to converge to its population counterpart in
norm. Therefore, for consistent estimation it is sufficient to impose this
upper bound. See also Said and Dickey (1984).
under which we derive the following
t-type test for δ = 0 in (3.8):
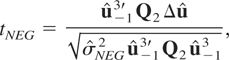
where
,
,
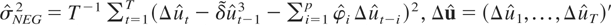
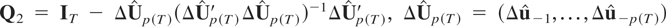
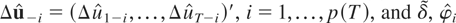
are the OLS estimates of δ and φi in
(3.8).
The main asymptotic distributional results for all these tests are
described in Theorem 3.1 under the following additional assumption.
Assumption 3. Partition Γxi =
(γxyi′,
Γxxi′)′ in (2.7) conformably
with zt =
(yt,xt′)′
and set γxyi = 0.
This assumption states that Δyt does
not Granger cause Δxt. Under Assumptions
1(i) and (ii), 2(i) and (ii), and 3, the well-known multivariate
invariance principle holds for et and
εxt:
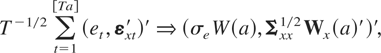
where [Ta] is the integer part of Ta,
⇒ denotes a weak convergence, and W(a) and
Wx(a), defined on a ∈
[0,1], are independent scalar and k-vector standard
Brownian motions. Without Assumption 3, W(a) and
Wx(a) are no longer independent
under the null of no cointegration because the weak exogeneity assumption
guarantees only that
,
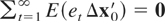
but not that
,
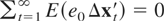
and therefore the long-run correlation between the partial sums of
et and Δxt
is possibly nonzero. See also Banerjee et al. (1998) and Pesaran et al. (2001). At the end of this section we discuss a
standard extension to the testing procedures that allows us to relax this
assumption without affecting asymptotic results.
THEOREM 3.1. Consider the conditional nonlinear ESTR ECM, (2.6),
and let Assumptions 1–3 hold. Under the null hypothesis of no
cointegration, the FNEC statistic, defined by
(3.3), has the following asymptotic distribution:
where B and W are shorthand notations for
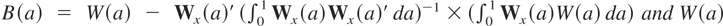
defined on a ∈ [0,1]. Next, imposing c =
0 and under the null of no cointegration, the
FNEC* statistic defined by (3.5) has the
following asymptotic distribution:
Further, imposing both φ = 0 and
c = 0, and under the null of no cointegration (3.1), the
tNEC and tNEG
statistics defined by (3.7) and (3.10) have the
following asymptotic distributions, respectively:5
It is worth noting that the asymptotic
distribution of the tNEC statistic is free of
any nuisance parameters as proved in the Appendix. In the literature it is
well established that the limiting null distribution of an ECM
t-test depends on the signal-to-noise ratio, though this
dependency is due to the use of known cointegrating parameters. It has
been proved in linear models that an ECM t-test obtained using
the residuals is free of any nuisance parameters, and a formal proof of
this is available upon request.
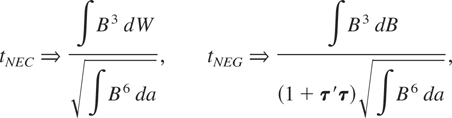
where
.
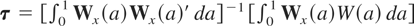
Under the alternative hypothesis that the cointegrating relationship
follows ESTR, all the tests are consistent.
To accommodate deterministic components in (2.3), we extend to
consider regressions with an intercept and with an intercept and a linear
time trend,
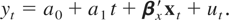
Alternatively, we take a simpler but equivalent approach and reexpress
(3.15) and (3.16) as
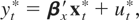
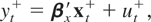
where the superscripts * and + indicate the demeaned and the detrended
data, respectively. The respective FNEC,
FNEC*, tNEC, and
tNEG statistics are then obtained as follows.
First, the appropriate residuals are obtained from either (3.17) or
(3.18), and then the corresponding regressions are constructed. For
example, we have
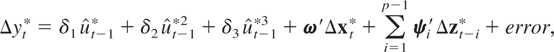
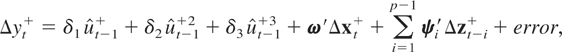
where
.
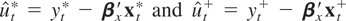
Then, the FNEC statistics are obtained as
the F-statistic for δ1 = δ2 =
δ3 = 0 in (3.19) or (3.20), respectively. The corresponding
FNEC*, tNEC, and
tNEG statistics are obtained in an analogous
way. For the regression with a nonzero intercept, (3.15), it is easily
seen that the asymptotic distributions of the
FNEC, FNEC*,
tNEC, and tNEG
statistics are the same as in Theorem 3.1, except that
W(a) and Wx(a) are
replaced by the demeaned Brownian motions, denoted
.
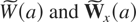
Similarly, for the regression with nonzero intercept and nonzero linear
trend coefficient, (3.16), the associated asymptotic distributions are
such that W(a) and
Wx(a) are replaced by the demeaned
and detrended Brownian motions, denoted
.
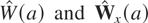
Asymptotic critical values of the FNEC,
FNEC*, tNEC, and
tNEG statistics for the preceding three cases
have been tabulated for k = 1,…,5, via stochastic
simulations with T = 1,000 and 50,000 replications in Table 1.
Asymptotic critical values for alternative statistics
We comment on one further modeling issue. An alternative popular
nonlinear STR adjustment scheme to the one favored in this paper is given
either by the first-order logistic function, 1 − b/(1 +
exp(−θut−1)), or by the
second-order logistic function, 1 − b/(1 +
exp(−θut−12)),
where b < 1 is a scaling constant. We note that the resulting
t-type tests against the alternative of the second-order logistic
function have exactly the same form as in (3.7) and (3.10). It is also
easily seen that adopting the first-order Taylor approximation to the
first-order logistic terms as we did before gives the regression
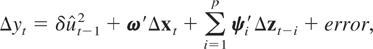
and we could develop a t-type test for δ = 0 in (3.21).
Though the asymptotics for this case are straightforwardly obtained via a
simple extension of the analysis in this paper, the interpretation of the
error correction coefficient in the first-order logistic STR error
correction model is problematic. By contrast, in the exponential case the
interpretation of this coefficient is both natural and intuitive (for a
discussion of this point, see Kapetanios et al.,
2003). Therefore, we focus on the exponential case.
Finally, we comment on how to relax Assumption 3 in practice. To purge
the potentially nonzero long-run correlation between the partial sums of
et and Δxt,
we should augment our conditional model (2.6) with leads of
Δxt, as is standard in the cointegration
literature; see, e.g., Banerjee et al. (1998)
and Saikkonen (1991). Then, following Theorem
4.1 of Saikkonen (1991), it is readily seen that
the limit distribution of these ECM-based tests will be identical to those
derived in Theorem 3.1, under the further condition that the number of
leads grows at a rate less than T1/3. We also
notice that the asymptotic result for the
tNEG test in this situation would be intact
too.
4. FINITE-SAMPLE PROPERTIES
In this section we undertake a small-scale Monte Carlo investigation
of the finite-sample size and power performance of our proposed
tNEC, tNEG,
FNEC, and FNEC*
tests in conjunction with the linear cointegration tests of Engle and
Granger and Johansen denoted tEG and
JOH, respectively.
We consider experiments based on a bivariate ECM similar to that
adopted by Arranz and Escribano (2000). We
generate the data as follows:
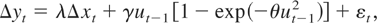
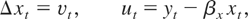
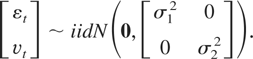
Here we fix βx = 1 and
σ12 = 1. In the tabulated experiments we fix
φ = 0 but also discuss (rather than tabulate) results for nonzero
φ. Under the null we set θ = 0, whereas we consider parameter
values for θ = {0.01, 0.1, 1} and γ =
{−1,−0.5,−0.3,−0.1} under the alternative. To
investigate the impact of the common factor (COMFAC) restriction, λ =
1 and the impact of different signal-to-noise ratios we consider different
parameter values for λ = {0.5,1} and σ22 =
{1,4}.
To save space we only report the results for the demeaned case (see
(3.17)) with T = 100.6
Overall
simulation results for the different sample sizes and for the detrended
data are qualitatively similar to the main findings reported in the paper
and are available upon request.
gives results on the size of alternative tests and shows that at this
sample size there are no substantial size distortions for any of the tests
under consideration. This is convenient as it allows a direct comparison
of test powers without the need to worry about size-adjusted critical
values.
Size of alternative tests for demeaned data (T =
100)
Turning to the power performance of the tests, which is summarized in
Table 3, a general finding is that
nonlinear-based tests dominate linear counterparts in terms of power for
almost all cases considered. As expected, the power gain of our suggested
NEC-based tests over the nonlinear analogue of the EG test becomes
substantial where the COMFAC restriction (λ = 1) does not hold. The
result that when the COMFAC restriction is violated the power superiority
of tNEC over
tNEG increases with the variance of the
innovation in x is both intuitive (a higher variance increases
the correlation with the regression error) and a reiteration of what is
now well known to occur in the linear case.
Power of alternative tests for demeaned data (T =
100)
Next, we focus on the results for θ = 0.01, because this value is
found to be close to empirically plausible estimates.7
Notice in our application that the estimates of θ (which
we obtain under the constraint that γ = −1 for convenience; see
also Taylor, Peel, and Sarno, 2001) indeed range
between 0.007 and 0.017. In general, it is hard to get an exact definition
of “small” and “large” θ because it is not a
scale-free parameter. But it is easily seen that given the values of
σ2 and γ, as θ grows, the
ut becomes less persistent, where we note
that the term
e−θut−12
here measures the root of the series at time t. For example, we
find via simulation that for σ2 = 1 and γ = −1
with T = 1,000, the average sample values of
e−θut−12
are 0.95, 0.83, and 0.34 for θ = 0.01, 0.1, and 1,
respectively.
For example, when (γ,λ,σ
2) =
(−1, 0.5, 1), the powers of the
tNEC,
FNEC*,
FNEC, and
tNEG tests are 48%, 45%, 43%, and 33%,
whereas the powers of
tEG and
JOH
are 24% and 26% only. What is surprising however is the relative
performance of
tNEC,
FNEC, and
FNEC*—in terms of power there is little
to choose between these three. This occurs despite the fact that the
F-statistics are testing more coefficients. Put another way, the
implicit alternatives of the
F-tests are “larger”
than that of
tNEC in the sense that they nest
approximations to a greater number of alternative nonlinear models than
does
tNEC. Allowing φ and/or
c to be nonzero does not alter the general tenor of these
results. In sum it seems that moving from
tNEC when its implicit alternative is true to
portmanteau
F-tests (whose alternatives nest the truth as a
special case) does not seem to significantly jeopardize power. We would
hesitate to draw general conclusions from a simple and single data
generating process, but we might cautiously recommend that if there is
some doubt as to the nature of the STR alternative and in particular if we
do not know for sure that
c = 0 then the
F-type tests
should be used.
5. EMPIRICAL APPLICATION TO ASSET PRICING IN
THE PRESENCE OF TRANSACTIONS COSTS
In a seminal paper, Campbell and Shiller (1987) investigate the existence of linear
cointegration between aggregate U.S. stock prices and U.S. dividends, as
predicted by a simple equilibrium model of constant expected asset
returns. Their results were ambiguous. A null hypothesis of no (linear)
cointegration was marginally rejected in their data, but the implied
estimate of long-run asset returns was implausible. Imposing a more
credible long-run return caused nonrejection of the null of no
cointegration. Subsequent literature has met with similar mixed results,
e.g., Campbell and Shiller (1988), Froot and
Obstfeld (1991), and Cuthbertson, Hayes, and
Nitzsche (1997).
In this section we apply our proposed tests for cointegration to asset
prices and dividends for 11 stock portfolios allowing for nonlinear
adjustment to equilibrium of the STR variety. The theoretical motivation
for STR nonlinearity has already been given in the introduction, and we
reemphasize that theoretical reasoning suggests that it is STR adjustment
rather than threshold adjustment that is likely to arise in our current
application.8
There is also some simulation
evidence that shows that even if bid-ask spreads are fixed, aggregation
across assets with different fixed spreads will in fact lead to STR-type
rather than TAR-type dynamic adjustment.
Gallagher and Taylor
(
2001) have applied the STR-based ECM to the
U.S. log dividend-price ratio and find that the speed of reversion of the
U.S. log dividend-price ratio toward the fundamental equilibrium follows a
nonlinear STR adjustment and is an increasing function of degree of
mispricing. In their study, however, they adopt linear cointegration tests
such as the Engle and Granger (
1987) and
Johansen (
1995) tests.
We collected monthly data from January 1974 to November 2002 on end
period real prices and within period real dividend yields for value
weighted market portfolio indexes of stocks traded on the main exchanges
of the following 11 countries: Germany, Belgium, Canada, Denmark, France,
Ireland, Italy, Japan, Netherlands, United Kingdom, and United States. A
dividend series was constructed as the product of dividend yield and
prices. Although not presented here, augmented Dickey–Fuller (ADF)
tests give overwhelming support to the hypothesis that all variates are
I(1).
As alluded to before, we test for the existence of a linear
cointegrating relationship between dividends and prices of the form
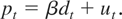
The existence of bid-ask spreads discussed previously motivates the
following nonlinear dynamic STR ECM specification:
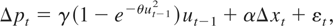
where ut−1 =
pt−1 −
βdt−1 and
εt is a (possibly autocorrelated) error term
that captures other microstructure effects such as specific kinds of noise
trading and dealer inventory control mechanisms whereby the adjustment of
prices to elicit inventory-correcting trades generates autocorrelated
price movements, e.g., Snell and Tonks (1998).
We computed three tests. The first two,
tEG and tNEG,
are the linear EG test and its nonlinear counterpart. The third,
tNEC, is the t-ratio on
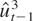
in the STR ECM formulation (see (3.6)) where
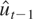
is the residual from the first stage (spurious under the null) regression
of pt on dt. The
price and dividend series appeared to have an upward trend so that all
series were demeaned and detrended before use.
9 The issue of whether or not stock prices and dividends contain
a deterministic time trend is contentious. However, there is a clearly
discernible trend in both dividends and prices in our data, and hence we
detrend. It is comforting to note that if we only demean, the results are
qualitatively almost identical.
We estimated the appropriate
auxiliary regressions for
p = 12 and then dropped all
insignificant lags in a general-to-specific modeling.
10 We should note that although further exploration revealed
some significant lags beyond twelfth order, the test statistics were not
in general very sensitive to the choice of lag length.
Finally,
we note that there is overwhelming prior theoretical justification for
restricting the switch point,
c, to be zero. As a result we do
not compute
F-type tests that test additional linear and
quadratic terms.
The results for the tests are in columns 2–4 in Table 4. Looking at the results we see that viewed
through the “eyes” of linear cointegration tests there is
little support for the hypothesis that dividends and prices move together
in the long run, with only two of the tEG
tests rejecting the null, albeit at the 1% level. Furthermore, none of the
remaining nine tEG statistics are significant
even at the 10% level. By contrast the nonlinear
tNEG test rejects in seven out of eleven
stock markets with four of these rejections occurring at the 1% level. A
further three statistics are quite close to the 10% critical value. The
success in rejecting the null of no cointegration is less marked for
tNEC, with only five rejections at standard
significance levels, although three of these reject also at the 1%. A
further two tNEC statistics are quite close
to the 10% critical value. If the alternative is really true then we could
interpret this finding as being somewhat at odds with the Monte Carlo
evidence presented before, which generally shows that
tNEC has more power than
tNEG. One possible explanation is that prior
empirical investigation of the data suggested that the COMFAC restriction
may hold here. If true, a bivariate ECM would lack parsimony compared with
the univariate specification, and this may lead to a loss in power when
moving from tNEG to
tNEC.
Cointegration tests and estimates of the ESTR parameter for asset
prices and dividends
Given the strength of evidence against the null and support for the
alternative we could obtain estimates of adjustment parameters under the
alternative. Focusing on the univariate model we obtained nonlinear least
squares estimates of θ from the alternative ESTR model,
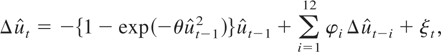
where the model has been specialized compared with the general ESTR
considered previously by imposing a unit coefficient on γ. Early
attempts to estimate γ jointly with θ foundered on severe
identification problems, and our nonlinear algorithm failed to converge in
most cases—hence the specialization. Under the alternative (and
estimation of (5.3) only makes sense if the alternative is true), θ
is scale dependent. To clarify its interpretation and to facilitate
numerical convergence, we normalized the
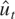
series to have unit sample variance (a procedure that only makes sense
under the alternative). The results for
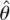
and its t-statistic are given in Table
4. Although we cannot interpret the t-statistic as a
significance from zero test (for obvious reasons) we refer to it as
“significant” if an asymptotic 95% confidence interval around
the estimate excludes zero. We see that
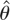
is “significant” in all cases and varies between 0.007 and
0.017.
To get a feel for what such values imply, Figure
1 plots IRFs for the error correction term for initial impulses of
one, two, three, and four standard deviation shocks, respectively. To be
explicit, we take the univariate specification in (5.3) and perturb its
disturbance by one to four standard deviation shocks. We trace the time
path implied by (5.3) following each of the four shocks and plot them on a
single IRF diagram.11
Alternatively, it
would be interesting to further investigate the IRF analysis in the
context of nonlinear STR ECMs in which both conditional and marginal
models (2.6) and (2.7) should be jointly considered. But this is beyond
the current study. For further discussions see van Dijk et al. (2002).
For completeness and comparison we
compare the corresponding IRF with that obtained from the estimated linear
models. The striking finding is the length of time taken to recover from
small shocks. In particular the time taken to recover one-half of a one
standard deviation shock varies between 5 and 20 years. By contrast, the
time taken to recover one-half of a large shock (such as three or four
standard deviations) is comparable to that of the linear case and varies
between just 4 and 18 months. This implies that data periods dominated by
extreme volatility may display substantial reversion of prices toward
their NPV relationship but in “calmer” times, where the error
in the NPV relationship takes on smaller values, the process driving it
may well look like a unit root. This suggests that in practice the ESTR
and threshold autoregressive (TAR) models may not be too dissimilar in
terms of overall inference in any given sample.
Impulse responses of error correction terms to k (= 1,2,3,4)
standard deviation shock for various countries.
6. CONCLUDING REMARKS
The investigation of nonstationarity in conjunction with nonlinear
autoregressive modeling has recently assumed a prominent role in
econometric study. It is clear that misclassifying a stable nonlinear
process as nonstationary can be misleading both in impulse response and
forecasting analysis. Similarly, not allowing for the presence of
cointegration when the speed of adjustment varies with the position of the
system as in the case of nonlinear cointegration can be equally
misleading. In this paper we have proposed a simple direct cointegration
test procedure that is designed to have power against STR nonlinear error
correction specifications. Our proposed tests are shown to have better
power than the linear cointegration tests that ignore the nonlinear nature
of the alternative. An empirical application clearly shows the potential
of our approach. Unlike linear cointegration tests, the nonlinear tests
find substantial evidence of cointegration in stock price and dividend
systems. Further research to develop similar tests for alternative
nonlinear models is currently under way.
APPENDIX: Proof of Theorem 3.1
Under the null δ1 = δ2 =
δ3 = 0, the FNEC statistic
given by (3.3) can be rewritten as
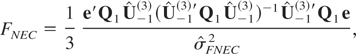
where
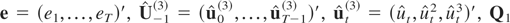
is the T × T idempotent matrix defined following
(3.7), and
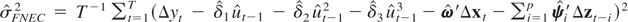
is the estimated variance with
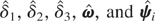
being the OLS estimators obtained from (3.2).
Notice under the null that (2.6) can be written alternatively as the
following autoregressive distributed lag (ARDL) specification:
where φ(L) = 1 − φ1 L
− ··· − φp
Lp and θ(L) =
θ0 + θ1 L +
··· + θp
Lp. Decomposing
ψi′ =
(ψyi,
ψxi′) in (2.6), and comparing
(A.2) with (2.6), we find that φi =
ψyi, i = 1,…,p,
θ0 = ω′, and
θi =
ψxi′, i =
1,…,p. Using the Beveridge–Nelson (BN) decomposition
(e.g., Phillips and Solo, 1992) we have
where φ*(L) = 1 − φ1*L
− ··· −
φp−1*Lp−1
and θ*(L) = θ0* +
θ1*L + ··· +
θp−1*Lp−1.
Summing both sides of (A.2) from 1 to t and using (A.3), we
obtain
where
.
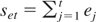
Under Assumptions 1(iii), 2(i) and (ii), and 3 and using (A.4), then it
is easily seen that the residual
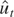
obtained from the spurious regression of yt
on xt becomes
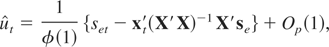
where se =
(se1,se2,…,seT)′
and X =
(x1,…,xT)′.
Therefore, using (3.11) we have
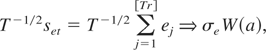
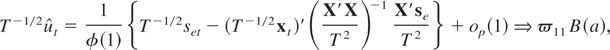
where
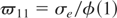
is defined in Theorem 3.1.
Next, noting that the
,
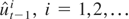
are a regular transformation of
in the sense of Park and Phillips (2001), we
can apply Lemma 2.1 of their paper and obtain
where st are the tth row of
S and S is the T × (k +
p(k + 1)) I(0) data matrix defined following (3.7).
Using the preceding results, and defining the scaling matrix
DT =
diag(T−1,T−3/2,T−2),
it is readily seen that
It is also straightforward to show under the null that
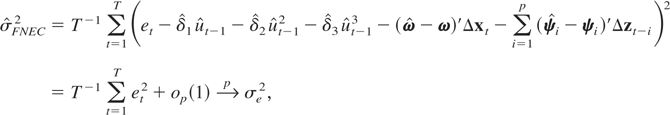
where we have used
.
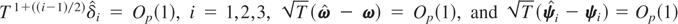
Using (A.7)–(A.9) in (A.1), we obtain the required asymptotic null
distribution of the FNEC test.
Under the alternative hypothesis, FNEC
can be expressed as
where
.
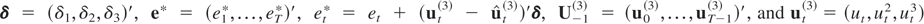
Because
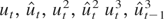
are all I(0) and
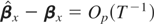
under the alternative, it is easily seen that
where we used that
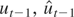
and all lagged I(0) regressors in S are uncorrelated with
et. Next, tedious but straightforward
computations can be used to show that
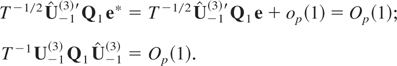
Also, we have
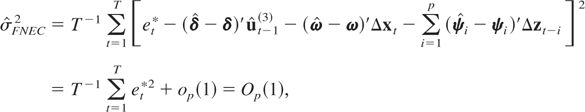
where we used
.
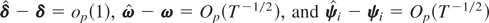
Therefore, using (A.11)–(A.13) in (A.10), we obtain
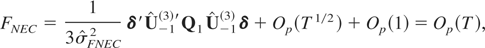
which clearly shows that the FNEC
statistic diverges to infinity as T → ∞.
It is trivial to derive the asymptotic distributions of the
FNEC* and tNEC
tests and prove their consistency as they are special cases of the
FNEC test.
We move on to prove results for the tNEG
test. Note that the AR representation of
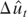
is given by
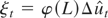
, where
;
see (3.9). The tNEG statistic can be written
as
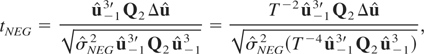
where Q2 is defined following (3.10). Following
Phillips and Ouliaris (1990), it is
straightforward to show that
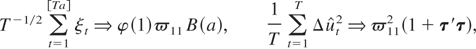
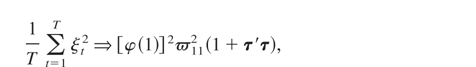
where τ is defined in Theorem 3.1. We also have
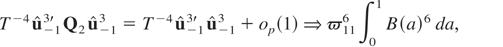
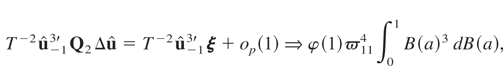
where ξ =
(ξ1,…,ξT)′ and the
equality in (A.18) and (A.19) follows from the straightforward adaptation
of the Said and Dickey (1984) approach as
employed in (A.16) of Phillips and Ouliaris (1990) and
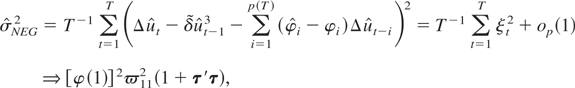
where we used (A.17),
.
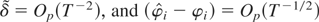
Using (A.18)–(A.20) in (A.15), we obtain the required results for
the asymptotic distribution of the tNEG
test.
Next, under the alternative hypothesis,
tNEG can be expressed as
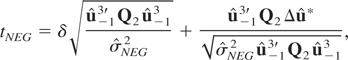
where
.
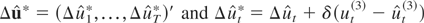
As before, it is straightforward to show that
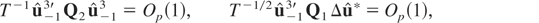
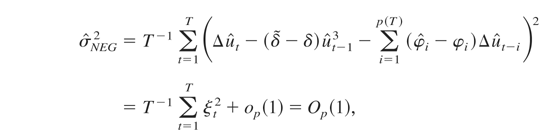
where we used
.
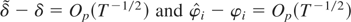
Using (A.22) and (A.23) in (A.21), we have
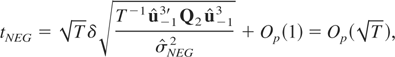
which shows that the tNEG statistic
diverges to negative infinity as T → ∞. █
